Introduction

As the core technology of power transmission for a new generation of high-performance helicopters and ships, the split-torque parallel gear transmission system has gradually replaced the traditional star and planetary power split transmission systems with its advantages of high efficiency and compactness, and has become an important direction for upgrading modern aviation and ship power systems1. However, the engineering application of the system faces a key bottleneck—dynamic load balance control among multi-power branches. In the transmission structure of split-torque parallel gear, the manufacturing error, assembly error and dynamic meshing phase difference of gear pair will lead to the load distribution mismatch between power channels. If there is no active load sharing mechanism, the system will show the phenomenon of "single channel overload leading": on the one hand, the transmission device needs to be redundantly designed according to the ultimate load of the maximum bearing channel, which leads to a significant increase in the overall structural weight and seriously restricts the lightweight goal of the power system. On the other hand, local stress concentration will accelerate tooth surface damage and fatigue failure, and significantly reduce the reliability of system operation2.

Therefore, the elastic web gear system is proposed to solve the above problems. The core mechanism of the design is to realize the adaptive adjustment of dynamic load by using the elastic deformation characteristics of the flexible web. When the gear is subjected to load, the multi-dimensional deformation generated by elastic web can dynamically adjust the gear meshing contact state, so as to redistribute the torque between the dual drive branches and effectively suppress the load deviation between the branches. At the same time, the damping characteristics of the flexible structure can absorb the high-frequency vibration energy in the transmission process and significantly reduce the noise radiation level, which is particularly important for the optimization of ship stealth performance. Therefore, the use of elastic web gear in helicopter main reducer and ship parallel transmission device can not only ensure the synchronization accuracy of power split through load sharing effect, but also realize the comprehensive goal of structural lightweight, reliability improvement and vibration characteristics optimization.

Hu et al.3 studied the effects of web thickness on dynamic responses by analyzing the dynamic deformations and stresses within web, and revealed that elasticity of web and shaft can reduce vibration energy transmitted to the supporting structure, which contributed to vibration reduction of gear transmission system. Sun et al. CitationID=“CR4”>4 calculated the time-varying meshing stiffness of spur gear pairs with webs and lightening holes. The results show that webs have a greater influence on the reduction of the average amplitude of stiffness than holes. Shi et al.5 established a nonlinear dynamic model of gear-bearing system with multi-meshing state and deterministic-random excitation, including backlash and time-varying meshing stiffness, and discussed the coupling effect of gear pair meshing vibration and gear bearing radial vibration. In addition, Shi et al. CitationID=“CR6”>6 established the nonlinear dynamic model of spur gear system with time-varying meshing stiffness and time-varying backlash, analyzed the bifurcation and evolution of five meshing behaviors, and found that the sudden change of dynamic meshing force direction led to the disengagement of gear teeth and the contact of single or double teeth on the back, resulting in multi-state meshing behavior. Shi et al.7 also proposed a new time-varying meshing stiffness model considering elastic contact, temperature and lubrication, and then established a nonlinear dynamic model of gear-rotor- bearing system with 5-state mesh including time-varying backlash and time-varying meshing stiffness, thus obtaining the influence law of gear temperature and lubrication effect on time-varying meshing stiffness and revealing the bifurcation and evolution law of different two-parameter planar systems. They CitationID=“CR8”>8 finally proposed a method of computing coexistence dynamics in a two-parameter plane considering multi-initial values based on the idea of gridding, and analyzed the formation mechanism of coexistence dynamics in the two- parameter plane for the spur gear system. The results show that the superposition of various dynamic response regions in the two-parameter plane produces a variety of coexistence dynamics, such as dynamic coexistence, bifurcation coexistence, and bifurcation and dynamic coexistence. Li et al.[9] analyzed both the in-plane and out-of-plane vibration modes of thin web gear based on the Timoshenko theory. The results show that instability will likely happen in out-of-plane vibration and the existence of discrete springs will deteriorate the instability. Guilbert et al.[10] analyzed the effect of thin-webbed/-rimmed and consequently flexible gear bodies on dynamic tooth loads. The results show that when thin-rimmed/webbed gears are considered, the outcomes from the approximate dynamic factor formula are still in reasonable agreement with those of the complete FE model. Blockmans et al.[11] presented a novel nonlinear parametric model order reduction technique for the solution of contact problems in flexible multibody dynamics, and verified the performance of the new technology by simulating a dynamic gear contact problem and comparing it with the traditional model reduction technology and commercial nonlinear finite element software. Liu et al.[12] used the finite element analysis method to establish a parametric model of the elastic web herringbone gear structure, and studied the steady-state response of the web thickness and the rim thickness to the herringbone gear structure. Bruzzone et al.[13] presented dynamic reduction technique for nonlinear analysis of spur gear pairs, and studied the influence of thin rim on the vibration characteristics of spur gear transmission. The results show that the nonlinear increase of vibration amplitude is actually caused by the unique self-excitation mechanism of gears and the contact loss under some rotation and load conditions. Yu et al.[14] established the nonlinear dynamic model of the parallel gear transmission system, and analyzed the influence of stiffness and damping of web on the system vibration. The results show that under different web stiffness conditions, the parallel transmission system will have typical nonlinear vibration characteristics such as sub-harmonic response, quasi-periodic response and chaotic response. Xu et al.[15] established a double-sided meshing impact dynamic model of herringbone planetary gear transmission system considering error, meshing phase, time- varying meshing stiffness and backlash, and studied the double-sided meshing process and mechanism of herringbone planetary gear. The results show that the change of excitation frequency will directly change meshing state of herringbone planetary gear. Li et al.[16] studied the influence of different system parameters on the nonlinear dynamic characteristics of the system before and after 3D modification by combining the 3D modification technology with the contact performance and dynamic characteristics of herringbone gear transmission, and found that the 3D modification technology can effectively reduce the system vibration. Shiva et al. [17] used multi-scale method to analyze the nonlinear vibration of elastic gear system, and studied the influence of system parameters on frequency response. The results show that the influence of external excitation amplitude and intensity on the system response amplitude is the same in first and second harmonic resonance. Mo et al.[18] established the nonlinear dynamic model of herringbone gear transmission system, and analyzed the main resonance characteristics by numerical method. The results show that when the external excitation frequency and torque gradually increase, the motion state of the system gradually changes from a stable one-cycle motion state to a chaotic state. Tatsuhito et al.[19] established the nonlinear dynamic model of the coupling between shaft and gear pair, and clarified the influence of the shaft on the vibration of the gear system by comparing the results without considering the shaft, considering one shaft and considering two shafts. Guan et al.[20] established the dynamic model of light straight cylindrical gear transmission system considering the elasticity of shaft and gear body, and studied the influence of gear body elasticity on dynamic characteristics. The results show that the elasticity of gear web can reduce the vibration intensity. Yang et al.[21] proposed a new temperature-controlled vibration- damping lightening polymer composite gear model with a modified web structure, and used additive manufacturing technology to make gears from three viscoelastic polymers for experimental purposes. Kahnamouei et al.[22] proposed a statistical linearization method based on energy to simulate the nonlinear dynamic model of spur gear pair, and analyzed the influence of input torque on the dynamic response of gear pair. The results show that for high input torque, the system runs in a linear range, and for low input torque, the system becomes strongly nonlinear. Guan et al.[23] simulated gear rim through the flexible ring, and gear web flexibility through the bearing spring, and analyzed the influence of the thickness-diameter ratio of gear ring and the bearing stiffness on the dynamic transmission error. The results show that the flexibility of gear body reduces the meshing vibration intensity. Kang et al.[24] established a two-degree-of-freedom helical gear nonlinear torsional vibration model, and analyzed the influence of the dynamic characteristics on external excitation conditions in a certain parameter domain and the influence of external excitation on the gear system dynamic characteristics. Guilbert et al.[25] analyzed the effect of thin-webbed/-rimmed and consequently flexible gear bodies on dynamic tooth loads. The results show that the outcomes from the approximate dynamic factor formula of thin-rimmed/webbed gears are still in reasonable agreement with those of the complete FE model, which is moderate for dynamic couplings between dynamic mesh forces and gear body elasticity. Lu et al.[26] developed a high power density polymer gear transmission system. The research shows that the optimized polymer gear transmission system reduces the weight by 49%. Sun et al.[27] established a multi-scale numerical prediction method for the elastic properties of anisotropic composite materials and uniformly laminated webs. The results show that the micro and macro parameter design of composite webs has advantages in adjusting the quality and stiffness and reducing the fluctuation of meshing stiffness. Hou et al.[28] established a rigid-flexible coupling dynamic model of gear system with shaft elasticity, bearing stiffness and shell flexibility, and analyzed the influence of gear web and rim thickness on dynamic meshing force and dynamic response at bearing and shell. The results show that changing gear web and rim thickness can reduce dynamic meshing force and dynamic response. Li et al.[29] established a puretorsion nonlinear dynamic model of six- branch herringbone gear transmission system with time- varying meshing stiffness and transmission error, and studied the system global vibration characteristics in the parameter domain. The results show that with the change of the parameter domain, the 3D modification technology can reduce vibration and improve the load sharing performance.

In summary, in the herringbone gear transmission, due to the influence of the torsional stiffness, bending stiffness and damping of the intermediate relief groove, coupled with the influence of processing and installation errors, the power and torque cannot be evenly transmitted from both sides of the herringbone gear, resulting in the reduction of the load sharing performance between the branches of the transmission system. Most scholars theoretically explore how to reduce the vibration and noise of gear system by introducing the damping of web structure, focus on the influence of the thickness and arrangement of the web on the gear transmission system, and less consider the influence of additional elasticity and damping. The influence of elastic web material on the dynamic load sharing performance is also rarely studied. When analyzing the dynamic characteristics of the elastic web gear transmission system, the influence of the bearing and the mechanical properties of elastic web are rarely considered. In addition, the stiffness and damping of the webs of different sizes not only affect the dynamic characteristics of gear pair, but also affect the load sharing characteristics and strength of parallel or coaxial gear pairs. Based on the above shortcomings, this paper comprehensively considers the time-varying meshing stiffness, damping and transmission error of gear pair, the stiffness and damping of the cylindrical sliding bearing, the bending, tension and compression, torsion stiffness and corresponding damping of the elastic web, and load fluctuation of input disk and output disk, and analyzes the nonlinear dynamic characteristics of elastic web herringbone gear system and the influence of four potentially applicable elastic materials on the system dynamic characteristics.

Vibration reduction mechanism of elastic web herringbone gear transmission

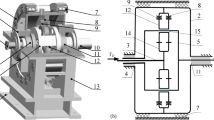
In order to improve the load sharing characteristics of herringbone gear transmission, the elastic web gear is adopted as the load sharing structure of split-torsion transmission, as shown in Fig. 1. In this structure, the passive gear ring and the web are divided into two parts, and the elastic material is placed between the two parts. The two parts of the web are connected together by bolts and isolation orifice plates to form an elastic web gear. In the joint part of gear ring and web, the uniform elastic material is used to make web plate obtain greater flexibility, such as rubber, resin and so on. The vibration reduction mechanism of elastic web herringbone gear mainly depends on the synergistic effect of various mechanisms such as elastic deformation to absorb energy, damping effect to suppress vibration, flexible connection to buffer impact, dynamic adjustment of backlash and phase tuning to offset vibration. The combined action of these mechanisms enables the elastic web herringbone gear to effectively reduce the vibration level of the transmission system under complex working conditions and improve the running stability and service life.

Fig.1
figure 1

The cross-section of elastic spoke herringbone gear.

Full size image

Figure 2 shows the 3D decomposition model of herringbone gear with elastic web. The herringbone gear ring, the elastic material ring and the isolation plate all have a cone angle with the same slope. This is to generate a certain pre-tightening force between the three, and ensure that the elastic material is in a tight state and the device is sealed. The elastic material ring is cast on the isolation hole plate, and the torque is transmitted through the friction force of the bolt connection. Even under a small preload, a large positive pressure can be generated between the web and the isolation plate, which can be multiplied by a certain friction coefficient to transmit the load torque of the gear teeth30. In practice, in the design load range, there will be a gap between the inner spline of gear ring and the outer spline of the web. When the actual load reaches 140% of the design load, the spline pair contacts and transmits additional torque load.

Fig.2
figure 2

3D decomposition model of elastic spoke herringbone gear.

Full size image

Nonlinear dynamic model of herringbone gear transmission

According to the mechanism characteristics of herringbone gear, the herringbone gear pair is regarded as two helical gear pairs with opposite rotation directions connected by an elastic shaft. When establishing the gear dynamic model, the coupling and helical gear of the system are equivalent to mass nodes, and each concentrated mass node is established at its center of mass, so that its mass and moment of inertia are all concentrated at the nodes. and the mass and moment of inertia of the shaft section between two adjacent concentrated mass nodes are equally distributed to the mass nodes at both ends according to the principle of constant center of mass, so that the supporting stiffness of gear bearings is equivalent to the corresponding gear nodes. According to the principle of constant center of mass, the mass and moment of inertia of the intermediate shaft section are equally distributed to the mass nodes at both ends, and the supporting stiffness of the gear bearing is equivalent to the corresponding gear nodes. The shaft between adjacent nodes is regarded as a massless spring and damper with bending, torsion and axial stiffness. At the same time, the meshing relationship of the gear pair is simplified as a spring and damper along the meshing line. The coupling mechanism of gear pair meshing vibration and elastic shaft is considered by the equivalent spring-damper. Therefore, the dynamic model of the elastic web herringbone gear system established in this paper is shown in Fig. 3.

Fig.3
figure 3

Dynamic model of herringbone gear pair.

Full size image

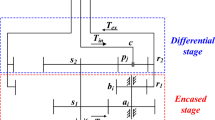
As shown in Fig. 3, the input and output shafts only consider the torsional stiffness and damping. This is because the vibrations of input and output shafts are mainly the torsional vibration around the axis, and the lateral and axial vibrations are relatively small. The input torque is directly applied to input disk, and it is assumed to be a simple harmonic torque \(\tilde{T}_{in}\) with \(2\pi \cdot n_{in}\) (\(n_{in}\) is input speed ) as circular frequency. The load torque is assumed to be a fluctuating torsional torque \(\tilde{T}_{out}\), and its circular frequency is \(2\pi b \cdot n_{out}\)( \(n_{out}\) is output speed, \(b\) is the number of propeller blades). Under the normal dynamic meshing force, the herringbone gear pair will generate translational vibration along three coordinate directions and torsional vibration around the axis, so each gear node has four degrees of freedom. \(x_{p1}\), \(y_{p1}\) and \(z_{p1}\) represent the translational vibration displacement of helical gear p1 along axes x, y and z. \(x_{p2}\), \(y_{p2}\) and \(z_{p2}\) represent the translational vibration displacement of helical gear p2 along x, y and z axes. \(x_{g1}\), \(y_{g1}\) and \(z_{g1}\) represent the translational vibration displacement of helical gear g1 along axes x, y and z. \(x_{g2}\), \(y_{g2}\) and \(z_{g2}\) represent the translational vibration displacement of helical gear g2 along axes x, y and z. \(\theta_{p1}\), \(\theta_{p2}\), \(\theta_{g1}\) and \(\theta_{g2}\) denote the axial torsional vibration displacement of each helical gear around axis z, respectively. The bearing stiffness and damping along the three coordinate axes are imposed on each gear mass node to constrain the mass point to move infinitely freely. In addition to considering the torsional stiffness and damping (\(k_{tp} ,c_{tp}\);\(k_{tg} ,c_{tg}\)), the bending stiffness and damping (\(k_{bp} ,c_{bp}\);\(k_{bg} ,c_{bg}\)) along the \(XY\) cross section and the tension and compression stiffness and damping (\(k_{bzp} ,c_{bzp}\);\(k_{bzg} ,c_{bzg}\)) along axis \(Z\) for web herringbone gear relief groove shaft section should also be considered. Because the dynamic model of the connection between elastic web and gear ring is not easy to be expressed in Fig. 3, the detailed description is shown in Fig. 4.

Fig.4
figure 4

Side view of herringbone gear dynamics model.

Full size image

When establishing the dynamic model of herringbone gear with elastic web, the gear ring is considered as a mass node alone, while the web, the isolation plate and elastic material ring are regarded as a concentrated mass node. The elastic web node considers four degrees of freedom, namely, torsional degree of freedom \(\theta_{egi} (i = 1,2)\) around the central axis, lateral degree of freedom \(x_{egi}\) and \(y_{egi}\), and axial degree of freedom \(z_{egi}\). The elastic web is supported by a cylindrical sliding bearing, and the elastic material between the web and gear ring and the the shaft are similarly simplified as the spring dampers with torsional stiffness and damping (\(k_{egi} ,c_{egi}\)) around axis \(Z\), bending stiffness and damping (\(k_{ebgi} ,c_{ebgi}\)) along XY cross section and tension- compression stiffness and damping (\(k_{ezgi} ,c_{ezgi}\)) along axis Z. The selection of the geometry shape and material of the elastic material ring will determine the torsional stiffness, transverse bending stiffness, axial stiffness and their corresponding damping in Fig. 4.

Figure 5 shows the angle relationship diagram of a single stage gear dynamic model. γ is the angle between the center distance of gear pair and axis \(X\) of the local coordinate, which indicates the relative position of active gear and gear ring. \(v_{t}\) is the rotational tangential velocity of the tooth, and \(\alpha_{t}\) is the angle between the steering direction of the gear and the normal meshing force. Because the position of the meshing plane in the local coordinate axis changes with the change of the load direction of the teeth, there is the following relationship:

$$\psi = \left\{ \begin{gathered} \alpha_{t} - \gamma ,\begin{array}{*{20}c} {} & {T_{in} :{\text{Counterclockwise}}} \\ \end{array} \hfill \\ - (\alpha_{t} + \gamma ),\begin{array}{*{20}c} {T_{in} :{\text{Clockwise}}} & {} \\ \end{array} \hfill \\ \end{gathered} \right.$$
(1)

where, \(T_{in}\) acts on the active gear, and its direction is the driving force direction of the loaded tooth profile.

Fig.5
figure 5

Angle relationship diagram of gear pair dynamics model.

Full size image

Each node considers three translational vibrations and torsional vibrations around the shaft, ignoring the tooth surface friction effect, and the entire transmission system has a total of 26 degrees of freedom. According to Newton’s second theorem, the dynamic equations of each mass point are established. When approaching the equivalent helical gear pair at the power input end, the vibration equations of the active gear \(p1\) and passive gear ring \(g1\) are shown as:

$$\left\{ \begin{gathered} m_{p1} \cdot \ddot{x}_{p1} + c_{p1x} \cdot \dot{x}_{p1} + k_{p1x} \cdot x_{p1} + k_{bp} \cdot (x_{p1} - x_{p2} ) + c_{bp} \cdot (\dot{x}_{p1} - \dot{x}_{p2} ) \hfill \\ = - k_{m} \cdot \delta_{1} \cdot \cos \beta_{1} \cdot sin\psi - c_{m} \cdot \dot{\delta }_{1} \cdot \cos \beta_{1} \cdot sin\psi \hfill \\ m_{p1} \cdot \ddot{y}_{p1} + c_{p1y} \cdot \dot{y}_{p1} + k_{p1y} \cdot y_{p1} + k_{bp} \cdot (y_{p1} - y_{p2} ) + c_{bp} \cdot (\dot{y}_{p1} - \dot{y}_{p2} ) \hfill \\ = - k_{m} \cdot \delta_{1} \cdot \cos \beta_{1} \cdot \cos \psi - c_{m} \cdot \dot{\delta }_{1} \cdot \cos \beta_{1} \cdot \cos \psi \hfill \\ m_{p1} \cdot \ddot{z}_{p1} + c_{p1z} \cdot \dot{z}_{p1} + k_{p1z} \cdot z_{p1} + k_{bzp} \cdot (z_{p1} - z_{p2} ) + c_{bzp} \cdot (\dot{z}_{p1} - \dot{z}_{p2} ) \hfill \\ = k_{m} \cdot \delta_{1} \cdot \sin \beta_{1} + c_{m} \cdot \dot{\delta }_{1} \cdot \sin \beta_{1} \hfill \\ I_{p1} \cdot \ddot{\theta }_{p1} + c_{in} \cdot (\dot{\theta }_{p1} - \dot{\theta }_{in} ) + k_{in} \cdot (\theta_{p1} - \theta_{in} ) + k_{tp} \cdot (\theta_{p1} - \theta_{p2} ) + c_{tp} \cdot (\dot{\theta }_{p1} - \dot{\theta }_{p2} ) \hfill \\ = - r_{p1} \cdot \cos \beta_{1} \cdot (k_{m} \cdot \delta_{1} + c_{m} \cdot \dot{\delta }_{1} ) \hfill \\ \end{gathered} \right.$$
(2)
$$\left\{ \begin{gathered} m_{g1} \cdot \ddot{x}_{g1} + k_{ebg1} \cdot (x_{g1} - x_{eg1} ) + c_{ebg1} \cdot (\dot{x}_{g1} - \dot{x}_{eg1} ) \hfill \\ = k_{m} \cdot \delta_{1} \cdot \cos \beta_{1} \cdot sin\psi + c_{m} \cdot \dot{\delta }_{1} \cdot \cos \beta_{1} \cdot sin\psi \hfill \\ m_{g1} \cdot \ddot{y}_{g1} + k_{ebg1} \cdot (y_{g1} - y_{eg1} ) + c_{ebg1} \cdot (\dot{y}_{g1} - \dot{y}_{eg1} ) \hfill \\ = k_{m} \cdot \delta_{1} \cdot \cos \beta_{1} \cdot \cos \psi + c_{m} \cdot \dot{\delta }_{1} \cdot \cos \beta_{1} \cdot \cos \psi \hfill \\ m_{g1} \cdot \ddot{z}_{g1} + k_{ezg1} \cdot (z_{g1} - z_{eg1} ) + c_{ezg1} \cdot (\dot{z}_{g1} - \dot{z}_{eg1} ) \hfill \\ = - k_{m} \cdot \delta_{1} \cdot \sin \beta_{1} - c_{m} \cdot \dot{\delta }_{1} \cdot \sin \beta_{1} \hfill \\ I_{g1} \cdot \ddot{\theta }_{g1} + k_{eg1} \cdot (\theta_{g1} - \theta_{eg1} ) + c_{eg1} \cdot (\dot{\theta }_{g1} - \dot{\theta }_{eg1} ) \hfill \\ = - r_{g1} \cdot \cos \beta_{1} \cdot (k_{m} \cdot \delta_{1} + c_{m} \cdot \dot{\delta }_{1} ) \hfill \\ \end{gathered} \right.$$
(3)

When away from the equivalent helical gear pair at the power input end, the vibration equations of the active gear \(p2\) and passive gear ring \(g2\) are shown as:

$$\left\{ \begin{gathered} m_{p2} \cdot \ddot{x}_{p2} + c_{p2x} \cdot \dot{x}_{p2} + k_{p2x} \cdot x_{p2} + k_{bp} \cdot (x_{p2} - x_{p1} ) + c_{bp} \cdot (\dot{x}_{p2} - \dot{x}_{p1} ) \hfill \\ = - k_{m} \cdot \delta_{2} \cdot \cos \beta_{2} \cdot sin\psi - c_{m} \cdot \dot{\delta }_{2} \cdot \cos \beta_{2} \cdot sin\psi \hfill \\ m_{p2} \cdot \ddot{y}_{p2} + c_{p2y} \cdot \dot{y}_{p2} + k_{p2y} \cdot y_{p2} + k_{bp} \cdot (y_{p2} - y_{p1} ) + c_{bp} \cdot (\dot{y}_{p2} - \dot{y}_{p1} ) \hfill \\ = - k_{m} \cdot \delta_{2} \cdot \cos \beta_{2} \cdot \cos \psi - c_{m} \cdot \dot{\delta }_{2} \cdot \cos \beta_{2} \cdot \cos \psi \hfill \\ m_{p2} \cdot \ddot{z}_{p2} + c_{p2z} \cdot \dot{z}_{p2} + k_{p2z} \cdot z_{p2} + k_{bzp} \cdot (z_{p2} - z_{p1} ) + c_{bzp} \cdot (\dot{z}_{p2} - \dot{z}_{p1} ) \hfill \\ = k_{m} \cdot \delta_{2} \cdot \sin \beta_{2} + c_{m} \cdot \dot{\delta }_{2} \cdot \sin \beta_{2} \hfill \\ I_{p2} \cdot \ddot{\theta }_{p2} + k_{tp} \cdot (\theta_{p2} - \theta_{p1} ) + c_{tp} \cdot (\dot{\theta }_{p2} - \dot{\theta }_{p1} ) = \hfill \\ - r_{p2} \cdot \cos \beta_{2} \cdot (k_{m} \cdot \delta_{2} + c_{m} \cdot \dot{\delta }_{2} ) \hfill \\ \end{gathered} \right.$$
(4)
$$\left\{ \begin{gathered} m_{g2} \cdot \ddot{x}_{g2} + k_{ebg2} \cdot (x_{g2} - x_{eg2} ) + c_{ebg2} \cdot (\dot{x}_{g2} - \dot{x}_{eg2} ) \hfill \\ = k_{m} \cdot \delta_{2} \cdot \cos \beta_{2} \cdot sin\psi + c_{m} \cdot \dot{\delta }_{2} \cdot \cos \beta_{2} \cdot sin\psi \hfill \\ m_{g2} \cdot \ddot{y}_{g2} + k_{ebg2} \cdot (y_{g2} - y_{eg2} ) + c_{ebg2} \cdot (\dot{y}_{g2} - \dot{y}_{eg2} ) \hfill \\ = k_{m} \cdot \delta_{2} \cdot \cos \beta_{2} \cdot \cos \psi + c_{m} \cdot \dot{\delta }_{2} \cdot \cos \beta_{2} \cdot \cos \psi \hfill \\ m_{g2} \cdot \ddot{z}_{g2} + k_{ezg2} \cdot (z_{g2} - z_{eg2} ) + c_{ezg2} \cdot (\dot{z}_{g2} - \dot{z}_{eg2} ) \hfill \\ = - k_{m} \cdot \delta_{2} \cdot \sin \beta_{2} - c_{m} \cdot \dot{\delta }_{2} \cdot \sin \beta_{2} \hfill \\ I_{g2} \cdot \ddot{\theta }_{g2} + k_{eg2} \cdot (\theta_{g2} - \theta_{eg2} ) + c_{eg2} \cdot (\dot{\theta }_{g2} - \dot{\theta }_{eg2} ) \hfill \\ = - r_{g2} \cdot \cos \beta_{2} \cdot (k_{m} \cdot \delta_{2} + c_{m} \cdot \dot{\delta }_{2} ) \hfill \\ \end{gathered} \right.$$
(5)

The vibration equations of the elastic webs \(eg1\) and \(eg2\) connected with gear ring \(g1\) and \(g2\) are shown as:

$$\left\{ \begin{gathered} m_{eg1} \cdot \ddot{x}_{eg1} + c_{eg1x} \cdot \dot{x}_{eg1} + k_{eg1x} \cdot x_{eg1} = - k_{ebg1} \cdot (x_{eg1} - x_{g1} ) - \hfill \\ c_{ebg1} \cdot (\dot{x}_{eg1} - \dot{x}_{g1} ) - k_{bg} \cdot (x_{eg1} - x_{eg2} ) - c_{bg} \cdot (\dot{x}_{eg1} - \dot{x}_{eg2} ) \hfill \\ m_{eg1} \cdot \ddot{y}_{eg1} + c_{eg1y} \cdot \dot{y}_{eg1} + k_{eg1y} \cdot y_{eg1} = - k_{ebg1} \cdot (y_{eg1} - y_{g1} ) - \hfill \\ c_{ebg1} \cdot (\dot{y}_{eg1} - \dot{y}_{g1} ) - k_{bg} \cdot (y_{eg1} - y_{eg2} ) - c_{bg} \cdot (\dot{y}_{eg1} - \dot{y}_{eg2} ) \hfill \\ m_{eg1} \cdot \ddot{z}_{eg1} + c_{eg1z} \cdot \dot{z}_{eg1} + k_{eg1z} \cdot z_{eg1} = - k_{ezg1} \cdot (z_{eg1} - z_{g1} ) - \hfill \\ c_{ezg1} \cdot (\dot{z}_{eg1} - \dot{z}_{g1} ) - k_{bzg} \cdot (z_{eg1} - z_{eg2} ) - c_{bzg} \cdot (\dot{z}_{eg1} - \dot{z}_{eg2} ) \hfill \\ I_{eg1} \cdot \ddot{\theta }_{eg1} + c_{eg1} \cdot (\dot{\theta }_{eg1} - \dot{\theta }_{g1} ) + k_{eg1} \cdot (\theta_{eg1} - \theta_{g1} ) \hfill \\ = - k_{tg} \cdot (\theta_{eg1} - \theta_{eg2} ) - c_{tg} \cdot (\dot{\theta }_{eg1} - \dot{\theta }_{eg2} ) \hfill \\ \end{gathered} \right.$$
(6)
$$\left\{ \begin{gathered} m_{eg2} \cdot \ddot{x}_{eg2} + c_{eg2x} \cdot \dot{x}_{eg2} + k_{eg2x} \cdot x_{eg2} = - k_{ebg2} \cdot (x_{eg2} - x_{g2} ) - \hfill \\ c_{ebg2} \cdot (\dot{x}_{eg2} - \dot{x}_{g2} ) - k_{bg} \cdot (x_{eg2} - x_{eg1} ) - c_{bg} \cdot (\dot{x}_{eg2} - \dot{x}_{eg1} ) \hfill \\ m_{eg2} \cdot \ddot{y}_{eg2} + c_{eg2y} \cdot \dot{y}_{eg2} + k_{eg2y} \cdot y_{eg2} = - k_{ebg2} \cdot (y_{eg2} - y_{g2} ) - \hfill \\ c_{ebg2} \cdot (\dot{y}_{eg2} - \dot{y}_{g2} ) - k_{bg} \cdot (y_{eg2} - y_{eg1} ) - c_{bg} \cdot (\dot{y}_{eg2} - \dot{y}_{eg1} ) \hfill \\ m_{eg2} \cdot \ddot{z}_{eg2} + c_{eg2z} \cdot \dot{z}_{eg2} + k_{eg2z} \cdot z_{eg2} = - k_{ezg2} \cdot (z_{eg2} - z_{g2} ) - \hfill \\ c_{ezg2} \cdot (\dot{z}_{eg2} - \dot{z}_{g2} ) - k_{bzg} \cdot (z_{eg2} - z_{eg1} ) - c_{bzg} \cdot (\dot{z}_{eg2} - \dot{z}_{eg1} ) \hfill \\ I_{eg2} \cdot \ddot{\theta }_{eg2} + c_{eg2} \cdot (\dot{\theta }_{eg2} - \dot{\theta }_{g2} ) + k_{eg2} \cdot (\theta_{eg2} - \theta_{g2} ) = \hfill \\ - c_{tg} \cdot (\dot{\theta }_{eg2} - \dot{\theta }_{eg1} ) - k_{tg} \cdot (\theta_{eg2} - \theta_{eg1} ) - \hfill \\ c_{out} \cdot (\dot{\theta }_{eg2} - \dot{\theta }_{out} ) - k_{out} \cdot (\theta_{eg2} - \theta_{out} ) \hfill \\ \end{gathered} \right.$$
(7)

where, δ1 and δ2 are the relative vibration displacement of helical gears on the left and right sides of the herringbone gear pair along the meshing line, respectively.

The vibration equations of input disk and output disk connected to active gear \(p1\) and web \(eg2\) are shown as:

$$\left\{ \begin{gathered} I_{in} \cdot \ddot{\theta }_{in} + c_{in} \cdot (\dot{\theta }_{in} - \dot{\theta }_{p1} ) + k_{in} \cdot (\theta_{in} - \theta_{p1} ) = \tilde{T}_{in} \hfill \\ I_{out} \cdot \ddot{\theta }_{out} + c_{out} \cdot (\dot{\theta }_{out} - \dot{\theta }_{eg2} ) + k_{out} \cdot (\theta_{out} - \theta_{eg2} ) = \tilde{T}_{out} \hfill \\ \end{gathered} \right.$$
(8)

The Eq. (2) ~ (8) are written in the form of matrix:

$${\mathbf{M}}\user2{\ddot{q}} + {\mathbf{C}}\dot{\user2{q}} + {\mathbf{K}}{\varvec{q}} = {\varvec{T}}$$
(9)

where, \({\varvec{q}}\), \({\varvec{T}}\), \({\mathbf{M}}\), \({\mathbf{C}}\), and \({\mathbf{K}}\) are displacement vector, torque vector, mass matrix, damping matrix and stiffness matrix.

Since the displacement \(\theta\) of each concentrated mass is not constrained, the torsional vibration equation is a semi-definite second-order differential equation group. In order to eliminate coaxial stiffness displacement, the angular displacement of mass nodes at both ends of elastic shaft is converted into the relative linear displacement along the tangential of shaft:

$$\left\{ \begin{gathered} \delta_{in} = (\theta_{in} - \theta_{p1} ) \cdot r_{in} \hfill \\ \delta_{p1p2} = (\theta_{p1} - \theta_{p2} ) \cdot r_{p} \hfill \\ \delta_{g1eg1} = (\theta_{g1} - \theta_{eg1} ) \cdot r_{eg1} \hfill \\ \delta_{eg1eg2} = (\theta_{eg1} - \theta_{eg2} ) \cdot r_{g} \hfill \\ \delta_{g2eg2} = (\theta_{g2} - \theta_{eg2} ) \cdot r_{eg2} \hfill \\ \delta_{out} = (\theta_{eg2} - \theta_{out} ) \cdot r_{out} \hfill \\ \end{gathered} \right.$$
(10)

In order to eliminate the stiffness displacement of meshing gear, the relative vibration displacement of the equivalent helical gear pair along the meshing line is shown as:

$$\left\{ \begin{gathered} \delta_{1} = (x_{p1} - x_{g1} ) \cdot \cos \beta_{1} \cdot sin\psi + (y_{p1} - y_{g1} ) \cdot \cos \beta_{1} \cdot \cos \psi \hfill \\ + ( - z_{p1} + z_{g1} ) \cdot \sin \beta_{1} + (r_{p1} \cdot \theta_{p1} + r_{g1} \cdot \theta_{g1} ) \cdot \cos \beta_{1} \hfill \\ \delta_{2} = (x_{p2} - x_{g2} ) \cdot \cos \beta_{2} \cdot sin\psi + (y_{p2} - y_{g2} ) \cdot \cos \beta_{2} \cdot \cos \psi \hfill \\ + ( - z_{p2} + z_{g2} ) \cdot \sin \beta_{2} + (r_{p2} \cdot \theta_{p2} + r_{g2} \cdot \theta_{g2} ) \cdot \cos \beta_{2} \hfill \\ \end{gathered} \right.$$
(11)

Then, define \(X_{i} {(}\tau {) = }{{x_{i} {(}t{)}} \mathord{\left/ {\vphantom {{x_{i} {(}t{)}} L}} \right. \kern-0pt} L}\) and \(\tau { = }\omega_{n} \cdot t\), and there is:

$$\left\{ \begin{gathered} \ddot{X} = {{\ddot{x}} \mathord{\left/ {\vphantom {{\ddot{x}} {(L \cdot \omega_{n}^{2} )}}} \right. \kern-0pt} {(L \cdot \omega_{n}^{2} )}} \hfill \\ \dot{X} = {{\dot{x}} \mathord{\left/ {\vphantom {{\dot{x}} {(L \cdot \omega_{n} )}}} \right. \kern-0pt} {(L \cdot \omega_{n} )}} \hfill \\ X = {x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L} \hfill \\ \end{gathered} \right.$$
(12)

where, L is the nominal scale of displacement, taking \(L = 10^{ - 5}\), \(\omega_{n}\) is circular frequency, taking \(\omega_{n} = \sqrt {{{k_{m} } \mathord{\left/ {\vphantom {{k_{m} } {M_{p1g1} }}} \right. \kern-0pt} {M_{p1g1} }}}\), \(M_{p1g1}\) is the equivalent mass of gear pair \(p1g1\), which has \(M_{p1g1} = {{\left( {I_{p1} \cdot I_{g1} } \right)} \mathord{\left/ {\vphantom {{\left( {I_{p1} \cdot I_{g1} } \right)} {\left( {I_{p1} r_{g1}^{2} + I_{g1} r_{p1}^{2} } \right)}}} \right. \kern-0pt} {\left( {I_{p1} r_{g1}^{2} + I_{g1} r_{p1}^{2} } \right)}}\).

The dimensionless vibration differential equation of the system under the new degree of freedom can be obtained from Eq. (9) to Eq. (12). The vibration response can be obtained by Runge–Kutta numerical iteration method, and the dynamic load coefficient and load sharing coefficient of the system can be further obtained. Before the solution of this method, the initial displacement is determined by the static deformation of the system under the theoretical load, and the initial velocity is determined by the initial state.

The time-varying mesh stiffness of gear pair

In the continuous meshing process of gear pair, the number of meshing teeth changes periodically with the time, which will cause periodic changes in the meshing stiffness of the teeth. Based on the tooth contact analysis technology of tooth surface, this paper calculates the time-varying meshing stiffness of gear pair31, which is shown as:

$$K_{s} = \frac{{F_{n} }}{{\delta_{n} }} = \frac{{\left( {{T \mathord{\left/ {\vphantom {T {r_{2} }}} \right. \kern-0pt} {r_{2} }}} \right) \cdot \cos \alpha_{n} \cdot \cos \beta }}{{\delta_{LTE} - \delta_{TE} }}$$
(13)

where, \(\delta_{LTE}\) and \(\delta_{TE}\) are the loaded transmission error and geometric transmission error of gear pair along the meshing line. \(\delta_{n}\) is the normal elastic deformation. \(T\) is load torque. \(r_{2}\) is the radius of base circle of the passive, \(\alpha_{n}\) is the normal pressure angle, and \(\beta\) is the spiral angle.

The time-varying meshing stiffness is expressed as Fourier series, and then directly introduced into the system dynamics equations, and its expression is shown as:

$$k(t) = k_{m} + \sum\limits_{i = 1}^{{n_{k} }} {\left( {A_{i} \cos i\omega_{m} t + B_{i} \sin i\omega_{m} t} \right)}$$
(14)

Here, in order to ensure a certain amount of work and solution accuracy, the fluctuation period of time-varying meshing stiffness is meshing period, \(\omega_{m}\) is its fundamental frequency, \(\omega_{m} { = }{{2\pi n_{in} z_{1} } \mathord{\left/ {\vphantom {{2\pi n_{in} z_{1} } {60}}} \right. \kern-0pt} {60}}\), \(n_{in}\) is input speed, \(z_{1}\) is the number of teeth of the active gear, and \(n_{k}\) is the order, taking \(n_{k} { = }50\).

The stiffness/damping of sliding bearing

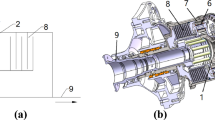
In gear transmission system, the oil film characteristics of sliding bearing is mainly characterized by the dynamic characteristic coefficient of sliding bearing, that is, the oil film stiffness coefficient and the oil film damping coefficient32. Figure 6 shows the structure diagram of cylindrical sliding bearing. According to hydrodynamic lubrication theory, the dimensionless Reynolds equation describing oil film pressure distribution in cylindrical bearings can be obtained as:

$$\frac{\partial }{\partial \varphi }\left( {\overline{h}^{3} \frac{{\partial \overline{p}}}{\partial \varphi }} \right) + \left( \frac{D}{L} \right)^{2} \frac{\partial }{\partial \lambda }\left( {\overline{h}^{3} \frac{{\partial \overline{p}}}{\partial \lambda }} \right) = - 3\left[ \begin{gathered} \varepsilon (1 - 2\dot{\theta })\sin \varphi \hfill \\ + 2\dot{\varepsilon }\cos \varphi \hfill \\ \end{gathered} \right]$$
(15)

where, \(\overline{p}\) is dimensionless oil film pressure, \(\overline{h}\) is oil film thickness, \(D\) is bearing diameter, \(L\) is bearing width, \(\varepsilon\) is eccentricity, and \(\theta\) is deflection angle.

Fig.6
figure 6

The structure diagram of cylindrical bearing.

Full size image

Given the small disturbance quantities \(\varepsilon\), \(\theta\), \(\dot{\varepsilon }\) and \(\dot{\theta }\), combined with Eq. (15), the disturbance pressures \({{\partial \overline{P}} \mathord{\left/ {\vphantom {{\partial \overline{P}} {\partial \varepsilon }}} \right. \kern-0pt} {\partial \varepsilon }}\),\({{\partial \overline{P}} \mathord{\left/ {\vphantom {{\partial \overline{P}} {\partial \theta }}} \right. \kern-0pt} {\partial \theta }}\), \({{\partial \overline{P}} \mathord{\left/ {\vphantom {{\partial \overline{P}} {\partial \dot{\varepsilon }}}} \right. \kern-0pt} {\partial \dot{\varepsilon }}}\) and \({{\partial \overline{P}} \mathord{\left/ {\vphantom {{\partial \overline{P}} {\partial \dot{\theta }}}} \right. \kern-0pt} {\partial \dot{\theta }}}\) under each disturbance quantity can be calculated, and then the oil film stiffness coefficient and oil film damping coefficient of bearing can be obtained as:

$$\left\{ \begin{gathered} \left\{ \begin{gathered} K_{ee} \hfill \\ K_{\theta e} \hfill \\ \end{gathered} \right\} = - \int_{ - 1}^{1} {\int_{{\phi_{{1}} }}^{{\phi_{2} }} {\frac{{\partial \overline{P}}}{\partial \varepsilon }} } \left\{ \begin{gathered} \cos \phi \hfill \\ \sin \phi \hfill \\ \end{gathered} \right\}d\phi d\lambda \hfill \\ \left\{ \begin{gathered} {\text{K}}_{{{\text{e}}\theta }} \hfill \\ K_{\theta \theta } \hfill \\ \end{gathered} \right\} = - \int_{ - 1}^{1} {\int_{{\phi_{1} }}^{{\phi_{2} }} {\frac{{\partial \overline{P}}}{\partial \theta }} } \left\{ \begin{gathered} \cos \phi \hfill \\ \sin \phi \hfill \\ \end{gathered} \right\}d\phi d\lambda \hfill \\ \left\{ \begin{gathered} {\text{D}}_{ee} \hfill \\ D_{\theta e} \hfill \\ \end{gathered} \right\} = - \int_{ - 1}^{1} {\int_{{\phi_{1} }}^{{\phi_{2} }} {\frac{{\partial \overline{P}}}{{\partial \dot{\varepsilon }}}} } \left\{ \begin{gathered} \cos \phi \hfill \\ \sin \phi \hfill \\ \end{gathered} \right\}d\phi d\lambda \hfill \\ \left\{ \begin{gathered} {\text{D}}_{e\theta } \hfill \\ D_{\theta \theta } \hfill \\ \end{gathered} \right\} = - \int_{ - 1}^{1} {\int_{{\phi_{1} }}^{{\phi_{2} }} {\frac{{\partial \overline{P}}}{{\partial \dot{\theta }}}} } \left\{ \begin{gathered} \cos \phi \hfill \\ \sin \phi \hfill \\ \end{gathered} \right\}d\phi d\lambda \hfill \\ \end{gathered} \right.$$
(16)

The oil film stiffness coefficient and damping coefficient are converted to the coordinate system SO to obtain:

$$\left\{ \begin{gathered} \left[ {\begin{array}{*{20}c} {K_{xx} } & {K_{xy} } \\ {K_{yx} } & {K_{yy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sin \theta } & {\cos \theta } \\ {\cos \theta } & { - \sin \theta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {K_{ee} } & {K_{e\theta } } \\ {K_{\theta e} } & {K_{\theta \theta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sin \theta } & {\cos \theta } \\ {\cos \theta } & { - \sin \theta } \\ \end{array} } \right] \hfill \\ \left[ {\begin{array}{*{20}c} {D_{xx} } & {D_{xy} } \\ {D_{yx} } & {D_{yy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sin \theta } & {\cos \theta } \\ {\cos \theta } & { - \sin \theta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {D_{ee} } & {D_{e\theta } } \\ {D_{\theta e} } & {D_{\theta \theta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sin \theta } & {\cos \theta } \\ {\cos \theta } & { - \sin \theta } \\ \end{array} } \right] \hfill \\ \end{gathered} \right.$$
(17)

Due to the influence of machining error, the herringbone gear often produces a small axial load. In order to support the transmission system in the axial, the easiest way is to use the squeezing effect of oil film in the thrust plate to give the axial bearing stiffness and damping, as shown in Fig. 7. In the analysis of squeeze film lubrication, assuming that there is no relative sliding between the supporting surfaces, and the viscosity of the lubricant is constant. the squeeze Reynolds equation can be expressed as:

$$\frac{\partial }{\partial x}\left( {h^{3} \frac{\partial p}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {h^{3} \frac{\partial p}{{\partial y}}} \right) = 12\eta \frac{\partial h}{{\partial t}}$$
(18)
Fig.7
figure 7

The thrust plate structure diagram.

Full size image

Assuming that the thrust side structure is circular, and the inner and outer radii are R1 and R2. The Eq. (18) is transformed into Reynolds equation in polar coordinates (r, θ), which is shown as follows:

$$\frac{\partial }{\partial r}\left( {rh^{3} \frac{\partial p}{{\partial r}}} \right) + \frac{1}{r} \cdot \frac{\partial }{\partial \theta }\left( {h^{3} \frac{\partial p}{{\partial \theta }}} \right) = 12\eta r\frac{\partial h}{{\partial t}}$$
(19)

where, r is radius, and its range is between R1 and R2. θ is the circumferential angle, h is oil film thickness, p is the pressure on thrust side, η is dynamic viscosity and t is time.

Because of symmetry, \({{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial \theta }}} \right. \kern-0pt} {\partial \theta }} = 0\), and h has nothing to do with r, the Eq. (19) is rewritten as:

$$\frac{d}{dr}\left( {r\frac{dp}{{dr}}} \right) = \frac{12\eta r}{{h^{3} }} \cdot \frac{\partial h}{{\partial t}}$$
(20)

The boundary condition of Eq. (20) is shown as:

$$\left\{ \begin{gathered} r = R_{1} \, p = P_{in} \hfill \\ r = R_{2} \, p = 0 \hfill \\ \end{gathered} \right.$$
(21)

Combining Eq. (20) and Eq. (21), the axial pressure distribution of the bearing is given as:

$$p = \frac{3\eta }{{h^{3} }}\left[ {r^{2} - R_{2}^{2} - \frac{{\ln r - \ln R_{2} }}{{\ln R_{1} - \ln R_{2} }}\left( {R_{1}^{2} - R{}_{2}^{2} } \right)} \right]\frac{dh}{{dt}} + \frac{{p_{in} \left( {\ln r - \ln R_{2} } \right)}}{{\ln R_{1} - \ln R_{2} }}$$
(22)

The axial load of bearing can be obtained by integrating the axial pressure distribution, which is shown as:

$$\begin{gathered} W = \int_{{R_{1} }}^{{R_{2} }} {2\pi prdr} = \frac{6\pi \eta }{{h^{3} }}\left[ {\frac{1}{2}R_{1}^{2} \left( {R_{1}^{2} - R_{2}^{2} } \right) - \frac{{\left( {R_{1}^{2} - R_{2}^{2} } \right)^{2} }}{4}\left( {1 + \frac{1}{{\ln R_{1} - \ln R_{2} }}} \right)} \right]\frac{dh}{{dt}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{2\pi p_{in} }}{{\ln R_{1} - \ln R_{2} }}\left[ {\frac{{R_{1}^{2} - R_{2}^{2} }}{4} - \frac{1}{2}R_{1}^{2} \left( {\ln R_{1} - \ln R_{2} } \right)} \right] \hfill \\ \end{gathered}$$
(23)

The lubricating oil between thrust side and thrust plate is simplified as a nonlinear spring and damper. The Eq. (23) is derived from the displacement and velocity respectively, and the influence of higher order term is neglected. The stiffness and damping coefficient of squeeze film are obtained as:

$$\left\{ \begin{gathered} K = \frac{\partial W}{{\partial h}} = - \frac{{18\pi \eta h^{\prime}}}{{h^{4} }}\left[ {\frac{{R_{1}^{4} - R_{1}^{2} R_{2}^{2} }}{2} - \frac{{\left( {R_{1}^{2} - R_{2}^{2} } \right)^{2} }}{4}\left( {1 + \frac{1}{{\ln R_{1} - \ln R_{2} }}} \right)} \right] \hfill \\ D = \frac{\partial W}{{\partial \dot{h}}} = \frac{6\pi \eta }{{h^{3} }}\left[ {\frac{{R_{1}^{4} - R_{1}^{2} R_{2}^{2} }}{2} - \frac{{\left( {R_{1}^{2} - R_{2}^{2} } \right)^{2} }}{4}\left( {1 + \frac{1}{{\ln R_{1} - \ln R_{2} }}} \right)} \right] \hfill \\ \end{gathered} \right.$$
(24)

In the actual calculation, the oil film thickness \(h\) and \(\dot{h}\) of Eq. (23) and Eq. (24) are converted into the corresponding axial displacement and speed of the shaft. Before and after calling the neural network for simulation calculation, the input and output of the neural network should be normalized and denormalized, which can be realized by the normalization processing function tramnmx and denormalization processing function postmnmx in Matlab.

Because the calculation of the dynamic characteristics of sliding bearing is carried out in the coordinate system with the load direction as the ordinate and the direction perpendicular to the load as the abscissa, the gear-sliding bearing-rotor dynamics analysis is carried out in the horizontal direction as the abscissa and the vertical direction as the ordinate, as shown in Fig. 6, θ is the angle between load and vertical direction. Therefore, it is necessary to transform dynamic characteristic coefficient of sliding bearing obtained by neural network simulation into the coordinate system where the gear-bearing- rotor system dynamics analysis is located, and then it can be applied to the system dynamics analysis.

The parameters of cylindrical sliding bearing in Table 1 are substituted into the compiled neural network program to calculate the bearing stiffness and damping along axis X and axis Y (Fig. 6) as the speed changes, and the results are shown in Fig. 8. From Fig. 8, under different eccentricity, the bearing stiffness of bearing oil film along axis X and axis Y decreases with the increase of the speed, and corresponding bearing damping first decreases, then increases, appears peaks, and finally remains unchanged. When the eccentricity reaches 0.7, the greater the slope of bearing support stiffness and damping, the more sensitive it is to the change of speed.

Table 1 The relevant parameters of dynamic characteristics of cylindrical sliding bearing.
Full size table
Fig.8
figure 8

The influence of journal speed on dynamic characteristics of cylindrical bearings under different eccentricity.

Full size image

The stiffness/damping of elastic material ring

The elastic web connects ring gear of passive gear with gear web, and its stiffness directly affects vibration characteristics of the whole gear transmission system, while its damping value will affect vibration waveform and amplitude of the meshing force of gear pair. The stiffness and damping of elastic web depend on structural design and material selection. Based on the theory of elastic mechanics, the bending stiffness \(k_{ebgi}\), axial tension–compression stiffness \(k_{ezgi}\) and torsional stiffness \(k_{egi}\) of elastic material ring are deduced respectively.

The Fig. 9 shows the geometric shape of the elastic material circle. The center of the maximum end of elastic material circle is the coordinate origin, and the center axis is axis z. L is the axial length of elastic material ring, ϕd0 is the minimum aperture of the ring, h is the thickness of the ring, and α is the inclination angle of the hole wall relative to axis z.

Fig.9
figure 9

The geometry shape of elastic material ring.

Full size image

The expression of hole wall in the coordinates is shown as:

$$\rho (z) = \rho_{0} + \tan \alpha \cdot z$$
(25)

where, ρ0 is the maximum aperture of elastic material ring, and when \(z = L\), \(\rho = {{d_{0} } \mathord{\left/ {\vphantom {{d_{0} } 2}} \right. \kern-0pt} 2}\), \(\rho_{0} = {{d_{0} } \mathord{\left/ {\vphantom {{d_{0} } 2}} \right. \kern-0pt} 2} - L\tan \alpha\) is obtained.

According to Hooke’s law, the total deformation after axial force \(F_{z}\) is shown as:

$$\Delta l_{m} = \int_{0}^{L} {\frac{{F_{z} dz}}{{E \cdot 2\pi (\rho_{0} + \tan \alpha \cdot z) \cdot h}}}$$
(26)

Then the axial tension and compression stiffness of the member along axis z is expressed as:

$$k_{ezgi} = \left| {\frac{2\pi h \cdot E \cdot \tan \alpha }{{\ln \left[ {{{(\rho_{0} + L \cdot \tan \alpha )} \mathord{\left/ {\vphantom {{(\rho_{0} + L \cdot \tan \alpha )} {\rho_{0} }}} \right. \kern-0pt} {\rho_{0} }}} \right]}}} \right|$$
(27)

When calculating the relative rotation angle \(\varphi\) of elastic ring around axis z, because the second moment \(I_{z}\) of each section of elastic ring on axis z is different, the relative torsion angle \(d\varphi = \left( {{T \mathord{\left/ {\vphantom {T {GI_{z} }}} \right. \kern-0pt} {GI_{z} }}} \right)dz\) at both ends of the ring should be calculated by the integral method, so as to obtain the total torsional deformation:

$$\begin{gathered} \Delta \varphi_{m} = \frac{T}{\tan \alpha \cdot \pi Gh}\ln \frac{{hd_{0} + h^{2} }}{{2h\rho_{0} + h^{2} }} - \hfill \\ \frac{2T}{{\tan \alpha \cdot \pi Gh}}(\arctan \frac{{d_{0} + h}}{h} - \arctan \frac{{2\rho_{0} + h}}{h}) \hfill \\ \end{gathered}$$
(28)

where, G is the shear modulus of the material.

Then the torsional stiffness of the member along axis z is:

$$k_{egi} = \left| {\tan \alpha \cdot \pi Gh\left[ {\ln \left( {\frac{{hd_{0} + h^{2} }}{{2h\rho_{0} + h^{2} }}} \right) - 2\left( \begin{gathered} \arctan \frac{{d_{0} + h}}{h} \hfill \\ - \arctan \frac{{2\rho_{0} + h}}{h} \hfill \\ \end{gathered} \right)} \right]^{{{ - }1}} } \right|$$
(29)

Supposing that the big end of the ring is fixed and a radial force F is applied to its small end, the bending moment M will be generated, which will make the component produce deflection deformation. Approximate differential equation of deflection curve by mechanics of materials is shown as:

$$\frac{{d^{2} x}}{{dz^{2} }} = \frac{{d^{2} y}}{{dz^{2} }} = \frac{4F \cdot (L - z)}{{E\pi \left[ {(\rho (z) + h)^{4} - \rho (z)^{4} } \right]}}$$
(30)

Then, by integrating the Eq. (30) twice, the maximum deflection expression is shown as:

$$\begin{gathered} \Delta x = \Delta y = \hfill \\ \frac{F \cdot L}{{\pi \cdot h^{3} \cdot \tan \alpha^{2} }}\left\{ \begin{gathered} (2\tan \alpha \cdot z + 2p_{0} + h) \cdot \ln \left[ \begin{gathered} 2\tan \alpha^{2} \cdot z^{2} + \hfill \\ (4p_{0} + 2h) \cdot \tan \alpha \cdot z \hfill \\ + 2p_{0}^{2} + 2hp_{0} + h^{2} \hfill \\ \end{gathered} \right] + \hfill \\ 2h \cdot \arctan (\frac{{2\tan \alpha \cdot z + 2p_{0} + h}}{h}) \hfill \\ - (4\tan \alpha \cdot z + 4p_{0} + 2h) \cdot \hfill \\ \ln (2\tan \alpha \cdot z + 2p_{0} + h) + 4p_{0} + 2h \hfill \\ \end{gathered} \right\} \hfill \\ + \frac{F}{{\pi \cdot h^{3} \cdot \tan \alpha^{3} }}\left\{ \begin{gathered} \left[ {(2p_{0} + h)\tan \alpha \cdot z + 2p_{0}^{2} + 2hp_{0} } \right] \cdot \ln \left[ \begin{gathered} 2\tan \alpha^{2} \cdot z^{2} + (4p_{0} + 2h) \cdot \hfill \\ \tan \alpha \cdot z + 2p_{0}^{2} + 2hp_{0} + h^{2} \hfill \\ \end{gathered} \right] \hfill \\ + (2h\tan \alpha \cdot z + 4hp_{0} + 2h^{2} ) \cdot \arctan (\frac{{2\tan \alpha \cdot z + 2p_{0} + h}}{h}) \hfill \\ - \left[ {(4p_{0} + 2h)\tan \alpha \cdot z + (4p_{0}^{2} + 4hp_{0} + h^{2} )} \right] \cdot \hfill \\ \ln (2\tan \alpha \cdot z + 2p_{0} + h) + 4p_{0}^{2} + 4hp_{0} + h^{2} \hfill \\ \end{gathered} \right\} \hfill \\ + Cz + D \hfill \\ \end{gathered}$$
(31)

From the initial condition \(z = 0\), \(\Delta x = \Delta y = \Delta x^{\prime} = \Delta y^{\prime} = 0\), we can get: \(C = 5866.1F,D = 266.2F\). Then the bending stiffness of elastic material ring along axis x and y can be shown as:

$$k_{ebgi} = F/\Delta x = F/\Delta y$$
(32)

The tension–compression, torsion and bending damping of elastic material ring are respectively expressed as:

$$c_{j} = 2 \cdot \xi_{j} \sqrt {k_{j} \cdot M}$$
(33)

where, kj (j = ezgi, egi and ebgi) represent the tension- compression, torsion and bending stiffness of the elastic ring, ξj is the corresponding damping ratio, and M is the equivalent mass of the concentrated mass node of elastic ring.

The input/output torque fluctuation excitation

Usually, in addition to the internal excitation caused by gear meshing, the transmission system is also subjected to external excitation caused by engine input torque disturbance and the impact of air or liquid medium. In this paper, the input torque fluctuation excitation is regarded as theoretical input torque acted by engine plus simple harmonic momentum fluctuating with the frequency of input shaft, which is given as:

$$\tilde{T}_{in} = T_{m1} \left[ {1 + bd_{1} \cdot \sin (\frac{{2\pi n_{in} \cdot t}}{{60w_{n} }})} \right]$$
(34)

Here, Tm1 is constant input torque, nin is speed, bd1 is input torque fluctuation rate, and wn is dimensionless time scale.

For the output torque fluctuation excitation, according to the helicopter propeller “exciter” in Ref. 33, the elastic vibration of propeller caused by alternating aerodynamic force and inertial force is transmitted to the transmission system through the “filter” hub, forming an alternating load force. The harmonic frequency of the load \(\tilde{T}_{out}\) is an integer multiple of the number of blades. Let b be the number of blades and \(\Omega\) be the rotational angular velocity of propeller, then the harmonic frequency of the moment \(\tilde{T}_{out}\) acting on the fuselage is \(mb\Omega\)(\(m = 1,2,3 \cdots\)), and its specific expression is shown as:

$$\tilde{T}_{out} = T_{m1} \cdot \frac{{z_{p1} }}{{z_{g1} }}\left[ {1 + bd_{2} \cdot \sin (\frac{mb\Omega \cdot t}{{60w_{n} }})} \right]$$
(35)

Here, zp1 and zg1 are the number of teeth of active and passive gear, and bd2 is output torque fluctuation rate.

Influence of elastic material of web on system dynamic characteristics

The elastic material layer of elastic web is core component of the whole system, and its mechanical properties, that is, the elastic modulus and shear modulus of materials, will directly affect the dynamic performance of the whole gear system. Therefore, the selection of elastic materials plays a vital role. In this section, the basic parameters of herringbone gear in Table 2 are taken as the research object. The four elastic materials, namely elastic copper alloy (beryllium copper), superalloy (Ni40Cr20Co20Mo), spring steel and silicon rubber, are selected from Ref. 34. By calculating the dynamic load coefficient(DLC) and load sharing coefficient (LSC) of the elastic web herringbone gear pair, the influence of the above elastic materials on the dynamic characteristics of the system is analyzed.

Table 2 The basic parameters of herringbone gear transmission.
Full size table

The elastic material ring is made of beryllium copper, and its mechanical characteristics: the elastic modulus is \(E = 130{\text{GPa}}\), Poisson’s ratio is \(\mu = 0.35\), and density is \(\rho = 8.3{{\text{g}} \mathord{\left/ {\vphantom {{\text{g}} {{\text{cm}}^{3} }}} \right. \kern-0pt} {{\text{cm}}^{3} }}\). When the elastic material is high temperature resistant and high elastic alloy (Ni40Cr20Co20Mo), the performance is good at 500 °C, and its mechanical properties: the elastic modulus is \(E = 1950{\text{MPa}}\), Poisson’s ratio is \(\mu = 0.25\), and density is \(\rho = 8.4{{\text{g}} \mathord{\left/ {\vphantom {{\text{g}} {{\text{cm}}^{3} }}} \right. \kern-0pt} {{\text{cm}}^{3} }}\). When spring steel is used for elastic material ring, the elastic limit and yield ratio can be significantly improved, and its mechanical properties: elastic modulus is \(E = 200000\;{\text{MPa}}\), shear modulus is \(G = 74100\;{\text{Mpa}}\), density is \(\rho = 7.85{{\text{g}} \mathord{\left/ {\vphantom {{\text{g}} {{\text{cm}}^{3} }}} \right. \kern-0pt} {{\text{cm}}^{3} }}\). When the elastic material is silicon rubber, the hardness increases slowly and the tensile strength and elongation at break decrease slowly at high temperature (> 250℃), and its mechanical properties: elastic modulus is \(E = 6{\text{MPa}}\), Poisson’s ratio is \(\mu = 0.47\), and density is \(\rho = 1.1{{\text{g}} \mathord{\left/ {\vphantom {{\text{g}} {{\text{cm}}^{3} }}} \right. \kern-0pt} {{\text{cm}}^{3} }}\). The bending stiffness, tension- compression stiffness and torsion stiffness of the component are obtained, and the dynamic load coefficient diagram of the left and right sides of gear pair is obtained when input power is 100 kW and input speed is 8000 rpm, as shown in Fig. 10.

Fig.10
figure 10

The dynamic load coefficient of the left and right sides of the herringbone gear pair.

Full size image

From Fig. 10 (a), it can be seen that when the elastic plate structure is not used, the DLCs of the left and right branches of the herringbone gear pair are 0.059387 and 0.059439, and the system vibration is too large. It can be seen from Fig. 10 (b) that when the elastic material is beryllium copper, there is still uneven power distribution on both sides of the tooth. The DLC of gear pair p2g2 is the largest, and its value reaches 1.158443. Compared with the system dynamic characteristics without considering the effect of elastic web, the system dynamic characteristics are improved, and the DLCs of the left and right branches are different by 21.68%. It can be seen from Fig. 10 (c) that when the elastic material is Ni40Cr20Co20Mo, the DLCs of the left and right branches differ by 7.64%. Compared with beryllium copper, the system dynamic load sharing performance is improved. From Fig. 10(d), when the elastic material is spring steel, the DLC different of the left and right branches is 21.55%, and the DLC of gear pair p2g2 is larger. Compared with Ni40Cr20Co20Mo of Fig. 10 (c), the system dynamic load sharing performance is worse and the vibration is unstable. From Fig. 10 (e), when the elastic material is silicone rubber, the DLCs of the left and right branches are very close to 1, the dynamic load amplitude of the gear pair changes little. The system dynamic load sharing performance is more stable. Table 3 shows the DLC and LSC of the system with different elastic materials.

Table 3 The DLC and LSC of the system under different elastic materials.
Full size table

The analysis of gear system nonlinear vibration characteristics

Based on the comparison of dynamic load-sharing characteristics of several elastic web materials, it can be seen that silicone rubber has the best performance, followed by superalloy Ni40Cr20Co20Mo. In the following, the nonlinear vibration behavior of elastic web herringbone gear under these two elastic materials is analyzed at different speeds. The curve of the root mean square (RMS) of relative comprehensive vibration acceleration of the left and right meshing lines of elastic web herringbone gear pair with the change of input speed is obtained, as shown in Fig. 11. From Fig. 11, with the increase of input speed, the vibration acceleration of gear pair appears multiple resonance peaks, which corresponding to the resonance frequency and 1/2 resonance fundamental frequency respectively. In addition, there are multiple jumps at low speed. At low speed, the damping effect of silicon rubber is obvious, while at high speed, the damping effect of superalloy is obvious, which shows that at high speed, the damping effect of silicon rubber is obvious, while superalloy material is more conducive to system stability.

Fig.11
figure 11

The change curve of RMS of acceleration with input speed changes.

Full size image

Figure 12 shows the system global bifurcation diagram as input speed changes. As can be seen from Fig. 12, with the increase of input speed, the change trend of relative vibration displacement on the meshing line of herringbone gear pair made of silicon rubber and superalloy is similar. At low speed, the system shows the superposition of multiple periodic motions and jumping motions. When rotational speed reaches 5000 rpm, the system is in chaotic motion, then it bifurcates into two periodic motion at about 7000 rpm, and then enters chaotic motion. At about 10000 rpm, there is a periodic window, and then it has been in single periodic motion. The difference is that when silicon rubber is used, the chaotic motion region is relatively large and there are multiple periodic windows. When using superalloy, the periodic motion area is larger, which is more conducive to improving the stability of the system.

Fig. 12
figure 12

The global bifurcation diagram with input speed changes.

Full size image

The curve of the RMS of relative comprehensive vibration acceleration of the left and right meshing lines of elastic web herringbone gear pair with the change of input power is obtained, as shown in Fig. 13. As can be seen from Fig. 13, with the increase of input power, the vibration acceleration of the system under the two materials also increases. At low power, the elastic web gear pair of two materials appears jumping behavior, while silicon rubber is more beneficial to improve the stability of the system than superalloy. At high power, there is no jumping behavior, while superalloy is more beneficial to improve the system vibration characteristics than silicon rubber. Figure 14 shows the global bifurcation diagram of the system with input power changes. From Fig. 14, with the increase of input power, the vibration of herringbone gear pair with elastic webs of two materials also increases. When the power is low, the silicon rubber web gear is in a state of superposition of chaotic motion and multiple periodic motion, while the superalloy web gear is in chaotic motion, and the chaotic motion area of silicon rubber is larger than that of superalloy web. When the input power exceeds 2000 kW, the web gears of two materials move in a single period. When the high power changes, the superalloy is more conducive to improving the gear system stability.

Fig.13
figure 13

The change curve of RMS of acceleration with input power changes.

Full size image
Fig. 14
figure 14

The global bifurcation diagram with input power changes.

Full size image

Influence of structural parameters on system dynamic characteristics

Under normal circumstances, in addition to the internal excitation caused by gear meshing, the transmission system is also subjected to vibration excitation such as engine input torque disturbance, load air or liquid medium slap, which is defined as the external excitation of gear dynamics system35. Figure 15 shows the dynamic load sharing coefficient of two kinds of elastic web gear transmission systems under input torque excitation fluctuation. As shown in Fig. 15(a), the DLC of herringbone gear pairs of two kinds of elastic material webs increases with the increase of input torque volatility, but the increase slope is not obvious. The DLC of half gear pair near power input end of the system under the superalloy elastic web is obviously larger than that of the gear with silicon rubber elastic web. As shown in Fig. 15 (b), the herringbone gear pair under the high temperature alloy elastic web has obvious uneven force at both ends and uneven power distribution compared with silicon rubber web. The input torque fluctuation rate has little effect on the LSC of gear pair of two material elastic web plates.

Fig.15
figure 15

Influence of input torque excitation on system dynamic characteristics.

Full size image

Figure 16 shows the influence of output torque fluctuation excitation on DLC and LSC of herringbone gear pair. As can be seen from Fig. 16(a), compared with the fluctuation of input torque, the DLC of herringbone gear pair with two kinds of elastic webs has a larger fluctuation of load torque. At this time, the power transmission of herringbone gear pair with silicon rubber elastic is uneven, and the difference between the DLCs at both ends becomes larger. This shows that the vibration reduction effect of silicon rubber elastic web is gradually weakened. As shown in Fig. 16(b), there is obvious uneven power distribution at both ends of herringbone gear pair under the superalloy elastic web. The fluctuation of output torque has little influence on the load sharing characteristics of gear pair of two materials elastic web. It can be seen that the influence of output external excitation on the system is greater than that of input external excitation, so the vibration amplitude of the load should be strictly controlled, and vibration dampers should be added at the output of the system to weaken the excitation influence of the load.

Fig.16
figure 16

Influence of output torque excitation on system dynamic characteristics.

Full size image

According to experimental gear parameters, the parameters smaller than, equal to and larger than the experimental relief groove diameter of 30 mm are selected respectively, and the influence of the relief groove diameter on the DLC and LSC of gear pair is analyzed. The results are shown in Fig. 17. From Fig. 17, the DLC and LSC of the silicon rubber elastic web gear system are not affected by the change of the relief groove diameter of active wheel, but the two ends of the herringbone gear with the superalloy elastic web have the same primary power flow when the diameter is between 30 and 45 mm. The big end of power flow gradually changes from the gear pair close to power input end to the far end. The difference of power flow between two gear pairs tends to increase with the increase of the relief groove diameter of active gear.

Fig.17
figure 17

Influence of relief groove diameter of active gear on the system dynamic load-sharing performance.

Full size image

Figure 18 shows the influence of relief groove diameter of passive gear on the system dynamic load sharing performance. As can be seen from Fig. 18, the herringbone gear system of silicone rubber elastic web still maintains good load sharing characteristics. When the DLC of gear pair remains at a very low, the system runs smoothly. However, the dynamic load of the superalloy elastic spoke herringbone gear pair decreases with the increase of relief groove diameter of passive gear, and the load-sharing characteristics at both ends of herringbone gear are greatly improved. When the diameter reaches 70 mm, the LSCs at both ends of herringbone gear are almost equal. This is because the relief groove diameter has reached or exceeded the diameter of tooth root. There is no uneven load phenomenon of herringbone tooth at this time.

Fig.18
figure 18

Influence of relief groove diameter of passive gear on the system dynamic load-sharing performance.

Full size image

By changing the length of relief groove of the active and passive gears, the influence of length of relief groove on the DLC and LSC of gear pair is analyzed. The results are shown in Fig. 19. It can be seen from Fig. 19 that the load sharing characteristics of gear pair with the superalloy elastic web gradually deteriorate with the increase of the length of relief groove. When the length is much smaller than the diameter of two retreating grooves, the system load sharing characteristics are the best and the vibration amplitude is the smallest. The silicon rubber elastic web herringbone tooth system maintains good load sharing characteristics, but when the length of the groove is much smaller than the diameter of two retreating grooves, the dynamic load tends to increase.

Fig.19
figure 19

Influence of the length of relief groove on the system dynamic load-sharing performance.

Full size image

Since the moment of inertia of web plate is proportional to its mass, the mass and moment of inertia of entire web can be adjusted by increasing or decreasing the number of web holes. By changing the mass of the passive gear web, the 0.01,0.1,1 and 10 times mass of the original web mass are selected respectively to observe the influence of the mass of the web on the DLC and LSC of gear pair. The results are shown in Fig. 20. It can be seen from Fig. 20 that when the mass of the web is reduced to 0.1 times the initial mass, the DLC and LSC of gear pair of both the silicone rubber and the superalloy elastic web gear do not change. However, when the mass is reduced to 0.01 times the initial mass of the web, the DLC of gear pair of silicon rubber and the superalloy elastic web gear increases rapidly, and the load sharing characteristics at both ends of herringbone teeth become worse. Therefore, in the design of elastic web herringbone gear, the number of web holes should be reasonably increased to improve the system dynamic load sharing performance.

Fig.20
figure 20

Influence of the mass of the plate on the system dynamic load-sharing performance.

Full size image

Conclusion

  1. (1)

    Under different eccentricity, the bearing stiffness of the bearing oil film along axis X and axis Y decreases with the increase of rotational speed, and the bearing damping decreases first, then increases and decreases, and finally remains unchanged.

  2. (2)

    Compared with the web without consideration, when the elastic material of the web is beryllium copper, there is still uneven power distribution on both sides of herringbone teeth. The DLC different of left and right branches are 21.68%. When the elastic material is Ni40Cr20Co20Mo, the DLC different of the left and right branches are 7.64%. When elastic material is spring steel, the DLC different of left and right branches are 21.55%. When elastic material is silicon rubber, the DLC difference of left and right branches is very small and close to 1. Therefore, when elastic web is silicon rubber, the dynamic load amplitude of gear pair changes little, and the system dynamic load sharing performance is more stable.

  3. (3)

    At low rotational speed, the damping effect of silicon rubber is obvious, while at high speed, the damping effect of superalloy is obvious. When silicone rubber is used, the chaotic motion region of the system is relatively large, and there are many periodic windows. When using superalloy, the periodic motion area of the system is larger, which is more conducive to improving the stability of gear system. At low power, silicone rubber is more beneficial to improve the system stability than superalloy. At high power, superalloy is more beneficial to improve the system vibration characteristics than silicon rubber. When the power is low, the silicon rubber web gear is in a state of superposition of chaotic motion and multiple periodic motion, while the superalloy web gear is in chaotic motion. When the high power changes, the web gears of two materials move in a single period, and the superalloy is more conducive to improving the system stability.

  4. (4)

    With the increase of the fluctuation of input torque, the silicon rubber elastic web is more beneficial to improve the system dynamic load sharing performance than the superalloy elastic web. With the increase of output torque fluctuation, the system dynamic load performance is greatly affected, and the superalloy elastic web is more beneficial to improve the system dynamic load sharing performance than silicon rubber elastic web. The output excitation has greater influence on the system dynamic load-sharing performance than input external excitation, so the vibration amplitude of load should be strictly controlled and vibration dampers should be added at the output to improve the adaptability of system to the environment.

  5. (5)

    With the change of diameter and length of relief groove of active and passive gears, the elasticity of silicon rubber is more beneficial to improve the system dynamic load sharing performance than that of the superalloy. When the mass of the web is reduced to 0.1 times of initial web mass, the DLC of the system under two materials does not change, while when the mass of the web is reduced to 0.01 times of initial web mass, the system dynamic load sharing performance under two materials becomes worse. Therefore, in the design of elastic web herringbone gear, the number of web holes should be reasonably increased, and the web mass should not be reduced just to reduce the mass of gear system.