Introduction

Background and motivation

Accurate measurement of bladder volume is an essential component in the assessment of patients with urinary retention and voiding dysfunction1. While ultrasound imaging can effectively calculate bladder volume using prolate ellipsoid formula2,3, high-quality images are essential to ensure reliable volume assessments, which directly impact clinical decision-making and patient care outcomes. Achieving such quality requires the careful acquisition of optimal views in both transverse and longitudinal orientations. However, inexperienced operators often struggle to acquire ultrasound images at the optimal transverse and longitudinal planes4. An effective and robust intelligent ultrasound imaging guidance system can assist operators in achieving optimal views and acquiring higher-quality images, ultimately contributing to more consistent and accurate diagnostic outcomes.

Recent advancements in artificial intelligence have enabled the development of automatic ultrasound guidance systems, which assist operators during scans by enhancing image quality5. Reinforcement Learning (RL), a rapidly growing area in artificial intelligence, has gained significant attention in healthcare for its ability to make adaptive, real-time decisions6,7. By interacting with their environment, RL models learn optimal strategies dynamically, making them particularly suited for tasks requiring continuous adaptation, such as ultrasound bladder application. In the context of ultrasound imaging, RL-based approaches have been developed to provide real-time guidance during image acquisition, adjusting continuously to maintain optimal imaging conditions.

Despite their promise, most existing RL models for ultrasound imaging8,9 rely primarily on simple coordinates and raw image features from their environments to predict actions during deployment without directly considering anatomical features in their objective functions. In real-world applications, where a deeper understanding of input information is crucial for decision-making, these models face significant limitations. Specifically, they often struggle to identify the most relevant features in the decision-making process due to limited supervision and reward structures. Additionally, the concept of creating an environment with real-world ultrasound data poses a major challenge in RL ultrasound application development.

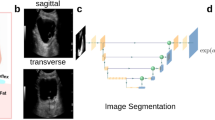
In this work, we present a RL-based ultrasound guidance pipeline that integrates a provable and practical variant of Deep Q-Networks (DQN)10 known as Adam LMCDQN11, which utilizes posterior sampling for RL. Fig. 1 illustrates the overall framework. Specifically, Adam LMCDQN performs noisy gradient descent updates with Langevin Monte Carlo (LMC), generating samples that approximate the posterior distribution of the Q-value function. By incorporating anatomical features as an additional domain knowledge, we show that the model concentrates better on the critical features and patterns. This integration allows the model to make more informed and context-aware decisions, addressing key shortcomings of existing approaches. The main contributions of this work are:

  • Generation of a realistic RL simulation environment based on 3D ultrasound bladder dataset collected from 17 healthy volunteers that features three degrees of freedom: left/right translation, up/down translation, and tilt which encompasses all necessary actions for optimal probe positioning to accurately estimate bladder volume.

  • We demonstrate that using LMC as an exploration strategy, as implemented in Adam LMCDQN, yields superior efficiency in discovering optimal trajectories compared to baseline methods in the context of ultrasound guidance. To the best of our knowledge, this work marks the first deployment of this exploration strategy with real-world data and represents the first RL-based application in ultrasound guidance for bladder assessment.

  • We introduce a novel domain-specific reward function that leverages bladder’s anatomical information to guide RL-based navigation explicitly.

Fig. 1
figure 1

An overview of the presented method for navigation an ultrasound probe . At each time step, a RL model, specifically a deep Q network, receives the current ultrasound image as d states, along with the corresponding e reward from the b bladder simulation environment. The optimal movement action is selected from the c action space based on the maximum output Q value. The action space encompasses both translation and tilt, where the details for different settings are described in.

Full size image

Related work

Automated ultrasound guidance

Deep learning has emerged as a prominent technique in image analysis, with numerous studies exploring its application to detect optimal views in 2D ultrasound image sequences. Convolutional neural networks (CNNs), in particular, have been used to find the probe location difference between the current and optimal view images5,12. However, these approaches often result in abrupt adjustments rather than smooth and continuous trajectories. Effective ultrasound navigation with optimal view requires a sequence of incremental movements based on observations such as ultrasound images and probe position. In this context, reinforcement learning (RL) offers a promising solution, as it can model the continuous decision-making process required for precise probe navigation.

Some studies have explored learning from demonstration for probe navigation12,13. However, obtaining comprehensive and accurate expert demonstrations remains a significant challenge, particularly in clinical ultrasound settings where data can be difficult and costly to acquire. In response, several works have utilized virtual probes within simplified, static simulators to define probe trajectories, aligning more closely with traditional RL development paradigms6. Nevertheless, these approaches fail to capture the complexities of real-world probe navigation, where detailed tissue structures, variations in probe coupling and decoupling, and the presence of artifacts can significantly alter the scenario.

Simulation-based learning using real ultrasound images offers a more reliable and cost-effective approach to training models9,14. Several studies have applied RL within simulated environments constructed from 2D ultrasound images. In Li’s work15, a simulator was developed using 3D ultrasound volumes to model the spinal region. A robotic arm was employed to maneuver a 3D probe, generating synthetic ultrasound images based on the probe’s position. This system achieved a translation and orientation accuracy of 4.91 mm within an intra-patient setting for reaching a target. Similarly, Milletari14 proposed a grid pattern over the chest, using both imaging and a 4-DOF tracking system to create a cardiac simulation. Hase9 also projected a grid onto a volunteer’s spine and used a robotic arm to manipulate the probe. These works predominantly utilized deep Q-networks (DQN) as the RL algorithm due to its simplicity and stability in discrete action spaces. While DQNs9,14 have significantly outperformed supervised learning methods and yielded promising results in ultrasound-guided procedures, they face limitations in terms of state-action space due to the inherent complexity of cardiac and spinal ultrasound images. Moreover, the exploration-exploitation dilemma remains a challenge in vanilla DQN approaches. A recent advancement in addressing this issue is posterior sampling for RL, which maintains a posterior distribution over the model parameters, enabling more efficient exploration and decision-making.

Posterior sampling for reinforcement learning

Randomized strategies in posterior sampling (i.e., Thompson sampling) often outperform deterministic approaches in practice by mitigating premature convergence to suboptimal actions16,17,18. The effectiveness of TS has spurred the development of variants such as Langevin Monte Carlo Thompson Sampling (LMCTS) for varying bandits19.

One notable approach of posterior sampling in RL is Randomized Least-Square Value Iteration (RLSVI), which incorporates random perturbations to approximate posterior distributions with frequentist regret analysis in tabular MDP20. This work has catalyzed subsequent theoretical advancements, with a focus on minimizing worst-case regret in both tabular21,22 and linear settings23,24. From a practical standpoint, several algorithms have emerged from RLSVI to approximate posterior samples of Q-functions in deep RL25,26. With the success of LMCTS, methods upon LMC has been proposed in tabular RL27, linear MDPs with neural network approximations11 and multi-agent RL28,29. While these LMC-based methods have demonstrated superiority in various contexts from both theoretical and empirical perspectives, their application to real-world problems remains largely unexplored, with most efforts focused on standard benchmark settings.

Results

Quantitative evaluation

Table 1 highlights the superior performance of reinforcement learning (RL) methods over supervised classification CNNs. Unlike RL, the supervised approach lacks memory and does not follow the Markov Decision Process (MDP), relying only on features from the current ultrasound image to determine the next action. This often leads to loops, preventing the model from reaching the optimal view. RL, on the other hand, uses the Markov property to estimate rewards and make decisions, enabling it to achieve better results with lower computational complexity and reduced data preparation requirement. The proposed model requires approximately 0.41 GFLOPs per inference, corresponding to an average inference time of approximately 4–7 ms per inference step when processing a single ultrasound frame on a standard CPU in an Android-based application. This computational efficiency supports real-time deployment.

Table 1 Baseline performance comparison in terms of success rate for different methods in transverse and longitudinal views.
Full size table

The Transverse and Longitudinal rows in Table 1 show that Adam LMCDQN with LMC outperforms the vanilla DQN with neural network approximation on real subject data, despite its theoretical guarantees being limited to a linear MDP setting. Additionally, we extend the RL agent’s capabilities by introducing tilting actions, enabling it to capture ultrasound images from different angles. The results for this configuration, labeled as (3D) in Table 2, demonstrate that expanding the action space enhances the agent’s ability to move toward the correct translational direction by accessing a wider range of diverse images. This improvement is evident when comparing (3D) to the non-3D setup in Table 1. A comparison with a classification CNN is not included for (3D) due to the inherent complexity of defining optimal actions in this scenario.

Table 2 Performance (success rate) comparison between RL methods with the access of tilting angles during training.
Full size table

The proposed segmentation-based reward function increased accuracy from 0.69 (using the standard distance reward) to 0.73, as shown in Table 3. These results support the hypothesis that a deeper understanding of the input image enables the agent to make more informed decisions about predicted actions. Given the high cost and time required for domain experts to label over 600 images per subject in a 3D framework, we focused on validating the reward function in a 2D transverse view for practicality.

Table 3 Improvement of segmentation-based reward. (D) represents distance reward function from Problem formulation under Method Section and (S) indicates segmentation reward function from Segmentation-based Reward Function.
Full size table
Fig. 2
figure 2

Navigation sequence in transverse view for subject 0018 (a 33-year-old male). The best view for 0018 is frame 23. The green line represents trajectories that successfully reached the target, while the red lines indicate trajectories where the model failed to reach the target.

Full size image
Fig. 3
figure 3

Navigation sequence in transverse view for subject 0012(a 64-year-old male). The best view of 0012 is 42.The green line represents trajectories that successfully reached the target, while the red lines indicate trajectories where the model failed to reach the target.

Full size image
Fig. 4
figure 4

Navigation sequence in longitudinal view for subject 0014 (a 51-year-old male). The best view of 0014 is 23. The green line represents trajectories that successfully reached the target, while the red lines indicate trajectories where the model failed to reach the target.

Full size image

Qualitative visualization

Typically, the best view in bladder scanning is achieved by positioning the probe just above the pubic bone, along the midline of the body. In our grid projection, this location was most often in the center line of the grids and the first or second rows of the grid. Here, we visually illustrate the navigation paths on three validation subjects generated by our trained policy using one of the random seeds in transverse and longitudinal views: (i) subject 0018, a 33-year-old male, attains the best view in the transverse view at grid 23 in Fig. 2, aligning with the midline, (ii) subject 0012, a 64-year-old male with his best view in the transverse view at grid 42 in Fig. 3, which is located slightly to the left, and (iii) subject 0014, a 51-year-old male with his best view in the longitudinal view at grid 23 in Fig. 4. The arrows in all three figures represent the trajectories originating from various grid points.

In Fig. 2, we observe that the probe can reach to the best view from any grid with \(93 \%\) accuracy. Specifically, when the probe starts at 21 or 22, our RL policy misguides the probe down to gird 12, which is further from the best view. However, the policy quickly rectifies this error, directing the probe toward grid 13 and then 23.

The edge contrast in ultrasound images for bladder measurements tends to be weaker in individuals with higher body mass index (BMI) or those who are older, compared to younger and more muscular individuals. This phenomenon is evident when comparing Figs. 2 and  3. Consequently, the navigation task for Subject 0012 is objectively more challenging than that for Subject 0018. Although the accuracy in this instance drops to \(80 \%\) in subject 0012, most failures occur in the bottom row of Fig. 3, where bladder features are absent. As a result, the trained policy lacks guidance in these areas. It is important to note that, despite the optimal view in this case not aligning with the center line and not being represented in the training set, our RL model is still able to generalize to this unseen scenario.

In the longitudinal orientation, more grid images lacked bladder features, making this view more difficult to train. Figure 4 shows the navigation task for subject 14 in longitudinal orientation. The model effectively guides the probe to grid 23 for all spots in the first three columns. However, it misguides the probe for spots in the last two columns. The figure shows that 9 out of 12 images in the last two columns lacked bladder features, leading to a decrease in performance.

Discussion

In this work, we introduced a RL based ultrasound active guidance for optimal-view localization in bladder imaging. We developed a scalable 3D bladder simulation environment, which can be extended to incorporate additional subject data in the future. This paper is the first work employing LMC exploration in DQN-based method for solving a real-world problem. Our experiments demonstrated the superiority of the proposed approach over traditional DQN and classification baselines. Specifically, we showed that incorporating a more effective exploration strategy consistently improves guidance accuracy across varying task settings. We also found that tilting the probe at the current grid significantly enhances performance by guiding the probe in the correct direction for the next step. Moreover, we proposed a novel segmentation image-based reward function that integrates domain knowledge with a better performance.

Here, we demonstrated the feasibility of the proposed RL-based guidance framework in identifying the optimal bladder imaging plane which is a precursor for getting the accurate bladder volume estimation. Once the optimal plane is identified, the subsequent bladder-volume calculation is well established in the literature. Within the RL framework, the actor network learns a policy that captures the dynamics of the environment through rewards and state–action trajectories explored during training. Once trained, the actor can make informed guidance decisions at deployment from any position (not constrained to the sparse grid positions) in the environment. The learned policy operates directly on incoming ultrasound frames and outputs directional guidance actions (e.g., left/right, up/down, and tilt), which can be communicated to the operator through simple visual cues such as on-screen arrows or textual prompts. A full assessment of end-user impact for this RL-based guidance framework would warrant for an extensive future clinical validation study involving multiple expert reviewers, which is beyond the scope of the present work. Additionally, it would be valuable to explore the use of pre-trained foundation models for segmentation to automatically generate reward functions and scale up the training pipeline. To further enhance clinical applicability, we aim to expand our dataset by including a larger number of subjects with a broader range of pathological conditions.

Methods

Reinforcement learning for probe navigation

This section presents a learning algorithm developed to enable an image-based navigation policy for ultrasound-guided active guidance in bladder scanning applications. We begin by outlining the data collection and prepossessing procedures used to generate a realistic reinforcement learning (RL) simulation environment based on a 3D ultrasound probe. We then formulate the problem of ultrasound active guidance as a Markov Decision Process (MDP). Finally, we introduce an RL algorithm that features a novel reward structure based on image segmentation.

Fig. 5
figure 5

Illustrations of data acquisition process. a Each subject is represented with grids that maintain a fixed spatial distance between each gird, where sonographers collect ultrasound images at each labeled location. The dataset obtained includes ultrasound images capture from two distinct views: b longitudinal and c transverse.

Full size image

Simulation of probe–subject interaction

To create an environment where the RL agent can interact and learn optimal trajectories through trial and error, we acquired ultrasound images and their corresponding probe locations independently of our learning procedure. Figure 5a illustrates our setup for data collection. For each participant in the study, we defined a work area that encompasses a significant portion of the pelvic region where the bladder is located. We drew a 6x5 with a spatial distance of 0.7 inches between each grid point. The grid-based setup was only used to simulate the bladder environment for model development. The model learns to navigate across the bladder in a relative positional manner Solely using ultrasound images, rather than being limited to a grid of fixed dimension. At each grid position, volumetric data were collected using a 3D Matrix transducer (Philips X5-1), which provided access to both longitudinal and transverse views. The 3D acquisition employs electronic beam steering in both the elevational and azimuthal planes with \(3^\circ\) increments, offering a richer range of probe orientations and greater exploration capability for the model.

Since only longitudinal and transverse views are used in clinical bladder scanner applications, there is no need for rotational motion of the probe in our acquisition process. Our acquisition covers the 3 degrees of freedom required for clinical bladder scanner applications: translation along the left-right and top-bottom axes, and tilting probe. We collected data for the first two degrees of freedom by systematically placing the probe at each grid point while ensuring it remained perpendicular to the subject’s abdominal region. This approach effectively captured the necessary translational movement in both longitudinal and transverse views, as illustrated in Fig. 5b and c,as well as the elevational and azimuthal tilts for each grid (Fig. 5d).

Problem formulation

The ultrasound active guidance problem can be formulated as a sequential decision-making task, typically modeled as a Markov Decision Process (MDP) defined by the tuple (\({\mathscr {S}}, {\mathscr {A}}, r, T, P\)). In this formulation, \({\mathscr {S}}\) and \({\mathscr {A}}\) represent the state and action spaces, respectively. The reward function is denoted by r, the set of terminal conditions by T, and \(P(s'|s, a)\) specifies the transition probability. The policy \(\pi = \{\pi _{h}\}_{h \in [H]}\) is a sequences of decision rules, where \(\pi _{h}: {\mathscr {S}} \rightarrow {\mathscr {A}}\) is a deterministic mapping at each step h.

For each \(h\in [H]\), the value function \(V_h^\pi : {\mathscr {S}} \rightarrow {\mathbb {R}}\) is defined as the expected cumulative reward under policy \(\pi\) starting from an arbitrary state \(s_h = s\) at h-th time step. Specifically, it is expressed as:

$$\begin{aligned} V_h^\pi (s) = {\mathbb {E}}_{\pi } [\sum _{h'=h}^H r_{h'} (s_{h'}, a_{h'})|s_h = s] \end{aligned}$$
(1)

Similarly, the action-value function, i.e., Q function, \(Q_h^\pi : {\mathscr {S}} \times {\mathscr {A}} \rightarrow {\mathbb {R}}\), is defined as the expected cumulative reward given the current state and action, with the agent following policy \(\pi\) thereafter. Concretely, it is formulated as:

$$\begin{aligned} Q_h^\pi (s,a) = {\mathbb {E}}_{\pi } [\sum _{h'=h}^H r_{h'} (s_{h'}, a_{h'})|s_h = s, a_h = a] \end{aligned}$$
(2)

In our work, the agent relies exclusively on visual input in the form of ultrasound frames. Therefore, it does not have direct access to the underlying state, which is its exact position and orientation relative to the optimal view. This limitation transforms the problem from a fully observable MDP into a Partially Observable Markov Decision Process (POMDP), where the agent must infer its state solely from observations. Specifically, the observation function O(s) maps each latent state s to a corresponding ultrasound image, requiring the agent to learn a policy over this high-dimensional, image-based observation space.

The transition to a POMDP framework introduces challenges such as partial observability and the need for visual representation learning. To address these, we define the RL framework for probe navigation as follows:

Action We consider two action space configurations in our setup: (i) a basic configuration involving four discrete translational actions—up, down, left, and right—that move the probe to adjacent grid locations; and (ii) an extended configuration that combines translation with incremental tilt control.

In the second configuration, the probe can tilt within a clinically plausible range of \(-30^\circ\) to \(+30^\circ\) relative to the perpendicular orientation. At each step, the agent may apply a discrete tilt adjustment of \(-3^\circ\) (counterclockwise), \(0^\circ\) (no change), or \(+3^\circ\) (clockwise). By combining the four translational directions with the three tilt adjustments, we define a total of twelve discrete actions in action space. This expanded action space enables the agent to explore both spatial positions and angular perspectives, better mimicking real-world ultrasound guidance.

State and observation The true state of the environment is defined by the probe’s position relative to the optimal viewing location in the parallel imaging plane. While the environment state is fully defined by the probe’s grid position and orientation (satisfying the Markov property), it remains hidden from the agent. Instead, the agent receives an observation O(s) in the form of an ultrasound frame and must infer its state accordingly under the POMDP framework.

Reward function To incentivize the agent to reach the optimal view efficiently, we define a distance-based reward function. The grid location corresponding to the best view is designated as the goal. Numerical rewards are assigned based on the agent’s actions relative to this goal. The reward function significantly penalizes unsuccessful trajectories, that is, failure to reach the goal within an episode, with a negative reward (\(-r_{\text {medium}}\)), and discourages movements that increase the distance to the goal with a small penalty (\(-r_{\text {small}}\)). Conversely, it provides positive rewards for actions that reduce the distance (\(r_{\text {small}}\)) and for successfully reaching the goal (\(r_{\text {large}}\)).

Because successful trajectories may occur less frequently than unsuccessful ones, we set \(r_{\text {large}} > r_{\text {medium}}\) to strongly encourage goal-reaching behavior. Additionally, to prevent the agent from moving the probe outside the 6x5 grid, we apply a penalty of \(-r_{\text {small}}\) for such actions and restrict the agent to remain in its current position.

After hyperparameter tuning, we use \(r_{\text {large}} = 1.0\), \(r_{\text {medium}} = 0.25\), and \(r_{\text {small}} = 0.1\). We refer to this setup as the distance reward. An alternative reward function based purely on image is introduced in Segmentation-based Reward Function Section.

3D bladder simulation reconstruction

We reconstruct a 3D bladder simulation environment based on the OpenAI Gym framework30, utilizing real subject data. Specifically, we use a training set of 14 healthy subjects to build the environment and validate both the environment and the RL policy with data from 3 additional subjects. Scans were collected under conditions that ensured adequate probe-skin coupling, providing images with sufficient quality for bladder volume estimation. All participants provided written informed consent prior to participating in data collection. The study was approved by the Institutional Review Board (IRB) of Philips under our System Validation Protocol for Human Subject Scanning (Protocol number 11526) and was conducted in accordance with the ethical standards of the committee and with the Declaration of Helsinki and its later amendments. For each subject, we generate a corresponding transition probability tabular that captures the relationship between observed ultrasound images, rewards, and actions. The results of this study were derived from 17 healthy subjects with limited anatomical variability and may not generalize to populations with atypical anatomy.

Reinforcement learning algorithm

Deep Q-networks (DQNs)10 serves as the backbone for many deep RL algorithms and are widely applied in real-world scenarios due to their scalability, ease of implementation, and effectiveness in tasks with discrete action spaces. A common exploration strategy for DQN is the \(\epsilon\)-greedy method, where the agent selects the action with the highest estimated reward with probability \(1 - \epsilon\), and a random action with probability \(\epsilon\). The parameter \(\epsilon \in (0,1)\) balances exploration and exploitation. However, the \(\epsilon\)-greedy strategy can be inefficient, especially in large action spaces or when \(\epsilon\) is poorly tuned, which is often the case in practical applications. This inefficiency motivates the use of better exploration strategies that adjust to the problem at hand and evolving data to effectively identify the optimal action.

To overcome these limitations, we adopt a randomized exploration strategy using Langevin Monte Carlo (LMC), following the LMC-LSVI framework11. This method employs LMC to approximate the posterior distribution of the Q functions with the following loss function for step h during the k-th episode:

$$\begin{aligned} L_{h}^k({\textbf{w}}_h)&= \textstyle \sum _{\tau =1}^{k-1} [r_h(s_h^\tau , a_h^\tau ) + \max _{a \in {\mathscr {A}}} Q_{h+1}^k(s_{h+1}^\tau , a)-Q({\textbf{w}}_h; \phi (s_h^\tau , a_h^\tau ))]^2 + \lambda \Vert {\textbf{w}}_h\Vert ^2 \end{aligned}$$
(3)

where \(\phi (\cdot , \cdot )\) is a feature representation of the state-action pair, and \(Q({\textbf{w}}_h; \phi (s_h^\tau , a_h^\tau ))\) denotes the parameterized approximation of the Q-function, with \({\textbf{w}}_h\) as the parameter vector and \(\phi (s_h^\tau , a_h^\tau )\) as input, using the trajectories collected over the first \(k-1\) episodes.

At each step h, we perform noisy gradient descent on \(L_h^k(\cdot )\) for \(J_k\) iterations, where \(J_k\) represents the number of updates in episode k. This noisy gradient update incorporates Gaussian noise, inspired by Langevin dynamics. Specifically, the model parameters are updated iteratively, and for iteration \(j=1, \ldots , J_k\), the update rule is given by:

$$\begin{aligned} {\textbf{w}}^{k,j}_{h} = {\textbf{w}}^{k,j-1}_{h} -\eta _{k}\nabla L_{h}^k\big ({\textbf{w}}^{k,j-1}_{h}\big ) + \sqrt{2\eta _{k}\beta _{k}^{-1}}\varvec{\epsilon }_{h}^{k,j} \end{aligned}$$
(4)

where \(L_{h}^k\) is defined in Eq. (3), \(\varvec{\epsilon }_{h}^{k,j}\in {\mathbb {R}}^d\) is a standard Gaussian noise, \(\eta _{k}\) is the learning rate, and \(\beta _{k}\) is the inverse temperature parameter. This exploration strategy is provable with a regret bound \(\tilde{O}(d^{3/2} H^{3/2}\sqrt{T})\) and eventually converges to the performance of posterior sampling in11, where d is the dimension of the feature mapping, H is the planning horizon, and T is the total number of steps. We use \(\tilde{O}(\cdot )\) to ignore poly-logarithmic factors.

In practice, the standard LMC method is replaced by Adam Stochastic Gradient Langevin Dynamics (SGLD) in Adam LMCDQN due to the frequent presence of pathological curvatures and saddle points in deep neural networks. Specifically, the update rule in Eq. (4) is modified to Eq. (5). \(\nabla \tilde{L}_h^k(\omega _h^{k,j-1})\) represents an estimate of the gradient \(\nabla L_h^k(\omega _h^{k,j-1})\) computed from a mini-batch of data sampled from the replay buffer. The parameter \(\alpha\) acts as a bias factor and \(C_1\) is a small constant to prevent division by zero. The bias term \(m_{h}^{k,j-1} \oslash \sqrt{v_h^{k,j-1} + C_1 {{\textbf {1}}}}\) as shown in Eq. (6), can be interpreted as the rescaled momentum, ensuring that the momentum is isotropic near stationary points. Additionally, \(v_h^{k,j}\) in Eq. (7) approximates the true second-moment matrix \({\mathbb {E}}(\nabla \tilde{L}^k_{h}(\omega ^{k,j-1}_{h}) \nabla \tilde{L}^k_{h}(\omega ^{k,j-1}_{h})^\top )\). Note that in these contexts, \(\odot\) and \(\oslash\) denote element-wise vector product and division, respectively. Furthermore, \(\alpha _1\) and \(\alpha _2\) are smoothing factors for the first and second moments of the stochastic gradients.

$$\begin{aligned}&{\textbf{w}}^{k,j}_{h} = {\textbf{w}}^{k,j-1}_{h} -\eta _{k} \nabla \tilde{L}^k_{h}({\textbf{w}}^{k,j-1}_{h}) + \alpha m_{h}^{k,j-1} \oslash \sqrt{v_h^{k,j-1} + C_1 {{\textbf {1}}}} + \sqrt{2\eta _{k} \beta _{k}^{-1}}\epsilon _{h}^{k,j} \end{aligned}$$
(5)
$$\begin{aligned}&m_{h}^{k,j} = \alpha _1 m_{h}^{k,j-1} + (1-\alpha _1)\nabla \tilde{L}^k_{h}({\textbf{w}}^{k,j-1}_{h}) \end{aligned}$$
(6)
$$\begin{aligned}&v_h^{k,j} = \alpha _2 v_h^{k,j-1} + (1-\alpha _2) \nabla \tilde{L}^k_{h}({\textbf{w}}^{k,j-1}_{h}) \odot \nabla \tilde{L}^k_{h}({\textbf{w}}^{k,j-1}_{h}) \end{aligned}$$
(7)
Fig. 6
figure 6

Visualization of the segmentation-based ultrasound reward function. The figure shows how the probe transitions from the current state grid to the next state grid. In this context, \(a_i\) represents the bladder area, and \(d_i\) denotes the distance between the bladder center and the midline of the ultrasound image, where \(i = 1, 2\) corresponds to the current and next state grid positions, respectively.

Full size image

Segmentation-based reward function

Previous studies9,14,15 demonstrated initial success by discretizing grid points for navigation within a discrete action space and utilizing distance-based rewards. However, these approaches did not incorporate task-specific domain knowledge31. To help the agent gain task-specific understanding about the inputs, we propose a new reward mechanism that leverages anatomical information extracted from a bladder segmentation mask. The bladder regions were manually segmented in the ultrasound images by an expert sonographer to ensure accurate and consistent annotations. This approach integrates the bladder’s anatomical context, guiding the agent to focus more effectively on the relevant part of the image. As the objective for bladder volume estimation is to navigate the probe to an optimal view that shows the largest bladder area at the center of the image, we define the segmentation-based reward function as

$$\begin{aligned} r_s = \zeta r_c + (1 - \zeta ) r_a \end{aligned}$$
(8)

where \(r_c\) measures the change in distance between the bladder center and the midline of the ultrasound image from the current state grid to the next state grid, \(r_a\) quantifies the change in bladder area from the current state grid to the next state grid, normalized by the total image area. \(\zeta\) is a tuning hyper-parameter with \(0< \zeta < 1\). Specifically, \(r_c = \frac{d_1 - d_2}{w}\) and \(r_a = \frac{a_2 - a_1}{\text {area}}\), as illustrated in Fig. 6, where both are normalized measurements.

Experiments

In this section, we investigate how improved exploration strategies can enhance the performance of baseline reinforcement learning (RL) algorithms, particularly Deep Q-Networks (DQN), within our discrete action space setting. In addition, we provide additional supervised learning models for comparison. Three different classifiers were tested: MobileNetv232, ResNet-5033, and a customized lightweight convolutional model with 5 CNN layers and 3 fully connected layers. The customized lightweight model demonstrated better performance in our experiments and was therefore used in our results. Since there may not only exist one optimal action in each step, it is relatively hard to model probe navigation task as a supervised learning problem. To have a fair comparison, instead of directly picking one of the optimal actions as the label for training supervised learning9, we divide the action labeling process in two steps: (i) we create a vector between the current grid and target grid with the angle as the label; (ii) we divide the vector in step 1 into x and y directions to map back to our original action space, i.e., up, down, left, right, with the priority of the longer directions. We pre-validate that using our action label can improve the performance against the setting in9. Results for supervised learning model in the following are all based on our proposed action setting.

From RL side, we firstly train Adam LMCDQN and vanilla DQN with only a single perpendicular image for each grid using distance reward introduced in Problem Formulation section under Methods. In other words, the RL agent can only access to the translational actions. Then we increase the action space with additional tilt to see how the flexibility of actions can help generalization. Finally, we demonstrate that using segmentation-based reward can improve performance compared with distance reward. For each task and method, we run 5 random seeds for evaluation.

Implementation details

Framework setup

The learning process comprises a simulation environment and RL algorithm. In addition to the description in 3D Bladder Simulation Reconstruction Section under Methods, we also build an auxiliary matrix for segmentation image-based reward function to directly infer the corresponding reward moving from the current grid to its neighborhood, saving computation cost and training time. Since the maximum values of \(r_c\) and \(r_a\) in the dataset are similar, we set \(\zeta = 0.5\) in \(r_s = \zeta r_c + (1-\zeta )r_a\) to equally weight both reward components. On the other hand, we implemented Adam LMCDQN with a convolutional neural network to take ultrasound images as input upon stable-baselines3 RL library via PyTorch.

Model training

At the start of each episode, a random bladder environment from the training set is initialized, allowing the RL agent to learn the optimal policy through interaction with the specific bladder environment within 20 steps. The episode terminates when the agent either achieves the best view earlier or reaches the maximal permitted step limits. During training, (vanilla) DQN follows \(\epsilon\)-greedy policy and Adam LMCDQN adopts LMC exploration. The hyper-parameters used in the training process are summarized in Table 4. For the supervised baseline approach, the same hyperparameter tuning strategy, including network architecture, optimizer selection, learning rate, and warm-up scheduling, was applied, and the results reported in this study are based on the model showing the best performance.

Table 4 The swept hyper-parameters of DQN and Adam LMCDQN. Note that DQN only uses the top 3 hyper-parameters.
Full size table

Metrics

To evaluate our model, we report the percentage of successful runs, defined as the proportion of test cases where the agent reaches the optimal view within 20 steps. Based on our test dataset, we consider a total of 90 initial states, derived from 3 unseen subjects, each with 6 \(\times\) 5 = 30 grid locations for both transverse and longitudinal directions. Each initial state is treated as a separate test run. The final success rate is computed as the number of successful runs divided by the total number of runs (90) for each scanning direction.