QPSODRL: an improved quantum particle swarm optimization and deep reinforcement learning based intelligent clustering and routing protocol for wireless sensor networks

Abstract

In wireless sensor networks (WSNs), energy-efficient clustering and adaptive routing are key to extending network lifetime and ensuring reliable communication under dynamic conditions. Although numerous metaheuristic- and learning-based schemes have been developed to address these challenges, existing methods may suffer from premature convergence, imbalanced energy utilization, and limited generalization capability when network conditions vary, which restricts their long-term effectiveness. To address these limitations, an intelligent clustering and routing protocol called QPSODRL (Quantum Particle Swarm Optimization and Deep Reinforcement Learning), that integrates an enhanced Quantum Particle Swarm Optimization (QPSO) and Deep Reinforcement Learning (DRL), is proposed in this paper. In the clustering phase based on QPSO, an entropy-guided activation strategy is introduced to dynamically switch between global exploration and local exploitation, based on the network’s energy distribution entropy. Additionally, an elite-guided quantum perturbation mechanism is adopted to drive particles toward promising regions while maintaining diversity, significantly improving convergence quality. In the routing phase, a modified Dueling Double Deep Q-Network (D3QN) is extended with an advantage entropy regularization term, which encourages policy diversity and avoids overfitting, thereby increasing robustness against topology variations. Furthermore, an Enhanced Prioritized Experience Replay (E-PER) strategy is integrated to adjust sampling priorities based on temporal-difference errors, residual energy, and communication cost, accelerating policy convergence in energy-constrained environments. Extensive simulation results demonstrate that QPSODRL outperforms four state-of-the-art protocols in terms of network lifetime, load balancing, throughput, and energy consumption, validating its superiority in optimization accuracy, learning efficiency, and environmental adaptability.

Introduction

Wireless Sensor Networks (WSNs) have emerged as a foundational technology for real-time monitoring and data acquisition in diverse application domains such as environmental sensing, battlefield surveillance, smart agriculture, and industrial automation^1,2. These networks consist of numerous sensor nodes deployed in a distributed manner to cooperatively collect, process, and transmit information to a central base station (BS). However, the practical deployment of WSNs faces critical problems, primarily due to the constrained energy resources and limited computational capabilities of sensor nodes. Frequent communication, redundant data transmission, and imbalanced energy consumption among nodes often lead to premature node failure, reduced data reliability, and shortened network lifetime^3,4. To address these issues, clustering and routing protocol has been widely adopted, wherein the nodes are organized into clusters, and cluster heads (CHs) are responsible for aggregating and forwarding data to the BS^5,6. Nevertheless, designing an energy-efficient and adaptive cluster-based routing protocol considered as a typical NP-hard problem remains a significant research challenge, especially under dynamic network conditions such as varying topology, traffic load, and energy distribution^5,7. However, when addressing this NP-hard problem, existing heuristic and learning-based methods often suffer from premature convergence, inadequate exploration, or limited generalization under dynamic network conditions^8,9. Thus, computational intelligence-based clustering and routing protocols have been extensively studied to tackle the dynamic changes and energy efficiency^10,11.

Various protocols primarily employed single computational intelligence algorithms, such as Fuzzy Logic System (FIS)¹², Particle Swarm Optimization (PSO)³, Genetic Algorithms (GA)¹³, and Artificial Rabbits Optimisation (ARO)⁶, to select CHs and optimize routing paths simultaneously. Among them, PSO has gained wide attention due to its simple implementation and fast convergence¹⁴. Moreover, to improve optimization robustness and global search capability, researchers introduced hybrid protocols that integrate the strengths of multiple computational intelligence techniques, such as whale optimization algorithm (WOA) combined with GA⁸, FLS integrated with barnacles mating optimization (BMO) and sunflower optimization (SFO)¹⁵, hybrid ant colony optimization (ACO), social spider optimization (SSO) and optics-inspired optimization (OIO)¹⁶, artificial bee colony (ABC) combined with ACO¹⁷, grey wolf optimization (GWO) integrated with sea lion optimization (SLO)¹⁸, to balance exploration and exploitation and enhance clustering and routing decisions. Although such hybrid frameworks can improve clustering and routing quality and energy balance, they often require extensive parameter tuning, introduce additional algorithmic complexity, and may exhibit limited adaptability when network topology or energy distribution changes rapidly^19,20. Building on these foundations, quantum-inspired computational intelligence algorithms including quantum annealing algorithm (QAA)²¹, quantum harris hawk optimization algorithm (QHHO)²², quantum gray wolf optimization (QGWO)²³ have demonstrated superior performance due to their enhanced global search ability and probabilistic movement mechanisms. Specifically, QPSO and its variants replaces traditional velocity-position models with a quantum potential well model, enabling particles to explore a broader solution space, making it highly effective in CH selection and energy-aware network organization^24,25. In parallel, reinforcement learning (RL) has emerged as a powerful technique for clustering and routing optimization by enabling agents to learn optimal policies through interactions with the environment^26,27. Classical Q-learning approaches have been used for optimal CHs selection and routing paths determination through continuously updating the Q-table, but they suffer from the curse of dimensionality and scalability issues^28,29. Thus, deep reinforcement learning (DRL) methods such as Deep Q-Networks (DQN)¹¹, Double DQN (DDQN)²⁰, and particularly Dueling Double DQN (D3QN)⁹ have been adopted to overcome these limitations. Nonetheless, existing DRL-based protocols for WSNs may still face issues such as slow convergence, insufficient exploration of critical states, and limited adaptability to dynamic energy and traffic patterns, particularly when reward design or experience sampling is not well tailored to energy-constrained environments. These limitations across single, hybrid, quantum, and learning-based methods highlight the need for a unified and adaptive protocol that combines intelligent clustering with efficient and robust routing.

In this paper, an intelligent clustering and routing protocol named QPSODRL (Quantum Particle Swarm Optimization and Deep Reinforcement Learning) is proposed, which integrates an improved QPSO for clusters formation and an enhanced D3QN for routing optimization. In the clustering phase, a novel entropy-guided activation mechanism is introduced to dynamically switch between global exploration and local exploitation based on the real-time energy distribution entropy of the network. Furthermore, an elite-guided quantum perturbation strategy is employed to guide particle movement toward promising regions, effectively accelerating convergence and avoiding premature stagnation. In the routing phase, the proposed PSODRL utilizes D3QN to learn energy-efficient and adaptive routing strategies. To improve learning robustness and avoid overfitting, an advantage entropy regularization term is added to the value function, encouraging policy diversity. Moreover, a customized enhanced prioritized experience replay (E-PER) mechanism is incorporated to increase the sampling frequency of critical experiences, with priority scores jointly determined by temporal-difference error, node energy, and communication cost. The main contributions of this work are summarized as follows:

• The problem of energy imbalance in CH selection is investigated, which often leads to premature node depletion and unstable clustering structures in WSNs. To address this issue, an entropy-aware clustering strategy is developed to dynamically reflect the global energy distribution of the network, enabling adaptive clustering decisions under heterogeneous and evolving energy conditions.

• The challenge of maintaining robust and adaptive inter-cluster routing is addressed when network topology and residual energy continuously change. A D3QN learning-based routing framework with advantage entropy regularization and enhanced prioritized experience replay is constructed to couple routing decisions with energy-awareness, improving route stability and adaptability while mitigating performance degradation caused by dynamic network states.

• The proposed protocol under multiple network scales and configurations is systematically evaluated, demonstrating that the joint consideration of energy balance, adaptive routing, and learning robustness leads to consistent improvements in network lifetime, load balancing, throughput, and overall energy efficiency compared with state-of-the-art protocols.

The rest of this paper is organized as follows. Section 2 reviews related work on intelligent clustering and routing protocols in WSNs. Section 3 introduces the preliminaries. Section 4 presents the proposed QPSODRL protocol, including the improved QPSO-based clustering and D3QN-based routing mechanisms. Section 5 provides simulation results and performance analysis. Section 6 concludes the paper and discusses future work.

Related work

Clustering and routing protocols have been widely recognized as effective strategies for enhancing energy efficiency and prolonging the operational lifetime of WSNs. However, due to the complexity and dynamic nature of WSN environments, traditional deterministic methods often fail to achieve optimal performance. In response, numerous intelligent clustering and routing protocols have been proposed, leveraging computational intelligence and reinforcement learning to enhance decision-making under uncertainty. This section presents a brief review of recent advancements in this field.

Different clustering and routing protocols based on single computational intelligence algorithms have emerged to address the NP-hard nature of CH selection and routing path optimization in WSNs. In¹², a fuzzy logic-based protocol is proposed that applies Fuzzy C-Means (FCM) clustering at the BS, followed by fuzzy rule-based CH selection considering intra-cluster communication cost and residual energy. Multi-hop routes are established through fuzzy inference, achieving good performance in dense networks with uncertain topologies. Building upon rule-based adaptability, GA-UCR¹³ introduces GA to optimize both CH selection and relay determination. By iteratively applying genetic operations and evaluating candidates based on parameters including residual energy, distance to the BS, inter-cluster spacing, and hop count, GA-UCR effectively searches for energy-efficient configurations. Experiment results demonstrate its enhanced energy balance, scalability, and network longevity. To further mitigate the hot-spot problem, HHO-UCRA³⁰ leverages Harris Hawks Optimization (HHO) for unequal clustering and multi-hop routing. The protocol adapts CH density based on proximity to the BS and incorporates residual energy and node degree into its fitness functions, improving data delivery and convergence. M-PMARO⁶ takes a step forward by applying ARO with multi-objective perturbed learning and mutation strategies. This design enhances exploration and avoids local optima, while routing decisions are refined using both single-hop and multi-hop options based on energy and distance. Among these approaches, the PSO-based protocol NPSOP³ offers a unified model by encoding both CH selection and routing into a single particle. It introduces an adaptive inertia weight mechanism and a composite fitness function considering residual energy and clustering metrics. This joint optimization leads to significant gains in energy efficiency, convergence, and network lifetime compared to traditional two-stage models. Overall, single computational intelligence based protocols provide solid foundations for energy-aware clustering and routing. However, their performance is often constrained by limited adaptability, parameter sensitivity, and local optima issues. So, hybrid intelligent based protocols have been proposed, by integrating the strengths of multiple computational intelligence algorithms, to address these limitations.

In¹⁷, a hybrid clustering and routing protocol is introduced for WSNs, combining ABC and ACO. ABC is applied for CH selection, considering multiple factors including residual energy, number of neighbors, node degree, distance to the BS, and node centrality. These are integrated into a fitness function to identify optimal CHs. For routing, ACO is enhanced to discover energy-efficient paths by evaluating distance, residual energy, and node degree. The proposed protocol significantly reduces energy consumption and prolongs network lifetime under various WSN scenarios. In GWO-MSLO¹⁸, a hybrid clustering and routing protocol is proposed that integrates GWO for CH selection and a Modified SLO (MSLO) algorithm for routing. During the clustering phase, GWO identifies optimal CHs based on parameters such as residual energy, distance, and trust factors. For the routing phase, MSLO constructs secure and energy-efficient routes by considering residual energy, distance, hop count, node degree, and link quality. GWO-MSLO improves throughput, reduces energy consumption, and strengthens data security. In³¹, a hybrid clustering and routing protocol is proposed based on FLS, Adaptive Sailfish Optimization (ASFO), and Improved Elephant Herd Optimization (IEHO). FLS and ASFO are jointly used for clusters formation, considering residual energy, node centrality, and neighbor overlap. IEHO is applied in the routing phase to find energy-efficient and low-latency multi-hop paths by updating elite individuals and discarding the weakest. IEFCRP significantly improves packet delivery, energy efficiency, and network lifetime. In³², a hybrid clustering and routing protocol is proposed that combines the Spider Wasp Optimizer (SWO) with Dijkstra’s algorithm. SWO is used to select optimal CHs considering factors such as energy, distances, cluster members, and communication length. CHs are grouped using K-means, and relay points are added between groups to reduce transmission distance. Dijkstra’s algorithm is then applied to compute shortest multihop paths from CHs to the BS. Simulation results show that the poposed protocol outperforms others in energy efficiency and network lifetime. In QoSCRSI³³, a hybrid protocol is proposed that first employs FLS and glowworm swarm optimization (GSO) to select optimal CHs, followed by a Quantum Salp Swarm optimization Algorithm (QSSA) to establish QoS-aware routing paths. The population is initialized using quantum encoding, and individual solutions are evaluated through a fitness function that integrates residual energy, distance to the base station, and neighbor density. To guide the search toward global optima, a quantum rotation gate is used to update individuals iteratively. Simulation results show that QoSCRSI effectively enhances energy efficiency, prolongs network lifetime, and improves performance in terms of throughput, delay, and communication overhead. Specifically, in QPSOFL²⁴, a QPSO algorithm is developed to determine the optimal CHs according to an innovative fitness function considering energy efficiency and balance, while sobol sequences, levy fight, and Gaussian perturbation mechanisms are embedded into the QPSO to broaden the search space, enhance convergence speed, and escape from local optima. Subsequently, FLS with descriptors residual energy, energy deviation, and relay distance is utilized to find the effective relays for mitigation of the uncertainties. Fuzzy rules derived from expert experiences are provided to make decision. Its superiority is demonstrated by intensive tests in terms of network lifetime, throughput, energy consumption, and scalability. While these hybrid protocols improve overall performance by combining complementary strengths, they often require careful parameter tuning and may still suffer from weak adaptability to dynamic network changes. To address these issues, RL-based clustering and routing protocols have been introduced, enabling autonomous decision-making through continuous interaction with the network environment.

In PSO-QLR³⁴, a routing protocol is proposed that integrates PSO and Q-learning to achieve energy-efficient and congestion-aware communication. In the first phase, based on the CHs selected by LEACH³⁵, PSO is employed to select optimal relay nodes using a fitness function that considers congestion index, energy consumption, and delay cost. In the second phase, Q-learning dynamically refines the data transmission paths by leveraging real-time network feedback. The Q-values are updated based on reward functions that incorporate residual energy and delay sensitivity. PSO-QLR significantly reduces energy consumption and end-to-end delay, while improving throughput, packet delivery ratio, and reducing. In MRP-ICHI³⁶, a hybrid clustering and routing protocol is proposed using an improved Coronavirus Herd Immunity Optimizer (CHIO) for CH selection and Q-learning for multi-hop routing. CHs are selected by using CHIO minimizing a fitness function that considers residual energy and location of the nodes, while incorporating nonlinear decreasing and perturbation strategies to improve convergence and solution diversity. For routing, Q-learning determines optimal paths between CHs and the BS based on a reward function reflecting energy consumption. Although effective in reducing energy use and balancing load, the protocol may face scalability issues due to the Q-table’s dimensionality growth with increasing network size. Accordingly, in EDRP-GTDQN¹⁹, an adaptive routing protocol is proposed that integrates game theory with DRL to optimize energy usage and reduce delays. CHs are selected based on a game-theoretic model considering both node fusion centrality and residual energy, capturing both local and global topological features. Routing is then handled by a DQN, which learns optimal paths from CHs to the BS using rewards derived from energy, distance, and communication delay. A graph convolutional network (GCN) is used to extract topological features for improved routing decisions. The protocol adapts well to network dynamics and enhances performance in terms of energy balance and end-to-end delay. Moreover, in ADDQL-IRHO²⁰, a routing strategy is proposed that combines adaptive double deep Q-learning (DDQL) with federated learning to enhance energy efficiency and scalability in IoT-based WSNs. To address Q-value overestimation, DDQL is adopted, and its parameters are optimized using the Iteration-based Random Hippopotamus Optimizer (IRHO). A double-cluster pairing mechanism is used to balance energy among strong and weak nodes, while federated learning enables decentralized model training without sharing raw data. Simulation results show that ADDQL-IRHO improves performance in energy consumption, delay, and packet delivery ratio. In WOAD3QN-RP⁹, a clustering and routing protocol is proposed that combines WOA for CH selection and D3QN for routing. WOA selects CHs based on residual energy, distance, and communication delay. For routing, D3QN addresses Q-value overestimation via DDQN and reduces redundancy in value estimation by decoupling the Q-function into state-value and advantage-value components. Experimental results show that WOAD3QN-RP achieves super performance in energy efficiency, packet delivery, and network lifetime.

In summary, extensive research has explored intelligent clustering and routing protocols in WSNs, including single computational intelligence based approaches, hybrid metaheuristics, quantum-inspired models, and deep reinforcement learning-based protocols. While single strategies often suffer from limited adaptability and local optima, hybrid methods introduce complexity and parameter sensitivity. Quantum algorithms enhance exploration capabilities, but lack policy learning, while DRL methods offer adaptability but suffer from convergence and scalability problems. Therefore, there remains a critical need for a unified protocol that can combine efficient global optimization with adaptive routing in dynamic environments. The proposed QPSODRL protocol addresses this gap by integrating entropy-aware QPSO for energy-balanced clustering and E-PER driven D3QN for robust, low-delay routing, offering a holistic solution to energy efficiency, scalability, and adaptability in WSNs.

Preliminaries

This section outlines the foundational components of the proposed QPSODRL protocol, including the network model, energy model, and an overview of the QPSO algorithm. These components collectively define the operating environment and energy assumptions used throughout the system design.

Network model

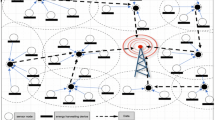
In the proposed QPSODRL protocol, it considers a WSN composed of n sensor nodes $\:WSN=\{{s}_{1},\:{s}_{2},\:...,\:{s}_{n}\}$, randomly distributed in a two-dimensional monitoring area. All nodes are homogeneous, possessing equal initial energy as well as identical sensing, processing, storage, and communication capabilities. The BS is assumed to be static and placed either inside or outside the sensing field. Node mobility is not considered in this work. Each node is uniquely identified by an assigned ID. Clustering is employed to structure the network, with nodes grouped into clusters composed of CHs and CMs. Data is transmitted from CMs to CHs using a TDMA-based schedule, and then forwarded to the BS using a multi-hop strategy. Each transmission cycle is considered a round, comprising intra-cluster and inter-cluster communication phases. At the beginning of each round, the protocol executes the entropy-aware QPSO to determine the CH set and cluster memberships under a predefined CH ratio. The selected CHs keep their roles only during the current round. At the next round, clustering is re-optimized using updated residual energy and topology information, which naturally enables CH rotation and prevents persistent energy depletion of a small subset of nodes. Additionally, the network model includes the following assumptions^3,22:

All nodes are aware of their locations, and Euclidean distance is used for measuring their distances.

• Only symmetric links are considered for communication.

• The BS has unlimited energy, computing, and other resources.

• Transmission power is dynamically adjustable according to communication needs.

The overall network architecture is illustrated in Fig. 1.

Fig. 1

The network architecture of QPSODRL.

Energy model

To model energy consumption during communication, a widely adopted first-order radio energy dissipation model is used in QPSODRL^3,25. In this model, each sensor node expends energy for transmitting and receiving data. The energy consumed for transmitting a bit of data between nodes $\:{s}_{i}$ and $\:{s}_{j}$, separated by distance $\:d$, is calculated as:

$$\:{E}_{Tx}=\left\{\begin{array}{c}\:\:\:{E}_{elec}+{\epsilon\:}_{fs}*{d}^{\theta\:},\:\:if\:d<{d}_{0}\\\:\:\:\:{E}_{elec}+{\epsilon\:}_{mp}*{d}^{\theta\:},\:if\:d\ge\:{d}_{0}\end{array}\right.$$

(1)

Here, $\:{E}_{elec}$ is the energy consumed by transmitter circuitry, $\:{\epsilon\:}_{fs}$ and $\:{\epsilon\:}_{mp}$ are the amplification factors for free space and multipath fading model respectively. The distance threshold $\:{d}_{0}=\sqrt{{\epsilon\:}_{fs}/{\epsilon\:}_{mp}\:}$ determines the model to be used, if $\:d$ is less than $\:{d}_{0}$, then free space model is applied ($\:\theta\:$=2), otherwise multipath fading model is used ($\:\theta\:$=4). The energy required for receiving one bit is expressed as:

$$\:{E}_{Rx}={E}_{elec}$$

(2)

This energy model provides the basis for evaluating energy efficiency in both clustering and routing phases of the QPSODRL protocol.

QPSO algorithm

QPSO is a hybrid computational intelligence algorithm that integrates PSO with quantum mechanics principles to overcome the limitations of standard PSO such as premature convergence, susceptibility to local optima, and difficulties in achieving global search capability under complex environments. In QPSO, the states of particles is represented by the wave function instead of position and velocity in PSO. Morevoer, QPSO makes particles reach any region within the search space according to the probability density function. Specifically, only a position vector in QPSO enables it has powerful optimization ability. Then, each particle in the QPSO can be denoted by a position vector $\:{X}_{i}=({x}_{i,1},\:{x}_{i,2},\:...,\:{x}_{i,D})$, where D is the dimension of the search space. Using the Monte Carlo method, the position of the i-th particle in the $\:d$th dimention is updated according to:

$$\:{x}_{i,d}^{t+1}={p}_{i,d}^{t}\pm\:\alpha\:\times\:\left|{Mbest}_{i}^{t}-{x}_{i,d}^{t}\right|\times\:ln\left[\frac{1}{{\mu\:}_{i,d}^{t}}\right]$$

(3)

Here, $\:\alpha\:$ is the contraction-expansion coefficient that regulates the convergence speed of QPSO. The variable $\:{\mu\:}_{i,d}$ is a random number uniformly distributed in the interval [0, 1], and $\:{p}_{i,d}$ is the local attractor determined by the personal best position $\:{Pbest}_{i}$ and the global best position $\:Gbest$, which formulated as:

$$\:{p}_{i,d}^{t}={\phi\:}_{i,d}^{t}\times\:{Pbest}_{i,d}^{t}+(1-{\phi\:}_{i,d}^{t})\times\:{Gbest}_{i,d}^{t}$$

(4)

where $\:{\phi\:}_{i,d}$ is a uniformly distributed random number in [0,1]. In addition, the average personal best position can be expressed by:

$$\:{Mbest}_{i}^{t}=\frac{{\sum\:}_{j=1}^{D}{Pbest}_{i,d}^{t}}{{N}_{p}}=\frac{{Pbest}_{i,1}^{t}+{Pbest}_{i,2}^{t}+...+{Pbest}_{i,D}^{t}}{{N}_{p}}$$

(5)

where $\:{N}_{p}$ denotes the population size. This quantum behavior allows QPSO to achieve improved exploration and exploitation balance, making it more effective for solving high-dimensional and nonlinear optimization problems^37,38.

The proposed QPSODRL protocol

In this section, the proposed QPSODRL is introduced in detail, which consists a joint optimization framework that tightly couples quantum-behavior-enhanced swarm intelligence with DRL. First, an entropy-aware QPSO-based clustering method leverages global-local adaptive search mechanisms to improve energy-balanced cluster formation. Second, an enhanced D3QN routing scheme integrates advantage entropy regularization and E-PER, enabling intelligent and robust path selection. They work collaboratively to achieve optimal performance in dynamic and energy-constrained environments. The following subsections detail their design and operation.

Cluster construction based on QPSO

In the proposed QPSODRL, a two-level adaptive mechanism is embedded in QPSO to enhance convergence stability and energy awareness. At the global level, the entropy-guided activation strategy dynamically modulates the QPSO contraction coefficient to balance exploration and exploitation based on real-time energy distribution. At the local level, the elite-guided quantum perturbation strategy selectively refines particles that experience stagnation, by combining elite attraction with stochastic Lévy flight. These two strategies act in coordination to adjust overall search behavior and enhance recovery and diversity, jointly improving the robustness and energy-efficiency of clustering.

Particle encoding and initialization

In QPSODRL, each particle in QPSO represents a complete clustering scheme encoded as a real-valued vector:

$$\:{P}_{i}=({x}_{i,1},\:{x}_{i,2},...,\:{x}_{i,d},\:...,{x}_{i,n}),\:i\in\:[0,{n}_{p}]$$

(6)

where $\:n$ is the number of nodes, and $\:{n}_{p}$ is the population size. Each dimension $\:{\text{x}}_{\text{i,d}}\in\text{[1,\:n]}$ represents the CH ID assigned to node $\:{\text{s}}_{\text{d}}$ in the $\:\text{i}$-th particle. Initially, the particles are randomly initialized to ensure population diversity. In each particle, CHs and their corresponding member nodes are implicitly represented, namely nodes that share the same CH ID in their encoding are considered to belong to the same cluster. This direct encoding approach eliminates the need for excessive message exchanges commonly required in conventional clustering methods, thereby significantly improving energy efficiency. Moreover, if a randomly assigned CH ID does not belong to the neighborhood of the current node, the protocol rectifies this by randomly selecting a valid CH from its immediate neighbors. This correction ensures local connectivity and reliability of the clustering structure from the early stage of population initialization. The total number of CHs is constrained by the target CH ratio. After QPSO converges, the best particle is adopted for the current round, and the obtained CH set remains fixed within that round. In the subsequent round, QPSODRL reruns the clustering procedure with updated residual energy, thereby updating the CH set and refreshing CH roles on a per-round basis.

Fitness function design

To evaluate the quality of each particle, a multi-objective fitness function is constructed:

$$\:Fitness={w}_{1}\times\:{RES}_{avg}+{w}_{2}\times\:{H}_{entropy}+{w}_{3}\times\:{DIS}_{avg}$$

(7)

where:

• $\:{RES}_{avg}$is the average residual energy of selected CHs, which can be obtained by:

  $$\:{RES}_{avg}=\frac{{\sum\:}_{i=1}^{m}{RES}_{{ch}_{i}}}{m}$$

  (8)

  Here, $\:m$ denotes the total number of CHs, $\:{RES}_{{ch}_{i}}$ represents the residual energy of $\:{\text{c}\text{h}}_{\text{i}}$.

• $\:{H}_{entropy}$ is the Shannon entropy of energy distribution among CHs:

  $$\:{H}_{entropy}=-\sum\:_{k=1}^{m}{p}_{k}log\left({p}_{k}\right),\:where\:\:{p}_{k}=\frac{{RES}_{k}}{{\sum\:}_{j=1}^{m}{RES}_{j}}$$

  (9)

  Here, $\:{RES}_{k}$ denotes the residual energy of the $\:k$-th CH.

• $\:{DIS}_{avg}$ is the average intra-cluster distance:

  $$\:{DIS}_{avg}=\frac{1}{m}\sum\:_{k=1}^{m}\frac{1}{\left|{C}_{k}\right|}\sum\:_{j\in\:{C}_{k}}{d}_{k,j}$$

  (10)

where $\:{\text{d}}_{\text{k}\text{,}\text{j}}$ is the Euclidean distance between CH $\:\text{k}$ and its member node $\:\text{j}$, and $\:{\text{C}}_{\text{k}}$ is the set of cluster members of CH $\:\text{k}$. Weights $\:{w}_{1}$, $\:{w}_{2}$, $\:{w}_{3}\in\:[0,\:1]$ are normalized such that $\:{w}_{1}+{w}_{2}+{w}_{3}=1$, enabling balanced evaluation of energy efficiency, load uniformity, and communication cost.

Entropy-guided activation strategy

In dynamic WSNs, balancing global exploration and local exploitation is crucial for robust and energy-efficient clustering. To address this, an entropy-guided activation strategy is introduced in QPSODRL to dynamically regulate the search behavior of particles based on the real-time energy distribution entropy of the network. According to Eq. (9), the entropy is calculated at each iteration $\:t$ as $\:{H}_{entropy}^{t}$. Then, normalized by $\:logn$, and obtain:

$$\:{\gamma\:}_{t}=\frac{{H}_{entropy}^{t}}{logm}$$

(11)

This normalized entropy $\:{\gamma\:}_{t}\in\text{(0,\:1]}$ acts as an activation signal. When $\:{\gamma\:}_{t}$ is low, it suggests energy imbalance, thus triggering global exploration. Otherwise, energy is well balanced, favoring local refinement. Instead of switching strategies explicitly, this behavior is embedded into the QPSO update (Eq. (3)) by modulating the contraction-expansion coefficient $\:{\upalpha\:}$:

$$\:{\alpha\:}_{t}={\alpha\:}_{min}+({\alpha\:}_{max}-{\alpha\:}_{min})\times\:{\gamma\:}_{t}$$

(12)

A smaller $\:{\alpha\:}_{t}$ expands the search space, while a larger $\:{\alpha\:}_{t}$ focuses on exploitation. This mechanism serves as a macro-level controller, providing real-time behavioral adaptation across all particles. However, macro-level control alone may be insufficient to maintain search diversity and convergence. Thus, QPSODRL complements this with a micro-level elite-guided strategy, as detailed below.

Elite-guided quantum perturbation

To support the entropy-guided activation with finer control and targeted refinement, an elite-guided quantum perturbation strategy is proposed to enhance local search precision without sacrificing diversity. During clustering, a fixed proportion 20% of particles with the best fitness values is selected as the elite pool³⁹. For each particle $\:{P}_{i}$, the perturbation is performed only when its personal best $\:{Pbest}_{i}$ has stagnated for a predefined number of iterations. The updated position is calculated as:

$$\:{x}_{i,d}^{t+1}={x}_{i,d}^{t}+\eta\:\times\:\left|{x}_{elite,d}^{t}-{x}_{i,d}^{t}\right|+\xi\:\times\:L\left(\lambda\:\right)$$

(13)

where $\:{\text{x}}_{\text{elite,d}}^{\text{t}}$ is a randomly selected elite in dimension $\:\text{d}$, $\:\eta\:\in\:\left(\text{0,1}\right)$ controls the attraction strength to the elite. $\:\xi\:\times\:L\left(\lambda\:\right)$ introduces quantum-level stochastic perturbation, where $\:L\left(\lambda\:\right)$ is sampled via Lévy flight:

$$L\left( \lambda \right) = \frac{\mu }{{\left| \nu \right|^{{1/\beta }} }},\mu \in N\left( {0,\sigma _{\mu } ^{2} } \right),~\nu \in N\left( {0,\sigma _{\nu } ^{2} } \right) $$

(14)

Usually, $\sigma _{v} = 1$, $\beta = 3/2$⁴⁰. $\:\xi\:\in\:[0.05,\:0.2]$ is the perturbation amplitude used to encourage exploration of the search space. Unlike pure random jumps, this strategy performs biased stochastic movement toward promising regions, while Lévy jumps help escape local optima. Importantly, the decision to apply this perturbation is jointly influenced by the particle’s stagnation history and the entropy signal $\:{\gamma\:}_{t}$ with low entropy implying higher chance to perturb. Thus, the entropy-guided activation strategy acts globally, while the elite-guided perturbation strategy works locally, forming a hierarchical adaptation framework that enables QPSO to adjust search scale based on energy balance (global) and refine promising solutions and escape traps (local). Together, they form a cohesive mechanism that ensures QPSO can effectively handle energy heterogeneity, topological shifts, and convergence challenges in clustering.

Finally, the clustering process terminates when a maximum iteration count is reached. The best CHs and formed clusters are extracted from the optimal particle and used to initialize the routing phase.

Route path determination based on D3QN

After the clustering phase, each CH is responsible for forwarding the aggregated data to the BS. To construct energy-aware and adaptive multi-hop routes from CHs to the BS, an enhanced D3QN is employed in QPSODRL to optimize the routing policy based on DRL. The proposed routing strategy is adaptive in nature. Instead of using a static next-hop rule, QPSODRL makes routing decisions online at each forwarding step based on the current network state. As the residual energy of nodes changes after each communication round and link costs vary with hop choices, the agent continuously re-evaluates candidate next hops and updates its action selection accordingly. This enables the routing policy to dynamically adjust to energy depletion, topology evolution, and varying communication costs, thereby maintaining long-term network sustainability.

Problem formulation

To address the routing problem under energy-constrained and dynamically evolving environments, the route decision task is modeled as a Markov Decision Process (MDP), defined by the tuple <$\:S,\:A,\:P,\:R$>, where S is the state space describing the current network status perceived by each CH, A is the action space specifying the next-hop selection decisions, P is the transition probability which is implicitly learned via experience interaction, R is the reward function reflecting the quality of each routing action. The goal is to enable each CH agent to autonomously determine energy-efficient and low-latency routes to the BS based on observed features and learned policies.

• (1) State space $\:S$.

  Each agent (i.e., CH) observes the local and contextural features to form its state representation $\:{\text{s}}_{\text{i}}^{\text{t}}$ at time step $\:\text{t}$, including both topological and energy-aware information $\:{\text{s}}_{\text{i}}^{\text{t}}=({RES}_{i}^{t},\:{DST}_{i}^{t},\:{DLY}_{i}^{t},\:{TD}_{i}^{t},\:{CE}_{i}^{t})$, where:

  • $\:{RES}_{i}^{t}=\left\{{RES}_{i}^{t}\right\}\:\cup\:\:\left\{{RES}_{j}^{t}\right|\:j\in\:{N}_{chi}\}$: residual energy of $\:{\text{c}\text{h}}_{\text{i}}$ and its neighbor CHs $\:{N}_{chi}$;

  • $\:{DST}_{i}^{t}=\left\{{d}_{i,j}\right|\:j\in\:{N}_{chi}\}\:\cup\:\:\{BS\}$: Euclidean distances to neighbor CHs and the BS;

  • $\:{DLY}_{i}^{t}=\{{d}_{i,j}/spd|\:j\in\:{N}_{chi}\}$: estimated communication delay, where $\:spd$ is the speed of light or medium prapagation constant;

  • $\:{TD}_{i}^{t}={Q}_{i}^{t}$: the temporal-difference (TD) error from previous episodes, stored in experience replay buffer;

  • $\:{CE}_{i}^{t}$: a scalar denoting communication entropy, defined as:

    $$\:{CE}_{i}^{t}=-\sum\:_{j\in\:{N}_{chi}}{p}_{j}^{t}log{p}_{j}^{t},\:\:{p}_{j}^{t}=\frac{{RES}_{j}^{t}}{\sum\:_{k\in\:chi}{RES}_{k}^{t}}$$

    (15)

• (2) Action space $\:A$.

  At each time step $\:\text{t}$, CH $\:i$ selects an action $\:{a}_{i}^{t}$ from its action set $\:{A}_{i}^{t}=\left\{{N}_{chi}\right\}\cup\:\left\{BS\right\}$, each action corresponds to selecting a neighbor CH or the BS as the next-hop relay. The routing agent uses D3QN to predict the Q-value for each possible action:

  $$\:{a}_{i}^{t}=arg\underset{a\in\:{A}_{i}^{t}}{\text{max}}Q({s}_{i}^{t},\:a;\:\theta\:)$$

  (16)

  where $\:\theta\:$ denotes the neural network parameters.

• (3) Reward function $\:R$.

  The reward function is designed to guide the agent toward paths that optimize energy balance, delay, and robustness, which is expressed as:

  $$\:{R}_{i}^{t}={\omega\:}_{1}\times\:{r}_{E}+{\omega\:}_{2}\times\:{r}_{D}+{\omega\:}_{3}\times\:{r}_{PER}$$

  (17)

  where:

  • $\:{r}_{E}=1-\left|\frac{{RES}_{j}^{t}-\stackrel{-}{{RES}_{i}^{t}}}{\stackrel{-}{{RES}_{i}^{t}}}\right|$: pernalizes deviation of selected relay’s residual energy $\:{RES}_{\text{j}}^{\text{t}}$ from neighborhood mean $\:\stackrel{-}{{RES}_{\text{i}}^{\text{t}}}$;

  • $\:{r}_{D}=\frac{1}{1+{d}_{i,j}}$: inversely propotional to the distance to next-hop CH $\:\text{j}$, encouraging short communications;

  • $\:{r}_{PER}$: entropy-regularized priority score, derived from

    $$\:{r}_{PER}=\frac{\left|{TD}_{i}^{t}\right|}{\sum\:_{k}\left|{TD}_{i}^{t}\right|}+\lambda\:\times\:{CE}_{i}^{t}$$

    (18)

    where $\:\lambda\:\in\:\left[\text{0,1}\right]$ adjusts entropy weight. The coefficients $\:{\omega\:}_{1}+{\omega\:}_{2}+{\omega\:}_{3}=1$ control the trade-off between energy, delay, and exploration learning.

Enhanced prioritized experience replay

To improve the learning efficiency, convergence speed, and robustness of D3QN under dynamic environments, an Enhanced Prioritized Experience Replay (E-PER) strategy is introduced. Unlike conventional PER that relies solely on temporal-difference (TD) error to determine the sampling probability of transitions, E-PER incorporates energy-awareness and communication cost into the priority estimation, allowing the agent to focus more on energy-critical and high-impact experiences.

Each transition $\:{e}_{i}^{t}=({s}_{i}^{t},\:{a}_{i}^{t},\:{r}_{i}^{t},\:{s}_{i}^{t+1})$ stored in the experience buffer is assigned a priority score $\:{Pri}_{i}^{t}$, which is defined as:

$$\:{Pr}_{i}^{t}={\rho\:}_{1}\times\:norm\left({TD}_{i}^{t}\right)+{\rho\:}_{2}\times\:(1-norm({E}_{i}^{t}\left)\right)+{\rho\:}_{3}\times\:(1-norm({DLY}_{i}^{t}\left)\right)$$

(19)

where $\:norm(\bullet\:)$ is a min-max normalization function mapping each component to [0, 1], $\:{\rho\:}_{1}+{\rho\:}_{2}+{\rho\:}_{3}=1$, controlling the influence of each factor. Higher $\:{P}_{i}^{t}$ implies the transition is both informative and critical, thus increasing its chance of being sampled. The sampling probability for each transition is defined by:

$$\:{pb}_{i}^{t}=\frac{{({P}_{i}^{t}+\epsilon\:)}^{\beta\:}}{\sum\:_{j}{({P}_{i}^{t}+\epsilon\:)}^{\beta\:}}$$

(20)

where $\:\epsilon\:>0$ prevents zero priority, and $\beta \in [0,1]$ adjusts the degree of prioritization with $\beta = 0$ equivalent to uniform sampling. To correct the bias introduced by prioritized sampling during gradient updates, importance sampling weights are used:

$$\:{w}_{i}^{t}={\left(\frac{1}{\mathcal{D}\times\:{pt}_{i}^{t}}\right)}^{\lambda\:}$$

(21)

where $\:\mathcal{D}$ is the buffer size, $\:\lambda\in\text{[0\:,1]}$ is a factor annealed from 0 to 1 during training. The weights $\:{\text{w}}_{\text{i}}^{\text{t}}$ are normalized and multiplied with the TD error in the loss function to preserve unbiased estimation. After each training, the TD error $\:{TD}_{i}^{t}$ is recalculated as:

$$\:{TD}_{i}^{t}=|{r}_{i}^{t}+{\rm\:Y}\times\:{Q}_{target}({s}_{i}^{t+1},\:arg\underset{a}{\text{max}}({s}_{i}^{t+1},\:a))-Q({s}_{i}^{t},\:{a}_{i}^{t})|$$

(22)

The new priority $\:{Pr}_{i}^{t}$ is then updated accordingly using Eq. (19), ensuring that E-PER always reflects the latest feedback, energy state, and communication environment. The E-PER strategy can focuse learning on energy-critical transitions to prolong network lifetime, guide the agent away from costly or inefficient routes by embedding transmission cost, and maintain diversity and convergence stability by leveraging TD error and IS correction.

D3QN architecture and training process

To optimize routing decisions under dynamic WSN environments, a D3QN is adopted as the backbone of the learning agent. Compared with conventional DQN, D3QN effectively addresses two critical issues Q-value overestimation and representation inefficiency. It separates the estimation of state-value and action advantage, while employing Double Q-learning to reduce overestimation bias. In addition, an advantage entropy regularization term is embedded in the loss to encourage exploration and policy diversity, which is critical for adapting to frequent topology and energy changes in WSNs.

• (1) Network architecture.

The D3QN architecture is dipicted in Fig. 2, which consists of the following key components:

• Input layer: encodes the current CH state $\:{\text{s}}_{\text{t}}$, including CH energy level, load overhead, neighbor residual energy, and communication delay.

• Shared feature extractor: a multi-layer perceptron (MLP) extracts latent features from $\:{\text{s}}_{\text{t}}$.

• Dueling streams: value stream estimates the state value $\:V({s}_{t};\:{\theta\:}_{v})$, and advantage stream estimates the advantage of each action $\:A({s}_{t},\:{a}_{t};\:{\theta\:}_{a})$.

$$\:\text{Q}({s}_{t},\:{a}_{t};\:\theta\:)=V({s}_{t};\:{\theta\:}_{v})+\left(A\right({s}_{t},\:{a}_{t};\:{\theta\:}_{a})-\frac{1}{\left|A\right|}\sum\:_{{a}^{{\prime\:}}}A({s}_{t},\:{a}^{{\prime\:}};\:{\theta\:}_{a}))$$

(23)

• (2) Training objective with advantage entropy regularization.

To avoid overfitting and encourage diverse routing policies, an advantage entropy regularization term is introduced into the loss function:

$$\:\mathcal{L}\left(\theta\:\right)={E}_{(s,a,r,{s}^{{\prime\:}})\sim\:D}\left[{({y}_{t}-Q({s}_{t},{a}_{t};\:\theta\:\left)\right)}^{2}\right]+{\lambda\:}_{ent}\times\:\mathcal{H}\left(A\right({s}_{t},\:\bullet\:\left)\right)$$

(24)

Where $\:{y}_{t}={r}_{t}+\gamma\:\times\:Q({s}_{t+1},\:ar\text{g}\underset{{\text{a}}^{{\prime\:}}}{\text{max}}\text{Q}\text{(}{\text{s}}_{\text{t}\text{+1}}\text{,\:}{\text{a}}^{{\prime\:}}\text{;\:}\theta\text{);\:}{\theta\:}^{{\prime\:}}\text{)}$is the double Q-learning target, $\:\text{H}\text{(}\text{A}\text{)=-}{\sum\:}_{\text{a}\in\text{A}}\pi\text{(}\text{a}\text{|}{\text{s}}_{\text{t}}\text{)}\text{log}\pi\text{(}\text{a}\text{|}{\text{s}}_{\text{t}}\text{)}$ is the entropy of advantage-based action distribution, and $\:{\lambda}_{\text{ent}}$ is a regularization coefficient. This entropy term penalizes highly peaked action distributions, encouraging exploration and mitigating premature convergence in highly dynamic topologies.

• (3) Training procedure.

For adaptively training, the routing agent is trained in an episodic manner. In each episode, nodes are randomly deployed and the environment evolves as energy is consumed by transmissions and receptions. The state is constructed using time-varying features, so that the agent observes changing conditions across rounds. The reward is used to favor energy-efficient forwarding while penalizing excessive communication cost and premature energy depletion, encouraging a policy that remains effective under evolving network states. Moreover, the proposed E-PER mechanism prioritizes sampling of transitions with high TD-error and energy-critical conditions, and advantage entropy regularization further stabilizes learning in dynamic topologies. The D3QN agent is trained using the following steps:

• 1. Initialize the evaluation network $Q(s,a;\theta )$ and target network $\:\text{Q}\text{(}\text{s,a}\text{;}{\theta\:}^{{\prime\:}}\text{)}$ with random weights, and experience buffer $\:\mathcal{D}$;

• 2. For each training episode:

• 3. For each CH node, observe state $\:{s}_{t}$;

• 4. With probability $\:{\upepsilon\:}$, select a random action $\:{a}_{t}$ (relay CH or BS), else choose:

• 5.
  $$\:{a}_{t}=arg\underset{a}{\text{max}}Q({s}_{t},\:a;\theta\:)$$

  (25)

• 6. Execute $\:{\text{a}}_{\text{t}}$, receive reward $\:{\text{r}}_{\text{t}}$, and observe $\:{\text{s}}_{\text{t}\text{+1}}$;

• 7. Store ($\:{s}_{t},\:{a}_{t},\:{r}_{t},\:{s}_{t+1}$) in buffer $\:\mathcal{D}$, and compute TD-error and priority score using E-PER (Eq. (19)).

• 8. Sample a mini-batch from $\:\mathcal{D}$ based on priority $\:{\text{p}}_{\text{i}}$, compute loss using Eq. (24), and perform gradient descent on $\:\theta\:$;

• 9. Every $\:C$ steps, update the target network: $\:{\theta\:}^{{\prime\:}}\leftarrow\:\theta\:$;

• 10. End for

• 11. Repeat until convergence or maximum training episodes reached.

• 12. Routing inference.

  After training, each CH selects its next-hop relay (neighbor CH or BS) by executing:

  $$\:{a}_{t}^{*}=arg\underset{a}{\text{max}}Q({s}_{t},\:a;\theta\:)$$

  (26)

Fig. 2

The structure of D3QN with E-PER.

This ensures that each routing decision is energy-aware, adaptive to real-time states, and guided by long-term optimization via D3QN. This structured D3QN training, enhanced by AER and E-PER, ensures that routing policies are not only accurate and stable, but also capable of adapting to dynamic WSN conditions such as fluctuating energy, node density, and communication delays.

Routing execution

Once the D3QN routing model is trained using the proposed learning framework, each CH employs the trained policy to make real-time routing decisions in a fully distributed and adaptive manner. This is referred to as the routing execution stage and influences packet forwarding efficiency, energy consumption, and network longevity.

• (1) Real-time state acquisition.

  At the beginning of each round, every CH $\:i$ locally observes its current routing state $\:{s}_{i}^{t}$, which includes its own residual energy $\:{RES}_{i}^{t}$, the average residual energy of its one-hop neighbor CHs, the number of active neighbors, the estimated communication delay to each neighbor and the BS. This ensures that the agent has a compact but informative state representation, enabling fast and reliable decision-making.

• (2) Action selection based on trained D3QN.

  Given the observed state $\:{s}_{i}^{t}$, the CH uses the trained D3QN model to select the optimal next-hop relay $\:{a}_{t}^{\text{*}}$ according to:

  $$\:{a}_{t}^{\text{*}}=arg\underset{a\in\:{\mathcal{A}}_{i}}{\text{max}}Q({s}_{t}^{i},\:a;\theta\:)$$

  (27)

  Here, $\:{\mathcal{A}}_{i}$ is the available set of next-hop candidates for CH $\:i$. The selected action maximizes the estimated long-term utility by balancing energy efficiency, delay, and residual energy awareness, as encoded in the learned Q-values.

• (3) Data Packet Forwarding and Monitoring.

  After selecting the next-hop node, the data packet is forwarded to the selected CH or the BS. Penalization occurs by adjusting the TD target to reflect bad rewards, which lowers future Q estimates for bad actions. This interaction loop ensures that the routing agent remains responsive to runtime feedback even after the training phase.

• (4) Adaptability under dynamic conditions.

  Although the D3QN model is trained offline or semi-online, the routing decisions made during execution are fully adaptive, because the input state $\:{s}_{i}^{t}$ is updated in real time, the Q-network has learned generalized policies under varying conditions due to advantage entropy regularization and E-PER, new topological changes are inherently captured via updated local observations. As a result, QPSODRL ensures scalable, decentralized, and intelligent routing, even under challenging network dynamics.

Simulation experiments

To validate the effectiveness of the proposed QPSODRL protocol for clustering and routing in WSNs, extensive simulations were carried out and compared with four benchmark protocols NPSOP³, WOAD3QN-RP⁹, QPSOFL²⁴, and MRP-ICHI³⁶. The evaluation emphasizes key performance indicators including network lifetime, packet throughput, load distribution (measured by standard deviation), and overall energy consumption. All the simulations were implemented in MATLAB 2024a and executed on a workstation featuring a 12th Gen Intel^® Core™ i5-12400 F CPU @ 2.50 GHz, 16 GB RAM, and the Windows 11 OS. To comprehensively assess the protocol’s adaptability across different network scales and densities, two deployment configurations were tested. Scenario 1: 100 sensor nodes randomly distributed over a 100 m×100 m area, and Scenario 2: 200 nodes spread across a larger 400 m×400 m region.

Following insights from MRP-ICHI³⁶ highlighting the influence of the CH ratio on protocol behavior, two CH ratios (10% and 5%) were evaluated in both scenarios. In all experiments, the BS was centrally positioned to ensure fair communication distances, and each node started with an identical initial energy. Data aggregation was performed at the CHs to reduce redundancy and minimize transmission cost. To ensure statistical robustness, each experimental configuration was repeated 50 times using the Monte Carlo method, and the averaged results were reported for analysis. The adopted simulaiton settings including static node deployment, centralized BS placement, and energy consumption model are consistent with widely used assumptions in WSN clustering and routing literature, thereby enabling fair benchmarking and reflecting practical WSN deployment scenarios. For the DRL-based routing component, the agent is trained within the simulation environment using multiple episodes. Each episode consists of consecutive communication rounds in which node energies are updated according to the adopted radio energy model, and routing decisions are executed hop-by-hop using the current policy. During training, experience tuples are stored in a replay buffer and the network parameters are updated periodically using mini-batch sampling with E-PER. This training setup exposes the agent to continuously changing network states caused by energy depletion and varying communication costs, which is essential for learning an adaptive routing policy.

This experimental design allows a rigorous assessment of QPSODRL in terms of energy conservation, balanced workload allocation, and network sustainability under varying deployment conditions. A full list of simulation parameters and settings is provided in Table 1, ensuring reproducibility and facilitating comparison with existing state-of-the-art protocols.

Table 1 Simulation settings and network parameters.

Network lifetime

Network lifetime is a critical metric for evaluating the sustainability of WSNs, commonly defined as the total number of operational rounds until a specific portion of nodes deplete their energy. Figure 3; Table 2 compare the network lifetime performance of the proposed QPSODRL protocol against four representative baselines under varying network scales, CH ratios, and BS locations.

QPSODRL consistently demonstrates the longest network lifetime across all test scenarios. This improvement stems from its entropy-guided QPSO clustering, which adaptively adjusts exploration intensity based on energy distribution, thereby avoiding overuse of high-energy nodes and reducing clustering instability, as well as the hot spot effect near the BS. Meanwhile, the D3QN-based routing module, reinforced by advantage entropy regularization, improves policy robustness and responsiveness to topological dynamics, preventing excessive routing loads on specific nodes.

Compared to WOAD3QN-RP, which utilizes D3QN and WOA for routing and clustering respectively, QPSODRL avoids the cost of fixed dual-network architectures and achieves faster convergence via its E-PER. While MRP-ICHI benefits from frequent CH updates based on immunity rules, it incurs high control overhead and degraded stability in later phases. Similarly, NPSOP achieves fast convergence using inertia-weight-tuned PSO, yet suffers from insufficient diversity under topological changes. QPSOFL, although incorporating fuzzy logic, relies on static rule bases that limit adaptability in large-scale or dynamic settings. Thus, in Scenarios #1 and #2, the network lifetime achieved by QPSODRL exceeds WOAD3QN-RP over 14.94%, 11.62%, 17.11%, and 31.65%, QPSOFL over 18.18%, 15.43%, 22.10%, and 23.41%, NPSOP over 9.12%, 11.14%, 23.94%, and 11.29%, and MRP-ICHI over 17.63%, 17.17%, 6.67%, and 12.37%, respectively. Notably, under the more challenging BS-Top configurations, QPSODRL maintains a clear advantage in half-node death round, validating its effectiveness in sustaining long-term network operation through a unified optimization-learning framework that balances energy awareness, adaptability, and robustness.

Fig. 3

Network lifetime comparison of QPSODRL and benchmark protocols.

Table 2 Comparison of half node death in rounds.

Standard deviation of chs’ load

To assess the effectiveness of load distribution among CHs, the standard deviation of CHs’ load is evaluated, which reflects disparities in energy consumption and traffic forwarding. Since all CMs incur similar communication overhead, this metric focuses solely on CHs. A lower standard deviation implies more balanced energy usage and better mitigation of hotspot formation, which contributes to longer network lifespan. The comparison results with the BS located at the center are illustrated in Fig. 4.

Fig. 4

Comparison of CH’s load deviation.

As shown in Fig. 4, QPSODRL consistently achieves the lowest standard deviation across all simulation scenarios, indicating a high level of load balance. This performance stems from the synergy between the entropy-aware QPSO, which promotes globally even CH distribution, and the D3QN routing module, which adaptively shifts traffic away from overloaded nodes. Among the benchmark protocols, WOAD3QN-RP exhibits moderate load balance, thanks to its use of WOA for CH selection. However, during initial learning phases, its D3QN module suffers from Q-value overestimation, leading to imbalanced routing assignments. MRP-ICHI relies on frequent CH role switching based on herd immunity principles, but this often results in unstable traffic patterns and significant fluctuations in load distribution. Although QPSOFL shows reasonable balance in smaller networks, it becomes less effective as network size increases due to fuzzy rule complexity and scalability limitations. NPSOP includes load-related terms in its fitness function, but its dynamic inertia weight strategy sometimes fails to maintain equilibrium under highly dynamic traffic conditions. In contrast, QPSODRL leverages elite-guided diversity in the QPSO stage to prevent clustering around similar nodes, and its D3QN routing with advantage entropy regularization ensures that forwarding decisions are both energy-aware and traffic-sensitive. This dual-stage optimization achieves consistently superior load balancing across varying network sizes and topologies.

Network throughput

Network throughput represents the cumulative number of data packets successfully received by the BS throughout the network’s operational lifetime. This metric reflects the protocol’s effectiveness in ensuring stable and efficient data transmission under varying network conditions. The comparative results with the BS located at the center under two deployment scenarios are presented in Fig. 5.

Fig. 5

Comparison of total network throughput.

As illustrated in Fig. 5, QPSODRL consistently achieves the highest throughput across all experimental settings, surpassing the benchmark protocols in both medium and large-scale networks. This improvement stems from the joint impact of entropy-guided clustering and adaptive routing policy optimization. Compared with WOAD3QN-RP, which relies on a standard D3QN without entropy-based constraints or adaptive experience prioritization, QPSODRL demonstrates better adaptability and throughput consistency. MRP-ICHI suffers from instability due to frequent CH role changes, while QPSOFL is hindered by rule-based decision delays. NPSOP, though PSO-based, lacks learning-based routing refinement and struggles in dynamic scenarios. Quantitatively, in Scenarios #1 and #2, QPSODRL outperforms WOAD3QN-RP by 12.66%, 10.19%, 20.94%, and 33.71%, QPSOFL by 16.46%, 12.45%, 27.07%, and 25.60%, NPSOP by 6.63%, 8.20%, 33.43%, and 13.00%, MRP-ICHI by 16.14%, 13.89%, 10.40%, and 10.96%.

Energy consumption

Energy consumption is a fundamental metric in evaluating the overall energy efficiency and sustainability. It reflects how effectively the protocol minimizes power usage across all nodes throughout the network’s operational lifetime. Figure 6 presents the total energy consumption results of the five protocols under two deployment scenarios with different CH ratios, and various BS locations.

Fig. 6

Comparison of the total energy consumption.

As illustrated in Fig. 6, QPSODRL consistently exhibits the lowest total energy consumption, highlighting its superior energy management capability and robustness under different BS placement conditions, particularly in the BS-Top scenario. This performance is primarily attributed to the protocol’s joint design, which optimizes both the clustering and routing phases through intelligent mechanisms tailored to energy-constrained WSNs. In the clustering stage, the entropy-aware QPSO framework promotes balanced CH selection by adapting to the real-time energy distribution. In the routing stage, QPSODRL’s D3QN module with advantage entropy regularization learns adaptive routing policies that favor energy-efficient paths while maintaining robustness against fluctuating network conditions. Additionally, the E-PER strategy prioritizes learning from critical experiences to accelerate convergence and reduce wasted energy during training. Comparatively, WOAD3QN-RP involves computationally expensive D3QN training and frequent memory updates, which increase early-stage energy use. MRP-ICHI suffers from energy overhead due to frequent CH transitions and immune mechanism-driven control messages. QPSOFL experiences high inference costs per round from complex fuzzy rule evaluation. NPSOP, though efficient in clustering, lacks routing flexibility, often resulting in suboptimal or lengthy paths. This drawback becomes particularly pronounced in the BS-Top scenario, where long-range transmissions cannot be effectively mitigated, leading to rapid energy depletion. In terms of quantitative performance, averaging across different BS locations under Scenarios #1 and #2, QPSODRL reduces total energy consumption by 6.34%, 7.49%, 10.09%, and 15.98% compared to WOAD3QN-RP, 7.39%, 8.00%, 11.64%, and 19.27% over QPSOFL, 4.00%, 5.48%, 6.98%, and 8.94% over NPSOP, and 7.57%, 8.48%, 10.63%, and 16.42% over MRP-ICHI, respectively. Notably, in the challenging BS-Top configuration, QPSODRL exhibits a significantly lower energy consumption growth rate than the steep increases observed in baseline protocols, effectively delaying the network energy saturation point and demonstrating strong robustness against unfavorable BS placement.

Conclusion

This paper presents QPSODRL, a novel clustering and routing protocol designed to enhance energy efficiency, scalability, and adaptability in WSNs. Unlike conventional approaches, QPSODRL unifies a global optimization-driven clustering mechanism with a learning-based routing strategy. Specifically, an entropy-aware QPSO algorithm is introduced for cluster formation, where energy distribution entropy guides the dynamic transition between exploration and exploitation phases, ensuring balanced energy utilization and improved convergence. In addition, an elite-guided quantum perturbation is further incorporated to avoid premature stagnation and promote global diversity during the optimization process. For routing optimization, QPSODRL integrates a D3QN framework enhanced with advantage entropy regularization, which mitigates value overestimation and improves routing robustness in dynamic topologies. To accelerate policy convergence and maintain energy-aware decision-making, an E-PER mechanism is employed, adjusting sampling priorities based on temporal-difference error, residual energy, and communication cost. Together, these innovations enable the protocol to adaptively construct energy-efficient routes while maintaining balanced load distribution across the network. Comprehensive simulation results under varying network scales demonstrate that QPSODRL significantly outperforms four state-of-the-art protocols in terms of network lifetime, throughput, energy consumption, and load balancing, confirming its effectiveness and generalization capability in dynamic environments. It is worth noting that simulation-based evaluation remains the dominant and widely accepted methodology in WSN research, as it enables systematic and reproducible performance assessment under controlled conditions.

Nevertheless, the proposed QPSODRL still has limitations. The current study assumes static sensor nodes and relies on idealized simulation models, which may not fully capture all practical deployment uncertainties. Future work will focus on extending this approach toward more realistic scenarios, including node mobility, heterogeneous hardware constraints, and distributed learning paradigms such as federated reinforcement learning, in order to further reduce communication overhead and enhance scalability and real-world applicability.