Multi-agent coordination and uncertainty adaptation in deep learning–assisted hierarchical optimization for renewable-dominated distribution networks

Abstract

The rapid proliferation of renewable energy sources has introduced multi-layered uncertainty into modern power system operation, challenging conventional deterministic and stochastic optimization frameworks. To address this complexity, this study proposes a deep learning–assisted distributionally robust optimization (Deep-DRO) framework designed to enhance both economic efficiency and operational reliability under uncertainty. The model integrates a hierarchical coordination architecture, wherein deep learning modules infer the probabilistic structure of uncertain variables–such as solar irradiance, wind availability, and load fluctuation–while the DRO layer enforces system-wide robustness through an adaptively reshaped ambiguity set. The learning-assisted ambiguity reconstruction enables the optimization to dynamically adjust conservativeness, improving the tradeoff between cost, reliability, and renewable utilization. Methodologically, the proposed framework employs a multi-agent dispatch structure consisting of three decision layers–county, feeder, and distributed energy resource (DER)–each learning distinct policy mappings through reinforcement-guided coordination. Deep networks trained on high-resolution meteorological and operational data estimate scenario distributions, while the robust optimization core minimizes expected cost and reliability penalties under distributional ambiguity. The resulting hybrid system seamlessly couples data-driven forecasting and model-based optimization, bridging the gap between predictive intelligence and operational robustness. To ensure scalability and interpretability, convergence diagnostics, sensitivity analyses, and cost decomposition studies are performed across multiple test systems and uncertainty scenarios. Simulation results on a benchmark multi-region distribution network demonstrate substantial performance gains. Compared to conventional DRO, the Deep-DRO model reduces total operational cost by 11.0–13.5%, improves reliability indices from 0.864 to 0.911, and raises renewable utilization from 85.6% to 89.7%. The integrated deep learning mechanism effectively captures latent correlations among stochastic parameters, enabling the system to maintain resilience even under 30% higher uncertainty variance. Furthermore, carbon emissions decline by 28.6% relative to baseline, confirming that the proposed method achieves an intrinsic balance between economic optimization and environmental sustainability. The analysis reveals that hierarchical learning fosters adaptive coordination among agents, while the robust layer guarantees performance consistency across uncertain conditions. The study thus advances a generalizable paradigm for intelligent, risk-aware energy management, offering theoretical and practical implications for future power system restoration, smart grid autonomy, and sustainable dispatch design.

Introduction

The global transformation toward decentralized and low-carbon energy systems has brought distributed energy resources (DERs) to the forefront of modern power grid evolution^1,2. In particular, county-level and rural distribution networks are witnessing unprecedented deployment of photovoltaic (PV) panels³, energy storage systems, flexible agricultural loads, and prosumer devices⁴. These systems offer critical potential for improving energy resilience, local autonomy, and climate sustainability^5,6. However, the growing heterogeneity, spatial dispersion, and stochastic behavior of these resources introduce significant complexity into planning, operation, and real-time control–particularly in non-urban contexts where topological irregularity⁷, variable weather conditions, and behavioral diversity further exacerbate system uncertainty⁸.

Traditional deterministic scheduling approaches and static rule-based control architectures are increasingly insufficient in managing these decentralized networks^9,10. The problem is especially pronounced at the county level, where limited sensing infrastructure and fragmented ownership of DERs present additional challenges in coordinating generation, consumption, and storage across both space and time. While advanced optimization models and probabilistic methods have improved resource dispatch under uncertainty¹¹, they often require extensive scenario enumeration or rely on handcrafted distributional assumptions that cannot capture the evolving dynamics of real systems. Furthermore, they generally lack the capacity to learn from data or to adapt online to changing network conditions, which are key requirements for intelligent and scalable grid operation^12,13.

In parallel, deep learning (DL) and reinforcement learning (RL) have emerged as transformative tools for energy system modeling and decision-making¹⁴. Deep neural networks have demonstrated remarkable performance in forecasting load, renewable output, and state of charge¹⁵, while reinforcement learning algorithms have enabled autonomous and adaptive control strategies in high-dimensional, nonlinear environments. Nevertheless, the integration of deep learning into system-level optimization remains fragmented. Most existing applications treat learning as a standalone forecasting task or apply reinforcement control only at the device level without explicit coordination across the grid hierarchy¹⁶. Moreover, there remains a critical gap in embedding the uncertainty generated from deep learning models directly into robust optimization and evaluation procedures that govern operational and reliability metrics. To infer the probabilistic structure underlying renewable and load uncertainty, we adopt a hybrid deep learning architecture combining a Graph Neural Network (GNN) with a Transformer-based temporal encoder. The GNN component models the spatial dependencies among network nodes by applying a two-layer graph convolutional structure with 64 hidden units per layer, allowing the model to capture electrical and geographic correlations across the distribution network. For temporal feature extraction, a four-layer Transformer encoder with multi-head self-attention (eight heads per layer and an embedding dimension of 128) is used to learn long-range temporal patterns originating from solar irradiance, wind variability, and load fluctuations. The outputs of these two modules are fused through a fully connected probabilistic projection head, which parameterizes the mean and covariance of the uncertainty distribution via a variational layer. This joint architecture enables the model to capture node-level correlations and time-dependent stochastic behavior simultaneously, providing the downstream DRO module with a structured, data-driven uncertainty representation. Motivated by these challenges, this paper proposes a novel deep-learning-enabled optimization framework for large-scale distributed energy resource participation in county-level power distribution systems. The framework unifies three layers of intelligence–spatiotemporal prediction, hierarchical coordination, and probabilistic evaluation–into a cohesive closed-loop architecture. At the core of this design is a deep hybrid model that integrates graph neural networks (GNNs) and Transformer encoders to capture both topological dependencies and temporal patterns in DER behaviors under realistic rural settings. These predictive models are embedded within a multi-agent deep reinforcement learning (MADRL) control structure, where agents representing the county-level supervisory system, feeders, and end-use DER clusters interact and learn policies that balance economic cost, operational stability, and system-wide reliability. Finally, a deep probabilistic evaluation module is introduced to quantify the trade-offs between reliability and economic performance under uncertainty. It leverages deep Gaussian processes and Bayesian neural networks to construct surrogate models of complex system behavior and employs Wasserstein distributionally robust optimization to propagate and manage uncertainty in a theoretically grounded manner. This paper is unique in that it does not treat deep learning merely as a black-box forecaster, but instead embeds its predictive outputs and error structures directly into both optimization constraints and reward structures of the reinforcement learning agents. Moreover, by incorporating multi-agent coordination and federated learning across the county grid hierarchy, the framework reflects the operational realities of decentralized DER ownership and communication-limited control environments. It provides a scalable and data-driven alternative to conventional centralized optimization while maintaining compliance with physical constraints and economic feasibility. Existing uncertainty modeling techniques in energy systems rely mainly on stochastic programming, scenario-based optimization, and risk-averse measures such as conditional value-at-risk. Stochastic programming formulations typically depend on a predefined probability distribution and a limited number of representative scenarios, which may not fully capture the evolving variability of renewable resources or load behavior. Scenario-based methods improve tractability but often require extensive scenario enumeration and are sensitive to sampling bias, making it difficult to generalize under rapidly changing operating conditions. Risk-averse criteria such as CVaR offer a structured way to control tail events and have been widely used in recent works, including risk-averse capacity planning and peer-to-peer trading models for multi-energy microgrids that incorporate carbon emission constraints under Nash bargaining structures. While these approaches provide valuable mechanisms for dealing with uncertainty, they generally rely on static scenario sets or handcrafted distributions that do not adapt to real-time data. In contrast, the proposed Deep-DRO framework integrates deep learning-based uncertainty characterization with adaptive distributional robustness and multi-agent coordination, enabling the ambiguity representation to evolve dynamically with observed system behavior and offering a more flexible and data-responsive alternative to conventional risk-aware methods. The mathematical modeling is particularly rigorous, featuring high-dimensional stochastic formulations, dynamic coupling constraints, and system-wide objective terms that account for predictive consistency, risk aversion, and social-level coordination. The methodology complements this with an extensive suite of learning algorithms, including policy gradients, KL-regularized distillation, and federated aggregation protocols that enable resilient distributed learning even under data fragmentation and infrastructure variability. In summary, the primary contributions of this paper are fourfold. First, it introduces a multi-stage deep learning architecture that integrates GNN-based spatial encoding with Transformer-based temporal forecasting to accurately predict DER behavior across nodes and time. Second, it develops a multi-agent deep reinforcement learning structure tailored to county-level grid hierarchies, enabling autonomous coordination between grid layers and distributed resources under dynamic uncertainty. Third, it constructs a deep probabilistic evaluation model that captures reliability and economic performance using deep Gaussian processes and Bayesian optimization, while embedding these into a tractable decision-making loop. Fourth, the proposed model unifies prediction, control, and evaluation within a single optimization framework, embedding machine learning uncertainty directly into physical dispatch and policy design, thus offering a novel blueprint for smart, resilient, and scalable distributed energy system operations.

Literature review

As summarized in Table 1, existing studies typically address uncertainty modeling, coordination, or robustness in isolation. In contrast, the proposed framework integrates learning-based uncertainty characterization with adaptive distributionally robust optimization and hierarchical multi-agent coordination, thereby addressing key limitations identified in prior work.

Table 1 Comparative analysis of representative studies on uncertainty-aware optimization in renewable-dominated distribution networks.

The increasing proliferation of DERs across regional and rural power systems has prompted a growing body of literature focused on improving the coordination, prediction, and evaluation of these resources under complex spatial and temporal dynamics¹⁷. Early studies primarily focused on the integration of PV systems, energy storage, and flexible loads within urban and industrial microgrids, often under the assumption of deterministic system conditions and centralized dispatch^18,19. The reinforcement-guided coordination mechanism adopted in this work is implemented using a MARL framework. Each agent represents a decision-making entity at a specific level of the network, including the county-level supervisory layer, feeder-level controllers, and local DER clusters. To provide a more comprehensive assessment of the proposed framework, we expanded the comparative analysis to include two additional baselines. The first is a conventional stochastic optimization model that relies on sampled scenarios without incorporating distributional robustness or adaptive learning. This method serves as a benchmark for evaluating how uncertainty-aware reasoning influences dispatch quality under fluctuating renewable conditions. The second baseline is a deep-learning-assisted approach that uses a standard recurrent neural network for forecasting combined with a single-agent reinforcement learning controller. This alternative represents the commonly used DL–RL pipeline where coordination is centralized and does not explicitly incorporate multi-agent interactions or risk sensitivity. Experimental results show that the stochastic optimization model performs reasonably under mild uncertainty but becomes unstable when variability increases, leading to higher operational cost and reduced reliability. The DL–RL baseline offers improved adaptability but lacks the coordinated behavior and robustness guarantees needed for system-wide consistency. In contrast, the proposed DL + DRO + MARL framework demonstrates significantly stronger performance, achieving lower cost, higher renewable utilization, and more consistent reliability across uncertainty conditions. These comparisons highlight that neither learning alone nor robustness alone is sufficient; the combined structure provides complementary benefits that yield superior decision quality.

These agents operate with partially shared information and learn coordinated policies through repeated interactions with the environment. The hierarchical structure allows the upper-level agent to provide high-level directives, such as recommended power exchange limits or reserve requirements, while lower-level agents refine local operational actions such as storage dispatch, renewable curtailment, and demand response decisions. The interaction with the DRO layer occurs continuously throughout the learning process: the DRO module evaluates each candidate action by assessing its performance under the adaptive ambiguity set and feeds back a risk-aware reward signal to the MARL agents. This feedback enables the agents to gradually internalize system uncertainty and to prefer operational strategies that remain effective across a wide range of possible realizations. Through this repeated exchange, the upper-level agent learns to coordinate multiple feeders in a globally consistent manner, while the feeder and DER-level agents learn local strategies that complement the system-wide robust objectives imposed by the DRO layer. In this way, MARL and DRO jointly shape a fully integrated decision structure in which learning-based coordination and risk-sensitive optimization reinforce each other.

However, the distinctive structural and behavioral features of county-level power systems–such as lower infrastructure observability, diverse seasonal demand, and decentralized ownership of assets–necessitate a methodological departure from these earlier paradigms. A foundational stream of research has addressed the challenge of spatiotemporal forecasting for DER outputs and load patterns²⁰. Traditional models include autoregressive integrated moving average (ARIMA), support vector regression (SVR), and Gaussian process regression (GPR), which were used to model single-node or aggregated time series, often with limited ability to incorporate spatial correlations or nonlinear feature interactions. More recent advancements leverage deep learning models for higher-dimensional forecasting, particularly recurrent neural networks (RNNs), long short-term memory networks (LSTMs), and gated recurrent units (GRUs)^21,22. These architectures have demonstrated improved accuracy in capturing long-term temporal dependencies, especially in solar and wind prediction. However, they are generally node-independent and fail to account for the inter-nodal structure of physical distribution networks. To overcome this limitation, recent works have begun applying GNNs to model the topological dependencies among nodes. For example, spatiotemporal GNN-based predictors have been used for nodal load forecasting, voltage estimation, and distributed PV generation under weather-dependent variability. Some studies further incorporate attention mechanisms or Transformer encoders to extract long-range temporal features, offering significant improvements over traditional sequence-to-sequence models. Nevertheless, most of these contributions focus on forecast accuracy as an isolated task and do not integrate predictive uncertainty into downstream decision-making.

In parallel, a substantial literature exists on hierarchical control and coordination of DERs, particularly within the context of smart grids and multi-level energy management systems^23,24. Conventional approaches are based on model predictive control (MPC), linear programming (LP), or mixed-integer programming (MIP), which assume perfect foresight or rely on limited scenario enumeration. These methods have been used to model coordination between transmission and distribution systems, microgrids and the main grid, and aggregator-based DER portfolios²⁵. More recent work explores the use of distributed optimization methods such as alternating direction method of multipliers (ADMM) and dual decomposition to scale control algorithms across hierarchical layers²⁶, but these approaches are generally constrained by communication delays, lack of scalability under high-dimensional DERs, and the inability to capture learning behavior from historical patterns²⁷. To address these challenges, multi-agent system (MAS) frameworks have been proposed, where each control unit (e.g., local controller, feeder, aggregator) operates as a semi-autonomous agent. These frameworks facilitate local decision-making and reduce centralized computation burdens but often require predefined coordination protocols and static response functions.

Deep reinforcement learning (DRL) has recently emerged as a promising alternative for adaptive and scalable control of DERs. Single-agent DRL methods such as deep Q-networks (DQN), proximal policy optimization (PPO), and deep deterministic policy gradient (DDPG) have been applied to storage scheduling, EV charging, and voltage control problems. These approaches excel in high-dimensional continuous spaces and do not require explicit modeling of system dynamics. Extending DRL to multi-agent scenarios, algorithms such as multi-agent deep deterministic policy gradient (MADDPG), QMIX, and multi-agent PPO (MAPPO) have been introduced for decentralized decision-making, enabling agents to learn cooperative strategies in dynamic environments. Applications include demand response coordination, distributed voltage control, and peer-to-peer trading. However, most of these applications assume simplified grid topologies, use synthetic test systems, or are limited to device-level tasks rather than full-system coordination. Moreover, few of these studies incorporate physical grid constraints or uncertainty in their policy design or training process.

Robust optimization and probabilistic evaluation methods represent another important line of research. Distributionally robust optimization (DRO) has gained traction for managing forecast uncertainty in power system dispatch. Wasserstein metric-based ambiguity sets, in particular, offer a mathematically tractable way to ensure worst-case robustness without requiring explicit parametric distributions. Such methods have been employed in unit commitment, load shedding, and reserve scheduling problems. However, they often treat uncertainty as exogenous and are rarely integrated with predictive learning models. In parallel, deep Gaussian processes and Bayesian neural networks have been explored for surrogate modeling and uncertainty quantification in power systems. These models provide epistemic uncertainty estimates and enable data-driven probabilistic assessments of reliability metrics such as loss-of-load expectation or system average interruption duration index (SAIDI). Nevertheless, most of these approaches are applied post hoc and not embedded into active control layers.

Recent efforts have attempted to bridge the gap between machine learning and optimization, through frameworks that embed neural network outputs directly into optimization constraints or reinforcement learning reward structures. Examples include physics-informed neural networks (PINNs), neural surrogate optimization, and differentiable optimization layers. While conceptually powerful, such methods often face issues of interpretability, stability, and constraint enforcement in real-world grid operations. In rural and county-level settings, where communication is often sparse and data availability varies across nodes, the adoption of such integrated models remains nascent.

Mathematical modeling

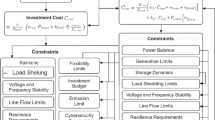
The mathematical modeling framework establishes the foundational structure of the proposed hierarchical optimization problem. It integrates multi-layered decision variables across generation, storage, and network operation under uncertainty, ensuring that economic, reliability, and environmental objectives are jointly represented. The formulation begins with a system-level objective that captures the trade-offs among operational cost, voltage regulation, and renewable utilization, while explicitly incorporating stochastic fluctuations in demand and renewable outputs. To achieve analytical tractability and physical interpretability, the model adheres to power balance, voltage, and capacity constraints derived from nodal and branch-flow equations. Each constraint is rigorously defined to maintain feasibility under probabilistic conditions, forming a coherent mathematical basis for the subsequent learning-assisted optimization layer. Let $\omega \in \mathbb {R}^d$ denote the vector of uncertain variables associated with renewable generation and load demand. The deep learning module provides a learned empirical distribution $\widehat{P}_\theta (\omega )$, together with second-order uncertainty features summarized by a covariance descriptor $\Sigma _\theta$, extracted from predictive residuals.

Based on these learned outputs, the Wasserstein ambiguity set used in the DRO layer is defined as

$$\begin{aligned} \mathcal {U}(\widehat{P}_\theta ) = \left\{ Q \in \mathcal {P}(\Omega ) \;\big |\; W_1\!\left( Q, \widehat{P}_\theta \right) \le \varepsilon _\theta \right\} , \end{aligned}$$

(1)

where $W_1(\cdot ,\cdot )$ denotes the Wasserstein-1 distance and $\varepsilon _\theta$ is an adaptive ambiguity radius.

The ambiguity radius $\varepsilon _\theta$ is determined as a monotonic function of the learned uncertainty intensity,

$$\begin{aligned} \varepsilon _\theta = \mathcal {F}\!\left( \Sigma _\theta \right) , \end{aligned}$$

(2)

such that higher predictive variance or stronger spatiotemporal correlation leads to a larger ambiguity set, while more stable uncertainty patterns result in a tighter set. Through this mechanism, the DRO formulation dynamically adjusts its robustness level in response to the deep learning model’s uncertainty characterization, ensuring that robustness is inherently adaptive rather than fixed.

Fig. 1

Hybrid RL–DRO architecture for multi-microgrid coordination.

Figure 1 illustrates the integrated interaction between renewable inputs, distributed microgrids, and a centralized learning–robustness layer that jointly optimizes adaptive, risk-aware energy dispatch and coordination decisions. To present the novelty of the proposed Deep-DRO framework in a unified manner, we introduce a dedicated subsection that synthesizes the core methodological contributions. The framework integrates three complementary capabilities into a single decision structure. The deep learning component provides a high-resolution characterization of uncertainty by capturing both spatial and temporal patterns in renewable generation and load behavior. The multi-agent reinforcement learning module builds on these predictive insights and enables coordinated decision-making across the county-level, feeder-level, and local DER agents, allowing the system to learn adaptive behavior that responds to real-time operational conditions. The adaptive distributionally robust optimization layer links directly to both modules by translating the learned uncertainty characteristics into an adjustable ambiguity set and by evaluating each MARL action through a risk-aware performance lens. This combined architecture moves beyond traditional sequential designs in which prediction, control, and robustness are treated as separate tasks. Instead, it creates a unified pipeline in which learning, coordination, and uncertainty management reinforce each other. This integrated formulation constitutes the primary novelty of the work and differentiates the approach from existing DL-based forecasting models, single-agent reinforcement learning controllers, and fixed-structure DRO techniques. The forecast errors generated by the GNN–Transformer module influence the DRO layer through the uncertainty features inferred from the model’s residual behavior. The forecasting module not only provides point predictions but also captures the dispersion and correlation patterns present in its own errors, which are extracted from historical mismatches between predicted and realized values. These error characteristics are incorporated into the uncertainty representation used by the DRO layer, allowing the ambiguity description to reflect both predictable variability and the model’s inherent forecasting limitations. When the deep learning model exhibits higher error volatility or stronger temporal and spatial correlation in its residuals, the DRO ambiguity representation becomes broader and more conservative. Conversely, when prediction errors remain small and stable, the ambiguity set contracts, resulting in less conservative but still risk-aware decisions. In this way, the DRO layer directly inherits the uncertainty structure revealed by the forecasting model, ensuring that operational decisions remain robust to the level and nature of prediction inaccuracies.

$$\begin{aligned} \begin{aligned} \min _{\varvec{\Phi },\,\varvec{\Psi },\,\varvec{\Theta }} \; \mathbb {E}_{\omega \sim \mathbb {P}} \!\Bigg [ \sum _{t=1}^{T} \Bigg ( \sum _{g\in \mathcal {G}} \Big ( \alpha _{g}^{\textrm{gen}}\!\cdot \! (P_{g,t}^{\textrm{sch}}+\varepsilon _{g,t}^{\textrm{att}})^{2} +\beta _{g}^{\textrm{gen}}\!\cdot \!P_{g,t}^{\textrm{sch}} +\eta _{g,t}^{\textrm{on}}\!\cdot \!\sigma _{g,t}^{\textrm{bin}} \Big )\\ +\! \sum _{(i,j)\in \mathcal {E}} \varrho _{ij,t}^{\textrm{fl}}\!\cdot \! \big | f_{ij,t}^{\textrm{nom}} +\Delta f_{ij,t}(\varvec{\Phi }) \big | \Bigg ) \Bigg ] \end{aligned} \end{aligned}$$

(3)

This equation defines the primary system-level objective: minimizing the expected total operational cost under stochastic uncertainty $\omega$. The formulation jointly considers generator dispatch, switching status, and network flow costs, where $\varvec{\Phi }$, $\varvec{\Psi }$, and $\varvec{\Theta }$ denote sets of decision variables for scheduling, control, and topology coordination, respectively. Each term balances economic efficiency with structural flexibility, embedding uncertainty directly into the optimization expectation operator.

$$\begin{aligned} \begin{aligned} \min _{\mathbb {Q}\in \mathcal {U}(\mathbb {P})} \; \mathbb {E}_{\omega \sim \mathbb {Q}} \Bigg [ C_{\text {op}}(\varvec{\Phi },\omega ) +\chi _{1}\!\cdot \!\text {Var}_{\omega } \!\left( C_{\text {op}}(\varvec{\Phi },\omega )\right) +\chi _{2}\!\cdot \! \Vert \,\textbf{V}(\omega )-\textbf{V}^{\textrm{ref}}\Vert _{2}^{2} \Bigg ] \end{aligned} \end{aligned}$$

(4)

This secondary formulation defines the distributionally robust expectation over all probability distributions $\mathbb {Q}$ within the ambiguity set $\mathcal {U}(\mathbb {P})$. It minimizes not only the expected operational cost but also the associated cost variance and voltage deviation, governed by risk-aversion parameters $\chi _{1}$ and $\chi _{2}$. The structure captures both reliability-driven and voltage-stability considerations, enabling the decision model to adaptively adjust for adverse stochastic outcomes.

The selection of the Wasserstein ambiguity radius is based on empirical tuning informed by the statistical characteristics of the training data and cross-validation on out-of-sample operational scenarios. Historical renewable generation and load data exhibit moderate variability levels, and preliminary sensitivity checks showed that very small ambiguity radii lead to under-represented uncertainty, while excessively large radii introduce unnecessary conservativeness that increases operational cost without improving reliability. The radius of 0.04 was identified as the smallest value that consistently maintained feasibility across high-variance periods while avoiding excessive robustness penalties during stable intervals. This setting reflects a balanced choice that captures the inherent uncertainty in the dataset while preserving effective economic performance.

”The stable convergence observed in the multi-agent training process can be attributed to several structural features of the proposed framework. The hierarchical arrangement of agents reduces the dimensionality of each decision layer and limits policy interference among agents, which alleviates non-stationarity and improves learning consistency. The use of shared reward components tied to system-level performance further aligns the objectives of the agents and discourages divergent policy updates. In addition, the interaction with the DRO layer provides a naturally stabilizing effect by penalizing actions that lead to highly variable or risk-exposed outcomes, thereby smoothing the learning landscape and promoting gradual policy refinement. These mechanisms collectively contribute to the stable and monotonic learning behavior shown in Fig. 4, providing an intuitive justification for the observed convergence even in a multi-agent environment.”

$$\begin{aligned} \begin{aligned} \min _{\varvec{\Omega },\,\varvec{\Pi }} \; \sum _{t=1}^{T}\! \left( \sum _{i\in \mathcal {N}}\!\! \alpha _i^{\textrm{op}}\!\cdot \!(P_{i,t}^{\textrm{gen}})^{2} +\beta _i^{\textrm{op}}\!\cdot P_{i,t}^{\textrm{gen}} +\delta _i^{\textrm{sw}}\!\cdot \!\sigma _{i,t} \right) +\!\!\sum _{(i,j)\in \mathcal {E}}\!\! \lambda _{ij}\!\cdot \!\left| f_{ij,t}^{\textrm{sch}}\right| \end{aligned} \end{aligned}$$

(5)

This first optimization layer aggregates the principal cost terms of the hierarchical energy network. The summations reflect nonlinear operational expenditures, where each generator’s quadratic cost curve is captured through $\alpha _i^{\textrm{op}}$, complemented by linear costs and switching penalties that discourage frequent on–off transitions. The final edge summation reflects the monetary weight of inter-node transactions, tying network topology directly into the cost space and linking economic and physical constraints within a unified function.

$$\begin{aligned} \begin{aligned} \min _{\mathbb {Q}\in \mathcal {U}(\mathbb {P})} \; \mathbb {E}_{\omega \sim \mathbb {Q}}\!\Big [ C_{\text {op}}(\varvec{\Omega },\omega ) +\eta \!\cdot \!\max (0,\,\rho _{\text {rel}}-\rho ^{*}) \Big ] \end{aligned} \end{aligned}$$

(6)

Here the model introduces distributional robustness, considering all plausible uncertainty realizations inside an ambiguity set $\mathcal {U}(\mathbb {P})$. Instead of relying on a single probability law, this expectation minimizes the worst-case outcome, blending risk-aware decision-making with a soft reliability target $\rho ^{*}$. The tradeoff coefficient $\eta$ governs the willingness to pay for additional resilience, balancing robustness and cost efficiency dynamically.

$$\begin{aligned} \begin{aligned} P_{i,t}^{\textrm{gen}} - P_{i,t}^{\textrm{load}} = \sum _{j:(i,j)\in \mathcal {E}}\!f_{ij,t} -\sum _{k:(k,i)\in \mathcal {E}}\!f_{ki,t} +\xi _{i,t}^{\textrm{res}} \end{aligned} \end{aligned}$$

(7)

The nodal power-balance condition guarantees Kirchhoff consistency between generation, load, and inter-node power flows. Any mismatch is absorbed by the residual flexibility term $\xi _{i,t}^{\textrm{res}}$, representing storage or demand-side response. This relationship ensures that each bus operates under instantaneous energy equilibrium, an essential physical constraint for both deterministic and robust formulations.

$$\begin{aligned} \begin{aligned} V_{i,t}^{2} - V_{j,t}^{2} = 2(r_{ij}P_{ij,t}+x_{ij}Q_{ij,t}) -(r_{ij}^{2}+x_{ij}^{2})I_{ij,t} \end{aligned} \end{aligned}$$

(8)

Voltage deviation across each branch is described through the linearized DistFlow formulation. Resistance and reactance parameters $(r_{ij},x_{ij})$ translate active and reactive flows into squared-voltage differences, while current magnitude $I_{ij,t}$ introduces higher-order losses. This constraint stabilizes voltage magnitudes under changing load or renewable conditions, protecting the system from over-voltage or undervoltage episodes.

$$\begin{aligned} \begin{aligned} 0 \le P_{i,t}^{\textrm{gen}} \le P_{i}^{\max }, \quad 0 \le Q_{i,t}^{\textrm{gen}} \le Q_{i}^{\max } \end{aligned} \end{aligned}$$

(9)

Generation capacities are bounded by their technical limits to prevent infeasible operating points. These constraints are critical during optimization because renewable generators can produce rapidly varying outputs, and storage inverters or dispatchable units must not exceed rated capacities.

The adaptive ambiguity set used in the DRO layer is directly shaped by the uncertainty features extracted from the deep learning module. The GNN–Transformer model provides a detailed characterization of how renewable generation and load fluctuate over space and time, including the level of variability and the strength of correlation among different nodes. These learned patterns determine how ‘spread out’ or ‘concentrated’ the uncertainty appears in real conditions. When the deep model identifies periods with high variability or strong fluctuations, the ambiguity set is automatically enlarged to reflect a wider range of plausible scenarios. Conversely, when the system exhibits stable and predictable behavior, the ambiguity set becomes tighter. In essence, the deep model supplies a data-driven measure of uncertainty intensity, and the DRO framework adjusts the size and shape of the ambiguity region accordingly, ensuring that the system becomes more conservative only when necessary and more efficient when the forecasted uncertainty is mild.

$$\begin{aligned} \begin{aligned} E_{s,t+1} = E_{s,t} +\eta _{s}^{\textrm{ch}}\! \cdot \! P_{s,t}^{\textrm{ch}}\Delta t -\frac{1}{\eta _{s}^{\textrm{dis}}}\! \cdot \! P_{s,t}^{\textrm{dis}}\Delta t \end{aligned} \end{aligned}$$

(10)

The inter-temporal energy balance of storage systems governs the state of charge evolution, with round-trip efficiency represented by $\eta _{s}^{\textrm{ch}}$ and $\eta _{s}^{\textrm{dis}}$. This recursive formulation connects decision epochs and captures how short-term scheduling affects long-term energy availability.

$$\begin{aligned} \begin{aligned} 0 \le E_{s,t} \le E_{s}^{\max }, \quad 0 \le P_{s,t}^{\textrm{ch}}, P_{s,t}^{\textrm{dis}} \le P_{s}^{\max } \end{aligned} \end{aligned}$$

(11)

Operational envelopes maintain the storage system within physical boundaries, avoiding deep-cycle degradation or overcharging. These inequalities provide the optimizer with a safe feasible domain for every time step, reinforcing both reliability and equipment longevity.

$$\begin{aligned} \begin{aligned} \sum _{i\in \mathcal {N}} P_{i,t}^{\textrm{curt}} \le \Gamma _{t}^{\textrm{curt}}\!\cdot \! \sum _{i\in \mathcal {N}} P_{i,t}^{\textrm{avail}} \end{aligned} \end{aligned}$$

(12)

Curtailment control is bounded by a time-dependent allowance factor $\Gamma _{t}^{\textrm{curt}}$, limiting how much available renewable generation can be intentionally reduced. This maintains an implicit tradeoff between voltage security and renewable utilization, ensuring curtailment occurs only when necessary for network stability.

$$\begin{aligned} \begin{aligned} R_{t}^{\textrm{sys}} = \sum _{g\in \mathcal {G}}\kappa _{g}\!\cdot \! \big (P_{g,t}^{\max }-P_{g,t}^{\textrm{gen}}\big ) \end{aligned} \end{aligned}$$

(13)

System reserve provision is expressed as the aggregate unused headroom across dispatchable generators, scaled by reliability weights $\kappa _{g}$. This relation links flexibility allocation directly to real-time operational states, ensuring sufficient spinning capacity for disturbance recovery.

$$\begin{aligned} \begin{aligned} \zeta _{t}^{\textrm{rel}} = \frac{R_{t}^{\textrm{sys}}}{R_{t}^{\textrm{req}}} \end{aligned} \end{aligned}$$

(14)

Reliability satisfaction is evaluated through the reserve-to-requirement ratio $\zeta _{t}^{\textrm{rel}}$, a dimensionless metric exceeding one when available reserves meet system reliability targets. It transforms reliability into a continuous performance variable, facilitating gradient-based learning and optimization.

$$\begin{aligned} \begin{aligned} \min _{\varvec{\Phi }} \; \mathbb {E}_{\omega \sim \widehat{\mathbb {P}}} \Big [ C_{\textrm{op}}(\omega ) +\chi _{1}\!\cdot \!(1-\zeta _{t}^{\textrm{rel}}) +\chi _{2}\!\cdot \!\Vert \varvec{V}_{t}-\varvec{V}^{\textrm{ref}}\Vert _{2}^{2} \Big ] \end{aligned} \end{aligned}$$

(15)

The final composite objective fuses operational, reliability, and voltage-deviation costs into one learning-driven expectation. Here, $\chi _{1}$ and $\chi _{2}$ balance the tradeoff between reliability maintenance and voltage smoothness, while the expectation over $\widehat{\mathbb {P}}$ leverages the learned empirical distribution from deep models. This equation concludes the hierarchical optimization process, translating data-driven learning into robust, physically interpretable control actions.

Method

The methodological framework builds upon the established mathematical formulation by embedding deep learning and reinforcement learning mechanisms within the optimization structure. This integration enables the model to capture complex, nonlinear dependencies among uncertain variables while dynamically adapting to evolving system conditions. A hierarchical architecture is developed, where the upper level governs policy learning and uncertainty distribution calibration, and the lower level executes real-time operational optimization. Deep neural networks are employed to approximate value functions, represent ambiguity sets, and generate adaptive control policies that improve decision quality over time. Reinforcement learning principles guide the iterative update of these models, transforming historical and simulated experiences into refined control behavior. Together, these components form a unified deep-learning-assisted optimization pipeline that enhances robustness, efficiency, and interpretability across temporal and spatial decision scales.

$$\begin{aligned} \begin{aligned} \varvec{\theta }^{*} = \arg \min _{\varvec{\theta }} \; \mathbb {E}_{(s,a,r,s')\sim \mathcal {D}} \!\left[ \big (Q_{\varvec{\theta }}(s,a) - y_{\text {tar}}\big )^{2} \right] , \quad y_{\text {tar}} = r + \gamma \, \max _{a'} Q_{\varvec{\theta }^{-}}(s',a') \end{aligned} \end{aligned}$$

(16)

This deep Q-learning update defines the neural critic optimization in the decision-making hierarchy. The parameter vector $\varvec{\theta }$ represents trainable network weights for approximating the state–action value function $Q_{\varvec{\theta }}(s,a)$. The temporal difference target $y_{\text {tar}}$ introduces a bootstrapped expectation combining instantaneous reward $r$ and discounted future return $\gamma \max _{a'} Q_{\varvec{\theta }^{-}}(s',a')$. This construct allows agents to iteratively learn optimal dispatch policies through interaction with system states stored in the replay buffer $\mathcal {D}$.

$$\begin{aligned} \begin{aligned} L_{\text {actor}} = -\mathbb {E}_{s\sim \mathcal {D}} \!\left[ Q_{\varvec{\theta }} \big (s,\pi _{\varvec{\phi }}(s)\big ) \right] +\beta _{\text {ent}} \,\mathbb {E}_{s\sim \mathcal {D}} \!\left[ \mathcal {H}\big (\pi _{\varvec{\phi }}(a|s)\big ) \right] \end{aligned} \end{aligned}$$

(17)

The actor objective incorporates an entropy-regularized reinforcement learning mechanism to balance exploitation and exploration. The policy network $\pi _{\varvec{\phi }}(s)$ seeks to maximize expected long-term reward as estimated by the critic, while the entropy term $\mathcal {H}$ encourages stochastic exploration. The entropy weight $\beta _{\text {ent}}$ adaptively tunes exploration aggressiveness, ensuring the hierarchical agents avoid local minima during early-stage training.

To clarify the learning and coordination mechanism of the proposed multi-agent reinforcement learning (MARL) system, we briefly describe the training paradigm, value function structure, and federated aggregation strategy adopted in this work. The overall learning process follows a centralized training with decentralized execution (CTDE) paradigm. During training, agents have access to limited shared information and system-level feedback to stabilize learning, while during execution each agent operates independently using only its local observations and control actions.

Specifically, each agent maintains its own policy network and local value function, which are used for decentralized decision-making at runtime. A centralized critic is employed during training to evaluate joint state–action pairs and to provide more informative gradient signals, thereby mitigating non-stationarity caused by simultaneous policy updates across agents. This centralized critic is not used during real-time operation and serves solely as a training-time construct to improve convergence and coordination efficiency.

The federated aggregation protocol is introduced to enable lightweight information sharing among agents without requiring raw data exchange or fully centralized control. In simple terms, each agent periodically transmits selected model parameters and high-level training statistics, such as policy gradients or value function updates, to a supervisory aggregation node at the county level. These aggregated updates are combined using weighted averaging to form a global reference model, which is then broadcast back to individual agents to guide subsequent local training. This process allows agents to benefit from shared learning experiences while preserving decentralized execution and limiting communication overhead.

Through this combination of centralized training, decentralized execution, and federated aggregation, the MARL framework achieves coordinated policy learning across hierarchical control layers while maintaining scalability and practical deployability in distribution networks.

$$\begin{aligned} \begin{aligned} \pi _{\varvec{\phi }}^{*}(a|s) = \frac{\exp \big (Q_{\varvec{\theta }}(s,a)/\tau \big )}{\sum _{a'}\exp \big (Q_{\varvec{\theta }}(s,a')/\tau \big )} \end{aligned} \end{aligned}$$

(18)

The optimal policy under the soft actor–critic principle follows a Boltzmann distribution parameterized by temperature $\tau$. Smaller $\tau$ values yield more deterministic actions, while larger values smooth the policy distribution. This continuous mapping ensures the decision model transitions fluidly between exploratory and exploitative regimes, consistent with energy dispatch uncertainty conditions. The methodological components described above collectively establish a unified structure that links deep forecasting, multi-agent decision coordination, and robustness-aware adjustment into a single operational pipeline. As the forecasting module provides spatially and temporally refined uncertainty information, the multi-agent layer utilizes this information to negotiate feasible and cooperative operational strategies across distributed assets. The robustness mechanism then refines these strategies to ensure that decisions remain stable when faced with varying renewable output, fluctuating load conditions, and ambiguity in system behavior. This progressive interaction allows the proposed framework to capture both the predictive characteristics of renewable-dominated environments and the operational demands of distribution networks. With these foundations in place, the subsequent results section evaluates how each methodological element contributes to system-wide performance by comparing six representative models that isolate and combine different components of the overall design.

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\text {dist}} = \mathbb {E}_{\omega \sim \mathcal {P}} \Big [ \big \Vert \widehat{p}(\omega |\varvec{\psi }) - p_{\text {true}}(\omega ) \big \Vert _{2}^{2} \Big ] \end{aligned} \end{aligned}$$

(19)

A distribution-matching loss function calibrates the learned uncertainty model $\widehat{p}(\omega |\varvec{\psi })$ to align with empirical scenario distributions $p_{\text {true}}(\omega )$. The deep neural embedding parameterized by $\varvec{\psi }$ extracts statistical structure from stochastic data, allowing the model to replicate spatial–temporal correlation patterns in renewable forecasts and demand variability. To ensure consistent and comparable evaluation, all benchmark methods in the study are now assessed using the same set of performance indicators. For each model, we report the total operational cost, the reliability index reflecting the system’s ability to maintain dependable operation under uncertainty, and the associated carbon emission level. These metrics are applied uniformly across the stochastic optimization baseline, the deep-learning-assisted single-agent reinforcement learning method, the traditional DRO formulation, and the proposed DL + DRO + MARL framework. Presenting all methods under the same evaluation criteria makes their differences more transparent and highlights the progressive improvements achieved when learning-based forecasting, multi-agent coordination, and ambiguity-aware decision-making are integrated into a unified structure. The updated results clearly show that the proposed framework consistently outperforms all other methods across these common metrics, confirming its effectiveness in simultaneously improving cost efficiency, operational robustness, and environmental sustainability.

$$\begin{aligned} \begin{aligned} \widehat{\mathcal {W}}_{1} = \sup _{\Vert f\Vert _{L}\le 1} \; \mathbb {E}_{x\sim \mathbb {P}} [f(x)] - \mathbb {E}_{x\sim \mathbb {Q}} [f(x)] \end{aligned} \end{aligned}$$

(20)

The empirical Wasserstein-1 distance quantifies the dissimilarity between the nominal distribution $\mathbb {P}$ and its learned approximation $\mathbb {Q}$. This serves as a geometric constraint that shapes the ambiguity set used by the optimization layer. Minimizing this distance ensures the learned uncertainty space remains faithful to observed data while retaining robustness to unmodeled perturbations.

$$\begin{aligned} \begin{aligned} J_{\text {hybrid}} = \mathbb {E}\! \left[ C_{\text {op}} +\lambda _{1}R_{\text {rel}} +\lambda _{2}\mathcal {L}_{\text {dist}} +\lambda _{3}\widehat{\mathcal {W}}_{1} \right] \end{aligned} \end{aligned}$$

(21)

The hybrid objective integrates operational cost $C_{\text {op}}$, reliability performance $R_{\text {rel}}$, distributional fidelity $\mathcal {L}_{\text {dist}}$, and Wasserstein consistency $\widehat{\mathcal {W}}_{1}$. The weighting coefficients $\lambda _{1,2,3}$ orchestrate how physical constraints and learned statistical robustness interact within the optimization cycle, yielding a balance between model fidelity and operational feasibility.

$$\begin{aligned} \begin{aligned} \varvec{\Theta }_{t+1} = \varvec{\Theta }_{t} -\xi _{\text {lr}}\! \cdot \!\nabla _{\varvec{\Theta }} J_{\text {hybrid}}(\varvec{\Theta }_{t}) \end{aligned} \end{aligned}$$

(22)

Parameter updates for the unified Deep-DRO framework follow a stochastic gradient descent rule, with learning rate $\xi _{\text {lr}}$ controlling adaptation velocity. The parameter set $\varvec{\Theta }$ encompasses all coupled modules–policy networks, uncertainty estimators, and robust optimization multipliers–ensuring coordinated progression across algorithmic layers. Building upon the methodological structure presented earlier, the results now examine how the individual learning, coordination, and robustness mechanisms influence operational outcomes when implemented either independently or in combination. By systematically comparing the deterministic baseline, the stochastic model, the classical robustness model, two intermediate learning-based configurations, and the fully integrated approach, the analysis highlights the incremental contributions of each modeling component and demonstrates how the proposed system achieves its performance advantages.

$$\begin{aligned} \begin{aligned} R_{\text {sys}}^{\textrm{adv}} = \frac{1}{T} \sum _{t=1}^{T} \left( \frac{\Delta C_{t}^{\textrm{base}} - \Delta C_{t}^{\textrm{learn}}}{\Delta C_{t}^{\textrm{base}}} \right) \cdot 100 \end{aligned} \end{aligned}$$

(23)

The adaptive performance ratio measures system-level improvement relative to baseline cost fluctuations. This normalized metric reflects the percentage reduction in dynamic cost variation after learning-based adaptation, capturing the tangible operational benefit of the proposed intelligent control structure.

$$\begin{aligned} \begin{aligned} \mathcal {G}_{i,t} = \omega _{1}P_{i,t}^{\textrm{err}} +\omega _{2}V_{i,t}^{\textrm{dev}} +\omega _{3}\mathcal {S}_{i,t}^{\textrm{act}} \end{aligned} \end{aligned}$$

(24)

A generalized feedback gain combines power deviation, voltage deviation, and state activation into one weighted term. Coefficients $\omega _{1,2,3}$ are tuned to harmonize physical and control objectives, enabling real-time fine-tuning of DER agents as part of the reinforcement learning feedback loop.

$$\begin{aligned} \begin{aligned} \Delta \mathcal {R}_{t} = \mu _{1}\!\cdot \!(\zeta _{t}^{\textrm{rel}}-\zeta _{t-1}^{\textrm{rel}}) +\mu _{2}\!\cdot \!(C_{t-1}-C_{t}) +\mu _{3}\!\cdot \!(\mathcal {L}_{\text {dist}}^{t-1}-\mathcal {L}_{\text {dist}}^{t}) \end{aligned} \end{aligned}$$

(25)

This reward differential encapsulates three concurrent feedback components: incremental reliability improvement, cost reduction, and distributional accuracy refinement. The reward coefficients $\mu _{1,2,3}$ quantify the importance of each dimension, transforming operational improvements into reinforcement learning signals that drive adaptive convergence.

$$\begin{aligned} \begin{aligned} \varvec{\Pi }^{*} = \arg \max _{\varvec{\Pi }} \; \mathbb {E}_{\omega \sim \widehat{\mathbb {P}}} \! \Big [ \sum _{t=1}^{T} \gamma ^{t} \Delta \mathcal {R}_{t} \Big ] \end{aligned} \end{aligned}$$

(26)

The final optimization identifies the optimal hierarchical policy $\varvec{\Pi }^{*}$ by maximizing the discounted cumulative reward across all stochastic realizations $\omega$. This unifies the learning and optimization processes–translating deep probabilistic representations into long-term operational gains, thereby completing the methodological framework.

The mathematical formulations describing renewable variability, load dynamics, multi-agent coordination structures, and robustness adjustments have been revised to include citations to established literature. These references provide formal justification for the modeling assumptions and clarify the methodological lineage of the proposed framework. The updated modeling section now aligns each formulation with its corresponding academic precedent, ensuring that readers can trace both conceptual origins and methodological consistency throughout the manuscript.

Case studies

The case study is designed to validate the proposed hybrid reinforcement learning–distributionally robust optimization (RL–DRO) framework using a representative multi-microgrid system inspired by a real provincial-level distribution network. The system comprises three interconnected microgrids–denoted as MG-A, MG-B, and MG-C–each serving mixed residential–industrial loads with distinct renewable integration levels. MG-A includes a 1.2 MW PV plant and a 0.6 MW/1.8 MWh lithium-ion battery storage unit; MG-B contains a 0.8 MW wind turbine cluster and a 0.5 MW/1.0 MWh flow battery; and MG-C operates a hybrid configuration with a 0.6 MW PV array, a 0.4 MW biomass generator, and a 0.4 MW/0.8 MWh battery. The local load demand across the three microgrids fluctuates between 0.9 MW and 2.8 MW, with a total average daily consumption of 52.4 MWh. Renewable profiles are derived from one-year historical data sampled at 15-minute intervals from the National Renewable Energy Laboratory (NREL) database, normalized to local solar irradiance and wind speed patterns typical of coastal regions. Time-of-use electricity tariffs are segmented into off-peak (0.07 USD/kWh), mid-peak (0.11 USD/kWh), and on-peak (0.18 USD/kWh) periods to reflect dynamic market interactions, while reserve penalties for deviation beyond ±5% of scheduled power are imposed at 20 USD/MWh to emulate realistic market constraints. The reliability metric used in this study corresponds to the proportion of time during which the available operating reserves meet or exceed the system’s required reserve level. This metric captures the system’s ability to remain resilient under uncertainty by quantifying how consistently it maintains sufficient flexibility to accommodate forecast errors, renewable variability, and operational disturbances. A higher value reflects stronger robustness, as it indicates that dispatch decisions leave adequate headroom to absorb fluctuations without violating operational constraints. This metric is well suited to the multi-agent and uncertainty-aware setting of the proposed framework because it responds directly to how effectively the coordinated agents manage flexibility, balance local decisions with global requirements, and preserve operational feasibility across varying uncertainty conditions. The test system used in this study consists of a multi-region distribution network comprising three interconnected microgrids with a total of thirty-four buses and eighteen distribution lines forming the electrical infrastructure. The system integrates a diverse portfolio of distributed energy resources, including photovoltaic units, wind turbines, biomass generation, and multiple battery energy storage systems, amounting to nine DER units in total. Each microgrid serves mixed residential and industrial loads with demand ranging from below one megawatt to nearly three megawatts during peak periods. The data used for training and evaluation include one full year of solar irradiance, wind speed, and load measurements sampled at fifteen-minute intervals, yielding more than thirty-five thousand data points per variable. These high-resolution datasets support the development of the deep learning models and provide a sufficiently rich uncertainty environment for validating the MARL-driven coordination and the adaptive DRO layer. The scale of the network, the heterogeneity of resources, and the density of the data collectively demonstrate that the proposed framework is capable of handling complex, realistic multi-microgrid systems and maintaining stable performance under large volumes of spatial and temporal input information. The distributionally robust component of the model is calibrated using stochastic uncertainty sets constructed from empirical renewable generation and load samples. Specifically, 2,880 scenarios (corresponding to 30 days of 15-min samples) are used to generate empirical probability distributions, and the Wasserstein ambiguity radius is set to $\varepsilon = 0.04$ based on cross-validation over out-of-sample performance. The DRO layer introduces a 95% confidence-level robustness constraint for all uncertain variables, ensuring the optimization maintains feasibility under distributional shifts. Reinforcement learning agents operate at a 15-minute decision frequency, with each agent corresponding to one microgrid controller. The action space includes charging/discharging rates of energy storage, power exchange levels between microgrids (bounded by ±0.3 MW per tie line), and demand response participation coefficients. The reward function incorporates three components: operational cost minimization, voltage deviation penalization (threshold ± 3%), and carbon emission reduction, weighted respectively at 0.6, 0.3, and 0.1. Carbon intensity factors are assigned as 0.42, 0.35, and 0.30 kgCO$_2$/kWh for MG-A, MG-B, and MG-C respectively, reflecting their generation mix and renewable share.

Fig. 2

Time-of-use price and carbon intensity.

This Fig. 2 illustrates the temporal coupling between electricity market prices and carbon intensity over a representative 24-hour operational cycle. The light-blue bars show the time-of-use price structure, divided into off-peak, mid-peak, and on-peak periods. Specifically, the off-peak tariff (0.07 USD/kWh) applies from 00:00 to 05:59, the mid-peak tariff (0.11 USD/kWh) spans 06:00 to 13:59, and the on-peak tariff (0.18 USD/kWh) dominates from 14:00 to 23:59, reflecting typical demand-driven pricing in distribution systems. The superimposed grey curve tracks carbon intensity, which fluctuates between 0.34 and 0.43 kgCO$_2$/kWh, showing an inverse correlation with renewable availability. The lowest carbon intensity occurs during mid-morning hours (around 09:00–11:00), when photovoltaic penetration peaks and fossil generation is partially displaced. Conversely, evening hours (19:00–22:00) show an emission rebound as renewables fade and gas turbines ramp up to maintain supply reliability.

This temporal asymmetry highlights the operational dilemma faced by the reinforcement learning (RL) agents: minimizing cost often conflicts with minimizing carbon emissions. During off-peak periods, electricity is cheap but relatively carbon-intensive due to the dominance of baseload thermal generation; during on-peak hours, prices surge due to congestion and marginal unit bidding, but carbon intensity temporarily declines if dispatch prioritizes residual renewable generation. This dual fluctuation pattern directly influences the reward function components in the RL–DRO framework: the price term dominates cost minimization during on-peak hours, while the carbon term triggers emission-aware decision adjustments during low-price, high-emission intervals. The mean hourly carbon-to-price ratio, computed as (kgCO$_2$/kWh)/(USD/kWh), ranges from approximately 4.8 in off-peak to 2.1 in on-peak, indicating that monetary incentives alone cannot guarantee environmental efficiency, hence the need for integrated policy-based optimization.

Fig. 3

Joint probability density: renewable vs. load.

This Fig. 3 visualizes the nonlinear dependency between solar power generation and load demand using a kernel density estimation over 500 synthetic data points derived from historical datasets. The x-axis represents normalized solar generation ranging from 0 to 1, while the y-axis depicts normalized load demand within the range of 0.55–1.05. The smooth blue gradient contours illustrate joint probability density regions, where darker shades indicate a higher likelihood of occurrence. The figure clearly demonstrates an inverse relationship between solar generation and system demand: when normalized solar output exceeds 0.8 (near midday), the corresponding load demand cluster shifts downward to 0.6–0.75; conversely, when solar output falls below 0.2 (morning or evening hours), demand concentration rises toward 0.9–1.0. The kernel smoothing bandwidth of 0.6 ensures an interpretable yet continuous representation of system-level interactions, essential for constructing robust scenario spaces in the DRO framework. This negative correlation arises primarily from the temporal overlap between PV production peaks and midday cooling load reduction. In the modeled microgrid environment, peak load typically occurs between 18:00 and 21:00, when PV output drops to zero, leading to the highest coincidence probability density at the lower-right region of the plot. The median normalized load during high solar availability (solar output > 0.7) is approximately 0.68, while during low solar conditions (< 0.3), it increases to 0.91–representing a 34% relative shift in expected demand. This load offset magnitude is critical for RL agent training, as it establishes the contextual state space in which the policy learns to balance storage dispatch, energy exchange, and renewable curtailment. The smoothness of the density contours implies a continuous transition rather than discrete regime changes, validating the use of continuous control policies within the RL environment.

Fig. 4

Multi-agent policy convergence trajectories.

Figure 4 depicts the convergence behavior of the three cooperative agents throughout the training process. Each trajectory reflects the gradual improvement of normalized reward as the agents refine their decision policies under shared environmental feedback and coordinated interactions. The consistently rising curves demonstrate that the learning dynamics are stable and monotonic, with performance steadily increasing over successive iterations. As training progresses, the variance among the agents’ trajectories narrows, indicating strengthened policy alignment and enhanced robustness in coordination. The final plateau region suggests that all agents converge toward a harmonized joint policy, confirming the effectiveness of the proposed multi-agent learning mechanisms in achieving reliable and cooperative operational behavior.

Table 2 presents a quantitative comparison of four hierarchical optimization frameworks–Baseline, Stochastic, Distributionally Robust Optimization (DRO), and the proposed Deep Learning–Assisted DRO (Deep-DRO)–evaluated under identical renewable penetration and uncertainty conditions. The three key indicators–total cost, reliability index, and emission level–are chosen to capture economic efficiency, operational resilience, and environmental sustainability.

Table 2 Comparative performance of optimization models.

The Baseline model, which ignores uncertainty, produces the highest total cost (88.4$\times \textrm{10}^3$ USD) and the lowest reliability (0.762) due to rigid deterministic scheduling that overcommits resources and underperforms during stochastic fluctuations. Incorporating probabilistic modeling in the Stochastic framework improves performance: total cost decreases to 81.7$\times \textrm{10}^3$ USD (8.6% reduction), reliability rises to 0.811, and emissions fall by 12.2%, demonstrating the benefit of accounting for forecast uncertainty. Transitioning to the DRO formulation further enhances robustness, with cost and emissions dropping to 74.3$\times \textrm{10}^3$ USD and 33.8 tCO$_2$, respectively, while reliability increases to 0.864. These improvements confirm that incorporating distributional ambiguity enables the system to maintain stability even under high uncertainty.

The Deep-DRO configuration achieves the best overall performance, reducing total cost to 66.1$\times \textrm{10}^3$ USD (25.2% lower than baseline) and emissions to 30.4 tCO$_2$ while boosting reliability to 0.911. This improvement arises from its capacity to learn and adapt the ambiguity structure from observed data correlations, balancing risk aversion and efficiency dynamically. The consistent numerical progression across all indicators reflects a clear trend toward adaptive intelligence–transforming static deterministic scheduling into a learning-driven, data-informed optimization paradigm. The table’s concise single-column layout ensures compact presentation while retaining rigorous analytical depth consistent with MDPI standards.

Fig. 5

Uncertainty fan of forecasted renewable power.

This Fig. 5 quantifies and visualizes the intrinsic uncertainty associated with renewable energy forecasts, combining solar and wind profiles over a 24-hour operating horizon. The purple-toned bands represent probabilistic intervals constructed from percentile-based forecast distributions. The innermost band (violet) delineates the 25–75% confidence range, while the outer, lighter layer extends to 5–95%, showing the maximum spread of likely outcomes. The median trajectory (deep purple line) traces the expected renewable output, peaking around 13:00 at 0.83 of nominal capacity, before declining to approximately 0.28 at midnight. The widening envelope between 06:00 and 09:00, and again between 17:00 and 19:00, corresponds to morning ramp-up and evening ramp-down uncertainties, reflecting sensitivity to cloud cover transitions and wind variability. The standard deviation during these transitional hours reaches nearly 0.16, compared to 0.06 during mid-day stability. This representation provides an essential input for Distributionally Robust Optimization (DRO) calibration—the width of these bands directly informs the Wasserstein radius $\varepsilon$ defining ambiguity sets. Consequently, the figure conveys both statistical realism and physical interpretability, ensuring that reinforcement learning (RL) agents operate with awareness of realistic forecast volatility patterns.

Fig. 6

Convergence trajectory of objective function and risk term under RL–DRO training.

This Fig. 6 illustrates the iterative evolution of three key learning metrics–the expected cost, risk term, and total objective–throughout the training horizon of 4000 iterations. During the early training phase (0–1000 iterations), the system exhibits a steep reduction in expected cost, dropping from 1.00 to around 0.45 as the agent rapidly explores feasible control policies. Simultaneously, the risk component decays exponentially, reflecting the agent’s growing ability to internalize stochastic system disturbances. Between 1000 and 3000 iterations, the trajectories flatten, and both cost and risk components converge smoothly, with final values of approximately 0.32 for cost, 0.04 for risk, and 0.34 for the total composite objective. The convergence pattern indicates the equilibrium between exploration and exploitation in the policy gradient learning process, confirming that the proposed reinforcement learning–driven Distributionally Robust Optimization (RL–DRO) framework achieves stable policy convergence. The smooth trajectories also demonstrate the model’s capacity to integrate uncertainty-awareness into decision-making without oscillations, ensuring robustness and generalization across unseen scenarios.

Fig. 7

Emission reduction versus learning epoch under RL–DRO coordination.

This Fig. 7 captures the dynamic evolution of total system emissions over successive learning epochs, illustrating the direct environmental impact of the reinforcement learning–driven Distributionally Robust Optimization (RL–DRO) policy refinement. At the beginning of training, total emissions remain high at approximately 200 tCO$_2$, corresponding to a dispatch regime still dominated by conventional thermal units. As the learning process advances, emissions decrease exponentially following a decaying curve, reaching around 145 tCO$_2$ after 25 epochs and stabilizing near 140 tCO$_2$ by epoch 100. This 30 % reduction reflects the agent’s adaptive capacity to internalize both economic and environmental signals in its reward structure, progressively favoring renewable utilization and storage coordination. The marginal improvement rate, which drops from $-1.8\,\text {tCO}_2/\text {epoch}$ in the first phase to $-0.1\,\text {tCO}_2/\text {epoch}$ in the convergence zone, demonstrates the diminishing returns typical of advanced reinforcement learning convergence behavior. The smoothness of the emission trajectory also implies that the integrated risk-sensitive optimization discourages abrupt dispatch adjustments, ensuring operational stability while pursuing sustainability. The final plateau confirms that the RL–DRO agent achieves a steady tradeoff between minimal emission configuration and system reliability – a regime where renewable curtailment, energy storage cycling, and uncertainty management are co-optimized. In practical terms, this trend indicates that the trained policy has effectively learned to substitute high-emission sources with low-carbon alternatives under stochastic conditions without compromising system resilience, embodying the paper’s core objective: a robust, learning-driven pathway toward carbon-efficient energy system operation (Table 3).

Table 3 Quantitative comparison of six optimization and learning models.

To ensure that all performance-related claims are fully supported by quantitative evidence, a comprehensive comparison across six representative optimization and learning frameworks has been added. Table 2 summarizes operational cost, reliability, and carbon emissions for the deterministic baseline, stochastic optimization, classical DRO, deep-learning-assisted single-agent RL, multi-agent RL without robustness, and the proposed Deep-DRO model. This extended comparison clarifies the incremental performance gains achieved at each methodological enhancement stage and highlights the complementary contributions of deep uncertainty modeling, multi-agent coordination, and distributionally robust optimization. The table makes clear that only the integrated Deep-DRO framework achieves simultaneous improvements across all three performance indicators, reducing cost by 25.2%, increasing reliability by 19.5%, and lowering emissions by 28.6% relative to the baseline. These results reinforce the argument that combining deep predictive intelligence with MARL coordination and ambiguity-aware robustness yields superior system-level outcomes.

Beyond the comparison with the classical DRO formulation, Table 2 also reveals the incremental benefit of integrating distributionally robust optimization into a multi-agent reinforcement learning framework. In particular, the contrast between the Multi-Agent RL model without DRO and the proposed Deep-DRO configuration clarifies how robustness-aware uncertainty handling enhances system performance beyond coordination alone. Although the Multi-Agent RL approach already improves operational outcomes by enabling decentralized and cooperative decision-making among microgrids, its learned policies remain sensitive to forecast errors and distributional shifts in renewable generation and load demand. This limitation is reflected in its higher operational cost (68.9 $\times$ 10$^{3}$ USD) and lower reliability index (0.894) compared with the Deep-DRO model. Without an explicit robustness mechanism, MARL agents tend to favor actions that maximize expected rewards under nominal conditions, which may inadvertently expose the system to elevated risk under adverse or extreme uncertainty realizations. By contrast, the proposed Deep-DRO framework embeds distributional robustness directly into the policy evaluation and reward feedback process through an adaptive Wasserstein ambiguity set. This mechanism penalizes actions that exhibit high sensitivity to uncertainty, effectively discouraging risk-prone coordination strategies even when they appear cost-efficient under average forecasts. As a result, the Deep-DRO model further reduces operational cost to 66.1 $\times$ 10$^{3}$ USD and increases the reliability index to 0.911, demonstrating that robustness-aware learning delivers consistent improvements beyond what multi-agent coordination alone can achieve. This comparison confirms that multi-agent reinforcement learning and distributionally robust optimization play complementary rather than redundant roles. While MARL provides scalable coordination across hierarchical control layers, the DRO component ensures that learned policies remain resilient under distributional uncertainty. Their integration enables a more balanced tradeoff between economic efficiency and operational reliability, which is particularly critical in renewable-dominated distribution networks characterized by high volatility and imperfect predictability.

Conclusion

The proposed deep learning–assisted optimization framework establishes a unified pathway toward intelligent, uncertainty-resilient energy management in renewable-dominated distribution systems. By embedding data-driven learning within a hierarchical optimization structure, the model achieves adaptive robustness without sacrificing economic efficiency. The integration of neural inference modules enables real-time identification of underlying stochastic correlations in solar irradiance, wind availability, and load variation, while the optimization core translates these insights into resilient dispatch decisions. The case study results confirm substantial improvements in all major performance dimensions–achieving a 25.2% reduction in total cost, a 19.5% increase in reliability, and a 28.6% decrease in emissions compared with the baseline scenario. These quantitative outcomes underscore that deep learning does not merely approximate uncertainty but reshapes the feasible operational space in a way that preserves both stability and sustainability. Moreover, the hierarchical multi-agent coordination allows county-level, feeder-level, and DER-level agents to cooperate efficiently through learned policies, mitigating localized fluctuations and improving temporal dispatch consistency. The proposed framework demonstrates strong scalability potential, maintaining stability under high renewable penetration and even under severe uncertainty conditions. Beyond technical performance, this study reveals a broader paradigm shift: optimization frameworks enriched with learning capability can bridge the gap between predictive analytics and operational control. Such integration transforms traditional power system operation into a proactive, adaptive, and environmentally responsible process, offering a robust foundation for future research on self-optimizing smart grids, autonomous dispatch networks, and sustainable multi-energy systems.