Introduction

Industry accounts for 40% of total final energy use (IEA2023) and generates more than 30% of global CO2 emissions, most of which is related to the energy consumption1,2. Under the Paris Agreement, more and more factories are choosing to increase the proportion of renewable energy supply to form a multi-energy system (MES)3,4. The recent target of tripling the renewable energy capacity as stated at the COP 28 held in the UAE provides a clear indication of the scale and urgency of this integration5.

Research in MES operation primarily focuses on optimizing dispatch strategies, managing system uncertainty, and performing risk analysis6,7. Optimized design of energy supply becomes more complex as the sources become more diverse4,8. There are many studies on the optimization of multi-energy supply systems proposed configuration planning for community-level MES, where the model is described as a linear system and solved based on fixed demand9. The facilities were described as having fixed capacity and cost, and the decision variables determined the number of components selected in the system. The case study in the paper demonstrates the capability of simultaneously optimizing the selection of energy convertors, storage devices and transmission10,11. Ma et al. performed similar work, which contained a solar panel and a wind turbine together with other conversion facilities including a gas turbine CHP, a gas boiler, an absorption chiller and an electric chiller12. Similar to above, the problem was formulated as a mixed integer linear program13,14. MES has many applications in the industrial sector, and some researchers have carried out studies on sizing the corresponding energy supply system in single plant15,16. Alessandro Mati et al. proposed a multi-energy system solution including PV, hydrogen, CHP for paper mills. The system was sized by a general grid search method rather than optimization algorithm to pair different PV capacities and electrolysis capacities and simulate the solutions accordingly. The best solution was selected based on their economic performance17. Patrizia Simeoni et al. designed an energy supply for an Italian ham-processing industrial area with a combination of PV, CCHP (CHP with absorption chiller) and energy storage systems. The sizing was done through a multi-objective optimisation approach through evolutionary algorithm18. Pazouki and Haghifam proposed the planning and scheduling of a multi-energy system containing wind turbines, electricity and thermal storage and CHP units19. The demand response is also included in the model. Additional uncertainty studies were conducted via Monte Carlo simulation. The model was described as a mixed integer linear program and demonstrated the response of various facilities to scenarios involving uncertainty in different sources. WT was considered important to reduce the total cost. When considering the uncertainties, CHP played a more important role, appearing in related scenarios with increased capacity. The capacity of facilities was set as a continuous variable, and it could lead to an integration problem in the installation phase.

Motivated by market demand, many commercial software have been developed for the optimization of MES, such as Hybrid Optimization of Multiple Energy Resources (HOMER), System Advisor Model (SAM), RETScreen, TRNSYS and EnergyPlan20,21. HOMER is a powerful software package designed by the National Renewable Energy Laboratory of the US Department of Energy. The most powerful option, HOMER Pro, contains multiple energy options, including solar, wind, hydro, hydrogen, battery, generator and CHP systems. It is the most used software by researchers in renewable energy sizing. The HOMER simulation tool is very powerful and supports detailed modifications of the dispatch strategy and battery charging strategy. By introducing a multi-year feature, grid price variation and performance degradation, demand growth can be modelled to assist long-term planning. HOMER is also a proven software used by many researchers for result verification22,23, especially in the electricity sector.

However, most of the studies only consider energy supply optimization and margins at the initial stage of the energy supply system installation and do not take into account the situation where the energy demand of a plant or campus is dynamic over time, e.g., as the market share increases, the plant’s production increases, and the energy demand increases, and even if it is taken into account, it is mainly used with a fixed expansion sub-cycle24,25. A fixed sub-period of capacity expansion limits the flexibility of the suggested energy system, and continuous variables could not properly represent the installation activity in small-scale projects26,27. The capacity growth of energy systems, termed the Generation Expansion Planning (GEP) problem, generally focuses on long-term, regional planning problems as a specific extension of capacity planning problems in direction of energy system sizing28. Demand is at the regional scale, while capacity is usually at the utility scale. At the same time, the conventional GEP problem only focuses on a single energy type29,30,. Zhang et al. proposed a method for expansion planning of MES considering transformers, CHP plants and gas furnaces for community-scale projects31. By integrating CHP units, the capacity influences both electricity and heat demand, and the total cost of project is reduced with less unserved electricity load. Luz et al. included multiple renewable sources into the system planning including hydro power, wind turbines, solar photovoltaic and biomass in project time of 15 years32. The expanded capacity would be installed in each sub-period of 5 years. By studying various scenarios, different solutions were suggested. The base case utilized large portion of hydro power, combined with smaller amount of wind started to be installed from second sub-period. After considering other political targets, solar photovoltaic and biomass started to participate. These selections were mainly guided by the cost as hydro power has the lowest LCE in the paper, followed by wind, biomass and solar photovoltaic. Comparing to wind, solar could contribute more peak power (83% from solar and 10% from wind), which encouraged more solar installation in scenarios with higher peak power requirements. Other papers contain renewable capacity planning are all fall in larger scale project planning33. Typical representation of installed capacity of renewable energy options using continuous variables would cause integration problems due to the unit size of renewable options (especially for wind turbine). Especially for small-scale planning problems with large demand growth such as the factories34,35,36, multi-round installation may reduce the initial investment, initial installation time and the payback period of the investment37, 38. In summary, existing researches lack a comprehensive planning tool that can simultaneously address dynamic demand growth, support flexible, discrete installation stages, and is specifically tailored for small-scale, multi-energy industrial systems.

To address this critical gap, a Genetic Algorithm (GA) based optimization model was developed for Multi-Energy Expansion Supply systems. The proposed framework is engineered for dynamic, multi-stage planning, enabling energy infrastructure to strategically scale with industrial operational growth. The model’s efficacy is quantitatively validated by its superior performance: it achieves 23.19% greater total cost savings over commercial software. Consequently, the model provides a robust and financially compelling framework for industrial facilities to navigate the transition towards sustainable and economically optimized energy systems.

Methodology

Optimization objectives

Two objectives were selected to be performed in the optimization. The main objective is to minimize the total cost of the project, including facility cost, grid cost etc. After which, payback as the second objective is calculated by comparing the total cost of each year with the business-as-usual case (BAU case). In the BAU case, all energy is supplied by the electricity and gas grid. Unlike the estimation performed in pre-screening, the cost calculated include detailed tracking of demand and grid cost growth trend, and economical factors including discount rate for an accurate calculation. Though two objectives were proposed, these two objectives were optimized individually as single objective optimization, and the selection between optimization objective could be performed based on the company preference.

Total cost

The first objective is to minimize the total cost of the project during the entire project length of 20 years. The total cost consists of multiple parts as shown in Eq. (1):

$$\:\begin{array}{c}{\text{C}}_{\text{T}\text{o}\text{t}\text{a}\text{l}}=\sum\:_{\text{j}=1}^{\text{t}}\frac{{\text{C}}_{\text{F}\text{a}\text{c}\text{i}\text{l}\text{i}\text{t}\text{y},\text{j}}+{\text{C}}_{\text{L}\text{a}\text{b}\text{o}\text{r},\text{j}}+{\text{C}}_{\text{O}\&\text{M},\text{j}}+{\text{C}}_{\text{B}\text{a}\text{l}\text{a}\text{n}\text{c}\text{i}\text{n}\text{g},\text{j}\:}}{{\left(1+\text{r}\right)}^{\text{j}-1}}\end{array}$$
(1)

Total cost of the project (\(\:{\text{C}}_{\text{T}\text{o}\text{t}\text{a}\text{l}}\)) is calculated by cumulating yearly cashflow with discount rate of r, where j represents the year (starting from 1) and t is the project length. Therefore, discount rate in the denominator calculate from power of 0 (j − 1). In the yearly cashflow, it contains the facility cost (\(\:{\text{C}}_{\text{F}\text{a}\text{c}\text{i}\text{l}\text{i}\text{t}\text{y},\text{j}}\)), the labor cost (\(\:{\text{C}}_{\text{L}\text{a}\text{b}\text{o}\text{r},\text{j}}\)), operating and maintenance cost (\(\:{\text{C}}_{\text{O}\&\text{M},\text{j}}\)), and balancing cost (\(\:{\text{C}}_{\text{B}\text{a}\text{l}\text{a}\text{n}\text{c}\text{i}\text{n}\text{g},\text{j}}\)).

Payback period

Since dynamic installation is enabled, and the total cost is calculated by cummulating the yearly cost based on yearly simulation, no mathematical formula could be used directly to calculate the payback period. The payback period is recorded as the year that BAU cost is higher than total cost.

As the calculated payback period was an integer, multiple solutions could have exactly the same payback period. The total cost of the project was required to assist determining the better solution. For two solutions, the solution 1 was identified as better than solution 2 when the criteria was satisfied as shown in Eq. 2.

$$\:\begin{array}{c}\text{min}\left(\text{P}{\text{B}}_{1},\text{P}{\text{B}}_{2}\right)=\left\{\begin{array}{c}\text{min}\left(\text{P}{\text{B}}_{1},\text{P}{\text{B}}_{2}\right),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:P{\text{B}}_{1}\ne\:P{\text{B}}_{2}\\\:\text{min}\left({\text{C}}_{\text{T}\text{o}\text{t}\text{a}\text{l},1},{\text{C}}_{\text{T}\text{o}\text{t}\text{a}\text{l},2}\right),\:\:if\:P{\text{B}}_{1}=P{\text{B}}_{2}\end{array}\right.\left(\right)\end{array}$$
(2)

Installation range and increment of the renewable supply options

Before conducting the optimization, the installation range and increment of the renewable supply options need to be determined due to the scale of on-site project as well. For each supply option, the determination was performed separately. To integrate capacity expansion into the supply sizing, additional parameters other than a fixed capacity of options were required. Four parameters are currently used, which are year 1 installation, installation increment, increment gap, and the selection of modules.

The first variable is the year 1 installation. The number of units to be installed in year 1 is described as the starting point of the installation activity of each supply option. The second variable is the installation increment. Same as the first variable, this variable has the same unit, but refers to the size expansion of each supply option. The third variable is the increment gap. It described the time between each size expansion applied for each supply option. The unit of this variable is year. The direct calculation of these three variables represented the installation plan of the selected option, which cooperated with the lifespan of selected option to form the operating capacity of each year during the project. The fourth parameter is the selection of different modules, which is optional. When multiple modules were included in the optimization, this variable was introduced to identify the selection in each option and provide associated cost and performance parameters to the optimization algorithm.

These variables collectively define the complete installation and expansion plan for the energy supply system over the project’s lifespan. Based on the installation activity, the number of installations, represented by \(\:\text{I}\text{n}\text{s}\text{t}\text{a}\text{l}{\text{l}}_{\text{k},\text{j}}\), could be extracted and used to calculate related cost. Other energy usage related costs could also be calculated by simulation of each year based on available units in each year.

After the four variables were identified, the next step was to determine the range and increment of each variable. The range and increment were influenced by the area availability, type of technology, unit size and other factors.

Solar installation

After the required variables were described in previous section, the range and accuracy of each variable for each option need to be determined. First is the area limitation. The installation of solar panels should fall in the range of zero installation and full installation based on the total area availability. The actual capacity range was calculated based on the installation density of the selected PV module.

For the installation increment, it is limited by multiple parameters. First is the technical minimum size of solar panel, which is normally one panel. Depending on the module type, different nameplate power of a single panel was observed. Secondly is the possible installation option. For rooftop or installation with tracking system, the minimum installation is one array. The array size was related to the actual size, shape, and installation arrangement. Based on the number of panels holding by one single array, and the nameplate of the panel, the minimum increment size was determined. Thirdly is the economic consideration. The total installed cost of solar panel consisted of module cost, frame and other support facility cost, system balancing cost, and labour cost. When the number of panels installed in each installation is too small, the cost of panels is taking a smaller portion as the labour cost is taking the lead. This information could be accessed from solar companies as well.

Besides the requirements from technical and economical perspective, the installation increment is having impact on the operating of optimization algorithms. While a smaller increment size can yield higher solution accuracy, it does so at the expense of increased computational cost. A reasonable increment size of the variables provides a good balance between solution accuracy and computation speed.

Wind turbine

Wind turbines have large size in general, both in area taken and height. The maximum unit size of wind turbines in manufacturing sites was limited to the maximum height of facilities allowed to be installed on-site. Other than the unit size, the maximum number of installations of wind turbines was limited by the area like solar panel. However, wind turbines, especially when the unit size is growing, are taking up more space than the previous generations. In addition, due to the turbulence flow of wind after going through the wind turbine, the turbines need to be spaced apart from each other to maintain the performance of each other. Based on the research of Johan Meyers34,39, the conventionally used spacing between turbines are 7D (rotor diameter), which may be lower than the optimal spacing found by Meyer (15D). The maximum number of turbines that could be installed on the site was calculated based on the total area availability and the required turbine spacing calculated based on the size of turbine blades.

Since the potential of installing wind turbine and solar panel existed, the actual area taken by the wind turbine needs to be determined to calculate the actual area availability after the installation of wind turbine. Based on research from Scott et al40 other properties were suggested to be spaced two times of the turbine height away from the turbine itself. Based on this, the actual area taken by each wind turbine was calculated and used as input to the optimization stage. The increment of wind turbine is one unit and the economical consideration of wind turbines was considered in the later optimization stage.

CHP

For CHP units, the maximum installation was determined by the factory demand and the energy output of each CHP unit. When all the energy demand is covered by output from CHP units, the number required is the maximum number of units to be installed. Further installation would only reduce the cost performance of the entire energy supply system. Most of current CHP units were integrated with modular design, which made the minimum increment of the CHP units is one unit as well. The model optimizes the number of discrete CHP units to be installed. For the case study in this paper, a standard unit capacity of 1000 kW per CHP system is assumed, a common size for industrial-scale applications.

Optimization algorithm

The project required a single objective optimization, and the optimization objective was the total cost in current stage. Since the total cost was calculated by cumulating the cost of each year during the project, the total cost cannot be analytical represented as the calculation was based on long-term system simulation. This made the optimization method using the gradient of the function not applicable. Additional parameters, which were discrete in current case, were added to the supply sizing optimization to represent capacity expansion. Therefore, the actual optimization could be defined as a searching process. Particle Swarm Optimization (PSO) and Genetic Algorithm (GA), and Simulated Annealing (SA) are well developed optimization categories, each has its pros and cons.

Table 1 Comparison between algorithms.
Full size table

To provide a suitable supply option and their sizing, a suitable optimization algorithm needs to be selected. As the project was focusing on on-site installation, the capacity of each supply option was required to be integrated based on their installation details. Especially for larger units like wind turbines, the capacity has too large increment-size to be considered as a continuous variable. In addition, the optimization requirement of the project included capacity expansion of supply facilities, which was represented by multiple variables including year 1 installation, incremental gap, and installation of each increment. As a result, since the project focused on the on-site installation, and the supply option contained wind turbine, the installation of facilities contained also incremental components. The discrete nature of the problem made GA a better option comparing to PSO algorithm. The SA is also included to enhance the performance of the selected algorithm. However, the original SA is an unguided search, and has much slower computation speed comparing to other algorithms. Overall, GA was selected as the optimization algorithm after comparing the three algorithms (Table 1).

The flow chart, shown in Fig. 1, described the algorithm that was used in this study. First, the optimization was initialized based on the problem setting, and a binary matrix was generated. It was then decoded to obtain the actual value of the design variable, such that the objective value could be calculated for each solution. There were three operators in the algorithm: the selection operator, the crossover operator, and the mutation operator. These operators updated the solution population based on available information and proceed with the optimization process.

Fig. 1
figure 1

Algorithm flow chart.

Full size image

Decoding

Since the number of solutions provided by certain number of binary digits was fixed, and the actual possible selection of variables was determined during the formulation of the problem, mismatch between the possible representation and the actual variable was generated. In addition, when multiple modules were included in the optimization and represented by same group of variables using the additional factor of module selected, the different area and installation requirement provided different variable range and increment.

$$\:\begin{array}{c}{\text{n}}_{\text{a}\text{c}\text{t}\text{u}\text{a}\text{l}}=\frac{{\text{n}}_{\text{d}\text{e}\text{c}\text{o}\text{d}\text{e}\text{d}}}{{2}^{\text{b}\text{i}\text{n}\text{a}\text{r}\text{y}\:\text{l}\text{e}\text{n}\text{g}\text{t}\text{h}}}\times\:{\text{n}}_{\text{v}\text{a}\text{r}\text{i}\text{a}\text{b}\text{l}\text{e}\:\text{r}\text{a}\text{n}\text{g}\text{e}}\:\left(3\right)\end{array}$$

To cover the gap and spread the variables in the entire solution space evenly, an expansion tool was integrated in the decoding of solutions as shown in Eq. (3). The expansion tool took the maximum range of the variable, the maximum range supported by the binary list, and the decoded value as the input, the actual value represented by the binary list was calculated by dividing maximum range supported by the binary list from the decoded value and multiply the maximum range of the variable. This operation could assist in adjusting the required accuracy (adjusting the length of binary list) without influencing the range of output variable. An even distribution of variables in the binary list could also assist the updating of population matrix.

Selection operator

Comparing these four operators, the tournament selection was selected (Table 2). Due to the discrete change of variables, there are larger gaps between individuals, which does not require rank selection. The tournament selection was selected due to its ease of application. It does not require the sorting of solutions, and a selection rate was added to maintain the variance in the population.

Table 2 Comparison between selection operators.
Full size table

Crossover operator

The first operator is the single point crossover. It is the simplest, and most widely used operator. Two individuals were recombined at a randomly selected point. The first child takes the front part of the first parent, and the rear part of the second parent. The second child takes the opposite part of the parents.

The second operator is the multiple point crossover. It operates in an analogous way to the single point operator, but with multiple crossover points.

The third operator is the uniform crossover. In uniform crossover, each gene is treated separately such that there are more crossover activities occurred in single crossover operator compared to the previous two operators.

The fourth operator is the shuffle operator. The entire gene is shuffled before crossover, and the individuals after crossover would be shuffled back to retain the previous sequence.

At the current stage, not much difference was observed between different crossover operators, so the single point crossover is selected due to its simplicity, the formula used was shown in Eq. (4).

\(\:\begin{array}{c}{\text{c}}_{1}={\text{p}}_{1}\left[0:\text{c}\text{r}\text{o}\text{s}\text{s}\text{p}\text{o}\text{i}\text{n}\text{t}\right]+{\text{p}}_{2}\left[\text{c}\text{r}\text{o}\text{s}\text{s}\text{p}\text{o}\text{i}\text{n}\text{t}:\right]\:\end{array}\)\(\:\begin{array}{c}{\text{c}}_{2}={\text{p}}_{2}\left[0:\text{c}\text{r}\text{o}\text{s}\text{s}\text{p}\text{o}\text{i}\text{n}\text{t}\right]+{\text{p}}_{1}\left[\text{c}\text{r}\text{o}\text{s}\text{s}\text{p}\text{o}\text{i}\text{n}\text{t}:\right]\left(4\right)\end{array}\)

Mutation operator

The mutation operator is used in the Genetic algorithm to avoid trapping in local optimal points, and addition variance to the entire population. Every gene is mutating at a certain rate, such that one gene is mutated in each individual on average.

Calculation

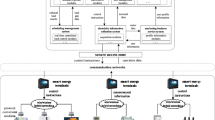
All the costs introduced in the total cost calculation were calculated for each year and cumulated up to obtain the total cost for the option. The calculation contains several steps, shown in Fig. 2.

The first step was to decode the binary string and obtain the variable of each solution. All variables were included in the binary string, taking a certain number of digits as determined during the problem formulation. The binary string was sliced according to the information based on the problem formulation, and then transferred to actual number based on the sliced string. For certain variables, the incremental gap, which is not a continuous number, was obtained in alternative ways. The obtained number was used as an index to obtain the required value of this variable.

Based on the variables and input information including the lifespan of the facilities, the installation plan was formulated. The amount of installation of each supply option required for each year was calculated. At the same time, the number of operating units in each year was calculated as well.

Fig. 2
figure 2

Calculation procedure of optimization objectives.

Full size image

When proceeded to the actual calculation, the cost was calculated for each year. The first step of the calculation in each year was to obtain the number of installation and operating units in a certain year from the output of previous step. The facility cost and labour cost were calculated accordingly. Based on the operating units, the availability of each energy source was calculated, and imported to the CHP optimizer to determine the best CHP operating level in each period. Based on the output, which was the actual usage from each supply option, the O&M cost, and the balancing cost from the electricity and gas grid were calculated.

After the total cost of the year was calculated, financial parameters including a discount rate could be applied to evaluate the effect on the final decision-making procedure. The final total cost was obtained by summing up the total cost of each year. At the same time, by comparing with the BAU case of the system, the payback period of the option was calculated simultaneously and included in the final result.

The verification of the proposed model

To verify the proposed method, a verification case was studied by comparing the results between model output and commercial software output (HOMER). The details parameters of validation case were shown in Supplementary S1. The demand growth rate was set as 5% per year. The grid cost of each period was calculated based on the length and the associated cost of this period. The heat demand was calculated based on steam consumption, and the standard steam unit to convert unit from T steam to kWh of heat required. The demand was analyzed and assumed to be distributed evenly among the year, with the demand power shown in Supplementary S2. The Limitation and Constraints of the validation case were shown in Supplementary S3.

The final supply option suggested consisted of 400 kW of solar panel, one wind turbine unit, and six units of CHP at the start of the project. At year 11, the capacity of solar panel was increased to 450 kW, and the number of CHP units operating was increased to nine units as well. This option provided a total cost of 106 million $, with a simple payback time of 5 years. The total cost and BAU cost, together with the yearly cash flow, were shown in Figs. 3 and 4 and the detail of BAU Cost Comparison was shown in Supplementary S8:

Fig. 3
figure 3

Total cost vs. BAU cost of proposed method.

Full size image
Fig. 4
figure 4

Yearly cash flow of proposed method.

Full size image

Most of the cost came from year 1 and year 11, where installation activities occurred. Different from HOMER model, the replacement of CHP occurred in year 11 as the lifespan of CHP units in the proposed method was counted as 10 years. The salvage value of the project was also lower, as the CHP system reached its end of life at the end of the project as well.

Besides year 1 and year 11, the operating cost of CHP units, marked as “CHP OPEX”, took the most place in the cost of each year. The details could be seen in the following energy usage detail graphs (Fig. 5).

Fig. 5
figure 5

(a) Energy usage of the Pharmaceutical manufacturing company; (b) Electricity usage details; (c) Heat usage details of proposed method.

Full size image

Figure 5(a) showed the growing trend of the electricity and heat usage. The detailed energy usage of electricity and heat energy was shown in Fig. 5(b) and 5(c) respectively. The usage of CHP units in the proposed method was aggressive since most of the energy demand was fulfilled by CHP units from the beginning of the project to the end. This led to the result that most of cost was the operating cost of CHP units, which was the fuel cost of CHP units. Grid usage was observed in Fig. 5(b) in year 9 & 10, before capacity expansion, and year 18–20 which is end of the project. This showed a balance of the suggested option between over-capacity and lack-capacity during the entire project.

Comparing between the optimized result from HOMER and the proposed method, a less total project cost was observed (138 million $ from HOMER vs. 106 million $ from proposed method). In addition, the payback period was reduced from 9 years to 5 years. This was mainly due to the integration of capacity expansion of options in the proposed supply system sizing module. The total cost comparison of HOMER and proposed method was shown in Fig. 6.

Fig. 6
figure 6

Comparison of total cost from HOMER and this work.

Full size image

Large difference in planned CHP operation was observed (low to high CHP usage in HOMER vs. high usage from beginning in proposed method). This was mainly due to the calculation time unit of the two methods. A larger calculation time unit led to a more aggressive dispatch of CHP units as it had cost performance advantage in the entire calculation time unit. This operation mode was similar to existing factory operation strategies as well. In addition, a great difference in the payback period was observed as well, mainly by the integration of capacity expansion in the proposed method. From the calculation results, using the proposed optimization method has a large improvement compared to HOMER.

Results and discussion

The detail parameters of the case

The case selected is a Multi-energy Expansion Supply system of an industrial park, located in Hainan province, China, requiring large amount of cooling demand to support production process. The owners of the industrial park were seeking a clean way to fulfill the energy demand and reduce the cost.

Growth mode

The growth rate of factory demand, electricity grid price and natural gas price are 5% exponentially.

Electricity grid

The grid structure used in the verification was based on the grid contract of the site (Table 3).

Table 3 Electricity grid cost of the model.
Full size table

Natural gas grid

The cost structure of the natural gas grid was calculated based on gas price in unit of yuan/m3. It was further converted to yuan/kWh using the calorific value of natural gas such that it is having the same unit as electricity for ease of calculation. For the cooling demand, the cost of providing required cooling demand was obtained from the site, listed below as well. The summarized natural gas grid cost structure was shown in Table 4:

Table 4 Natural gas grid cost summary.
Full size table

Factory demand

The electricity and cooling demand was calculated based on site data, and cumulated into working demand (daytime) and night demand The demand was assumed to be distributed evenly among the year, with details shown in Table 5:

Table 5 Demand details of selected case.
Full size table

Available options

Due to site limitations, wind turbines were not included in this case. Therefore, the available options in this site are CHP systems and solar panels.

CHP system

In the proposed method, the CHP was described as a % of the maximum operation capacity in each period, with its lifespan in years. The lifespan of CHP units was based on previous technology specification41, which was 10 years (Table 6). The performance parameter came from the same source.

Table 6 CHP cost and performance parameters.
Full size table

Solar panels

For an on-site solar installation, the factory has a limited area available. In this study, the available area for renewable energy installation was 8000 m2. For the solar panel module selected for this project, the average installation density was 200 W per meter square, which led to a maximum installation of 1600 kW of solar panel (Table 7).

For the installation setting of solar panel, the minimum installation unit size was assumed to be 10 kW, which was equivalent to 50 m2 of installation, about the size of installing solar panel as a full row same as the length of warehouse (around 30 m).

Table 7 Solar panel cost and performance parameters.
Full size table

Discount rate

The discount rate is a key parameter that has a large impact on the net present value and payback period of the project. In this case, the discount rate was set as 7%, which is the most used discount rate of the company.

Limitation and constraints

The installation of renewable facilities must maintain in 8000 m2, which is the maximum area available of the factory.

Optimized result from the proposed method

The primary outcome of the proposed optimization is a drastic 77% reduction in total energy costs compared to the Business-As-Usual (BAU) mode, as shown in Fig. 7. The final suggested supply option, which achieves this saving, consists of an initial 1600 kW of solar panels and nine CHP units, with CHP capacity expanding by two units every two years. This optimized plan results in a total 20-year cost of 238.41 million USD and a rapid simple payback time of 2 years.

Fig. 7
figure 7

Total cost vs. BAU cost of proposed method.

Full size image
Fig. 8
figure 8

Yearly cash flow of proposed method.

Full size image

The yearly cash flow analysis in Fig. 8 reveals a strategic capital deployment over the project’s lifespan. The significant costs in year 1 and year 11 are not operational burdens, but planned capital expenditures for the initial system installation and the scheduled replacement of CHP units. The higher replacement cost after year 11 is a direct result of the phased expansion strategy. Outside these investment years, annual costs are dominated by the highly efficient CHP operational expenses (CHP OPEX), which, as shown in Fig. 9, are substantially lower than relying on the grid.

Fig. 9
figure 9

Energy usage detail. (a) Energy usage of the industrial park; (b) Electricity usage details; (c) Heat usage details of proposed method.

Full size image

Lack of CHP capacity was observed at the beginning of the project, as CHP output reaching its maximum in both electricity and heat usage. After year 3, which the first capacity expansion occured, the lack of capacity was shrinked, more demand was fulfilled by the CHP outputs as it has economical performance advantage. Later energy usage showed a better tracing of the demand. This could be due to the difference of growth mode between capacity expansion and demand growth. The mismatching of exponential growth of demand and linear growth of facility capacity caused the lack of capacity in the beginning. Further study of different capacity expansion representation could be conducted to investigate this issue.

The case was repeated with fixed installation (proposed methodology with dynamic optimization disabled). The fixed installation suggested 1600 kW of PV (same as dynamic installation, reaching maximum installation), and 26 units of CHP units. The total cost is similar to the dynamic optimization, reaching 258.44 million USD, and a payback period of 4 years. The details were shown below:

The total cost of dynamic installation is 8.4% less than the fixed installation. Shown in Fig. 10(a), the initial system investment of the energy system from the fixed installation was 33.84 million USD, more than double of the dynamic optimization suggestion (11.98 million USD). Small initial investment could engage more users to take clean energy integration into consideration into their energy system, contribute to the global carbon neutral target.

Beyond direct cost savings, the dynamic model delivers significant operational and strategic advantages. Operationally, the dynamic approach achieves a much higher asset utilization rate. The fixed plan requires a large upfront installation of 26 CHP units, leading to significant underutilization in early years, whereas the dynamic plan matches capacity to demand, running fewer units more efficiently (Fig. 10c). Strategically, this phased investment approach enhances financial resilience, as evidenced by the smaller capital outlay for unit replacements in year 11 compared to the fixed plan (Fig. 10b). This inherent flexibility also provides better risk management, allowing the system to adapt to future uncertainties in demand forecasting.

Fig. 10
figure 10

Comparison between dynamic optimization and non-dynamic installation. (a) Cost comparison; (b) Annual-cost comparison; (c) Operating CHP units comparison.

Full size image

Conclusion

This study developed and validated a dynamic optimization model for multi-energy supply systems, addressing a critical gap in long-term capacity expansion planning for small-scale industrial applications. The findings demonstrate that by staging capital investment to correspond with evolving energy demand profiles, the proposed Genetic Algorithm-based framework significantly outperforms conventional static-planning paradigms. The model’s efficacy is evidenced by its capacity to reduce life-cycle costs through the maximization of asset utilization and the minimization of initial capital expenditure.

The practical implications of this research are substantial. For industrial asset management, the model serves as a quantitative framework for aligning energy infrastructure investment with operational expansion forecasts, thereby mitigating the financial risks associated with premature or oversized capital deployment. The demonstrated reduction in initial investment (up to 40%) enhances the economic feasibility of adopting high-efficiency, low-carbon technologies, particularly for small- and medium-sized enterprises. For the broader energy sector, this work provides a validated methodology for facilitating the cost-effective decarbonization of industrial energy consumption.

The limitations of the present study suggest several avenues for future research. The current model utilizes a discrete, step-wise expansion function, which may not fully optimize planning for non-linear demand trajectories. Future investigations could incorporate more complex, non-linear expansion models or integrate energy storage systems (e.g., batteries) to enhance short-term operational flexibility. Furthermore, the implementation of stochastic modeling to account for uncertainties in energy price and demand forecasts would represent a valuable extension of the model’s deterministic approach.

In conclusion, this research contributes a robust optimization framework and a quantitatively supported approach for industries to transition towards more sustainable and economically efficient energy systems.