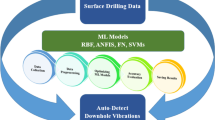
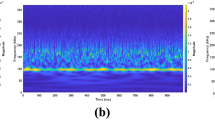
Abstract
Reliable tool condition monitoring (TCM) plays a critical role in precision machining, where progressive wear can lead to dimensional inaccuracies, degraded surface finish, and unplanned downtime. Despite advances in data-driven diagnostics, most machine-learning solutions remain constrained by their reliance on extensive labelled datasets, which poses a major barrier to industrial adoption. To address this limitation, this work introduces a Self-Supervised Masked-Feature Pretraining (SSL-MFP) framework that learns latent vibration representations by reconstructing partially masked time–frequency features, thereby eliminating the need for class labels during the initial learning stage. The pretrained encoder is subsequently fine-tuned using only a small subset of the labelled dataset for downstream drill-wear classification, markedly reducing annotation demands. The framework is evaluated on a fused vibration-feature dataset and benchmarked against established supervised baselines spanning machine-learning and deep-learning architectures. Results indicate that the proposed approach achieves classification accuracy comparable to that of fully supervised models while utilizing significantly fewer labelled samples, demonstrating effective generalization under limited annotation conditions. Furthermore, the learned feature manifold exhibits distinct class separability, evidencing the representational strength of the self-supervised encoder. Overall, the SSL-MFP paradigm provides a data-efficient foundation for TCM, enabling industrial deployment where labelling costs and adaptation are critical challenges.
Similar content being viewed by others
Data availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
References
Chandan, M. N., Majumder, H. & Badadhe, A. A Dual-Stream gated attention network for fault diagnosis of drill bit using time and frequency Domain-based vibration features. J. Vib. Eng. Technol. 13 (8), 626 (2025).
Hegde, K. A., Talla, G. & Gangopadhyay, S. Tool condition monitoring and hole quality analysis during micro-drilling of NiTi shape memory alloy using artificial neural network. Measurement 253, 117487 (2025).
Lins, R. G., Guerreiro, B., de Araujo, P. R. M. & Schmitt, R. In-process tool wear measurement system based on image analysis for CNC drilling machines. IEEE Trans. Instrum. Meas. 69 (8), 5579–5588 (2019).
Dai, Y. & Zhu, K. A machine vision system for micro-milling tool condition monitoring. Precis. Eng. 52, 183–191 (2018).
Lee, S. K. et al. In-situ evaluation of hole quality and cutting tool condition in robotic drilling of composite materials using machine learning. J. Intell. Manuf. (2025). https://doi.org/10.1007/s10845-024-02528-7
Gu, P. et al. Evaluation and prediction of drilling wear based on machine vision. Int. J. Adv. Manuf. Technol. 114, 2055–2074 (2021).
Dayam, S. & Desai, K. A. Smart tool wear state and chatter onset identification system for legacy manual drilling machine operators. Int. J. Adv. Manuf. Technol. 136 (2), 675–692 (2025).
Chen, N. et al. Research on tool wear monitoring in drilling process based on APSO-LS-SVM approach. Int. J. Adv. Manuf. Technol. 108, 2091–2101 (2020).
Matthew, D. E., Cao, H. & Shi, J. Artificial intelligent denoising spectrograms approach for enhanced chatter detection in robotic machining. Int. J. Mechatronics Manuf. Syst. 17 (4), 387–410 (2024).
Rajput, H. S., Raizada, V. & Law, M. Deep learning-based recovery of cutting tool vibrations from Spatiotemporally aliased video. Int. J. Mechatronics Manuf. Syst. 17 (3), 276–294 (2024).
Chauhan, S., Trehan, R., Singh, R. P. & Sharma, V. S. Intelligent tool wear prediction in milling of nickel-based Superalloy using advanced signal processing and bi-transformer. Int. J. Mechatronics Manuf. Syst. 17 (3), 295–318 (2024).
Fu, X., Fan, Z., Sencer, B. & Haapala, K. Thermal signal-enhanced unscented Kalman filter for tool wear prediction. Int. J. Mechatronics Manuf. Syst. 17 (2), 117–131 (2024).
Matthew, D. E., Cao, H. & Shi, J. Development of a robust indicator for online chatter detection. Int. J. Mechatronics Manuf. Syst. 17 (2), 132–149 (2024).
Chai, C., Deng, Z., Liu, J. & Wu, H. Intelligent fault diagnosis framework of mechatronics systems on high resolution sensory data. Int. J. Mechatronics Manuf. Syst. 17 (1), 69–83 (2024).
Rajput, H. S. & Law, M. Rapid online chatter detection in milling using aliased signals. Int. J. Mechatronics Manuf. Syst. 17 (1), 84–95 (2024).
Patange, A., Soman, R., Pardeshi, S., Kuntoglu, M. & Ostachowicz, W. Milling cutter fault diagnosis using unsupervised learning on small data: A robust and autonomous framework. Eksploatacja I Niezawodność, 26(1). (2024).
Assafo, M. & Langendoerfer, P. Unsupervised and semisupervised machine learning frameworks for multiclass tool wear recognition. IEEE Open. J. Indus. Electron. Soc. 5, 993–1010. (2024).
Yusoff, A. R., Jamil, N. & Nur Rosyidi, C. Classification of acceleration signal in milling process of FCD 450 cast iron for surface roughness using tuned support vector mechanics. Adv. Mater. Process. Technol. (2025). https://doi.org/10.1080/2374068X.2025.2559502
Shi, C. et al. Using multiple-feature-spaces-based deep learning for tool condition monitoring in ultraprecision manufacturing. IEEE Trans. Industr. Electron. 66 (5), 3794–3803 (2018).
Madhusudana, C. K., Kumar, H. & Narendranath, S. Condition monitoring of face milling tool using K-star algorithm and histogram features of vibration signal. Eng. Sci. Technol. Int. J. 19 (3), 1543–1551 (2016).
Kuntoğlu, M. & Sağlam, H. Investigation of signal behaviors for sensor fusion with tool condition monitoring system in turning. Measurement 173, 108582 (2021).
Patange, A. D. & Jegadeeshwaran, R. A machine learning approach for vibration-based multipoint tool insert health prediction on vertical machining centre (VMC). Measurement 173, 108649 (2021).
Krishnamurthy, B., Rakkiyannan, J., Gnanasekaran, S. & Thangamuthu, M. Condition monitoring of friction stir welding tool with vibration signals using support vector machine classifiers. Eng. Res. Express. 7 (1), 015564 (2025).
Patange, A. D. & Jegadeeshwaran, R. Application of bayesian family classifiers for cutting tool inserts health monitoring on CNC milling. Int. J. Prognostics Health Manag. 11(2). (2020).
Aravinth, S. & Sugumaran, V. Prediction of air compressor condition using vibration signals and machine learning algorithms. J. Vib. Control. 29 (5–6), 1342–1351 (2023).
Funding
The authors received no funding for this work.
Author information
Authors and Affiliations
Contributions
Chandan M. N.: original draft, Methodology, Conceptualization, Avinash Badadhe: Investigation, Conceptualization, Alemu Workie Kebede: Writing—review & editing and Himadri Majumder: Data curation, review and editing.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
A. Mathematical formulas of extracted vibration features
Feature | Domain | Formula |
|---|---|---|
Mean | Time | \(\:\mu\:=\frac{1}{N}{\sum\:}_{i=1}^{N}{x}_{i}\) |
Median | Time | \(\:Median\:\left(x\right)=\left\{\begin{array}{c}{x}_{\frac{N+1}{2}},N\:odd\\\:\frac{1}{2\left({x}_{\frac{N}{2}}+{x}_{\frac{N}{2}+1}\right)},N\:even\end{array}\right\}\) |
Standard deviation | Time | \(\:\sigma\:=\sqrt{\frac{1}{N}{\sum\:}_{i=1}^{N}({x}_{i}-\mu\:{)}^{2}}\) |
Root mean square (RMS) | Time | \(\:\text{RMS}=\sqrt{\frac{1}{N}{\sum\:}_{i=1}^{N}{x}_{i}^{2}}\) |
Peak-to-Peak | Time | \(\:\text{max}\left({x}_{i}\right)-\text{min}\left({x}_{i}\right)\) |
Skewness | Time | \(\:\frac{1}{N}{\sum\:}_{i=1}^{N}{\left(\frac{{x}_{i}-\mu\:}{\sigma\:}\right)}^{3}\) |
Kurtosis | Time | \(\:\frac{1}{N}{\sum\:}_{i=1}^{N}{\left(\frac{{x}_{i}-\mu\:}{\sigma\:}\right)}^{4}\) |
Crest factor | Time | \(\:\frac{\text{max\:}\left|{x}_{i}\right|}{RMS}\) |
Shape factor | Time | \(\:\frac{RMS}{\frac{1}{N}{\sum\:}_{i=1}^{N}\left|{x}_{i}\right|}\) |
Maximum amplitude | Time | \(\:\text{max}\left({x}_{i}\right)\) |
Minimum amplitude | Time | \(\:\text{min}\left({x}_{i}\right)\) |
Spectral centroid | Frequency | \(\:{f}_{c}=\frac{{\sum\:}_{k}{f}_{k}{P}_{k}}{{\sum\:}_{k}{P}_{k}}\) |
Spectral bandwidth | Frequency | \(\:\sqrt{\frac{{\sum\:}_{k}({f}_{k}-{f}_{c}{)}^{2}{P}_{k}}{{\sum\:}_{k}{P}_{k}}}\) |
Spectral flatness | Frequency | \(\:\frac{{\left({\prod\:}_{k}{P}_{k}\right)}^{\frac{1}{K}}}{\frac{1}{K}{\sum\:}_{k}{P}_{k}}\) |
Spectral entropy | Frequency | \(\:-{\sum\:}_{k}{p}_{k}\text{log}\left({p}_{k}\right)\) \(\:where\:{p}_{k}=\frac{{P}_{k}}{{\sum\:}_{k}{P}_{k}}\) |
Spectral rolloff (85%) | Frequency | \(\:{\sum\:}_{k=1}^{R}{P}_{k}\ge\:0.85{\sum\:}_{k}{P}_{k}\) |
Mean frequency | Frequency | \(\:\frac{1}{K}{\sum\:}_{k}{f}_{k}\) |
Dominant frequency | Frequency | \(\:{\text{arg}max\:}_{k}\left({P}_{k}\right)\) |
Total power | Frequency | \(\:{\sum\:}_{k}{P}_{k}\) |
Band power (0–1000 Hz) | Frequency | \(\:{\sum\:}_{{f}_{k}=0}^{1000}P\left({f}_{k}\right)\) |
List of symbols
Symbol | Description |
|---|---|
\({x}_{i}\) | i-th sample of the time-domain vibration signal |
\(N\) | Total number of time-domain samples |
\(\mu\) | Mean value of the vibration signal |
\(\sigma\) | Standard deviation of the vibration signal |
\({\text{RMS}}\) | Root mean square value of the vibration signal |
\(\text{max}({x}_{i})\) | Maximum amplitude of the vibration signal |
\(\text{min}({x}_{i})\) | Minimum amplitude of the vibration signal |
\({f}_{k}\) | Frequency at the \(k\)-th spectral bin |
\({P}_{k}\) | Power spectral density at frequency bin \({f}_{k}\) |
\(K\) | Total number of frequency bins |
\({f}_{c}\) | Spectral centroid frequency |
\({p}_{k}\) | Normalized spectral power, pk = \(\frac{{P}_{k}}{{\sum }_{k}{P}_{k}}\) |
\({f}_{\text{dom}}\) | Dominant frequency corresponding to maximum spectral power |
\(R\) | Frequency bin index at which the spectral roll-off criterion is satisfied |
B. Model architectures and hyperparameters
B.1 Self-supervised pretraining (masked feature modelling)
Component | Setting |
|---|---|
Input dimension | 40 (20 features + 20 mask indicators) |
Masking probability | 25% (tested 15%, 25%, 30%) |
Encoder hidden layers | 2 fully connected layers, 128 units each |
Normalization | Layer Normalization after each hidden layer |
Activation | ReLU |
Embedding dimension | 128 |
Reconstruction head | Dense layer → 20 outputs (linear) |
Loss function | Masked mean squared error (MSE) |
Optimizer | Adam, learning rate = 3 × 10−4, weight decay = 1 × 10−6 |
Batch size | 128 |
Epochs | up to 80 with early stopping (patience = 10) |
Regularization | Gaussian noise σ = 0.01 × feature std on unmasked features |
B.2 Fine-tuning for classification
Component | Setting |
|---|---|
Input (from pretrain) | 128-dim pretrained embedding |
Dropout | 0.2 (after embedding layer) |
Dense layers | 64 → 32 units |
Normalization | Layer Normalization after dense layers |
Output layer | Softmax over 7 tool classes |
Loss function | Cross-entropy |
Optimizer | Adam |
Learning rate | 1 × 10−3 for classifier head, 1 × 10−4 for pretrained encoder |
Batch size | 64 |
Epochs | up to 60 with early stopping (patience = 8) |
Regularization | L2 weight decay (1 × 10−5) |
B.3 Baseline models
Model | Key settings |
|---|---|
Random forest | 300 trees, max depth = auto, bootstrap = True |
Logistic regression | L2 regularization, max_iter = 2000, C = 1.0 |
XGBoost | 300 estimators, learning_rate = 0.1, max_depth = 6 |
GRN-AttnNet | Dual-stream gated residual attention network, hidden size = 128, attention heads = 4 |
C. Implementation and reproducibility
Hardware: Intel Core i7-11700 CPU @ 2.50 GHz, 32 GB RAM, NVIDIA RTX 3080 GPU (10 GB VRAM).
Software: Python 3.10, PyTorch 2.0.1, Scikit-learn 1.3.0, NumPy 1.24, Pandas 1.5, UMAP-learn 0.5, Matplotlib 3.7, Seaborn 0.12.
Operating system: Ubuntu 22.04 LTS.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Chandan, M.N., Badadhe, A., Kebede, A.W. et al. Reducing label dependence in vibration-based drill-bit condition monitoring with masked feature pretraining. Sci Rep (2026). https://doi.org/10.1038/s41598-026-37192-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-37192-9