Abstract
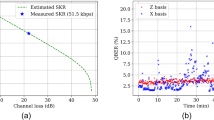
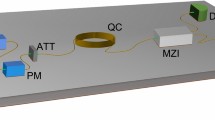
Quantum key distribution (QKD) provides a foundation for information-theoretic security based on quantum mechanics, yet its practical deployment is often constrained by intrinsically low secure key generation rates, particularly in high-bandwidth or low-latency settings. This work introduces a hybrid cryptographic technique that integrates conventional QKD with deterministic chaos, modeled using the Lorenz attractor, to provide a software-based enhancement of the effective key expansion rate. From a short 20-bit QKD seed, the system generates long bitstreams within milliseconds; although these streams exhibit high empirical randomness, their fundamental entropy remains bounded by the seed, consistent with standard cryptographic principles. The method employs the exponential divergence of chaotic trajectories, such that even minute uncertainties in an adversary’s estimate of the initial state lead to rapid desynchronization and, as established in Appendix A, an exponential decay of Eve’s mutual information with respect to the expanded key. Simulation results confirm this theoretical behavior and demonstrate an effective rate amplification exceeding two orders of magnitude over the baseline QKD seed rate. The proposed chaotic expansion operates entirely in software and requires no modifications to existing QKD hardware, offering a practical pathway to enhance throughput for applications ranging from secure video communication to low-latency IoT and edge-computing environments.
Similar content being viewed by others
Data availability
The original contributions presented in this study are included in the article.
References
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theoret. Comput. Sci. 560, 7–11 (2014).
Pirandola, S. et al. Advances in quantum cryptography. Adv. Opt. Photonics 12(4), 1012–1236 (2020).
Yang, J. et al. High-rate intercity quantum key distribution with a semiconductor single-photon source. Light Sci. Appl. 13(1), 150 (2024).
Alessa, A. S. Hammoudeh, M. & Singh, H. A peek into the post- quantum era—PQA PQC: What will happen in 2030. In Quantum Technology Applications, Impact, and Future Challenges, 163–180 (CRC Press, 2025).
Cacciapuoti, A. S. et al. Quantum internet: Networking challenges in distributed quantum computing. IEEE Netw. 34(1), 137–143 (2019).
Okey, O. D. et al. Quantum key distribution protocol selector based on machine learning for next-generation networks. Sustainability 14(23), 15901 (2022).
Shannon, C. E. Communication theory of secrecy systems. Bell Syst Tech. J. 28(4), 656–715 (1949).
Wang, Z. H. et al. Tight finite-key analysis for mode-pairing quantum key distribution. Commun. Phy. 6(1), 265 (2023).
Boaron, A. et al. Secure quantum key distribution over 421 km of optical fiber. Phys. Rev. Lett. 121(19), 190502 (2018).
Clivati, C. et al. Coherent phase transfer for real-world twin-field quantum key distribution. Nat. Commun. 13(1), 157 (2022).
Zhang, L. et al. Experimental mode-pairing quantum key distribution surpassing the repeaterless bound. Phys. Rev. X 15(2), 021037 (2025).
Wang, H. et al. High-efficiency multiphoton boson sampling. Nat. Photonics 11(6), 361–365 (2017).
Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat. Commun. 5(1), 5235 (2014).
Lorenz, E. N. Deterministic nonperiodic flow. In Universality in Chaos, 2nd ed., pp. 367–378 (Routledge, 2017).
Cowper, N., Shaw, H. & Thayer, D. Chaotic quantum key distribution. Cryptography 4(3), 24 (2020).
Keuninckx, L. et al. Encryption key distribution via chaos synchroniza- tion. Sci. Rep. 7(1), 43428 (2017).
Sykot, A. et al. Multi-layered security system: Integrating quantum key distribution with classical cryptography to enhance steganographic security. Alex. Eng. J. 121, 167–182 (2025).
Cho, K. & Miyano, T. Chaotic cryptography using augmented Lorenz equations aided by quantum key distribution. IEEE Trans. Circuits Syst. I Regul. Pap. 62(2), 478–487 (2014).
Kotangale, A., Kumar, M. S. & Bhagat, A. P. Improved big data security using quantum chaotic map of key sequence. Computers 14(6), 214 (2025).
Purohit, K. & Vyas, A. K. Quantum key distribution through quantum machine learning: A research review. Front. Quantum Sci. Technol. 4, 1575498 (2025).
Rahmanpour, M. et al. A new quantum key distribution protocol to reduce afterpulse and dark counts effects. Res. Opt. 16, 100718 (2024).
Zahidy, M. et al. Practical high-dimensional quantum key distribution protocol over deployed multicore fiber. Nat. Commun. 15(1), 1651 (2024).
Du, Z. et al. Advantage distillation for quantum key distribution. Quantum Sci. Technol. 10(1), 015050 (2024).
Song, K. Imran, N. Chen, J. Y. & Dobbins, A. C. A hybrid chaos- based cryptographic framework for post-quantum secure communica- tions. Preprint at https://arxiv.org/abs/2504.08618, 2025.
Shor, P. W. & Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85(2), 441–444 (2000).
Begimbayeva, Y. & Zhaxalykov, T. Research of quantum key dis- tribution protocols: BB84, B92, E91. Sci. J. Astana IT Univ. 2022.
Yin, H.-L. et al. Tight security bounds for decoy-state quantum key distribution. Sci. Rep. 10, 14312. https://doi.org/10.1038/s41598-020-71107-6 (2020).
Acknowledgements
The authors acknowledge support from Khon Kaen University.
Author information
Authors and Affiliations
Contributions
Conceptualization, P.D., S.W., H.T.M. and C.S.; Methodology, P.D. and C.S.; Formal Analysis, P.D., S.W., and C.S.; writing—original draft, P.D.; supervision, S.W.; writing—review and editing, C.S., H.T.M. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: proof of mutual information decay for discrete chaotic maps
Theorem statement
Let \(f:M\to M\) be a discrete-time chaotic map on a compact metric space \(M\), preserving an ergodic invariant probability measure \(\mu\).
Assume \(f\) exhibits exponential decay of correlations for Hölder-continuous observables:
Let \({x}_{0}\) be a random variable with density \({p}_{0}\). Define the trajectories
with \(\delta >0\). Then the mutual information satisfies
Spectral properties of the Perron–Frobenius operator
Let \(\mathcal{P}\) denote the Perron–Frobenius operator, defined by
For a broad class of chaotic dynamical systems, this operator exhibits a spectral gap: the eigenvalue \(1\) corresponding to the invariant density is simple, and all remaining eigenvalues lie strictly inside the unit disk, satisfying \(\mid \lambda \mid <1\). As a consequence, for any observable \(\varphi\) with zero mean (\(\int \varphi \text{\hspace{0.17em}}d\mu =0\)), iterates under the operator contract exponentially, obeying
for some constants \(C^{\prime} > 0\) and \(0<r<1\). This exponential contraction reflects the strong mixing properties essential for the decay-of-correlation estimates used throughout the proof.
Evolution of the joint distribution
Let \(\text{f}:\text{M}\to \text{M}\) be the chaotic map under study, and define the product map
acting on the product space \(\text{M}\times \text{M}\). Let \({\text{p}}_{0}(\text{x})\) denote the initial density of the random variable \({\text{X}}_{0}\), and let \(\updelta >0\) denote the initial offset between Alice’s and Eve’s trajectories. The corresponding joint initial density is
where \(\updelta (\cdot )\) is the Dirac delta. After a single iteration under the smooth map \(\text{F}\), this singular distribution becomes regular (absolutely continuous). Let \({\mathcal{P}}_{\text{F}}\) be the Perron–Frobenius operator associated with the product map. For chaotic systems with exponential mixing, this operator satisfies
for any density \(\text{q}\), where \(0<{\text{r}}_{\text{F}}<1\), \({\text{C}}_{\text{F}}>0\), and
denotes the product invariant density of the marginals. Consequently, the joint density \({p}_{t}(x,y)\) at time \(t\ge 1\) satisfies
showing that the joint distribution is attracted exponentially toward the product of marginals.
Convergence of marginals
The marginal distributions of \({\text{X}}_{\text{t}}\) and \({\text{Y}}_{\text{t}}\) are given by
Both marginals converge exponentially to the invariant density \(\uprho\). Specifically, for constants \({\text{C}}_{\text{M}}>0\) and \(0<\text{r}<1\),
Thus, regardless of the initial mismatch \(\updelta\), the marginals relax toward equilibrium at an exponential rate.
Total variation convergence
Since the Banach-space norm used above dominates the \({\text{L}}^{1}\) norm, there exists a constant \({\text{K}}_{\text{B}}>0\) such that
Combining this with the marginal convergence, we obtain
where \({\text{K}}_{1}>0\). This shows that the joint distribution becomes indistinguishable from the product of the marginals at an exponential rate.
Mutual information decay
The mutual information between the trajectories \({X}_{t}\) and \({Y}_{t}\) is defined as
where \({D}_{\text{KL}}\) denotes the Kullback–Leibler divergence, \({p}_{t}\) is the joint density of \(\left({X}_{t},{Y}_{t}\right)\), and \({p}_{t}^{\left(X\right)},{p}_{t}^{\left(Y\right)}\) are the marginal densities.
Using Pinsker’s inequality, the mutual information is bounded in terms of the total variation distance (TV)
where \(\parallel \cdot {\parallel }_{1}\) denotes the \({L}^{1}\)-norm. Thus,
Substituting the exponential \({L}^{1}\)-convergence bound derived in Sections A.2–A.4 yields
for constants \({K}_{2}>0\) and \(\gamma^{\prime} > 0\), establishing that the mutual information decays exponentially and approaches zero as \(t\to \infty\).
Applicability to standard chaotic systems
The assumptions underlying the proof—namely the existence of an ergodic invariant measure, a spectral gap for the Perron–Frobenius operator, and exponential decay of correlations—are satisfied by a broad class of well-studied chaotic dynamical systems. These include uniformly expanding maps, Anosov diffeomorphisms, and piecewise expanding systems, all of which admit the functional-analytic structure required for the convergence bounds established above. Although the Lorenz system is a continuous-time flow rather than a discrete map, the same reasoning applies to its time-\(\tau\) discretization \({\Phi }_{\tau }\). For any fixed sampling interval \(\tau >0\), the map \({\Phi }_{\tau }\) inherits exponential mixing properties on appropriate anisotropic Banach spaces, ensuring that the mutual-information decay proven in this appendix holds for the Lorenz attractor as well.
Conclusion
For continuous-time flows (such as the Lorenz system), apply the argument to the time-\(\tau\) map \({\Phi }_{\tau }\), giving
Appendix B: entropy bound for deterministic post-processing of an \({\varvec{N}}\)-Bit Seed
Let
denote the initial \(N\)-bit seed with probability mass function \({P}_{K}\). Its Shannon entropy is
and satisfies \(H(K)\le N\), with equality when \(K\) is uniformly distributed.
Let the entire key–generation pipeline—mapping to a chaotic system, evolving the trajectory, sampling, quantizing, and producing the final key—be represented as a deterministic function
and define the output random variable
The following theorem establishes that the output entropy cannot exceed the seed entropy.
Theorem B.1
(Deterministic Post-Processing Cannot Increase Entropy). If \(Y=f(K)\) for a deterministic function \(f\), then
Proof
Because \(Y\) is a deterministic function of \(K\), the conditional entropy vanishes:
Using the chain rule for entropy in two equivalent ways gives
and also
Equating the expressions yields
Since conditional entropy is non-negative,
we obtain the bound
Because \(H(K)\le N\) for any \(N\)-bit seed, the result follows.
Corollary B.2.
For a uniformly random \(N\)-bit seed, the entropy of any derived key obtained through deterministic chaotic evolution and bit extraction satisfies.
Thus, no deterministic expansion procedure—including those based on chaotic dynamics—can increase the entropy beyond that already present in the initial \(N\)-bit seed.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Danvirutai, P., Wongthanavasu, S., Hoang, TM. et al. Hybrid quantum–chaotic key expansion enhances QKD rates using the Lorenz system. Sci Rep (2026). https://doi.org/10.1038/s41598-026-37470-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-37470-6