Abstract
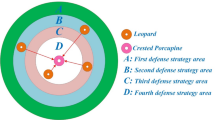
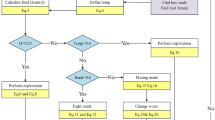
The Crested Porcupine Optimizer (CPO), an emerging intelligent optimization algorithm, exhibits considerable potential for addressing complex engineering problems, yet its capabilities remain insufficiently investigated. Nevertheless, the original CPO is susceptible to premature convergence and suffers from insufficient population diversity. To effectively address these limitations, this paper proposes a multi-mechanism enhanced Crested Porcupine Optimizer (SDHCPO). Its core innovation lies in the integration of four key strategies: a Sobol-Opposition-Based Learning (Sobol-OBL) initialization strategy, which combines the Sobol sequence with opposition-based learning to generate an initial population that is more uniformly distributed in the high-dimensional search space; a cosine-annealing-based dynamic adjustment strategy that replaces the original random weights and substantially enhances convergence stability; the incorporation of the DE/rand/1 strategy in the first defense phase to disrupt positional dependence and prevent premature convergence; and a horizontal-vertical crossover strategy employed in the second defense phase to eliminate dimensional stagnation. Experimental results on two authoritative benchmark suites, CEC2017 and CEC2022, demonstrate that the proposed algorithm outperforms seven representative metaheuristic algorithms in terms of global exploration capability, local exploitation accuracy, and convergence robustness. Furthermore, empirical studies on five representative engineering design optimization problems show that SDHCPO consistently attains either the best-known solutions or highly competitive results reported in the literature, thereby further confirming its effectiveness and broad application potential for complex real-world engineering optimization tasks.
Similar content being viewed by others
Data availability
This study is a benchmark based algorithm study and does not rely on any proprietary or externally collected dataset. All data generated or analyzed during this study are included in this published article . The implementation code and analysis scripts used to reproduce the reported tables, figures, and statistical analyses are available from the corresponding author upon reasonable request.
References
Floudas, C. A., Akrotirianakis, I. G., Caratzoulas, S., Meyer, C. A. & Kallrath, J. Global optimization in the 21st century: Advances and challenges. Comput. Chem. Eng. https://doi.org/10.1016/j.compchemeng.2005.02.006 (2005).
Mandal, P. K. A review of classical methods and Nature-Inspired algorithms (NIAs) for optimization problems. Results Control Optim. https://doi.org/10.1016/j.rico.2023.100315 (2023).
Abualigah, L. et al. Meta-heuristic optimization algorithms for solving real-world mechanical engineering design problems: a comprehensive survey, applications, comparative analysis, and results. Neural Comput. Appl. https://doi.org/10.1007/s00521-021-06747-4 (2022).
Zhang, Z., Li, X., Gao, L., Liu, Q. & Huang, J. Tackling dual-resource flexible job shop scheduling problem in the production line reconfiguration scenario: an efficient meta-heuristic with critical path-based neighborhood search. Adv. Eng. Inform. https://doi.org/10.1016/j.aei.2025.103282 (2025).
Chopard, B. & Tomassini, M. Performance and limitations of metaheuristics. In: An Introduction To Metaheuristics for Optimization, 191–203. Springer International Publishing, Cham https://doi.org/10.1007/978-3-319-93073-2_11 (2018).
Kennedy, J. & Eberhart, R. Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks, Vol.4, pp.1942–1948. IEEE (1995). https://doi.org/10.1109/ICNN.1995.488968
Holland, J. H. Adaptation in Natural and Artificial Systems: an Introductory Analysis with Applications To biology, control, and Artificial Intelligence (MIT Press, 1992).
Storn, R. & Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. https://doi.org/10.1023/A:1008202821328 (1997).
Mirjalili, S., Mirjalili, S. M. & Lewis, A. Grey Wolf optimizer. Adv. Eng. Softw. https://doi.org/10.1016/j.advengsoft.2013.12.007 (2014).
Mirjalili, S. & Lewis, A. The Whale optimization algorithm. Adv. Eng. Softw. https://doi.org/10.1016/j.advengsoft.2016.01.008 (2016).
Yang, X. S. Firefly algorithms for multimodal optimization. In: International Symposium on Stochastic Algorithms, pp.169–178. Springer Berlin Heidelberg, Berlin, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04944-6_14
Rajwar, K., Deep, K. & Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: taxonomy, applications, and open challenges. Artif. Intell. Rev. https://doi.org/10.1007/s10462-023-10470-y (2023).
Qiao, J. et al. A hybrid particle swarm optimization algorithm for solving engineering problem. Sci. Rep. https://doi.org/10.1038/s41598-024-59034-2 (2024).
Vie, A., Kleinnijenhuis, A. M. & Farmer, D. J. Qualities, challenges and future of genetic algorithms: a literature review. ArXiv Preprint. https://doi.org/10.48550/arXiv.2011.05277 (2020). arXiv:2011.05277.
Qin, Y., Deng, L., Li, C. & Zhang, L. CIR-DE: A chaotic individual regeneration mechanism for solving the stagnation problem in differential evolution. Swarm Evol. Comput. https://doi.org/10.1016/j.swevo.2024.101718 (2024).
Chen, S. & Zheng, J. A hybrid grey Wolf optimizer for engineering design problems. J. Comb. Optim. https://doi.org/10.1007/s10878-024-01189-9 (2024).
Deng, L. & Liu, S. Deficiencies of the Whale optimization algorithm and its validation method. Expert Syst. Appl. https://doi.org/10.1016/j.eswa.2023.121544 (2024).
Fister, I., Fister Jr, I., Yang, X. S. & Brest, J. A comprehensive review of firefly algorithms. Swarm Evol. Comput. https://doi.org/10.1016/j.swevo.2013.06.001 (2013).
Li, Y., Zhao, Y., Shang, Y. & Liu, J. An improved firefly algorithm with dynamic self-adaptive adjustment. PLOS ONE. https://doi.org/10.1371/journal.pone.0255951 (2021).
Branke, J. Memory enhanced evolutionary algorithms for changing optimization problems. In: Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Vol.3, pp.1875–1882. IEEE (1999). https://doi.org/10.1109/CEC.1999.785502
Liang, Y. & Leung, K. S. Genetic algorithm with adaptive elitist-population strategies for multimodal function optimization. Appl. Soft Comput. https://doi.org/10.1016/j.asoc.2010.06.017 (2011).
Zhang, Z., Gao, Y., Liu, Y. & Zuo, W. A hybrid biogeography-based optimization algorithm to solve high-dimensional optimization problems and real-world engineering problems. Appl. Soft Comput. https://doi.org/10.1016/j.asoc.2023.110514 (2023).
Wolpert, D. H. & Macready, W. G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. https://doi.org/10.1109/4235.585893 (2002).
Zhang, Z. & Gao, Y. Solving large-scale global optimization problems and engineering design problems using a novel biogeography-based optimization with Lévy and brownian movements. Int. J. Mach. Learn. Cybernet. https://doi.org/10.1007/s13042-022-01642-3 (2023).
Abdel-Basset, M., Mohamed, R. & Abouhawwash, M. Crested Porcupine optimizer: A new nature-inspired metaheuristic. Knowl. Based Syst. https://doi.org/10.1016/j.knosys.2023.111257 (2024).
Liu, S., Jin, Z., Lin, H. & Lu, H. An improve crested Porcupine algorithm for UAV delivery path planning in challenging environments. Sci. Rep. https://doi.org/10.1038/s41598-024-71485-1 (2024).
Liu, H. et al. Multi-strategy enhanced crested porcupine optimizer: CAPCPO. (2024). https://doi.org/10.3390/math12193080
Villaruz, J. A., Gerardo, B. D., Gamao, A. O. & Medina, R. P. Scouting firefly algorithm and its performance on global optimization problems. Int. J. Adv. Comput. Sci. Appl. https://doi.org/10.14569/IJACSA.2023.0140350 (2023).
Zhang, Z., Gao, Y. & Guo, E. A supercomputing method for large-scale optimization: a feedback biogeography-based optimization with steepest descent method. J. Supercomputing. https://doi.org/10.1007/s11227-022-04644-8 (2023).
Altay, O. & Altay, E. V. A novel chaotic transient search optimization algorithm for global optimization, real-world engineering problems and feature selection. PeerJ Comput. Sci. https://doi.org/10.7717/peerj-cs.1526 (2023).
Li, J., Bai, J. & Wang, J. High-Precision Trajectory-Tracking Control of Quadrotor UAVs Based on an Improved Crested Porcupine Optimiser Algorithm and Preset Performance Self-Disturbance Control. Drones (2025). https://doi.org/10.3390/drones9060420
Tizhoosh, H. R. Opposition-based learning: a new scheme for machine intelligence. In: International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vol.1, pp.695–701. IEEE (2005). https://doi.org/10.1109/CIMCA.2005.1631345
Das, S. & Suganthan, P. N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. https://doi.org/10.1109/TEVC.2010.2059031 (2010).
Meng, A. B., Chen, Y. C., Yin, H. & Chen, S. Z. Crisscross optimization algorithm and its application. Knowl. Based Syst. https://doi.org/10.1016/j.knosys.2014.05.004 (2014).
Doerr, C. Complexity theory for discrete black-box optimization heuristics. In: Theory of Evolutionary Computation: Recent Developments in Discrete Optimization, 133–212. Springer International Publishing, Cham (2019).
Wu, G., Mallipeddi, R. & Suganthan, P. N. Problem definitions and evaluation criteria for the CEC 2017 competition on constrained real-parameter optimization. National University of Defense Technology, Changsha, Hunan, PR China and Kyungpook National University, Daegu, South Korea and Nanyang Technological University, Singapore, Technical Report (2017).
Luo, W., Lin, X., Li, C., Yang, S. & Shi, Y. Benchmark functions for CEC 2022 competition on seeking multiple Optima in dynamic environments. ArXiv Preprint arXiv. https://doi.org/10.48550/arXiv.2201.00523 (2022). :2201.00523.
Jia, H., Wen, Q., Wang, Y. & Mirjalili, S. Catch fish optimization algorithm: a new human behavior algorithm for solving clustering problems. Cluster Comput. https://doi.org/10.1007/s10586-024-04618-w (2024).
Bouaouda, A., Hashim, F. A., Sayouti, Y. & Hussien, A. G. Pied kingfisher optimizer: a new bio-inspired algorithm for solving numerical optimization and industrial engineering problems. Neural Comput. Appl. https://doi.org/10.1007/s00521-024-09879-5 (2024).
Shehadeh, H. A. Chernobyl disaster optimizer (CDO): a novel meta-heuristic method for global optimization. Neural Comput. Appl. https://doi.org/10.1007/s00521-023-08261-1 (2023).
Mirjalili, S., Mirjalili, S. M. & Hatamlou, A. Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput. Appl. https://doi.org/10.1007/s00521-015-1870-7 (2016).
Oladejo, S. O., Ekwe, S. O. & Mirjalili, S. The hiking optimization algorithm: A novel human-based metaheuristic approach. Knowl. Based Syst. https://doi.org/10.1016/j.knosys.2024.111880 (2024).
Wilcoxon, F. Individual comparisons by ranking methods. In: Breakthroughs in Statistics: Methodology and Distribution, 196–202. Springer, New York https://doi.org/10.1007/978-1-4612-4380-9_16 (1992).
Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. https://doi.org/10.1080/01621459.1937.10503522 (1937).
He, Q. & Wang, L. An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Eng. Appl. Artif. Intell. https://doi.org/10.1016/j.engappai.2006.03.003 (2007).
Mohammed, H. & Rashid, T. A novel hybrid GWO with WOA for global numerical optimization and solving pressure vessel design. Neural Comput. Appl. https://doi.org/10.1007/s00521-020-04823-9 (2020).
Akdağ, O. A modified tunicate swarm algorithm for engineering optimization problems. Arab. J. Sci. Eng. https://doi.org/10.1007/s13369-023-07803-y (2023).
Qiu, Y., Yang, X. & Chen, S. An improved Gray Wolf optimization algorithm solving to functional optimization and engineering design problems. Sci. Rep. https://doi.org/10.1038/s41598-024-64526-2 (2024).
Mashinchi Joubari, M., Pashaei, M. H. & Fathi, A. Sizing optimization of truss structures under frequency constraints with artificial bee colony algorithm. J. Math. Comput. Sci. https://doi.org/10.22436/jmcs.09.02.01 (2014).
Funding
This research received no external funding.
Author information
Authors and Affiliations
Contributions
H. Xie led the algorithm design and improvement, performed code implementation, experimental design, and statistical analysis, and drafted the manuscript. X. Wan created the visualization for the engineering application section (Figs. 19, 20, 21 and 22) using AutoCAD. J. Mao was responsible for coordination and communication management. Y. Bai contributed to the validation process by providing constructive suggestions and feedback. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xie, H., Mao, J., Wan, X. et al. Adaptive multi mechanism integration in the crested porcupine optimizer for global optimization and engineering design problems. Sci Rep (2026). https://doi.org/10.1038/s41598-026-39222-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-39222-y