Experimental and theoretical band alignment study of MPS₃ (M = Mn, Fe, Co, Ni) for designing tailored 2D heterostructures

Abstract

Van der Waals crystals offer opportunities to engineer material properties by stacking diverse 2D layers into heterostructures. Charge redistribution at these interfaces, governed by band alignment and Fermi levels, enables control over optical, electronic, and magnetic behavior. In this study, we investigated the band alignment and excitation spectra of exfoliated MPS₃ (M = Mn, Fe, Co, Ni) using X-ray and UV photoelectron spectroscopy, optical absorption, and DFT + U calculations. Ionization potentials from 5.4 eV (FePS₃) to 6.2 eV (NiPS₃) were determined. The resulting band diagrams differentiate localized d states from hybridized p-d states, offering insights for designing functional heterostructures. Selective occupation of unoccupied 3d states provides a pathway to tune magnetic order. Theoretical results show that MnPS₃ is well-aligned for both hydrogen and oxygen evolution reactions (HER and OER), while other MPS₃ are promising for OER. MnPS₃/NiPS₃ heterostructure exhibits optimal band alignment for efficient water splitting across a broad pH range.

Introduction

The study of magnetic ordering in two-dimensional (2D) systems has been a central focus of condensed matter physics for several decades¹. Recently, magnetism in 2D van der Waals (vdW) materials has gained prominence as a promising avenue for exploring this phenomenon^2,3,4,5. These materials exhibit intriguing properties and hold significant potential for applications in fields such as topological magnonics, low-power spintronics, quantum computing, and optical communications^{6,7,8,9,10,11,12,13,14,15,16,17}. Metal phosphorus trichalcogenides (MPX₃), where M represents a transition metal, P is phosphorus, and X is sulfur or selenium, exhibit M^II, M^I, and M^III states that are stably located within octahedral sulfur environments^18,19,20. The strong ionic bonds between the metal cations and the [P₂X₆]⁴⁻ anions provide MPX₃ materials with a wide range of functionalities¹⁸. Significantly, MPS₃ displays magnetic properties for M = Mn, Fe, Co, and Ni, characterized by Curie-Weiss susceptibility at high temperatures and antiferromagnetic order at low temperatures^3,6,20,21,22. The magnetic behavior arises from a competition between direct M-M exchange and indirect M-S-M super-exchange interactions within the layers, along with interlayer exchange interactions^3,20,21,22. Furthermore, theoretical and experimental studies indicate that the band gaps within this family range from 1.3 to 3.5 eV, significantly expanding the potential applications of 2D materials across a broad wavelength spectrum^23,24. These properties of MPX₃ nanocrystals are particularly promising for applications in catalysis and optoelectronics^18,24. Moreover, these materials exhibit unusual behaviors such as intercalation-substitution or intercalation-reduction, along with notable ionic conductivity, making them suitable for use in Li-ion batteries^25,26, hydrogen storage²⁷, photodetectors²⁸, and photoelectrochemical reactions^29,30,31.

A crucial aspect of vdW materials is the limitless possibility for combining and modifying their properties by stacking different types of 2D materials into heterostructures with atomically sharp interfaces^19,32,33,34. Studying band alignment and charge transfer across such heterostructures is a powerful method for tailoring their optical and electronic properties³⁵. Designing heterostructures with magnetic vdW materials offers the potential to modulate the intrinsic magnetic order within the layers, enabling the creation of materials with elevated critical temperatures or the development of magneto-tunnel junctions³⁶.

Despite the recent surge of interest in MPS₃ as functional materials, the understanding of their fundamental physical quantities, such as work function or ionization potential, remains limited^18,19,37,38. These properties are crucial in determining the characteristics and performance of potential devices based on heterojunctions, where an electron barrier might form. In this report, the electronic properties of exfoliated MPS₃, such as MnPS₃, FePS₃, CoPS₃, and NiPS₃, were determined by using X-ray and UV photoelectron spectroscopies (XPS and UPS). Additionally, the band gap widths for all studied MPS₃ were determined using the optical absorption technique. The obtained data allowed us to construct band energy diagrams for MPS₃ relative to the vacuum level, which can be advantageous for tailoring the optical and electronic properties of devices based on 2D material heterostructures. To interpret the experimentally measured ionization potentials, theoretical calculations were conducted in the framework of density functional theory (DFT) to determine the valence band position relative to the vacuum level. The resulting band alignment, with distinguished localized d states from purely ligand or strongly hybridized states, serves as a crucial tool for designing heterostructures with customized optoelectronic properties and offers a pathway to manipulate magnetic behavior. Additionally, the layered structures of MPX₃ materials provide a high surface area and active sites for catalytic reactions. The ability to intercalate ions between layers can further improve catalytic efficiency, while magnetic interactions in these materials can influence reaction selectivity. By selectively filling the localized, unoccupied 3d states of transition metals, distinct from ligand states, it becomes feasible to regulate the intrinsic magnetic order within the layer. Additionally, the localized d-orbitals can enhance the adsorption and activation of reactants in water-splitting reactions.

Results

XPS measurements

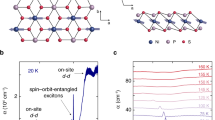
To examine the physicochemical properties and evaluate the purity of the obtained MPS₃ samples, XPS analysis was performed. Each sample was exfoliated under ultra-high vacuum and then measured (see Fig. 1a, b), ensuring the removal of air-contaminated layers to obtain pristine surfaces.

Fig. 1: XPS analysis.

a Mounting of NiPS₃ sample on a molybdenum plate using silver paste. b The sample is exfoliated under ultra-high vacuum conditions. Adhesive tape is affixed to the side of the preparation chamber, and the forward motion of the transfer arm allows for the exfoliation process. c Wide XPS spectrum and d high-resolution XPS spectra of S-2p, Ni-2p, and P-2p core level lines for exfoliated NiPS₃ relative to the valence band maximum.

Figure 1 shows a wide XPS spectrum and high-resolution XPS spectra of Ni-2p, S-2p, and P-2p core level lines for exfoliated NiPS₃. For a more accurate analysis, the binding energies of the main core level lines are presented relative to the valence band maximum (VBM), as the Fermi level may lie within the sample’s band gap, potentially affecting the measured absolute values. The survey XPS spectrum obtained for NiPS₃, Fig. 1c, shows a series of characteristic emission peaks with no additional lines from possible oxygen and carbon contaminants. In Fig. 1d, six fitted peaks observed at 854.4 and 871.7 eV, 859.1 and 876.0 eV, 864.5 and 881.7 eV in the Ni-2p spectrum are attributed to the characteristic multiplet structure of typical Ni²⁺ species, along with the expected satellite peaks^39,40,41. In the S-2p spectrum, two fitted peaks at 161.9 and 163.3 eV correspond to the spin-orbit 2p_3/2 and 2p_1/2 split. The P-2p spectrum shows two distinct fitted peaks at 131.4 and 132.4 eV, corresponding to a single spin-orbit split doublet. The XPS spectra for other studied MPS₃ are presented in Fig. S1 in Supporting Information. The obtained results indicate the high quality of the analyzed MPS₃ layers.

UPS measurements

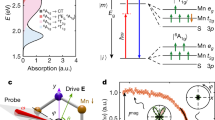
To investigate fundamental physical quantities such as the work function and ionization potential of the examined MPS₃ samples, UPS analysis was conducted. Measurements of parameters such as the VBM position and the work function can be affected by charging effects, as both are referenced to the Fermi level, which may shift due to surface charging. Thus, even if the XPS/UPS measurements are performed correctly, the Fermi level may be located within the sample’s band gap. However, in such cases, the ionization potential - defined as the energy difference between the VBM and the vacuum level - remains unaffected, since both the VBM and the vacuum level shift together. As a result, their relative positions stay constant. Figure 2a shows UPS spectra of all studied MPS₃ measured using He I photons (hν = 21.2 eV), referenced to the vacuum level. As a result, the cutoff energy (E_cutoff) for all samples was set to 21.2 eV. The ionization potential can be determined by linearly extrapolating the onset of the spectrum and identifying the point where it intersects with the background in the valence band region. The lowest ionization potential of 5.4 eV was observed for FePS₃. Subsequently, values of 6.0 and 6.1 eV were determined for materials MnPS₃ and CoPS₃, respectively. The highest value of ionization potential was observed for NiPS₃, equal to 6.2 eV. It can also be observed that the valence band shapes of the studied MPS₃ samples differ from those of typical semiconductors, such as GaN⁴², where the electron density of states begins below the Fermi level, forming a distinct valence band edge. In contrast, the states associated with high kinetic energy electrons in MPS₃ samples exhibit low photoelectron emissivity. Among the samples, the most well-defined valence band edge was observed for FePS₃. The experiment on exfoliated samples following air exposure was also conducted. The UPS results for NiPS₃, shown in Fig. S2 in Supporting Information, reveal that air exposure shifts the ionization energy only by 0.1 eV. This result suggests that although surface chemistry may change upon exposure, the electronic levels relevant for band alignment remain relatively stable within the timeframe and conditions tested.

Fig. 2: UPS analysis, absorption spectra and experimental band alignments.

a UPS spectra relative to the vacuum level, measured using He I photons (hν = 21.2 eV) for all studied and exfoliated MPS₃. Gray dashed lines represent experimentally determined values of ionization potential. b Room temperature optical absorption spectra. c The excitation scheme of d–d and charge transfer (CT) transitions for all employed systems. d Schematic band alignment diagram for all studied MPS₃ constructed based on a UPS and b absorption results.

Absorption measurements

The next step of our experimental study involved determining the electron affinity (EA), defined as the difference between the vacuum level and the conduction band minimum, which corresponds to the difference between the ionization potential and the optical band gap. To achieve this, optical absorption measurements were conducted. Figure 2b presents room temperature optical absorption spectra of all studied MPS₃. These transitions primarily take place between the metal ion states and its surrounding sulfur ligand p states (CT transitions) or occur between 3d states of the same ion (d–d transitions). Ligand arrangement yields a nearly octahedral (trigonal antiprismatic) crystal field that splits the 3d states into even and odd levels, as reported previously^43,44. Due to the different electronic configuration in the 3d shell of the ion states, excited states represent different symmetries, typically named using Mullikan notation (see Fig. 2c)⁴⁵. In general, in a centrosymmetric environment within metal complexes, d–d transitions are typically forbidden in the electric-dipole transition regime due to the parity rule. However, while this restriction does not generally apply to magnetic-dipole transitions, they are usually several orders of magnitude less intense⁴⁶. Additionally, according to ref. ⁴⁷, even a slight change in parity can cause electric-dipole transitions to dominate. Moreover, in the case of MPS₃, the occupied 3d states are not entirely isolated from the rest of the states but hybridize with ligand states, a topic that will be discussed later. For these reasons, such transitions can occur and are observed in absorption spectra, particularly in systems containing transition metals^48,49,50, including MPS₃. The spectrum of a bulk MnPS₃ crystal reveals three distinct absorption bands associated with electronic transitions within the 3d shell of the Mn²⁺ (3d⁵) configuration⁵¹. For MnPS₃, the Mn²⁺ ground state is ⁶A_1g (S), characterized by the orbital configuration (t_2g³ e_g²) with five unpaired spins. In the presence of an octahedral field, the free-ion ⁴G state is split into several levels: two triply degenerate states, ⁴T_1g (G, t_2g⁴ e_g¹) and ⁴T_2g (G, t_2g⁴ e_g¹); a doubly degenerate state, ⁴E_g (G, t_2g³ e_g²); and a nondegenerate state, ⁴A_1g (G, t_2g³ e_g²)⁵². These represent the first four excited states of Mn²⁺. Hence, the observed transitions correspond to ⁶A_1g (⁶S)→⁴T_1g, {⁴A_1g, ⁴E_g (⁴G)}, and P,S 3p_xp_y → ⁶A_1g (⁶S) with respective energies of 1.91, 2.7, and 2.85 eV^51,52. The optical absorption spectrum of a bulk FePS₃ crystal exhibits a broad, symmetric absorption feature centered around 1.03 eV, followed by a steep absorption edge at 1.35 eV. The 1.03 eV absorption peak corresponds to a 3d–3d transition in Fe²⁺, specifically from the ground ⁵T_2g state to the first excited ⁵E_g state (hereafter referred to as the d–d transition), within the forbidden energy region³⁸. Similarly, for CoPS₃, an on-site d–d transition is visible around 0.94 eV (⁴T_1g → ⁴T_2g), followed by a steep absorption edge at 1.3 eV⁵³, while NiPS₃ displays an on-site d–d transition near 1.05 eV (³A_2g → ³T_2g), with a subsequent absorption edge at 1.4 eV⁵⁴. To evaluate the practical relevance of the optical absorption properties of the investigated materials, we compared the calculated absorption spectra with the AM1.5G solar spectrum, as shown in Fig. S3 (Supporting Information). This comparison highlights the spectral range in which the materials can effectively harvest solar energy. While the absorption characteristics suggest promising light-harvesting potential, we note that experimental determination of photocatalytic spectral efficiency lies beyond the scope of this work and is not quantitatively assessed here.

The determined parameters allow us to construct band diagrams for all studied MPS₃ samples, as presented in Fig. 2d, where the electron affinity for all materials refers to the position of the vacuum level. The conduction and valence band offsets between the two materials were estimated using a first-approximation method, calculated as the differences in their electron affinities and ionization potentials, respectively. The results indicate that an interface consisting solely of MnPS₃ and FePS₃ forms a type I (straddling gap) heterojunction, while other heterostructure configurations result in type II (staggered gap) heterojunctions.

Ionization potential (IP) – theoretical considerations

To comprehend the experimentally obtained ionization potentials, ab initio calculations were performed, comparing the valence band position relative to the vacuum level using a state-of-the-art slab method (see Fig. 3a and Computational Details). In all studied systems magnetic ground state was assumed (an AFM-Neel arrangement for MnPS₃ and an AFM-ZigZag spin ordering for the rest of the compounds), where the spin magnetic moments were aligned along the easy axis of magnetization, as reported in refs. ^55,56. Partially filled d-orbitals exhibit strong Coulomb repulsion between electrons due to their localized nature, which is just partially accounted for in standard DFT calculations (LDA, GGA exchange functionals)⁵⁷. To improve this description, the additional on-site Coulomb interaction U and Hund’s exchange J_H of the half-filled 3d states are included.

Fig. 3: DFT calculations - effect of magnetic state, electron correlations and layer thickness.

a Calculation of the vacuum level for all employed systems based on the macroscopic planar average of the Hartree potential for 7-layer slab of MPX₃ crystals in the direction normal to the surface. At the top, additional visualization of the geometric structure of the slab. Ionization potential (b–d). Position of the valence band peak relative to vacuum level for b different antiferromagnetic ordering of MnPS₃, c as a function of the Hubbard parameter U for MnPS₃, d for all employed bulk crystals and monolayers. VB denotes the energy of the valence band maximum.

The effect of electron correlations on IP

First, the effect of the U parameter on the results is examined. To this end, various U values (U = 3, 5, 7, 9 eV) were considered for a representative system (MnPS₃, see Fig. 3c). The maximum difference between the IP calculations for U = 3 eV and U = 9 eV was 280 meV. Given that this family of materials is typically classified as relatively weakly correlated, the U = 9 eV value is unphysically high and was intentionally overestimated to assess the error of IP within the DFT + U framework. The resulting error, on the order of several hundred meV, is acceptable considering the complexity of the studied materials. Finally, the choice of a single U parameter for further calculations is justified. A recent self-consistent evaluation of the Hubbard parameter has reported U = 5 eV for MPX₃ materials, regardless of the type of material in this family⁵⁵. In our study, we focused on the accurate energetic positioning of electronic states near the band gap. For this purpose, we consider ARPES experiments particularly reliable^{40,58,59,60,61,62,63}, as they provide direct insight into the dispersion and relative energies of occupied states. Based on this, fitting the calculated electronic band structures to experimental ARPES data yields U = 1.8 eV for MnPS₃⁵⁸, U = 2.0 eV for NiPS₃⁵⁹, and U = 1.2 eV for FePS₃^60,61. These values suggest that correlation effects in this family of materials are moderate and that a mean-field DFT + U approach is sufficient to effectively reproduce the experimental photoemission spectra. Unlike strongly correlated materials such as cuprates⁶⁴ or iridates⁶⁵ where mean-field DFT + U is insufficient, the DFT + U method remains a valid approximation for MPX₃ compounds. Based on these considerations, U = 3 eV and J_H = 1 eV were set for all employed systems, following the Lichtenstein approach⁶⁶ (which corresponds to U_eff = 2 eV in the Dudarev scheme)⁶⁷.

The impact of magnetic state on IP

Next, the effect of various spin arrangements on ionization potentials is considered. Hence, various collinear AFM phases, using MnPS₃ as an example (Fig. 3b) is considered. These energies for a fully relaxed system of each antiferromagnetic phase (Neel, ZigZag, Stripy) were determined. The difference between the Neel (magnetic ground state) and the ZigZag orders is around 25 meV - but for the Stripy ordering, which is energetically much less favorable, the difference is significant (316 meV).

IP – comparison theory vs. experiment

Let us now compare the theoretical results with experimental findings presented in the previous section. To account for possible variations in layer thickness, the performed theoretical analysis includes calculations for both monolayer and bulk systems. However, for direct comparison with the experimental data - obtained from bulk MPS₃ crystals - the bulk parameters were considered. The theoretically obtained IP, defined here as IP = E_VAC – E_VBM (see Fig. 3d) correlates quite well with IP from experimental data (see Fig. 2a), fully reproducing experimental trends and differing in absolute value by a maximum of ~2.5%. In particular, the smallest and the largest absolute difference (ΔIP = |IP_exp - IP_th | ) were 65 meV and 159 meV for NiPS₃ and for CoPS_3, respectively. The IP of MPX₃ materials falls in the range of 5.5-6.1 eV, which is generally similar to the ionization potential reported for transition-metal dichalcogenides (TMDs) with sulfur⁶⁸, and higher than that of TMDs with selenium. The higher ionization potential reflects their deeper valence band levels, which can impact their optical properties and charge transfer behavior. Generally, our results demonstrated that IP energies obtained for the monolayers are larger than those obtained for bulk systems (Fig. 3d), which is in line with previous reports⁶⁹. In bulk materials, electrons experience stronger dielectric screening from surrounding layers, which lowers the energy required to remove an electron. In other words, in monolayers, this screening is significantly reduced, leading to a higher ionization potential. The only material for which the difference seems significant is FePS₃, in which prominent structural anisotropy exists, compared to other family members. Particularly, in FePS₃, structural anisotropy occurs within the layer plane (lattice constant b ≠ √3a), so the iron sublattice is not precisely hexagonal. The magnitude of this anisotropy (defined as Δ = (b –a √3)/a) varies depending on whether the studied system is 3D or 2D (2.6% vs. 2.8%). It appears that due to this structural in-plane anisotropy, greater coupling with subsequent layers might be possible. However, investigations of the origins and consequences of FePS₃ anisotropy are beyond the scope of this work. Nevertheless, this relationship is considered valuable to highlight when determining band alignment.

It is important to note that the presented band alignment diagrams are based on idealized, pristine surfaces. As such, this study should be viewed as exploratory and intended to establish a baseline for identifying promising material combinations. The actual performance of MPS₃-based heterostructures will strongly depend on interfacial quality. Factors such as interface dipoles, defect-induced states, and potential band bending may significantly influence charge transfer dynamics^{19,32,33,34,35}. Therefore, future experimental and theoretical efforts focusing on interfacial engineering and device-level fabrication will be crucial for validating and optimizing the proposed heterostructure concepts under realistic operational conditions.

Band alignments

The absorption spectra of MPX₃ crystals are rich due to low-intensity optical transitions known as d–d transitions (see arrows in Fig. 2b), occurring below the absorption edge and the charge transfer excitations contributing to a strong absorption onset. As was mentioned before, ligand arrangement yields a nearly octahedral crystal field that splits the 3d states into even and odd levels, as presented schematically in Fig. 4a. Let us now take a closer look at the composition of the states that yield d–d transitions for all employed systems. The PDOS plots uncover hybridization between the occupied M(d) and S(p) orbitals below the Fermi level (see red-green shaded region in Fig. 4b) for all employed systems. On the other hand, the unoccupied energy bands close to the Fermi level are primarily composed of 3d states. Such states for the FePS₃, CoPS₃ and NiPS₃ are well separated from the continuum of the bands and localized, whereas in the case of MnPS₃, part of the empty d states hybridizes with ligand states (detailed explanation in ref. ⁷⁰). These unoccupied 3d states, except in the case of MnPS₃, can act as band gap traps. Additionally, the partially filled 3d states of transition metals determine the material’s magnetic properties, as their occupation affects the spin state and exchange interactions. On the other hand, the absorption edge most likely originates from optical transitions associated with charge transfer between the occupied ligand p states and unoccupied metal d states, which are denoted in violet in the excitation scheme shown in Fig. 4d (onset of a significant absorption in Fig. 2b). Qualitatively, the excitation and absorption edge energies align well with transitions arising from the electronic structure calculations.

Fig. 4: DFT calculations - pDOS and band alignment.

a Visualization of the nearest environment of the transition metal ion (MS₆ cluster) with a description of the splittings associated with the crystal field of this cluster. b Density of states with projection onto the transition metal (M), sulfur (S), and phosphorus (P) states. VBM is set to 0. c Calculated band alignments and band offsets for MPX₃ bulk crystals, referenced to the vacuum level. The dotted line separates occupied (below) and unoccupied levels (above). Green color represents ligand region (1), while red denotes d states localized and unoccupied above the dotted line (2), and red-green shaded region – d states hybridized with p states below the dotted line (3). d Green and violet lines indicate the energy of d–d transitions (peak maxima, with green areas representing peak widths) and the absorption edge from absorption measurements (see Fig. 2b), respectively. Charge transfer excitation involves electron transfer from ligand states to ion d states, resulting in a ligand-to-metal transition. These transitions are typically more intense than d–d transitions and contribute to a strong absorption onset.

Heterojunctions

Understanding the band alignment in MPS₃ compounds allows us to predict the types of heterojunctions that can form within this material system. This, in turn, facilitates a more informed evaluation of their potential applications in spintronics and photocatalysis. Localized, unoccupied 3d states of transition metals, well separated from ligand states, enable the control of the intrinsic magnetic order by choosing a material with suitable band alignment. Creating a heterostructure allows a charge transfer (electrons or holes) across the interface. This can selectively fill unoccupied localized 3d states of the MPX₃ layer, modulating its magnetic properties. Beyond controlling the magnetic order in such heterostructures, optoelectronic devices can be more precisely designed by determining the nature and dispersion of the bands, which is crucial for optical transitions between the layers of the structure.

Additionally, when d states are localized away from ligands, they can participate in specific reactions without interference from ligand dynamics. This separation allows for more controlled reactivity, which is particularly beneficial in catalytic processes where selectivity is essential. Localized d states can facilitate electron transfer processes by providing distinct energy levels that are accessible for redox reactions.

The band alignment plays a crucial role in the efficiency of water-splitting reactions. The primary goal of the water-splitting reaction is to produce hydrogen (H₂) and oxygen (O₂) gases in hydrogen and oxygen evolution reactions (HER and OER), respectively, in a sustainable and efficient manner using sunlight as the energy source. HER occurs efficiently when the conduction band maximum (CBM) of the photocatalyst is above the hydrogen reduction potential ${\rm{E}_{{{\rm{H}}}^{+}/{H}_{2}}}$. Then, the photocatalyst can donate electrons to protons to form hydrogen. In the OER reaction, the VBM of the photocatalyst must be located below the oxygen oxidation potential ${\rm{E}_{{O}_{2}/{H}_{2}O}}$. Hence, it can provide holes efficiently to oxidize water molecules to oxygen. Both potentials depend on the pH value according to the formula:

$${E}_{{O}_{2}/{H}_{2}O}^{{ox}}=-5.67\,{eV}+{pH}\times 0.059\,{eV},$$

(1)

$${E}_{{{\rm{H}}}^{+}/{H}_{2}}^{{red}}=-4.44\,{eV}+{pH}\times 0.059\,{eV},$$

(2)

respectively^71,72. Only for MnPS₃ case, CBM lies above the hydrogen reduction potential E_H+/H2 in wide range of the pH of environment, whereas for FePS₃ this condition is fulfilled for low pH, making them suitable as HER photocatalyst (see Fig. 5a). In addition, almost all employed MPX₃ materials, except FePS₃, have VBM located below the oxygen evolution potential, which allows them to function as photocatalysts with the holes driving OER. The previous report suggested that MPX₃ materials are promising photocatalysts for both OER and HER applications²⁴. However, these conclusions relied on overestimated theoretical values of the fundamental band gap; for example, HSE06 yields 3.01 eV for NiPS₃²⁴, whereas experimental measurements report values between 1.4 and 1.5 eV. Moreover, the unoccupied d states were assumed to define the onset of the absorption edge. As a result, the band alignment in ref. ²⁴ was misinterpreted. It is important to emphasize that the absorption edge was assumed to lie between the occupied states (VBM) and the unoccupied d states²⁴. However, since these localized unoccupied d states typically fall within the fundamental band gap, the reported band gap would, in our interpretation, correspond to a d–d transition - further increasing the discrepancy between the theoretical prediction and experimental observations.

Fig. 5: Band alignment with OER/HER regions and proposed heterostructure for water splitting.

a The band alignments with the indicated hydrogen reduction potential ${\rm{E}_{{H}^{+}/{H}_{2}}}$ and oxidation potential ${\rm{E}_{{O}_{2}/{H}_{2}O}}$ in all pH range (blue areas). b Illustrative band diagram for MnPS₃/NiPS₃ heterostructure serving as a potential water-splitting system. The numbers (1–3) indicate the initial stages of the process that lead to the water-splitting reaction. (1) The semiconductors MnPS₃ and NiPS₃ absorb the light and create photogenerated carriers (electrons and holes). (2) Non-radiative interlayer recombination of the electron and hole at the interface (charge transfer – electron located at CBM in NiPS₃ is transferred to VBM in MnPS₃). (3) Photoexcited electrons in MnPS₃ (photocathode) participate in the reduction of protons (H⁺) to hydrogen gas (H₂) (HER), whereas photoholes at the NiPS₃ (photoanode) oxidize water molecules, generating oxygen gas (O₂).

Additionally, based on optimal band alignments, two heterostructures are theoretically proposed for water-splitting applications: MnPS₃/NiPS₃ and FePS₃/NiPS₃ (see Fig. 5a). However, MnPS₃/NiPS₃ could potentially work across a wider pH operating range and exhibits a favorable band alignment conducive to effective charge separation and water-splitting reactions. In contrast, the FePS₃/NiPS₃ system shows significantly smaller band offsets, which may lead to less efficient charge transfer and increased carrier recombination at the interface - factors that could limit its overall photocatalytic performance. Band alignment between MPS₃ samples was evaluated using the vacuum-level alignment method applied to individual, pristine monolayers. This widely used first-principles approach allows for a qualitative prediction of band alignment types by comparing the relative positions of electronic states, without the need to explicitly model the full heterostructure or include interfacial effects. Consequently, charge transfer was not quantified explicitly; however, the resulting band offsets indicate which directions of electron transfer are energetically favorable. The proposal of MnPS₃/NiPS₃ and FePS₃/NiPS₃ as potential heterostructures for photocatalysis is exploratory and based on band alignment considerations derived from both experimental and theoretical analyses. This approach was taken due to the practical challenges associated with performing photoelectrochemical measurements on these materials, particularly their sensitivity to humidity, oxygen, and illumination, and anisotropic surface properties^{31,73,74,75,76}. While these constraints limit experimental validation, they do not diminish the relevance or potential of our findings, which offer valuable guidance for future research in the field. In both configurations, NiPS₃ could potentially serve as the photoanode⁷⁷, efficiently transporting photogenerated holes to oxidize water molecules (OER reaction), while FePS₃ (or MnPS₃) acts as the photocathode, facilitating the transport of photogenerated electrons to participate in the reduction of protons (H⁺) to hydrogen gas (H₂) (HER reaction) (see Fig. 5). Efficient charge separation can occur at the NiPS₃/MnPS₃ interface due to electron transfer from CBM of NiPS₃ to the lower lying VBM of MnPS₃ systems (see (2) in Fig. 5b), thus preventing radiative carrier recombination within each material. Note that both CBM and VBM are made from localized d states (as discussed above), and due to such localized states, an effective charge transfer occurs at the interface. Namely, the photoexcited electron is transferred from NiPS₃ to recombine with the hole in MnPS₃ at the interface. Hence, the photohole in NiPS₃ and photoelectron in MnPS₃ are more likely to take part in OER and HER reactions, respectively (see Fig. 5b).

Discussion

The electronic and optical properties of exfoliated magnetic MPS₃ compounds - MnPS₃, FePS₃, CoPS₃, and NiPS₃ - were explored using X-ray and UV photoelectron spectroscopies, and optical absorption technique. Key electronic parameters, such as ionization potentials, were determined, ranging from 5.4 eV for FePS₃ to 6.2 eV for NiPS₃. The determined parameters allowed us to construct band diagrams for all studied MPS₃ samples. Our analysis revealed that a heterostructure comprising MnPS₃ and FePS₃ forms a type I (straddling gap) heterojunction, whereas other configurations construct type II (staggered gap) heterojunctions. In addition, the ionization potential values reported here suggest promising potential for catalysis and energy conversion. In particular, the MnPS₃ exhibits promising band alignment for photocatalytic applications in both HER and OER, whereas all employed MPX₃ materials facilitate OER effectively.

The calculated ionization potentials closely match experimental data, reproducing trends with a maximum deviation of ~2.5% (65 meV for NiPS₃ and 159 meV for CoPS₃). The impact of magnetic ordering on ionization potentials was also investigated using MnPS₃ as a case study. Our results confirm that electron correlations in these materials are moderate and that mean-field DFT + U methods can reliably reproduce experimental photoemission data. Moreover, the observed excitation and absorption edge energies correlate well with transitions derived from the electronic structure calculations (neglecting the excitonic effects). The resulting band alignment provides critical insights for tailoring the optoelectronic properties of heterostructures. The presence of d–d transitions and charge transfer states in MPX₃ contributes to a rich and complex absorption spectrum, distinct from the simpler spectra of transition-metal dichalcogenides or black phosphorus. Namely, d–d transitions occur below the absorption edge, and the charge transfer excitations contribute to a strong absorption onset. The transitions in MPS₃ are lower-energy than those in wide-band gap materials like h-BN, making them better suited for near-infrared and visible applications. Finally, MnPS₃/NiPS₃ and FePS₃/NiPS₃ heterostructures were proposed as potential candidates in water-splitting applications to effectively separate photogenerated electrons in MnPS₃ and FePS₃ (holes in NiPS₃) and prevent their recombination in these materials, before they participate in HER (OER) reactions. Effective charge separation occurs at the interface through non-radiative interlayer recombination. Our findings offer a robust foundation for designing advanced 2D material-based heterostructures, enabling optimized performance in electronics, photovoltaics, and photocatalytic applications.

Methods

Sample preparation

MPS₃ compounds were synthesized in quartz ampoules using the chemical vapor transport (CVT) method. The following high-purity starting materials were used as received: manganese (99.95%, -100 mesh, Abcr, Germany), iron (99.9%, -100 mesh, Abcr, Germany), cobalt (99.9%, -100 mesh, Alfa Aesar, Germany), nickel (99.99%, -100 mesh, Abcr, Germany), phosphorus (99.9999%, granules 2–6 mm, Wuhan Xinrong New Materials Co., China), sulfur (99.9999%, granules 2–6 mm, Wuhan Xinrong New Materials Co., China) and iodine (99.9%, granules, Fisher Scientific, Czechia). For the synthesis of MnPS₃, FePS₃, and NiPS₃, the corresponding elements (sufficient for 30 g of the desired MPX₃ compound) were placed in quartz ampoules along with 0.5 g of iodine and a 1 at.% excess of sulfur and phosphorus. The ampoules were melt-sealed under high vacuum (<1 × 10^-3 Pa, oil diffusion pump with liquid nitrogen cold trap) using an oxygen-hydrogen welding torch. The ampoules were placed in a muffle furnace and heated at 450 °C for 25 h, at 500 °C for 50 h, and at 600 °C for 50 h, and finally at 70 °C for 25 h. The heating and cooling rates were 1 °C/min. The ampoule with pre-reacted MPX₃ was placed in a two-zone furnace. First, the growth zone was heated at 750 °C, while the source zone was kept at 600 °C. After 2 days thermal gradient was reversed, and the source zone was heated at 750 °C and the growth zone at 650 °C for 10 days. The ampoule was cooled at room temperature and opened in an argon glovebox. For CoPS₃, stoichiometric amounts of the elements corresponding to 15 g of the final compound were placed in a quartz ampoule with 0.5 g of iodine and a 1 at.% excess of phosphorus and sulfur. The ampoule was sealed under the same vacuum conditions as described above. The ampoule was placed in a muffle furnace and heated at 450 °C for 25 h, at 500 °C for 50 h, and finally at 560 °C for 3 weeks. The ampoule was cooled at room temperature and opened in an argon glovebox.

XPS/UPS measurements

Photoelectron experiments were performed using a hemispherical electron energy analyzer (Argus CU) with either UV or X-ray illumination. The used light sources included nonmonochromatic He I (21.21 eV) and monochromatic Al Kα (1486.6 eV). For UPS measurements, photoelectrons were collected with a 0.01 eV step size and a pass energy of 2 eV, while for XPS measurements, a 0.1 eV step size and a pass energy of 20 eV were applied. Binding energy values were referenced to the Fermi level of the electron analyzer, which was calibrated using a clean Ag reference sample. Samples were mounted on a plate using ultra-high vacuum-compatible, silver-filled conductive paste to ensure good electrical conductivity. For XPS and UPS measurements, we used exfoliated bulk crystals to ensure a clean, uncontaminated surface, as these are surface-sensitive techniques. Prior to measurement, each sample was exfoliated under ultra-high vacuum and then transferred to the analysis chamber.

Transmission/absorption measurements

Energy band gaps for the studied samples were determined through transmission (absorption) measurements. For these measurements, well-defined and uniform bulk MPS₃ crystals were used. Exfoliation was not necessary, as the technique employed is bulk-sensitive and probes the entire thickness of the sample. The samples, each measuring 1 × 1 mm², had varying thicknesses: approximately 7 µm for CoPS₃, 13 µm for MnPS₃, 15 µm for FePS₃, and 18 µm for NiPS₃. Sample thicknesses were achieved through a polishing and lapping process using a Kemet 300 L machine with a Kemet Chem H polishing cloth. A suspension of Al₂O₃ powder with a grain size of 300 µm, mixed with deionized water, was used to control the polishing process. For optimal transmission measurements, both sides of each sample were dulled to prevent the formation of a Fabry-Perot interference effect. Each sample was secured to a brass holder with silver paste and aligned parallelly using 100 µm copper wire on either side, ensuring precise attachment. The transmission (absorption) spectra were collected using a “dark configuration” setup. In this setup, light from an OSRAM HLX 64642 150 W 24 V halogen lamp was modulated at 270 Hz by a STANFORD RESEARCH SYSTEMS SR540 CHOPPER and directed to a single-grating OMNI-λ 300 ZOLIX monochromator. Within the monochromator, the probe beam (white light) was dispersed before passing through the sample, which was positioned in a closed-cycle helium-cooled CTI-CRYOGENICS 22 JANIS cryostat, enabling measurements over a temperature range of 20–325 K. Transmission through the sample was detected by a HAMAMATSU S2386 Si diode, a PDA25K-EC GaP diode, and a PDA30G PbS diode. The resultant signal was measured using a lock-in technique with a STANFORD SR810 DSP phase-sensitive nanovoltmeter, capturing the spectra point by point along with the reference signal. The absorption α spectrum was calculated from the reflectance and transmission spectra using the formula:

$$\alpha =-\frac{1}{d}{ln}\frac{T}{{\left(1-R\right)}^{2}},$$

(3)

where d - sample thickness, T - transmission signal, R - reflectance signal.

Theoretical calculations

The calculations were performed in the framework of DFT using the generalized gradient approximation within the PBE flavor, as implemented in the VASP software⁷⁸. The ion-electron interactions were described by the projector augmented wave (PAW) method^79,80. Plane-wave basis cutoff and Γ-centered Monkhorst-Pack⁸¹ k-point grid were set to 500 eV and 15 × 9 × 15, respectively. A Gaussian smearing of 0.03 eV was employed for the Brillouin zone (BZ) integration. The interlayer vdW forces were treated within the Grimme scheme using D3 correction⁸². Most of the results were obtained using the PBE + U method based on Lichtenstein’s approach⁶⁶, with the effective on-site Hubbard U and Hund’s exchange J parameters assumed for the 3d orbitals. The spin-orbit coupling within the collinear treatment of magnetism was taken into account on top of the PBE + U scheme. The position of the atoms and unit cell were fully optimized within the PBE + U approach.

The work function and ionization potential were determined by adjusting the highest occupied eigenvalue of the bulk structure. This adjustment accounted for the energy difference between the vacuum level in slab calculations and the macroscopic planar average of the ionic and Hartree potential for the slab (excluding the exchange-correlation potential). For the slab calculations, 7 layers were taken and a vacuum corresponding to the length of the slab in the z direction (perpendicular to the plane of the layers). The work function (ϕ) and ionization potential (IP) in a solid are defined as ϕ = E_VAC–E_F and IP = E_VAC–E_VBM, where E_VAC, E_F, E_VBM denote the energy of the vacuum level, Fermi level, and valence band maximum, respectively. The vacuum level (E_VAC) was obtained using the macroscopic planar average of the ionic and Hartree potentials calculated for the slab. The slab represented a bulk surface and consisted of 7 layers and a vacuum thickness corresponding to the length of the slab in the direction normal to the surface. A vacuum of the thickness equal to 20 Å was added to mimic the isolated monolayer. Generally, for insulators and semiconductors, the ionization potential is larger than the work function due to the Fermi level position that is typically closer to mid-gap than the top of the valence band.

While this study focuses on ground state DFT-based band alignment and catalytic band edge positions, it does not include optical spectra or excitonic properties (e.g., via GW-BSE), as these effects are beyond the scope of the present work. However, dielectric screening and exciton binding energies are known to significantly influence charge carrier dynamics in MPX₃ materials. A comprehensive discussion of these effects, including their dependence on dimensionality and composition, is provided in our earlier publications^55,83.