Introduction

Microangiopathy of the skin refers to a kind of clinical disease involving changes in the morphology, structure, and function of the microvasculature, frequently observed not only in the category of dermatosis but in hemodynamic microcirculatory dysfunctions and fibrosis such as peripheral arterial disease1 and systemic sclerosis2. The microvascular and macrovascular dysfunction in type 2 diabetes mellitus (DM) are considered the main factors in diabetic foot ulcers, which finally cause amputations3. The macrovascular especially in arterial occlusive disease leads to impaired microvascular perfusion, hindering the ulcer’s healing3. The dysfunction of microvascular is commonly considered manifested in the thickening of the capillary basement membrane impairing normal substance transport, the reduction in the size of the capillary lumen limiting the vasodilatation, the degeneration of the pericytes relating to vascular regeneration4, and the contraction of connection in microcirculation declining complexity of the network5.In addition to structural changes, factors such as blood viscosity, osmotic pressure, vascular wall permeability, and cell behavior have a direct relationship with microcirculation disorders. A series of physiological and pathological changes are involved in the microcirculation disorders of diabetic foot: for example, hyperglycemia causes increased plasma osmotic pressure, cell dehydration, and hemoglobin glycation; The oxygen-carrying and oxygen-releasing capacity of red blood cells is decreased, which aggravates tissue hypoxia. In addition, diabetic foot ulcers are significantly influenced by peripheral neuropathies1,2 may be due to the intimate neurovascular association. Diabetic foot with or without neuropathy showed a difference in epidermal thickness and subepidermal edema leading to the formation of ulcers6.

Histopathology like skin biopsy, provides the most reliable way of diagnosing skin diseases as the ‘gold standard’7. However, the invasive method is a risk for the microangiopathy of the skin because the injury is hard to heal. Additionally, the morphology of the skin samples may change during the slicing process8. Many noninvasive technologies such as capillaroscopy, laser Doppler flowmetry, hyperspectral imaging, and transcutaneous oxygen pressure have been developed to assess and quantify microcirculation4. Capillaroscopy is the standard for visualizing capillaries, but it is limited to the fingernail bed1,4. Transcutaneous oxygen pressure reveals the function of the microcirculation, still not standardized4. For optical methods, Laser Doppler and Laser speckle contrast imaging with monochromatic light, while hyperspectral imaging utilizes lights with different wavelengths to distinguish substances can display the blood perfusion and measure the hemodynamic parameter but the limited penetration unable to image deep flow, and cannot identify anatomical changes as a 2D method5. Recently, optoacoustic tomography provides the ability to reconstruct a three-dimensional skin model at the 10-micron scale to discover microangiopathy phenotypes. A method called raster-scan optoacoustic mesoscopy (RSOM) shows microangiopathy with different diabetes stages5. However, the device systems, algorithms of reconstruction, and recognition are complex for clinical diagnosis and classifications. Additionally, the ankle-brachial index (ABI) is a global estimator for macrovascular, which ≤0.9 should be considered peripheral artery disease (PAD)9, while stenotic disease cannot be detected when circumferential arterial calcification in diabetes mellitus1,9. A single assessment cannot possess complete specificity and encompass all the characteristics of microangiopathy.

The electrical characteristics of skin have garnered extensive attention, which can mirror its structural and physiological changes10,11, but have not been used in microangiopathy as far as we know. Bioimpedance and electrodermal activity (EDA) are the main ways to measure electrical characteristics12,13,14,15. Bioimpedance analysis is widely utilized to differentiate components including temperature, pH, and sweat, on account of their respective sensitivity to frequency16, by applying multi-frequency voltage or current source in the predetermined range10,17. Recently, electrical impedance tomography (EIT) allows visualizing the 3D image of the resistivity distribution or its changes inside the human body18 by controlling the electrode array size and distance to provide different penetration depths and resolutions, even equally to that provided by magnetic resonance imaging (MRI)19. Accounting for the differences in dielectric properties of various skin layers and their respective sensitivity to frequency, result in varying penetration depths at different frequencies20. Many electrical models of skin are proposed to simulate the relations between the various structures and properties10,21. The measurement will be mapped to the parameters in electrical models22,23,24 representing one structure or physiological process. Khadka’s model25 shows the current pathway flowing along the ultra-structure such as the sweat gland and vessel network instead of the traditional concept that concentrates around electrode edges. The selectivity suggests the potential for microcirculation assessment, that is the current modulated by ultra-structure could contain the pathological information. However, the properties indirectly correspond with one specific disease but rely on regression26 and machine learning methods to establish the relationship as a low-cost solution instead of traditional diagnosis. Thus, derived from bioimpedance, we first proposed a clinically interpretable recognition model based on skin conductance to assess the skin surface’s microangiopathy aiming to replenish the diagnosis and improve the comprehension of electrical properties in diseased microvasculature and their impact on surrounding tissues. Besides, we have also utilized a 3D visualization approach based on Airy light sheet microscopy to verify the microcirculatory disturbance in the structure, and the results could support the correlation with our model.

Results

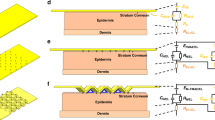
Figure 1 shows the framework. 28 patients with lower extremity arterial occlusion have participated in this study. 7 patients had a healthy side on one limb, 21 had a slight disorder on one limb, and all contralateral limbs that needed surgical intervention were assessed as disease side. Skin conductance (SC), laser speckle (LS), and ankle-brachial index (ABI) were measured in both limbs of all patients before and after surgery. Supplementary Fig. 1 shows the schematic diagram of skin conductance measurements.

Fig. 1: The framework of Module 1 and Module 2.
figure 1

A two-stage classifier structure was established. The first stage (module 1) was based on a decision tree classifier, and the skin conductance and angular distance were used as output features to perform a preliminary score. The second stage (module 2) combines module 1, patient record information, ABI, and LS to make predictions for the Wagner Grade based on ensemble learning.

Full size image

Participants

Table 1 shows the basic information of the participants, including age, gender, diabetes mellitus, wound and Wagner score on the affected side, ankle-brachial index, laser speckle, and skin conductance before and after surgery. This study mainly enrolled elderly patients (min 40, max 90, mean 73.3), and to examine whether the age of enrolled patients significantly affected skin conductance, we divided patients into two groups: 40–70 (n = 24) and 71–90 (n = 32). The results showed no significant difference (Mann-Whitney U test, p = 0.18), although the two groups did have different medians (40–70:78.6, 71-90:53.9).

Table 1 Characteristics of participants
Full size table

Microangiopathy’s features

The angle distance (AD) and average conductance (AC) are calculated as input vectors for the classification model. Figure 2 shows the calculation and results of AD in categories H, S, and D. Figure 2a represents the results of pairing data arranged in ascending order for each subject in category H, that is, the conductance data of the healthy side before and after the operation on (Hside1, Hside2) were used as the horizontal and vertical coordinate. The black line was the reference to slope 1. The above scatters represent the asymmetry change within individuals under multiple measurements. Similarly, Fig. 2b represent the asymmetry of conductance of each subject in S (Sside1, Sside2) and D (Hside1+ Dside1, Sside1+ Dside3). Subsequently, the least square linear regression model was used to fit the parametric curve of the scatter point to calculate the slope k and the coefficient of determination \({R}^{2}\). Figure 2g shows the fitting for one instance of D. Figure 2d–f shows the set of k distributions for each instance (Degree), and the distance of polar coordinates represents the number of samples. As can be seen, the asymmetry of healthy limbs is relatively low, around 45°. As the severity increases, the angle distribution spreads to both sides (Fig. 2b, e). This widening signifies a corresponding rise in uncertainty associated with the data. This feature used to assess microangiopathy is based on the following premise, there are different degrees of damage in the bilateral limbs of patients. If the bilateral limbs were damaged equally, the validity would be reduced. The features distribution of LS did not show this rules obviously (Supplementary Fig. 2).

Fig. 2: The angle distance of the three classes.
figure 2

With the increased severity, the angle distribution shows more bias. a data of class H. b data of class S. c data of class D. d The angle distribution of H. eThe angle distribution of S. f The angle distribution of D. g A fitting example of asymmetry. h The asymmetry of the three classes.

Full size image

Figure 3 shows the distribution of AC (Fig. 3a), AD (Fig. 3b), and linearly fitted \({R}^{2}\) (Fig. 3c) vary in three categories. As the severity rose, the conductance declined and the asymmetry increased, and the difference was significant (p < 0.05, one-way ANOVA). However, \({R}^{2}\) has no difference between the three classes (p = 0.97), thus it is not considered in the model for subsequent analysis.

Fig. 3: The distribution of features.
figure 3

The conductance declined and the asymmetry increased, and the difference was significant.a Skin conductance (AC). b Angle distance (AD). c linearly fitted \({R}^{2}\).

Full size image

Module 1: Classifier and estimator based on skin conductance

To establish the assessment model of the affected side, decision trees (DT) are used to enhance the interpretability as comprised by subdivided thresholds (Fig. 4b, e), endowing the DT with inherent interpretability and resulting in a linear boundary.

Fig. 4: Classification model based on decision trees.
figure 4

The model boundary exhibits transitional features. a first trained model’s response via features. b Model’s structure before pruning. c pruning progress, the cost via nodes. d model’s response after pruning. e Model’s structure after pruning. f Confusion matrix of the binary classification model. g H-S-D models respond after pruning. h H-S-D model’s pruning progress. i The confusion matrix of H-S-D model.

Full size image

Figure 4 shows the process of constructing classification boundaries. First, two categories (H, D) are input into a classification toolbox to train an optimizable binary decision tree model (Fig. 4b, with 1 representing H, 3 representing D, and Colum1/3 indicating two features). Given only two features, the model predicts all angular distances within the 0-1 range and average conductance within the 0–800, as depicted in Fig. 4a. Subsequently, the tree is pruned to mitigate overfitting and complexity, as seen in Fig. 4c. The error of resubstitution decreases with tree size but increases with cross-validation error beyond a certain point (marked by purple circles), which is chosen as the simplest tree with a distance to the minimum within a standard error range. As the procedure in Fig. 4a, the pruned model is demonstrated with the visualized prediction results (Fig. 4d) and tree structure (Fig. 4e). As can be seen, the original boundaries demonstrated characteristics of clustering (Fig. 4a), but pruning smoothed the boundaries (Fig. 4d) and reduced complexity by decreasing the number of model nodes (Fig. 4e). The boundaries revealed the interaction between feature variables affecting prediction outcomes, that is, higher conductivity and lower asymmetry were more likely to be predicted as H, whereas the opposite was D. Conductivity below 90 was more likely to be predicted as Class D regardless of symmetry. Figure 4f shows the confusion matrix of the pruned model on the original dataset, with 1 representing Class H and 3 representing Class D, exhibiting a specificity of 67.4%, sensitivity of 82.9%, and accuracy of 71.7%.

The same method was applied to the multiple classification models (Fig. 4g, h, i), mainly aimed at observing the changes in classification boundaries after adding Class S. The results showed (Fig. 4g) that the boundary of slight patients was between class H and class D, and was mixed in the low conductivity region, regardless of symmetry changes. Meanwhile, it proves the boundary division in Fig. 4 on the detection of class H. Figure 5i shows the classification effect of the three-classification model, with an accuracy of 72.2%, equivalent to that of the two-classification model.

Fig. 5: Schematic diagram of the estimator for assessing the severity.
figure 5

A simple algorithm is used to quantify the severity based on the boundaries. a The green arrow indicates the shortest distance as an output of severity. b A visual heat map of the severity of the method.

Full size image

Based on the boundaries established by the binary classification model, a simple algorithm is used to quantify the severity of the patient. Figure 5a shows the principle of the algorithm: The minimum Euclidean distance (green arrow) between the sample and all boundaries in the feature space is used to quantify the degree, to which the sample deviates from the boundary. The boundary is defined as 0, and the sample is negative in class D and positive in class H. When the distance is greater than a certain threshold, it will no longer increase, as the upper output of the model. The threshold was set as 10 in the study to regulate its distribution (Supplementary Fig. 3). Figure 5b presents the scoring distribution of this rule in a heat map.

Consistency analysis

First, the intra-class correlation coefficient (ICC) was used to measure the consistency among the estimator’s score, ABI, and laser speckle. ICC = 0.43 (P = 0.020) with laser speckle, coefficient 3.65, ICC = 0.55 (P = 0.0026) with ABI, coefficient 0.08. The difference between the model and ABI is normality (p = 0.37, Shapiro-Wilk test) and laser speck (p = 0.22, Shapiro-Wilk test).

Figure 6 shows the Bland-Altman plot between model score and ABI (Fig. 6a), score and laser speckle (Fig. 6b), and laser speckle and ABI (Fig. 6c). The results show that the agreement limit with laser speckle is 41.69, and the agreement limit with ABI is 0.76. Most of the scattered points fall within the agreement limit, which is an acceptable agreement.

Fig. 6: Bland-Altman analysis for the model.
figure 6

The model shows the normal consistency withABI and LS. a model and ABI. b model and LS. c ABI and LS.

Full size image

To verify the microcirculatory disturbance in the structure. Figures 7a, b show pathological tissues in the ulcers from two patients, which were analyzed to confirm microvascular abnormalities. As can be seen, brighter areas indicate denser vasculature, with the red dashed lines highlighting the regions of prominent microcirculatory disorder. In the normal area near the diabetic foot, the blood vessels in the normal area were stratified, showing a bifurcated shape, and the shape was normal (Fig. 7c). In the ulcerative area of diabetic foot, no normal blood vessel morphology was observed, and immunofluorescence results showed complete changes in blood vessel morphology (region I, II, III), which may cause blood transport dysfunction (Fig. 7d).

Fig. 7: Contrast imaging of microangiopathy.
figure 7

The ulcerative area shows complete changes in blood vessel morphology. a 3D microcirculation imaging of sample 1. b 3D microcirculation imaging of sample 2. c Vascular morphology of normal tissue. d Vascular morphology of the lesion area.

Full size image

Module 2: A multimodal model based on medical record and module 1

As the last part of the assessment, a multimodal detection model was developed to predict the Wanger grade which indicates the severity of ulcers. The features from the skin conductance (Mean, Angle) and the output (mOutput) shown in Fig. 5b are combined with other medical record information including the age, gender, wounded or not(isWound), diabetes or not (DB), the ankle-brachial index (ABI) and the laser speckle (LS).

First, the importance of the predictor was examined statistically by using the Chi-square test (Fig. 8a). As can be seen, the “isWound” is the main factor for Wanger Grade consistent with clinical judgment. The features derived from the skin conductance (green text) have similar performance to those of conventional detection methods such as ABI and LS.

Fig. 8: Wanger Grade prediction based on model output and medical record.
figure 8

The accuracy is improved by about 15% in multimodal ensemble learning. a The Chi-square test is used to measure the importance of the predictor. b the confusion matrix of the optimized multimodal model. c Receiver operating characteristic curves for four categories. d Features’ contribution based on optimization model. e Shapley value of all samples. f The predictions for individual patients.

Full size image

Next, the AdaBoost classifier containing those features was trained to predict the Wanger Grade. The model was assessed by the confusion matrix (Fig. 8b) and receiver operating characteristic (ROC) curve (Fig. 8c). The AdaBoost method exhibits an accuracy of 85.3% and the area under the curve (AUC) > 0.9 in all categories.

At last, the SHAP method is used to measure each feature’s contribution to the model’s prediction. Figure 8d shows the feature importance of each feature in the model and the Shapley value of all samples is shown in Fig. 8e. The results show that “isWound,” “Age,” “Mean,” and “Angle” play major roles in determining the results, same as Fig. 8a, and verified the tendency that higher “Mean” and lower “Angle” are associated with healthy status. Figure 8d may reveal the sensitivity of each feature in different stages of wound formation, such as the ABI, whose contribution in level 0 and level 2 outstrip the level 1 and level 3.

Figure 8f interprets how Module 2 uses the information in the medical record to predictions for individual patients, which could help the user comprehend and collate the result from Module 2.

The corresponding graphical user interface of the model was developed to facilitate clinical use (Fig. 9). The interface includes acquisition device control (top left), result analysis (bottom left), and real-time acquisition waveform display (right, from top to bottom: the original waveform, Fourier transform, and conductance estimates output).

Fig. 9: Graphical user interface based on model.
figure 9

The interface includes acquisition device control (top left), result (bottom left), and real-time waveform display (right panel).

Full size image

Discussion

Microangiopathy in the skin is a severe problem, especially for diabetes mellitus complicating with diabetes foot ulcer (DFU), which leads to tissue necrosis, non-traumatic amputation, and increased risk of death27. Many noninvasive methods have been used for the assessment of microcirculation in the skin. Due to the skin’s electric properties, that is, the different conductance and resistance of epidermal, dermal, and other ultra-structures, the current has distribution patterns reflecting structural changes, also influenced by the electrodes’ design, position, interface impedance, and the parameter of current. Although bioimpedance demonstrated the ability to distinguish body components, the application in microangiopathy evaluation seems has not been reported. This study shows the prospect of the assessment of microcirculation. Table 1 shows the metrics of the study participants. Compared to skin conductance (p = 0.125, Mann-Whitney U test), ABI and LS were better at distinguishing between pre-operative (n = 28) and post-operative (n = 28) states on the affected side (both p < 0.0001, Mann-Whitney U test). On the healthy side (n = 7) and the affected side (n = 28), skin conductance performed better in the task of distinguishing the healthy side from the affected side (skin conductance p = 0.003, ABI p = 0.132, LS p = 1, Mann-Whitney U test). As the initial model, we aimed to the simplest feature and algorithm of classification for interpretability and explored the possibility of related indicators in clinical application. As Figs. 2, 3 show, the affected side has a lower conductance and a higher asymmetry paired with the health side. Furthermore, the classification indicated the estimated boundary when divided into H-D for disease presence (Fig. 4) or H-S-D for disease status. Beyond aiming for the model to align with the results of other diagnostic criteria, we also seek new insights into microcirculation disorders from an electrophysiological perspective. Based on the estimated boundary, an equally straightforward distance metric (Fig. 5) was employed to quantify the severity level instead of the common regression which fits the existing diagnosis and was verified in the consistency analysis of ABI and laser speckle (Fig. 6) and the immunofluorescence staining of the abnormal tissues (Fig. 7). Based on the above measures, a multimodal model that incorporates patient medical record information was developed to predict a patient’s wanger rating and the interpretability of the model was analyzed using SHAP (Fig. 8). Although it is not the factor with the highest contribution to the prediction model, the importance of DB in the wanger can be seen in Fig. 8D. DB is more sensitive to the label of level 0 and level 1 and is not a decisive factor in levels 2 and 3. This may represent some role of diabetes in the different stages of wound formation.

The excitation signal parameters in electrical impedance measurement are critical and complex. The frequency, waveform, and amplitude should be considered. As mentioned before, Khadka’s fine model25 shows that the current under direct current (DC) excitation is mainly distributed in sweat gland ducts and vascular microstructures. That is, lower frequency currents can only enter the skin interior along high conductance structures such as sweat gland ducts and propagate in the dermis and blood vessels due to the high resistance characteristics of the stratum corneum, while higher frequency currents may weaken this effect. To avoid electrode polarization, alternating current is considered safer than DC due to charge recovery and thermal effects28, although DC is the mainstream application in skin conductance studies29. In addition, considering the limitation of the patient’s measurement duration and the engineering design of the device, we finally selected 100 Hz as the excitation frequency for the initial evaluation of microcirculation. The sampling rate should be set at least twice the frequency of interest to satisfy the Nyquist theorem for signal recoverability. However, an exorbitant sampling rate usually means more noise, power consumption, and data processing costs.

Regarding signal waveform, the square wave appears as a series of discrete periodic harmonic components in the frequency domain, which contains more information and exhibits better expandability than the sine wave. Such as low power consumption and fast measurement of different frequencies, and can be conveniently generated or modulated by timers in embedded systems without the additional digital-to-analog converters to reduce cost. However, due to its harmonic attenuation, there is a problem of accuracy in multi-frequency measurement.

The amplitude of the signal needs to consider the size of the load, larger voltages may mitigate the effects of the human body and circuit noise, but excessive injection currents should be avoided. Most devices inject currents less than 1 mA according to international safety standards specified in the standard IEC 6060130. Typical values of skin resistance are 95 kΩ31. The 5 V voltage provides an uA level of current, which can ensure the safety requirements. Supplementary Table 1 summarizes the parameter configurations in other literature14,32,33,34,35.

By measuring bilateral limbs, we extracted symmetry-related metrics in the feature section to reduce intra-individual variation. The symmetry eliminates the dimension of absolute value, which can highlight the changes of both limbs in the condition of disease and subtract the influence of age, temperature, humidity, etc. There remain several areas of concern for the factors involved in skin conductance changes. The underlying model includes the skin thickness and hydration level, which can be associated with microangiopathy but the mechanism is unclear in diabetes mellitus36. Microcirculation affects the global status of the skin through substance transportation and body fluid balance. The hydration level rises with the increased evaporation driven by the blood flow. This association may be one of the variables we want to observe. Therefore, it did not interfere with the skin’s condition before measurement.

The current advanced techniques used to assess microvascular structure and microcirculation disorders are mainly imaging methods with different technical routes and results presentation. In the study of Li et al.37. The performance difference between transmissive-detected laser speckle contrast imaging (TR-LSCI) and traditional laser speckle contrast imaging was discussed. TR-LSCI has a better resolution of thick tissue and blood flow velocity. Huynh et al. proposed a Fabry-Perot-based scanner that, employing parallel sensor readout, high-excitation laser, and compression sensing, can obtain high-resolution 3D images of capillary rings, venules, arterioles, and large millimeter-scale arteries and veins in a few seconds at a depth of up to 15 mm, to overcome the early system slow speed38. Karlas et al. Proposed raster-scan optoacoustic mesoscopy (RSOM) images and combined with machine learning methods to extract 32 microvascular features from the images to distinguish diabetes, with a sensitivity/specificity of 0.80/0.78. The area under the ROC curve was 0.845. In this paper, the skin conductance of the healthy and affected sides of the patient was obtained using a 100 Hz excitation signal, and two features of conductance mean and asymmetry were extracted from the model based on the decision tree. The sensitivity/specificity of the healthy side-affected classification was 0.82/0.67. Nine features were fused in the multimodal model based on ensemble learning, including patient medical records, ABI, and laser speckle. The accuracy in the Wagner classification was 0.85, and the area under the ROC curve was >0.9.

Skin conductance was measured for a duration of approximately 3–5 min, including the time the patient entered the resting state and the device was deployed at the bedside, and depending on the patient’s state, this time may be prolonged (data instability) or decreased (pain from holding posture). After the model is trained, this time can be further reduced, and the model will output the prediction results every second. When it is stable, the measurement is considered complete. Data processing will not take place during the data collection phase. Our trained simple model (Module 1) predicts a speed of ~10000 obs/sec, and the final model (Module 2) predicts a speed of ~2500 obs/sec, which is negligible during application.

However, this study is a preliminary assessment of the possibilities of electrical methods for diagnosing microcirculation. First, 28 patients’ data was collected in this study. The sample size may not adequately capture the heterogeneity, and make it challenging to perform meticulous stratification according to disease states and medical records. This impedes a deeper exploration of distinct subpopulations’ characteristics, especially in the different stages of diabetes mellitus for forecasting the progress. Second, to simplify the system and model, only 100 Hz and 5 V square waves are applied on the skin but no further adjusting of the current parameters. Multi-frequency scanning such as electrical impedance tomography, with varying penetration depths, offers deeper insights but is a time-consuming process that requires optimization for clinical. In addition, the uncertainty about ohmic tissue conductivity prevents accurate calculation of the electric fields39. Fine structures such as blood vessels and sweat glands cannot be easily distinguished, which limits their pathological specificity. In other words, the method is not based on physiology but on electrical structure. Multimodal detection integrated with other methods can fortify the limitations of purely electrical methods, offering more insightful information for specificity. For the model, although the current one with two features shows the ability to classify diseases, a complex model incorporating more features is anticipated for the potential to enhance accuracy, and finding a compromise between model complexity and interpretability will be one of the directions in the future. Anyway, a low-cost, simple, effective, and clinically interpretable model was proposed for the assessment of microangiopathy in this study, indicating the potential for using electrical properties of the skin to characterize surface microcirculation disorders.

Methods

Framework and structure

A clinically interpretable model of a two-stage classifier structure was established. The first stage (module 1) was based on a decision tree classifier, and the skin conductance and angular distance were used as output features to perform a preliminary score on the involvement of limb microcirculation. The second stage (module 2) combines multimodal data from module 1, patient record information, ABI, and LS to make predictions for the Wagner Grade based on ensemble learning.

Data acquisition

The research has been performed in accordance with the Declaration of Helsinki. Study protocols were approved by the Medical Ethics Committee of Tianjin People’s Hospital: (2020) Quick review No. (C05). The consent to participate in the study were obtained from all participants. Participants were required to have peripheral artery disease, which includes occlusive lower limb arteries, resulting in impaired circulation, and were diagnosed as requiring surgical intervention.

For skin conductance measurement, the subject is in a resting state and does not require skin preparation. The testing was performed in a room with a temperature of 25 °C and a humidity from 40% to 60%. The patient was required to rest in the supine position for 3 minutes before each test to reduce the effects of emotion and exercise on sweat gland activity. The measurement site was located at the proximal edge of the wound (if any) and did not involve the inside. A 100 Hz square wave signal with a peak-to-peak value of 5 V generated by STM32F415 (STMicroelectronics) is applied to the measured position of the skin through the adhesive electrodes. The skin-modulated signal is converted to digital using the ADS1115 (Texas Instruments) at a sampling rate of 400 Hz. A 1 s window is employed for Fourier transformation, with the 100 Hz component as the estimated skin conductance value. Each sample processing requires 3–5 min. The procedure should be applied in the bilateral limbs. All data processing is done on MATLAB.

Dataset and features

Dataset 1 includes two features for Module 1: angle distance (AD), and average conductance (AC) are extracted as the model input, and three output categories indicate the classification: health (H), slight (S), and disease (D). The proposed AD metric assesses the deviation between two sequences by calculating the absolute difference between the 45°-line slope and the slope of a linear regression equation derived from the ascending data sequences of the healthy and affected sides, after excluding outliers with the default setting in the function of ‘rmoutliers’ provided by MATLAB. AC is defined as the average value of the estimated conductance per second. Every 50 data points form one sample to train the classification model.

For the AD, a health reference is needed. the skin conductance of the patient’s healthy side before (Hside1) and after surgery (Hside2) forms h1; Similarly, the conductance of the slighter side before and after surgery (Sside1, Sside2) forms s1. For patients with one limb health, the healthy side (Hside1) and the diseased side (Dside1) before surgery were paired, and the AD was calculated to form d1. Although several patients with slight disorders on the unoperated side could not get health reference, they had different degrees of impairment compared to the severe side, so the slight side before surgery (Sside1) and the severe side before surgery (Dside3) were still considered as a pair in d1.

For the AC, the conductance of the healthy side before and after surgery (Hside1, Hside2) constituted h2, the conductance of the light side before and after surgery (Sside1, Sside2) constituted s2, and the preoperative heavy conductance of the two types of patients (Dside1, Dside3) constituted d2. d1 and d2 form the input data for category D, and H and S are formed similarly. Three categories and their corresponding input eigenvalues are obtained.

Dataset 2 includes 9 features for Module 2: the age, gender, wounded or not(isWound), diabetes or not (DB), the ankle-brachial index (ABI), the laser speckle (LS), the Dataset 1, and the output of Module 1. One patient provided four samples for training when considering both the operative and non-operative sides before and after surgery. The unoperated side was coded None1 and None2 before and after surgery, and the operative side was Surgery1 and Surgery2. None1 and None2 represent a healthy state, while Surgery1 is a sick state, and Surgery2 is a post-treatment state. Since the assessment was based on the asymmetry of the contralateral limb parameters in dataset 1, the ABI and LS data were paired to match the form of mean conductance and Angle in dataset 1. For the same reason, the absolute values of the differences in None1-Surgery1, None2-Surgery1, and None2-Surgery1 are calculated as features with their own label of Wanger Grades. None1- Non2 is also calculated as the label “0”.

Module 1

Module 1 contains a classifier and a severity estimator. MATLAB’s classification toolbox is utilized to develop decision tree classifiers to define decision boundaries. Since the sample size H constitutes approximately one-third of D, the misclassification cost is set to 3 and implements 3-fold cross-validation. The trained model is then pruned to reduce the complexity of decision boundaries and improve overfitting.

In the context of model evaluation, True positive (TP) refers to the number of samples that the model correctly predicts to be positive, and false negative (FN) refers to the number of positive but the model predicts to be negative. True negatives (TN) refer to the samples where the model correctly identifies samples as belonging to the negative class, whereas false positives (FP) indicate the number of samples that are negative but are mistakenly predicted as positive. The specificity is calculated as follows:

$${Specificity}=\frac{TN}{TN+{FP}}$$
(1)

Sensitivity is

$${Sensitivity}=\frac{{TP}}{{TP}+{FN}}$$
(2)

Accuracy is:

$${Accuracy}=\frac{{TP}+{TN}}{{TP}+{FN}+{FN}+{FP}}$$
(3)

For the severity estimator, the minimum Euclidean distance between the sample and all decision boundaries in the feature space is used to quantify the degree to which the sample deviates from the boundaries. This part is based on the HD binary classification model. The classification boundary is defined as 0, and the samples located in class D are negative values, and those in class H are positive. When the distance exceeds a certain threshold, it ceases to increase, serving as the upper limit of the model’s output. In this study, the threshold was set at 10. For each subject, three samples were collected, and the average distance of the outputs is the severity estimation of the subject.

Module 2

An optimizable classifier with multiple ensemble learning methods is implemented and automatically finds the optimal accuracy on the verification set in MATLAB’s classification toolbox. The cost matrix is calculated directly from the proportion between the sample classes. The performance of classification algorithms was assessed using Receiver Operating Curve Analysis (ROC) and the confusion matrix (see Module 1). Shapley method is used to measure each feature’s contribution to prediction.

Consistency analysis

Bland-Altman plot and intraclass correlation coefficient (ICC) were used to test the consistency of model severity estimation with laser speckle and ankle-brachial index. Since the three scales are different, a variable constant will be multiplied with the output of the model to obtain the maximum ICC respectively. Where ICC is a 2-way fixed effects model, \({{MS}}_{R}\) is the mean square of scores, and \({{MS}}_{E}\) is the mean square of errors.

$$I{CC}(3,k)=\frac{{{MS}}_{R}-{{MS}}_{E}}{{{MS}}_{R}}$$
(4)

Statistical test

One-way analysis of variance was used to test for significant differences between the class (H, S, D) feature parameters. The Shapiro-Wilk test is used to test normality. The remaining comparison between the two groups was performed using the Mann-Whitney U test.

Immunostaining

Diabetic foot samples were collected via biopsy using a 4 mm punch and fixed in 4% paraformaldehyde (PFA) for 24 to 48 h and rinsed with PBS three times for 15 min. Then, endogenous peroxidase was extinguished, and antigen retrieval was performed in a citrate antigen retrieval solution. After cooling naturally, the tissues were blocked with 10% bovine serum albumin (BSA) at room temperature for 1 h, and the Au25 probes were added and incubated at 4 °C for 48 h. The incubating solution was then removed by rinsing three times for 15 min with PBS. Finally, the tissues were cleared and the fluorescence images were captured with a home-built NIR-II light-sheet microscopy (LSM). The information of the Au25 probes was as follows: Au25-Anti-CD31 (CD31, Abcam, ab281583).

Light sheet microscopy imaging

The Airy light-sheet microscope is similar with that described in the study of Liu et al. (Nano Today 47 (2022): 101628). In brief, An Airy beam was generated using a spatial light modulator (SLM, Thorlabs, EXULUS-4K1) with phase modulation. A femtosecond laser (Spectra-Physics, InSight ® X3™, 680–1300 nm) passed through a variable beam splitter (PBS, Thorlabs, VA5-PBS252) to control illumination power, and was then spatially filtered and expanded to fill the SLM’s active area. The modulated beam was directed onto a Galvano mirror (GM, Thorlabs, GVS011) after passing through a rectangle diaphragm, reserving the first-order diffraction. The system used identical illumination and detection objective lenses (Nikon LU Plan, 10×/0.3, 3.5 mm working distance; water immersion) in a “dual-inverted” geometry. The sample was mounted on an XYZ piezo stage (Thorlabs, RBL13D/M, ZST213B) for automatic positioning. Fluorescence was collected using a scientific CMOS camera (Hamamatsu Orca-Flash4.0 v2) through a tube lens and filters (Thorlabs, TTL200-C, FEL0850 & FES01000/FEL1150). Micro-Manager software controlled the system, and custom MATLAB software was used for data processing.

The effective numerical aperture (NA) of the system was estimated using NA = n sinα = n sin [arctan (D/2 f)], where n refers to the refractive index, α refers to the half of the aperture angle, D refers to the illumination pupil diameter of the light-sheet, which was adjusted by holographically controlling of SLM, and f refers to the focal length of the illumination objective. The SLM controlled the pupil diameter, yielding a maximum field of view of 632 μm. The samples were imaged in DBE to match the refractive index, with power maintained between 3.5 and 12.2 mW and a step size of 500 nm for scanning. The exposure time was 20 ms.