Topological resonances in a Möbius ring resonator

Abstract

A Möbius strip, fascinating for its unique topological property of being a one-side nonorientable surface, has inspired mathematicians, physicists, engineers, and artists for many centuries. In a coherent system, coherent waves on the nonorientable surfaces reveal rich topological dynamics due to the interplay of coherence and topology. Here we experimentally observe topological resonances in a Möbius ring resonator formed in a twisted optical fiber loop. The twisted polarization-maintaining fiber ring encourages the hybridization of two polarization states, giving rise to the crucial Berry phase. This geometrical phase leads to the frequency shifts of fiber resonant modes with a non-trivial fractional mode number. Moreover, the resonant modes are topological, only resonating with certain polarized modes with circular chirality. These topological features introduce geometrical factors into coherent wave resonances, paving the way for topological information processing for quantum information, and coherent wave dynamics.

Introduction

Möbius strips, featured with their peculiar property of being “nonorientable” surfaces with only one “side”, have fascinated mathematicians, physicists, chemists, engineers, artists, architects, and many others ever since their discovery in 1858. It helps to spur the development of an entire field of topology, which preserves the genus, i.e., the number of holes, in an object even under the deformation. A Möbius strip’s unique topological property of being a nonorientable surface has evolved from a mathematical concept to a recent topological design of materials¹, molecules², nanostructures³, and electronic and microwave devices⁴ across multiple disciplines. Particularly, this one-sided topology enables the topological twist of the band structure in topological insulators;⁵ A crystalline ribbon of material can be coaxed into a novel Möbius nanocrystal⁶, and the synthesis of the molecular Möbius strip plays an important role in medicine and drugs².

Coherent wave dynamics around a Möbius loop are particularly important to the fields of quantum physics, optics, acoustic, and condensed matter. The Möbius topology combined with the coherence, i.e., resonances, can lead to non-trivial wave evolution⁷. During this adiabatic process over the course of a cycle, the coherent wave acquires an additional topological phase, namely the Berry phase (also termed the geometric phase, Pancharatnam-Berry phase)^8,9. Berry phase has been extensively investigated when the waves evolve along the parameter space in polarization states¹⁰, spin–orbital coupling¹¹, and helical systems¹². Earlier works have demonstrated the appearance of Berry phases in coiled fibers¹³. Combined with a Möbius loop, it has been shown experimentally the spin–orbit coupling of photons in the Möbius nano/micro rings;^14,15 Möbius ring resonators exhibit Fermion–Boson rotational symmetry⁴, and the recent work shows a Möbius strip microlaser can be implemented as a platform for the investigation of non-Euclidean optics¹⁶. The most important impact of such a geometric phase on the resonances is theoretically predicted to be topological in a Möbius loop, shifting the resonance frequencies and polarization states⁷. For example, half-integer modes are theoretically predicted between the traditional well-known whispering-gallery modes which are based on integer constructive modes^4,17. Particularly, these topological resonances in a Möbius resonator are critical for manipulating topology-based signal processing¹⁸, but few experimental realizations have been implemented up to this work.

In this work, we experimentally demonstrate a Möbius ring resonator based on a twisted polarization-maintaining (PM) fiber ring, where the angle twisting allows the coupling between the two polarization modes along the fast and slow axes inside the PM fiber ring. This hybridization of polarized modes gives a rise to the additional geometrical phase, i.e. Berry phase, during the propagation in the ring resonator. Effectively, this additional Berry phase introduces extra frequency shifts to the resonances, making their mode numbers fractional as opposed to the integer ones in the traditional ring resonators. Furthermore, enhanced mode splitting and mode flipping are also observed at a higher twisting angle. Also, these resonant modes are topological, only resonating with certain polarized modes with circular chirality. These results should be general and universal among other coherent systems involving Möbius-like evolution, the critical geometrical phase can facilitate extra coherent control of topological properties, paving the way for practical applications in topological signal processing and quantum information.

Results

Theory model for Möbius ring resonator

The Möbius ring resonator consists of a typical polarization-maintaining fiber ring geometry¹⁹, but with a twisting angle at the splice point as shown in Fig. 1. In this manner, two linear polarization modes along the slow and fast axes can couple to each other at the splice point depending on the twisting angle. At a 0° twisting angle, this ring resonator represents the traditional PM fiber ring resonator with two degenerated modes each along the slow and fast axes, respectively¹⁹. While 90° twisting angle may ideally totally convert the slow mode into the fast one right at the splice point, and vice versa^20,21. Intuitively, the optical waves have to travel twice of resonator length to complete one resonance cycle, similar to the Möbius-strip ant’s problem. However, the polarization state of the wave evolves through a closed adiabatic journey in this scenario, this gives a rise to the well-known Berry phase in addition to the usual dynamical phase^8,9. As a result, this additional topological phase leads to the shift of the resonance modes⁷, which usually are formed based on constructive resonance interference conditions. Originally, the resonance modes in the traditional resonators without the twist are characterized by integer azimuthal mode numbers $m$, in contrast, such Berry phase in the Möbius ring resonator can turn the mode number into a fractional one, for example, a half-integer $m$ is predicted in a dielectric Möbius strip cavity^4,7.

Fig. 1: a Möbius ring resonator of twisted polarization-maintaining (PM) fiber loop.

A fiber-coupled PM fiber ring resonator with 90° polarization axis rotation at the splice, such that the modes in the fast and slow axis couple with each other, effectively forming the Möbius ring resonator. The eigenmodes in the fast axis (blue) will, after one round trip, be in the slow axis (red).

Quantitatively, we consider a fiber ring resonator of cavity length $L$ and the twisting angle $\theta$ at the splice point, such that the effective fiber loop torsion can be defined as $\tau =\theta /L$. With the help of Jones’ formula²², the polarized field vector along PM fiber’s fast and slow axes $E(z,t)={({E}_{F},{E}_{S})}^{T}$ evolves inside the Möbius ring resonator according to:²³

$$i\frac{\partial }{\partial z}\left(\begin{array}{c}{E}_{F}\\ {E}_{S}\end{array}\right)= \,H\left(\begin{array}{c}{E}_{F}\\ {E}_{S}\end{array}\right)=\left\{\left(\begin{array}{cc}i\beta & -\tau \\ \tau & i\beta \end{array}\right)\right.\\ +\left.\frac{1}{2}i\varDelta \beta \left(\begin{array}{cc}\cos (2\tau z) & \sin (2\tau z)\\ \sin (2\tau z) & -\,\cos (2\tau z)\end{array}\right)\right\}\left(\begin{array}{c}{E}_{F}\\ {E}_{S}\end{array}\right)$$

(1)

where $H$ is the Hamiltonian of the Möbius ring resonator system. We define $\beta =({\beta }_{F}+{\beta }_{S})/2$ and $\varDelta \beta ={\beta }_{F}-{\beta }_{S}$, ${\beta }_{F}$ and ${\beta }_{S}$ are the propagation constants of the fast and slow axis respectively (see Supplementary Note 1). It is convenient to remove the time dependence and the absolute phase by alternatively expressing the field vector as $E(z,t)=A(z)\exp [i(\beta L-\omega t)]$, the amplitude $A(z)$ can be expressed in the new Hamiltonian $H{{\hbox{'}}}$ as:

$$i\frac{\partial }{\partial z}\left(\begin{array}{c}{A}_{F}\\ {A}_{S}\end{array}\right) = H^{\prime} \left(\begin{array}{c}{A}_{F}\\ {A}_{S}\end{array}\right)\\ = \left(\begin{array}{cc}-\varDelta \beta \,\cos (2\tau z)/2 & -i\tau -\varDelta \beta \,\sin (2\tau z)/2\\ i\tau -\varDelta \beta \,\sin (2\tau z)/2 & \varDelta \beta \,\cos (2\tau z)/2\end{array}\right)\left(\begin{array}{c}{A}_{F}\\ {A}_{S}\end{array}\right)$$

(2)

The above equation is a Schrodinger-like equation, which can be solved by the adiabatic theorem²⁴ if the torsion term varies slowly along the twisting fiber. Under this adiabatic approximation, the corresponding eigenstates with two additional phase factors can be solved as:

$${A}_{\pm }(z)=\left[\begin{array}{c}\pm \varOmega +\frac{1}{2}\varDelta \beta \,\cos (2\tau z)\\ -i\tau +\frac{1}{2}\varDelta \beta \,\sin (2\tau z)\end{array}\right]\cdot \exp (\pm i\varOmega L)\cdot \exp (i{\gamma }_{\pm }(L))$$

(3)

which represent the two elliptically polarized modes in our Möbius ring resonator. Here $\pm \varOmega =\pm \sqrt{{(\varDelta \beta )}^{2}/4+{\tau }^{2}}$ are the two eigenvalues of $H^{\prime}$. There are two phases in the solution: ${\varphi }_{\pm }=\pm \varOmega L$ is the dynamic phase and ${\gamma }_{\pm }(L)$ is the geometrical Berry phase acquired during the adiabatic evolution. ${\gamma }_{\pm }(L)$ can be calculated in the parameter space in an integrated form:⁸

$${\gamma }_{\pm }(L) =i{\int }_{0}^{L}\langle {A}_{\pm }{(z)}_{Norm}\left|\frac{d}{dz}\right|{A}_{\pm }{(z)}_{Norm}\rangle dz \\ =\mp {\int }_{0}^{L}\frac{{\tau }^{2}}{{{\rm N}}^{2}}\frac{d}{dz}\left(\frac{\varDelta \beta \,\sin (2\tau z)/2}{2\tau }\right)dz$$

(4)

where ${\rm N}=\sqrt{2{\varOmega }^{2}+\varOmega \cdot \varDelta \beta \,\cos (2\tau z)}$ is the normalization factor, and ${A}_{Norm}$ is the normalization of the eigenvector A. Obviously, the twisting of the torsion $\tau$ term can modify both the dynamical phase and the geometrical one. In a traditional ring resonator without the twist, the resonance modes are purely determined by the dynamical phase, such that the integer azimuthal mode number $m{\prime}$ can be found as $2\pi {m}_{\pm }^{\prime} ={\varphi }_{\pm }+\beta L$, which only depends on the two propagation constants of the fast and slow axes, i.e. ${\beta }_{F}$ and ${\beta }_{S}$.

In contrast, in a Möbius ring resonator, the torsion term brings in an additional Berry phase, as a result, the new azimuthal mode number $m$ becomes:

$$2\pi {m}_{\pm }={\varphi }_{\pm }+\beta L+{\gamma }_{\pm }(L)$$

(5)

$${m}_{\pm }={m}_{\pm }^{\prime} +\frac{{\gamma }_{\pm }}{2\pi }$$

(6)

The azimuthal mode number now turns into a fractional one depending on the Berry phase term. Previously, half-integer azimuthal modes were studied in a single-strip dielectric Möbius cavity, where the three-dimensional surface of the strip can support both the transverse magnetic (TM) and transverse electric (TE) polarization modes⁷, in a similar manner of slow and fast modes in the current work. In both cases, the twisted segments depending on splicing angle give a rise to the geometrical dynamics resulting in the current fractional modes.

Topological resonances in a Möbius ring resonator

Experimentally, Fig. 2 shows the transmission resonance spectra of a normal ring resonator without the twist and the Möbius ring resonator with a 90° twist. Here the initial input signal is launched through a segment of normal optical fiber without PM, with a help of a fiber polarization controller, the signal input polarization state can be manipulated in order to couple into both degenerated modes (see “Methods” section). As shown in Fig. 2a, the transmission spectrum of the normal ring resonator reveals two consecutive modes along both slow and fast axes. The individual slow and fast modes remain close to each other due to the fact that $\varDelta \beta ={\beta }_{F}-{\beta }_{S}$ is small, ~0.1% (see Supplementary Note 4). And both modes share a similar free spectral range (FSR) of ~60 MHz as well. In contrast, the Möbius ring resonator clearly exhibits a distinct resonance spectrum for the slow and fast modes in Fig. 2b: the slow and fast modes shift oppositely to the two spectrum sides as compared to the normal ring resonator case. Now the “slow” modes (blue) now seem to be separated from the “fast” ones (red) for ~30 MHz, both modes still maintain the original FSRs. In fact, these resonances are hybrid modes coupled with both modes along the slow and fast axes^19,20,21. Consider the Möbius ring case when $\tau L={90}^{^\circ }$ in Eq. 3, the eigenstates read ${A}_{\pm }=\left(\begin{array}{c}\pm \varOmega -\varDelta \beta /2\\ -i\tau \end{array}\right)\approx \tau \left(\begin{array}{c}\pm 1\\ i\end{array}\right)$, assuming small $\varDelta \beta$. These two modes correspond to two circularly polarized eigenmodes, i.e. left and right, at the coupling point. Experimentally, we can choose the input signal’s polarization states to be solely left or right circular polarization by a polarization controller. As a result, the transmission spectra become distinguishably separated for the left and right circular polarized inputs as shown in Fig. 2c, d. These topological modes still maintain the same FSRs as in Fig. 2a, b, but shift the resonances in the spectra due to the combination of the extra dynamical phases and the Berry phase in Eq. 5.

Fig. 2: Transmission spectra of a polarization-maintaining (PM) fiber ring resonator.

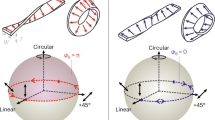
a At 0° twisting angle, with a linear polarization input, the PM fiber ring resonator has two eigenmodes characterized by azimuthal mode number n and m in the fast and slow axes, respectively, with a little separation due to the birefringence. b at 90° twisting angle, with a linear polarization input, the two eigenmodes are shifted due to the additional dynamic and geometric phases related to the twisting. At 90° twisting angle, the transmission spectrum of left circular polarized light (c) and right circular polarized light (d).

To gain more physical insights into these topological modes and understand the effect of Berry phases, we have studied the frequency spacing $\varDelta \omega =2\pi c({m}_{+}-{m}_{-})/L$ (see Supplementary Note 1)between the two classes of modes with mode number ${m}_{\pm }$ in Eq. (6) when varying the twisting angle at the splice point as shown in Fig. 3a. In this manner, the experimental measurement of the frequency spacing instead of individual modes can reduce some common external noises/perturbations like prior works^22,23. As shown in Fig. 2, this twisting process indeed induces some frequency shift of the modes as compared to the non-twisted case. However, it is hard to distinguish the Berry phase part from the dynamical one, moreover, there are some external perturbations like temperature, and fiber strain, which causes the shift of the whole resonance spectrum, this prevents us from directly comparing the twisted cases to the non-twisted one. Instead, the frequency spacing between the “+” and “-” modes only depends on the intrinsic properties, i.e. $\beta$ and $\varDelta \beta$, not external ones, enabling temperature-independent rotation sensing in prior works^19,21. This method helps to reveal the nature of the Berry phase in the current work.

Fig. 3: Observation of Berry phase-induced mode splitting.

a The twist angle denoted by $\theta$ is varied to observe the transmission spectrum. b Theoretically calculated Berry phase (without the dynamical one) at a different twisting angle, the referencing dashed line marks the zero-phase level. c The experimental observation of the mode spacing of fast and slow axes at various twist angles and the frequency spacing between the two modes is visualized in the inset. d Theoretically results of the mode spacing by including both the dynamical and Berry phase.

The direct analytical results of the Berry phase calculated from Eq. (4) are shown in Fig. 3b with a twisting angle from 0°−360°. There are two main features: (1) The deepest dip can be found around 125° angle. (2) the non-zero Berry phase is present at 360°, leading to an additional frequency separation between the “+” and “-“ modes. In the real experiment, it is accessible to obtain each mode’s resonance frequency, i.e. ${\omega }_{+}$,${\omega }_{-}$ and their difference $\varDelta \omega$. However, the main component in this frequency splitting is the dynamic one (See Supplementary Note 1), while the Berry phase’s contribution is much less. But the two main features brought in by the Berry phase do manifest themselves in the overall spectrum calculated from Eq. 5 in Fig. 3d. Here the frequency spacing does dip around 125° angle and does not return to zero (0° case) at 360° angle. These phenomena have also been observed experimentally in Fig. 3c, where the frequency spacing between the “+” and “-“ modes are recorded during the twisting angle variation from 0° to 360°.

Without the twist at 0°, the “+” and “-“ modes are initially close to each other in Fig. 4a. When increasing the twisting angle from 0°, the two classes of modes, i.e ± modes, begin to separate oppositely in the spectrum due to the polarization hybridization between the fast and slow axes of PM fiber^19,20,21. And the ${m}_{+}$ and ${m}_{-}+1$ modes (red and blue curves in Fig. 4a, respectively) are approaching each other. At 180°, these two resonance modes meet up, however, there is no mode crossing between the two. Above 180°, as the twisting angle increases, the ${m}_{+}$ and ${m}_{-}+1$ modes begin to separate (see Supplementary Note 2), while the ${m}_{+}$ and ${m}_{-}$ modes tend to remerge again until 360°. Note that, by comparing the frequency spacing $\varDelta \omega$ at 0° (Fig. 4a) and 360° (Fig. 4g), $\varDelta \omega$ has broadened from 5.4 MHz to 10.7 MHz. This extra frequency spacing clearly depicts the nonvanishing Berry phase occurred at 360° as shown in Fig. 3. Moreover, this nonvanishing Berry phase induced frequency spacing can be also extended to a higher twisting angle (see Supplementary Note 3).

Fig. 4: Berry phase enhanced mode separations.

a–c frequency spacing of two classes of resonance modes (red for + mode, blue for – mode) at 0° twisting angle. d–f The frequency spacing of two resonance modes and their consecutive ones during the variation of twisting angle. g–i Frequency spacing of two classes of resonance modes at 360° twisting angle. The pump wavelength is (a, d, g): 1550.2607 nm, (b, e, h): 1550.6989 nm, and (c, f, i): 1551.0745 nm. a, b The initial spacing (0°) is narrowed when the pump wavelength is increased and (g, h) the final spacing (360°) is both broadened due to the non-zero Berry phase. A flipping of the resonances is observed by comparing (c) 0° and (i) 360° cases also due to the additional Berry phase.

Ideally, such a Berry phase can also participate in the polarization hybridization between two modes with different order numbers. Without the twist, two polarized modes, possibly with different mode numbers $m$ and $n$, along the fast and slow axes are of different free-spectral range as shown in Fig. 4a–c. As a result, they firstly depict a frequency splitting ~ 5.4 MHz around 1550.2607 nm, but this separation is narrowing down to ~ 3.8 MHz around 1550.6989 nm, finally, they cross in the spectrum, i.e. with a spacing ~ −2.7 MHz. However, all the scenarios exhibit a similar evolution trend when varying the twisting angle in Fig. 4d, e: first, these modes are splitting apart until experiencing avoided mode crossing at 180°, then they remerge again till 360° as described above. Surprisingly, in Fig. 4f, this leads to an intriguing flipping of the two modes at 360° (Fig. 4i) as compared to their 0° case (Fig. 4c). In contrast, the other two cases in Fig. 4a, g and Fig. 4b, h only show a broadened mode splitting. But all three dynamics point to the same topological origin.

Conclusions

In summary, we experimentally demonstrate a Möbius ring resonator with topological resonances, in which their associated mode numbers are fractional, resulting from the additional Berry phases during the coherent evolution along two polarization axes in the Möbius ring. There are a few possible impacts on the optics, quantum physics, and coherent wave systems: the observed topological transport of circularly polarized light may enable uni-directional chiral transmitters/absorbers, i.e. only allowing one particular polarized wave to transmit in one direction while blocking/absorbing the others, meanwhile, this action will be reversed for the other polarized waves in the other transmission direction. Secondly, the additional Berry phase can be actively controlled through the twisting angle, hence, it may open an avenue for coherently controlling the frequency spacing between two classes of modes with different polarization. This is crucial for some fiber-based sensing applications²¹, e.g. gyroscope, temperature, and strain sensing, where the actual two-mode frequency spacing can be better immune from external perturbations, greatly enhancing the sensitivity. At last, we believe these results are universal across multidiscipline in microwaves, acoustics, mechanics, and matter waves, hence it provides opportunities for practical applications of coherent control in information processing and wave dynamics.

Methods

Experimental system

Experimentally, we use polarization maintaining fiber to change the polarization states on the Poincare sphere. The fast and slow axes of the PM fiber both work with a refractive index difference of ~0.1%. The experimental setup is illustrated in Fig. 5, we connect the two ports of the PM fiber coupler to form a ring loop with a tunable flange and the twist angle between the fast axis of the two ports can be changed conveniently.

Fig. 5: Experimental setup to observe the topological resonance.

The port2 and port3 are connected with a tunable flange to form a polarization-maintaining (PM) ring resonator, the transmission signal is collected with a detector and the transmission spectrum is observed on the oscilloscope (OSC).

In a general case, when the fast axes of port2 and port3 are aligned, there are two eigenmodes in the resonator, one is propagating in the fast axis and the other is in the slow axis, the two modes are close in frequency in the transmission spectrum. When the two fast axes are misaligned, the two modes begin to separate from each other in frequency. In the experiment, the angle is changed by 360° and the frequency difference is recorded at the corresponding angle.

Polarization state control

A special case exists at the angle 90°, where the fast axis is just connected to the slow axis. In this case, the polarization will be converted to its orthogonal state after one circle evolution and will be converted back to its original state during the next circle evolution to meet the resonance condition. The polarization state evolution behavior is similar to the Möbius strip. The eigenstates in this case are left/right circular polarized states. Experimentally, we input circularly polarized light and observe the Möbius ring resonator transmission.

The circularly polarized light can be produced with the setup in Fig. 6, where the PBS will split the polarized light into different arms. One arm is wrapped around cylindrical PZT tightly. The stress induced by the PZT will be controlled by the voltage to change the phase in this propagating arm.

Fig. 6: Experimental setup to produce circularly polarized light.

The whole setup is composed of polarization-maintaining (PM) fiber. The input laser is splitted by fiber polarization beam splitter (PBS). The Piezoelectric ceramics (PZT) will change the radius with an applied electric field to induce stress in the upper arm, so the phase can be modulated.