Introduction

Water under extreme conditions has been investigated for over a century due to its ubiquity throughout the universe and fundamental importance for life. Not only does water have a complex phase diagram, with at least 20 different ice phases1, it is one of the few materials known to freeze on nanosecond time scales2. Most liquids become too hot to solidify under single-shock (adiabatic) conditions, because thermal diffusion cannot keep up with the rapid temperature rise during compression. Even when freezing is thermodynamically possible, phase transformation times (hundreds of microseconds to seconds) are generally longer than dynamic compression can be maintained3.

Quasi-isentropic compression creates much lower temperatures than single-shock compression. Isentropic compression of water crosses the ice VII melt line around 2.5 GPa (Fig. 1), creating a metastable liquid until capabable of undergoing a first-order phase transition on nanosecond time scales. The 6–7 GPa pressure where this transition takes place has been defined as the metastable limit. That transition is characterized by contraction in particle-velocity measurements4,5,6,7, loss of optical transparency8, and x-ray diffraction patterns consistent with the ice VII phase9. Dynamic compression experiments allow both the metastable liquid and kinetic behavior to be investigated, which has huge implications for our general understanding of phase transitions and the classical nucleation theory (CNT) used to model transformations in extreme conditions10,11,12,13.

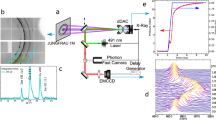
Fig. 1: Schematic representation of dynamic compression of liquid water to ice VII and the compression path followed.
figure 1

a An impactor imparts a shock wave on the sample, which rings back and forth between the sapphire windows creating pressure jumps. Velocimetry and pyrometry are collected from the backside of the sample. Even after crossing the melt line water remains a metastable liquid. Upon freezing the latent heat brings the water to the melt line. Previous results lead to the assumption of complete solidification to ice VII (bcc)2,4,5,6,7,9,12, which would result in the temperature dipping back into the ice VII phase. However the results in this paper show instead the creation of a mixed phase, where the temperature rides along the melt line. b The phase diagram for water showing the measured melt line from Reference20 and the calculated isentrope (compression path) from Reference4. For homogeneous nucleation it was previously established the liquid remained in a metastable state until 6-7 GPa, defining the commonly referenced metastable limit. Molecular dynamic snapshot of ice VII reprinted from Reference18 with the permission of AIP Publishing.

Full size image

The nucleation process can be divided into two categories depending on peak pressure and window material. Heterogeneous nucleation occurs over hundreds of nanoseconds below 5 GPa when water is dynamically compressed in the presence of silica8,14. Without such assistance from silica, water seems to remain a metastable liquid until 6–7 GPa, at which point homogeneous nucleation begins causing a rapid phase transformation (tens of nanoseconds, depending on the water layer thickness) evident from the particle-velocity pullback2,7. The pullback arises because ice VII is denser than liquid water and temporarily reduces the pressure exerted at the sample/window interface during the volume contraction. Optical transparency loss in both cases indicates coexistence of two phases with different refractive indices, leading to optical scattering. Optical transparency is quickly recovered in the homogeneous case, suggesting that the scattering sites have disappeared. One explanation for this behavior is the compressed sample becomes a fully solid transparent layer of ice VII2. Researchers have described this process as hypercooling2,11, a term used for deeply undercooled metallic systems15,16.

Hypercooling is achieved when the metastable liquid completely crystallizes during recalescence, i.e. latent heat of solidification is not sufficient to raise the sample to the equilibrium melting temperature (Tm). The temperature change due to crystallization is:

$$\Delta {T}_{Q}\approx \Delta {h}_{f}/{c}_{p}({T}_{m}).$$
(1)

where Δhf is the enthalpy of fusion and cp is the liquid’s isobaric specific heat (approximately constant). As long as temperature remains above Tm − ΔTQ, freezing heats the liquid phase to the melt line, suppressing subsequent growth of solid nuclei on short time scales. Temperatures below that threshold are said to be hypercooled because latent heat emission does not bring the liquid back to the melt line and solid nuclei can grow without the need for latent heat to diffuse away from the solid-liquid interface. Hypercooling has been used to describe extremely fast growth rates measured in dynamic compression experiments on water over the past decade2,7, and incorporated into a dual-temperature CNT-based kinetic model used to describe phase changes in both water and gallium in extreme conditions10,11,12,13.

In this paper we report the first, to the best of our knowledge, time-resolved optical pyrometry measurements during dynamic compression of liquid water to ice VII, where both the temperature during isentropic compression and latent heating during solidification are measured and compared to previous models4,11,17,18. These temperature observations expose two major inconsistencies with previous theories. First, solidification is clearly evident below the previously defined 6–7 GPa metastable limit, contradicting models that do not solidify when water is compressed to <6 GPa under similar loading rates11. Second, the hypercooling description is incorrect: latent heat given off during solidification raises the temperature to the melt line, where it exists in a mixed state. A theory is proposed to explain the contradiction between previous transmission loss followed by recovery, indicating complete solidification, and the results shown here, indicating a mixed phase (Fig. 1).

Results and discussion

All experiments described here begin at ambient conditions and become hotter due to adiabatic compression. As such, most of the ice structures available to water are thermodynamically irrelevant in this discussion. The ice VII region is the only verified equilibrium structure accessible to these experiments (Fig. 1).

Pressure and temperature versus time profiles for each experiment are shown in Fig. 2. The former was measured with photonic Doppler velocimetry (PDV), which tracks particle velocity at the sample-window interface. The latter was measured by mid-infrared pyrometry, using emission from the OH vibration near 3000 nm. As discussed in the Methods section, radiance throughout the water sample contributes to the pyrometry measurement. Hypothetically, material near the sapphire window could be significantly cooled by thermal conduction, reducing measured temperature below the bulk value. Such cooling would be limited to <0.5 μm length scales by the thermal diffusivity of water (10−7 m2/s) for the 1000 ns experiment time scale; finite boundary conductance further inhibits cooling through the sample-window interface19. Spectral calculations indicate that around 13% of light collected in the first three experiments originates from a 1 μm surface layer, dropping to much less than 1% in the second three experiments due to band pass filter change. Temperatures reported here are representative of the sample bulk, and the agreement between experiments 3–4 (same pressure state, different band pass filters) suggests that surface temperatures may not be all that different from the bulk.

Fig. 2: Pressure and temperature versus time profiles for each of the six experiments.
figure 2

The pressure is shown by the left/blue scale, while temperature is on the right/red scale for (a) experiments 1-3 (250 μm liquid layers), and (b) experiments 4–6 (500 μm liquid layers). Peak pressures were 4.7, 5.7, 7.5, 7.5, 10, and 12 GPa, respectively. Error bars were determined from the combination of the standard deviation over 300 ns at peak pressure and the 5% systematic uncertainty diagnosed from experiment-to-experiment.

Full size image

The first two experiments shown in Fig. 2 had peak pressures below the previously established metastable limit: no obvious pullback was observed at 4.7 GPa, but a long-lasting pressure decrease is evident at 5.7 GPa. Experiments 3–6 showed pullback features around 6–7 GPa, consistent with previous work2,7,12 despite each work using different experimental apparatus’, baseplate materials (sapphire and copper), and window materials (Al-coated α quartz, Al-coated sapphire, and uncoated sapphire). This agreement suggests homogeneous nucleation in the bulk water dominates as opposed to heterogeneous nucleation at the different interfaces or at impurity sites in the bulk12.

In experiments 1–2, temperature increased gradually with each pressure jump until reaching the peak pressure where the temperature rate rapidly increases. This feature is much more apparent in Fig. 3, where pressure vs. temperature for each experiment is plotted against the phase diagram20 and calculated isentropic compression path4. In experiments 3–6, there is a rapid increase in temperature that coincides with the pullback feature shown in the pressure profiles. These two features indicate a first-order phase transition: the pullback is consistent with density increase, which momentarily reduces pressure on the rear window; and the rapid temperature increase results from latent heat emission. Previously, the trough of the pressure pullback feature was interpreted as the end of nucleation and the onset of complete solidification2,11,12. However, Fig. 3 shows the trough of the pressure pullback coincides with when the latent heating reaches the melt, and then remains along the melt line indicating a mixed state. Experiment 6 is the only experiment that gives some indication of complete solidification; around 11 GPa the temperature dips into the ice VII phase. However, additional experiments to a higher peak pressure are needed to verify if the temperature continues to stay below the meltline and in the ice VII phase.

Fig. 3: Measured pressure versus temperature profiles for each experiment shown against the melt line, calculated isentropic compression path, and calculated hypercooling limit.
figure 3

Pressure versus temperature profiles for (a) experiments 1-3 and (b) experiments 4-6; legends show peak pressure in GPa. Steep temperature increases indicate latent heat emission from the formation of ice. Error bars were only added to the last data point in each set to avoid clutter. Error bars represent the 5% systematic uncertainty from experiment-to-experiment. Note there is no indication of time in these plots, so the rapid increase in temperature during the lower pressure shots (1–2) occurs after peak pressure state has been held for tens to hundreds of nanoseconds. For example, temperature change over 450-550 K takes place during ~ 700 ns in shot 2 but only ~ 130 ns in shot 4.

Full size image

The undercooling values of pure metals necessary to reach the hypercooling limit are on the order of (0.3 − 0.4)Tm16. If this criterion is applied to the liquid-ice VII melt boundary, then it can be seen from Fig. 3, quasi-isentropic compression would not reach the hypercooling limit until ~13 GPa.

It is evident from Fig. 3 that water froze in the lower pressure experiments (1–2), but no transmission loss was reported in previous experiments using sapphire windows at 5 GPa8, indicating there was no ice formation through either type of nucleation process. Although the pressure pullback features are difficult to pinpoint in the velocity profiles, latent heat is obvious in the temperature measurements. Previous work may also have missed the freezing transition because peak pressure was not held long enough. Smaller sapphire windows limited the duration of uniaxial strain to 800–900 ns6,14, but the transition just starts to appear around 800 ns at 5.7 GPa in experiment 2 and even later in experiment 1. This suggests the ice clusters could form via heterogeneous or homogeneous nucleation in experiments 1–2, and transmission loss experiments with thicker sapphire windows at these lower peak pressures should be explored in the future to determine which type of nucleation process exists and if the metastability limit for homogeneous nucleation needs to be redefined.

The pressure and temperature were both constant at a handful of times during the six experiments, allowing P-T states to be extracted. These points are plotted in Fig. 4. Error bars were determined from the combination of the standard deviation at each plateau and the 5% systematic uncertainty diagnosed from experiment-to-experiment (fiber bends, feed through coupling, and calibrating outside the chamber). Since the detector limit was roughly 375 K, it was difficult to accurately detect temperatures during the first pressure jumps.

Fig. 4: Measured P-T states during dynamic compression compared to three calculated isentropic compression paths, the dual-temperature model, and the hypothesized plastic ice phase.
figure 4

Steady pressure-temperature states (green circles) extracted from each plateau in experiments 1–6 compared to the melt line from Reference20 (black) and three calculated isentropes from Reference4 (blue and maroon, 3 & 4 J/g ⋅ K) and Reference17 (purple, Myint). Plastic bcc phase boundaries from Reference18 are shown in red, and the dual-temperature kinetic model from Reference11 is shown in purple (dashed). Error bars were determined from the combination of the standard deviation at each plateau and the 5% systematic uncertainty diagnosed from experiment-to-experiment.

Full size image

The obvious structure for solid water clusters is ice VII, but this is not the only explanation. A plastic crystal phase18 predicted to be thermodynamically stable with respect to ice VII water is depicted in Fig. 4; the slope is curiously similar to the trajectory observed here. The plastic crystal phase has oxygen atoms arranged the same as in ice VII (bcc), but the water molecules are able to rotate freely. Limited structure information is available in dynamic compression experiments, and time-resolved x-ray diffraction on water could not distinguish between crystalline ice VII and plastic ice9. Supercooled water could form a plastic ice phase, which might then transition to ice VII. Molecular rotation during dynamic compression needs to be explored before concluding which structure is formed.

Current EOS models from both Dolan4 and Myint17 use a constant heat capacity of 3 & 4 J/g ⋅ K and 3.23 J/g ⋅ K, respectively. It is clear from Fig. 4, an isentrope with a heat capacity of 4 J/g ⋅ K (closer to ambient liquid) has better agreement with the early temperatures than an isentrope with a heat capacity of 3 J/g ⋅ K, while the opposite is true for the higher temperatures around 6 GPa. Since Myint’s isentrope captures the metastable liquid points within error, that heat capacity can be used with Eq. (1) and the average temperature change (measured between 6–7 GPa during solidification) from experiments 1–6 ( ~ 109 K) to estimate the latent heat of fusion for ice VII, 6.3 kJ/mol. This is a rough estimate because it assumes all of the liquid froze and ignores if there are any compression heating effects during the transition. The rest of the data points all have excellent agreement with the previously measured melt line.

The dual-temperature model, depicted in Fig. 4, from Myint et al. is a posteriori analysis derived from coupling CNT and growth with hydrodynamic simulations to reproduce observed transition kinetics in dynamic compression experiments11. This model assumes there is essentially no thermal boundary layer at the solid-liquid interface and tracks the liquid and ice temperatures separately. This means there is only one temperature along the isentrope until the phase transition begins around 6–7 GPa, then the ice phase fraction becomes much hotter than the liquid phase until complete solidification. The ice phase fraction temperature is plotted in Fig. 4 (the liquid phase temperature is excluded for simplicity). Myint et al. showed the model does an excellent job of tracking the pressure and replicating the pullback feature. It is clear from Fig. 4 the temperature prediction for latent heat release is within error of the measured temperature, but remains within the ice VII phase due to the phase fraction reaching unity (aka complete solidification). It is important to note the authors compare this model to a single temperature model, where the phase fraction only reaches ~ 60%, has the correct pullback feature in pressure, but kinetics are slightly faster during the pullback than in experiments. It would be useful to compare the temperatures predicted from the single temperature model to the data here, however it has only been published for a synthetic drive, and is not a direct comparison13.

It was previously hypothesized that water completely solidified to ice VII at ~ 7 GPa because of the simultaneous loss and recovery in pressure and transmission. The current results indicate otherwise—the mixed state continues well above 7 GPa—so an alternative explanation is presented here. Clusters of ice form spontaneously behind the shock front that drives the nucleation rate to some sufficiently high level; liquid ahead of this shock is already metastable due to previous compression. When the clusters are sparse, they scatter light incoherently and reduce the optical transparency of the sample. However, when cluster density increases to the point where many clusters are present over the optical wavelengths passing through the sample, coherent scattering reduces loss until the sample appears transparent once more21.

A similar argument explains transparency of the mammalian cornea and lens22,23, where regions of high refractive index are densely packed in a low refractive medium. Although scattering occurs at all region interfaces, collective effects drastically reduce overall scattering23. The total cross-section of N scatterers is24:

$${C}_{total}=N{C}_{sca}S(\phi )$$
(2)

where Csca is the scattering cross-section of an individual scattering region, ϕ is the volume concentration of scattering regions ( ∝ N), and S(ϕ) is the structure factor. The structure factor gives the amount of reduction in total scattering due to destructive interference. For the simple case of small “hard sphere” scattering (r ≤ 70 nm) the structure factor is given by25:

$$S(\phi )={(1-\phi )}^{4}/(1+4\phi +4{\phi }^{2}-4{\phi }^{3}+{\phi }^{4}).$$
(3)

As shown in Fig. 5, as the concentration of scatters increases, there are more scattering events, but also more destructive interference. The maximum total scattering occurs around 13% and decreases beyond this concentration22,23,24. To put this in perspective, it was recently proposed the critical cluster size for homogeneous nucleation was <10 nm using TIP4P/2005 and TIP4P/ice water models26. Using that cluster size, a 1% volume fraction of ice would mean that the average number of scatterers in every 500 nm wide cubic volume is greater than 2000. Coherent effects would surely be important in the passage of visible light, reducing sample extinction. Dynamically compressed water does not have be completely frozen to become optically transparent.

Fig. 5: The transition from incoherent to coherent scattering.
figure 5

The total scattering for small hard sphere scatters vs. their volume fraction.

Full size image

At this point, heterogeneous nucleation needs to be discussed in order to avoid confusion. This is because heterogeneous nucleation also produces a mixed state; however, the transmission decreases from 1 to 0 as the phase change goes towards completion. Heterogeneous nucleation creates big crystals that continue to grow outward from the surface in a dendrite fashion; while, homogeneous nucleation creates small (<10 nm) clusters all throughout the sample. Instead of the clusters growing into dendrites, more clusters appear of similar sizes. Thus, the different transmission responses.

In summary, temperature measurements on dynamically compressed water have been reported for the first time, to the best of our knowledge, as the metastable liquid transformed to a solid phase. Quasi-isentropic compression does not hypercool the sample, and instead a mixed state is formed that follows the melt line. Nucleation occurs at pressures as low as 4.7 GPa, but additional experiments are needed to verify the nucleation process. These results provide constraints for nucleation models, and suggest an updated EOS with a variable heat capacity could better fit the data. Additional measurements are needed to characterize the solid phase created by dynamic compression. This technique should be used to further investigate other materials with absorption bands located between 2–5 μm, as described in the methods section.

Methods

Quasi-isentropic compression was achieved through multiple shock wave loading using the experimental configuration in Fig. 1. A thin water sample was sandwiched between two optical sapphire windows. The impact surface of the buffer window was vapor deposited with 0.2 μm of aluminum to prevent light collection from an impact flash. The back window was coated with a half-moon-shape of aluminum for photonic Doppler velocimetry (PDV)27,28 measurements at the liquid/window interface while also allowing a clear view of the water sample for pyrometry. An impactor was accelerated using a gas gun, which produced a shock wave upon collision with the buffer window. The shock wave propagated through this window into the liquid sample, leading to reverberating shocks that compressed the sample to a peak pressure state. The sapphire impactor, buffer plate, and back window were 32 × 10 mm, 40 × 2 mm, and 42 × 16 mm in diameter and thickness, respectively.

Although water samples are significantly compressed (20-40%) during these experiments, density changes in the sapphire windows are quite small (<2–3%). Minor temperature increases (<5–10 K)29 in the windows are neglected here, as are distinctions between the primary Hugoniot and release/reshock states. In each experiment, the pressure histories were calculated from the apparent velocity, recorded by PDV, using the window-specific velocity correction30 and the Hugoniot curve for sapphire31. The reverberating shock compression path nearly follows the calculated isentrope for water4 until freezing occurs.

Pyrometry measures the time-resolved temperature of a thermal emitter. In this paper, temperature was extracted from voltage by calibrating an InSb detector with a blackbody source through a sapphire window at multiple temperature points, as shown in Fig. 6. The detector was calibrated on each shot day and Fig. 6 shows the calibration curve for shot 6. Sapphire emits no light in the spectral range of interest because of its transparency; interface (Fresnel) reflections accounted for by calibrating through a sapphire window, somewhat overcompensating for the sample-window reflection with a vacuum-window reflection (temperature calculations are slightly biased upward). During each experiment, infrared radiance from the water sample was collected from a 2 m long, 400 μm diameter ZrF4 fiber transparent to 1–4.5 μm. Light exiting the fiber was sent through a long-pass filter onto an amplified liquid-nitrogen-cooled InSb detector with a time-resolution of about 10 ns.

Fig. 6: Pyrometry schematic and calibration.
figure 6

The (a) schematic diagram of the calibration setup that was performed on each shot day, and (b) a representative calibration curve (shot 6).

Full size image

Water emits strongly around its 3 μm absorption peak, which can be described by absorption α(λ) at sample positions from x = 0 to x = d. The infinitesimal spectral radiance dBint ≡ dL/dλ at x = d due to emission from a sample layer at position x is:

$$d({B}_{int})=(\alpha dx)B(x)\,\exp \left[-\alpha (d-x)\right]$$
(4)

where B is the spectral radiance of a blackbody at temperature T(x). Integrating over the entire sample:

$${B}_{int}=\alpha {e}^{-\alpha d}\int\nolimits_{0}^{d}B(x){e}^{\alpha x}\,dx$$
(5)

leads to the standard result for an isothermal slab32.

$${B}_{int} ={B}_{1}\left(1-{e}^{-\alpha d}\right)\\ {B}_{1} \equiv \frac{{c}_{1}}{{\lambda }^{5}\left[{e}^{{c}_{2}/\lambda {T}_{1}}-1\right]}$$
(6)

In the opaque limit αd ≫ 1, an isothermal sample acts as a blackbody. If the sample were divided into two isothermal regions—bulk temperature T1 from x = 0 over thickness d1 and surface temperature T2 over thickness d2—the combined spectral radiance for these regions is as follows.

$${B}_{int}={B}_{1}{e}^{-\alpha {d}_{2}}\left(1-{e}^{-\alpha {d}_{1}}\right)+{B}_{2}\left(1-{e}^{-\alpha {d}_{2}}\right)$$
(7)

Both contributions are similar to Eq. (6), with the bulk contribution attenuated by passage through the surface layer.

Figure 7 illustrates how the absorption depth (1/α) of ambient liquid water varies across the pyrometer’s operating range. Spectral integration of Eq. (7) indicates that around 13% of emitted light through a 1.9 μm long-pass filter (chosen to filter any stray light from PDV) originates from a 1 μm surface layer of water; experiments 1–3 used this configuration with 250 μm thick water samples. To further emphasize bulk temperature over a (possibly cooler) surface temperature, experiments 4–6 switched to a 3.5 μm long-pass filter and 500 μm thick water samples, making surface contributions to the pyrometry signal negligible. In all cases, blackbody emission from the bulk occurs over a significant portion of the pyrometer spectrum.

Fig. 7: Absorption depth dependence across the pyrometer’s operating range.
figure 7

Optical absorption depth34,35 shown in blue, the vertical lines indicate long-pass filter edges used in the experiments.

Full size image

Cross-timing between the radiance and velocimetry detectors was measured to be 101 ns. However, since the radiance and PDV fibers view different sample locations, small amounts of impactor tilt add an additional and unknown time shift. Radiance profiles were time-shifted according to the distinct coinciding temperature and pressure steps from the PDV data. When clearly defined steps were not visible in the radiance profile, matching signatures between the radiance and release wave were used. The shifts were between 85 and 100 ns, with exception to experiment 4, which was corrected by only 50 ns. Impact flash leaked onto the pyrometer in experiment 3 but quickly recovered and the saturated signal was discarded for clarity. The detector noise floor was about 375 K, and the pyrometry systems were calibrated with a blackbody source prior to each experiment. The emissivity is assumed to be 1, which is plausible because the samples were thick enough to be opaque around the absorption peak and reflectance is low at the water-sapphire interface. Previous work on vibrational overtones in water indicate that the absorption peak does not move significantly during isentropic compression33.