Machine-learning-enhanced automatic spectral characterization of x-ray pulses from a free-electron laser

Abstract

A reliable characterization of x-ray pulses is critical to optimally exploit advanced photon sources, such as free-electron lasers. In this paper, we present a method based on machine learning, the virtual spectrometer, that improves the resolution of non-invasive spectral diagnostics at the European XFEL by up to 40%, and significantly increases its signal-to-noise ratio. This improves the reliability of quasi-real-time monitoring, which is critical to steer the experiment, as well as the interpretation of experimental outcomes. Furthermore, the virtual spectrometer streamlines and automates the calibration of the spectral diagnostic device, which is otherwise a complex and time-consuming task, by virtue of its underlying detection principles. Additionally, the provision of robust quality metrics and uncertainties enable a transparent and reliable validation of the tool during its operation. A complete characterization of the virtual spectrometer under a diverse set of experimental and simulated conditions is provided in the manuscript, detailing advantages and limits, as well as its robustness with respect to the different test cases.

Introduction

X-ray free electron lasers (XFELs) produce x-ray pulses characterized by extreme brightness, high degree of transversal coherence, and temporal duration of the order of femtoseconds or shorter^1,2,3,4,5. The most common mean of generating these pulses is the self-amplified spontaneous emission (SASE) process^6,7,8, which is initiated by the intrinsic shot noise of accelerated electrons, and is therefore stochastic in nature. As such, x-ray pulses inherently fluctuate in spectral, spatial and temporal properties. A detailed characterization of these properties is instrumental to accurately interpret measurements at XFELs, and to ensure full exploitation of the potentialities of these machines, even more so accounting for the steady increase in breadth and complexity of operation modes being developed^9,10.

To this end, several x-ray beam diagnostics devices are available, each with a set of advantages and disadvantages. These are characterized by a certain degree of compatibility with experimental requirements, in terms of measurement accuracy, fraction of x-ray pulses characterized, and invasiveness. Furthermore, diagnostic devices require a varying level of expert intervention for their usage, such as in the derivation of calibration constants to transform their readings into physically-meaningful output.

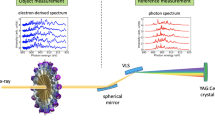
The European XFEL^5,11 is a megahertz-repetition-rate XFEL operating in burst mode. It delivers 10 Hz trains of up to 2700 x-ray pulses, whose separation can be as low as 222 ns, which is equivalent to a repetition rate of 4.5 MHz. Among the diagnostic tools available at European XFEL¹², a non-invasive x-ray gas monitor (XGM)^13,14 is used to quantify the energy of the x-ray pulses and their average position. To characterize spectral properties of soft x-ray pulses produced by the SASE3 beamline, mainly two different devices can be utilized. The grating-based spectrometer (GS, example data in Fig. 1a)¹⁵ consists of a variable-line-spacing grating monochromator operating in spectrometer mode together with an imager¹⁶. The GS provides high-resolution spectral measurements with an energy-dependent resolution δE/E < 0.05%¹⁵, but it is fully invasive and thus disrupts the beam for further downstream experiments. Additionally, owing to its detection system, only one spectrum per train can be collected. The gas-based photo-electron spectrometer (PES, example data in Fig. 1b)^17,18 consists of 16 detectors measuring the time-of-flight of photo-electrons at angles relative to the beam (further details are given in Supplementary note I). Differently from the GS, it allows for pulse-resolved beam spectral diagnostics at up to 4.5 MHz in a non-invasive manner¹². While the grating spectrometer has a high signal-to-noise ratio and a simple calibration, the PES has a much more complex non-linear calibration by virtue of the underlying measurement principle, and a lower signal-to-noise ratio and resolution.

Fig. 1: Schematic of the virtual spectrometer input and output sources, and of the different operational phases.

a Representative data from the grating spectrometer (blue solid line), which is used during the training phase (dashed line), and b time-of-flight data from the photo-electron spectrometer (dark green and orange lines), which is used during the training and inference (thick solid black line) phases. For the latter, only two out of sixteen channels are shown. Pulse energies provided by the x-ray gas monitor are employed during training and inference. c Representative data generated by the virtual spectrometer (red line), together with the 68% confidence level uncertainty band around the prediction (red band). d Selected region-of-interest of manually calibrated photo-electron spectrometer with energy axis on the top for each channel. Each channel has a different time-of-flight offset and independent calibration constants. e Comparison between grating spectrometer and virtual spectrometer in a selected region-of-interest. The Pearson correlation coefficient, ρ, between the GS and VS spectra can be seen in the plot.

Using an approach based on ghost imaging, Li et al.¹⁹ devised a method to combine the advantages of the two devices, providing therefore means to characterize each x-ray pulse precisely, non-invasively, and exploiting the calibration of the GS alone. To achieve so, data from both devices are collected for a short period of time, and a map between them is fitted. Once this relationship is known, the non-invasive device alone can be operated to obtain pulse-resolved, higher-resolution and calibrated spectra.

The routine utilization of similar procedures could significantly optimize the beamtime usage at XFELs, by providing higher-quality data to steer experiments and interpret their outcome. To sustain regular operation, procedures must be as automated and robust as possible. Nonetheless, there are several elements in the approach by Li et al. which might be difficult to automate. Due to the abundant amount of noise in the PES measurements, relevant data should be selected and denoising techniques applied, so that the fit is not affected by it. Those steps are often done through careful analysis of the data which are not trivial to automate. Another critical element to enable reliable automation is the provision of an estimate of data quality, as the devices in question have themselves limited resolution, which propagates into the algorithm. Given that such a method requires stable operating conditions, any deviation from them must be established, in order to immediately inform of a decrease in data quality, so that contingencies can be planned. Overall, such methods must be easy to use and robust, so that scientists focus on the science and not on tuning one extra tool.

In this paper, we present the virtual spectrometer (VS, example data in Fig. 1c), a nondestructive diagnostic tool leveraging machine learning (ML) which improves the data quality of the PES, and automates its operation, through the fusion of information coming from several data sources. This is particularly advantageous during quasi-real-time monitoring of the experiment, allowing for its more reliable steering. By applying this correlation method, higher spectral resolution and higher statistics is obtained, e.g., in core-level photoelectron²⁰ or x-ray emission spectra²¹, since the electron or photon spectra can be recorded using directly the broad and intense SASE pulse, and the reduced performances upon conventional monochromatization of the x-ray pulses are avoided. Other examples, for which this method would be beneficial, are related to experiments involving resonant excitations in the sequential photoionization²² or stimulated Raman processes²³. The detailed knowledge of the spectral content of each pulse is in fact essential for the quantitative analysis of these nonlinear phenomena. Furthermore, this machinery can be leveraged to enable improved temporal diagnostics of XFEL pulses, for instance exploiting the angular streaking technique^9,24,25,26, for which high-quality spectral characteristics of the pulse are required.

Advances in ML have already been shown to be instrumental to either improve control^27,28,29,30 or diagnostics quality^{31,32,33,34,35,36} in photon facilities. Key elements of the VS are the transparency in providing data quality assessment, obtained through continuous uncertainty and resolution evaluation, and automation of the calibration procedure. Such automation is achieved by taking advantage of the SASE beam inherent properties. The VS is robust against noise, and has been tested and deployed at European XFEL as part of the portfolio of photon diagnostics tools available to scientists and XFEL operators.

The underlying principles of the VS are explained in the “Methods” section, while in the “Results and discussion”, we demonstrate the enhancement in resolution with respect to the PES obtained with both experimental and artificially produced data. The underlying principles of the VS are explained in the next section. The following sections demonstrate enhancement in resolution with respect to the PES obtained with both experimental and artificially produced data. A summary and an outlook conclude the paper.

Methods

Virtual spectrometer

Spectral measurements contain two elements: the signal produced by the XFEL beam and low-variance noise. The highly stochastic pulse-to-pulse behavior of a SASE beam⁸ can be used to devise a method for automated selection of relevant data. We therefore exploit principal component analysis (PCA)³⁷ to preserve high variance components of the input data.

The operation of the VS entails two main phases, training and inference. During the initial training, the XGM, the PES and the GS collect data synchronously. Subsequently, during inference, the GS is removed and an approximate estimate of the GS spectrum is obtained in a non-invasive manner from the the PES data and XGM pulse energies. The resulting spectrum is pulse-resolved, and with better resolution, compared to the PES one (see the “Simulation results” section). Figure 2 illustrates the general approach, which is further discussed in the following paragraphs.

Fig. 2: Schematic of the virtual spectrometer operation.

a During the training phase, data generated from the photo-electron spectrometer (PES, x), the grating spectrometer (GS, y), and the x-ray gas monitor (XGM, I) are collected. From this, the principal component analysis (PCA) projection maps P_p( ⋅ ) and P_g( ⋅ ), together with the inverse PCA map U_g( ⋅ ), are derived. Finally, the function f( ⋅ ), which predicts GS data from the PES and XGM inputs using data projected after the PCA step, is defined. b During the inference phase, data generated from the PES (${{{\bf{x}}}}^{{\prime} }$) and the XGM (${I}^{{\prime} }$) are collected and used to infer the higher-resolution spectrum, using the PCA projection map P_p( ⋅ ), the function f( ⋅ ), and the inverse PCA map U_g( ⋅ ). Finally, uncertainty is propagated.

A region-of-interest of 600 samples is identified for all 16 PES sub-detectors, by using a low-pass filter and identifying the maximum peak as the region center. By taking such a large region-of-interest, we can ensure that the relevant spectral features are stored. The large amount of noise coming from such initial generous data selection is filtered out by performing PCA on the photo-electron spectra, while preserving the key features. The pulse energy is also included in the PCA input, so that correlations between the spectra and the pulse energy can be used to reduce the data dimensionality. The number of principal components is chosen by checking the fraction of variables contributing to at least 90% of the cumulative variance, with a minimum of 600 components. In the best scenario, such approach corresponds to a nine-fold data reduction of the input data. PCA is also applied to the grating spectrometer data, with a threshold for the number of variables corresponding to a 90% cumulative variance, or at least 20 components.

After this pre-processing stage, a fit is performed, which maps the principal components from the PES to the principal components of the GS. The fit is performed using the Automatic Relevance Determination (ARD)³⁸ method. Weights with large uncertainty are set to zero, leading to a very robust fit. Further information on the choicfe of hyper-parameters for the method is given in Supplementary note IV. An uncertainty is also made available by calculating the root-mean-squared error between the obtained spectra and the GS measurement convolved with the obtained resolution function (see Supplementary note V). This allows scientists and operators to understand limitations of the approach in different regions of the energy spectrum.

Furthermore, the consistency between the training data and input data during inference is continuously monitored using two methods, which ensures that drifts in the data are identified, informing the operators that a retraining is necessary. In general, such an operation may be needed in case of PES settings changes, or in case the training dataset is no longer representative of the current conditions. The first method calculates a Z-score between the XGM measured pulse energies and the training averages, such that if such a value deviates strongly from zero, the operator knows that a significant difference with respect to the training set arose. As a second method, the PES input data is compared to the mean and covariance estimated in training and an indication of out-of-dataset samples is produced.

The performance during the inference phase is sufficient to ensure compatibility with quasi-real-time requirements, that is, the VS can generate spectra which can be used to effectively steer experiments. In the tests performed, a typical training phase entailed 20 minutes of data-taking (corresponding to about twelve thousand spectra collected at 10 Hz) followed by roughly 2 minutes of model training. In case of retraining of the VS, the GS setup takes roughly 30 minutes.

In the following and if not explicitly mentioned otherwise, when making comparisons with the calibrated PES data, the measurement performed at the channel at 0^∘ (horizontal direction) is shown in this article. The reason for this choice is the high signal-to-noise ratio in this channel, due to the almost completely horizontal polarization of the XFEL beam.

Results and discussion

Experimental results

We have tested the VS under a diverse set of realistic operating conditions, and estimated its resolution relative to the GS. In all cases, the data has been collected in two separate datasets with identical configurations, such that the first run is used for the model fit (training), and a second, statistically independent one for producing the test results (inference). More information on the datasets is given in Supplementary note II. As the reference spectrum from the GS is also collected in our tests, we can model the resolution loss in the VS as the convolution with a response function directly, and estimate a resolution within the scope of such a model. The estimated resolution therefore assumes that the GS measurement is a very accurate reference in comparison to the virtual spectrometer. Details on the mathematical model used for the resolution estimate are given in Supplementary note V. An additional validation is shown in Supplementary note VI.

Figure 3 shows the resolution of the VS (filled markers), as a function of the photon energy for different PES and machine conditions. The resolution of the PES direct measurement for the 0^∘ channel is shown for comparison using the same method for datasets D_A, D_B, and D_C (unfilled markers), with a manual calibration derived from using Simion³⁹ simulations. Points with the same markers correspond to the same analysed dataset and therefore, the same beam conditions and instrument settings. For each of these, the four different points correspond to a resolution estimate obtained after applying a filter in the given energy range highlighted by the horizontal bar (energy bin). This energy binning allows us to analyse the resolution as a function of photon energy. The general loss of resolution as energy increases seen in the PES is explored in the “Simulation results” section and it is related to the non-linear relationship between the measured time-of-flight and the photon energy. It should also be noticed that the signal-to-noise ratio is significantly lower in the highest-energy bin, leading to a worse resolution in that bin in most datasets. The mean spectra and their root-mean-squared error over all trains for each dataset are shown in Supplementary note XI, where it can be appreciated that there is almost no signal in the last energy bin.

Fig. 3: Resolution estimates for several x-ray beam conditions and photo-electron spectrometer (PES) configurations.

Smaller values in the resolution axis (δE/E) mean better resolution. Virtual spectrometer (VS) results are shown in filled markers. Each marker style corresponds to results from one of the datasets mentioned in the legend. Each result is shown in four photon energy bins (see the “Experimental results” section for more details). The PES (channel at angle 0^∘) measurements are shown with open markers for a few test cases which have been calibrated directly on the data indicated in Supplementary Table 1. The vertical uncertainty band corresponds to a 95% confidence level band estimated through the root-mean-squared error of the resolution in four random splits of the dataset. The horizontal bar corresponds to different energy bins in a dataset. The vertical axis on the right-hand-side shows the resolving power, defined as E/δE.

Note that the VS in datasets D_A, D_B, and D_C has a significantly better resolution, compared to the PES resolution achieved, and such a result has been achieved in only approximately 20 min of data-taking and a few minutes of model fitting, while otherwise a tedious and time-consuming calibration procedure would be needed. In dataset D_A, for instance, the average resolution of the VS is about 40% better than the highest signal-to-noise ratio PES channel for the same data. The improvement given by the VS in dataset D_B is approximately 36%, while it is 25% in dataset D_C. The VS combines multiple PES channels using PCA to select high variance components, together with its correlation to the GS, thereby taking advantage of multiple sources of information at once. Several effects may contribute to the difference in the observed level of improvement. The resolutions observed in the PES data for datasets D_A, D_B, and D_C vary at least due to the different required PES settings in each acquisition energy range. In the “Simulation results” section, we use simulations to show that miscalibrations of the PES may affect the PES resolution significantly, while the VS is resilient to them, as it takes advantage of both PES and GS data.

Comparing the tests with average photon energy of 917 eV (datasets D_B, D_D, D_E, and D_G), we notice that the resolution is strongly influenced by the pulse intensity, gas pressure, and other elements of the PES configuration, which vary in those datasets (see Supplementary Table 1). Datasets D_C and D_F differ due to usage of the so-called “interleaved” mode, in which the sampling rate is doubled, but half of the channels are made unavailable. We can see that the resolution is slightly worse in interleaved mode, indicating that, in this particular test, the loss of the channels has a higher impact, compared to doubling the sampling rate. To further explore more challenging conditions, in addition to target gas Ne, we also operated with N₂ and Xe in datasets D_H and D_I. The high photo-electron kinetic energy and the broad lifetime widths when using Xe as the PES gas in dataset D_I leads to poorer resolution, compared to the previous situations. Additionally, the spin-orbit interaction leads to splitting of the Xe orbitals 3d_3/2 (binding energy 689 eV) and 3d_5/2 (binding energy 676.4 eV), which is expected to have an effect in the PES resolution, and thereby, in the VS resolution.

Discrepancies between the VS and GS are not explained alone by the mathematical description of the resolution in Supplementary note V. The remaining effect is modeled as a residual uncertainty, which estimates the potential effect of the PES noise in the results. Supplementary note VII of the Supplementary Material shows the signal-to-noise ratio for each dataset on average. Notice that the estimated uncertainty band includes both the effect of the resolution loss and such noise, although the breakdown of the uncertainty band into resolution and noise is available to operators through the graphical user interface (see Supplementary note X). One method to reduce the effect of such mismodelling effects is detailed in the Supplementary note VIII: the idea is to smear the initial GS data, such that the final VS resolution is decreased, while the signal-to-noise ratio is increased. Operators may profit from such a trade-off, in case a high signal-to-noise ratio is favored to a worse resolution. This might be the case when the number of spectral modes of the x-ray pulse is limited, and knowing the average shape of the spectrum is desired.

As an additional validation step, the mean spectra and their root-mean-squared error over all trains obtained by the VS are compared with those by the GS in Supplementary note XI. There, average PES results for datasets D_A, D_B, and D_C are also reported. Excellent agreement is observed between the output of GS and the VS, while large differences are observed when compared with the PES data.

We further assess the fit quality in dataset D_A, by examining the χ² normalized by number of degrees of freedom, calculated by measuring the deviation of the prediction after the PCA step, normalized by the fit uncertainty. Such a variable is defined as

$${\chi }^{2}/{N}_{{{\rm{DOF}}}}=\frac{1}{{N}_{{{\rm{DOF}}}}}\,\sum_{k}{\left(\frac{{\bar{y}}_{{{\rm{pred}}},k}-{\bar{y}}_{{{\rm{true}}},k}}{\delta {\bar{y}}_{k}}\right)}^{2},$$

(1)

where ${\bar{{{\bf{y}}}}}_{{{\rm{pred}}}}$ is the PCA-transformed prediction, ${\bar{{{\bf{y}}}}}_{{{\rm{true}}}}$ is the PCA-transformed expectation, $\delta \bar{{{\bf{y}}}}$ is the fit uncertainty, and N_DOF is the number of degrees of freedom. If the fit produces unbiased and uncorrelated predictions of the GS principal components, its mean value is expected to be one. By assessing its deviation from unity as a function of the experimental setup, one may identify variables that contribute to the degradation of the fit quality. The average normalized χ² for the dataset D_A is 1.14, with a sample variance of 0.26 over the test dataset. Figure 4 shows the pulse energy versus χ² normalized by number of degrees of freedom. As it can be observed, the quality of the fit decreases the more the pulse energy deviates from its average value. For this reason, one of the data quality checks performed in the VS is whether the pulse energy during inference is within three standard deviations from the same quantity during training. The PES, GS and VS spectra for the samples highlighted in Fig. 4 are shown in Supplementary note III. We have also compared the root-mean-squared deviation between the output of the PES and the GS, and between the VS and the GS in Fig. 5. It shows that the VS spectra have a higher similarity with the GS, than the PES does, while a clear correlation between them can still be observed. Variations in the spectral properties are therefore expected to be better modeled in the VS.

Fig. 4: Effect of pulse energy as a function of the fit quality for dataset D_A.

Pulse energy versus χ² normalized by the number of degrees of freedom a, together with the marginal normalized χ² distribution b, for dataset D_A. The χ² is calculated using the principal components' latent space, in which the features are — by construction — uncorrelated. The spectra for the highlighted examples are given in Supplementary note III of the Supplementary Material.

Fig. 5: Correlation between the PES and VS reconstructed spectra.

The root-mean-squared deviation between the PES (0^∘ channel) and grating spectrometer versus the root-mean-squared error between the virtual spectrometer and the grating spectrometer is shown for dataset D_A. The spectra in both cases are normalized to one, so that only the shapes are compared. The vertical and horizontal dashed lines are a guide for the eye showing the median of the marginal distributions.

A separate validation step has been taken by calculating the Pearson correlation coefficient between the VS and GS spectra. This is shown as ρ in Fig. 2d, as well as in Supplementary note III. The Supplementary note XII shows the average and root-mean-squared error values for the per-spectra correlation coefficients in each dataset. It is 91 ± 2% for dataset D_A, and always above 82% on average for the other datasets.

Simulation results

Statistical simulations of spectral data are an ideal proxy to investigate the behavior of the spectrometers under controlled conditions. As for experimental data, the reference spectrum of the GS is used to model the resolution loss as the convolution with a response function. Figure 6 shows the obtained resolution of the PES and VS relative to the GS for each simulation. Filled markers correspond to the VS, while unfilled markers of the same color correspond to the sum of all PES channels. Further simulation details are available in Supplementary note IX.

Fig. 6: Resolution estimate for simulated dataset.

Resolution as a function of the photon energy for several simulation datasets, for the VS a and the PES (b sum of 16 channels). Smaller values of the resolution axis (δE/E) The misaligned dataset contains channels with varying shifts in the time-of-flight axis, while the datasets with optimized calibration have no such shifts. The linearized dataset has a linear mapping between energy and time-of-flight, which leads to a relatively flat resolution response. The same applies to the simulation with only two spectral modes on average (in other cases, this is about ten). The vertical uncertainty band corresponds to a 95% CL band estimated through the root-mean-squared error of the resolution in four random splits of the dataset. The horizontal bar corresponds to different energy bins in a dataset. The vertical axis on the right-hand-side shows the resolving power, defined as E/δE.

We produced four simulations, and for each two statistically independent datasets, one for training and another for inference. In one simulation, the PES channels are calibrated perfectly, while in another random small shifts in the time-of-flight measurement simulate the effect of an incorrect offset in the calibration parameters. In fact, a perfect calibration of the PES relies on the precise alignment of the time-of-flight axis across different sub-detectors. In most experiment use-cases, there is no clear need for analysing separate PES channels, as they are expected to convey the same information and therefore, one would wish to combine the information of separate channels to maximize the signal-to-noise-ratio. In this case, the sum of all its channels is the simplest method to increase the signal-to-noise ratio of the data, provided that the channels are correctly aligned. In fact, when there is a misalignment, the sum has a worse resolution, due to the shifts in the energy axes between different sub-detectors. The VS achieves a better resolution by combining information from PES channels and correlating them with the simulated GS measurement. In particular, the impact of the channel misalignment is not significant in the VS, as it uses PCA for the selection of features.

In a third artificial dataset, the physical non-linear mapping between time-of-flight and energy has been linearized. Since the PES measurements happen as a function of time-of-flight and not photon energy, the non-linear effect compresses spectral modes at several photon energies into a smaller range of time-of-flight measurements, leading to a loss of resolution at higher kinetic energies of the photo-electrons. This is verified by comparing the resolution for the simulation in the perfect non-linear calibration dataset, and the linearized dataset. Note, that, as δE is constant for “Linearized” dataset, the value of δE/E in the plot decreases as a function of the photon energy.

In a fourth simulation, also linearized, the number of spectral modes has been reduced to only two on average, while in previous cases it was on average ten. The VS achieves an improved resolution in this case, by taking advantage of the correlation with the GS. This also explains how some differences observed in the previous section arise: different XFEL configurations produce different number of spectral modes.

Conclusions and outlook

The accurate characterization of spectral properties of XFEL pulses is critical for many experiments, and the ability to do so parasitically maximizes beamtime utilization. In this paper, we have presented a virtual spectrometer, which leverages on machine learning to significantly enhance the quality of x-ray diagnostics at the European XFEL. As part of our study, we have shown an improved resolution of up to about 40%. Additionally, the average spectra root-mean-squared deviation relative to the grating spectrometer is also shown to significantly improve (see Supplementary note XI).

This virtual device combines the benefits of two spectrometers, which are either based on a grating or on detection of photo-electrons, and a pulse energy monitor. The former spectrometer is high-resolution, but invasive and limited in repetition-rate. The latter one is lower in resolution and its calibration is non-trivial, time-consuming, and depends on several configuration parameters. However, it is non-invasive and can resolve each x-ray pulse. The virtual spectrometer combines the benefits of the two devices, by exploiting both in a training phase, and only the latter afterwards. It is non-invasive, pulse-resolved, and with resolution higher than the photo-electron spectrometer. Furthermore, the virtual device does not need any calibration or pre-processing, and therefore it enables a high degree of automation.

We firmly believe that any automation must found on extensive validation readily available to operators, so as to ensure that the data quality of both the input and of the output match the expectations of the underlying model. To this end, we designed and built in quality checks and alerts, so that operators can understand limitations of such a tool readily, and react appropriately.

The virtual spectrometer is implemented and available to scientists at European XFEL, both for quasi-real-time analysis, and after data has been stored to disk. Such implementation includes an interface to train the model from saved data, and to perform inference as soon as PES and XGM data are acquired, transforming them into an entry point to the virtual spectrometer. It provides, additionally, an estimate of the uncertainty band, the reliability of each input channel, and the compatibility of the pulse energy in training and inference. Images of the graphical user interface can be seen in Supplementary note X.

The performance and robustness of the virtual spectrometer have been carefully examined in this paper by calculating its resolution relative to a higher resolution device in a varied set of realistic experimental conditions and using simulations. In any considered case, the virtual device achieves better resolution than a direct measurement using only the PES, by taking advantage of multiple sources of information. It should be noted that, in this manuscript, the measurement conditions, in terms of x-ray properties and PES settings, were frozen between the model training and the virtual spectrometer operation phase. This limitation may be removed through the interpolation of the map for variable PES settings. Such procedure requires a non-linear interpolation method, which we have already implemented and tested using a Bayesian neural network (BNN)⁴⁰. Results using a BNN have not been reported in this paper, and are left for further research.

While the tests described here focused on x-ray diagnostics at the SASE3 FEL source, we intend to extend the procedure towards measurements at other European XFEL beamlines, where similar combinations of invasive/non-invasive devices can be exploited. The improvement of beam characterization through the provision of automated, higher resolution, angle- and pulse-resolved spectral measurements enables the automation of further diagnostics. In fact, the virtual spectrometer is essential to enable accurate temporal diagnostics, for instance based on angular streaking^9,24,25,26. This is the subject of active research at European XFEL, a critical step to enable the exploitation of attosecond XFEL science.

Accession codes

The Virtual Spectrometer software is open-source and available at https://git.xfel.eu/machineLearning/pes_to_spec. The software is licensed under the terms of 3-clause BSD. Details on how to reproduce the manuscript results with this software are provided in Supplementary note XIII.