Extreme shape coexistence observed in ⁷⁰Co

Abstract

The shape of the atomic nucleus is a property that underpins our understanding of nuclear systems, impacts the limits of nuclear existence, and enables probes of physics beyond the Standard Model. Nuclei can adopt a variety of shapes, including spheres, axially deformed spheroids, and pear shapes. In some regions of the nuclear chart where a spherical nucleus would naively be expected, deformed nuclear states can result from the collective action of constituent protons and neutrons. In a small subset of nuclei both spherical and deformed nuclear states have been experimentally observed, a phenomenon termed shape coexistence. We present spectroscopic evidence for the coexistence of J^π = 1⁺ spherical and deformed states in ⁷⁰Co, separated by less than 275 keV. This close degeneracy of levels with the same J^π and different shapes demonstrates an extreme example of shape coexistence resulting from the interplay of independent particle motion and collective behavior in highly unstable nuclear systems and identifies the Co isotopes as a transition point between deformed ground states observed in the Cr isotopes and spherical configurations observed in the closed-shell Ni isotopes.

Introduction

The nuclear shell model anchors our understanding of the atomic nucleus. It was developed 75 years ago by Mayer and Jensen^1,2 leading to the 1963 Nobel Prize in Physics and considers a single nucleon (either a neutron or a proton) moving in a mean field generated by the other nucleons. The emergence of shell structure is a common occurrence in interacting quantum systems^3,4,5 and provides a straightforward explanation for the experimentally observed “magic numbers” of 2, 8, 20, 28, 50, 82, and (for neutrons) 126. These numbers correspond to locations of large energy gaps between groups of single-particle states. Hence, completely filling the states up to one of these energy gaps imparts extra stability to the atomic nucleus relative to its immediate neighbors, analogous to the extra chemical stability encountered in the noble gases when an atomic electron shell is filled. Nuclei located near these closed shells are predominantly spherical in shape; however, promoting just a few nucleons across the large energy gap can induce a change in the shape of the nucleus, giving rise to the phenomenon of “shape coexistence”. The idea that the shape of the nucleus could change not only due to a different number of protons and neutrons but also from one state to another within the same nucleus was introduced almost 70 years ago in the case of ¹⁶O by Morinaga⁶. Since then, shape coexistence has been observed experimentally in more nuclei⁷ and continues to provide a stringent test of modern nuclear structure models. Studies of the shape of the atomic nucleus have been instrumental in a diverse set of areas, including nuclear structure^8,9,10,11, explorations of the limits of nuclear stability^12,13, and even in physics beyond the Standard Model⁸.

In the original study of ¹⁶O⁶, the coexisting states were the spherical 0⁺ ground state and a deformed 0⁺ excited state at an excitation energy of 6.05 MeV, resulting from the excitation of multiple particles across the large shell gap. Such a large energy separation is nominally expected from the nature of the excitation, but other observations have revealed a more varied picture. Generally, the relative energy between the spherical and deformed states is a result of a delicate balance between the energy cost of promoting particles across the shell gap and the energy gained from residual nucleon-nucleon interaction; The energy gained can more than offset the cost of the excitation and lead to the shape coexisting state dropping near, or below, the expected ground state. Therefore, shape-coexisting states provide a unique opportunity to study particle interactions within the same nucleus but under different conditions (different shapes).

Such shape-coexisting states are often found in transitionary regions of the nuclear chart, between mostly spherical nuclei found near closed shells and heavily deformed open-shell nuclei. Here we investigate nuclei in the A = 70 region near the doubly magic ⁷⁸Ni. Prior studies have suggested the prevalence of shape evolution in this region⁷, but thorough experimental study has been challenging due to the severe neutron-richness of the nuclei involved, and many prior investigations have focused on even-even isotopes^14,15. It is thought that these deformations are driven by a phenomenon known as Type II shell evolution, in which the traditional nuclear shell picture is restructured due to multiparticle-multihole excitations across shell gaps^16,17. Shape effects in odd-odd nuclei, like ⁷⁰Co, have been suggested as strong tests of the Type II shell evolution mechanism¹⁸, and their study is further necessary to understand broader scale transitionary effects that characterize nuclear structure in this region, like the possible merging of the N=40 and proposed N=50 islands of inversion¹⁹.

Experimental investigation of the ⁷⁰Fe → ⁷⁰Co  → ⁷⁰Ni β-decay chain was possible using the technique of total absorption spectroscopy (TAS). The TAS technique was introduced almost 50 years ago²⁰ as a solution to the so-called “Pandemonium Effect”, which refers to the erroneous assignment of β-decay feeding intensity (I_β) to lower excitation energies due to limitations in the detection efficiency and the presence of weak γ-ray transitions. TAS measurements avoid this issue by making use of large volume, high efficiency γ-ray calorimeters which allow for the accurate determination of the populated excitation energy, and hence accurate extraction of I_β. TAS detectors have been used extensively for I_β measurements, and in particular for extracting nuclear shapes. For some nuclei, changes in deformation result in a marked difference in the Gamow-Teller strength distribution²¹, B(GT), which is derived experimentally from I_β. Previous studies have compared TAS-measured and theoretical B(GT) distributions to infer the deformations of β-decaying states in ⁷⁶Sr²², ⁷⁸Sr²³, ⁷⁸Rb²³, ^100,101,102Zr^24,25, and ¹⁰⁹Tc²⁵. This method is optimal for the study of ⁷⁰Co, which has been found to have two β-decaying states²⁶: one with high-spin (J^π = 6⁻, 7⁻) and a half-life of  ≈ 65 ms²⁷, and a low-spin state with a half-life of  ≈ 470 ms²⁷. TAS measurement of the high-spin state was published by our group previously²⁸, in excellent agreement with shell-model calculations showing its weakly deformed character. However, the low-spin state has not been studied in the same manner until now.

In the present work, a ⁷⁰Fe beam was implanted at the center of a TAS detector called the Summing NaI(Tl) (SuN) detector²⁹. The β-decay of the J^π = 0⁺ ground state was used to preferentially populate the low-spin β-decaying state of ⁷⁰Co and fully detail its decay pattern with minimal limitations from the Pandemonium Effect. The observed distributions, summarized in Fig. 1, are interpreted quantitatively with the assistance of state-of-the-art shell model calculations and strongly support an assignment of J^π = 1⁺ and a strong deformation for the low-spin β-decaying state, which has a wavefunction dominated by multiparticle-multihole excitations across the Z=28 shell gap. Our results extend upon indications presented in Morales et al.¹⁷ and identify an extreme case of shape coexistence between the deformed J^π = 1⁺β-decaying state and near-spherical J^π = 1⁺ excited state  ~ 275 keV higher in excitation energy.

Fig. 1: Dominant decay paths for ⁷⁰Fe and ⁷⁰Co.

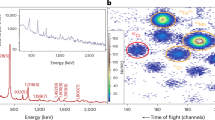
The most prominent transitions observed in the decay chain under study in the present work, which pass through the low-spin isomer of ⁷⁰Co, are shown as blue arrows. The green arrow shows the dominant transition from the high-spin isomeric state, observed in Spyrou et al.²⁸. The inset shows the configurations of the two relevant J^π = 1⁺ states in ⁷⁰Co. The label r represents the group of orbitals (0f_5/2, 1p_3/2, 1p_1/2). Open circles represent hole states within the orbitals; x’s represent states occupied by a particle excited across a shell gap. Symbols placed between orbitals indicate that configurations involving hole states in either orbital are possible. States interpreted as having a weakly deformed (WD) character are labeled with a white spherical shape, while states interpreted as having a strongly deformed (SD) character are labeled with a purple prolate shape (further details in text). All values are taken from the A=70 Nuclear Data Sheets²⁷, and the J^π value of the long-lived β-decaying state in ⁷⁰Co has been reassigned to 1⁺ in accordance with Morales et al.¹⁷ and the Discussion within the Results section.

Results

Experimental results and shell model calculations

Experimentally measured and theoretically calculated I_β and the extracted B(GT) distributions for the two decays are shown in Fig. 2. It can be observed that the ⁷⁰Fe β-decay predominantly populates a level in ⁷⁰Co that decays via emission of a 274 keV γ-ray. Following this γ-deexcitation, the low-spin isomeric state in ⁷⁰Co β-decays in a surprisingly selective pattern, predominantly feeding a highly localized set of levels with excitation energy of roughly 6 MeV in ⁷⁰Ni. To connect these unique decay patterns to a microscopic interpretation of the nuclear shape, we performed shell model calculations of the same β-decay chain.

Fig. 2: Cumulative β-Intensity and Gamow-Teller strength as a function of excitation energy for ⁷⁰Fe and ⁷⁰Co.

⁷⁰Fe decays are shown in (a) and (b); ⁷⁰Co decays are shown in (c) and (d). Experimental measurements are shown as a black line with a green band representing the uncertainty. For both nuclei, shell model calculations performed using the t1 truncation are shown as magenta dash-dot lines, while t2 truncation calculations are shown as a blue dotted line. Calculations are also labeled by the shape of the β-decaying state.

Gamow-Teller (GT) β-decay calculations were carried out with the NuShellX Code³⁰. They employ a model space called fpg9tn that consists of the five proton orbitals (0f_7/2, r, 0g_9/2) and four neutron orbitals (r, 0g_9/2), with r representing the (0f_5/2, 1p_3/2, 1p_1/2) orbital group. Due to the computational complexity of the calculations, truncations to the model space were necessary; The label “tn” indicates that at most n protons were allowed to be excited across the Z = 28 shell gap (i.e. from 0f_7/2 to (r, 0g_9/2)). Figure 3 shows some simple proton-neutron configurations allowed under the model space truncations used. Calculated T = 1 single-particle energies and two-body matrix elements for the (r, 0g_9/2) neutron orbitals were replaced with adjusted calculations using the jj44a Hamiltonian to improve agreement of the spectra with the Ni isotopes and reproduce relative binding energies of ⁷⁰Ni. More details about the Hamiltonians used can be found in the “Shell Model Hamiltonians” subsection of the Methods.

Fig. 3: Basic possible configurations for the β-decays of ⁷⁰Fe and ⁷⁰Co.

The top two rows (blue box) show the configurations related to the t1 truncation. Particle excitations are marked with x, while circles represent holes. Symbols placed between orbitals indicate that configurations involving particle/hole states in either orbital are possible. Orbitals are filled up to hole states. The last row shows the additional configurations allowed in the t2 truncation (green box). The t3 truncation, which is not included in the present calculations, would have the configuration shown in the white box.

Discussion

The Monte Carlo Shell Model calculations presented in Morales et al.¹⁷ feature two major types of states: a group of low-spin, strongly deformed (SD) states at low energies, and a group of weakly deformed (WD) J^π = (1⁺, 6⁻, 7⁻) states at around 900 keV. These WD states are analogous to those we obtain using the t1 truncation. While this t1 truncation is able to reproduce many features of the β-decays observed in this mass region, including those of ⁷⁰Fe (magenta dot-dash line in Fig. 2a) and the high-spin β-decaying state of ⁷⁰Co²⁸, it is not sufficient to accurately describe the observed I_β (Fig. 2c, magenta dot-dash line) or half-life (Fig. 4b) of the ⁷⁰Co low-spin β-decaying state of interest here. For this reason, the calculations were extended to the t2 truncation.

Fig. 4: Calculated energy levels below one MeV in ⁷⁰Co and associated β-decay patterns.

a shows the calculated states. The length of the lines is proportional to the J value and the color represents the parity (blue for negative, red for positive). States discussed in the text are labeled by their properties. b shows The cumulative β-decay intensities and T_1/2 for the β-decay of ⁷⁰Co to ⁷⁰Ni based on possible band-head J^π values in ⁷⁰Co. Decays from strongly deformed states are shown as dashed lines, while decays from weakly deformed states are shown as solid lines. The experimental intensity is shown as a dotted black line for comparison.

The t2 calculations predict 44 levels with energies less than 1 MeV, shown in Fig. 4a, separated by positive (red) and negative (blue) parity. Many of these are rather pure SD states connected by strong B(E2) values, but a variety of low-lying WD states are also present. It is not clear a priori which of these is the relevant β-decaying state. To elucidate this, I_β and the β-decay half-lives (T_1/2) were calculated for candidates and compared with the experiment, shown in Fig. 4b. The decay from the WD J^π = 1⁺ state is similar to that calculated in the t1 truncation. The J^π = 7⁻ WD state corresponds to the short-lived, near-spherical β-decaying state discussed in Spyrou et al.²⁸ The lowest energy state in the calculations is a WD J^π = 3⁻ state, but both its decay pattern and half-life are inconsistent with the experiment.

Decays from the SD states match the characteristics of the experimental distribution much more closely, exhibiting strong feeding to a range of states located between 5 − 7 MeV. We interpret the Gamow-Teller decay of the SD J^π = 1⁺ state in ⁷⁰Co to be populating a few neutron-hole proton-particle Nilsson states in ⁷⁰Ni (described further in the “Nilsson Model Interpretations” subsection of the Methods). The observed distribution of states comes from the mixing of these simple configurations with the high density of other types of J^π = 1⁺ states in ⁷⁰Ni that are present around 6 MeV in excitation energy. The observed TAS peak at 6 MeV (see the Experimental Description subsection of the Methods) supports this interpretation, as it is wider than what would be expected for a single level in this region²⁹. The J^π = 1⁺ SD state has the best half-life agreement and is the only SD state whose decay features direct ground state feeding, which is observed experimentally in Fig. 2c at an excitation energy of zero. This designation is also preferable because of the nonobservation of feeding to the lowest SD J^π = 0⁺ state in ⁷⁰Ni. Experimentally, this state is located at 1.57 MeV³¹ and is fed negligibly. In our SD J^π = 1⁺ calculations, the equivalent state appears at 3.2 MeV and is fed with only 0.8% of the total intensity. Thus, our evidence is consistent with an assignment of J^π = 1⁺ and a strongly deformed nature for the low-spin, long-lived β-decaying state as suggested by Morales et al.¹⁷.

The two low-lying SD J^π = 1⁺ states that appear in our calculations also have wave function occupancies similar to those shown in Fig. 4 of Morales et al.¹⁷ and large 2 particle-3 hole components. These states can be interpreted as members of deformed rotational bands with angular momentum projections of K^π = (0⁺, 1⁺). In these calculations, the K^π = 1⁺ band appears lower than the K^π = 0⁺ band. Adjusting the size of the Z=28 shell gap shifts the band energies relative to the predicted WD states, but they always appear close together and in the same order. A more detailed microscopic interpretation of these states using the Nilsson Model can be found in the “Nilsson Model Interpretations” subsection of the Methods.

The WD J^π = 1⁺ state, appearing 220 keV below the SD J^π = 1⁺ state in our calculations, is also of significant importance. The experimental ⁷⁰Fe β-decay (Fig. 2a) prominently feeds a J^π = 1⁺ state that deexcites via a 274 keV γ-ray. This state is understood to be of a WD character - hence why it is populated so strongly in the ⁷⁰Fe β-decay, while the SD β-decaying state is not despite having the same J^π. The reason that the WD state appears below the SD state in the calculations is due to a shift in the energies of SD states resulting from the model space truncation used. This is illustrated in the case of a “mirror” N=27 isotone, ⁵¹Cr, which is discussed in detail in “The N = 27 ‘mirror’ case” subsection of the Methods. This study is relevant since the ⁵¹Cr calculations can be performed in the full model space, providing an estimate of the limitations of the tn truncations used for ⁷⁰Co. ⁵¹Cr demonstrates a similar WD J^π = 7/2⁻ state and SD K^π = 1/2⁻ band in its lowest lying levels. Calculations that use the t2 neutron truncation see the K^π = 1/2⁻ SD band energies placed roughly 600 keV too high relative to the full space calculations. Correcting for this effect, the SD β-decaying state in ⁷⁰Co would fall a few hundred keV below the strongly β-fed WD J^π = 1⁺ state, in excellent agreement with present experimental observations.

Conclusions

We have presented spectroscopic evidence indicating that the low-spin β-decaying state in ⁷⁰Co has J^π = 1⁺ and a strongly deformed character. These results are consistent with and extend upon previous literature results, and identify one of the closest spacings between nuclear levels of the same J^π and different shapes yet observed. Such effects provide stringent tests for models at the limits of nuclear structure and could exert influence on complex astrophysical nucleosynthesis pathways far from stability. Investigation of nearby nuclei, including those near the N=50 shell closure, could reveal similar effects and is necessary for a complete understanding of the structural evolution in this region. In the case of ⁷⁰Co, future experiments, such as measurement of the lifetime of the 274 keV level and/or the angular distribution of its deexcitation to probe the multipolarity of the transition would further confirm the present interpretation. Additional theoretical calculations for the β-decays that extend to a t3 truncation and include the 1d_5/2 orbital also remain to be carried out.

Methods

Experimental Description

The experiment was conducted at the National Superconducting Cyclotron Laboratory at Michigan State University. The experimental setup was detailed in previous publications^32,33 and will be summarized here. A ⁸⁶Kr primary beam at 140 MeV/u was impinged on a ⁹Be target, and the isotopes of interest were separated using the A1900 fragment separator³⁴. Individual isotopes were identified using energy loss and time-of-flight information recorded by a plastic scintillator in the focal plane of the A1900, coupled with two silicon PIN detectors near the end-station. Following identification, the beam was implanted into a double-sided silicon strip detector (DSSD), which was used to detect the location and time for both the implanted ions and the electrons produced by their β-decays. γ-rays emitted following these β-decays were detected using the SuN detector²⁹. SuN is a cylindrical scintillator detector divided into 8 optically isolated NaI(Tl) segments. The segment signals can be evaluated individually (sum-of-segments), providing a measure of the γ-rays emitted during the deexcitation of a populated level, or summed over all 8 segments to provide a total absorption spectrum that is sensitive to the excitation energy of the nucleus. A third spectrum called “multiplicity” records the number of segments that register a signal in each event and is an indication of the number of γ-rays emitted from a deexcitation.

Events corresponding to ⁷⁰Fe ions were isolated by gating on the appropriate ranges for time-of-flight and energy loss measured by the silicon PIN detectors. The particle identification plot and gate are shown in Fig. 5. The DSSD allowed for both spatial and temporal correlation of implantations with subsequent β-decays. Decays detected within 150 ms of implantation were assigned to ⁷⁰Fe. Decays of the ⁷⁰Co child nucleus were isolated using the same particle ID gate, but a timing window of 400-1000 ms following the ⁷⁰Fe ion detection. Not every β detection within the correlation requirements corresponds to a real decay from a particular ion; therefore, the correlation process was repeated with β-detections that precede the ion implantation to produce a random correlation background. This background was subtracted from the raw ion-β correlated spectra produced for ⁷⁰Fe decays. For ⁷⁰Co decays, which have lower statistics, the background was included as a component of the fitting procedure outlined below and detailed thoroughly in Dombos et al.³⁵

Fig. 5: Particle identification plot showing the time of flight and energy loss measurements.

The gate used to isolate A = 70 fragments is also shown as a black oval.

To extract the β-decay feeding intensity (I_β) information, a χ² minimization method that simultaneously fits the total absorption, sum-of-segments and multiplicity spectra was employed. Simulated decays from each discrete level in the child nucleus were created using a GEANT4³⁶ simulation of SuN²⁹. For ⁷⁰Co, the discrete level spectrum presented in Morales et al.¹⁷ was used, and for ⁷⁰Ni the levels were taken from the National Nuclear Data Center’s A=70 Nuclear Data Sheets²⁷. For energies between the highest lying discrete level and Q_β, decays from pseudolevels spaced roughly equally to SuN’s energy resolution were simulated using the software RAINIER³⁷. RAINIER uses a user-defined nuclear level density (NLD) to create an artificial level scheme and follows the deexcitation of the nucleus using a Monte Carlo method with a γ-ray strength function (gSF). The extracted I_β is not very sensitive to small variations of the NLD or gSF. For the present work, the constant temperature NLD model³⁸ and the gSF extracted for ⁷⁰Ni in Liddick et al.³⁹ and Larsen et al.⁴⁰ were used. It was assumed that simulated pseudo-levels were populated by allowed decays, therefore they were assigned J^π = 1⁺ in the decay ⁷⁰Fe  → ⁷⁰Co and J^π = 0⁺, 1⁺, 2⁺ in the decay ⁷⁰Co  → ⁷⁰Ni, using our assignment of J^π = 1⁺ for the β-decaying state of ⁷⁰Co.

For each discrete level and each pseudolevel, GEANT4 was used to simulate total absorption, sum-of-segments, and multiplicity spectra. These spectra were used as components in a χ² fitting procedure that simultaneously fit the experimentally measured total absorption, sum-of-segments, and multiplicity spectra. The relative weight of each component determined the relative I_β at the given excitation energy. Experimental fits for both nuclei are shown in Fig. 6.

Fig. 6: Total absorption, sum-of-segments, and multiplicity fits for ⁷⁰Fe and ⁷⁰Co decays.

For ⁷⁰Fe, experimental spectra for ⁷⁰Co child decays were included as a component in the fit and are shown separately (magenta, a–c). For ⁷⁰Co, the random background was included as a component of the χ² minimization, instead of being subtracted prior to the fit, due to low statistics. It is shown in purple in d–f.

To account for unassigned J^π values in the discrete level schemes of these nuclei, a set of 10 RAINIER simulations was done for each nucleus, where any unassigned level’s spin was randomly varied within a ΔJ = 2 window of existing J^π estimates. For ⁷⁰Fe, these estimates were taken from shell model calculations presented in Morales et al.¹⁷ For ⁷⁰Ni, spin ranges for a given level were estimated based on the production mechanisms in the National Nuclear Data Center’s A=70 Nuclear Data Sheets²⁷. The results from the spin variation were included in the uncertainty estimate of I_β, along with statistical uncertainties and as a 10% efficiency uncertainty²⁹.

The extracted I_β distributions were used to calculate the associated Gamow-Teller strengths using

$$B(\,{{\mbox{GT}}})(E)={{\mbox{K}}}{\left(\frac{{g}_{v}}{{g}_{a}}\right)}^{2}\frac{{I}_{\beta }(E)}{{{\mbox{f}}}({Q}_{\beta }-E){T}_{\frac{1}{2}}}$$

(1)

where K = 6143.6(17) s⁴¹, $\frac{{g}_{a}}{{g}_{v}}$ = -1.2695(29)⁴², f(Q_β − E) is the Fermi Integral, and ${T}_{\frac{1}{2}}$ is the half-life.

Shell Model Hamiltonians

The starting Hamiltonian was obtained using the many-body perturbation theory code of Hjorth-Jensen et al.⁴³. We use the N³LO two-nucleon interaction, renormalized for short-ranged correlations with the v_lowk method with a cutoff of Λ = 2.2 MeV⁴⁴. Two-body matrix elements were obtained for a basis of states that contained up to 4ℏω excitations beyond a ⁶⁸Ni closed shell, where the 0f_7/2 orbital is filled for protons and the (r) orbitals are filled for neutrons. The radial integrals were calculated with harmonic-oscillator wavefunctions with ℏω = 9.16 MeV. The renormalized Hamiltonian for the fpg9 model space included up to second-order core-polarization corrections with folded diagrams. To improve agreement with the spectra of the Ni isotopes, the T=1 two-body matrix elements, and single-particle energies for the (r, 0g_9/2) neutron orbitals were replaced with those obtained in Lisetskiy et al⁴⁵. (called the jj44a Hamiltonian in Mukhopadhyay et al.⁴⁶). This Hamiltonian was designed for use in the t0 truncation (i.e. a Z = 28 closed shell). For the t1 truncation, the particle-hole components of the wavefunctions shifted the energies of states associated with the (r, 0g_9/2) neutron configurations relative to those obtained with the jj44a Hamiltonian. To reconcile this difference, the jj44a single-particle energies were adjusted and the two-body matrix elements were normalized by a factor of 0.80. The proton single-particle energies were adjusted to approximately reproduce the relative binding energies of ⁶⁹Co, ⁷⁰Ni, and ⁷¹Cu, and the low-lying states of ⁷¹Cu. All B(GT) calculations using this final Hamiltonian were carried out assuming a standard Quenching factor of R = 0.60. This is a typical reduction factor required for Gamow-Teller strengths observed in β-decays when compared to shell model calculations in the sd⁴⁷ and fp⁴⁸. A similar Quenching factor can be extracted from (p,n) reactions when compared to the 3(N − Z) Gamow-Teller Sum Rule⁴⁹.

Nilsson Model Interpretations

There is a small mixing between the WD J^π=1⁺ and SD J^π=1⁺ states in our calculations for ⁷⁰Co. This can be interpreted in terms of the Nilsson Model⁵⁰ and the potential energy surface (PES) shown in Fig. 3 of Morales et al.¹⁷. The WD J^π=1⁺ state is dominated by the coupling of the spherical π0f_7/2 and ν0f_5/2 configurations. However, as deformation increases, the proton [N, n_z, Λ]∣Ω_p∣^π = [3, 0, 3]7/2⁻ and [3, 2, 1]1/2⁻ Nilsson orbitals cross, resulting in a new PES minimum with a deformation of β ≈ + 0.3. The proton 1 particle-1 hole states at the t1 level of truncation can describe small changes around ${\beta }_{\min }$=0, but are not enough to describe these states with β = + 0.3; for such large deformations, the t2 truncation is necessary.

The Nilsson Model is also useful in understanding the origins of the WD and SD states in these nuclei. A proton Nilsson diagram for ⁷⁰Ni is shown in Fig. 7, with protons filling the 0f_7/2 orbital at small deformation. As such, one might expect the ground state of neighboring ⁶⁹Co to be well-described by one proton hole in the 0f_7/2 orbital with J^π = 7/2⁻. As the deformation increases, the ∣Ω_p∣^π = 7/2⁻ and ∣Ω_p∣^π = 1/2⁻ Nilsson orbitals cross, so that near β= + 0.3, the Nilsson state just below the Fermi surface has ∣Ω_p∣^π = 1/2⁻, arising from a proton 2 particle-2 hole structure in ⁷⁰Ni. Removing a proton would now result in a deformed K^π = 1/2⁻ rotational band. In calculations of ⁶⁹Co using the t2 truncation, shown in Fig. 8b, one sees the expected J^π = 7/2⁻ ground state and K^π = 1/2⁻ rotational band, dominated by 2 particle-3 hole configurations (although due to staggering its lowest-lying state has J^π = 3/2⁻, and also may be a β-decaying isomer). Experimentally, low-lying states of J^π = 7/2⁻⁵¹ and J^π = 1/2⁻⁵² have been observed that may be associated with these WD and SD shapes. Calculations for ^69,71,73Co with the LNPS Hamiltonian in a model space similar to ours are discussed in Lokotko et al.⁵³ Neutron orbitals exhibit the same pattern; In ⁴³S, one observes an SD K^π = 1/2 − band and WD J^π = 7/2⁻ state associated with the 0f_7/2 − r neutron configurations⁵⁴.

Fig. 7: Nilsson diagram for ⁷⁰Ni.

Calculations are performed with the deformed Woods-Saxon code WSBETA⁵⁸ with the potential choice ICHOIC=3. Positive-parity states are shown in red and negative-parity states are shown in blue. The proton and neutron 2∣Ω∣^π values that are related to the deformed states in ^69,70Co discussed in the text are labeled.

Fig. 8: E2-maps for ⁵²Mn, ⁶⁹Co, and ⁷⁰Co.

a shows full model space calculations for ⁵²Mn. Panels (b) and (c) show calculations using the t2 truncation for ⁶⁹Co and ⁷⁰Co, respectively. The width of the lines connecting the levels is proportional to the ∣M(E2)∣². Strong transitions involved in the K^π = 2⁺, 3⁺ bands in (a), K^π = 1/2⁺ band in (b), and K^π = 0⁺, 1⁺ bands in (c) are shown in red.

A clear pattern appears that can also describe the low-lying states observed in ⁷⁰Co. With our t1 Hamiltonian the lowest negative-parity state in ⁷⁰Co is 7⁻, and the lowest positive-parity state is 1⁺. The dominant configurations of these states are (π7/2⁻ ⊗ ν9/2⁺), and (π7/2⁻ ⊗ ν5/2⁻), respectively. Extending to the t2 truncation allows for stronger deformation, and thus the aforementioned crossing of the ∣Ω_p∣^π = 7/2⁻ and ∣Ω_p∣^π = 1/2⁻ orbitals. In this model space, SD positive-parity states in ⁷⁰Co can be interpreted as the coupling of the ∣Ω_p∣^π=1/2⁻ and ∣Ω_n∣^π=(1/2,5/2)⁻ Nilsson states to make proton-neutron bands with K = (0, 1, 2, 3)⁺. SD negative-parity states in ⁷⁰Co can be interpreted as the coupling of the ∣Ω_p∣^π=1/2⁻ and ∣Ω_n∣^π=5/2⁺ Nilsson state to make proton-neutron bands with K = (2, 3)⁻.

Finally, the Nilsson model provides a reason for the suppression of the nominally allowed β-decay transition to the SD J^π=0⁺ discrete state at 1.57 MeV ⁷⁰Ni. In our calculations, this decay is dominated by the forbidden neutron [3, 2, 1]1/2⁻ to proton [3, 0, 1]1/2⁻ GT transition.

The N=27 “mirror” case

The connection between the model-space truncation and the energies of the SD bands can be studied in ⁵¹Cr, which falls analogously below the N = 28 shell gap and can be fully calculated with no truncations to the model space. States starting with the 3/2⁻ level at 0.75 MeV and the 1/2⁻ level at 0.78 MeV^55,56 can be interpreted as the start of a K^π = 1/2⁻ SD band based on the neutron [3, 2, 1]1/2⁻ Nilsson orbtial. The levels of ⁵¹Cr can be described within the (0f_7/2, r) model space with the well-established GPFX1A Hamiltonian with effective charges of e_p = 1.5 and e_n = 0.5⁵⁷. This collective band is formed from exciting neutrons from 0f_7/2 to the r subset of orbitals. The WD and SD properties of ⁵¹Cr can be studied with an E2-map, where the levels are connected by lines whose width is proportional to the electric quadrupole transition matrix element ∣M(E2)∣², and the transition strength is given by B(E2) = ∣M(E2)∣²/(2J_i + 1). The results of the full-space calculation are shown in Fig. 9d. The energies and B(E2) are in excellent agreement with experimental measurements^55,56. These full-space results are compared to those from various levels of truncation tn in other panels of Fig. 9, where n is the maximum number of neutrons allowed in the r subset of orbitals. Weakly deformed (WD) states that are associated with those that start with the 7/2⁻ ground state are present even at the t1 level of truncation. On the other hand, SD rotational bands do not appear until excitation of multiple neutrons across the shell gap is allowed in the t2 truncation.

Fig. 9: E2-map for ⁵¹Cr.

a shows the E2-map calculated using the t1 truncation. b–d show the same, but utilizing the t2 truncation, t3 truncation, and full model space, respectively. The width of the lines connecting the levels is proportional to the ∣M(E2)∣², and the strong transitions involved in the K^π = 1/2⁻ band are shown in red. The number in each panel is the m-scheme dimension for M = 1/2.

Comparison between the ^69,70Co neutron neighbors and ⁵¹Cr,⁵²Mn proton neighbors is useful in completing this picture; In odd-odd ⁵²Mn there are SD states starting with J^π = 2⁺ and 3⁺ shown in Fig. 8a that can be interpreted as the coupling of the neutron [3, 2, 1]1/2⁻ and proton [3, 1, 2]5/2⁻ Nilsson states. These coexisting sets of states ⁵¹Cr and ⁵²Mn are analogous to those in ⁶⁹Co (shown in Fig. 8b) and ⁷⁰Co (shown in Fig. 8c), which are the ultimate focus of this paper. The deformed band in ⁵¹Cr obtained with the t2 truncation is 600 keV higher than that obtained with the full model space calculation. Given the similarities between the two pairs, we can expect the energy of the deformed bands in ^69,70Co obtained with the t2 truncation to be too high in energy by a similar amount. Taking this into account, the SD J^π = 1⁺ state would be lower in energy than the WD J^π = 1⁺ state, in agreement with the present experimental observation.