Introduction

In a real-world high-dimensional dynamic system, some variables or components are crucial for understanding the system’s behavior1,2. It is essential not only to predict their future dynamics but also to uncover the causal relationships of these variables within the system3. However, causal interaction information and temporal information are not independent or defined by a unidirectional dependency; rather, they are intricately interconnected elements that collectively contribute to a deeper understanding of the underlying mechanisms governing system dynamics—an aspect that has not been fully explored in most traditional research4,5,6. Temporal information provides the foundational materials and basis for discovering causal interactions7, while causal information can in turn facilitate the reliable prediction of future temporal state8. Meanwhile, most real-world systems are too complex to be accurately described by an explicit model. Therefore, it is imperative to develop a data-driven method aimed at conducting causal analysis and making future predictions simultaneously from a holistic perspective, addressing a persistent challenge in the fields of data science and deep learning.

Generally, time series forecasting can be broadly categorized into statistical methods and machine learning approaches. Classical statistical models (e.g., autoregressive integrated moving average (ARIMA)9, vector autoregression (VAR)10) are effective but struggle with nonlinearity and become computationally inefficient for high-dimensional or multivariate data11. In contrast, machine learning techniques excel at capturing complex patterns and managing multivariate inputs, with representative models including recurrent neural networks (RNNs)12, gated recurrent units (GRUs)13, long short-term memory networks (LSTMs)14,15, long- and short-term time-series networks (LSTNets)16, neural ordinary differential equations (NODEs)17, and transformer-based architectures (e.g., LogTrans18, Informer19, Reformer20, and iTransformer21). These forecasting methods inherently involve representation learning, as they rely on extracting high-level patterns and representations from raw time series data for accurate prediction. However, despite their predictive success, they often fail to fully exploit causal relationships within high-dimensional systems, constraining their generalization under distributional changes and diminishing their ability to elucidate the underlying causal interactions.

To better explore the intrinsic mechanisms of complex system, many studies focus on identifying causal relationships in dynamical systems. Based on the type of measurement data, these methods can be primarily categorized into statistical approaches for cross-sectional data and dynamical methods for time-series data11. While statistical methods, such as the potential outcome model (POM)22 and structural causal model (SCM)23,24,25, are effective for time-independent or intervention-based data, they struggle with time-series data, feedback loops, and Markov equivalence issues11,26,27,28,29. To address these challenges, dynamical methods such as Granger causality (GC)30, transfer entropy (TE), and reconstruction-based technique31, leverage time-series data to uncover causal relationships. However, GC is limited by its linear model assumption, and although TE extends GC to nonlinear dynamics, it still struggles with non-separability issues. In contrast, the reconstruction-based technique, derived from delay embedding theorem32,33, has been used to develop the state space reconstruction and widely applied in nonlinear time series causal analysis, including convergent cross mapping (CCM)34, cross map evaluation (CME)35, and cross map smoothness (CMS)36. However, these methods fail to effectively identify and orthogonally separate the causes and effects for key variables in systems and are often treated as an independent module from temporal information prediction, which hinders a comprehensive understanding of the dynamics of complex systems.

To fill the gaps, we introduce a self-supervised approach, i.e., causal-oriented representation learning predictor (CReP), to make multistep-ahead forecasting and conduct causal analysis for any target variable in a high-dimensional system. This framework aims to implicitly learn latent causal representations from observed data while making multistep predictions simultaneously, and explicitly interpret the representations for uncovering the causes and effects for target variable. The core idea of CReP is to decompose the original space into three latent orthogonal factors with causal representations for the target variable: cause representation, effect representation, and non-causal representation. Specifically, the effect representation is then used to reliably predict the future states of the target variable, which is ensured by our reconstruction-based dynamic causation extended through the spatiotemporal information (STI) transformation8,26,37,38.

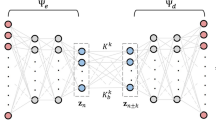
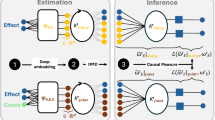
Our framework is characterized by three key features: 1) dynamic causation detection with the STI transformation mechanism (Fig. 1a), 2) causal-oriented representation learning for multistep predictions through the CReP (Fig. 1b), and 3) causal analysis of the target variable via \(\alpha \beta\)-LRP39,40 (Fig. 1c). To better puzzle everything together, the flowchart of our framework can be found in Supplementary Fig. 1. Note that the learned latent representations can be elucidated by utilizing the \(\alpha \beta\)-LRP interpretation method, mapping them back to the original space variables to uncover the causes and effects of the target variable. From a theoretical explanatory perspective, the generalized dynamic causation grounded in delay embedding theorem32,33,37 provides a theoretical foundation for understanding causal interactions and time series forecasting, while deep learning serves as the backbone for computationally implementing space decomposition and future predictions within a nonlinear system. Unlike the recently proposed spatiotemporal information conversion machine (STICM)8, which relies on Granger causality (GC), CReP is grounded in dynamic causation theory, inherently accommodating nonlinearity and non-separability. This theoretical advantage enables CReP to effectively handle a broader range of systems beyond those addressable by GC26,34. Moreover, CReP simultaneously identifies both causes and effects of the target variable within a single run, thus achieving higher computational efficiency than STICM.

Fig. 1: Schematic illustration of the CReP framework.
figure 1

a In a dynamical system where variable a causes variable b, the historical information of a is contained within the time series of b. Dynamic causation, grounded in Takens’ embedding theorem ensures reliable predictability from the delay embedding manifold \({M}_{b}\) to \({M}_{a}\). By incorporating the spatiotemporal information (STI) transformation, dynamic causation is extended to enable mappings between delay and non-delay manifolds, broadening the scope of causation analysis. b CReP is a self-supervised method to make multistep forecasting for a target variable y selected from the high-dimensional observables \(\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\}\). The original information \({{{{\bf{X}}}}}^{t}\) is transformed into temporal information \({{{{\bf{Y}}}}}^{t}\) by introducing three intermediary latent causal representations \({{{{\bf{S}}}}}^{t},{{{{\bf{Z}}}}}^{t},{{{{\bf{V}}}}}^{t}\) as bridges that capture the relationships with the target variable. The effect representation \({{{{\bf{Z}}}}}^{t}\) facilitates the future predictions \(\{{y}^{m+1},{y}^{m+2},\cdots ,{y}^{m+L-1}\}\) in \({{{{\bf{Y}}}}}^{t}\), while \({{{{\bf{Y}}}}}^{t}\) helps the temporal reconstruction for cause representation \({{{{\bf{S}}}}}^{t}\) based on generalized dynamic causation. c The latent representations remain too abstract to understand although they are causally informative. To make causal analysis for the target variable y from a practical perspective, \(\alpha \beta\)-LRP is employed in the CReP framework to calculate the relevance scores of input variables \(\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\}\) to the representations, which undirectedly quantify the causal strength of input variables to the target variable y.

Full size image

In this study, CReP is designed as a refined approach to the long-standing problem of comprehensively capturing system dynamics by integrating causal information mining and temporal information prediction through causal-oriented representation learning. To evaluate the performance of the CReP framework, it was applied on three representative models, i.e., a 60-dimensional Lorenz 96 system41, a 120-dimensional Kuramoto system42 and a 50-dimensional biological system. Additionally, we tested the CReP on two real-world datasets: predicting the daily number of cardiovascular inpatients in major hospitals in Hong Kong43,44, and forecasting the spread of COVID-19 in Japan45. The results demonstrate its effectiveness as a powerful tool for analyzing real causal networks and making reliable predictions for key variables based solely on observed data, indicating its potential for practical applications across various fields.

Results

Dynamic causation based on delay embedding scheme

According to dynamical systems theory, a necessary condition for two variables (e.g., \(a\) and \(b\)) to be causally linked is that they belong to the same dynamic system, meaning that they share a common attractor manifold46. Specifically, when the variable \(a\) acts as an environmental driver of the variable \(b\), the historical information from \(a\) is contained within the time series of \(b\), making it possible for the temporal reconstruction of \(a\) using \(b\). To illustrate, using the delay embedding scheme, we transform the original state space to the delay embedding space, represented as \({{{{\bf{A}}}}}^{t}={({a}^{t},{a}^{t+1},\cdots ,{a}^{t+L-1})}^{{\prime} }\in {{\mathbb{R}}}^{L}\) and \({{{{\bf{B}}}}}^{t}={({b}^{t},{b}^{t+1},\cdots ,{b}^{t+L})}^{{\prime} }\in {{\mathbb{R}}}^{L+1}\), where \(L\) is the embedding dimension and the symbol “\({\prime}\)” is the transpose of a vector. Based on the assumption of steady dynamics, \({\left({\left({{{{\bf{A}}}}}^{t}\right)}^{{\prime} },{({{{{\bf{B}}}}}^{t})}^{{\prime} }\right)}^{{\prime} }\) is an augmented \(2L+1\) dimensional vector on an attractive manifold with box-counting dimension \(d\). Clearly, \({{{{\bf{B}}}}}^{t}\) contains both its own temporal information and that of \(a\), whereas \({{{{\bf{A}}}}}^{t}\) contains only its own dynamic information. Therefore \({{{{\bf{A}}}}}^{t}\) can be predicted reliably using \({{{{\bf{B}}}}}^{t}\), but not vice versa47,48,49,50. Specifically, there exists an implicit function with the approximation error \({\epsilon }^{b,t}\):

$$\begin{array}{c}{{{{\bf{A}}}}}^{t}=h\left({{{{\bf{B}}}}}^{t},{\epsilon }^{b,t}\right),\end{array}$$
(1)

where \(h\) sufficiently exists when \(L > 2d\), and \(h\) is the embedding map from the delay manifold \({M}_{b}=\{{{{\bf{B}}}}^{t}{|t}{\mathbb{\in }}{\mathbb{R}}\}\) to \({M}_{a}=\{{{{{\bf{A}}}}}^{t}{|t}{\mathbb{\in }}{\mathbb{R}}\}\) according to Takens’ embedding theorem and its stochastic version11,26,32,33,51,52.

More generally, the mapping \(h\) in the causal equation Eq. (1) can be extended to map a non-delay manifold to a delay manifold. The generalized embedding theorem37, which expands Takens’ embedding theorem32, addresses more generic scenarios. According to the theory, the delay embedding manifold of the response variable \(b\) can be topologically conjugated to a non-delay embedding manifold53, which is summarized as the spatiotemporal information (STI) transformation8. Let \({{{{\bf{C}}}}}^{t}=({c}_{1}^{t},{c}_{2}^{t},\cdots ,{c}_{q}^{t})\) be the non-delay embedding vector that is topologically conjugated to the delay embedding vector \({{{{\bf{B}}}}}^{t}\), where \(q > 2\widetilde{d}\) and \(\widetilde{d}\) is the box-counting dimension of \({M}_{b}\). When variable \(a\) causes variable \(b\), \({{{{\bf{A}}}}}^{t}\) can be reliably predicted using \({{{{\bf{B}}}}}^{t}\) and we can also obtain the implicit function:

$$\begin{array}{c}{{{{\bf{A}}}}}^{t}=\widetilde{h}\left({{{{\bf{C}}}}}^{t},{\epsilon }^{c,t}\right),\end{array}$$
(2)

where \({\epsilon }^{c,t}\) is the approximation error, and \(\widetilde{h}\) maps from the non-delay manifold \({M}_{c}=\{{{{{\bf{C}}}}}^{t}{|t}{\mathbb{\in }}{\mathbb{R}}{{\}}}\) to the delay manifold \({M}_{a}=\{{{{{\bf{A}}}}}^{t}{|t}{\mathbb{\in }}{\mathbb{R}}{{\}}}\). Therefore, we generalize dynamic causation with the STI transformation, which is illustrated in Fig. 1a. This equation is referred to as the generalized causal equation in this study. Similarly, the delay embedding \({{{{\bf{B}}}}}^{t}\) can be used to reliably predict a non-delay embedding which is topologically conjugated to \({{{{\bf{A}}}}}^{t}\) under certain dimension conditions. More detailed descriptions are provided in Supplementary Note 3.

Multistep forecasting framework with dynamic causation

For each observed state \({{{{\bf{X}}}}}^{t}={({x}_{1}^{t},{x}_{2}^{t},\cdots ,{x}_{n}^{t})}^{{\prime} }\) with \(n\) variables at time \(t\) (\(t={{\mathrm{1,2}}},\cdots ,m\)), the temporal information \({{{{\bf{Y}}}}}^{t}={({y}^{t},{y}^{t+1},\cdots ,{y}^{t+L-1})}^{{\prime} }\) can be constructed using the delay embedding scheme for any target variable \(y\) (e.g., \({y}^{t}={x}_{k}^{t}\)) (\(k={{\mathrm{1,2}}},\ldots ,n\)), where the parameter \(L\) is the delay embedding dimension satisfying \(L > 2d\). Here, \({{{{\bf{X}}}}}^{t}\) is a known high-dimensional vector comprising multiple observed variables at time point \(t\), while \({{{{\bf{Y}}}}}^{t}\) is a temporal vector for the target variable \(y\) across multiple time points \(t,t+1,\cdots ,t+L-1\). Denote \(X=({{{{\bf{X}}}}}^{1},{{{{\bf{X}}}}}^{2},\cdots ,{{{{\bf{X}}}}}^{m})\) as the marix of observed states across all time points, and \(Y=({{{{\bf{Y}}}}}^{1},{{{{\bf{Y}}}}}^{2},\cdots ,{{{{\bf{Y}}}}}^{m})\) as the matrix of delay embedding vectors across all time points as follows:

$$\begin{array}{c}Y=\left({{{{\bf{Y}}}}}^{1},{{{{\bf{Y}}}}}^{2},\cdots ,{{{{\bf{Y}}}}}^{m}\right)={\left(\begin{array}{c}{y}^{1}\\ {y}^{2}\\ \vdots \\ {y}^{L}\end{array}\begin{array}{c}{y}^{2}\\ {y}^{3}\\ \vdots \\ {y}^{L+1}\end{array}\begin{array}{c}\cdots \\ \cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{y}^{m}\\ {y}^{m+1}\\ \vdots \\ {y}^{m+L-1}\end{array}\right)}_{L\times m}.\end{array}$$
(3)

Note that \(\{{y}^{1},{y}^{2},\cdots ,{y}^{m}\}\) located in the upper-left area is the known information, while \(\{{y}^{m+1},{y}^{m+2},\cdots ,{y}^{m+L-1}\}\) located in the lower-right area is the unknown information that remains to be predicted.

Observations from high-dimensional time series encompass rich information content on causal interactions. Based on their causal relationships with a selected target variable \(y\), the information can be divided into three mutually exclusive and collectively exhaustive categories: cause-related information, effect-related information, and independent information. Inspired by the temporal information of \(y\), the CReP directly decomposes the observed high-dimensional data \({{{{\bf{X}}}}}^{t}\) into three orthogonal latent representations St, Zt, Vt via a nonlinear function \(H\), capturing three types of causal information for \(y\), respectively, forming the following equations:

$$\begin{array}{c}\left\{\begin{array}{c}H\left({{{{\bf{X}}}}}^{t}\right)=\left(\begin{array}{c}{{{{\bf{S}}}}}^{t}\\ {{{{\bf{Z}}}}}^{t}\\ {{{{\bf{V}}}}}^{t}\end{array}\right),\\ {H}^{-1}\left(\begin{array}{c}{{{{\bf{S}}}}}^{t}\\ {{{{\bf{Z}}}}}^{t}\\ {{{{\bf{V}}}}}^{t}\end{array}\right)={{{{\bf{X}}}}}^{t},\end{array}\right.\end{array}$$
(4)

where \({{{{\bf{S}}}}}^{t}{=({s}_{1}^{t},{s}_{2}^{t},\cdots ,{s}_{q}^{t})}^{{\prime} }\), \({{{{\bf{Z}}}}}^{t}{=({z}_{1}^{t},{z}_{2}^{t},\cdots ,{z}_{q}^{t})}^{{\prime} }\) and \({{{{\bf{V}}}}}^{t}{=({v}_{1}^{t},{v}_{2}^{t},\cdots ,{v}_{q}^{t})}^{{\prime} }\). The mapping \({H}^{-1}\) is the conjugate function for reconstructing the original information. The decomposition and reconstruction processes can be realized by using an autoencoder (AE). According to the generalized causal equation (Eq. (2)), the effect representation \({{{{\bf{Z}}}}}^{t}\) can be utilized to effectively predict the temporal information of \(y\), and the cause representation \({{{{\bf{S}}}}}^{t}\) can be reconstructed from \(y\) based on dynamic causation. Let \(S=\left({{{{\bf{S}}}}}^{1},{{{{\bf{S}}}}}^{2},\cdots ,{{{{\bf{S}}}}}^{m}\right)\), \(Z=({{{{\bf{Z}}}}}^{1},{{{{\bf{Z}}}}}^{2},\cdots ,{{{{\bf{Z}}}}}^{m})\) and \(V=({{{{\bf{V}}}}}^{1},{{{{\bf{V}}}}}^{2},\cdots ,{{{{\bf{V}}}}}^{m})\) denote the matrices of cause, effect, and non-causal representations across all time points, respectively. Therefore, the original spatiotemporal information \(X\) is transformed into three orthogonal causal representations \(S,Z,V\), effectively facilitating multistep predictions for the target variable. Specifically, the non-delay embedding vector \({{{{\bf{Z}}}}}^{t}\) is mapped to the delay embedding vector \({{{{\bf{Y}}}}}^{t}\) via a nonlinear function \(g\), and \({{{{\bf{Y}}}}}^{t}\) is mapped to the non-delay embedding vector \({{{{\bf{S}}}}}^{t}\) via a nonlinear function \(f\), forming the following causal equations with the approximation errors \({\epsilon }^{z,t}\) and \({\epsilon }^{y,t}\):

$$\begin{array}{c}\left\{\begin{array}{c}g\left({{{{\bf{Z}}}}}^{t},{\epsilon }^{z,t}\right)={{{{\bf{Y}}}}}^{t},\\ f\left({{{{\bf{Y}}}}}^{t},{\epsilon }^{y,t}\right)={{{{\bf{S}}}}}^{t},\end{array}\right.\end{array}$$
(5)

where the first equation is to forecast the unknown values for \(y\) with \(g:{{\mathbb{R}}}^{q}{{\mathbb{\to }}{\mathbb{R}}}^{L}\), and the second equation is to recover the cause representation \({{{{\bf{S}}}}}^{t}\) with \(f:{{\mathbb{R}}}^{L}{{\mathbb{\to }}{\mathbb{R}}}^{q}\). The prediction and reconstruction process can be effectively implemented using Temporal Convolutional Network (TCN)54, which possesses multiple advantages including flexible receptive fields, stable gradient propagation and temporal consistency8. Let \({Z}_{{\mbox{win}}}=({{{{\bf{Z}}}}}^{t-w},{{{{\bf{Z}}}}}^{t-w+1},\cdots ,{{{{\bf{Z}}}}}^{t})\) and \({Y}_{{\mbox{win}}}=({{{{\bf{Y}}}}}^{t-w},{{{{\bf{Y}}}}}^{t-w+1},\cdots ,{{{{\bf{Y}}}}}^{t})\) with window size \(w+1\) denote the sliding window matrices from the whole spatiotemporal matrices \(Z\) and \(Y\), respectively. The causal equations based on the CReP are as follows:

$$\begin{array}{c}\left\{\begin{array}{c}g\left({Z}_{{\mbox{win}}},{\epsilon }^{z,t}\right)={{{{\bf{Y}}}}}^{t},\\ f\left({Y}_{{\mbox{win}}},{\epsilon }^{y,t}\right)={{{{\bf{S}}}}}^{t},\end{array}\right.\end{array}$$
(6)

where \({{{{\bf{Y}}}}}^{t}\) represents the temporal information of the target variable at time points \(t,t+1,\cdots ,t+L-1\), and \({{{{\bf{S}}}}}^{t}\) represents multi-dimensional cause representation at time point \(t\). The implementation details of CReP are illustrated in Supplementary Fig. 2. Given that the number of historical time points is \(m\), we can predict the values of the target variable for the next \(L-1\) time steps, i.e., \(\{{y}^{m+1},{y}^{m+2},\cdots ,{y}^{m+L-1}\}\), and reconstruct the cause representation \(S\) using the equation above. Clearly, properly determining the functions \(g\) and \(f\) are crucial for interpreting the causal relationships of \(y\) within the dynamic system and providing reliable multi-step forecasting of the future values. The details of delay embedding theorem and STI equations are provided in Supplementary Note 1 and Supplementary Note 2, respectively.

Explicit causation revealing based on layer-wise relevance propagation

As mentioned above, the original spatiotemporal information \(X=({{{{\bf{X}}}}}^{1},{{{{\bf{X}}}}}^{2},\cdots ,{{{{\bf{X}}}}}^{m})\) is causally decomposed into three orthogonal latent representations that suggest different causal interactions with the target variable. However, these causal representations, e.g., \(S=({{{{\bf{S}}}}}^{1},{{{{\bf{S}}}}}^{2},\cdots ,{{{{\bf{S}}}}}^{m})\), \(Z=\left({{{{\bf{Z}}}}}^{1},{{{{\bf{Z}}}}}^{2},\cdots ,{{{{\bf{Z}}}}}^{m}\right)\), are abstract and thus difficult to interpret in practical terms. To enhance the interpretability of these factors from a practical perspective, we focus on explaining the learned function \(H\) that performs the decomposition of the original space.

Layer-wise relevance propagation (LRP)39,40 is an effective method for explaining deep neural networks and has demonstrated its efficiency and accuracy for both classification and regression tasks55,56,57. Specifically, given a trained neural network, such as a Multilayer Perceptron (MLP)58, the observed \(n\) variables are processed through the network to produce a prediction output \(f(X)\). LRP then redistributes the output back to the input variables layer by layer and computes the relevance score \({R}_{k}^{(1)}(k={{\mathrm{1,2}}},\cdots ,n)\) to assess the importance of the \(k\)-th input variable in the network’s first layer to the output. To better understand the causal representations learned by CReP, the \(\alpha \beta\)-rule-based LRP method (\(\alpha \beta\)-LRP) is applied to interpret the decomposition function \(H\) by calculating the relevance scores of each input variable \({x}_{k}\) to \(S\) and \(Z\) (see Fig. 1c), denoted by \({{RS}}_{k,S}\) and \({{RS}}_{k,Z}\), respectively. These scores are obtained by aggregating the relevance scores to the vector outputs \({{{{\bf{S}}}}}^{t}\) and \({{{{\bf{Z}}}}}^{t}\), represented by \({{RS}}_{k,{{{{\bf{S}}}}}^{t}}\) and \({{RS}}_{k,{{{{\bf{Z}}}}}^{t}}\), over all time points. \({{RS}}_{k,S}\) quantifies the contribution of variable \({x}_{k}\) to the cause representation, thus indirectly used to infer the cause strength on \(y\). \({{RS}}_{k,Z}\) measures the contribution of variable \({x}_{k}\) to the effect representation, thus indirectly employed to infer the effect strength on \(y\). A higher value of \({{RS}}_{k,S}\) indicates a stronger causal link from \({x}_{k}\) to \(y\), while a higher value of \({{RS}}_{k,Z}\) indicates a stronger causal link from \(y\) to \({x}_{k}\). Consequently, the causal strength networks of \(y\) can be inferred by interpreting the latent causal factors \(S\) and \(Z\) from a practical perspective, which facilitates the identification of the causes and effects of \(y\). The detailed procedure for calculating the relevance scores is provided in Methods, Supplementary Fig. 3 and Supplementary Note 5.

Performance of the framework on simulation models

To illustrate the application of the CReP framework, simulated time series datasets were generated using the Lorenz 9641, Kuramoto models42 and gene regulatory network. Detailed results concerning the forecasting performance and causal inference are demonstrated in Supplementary Fig. 4 and Supplementary Fig. 5. The known data for each dataset is shown in Supplementary Table 1. The specific parameter settings of CReP are provided in Supplementary Table 2 and Supplementary Table 3. More experimental runs of different target variables are provided in Supplementary Table 5. In addition, we compared the results with other baseline methods (details provided in Supplementary Note 8) as shown in Supplementary Table 4.

Lorenz96 model

The Lorenz 96 system, introduced by Edward Lorenz in 199641, is a simplified mathematical model used to study atmospheric dynamics and chaotic behavior in weather prediction. The system consists of a set of ordinary differential equations for \(n\) variables that describe how a series of variables evolve over time with the following equations:

$$\begin{array}{c}\frac{d{x}_{i}}{{dt}}=\left({x}_{i+1}-{x}_{i-2}\right){x}_{i-1}-{x}_{i}+F,\end{array}$$
(7)

where \(i={{\mathrm{1,2}}},\cdots ,n\) and the parameter \(F\) is an external forcing term. Note that the causal link from \({x}_{j}\) to \({x}_{i}\) exists if \({x}_{j}\) is one of the independent variables of \({x}_{i}\), which is a standard criterion to identify dynamical causality in ordinary differential equations59,60,61.

We first apply the CReP to a Lorenz 96 system with \(n=60\), taking a time series of 50 steps (\(m=50\)) as known information and performing a 15-step ahead prediction (\(L-1=15\)) for a randomly selected target variable \({y}_{1}\). Note that the forecasted values for the target variable were obtained through a single prediction run, demonstrating the method’s capability for effective multi-step forecasting. As shown in Fig. 2a and Fig. 2b, the CReP framework shows satisfactory performance in terms of the Pearson correlation coefficient (PCC) and the root mean square error (RMSE) values. Specifically, the RMSEs for the randomly selected samples were as low as 0.0141 and 0.0299. The average RMSE and PCC across all samples are shown in Table 1. In addition, as presented in Fig. 2c and Fig. 2d, the relevance scores of variables to causal representations were computed to quantify the causal strength of variables on the target variable. The inferred cause and effect strength networks constructed from the relevance scores, shown in Fig. 2f and Fig. 2g, align well with the causal relationships derived from the original equations (see Fig. 2e). For the target variable \({x}_{2}\), the direct causes in the system are determined as \({x}_{60},{x}_{3},{x}_{1}\), while the direct effects in the system are determined as \({x}_{4}\), \({x}_{3}\) and \({x}_{1}\) (Fig. 2e). Based on the CReP, \({x}_{60}\), \({x}_{3}\) and \({x}_{1}\) were identified as the variables most likely to cause the target variable (Fig. 2f, inferred cause strength network with only the top six variables), while \({x}_{4}\), \({x}_{3}\) and \({x}_{1}\) were identified as being among those most likely to be caused by the target variable (Fig. 2g, inferred effect strength network with only the top six variables). The results validated the reliability of the causal inference conducted in this study.

Fig. 2: The forecasting performance and causal analysis of the CReP on the Lorenz 96 system.
figure 2

The time-series data were generated on the basis of the 60D Lorenz 96 system (Eq. (7)). The target variable was randomly selected among variables \(\{{x}_{1},{x}_{2},\cdots ,{x}_{60}\}\). Taking a time series of 50 steps (\(m=50\)) as known information, the CReP was applied to perform a 15-step-ahead prediction (\(L-1=15\)) for the target variable. The prediction performance of CReP is shown over two periods in (a) and (b). The root mean square errors (RMSEs) between the CReP predictions and the original values are 0.0141 in (a) and 0.0299 in (b), while the Pearson correlation coefficients (PCCs) are 0.9999 in (a) and 0.9995 in (b). By interpreting the causal representations via \(\alpha \beta\)-LRP, the relevance scores for variables \(\{{x}_{1},{x}_{2},\cdots ,{x}_{60}\}\) with regard to \(S\) and \(Z\) were calculated to quantify their causal strength on \(y\), and the top 10 variables are shown in (c) and (d). Based on the CReP, the inferred causal strength networks (f) and (g) were constructed to show the responsible causes and effects of the target variable, which align well with the gold standard in (e).

Full size image
Table 1 The average RMSEs and PCCs of each dataset across all samples
Full size table

Power grid system

The Kuramoto system is a mathematical model used to study synchronization phenomena in systems of coupled oscillators. It was introduced by Yoshiki Kuramoto in 197542. The model explores how a large number of oscillators, each with its own natural frequency, can synchronize when coupled together. We applied the CReP framework to a power grid system modeled by Kuramoto equations involving 120 units, which can be represented as follows:

$$\begin{array}{c}\frac{d{\theta }_{i}}{{dt}}={\omega }_{i}+\gamma {\sum }_{j=1}^{N}{A}_{{ij}}\sin \left({\theta }_{j}-{\theta }_{i}\right),\end{array}$$
(8)

where \({\theta }_{i}\) and \({\omega }_{i}\) are the phase and natural frequency of the \(i\)-th oscillator respectively, \(\gamma\) is the coupling strength, while pairwise interactions are encoded in the adjacency matrix \(A\)62.

For the 120-dimensional system (\(n=120\)), we used 30 known time points (\(m=30\)) and predicted 9 future time points (\(L-1=9\)). The target variable \({y}_{1}\) was randomly selected from \(\{{\theta }_{1},{\theta }_{2},\cdots ,{\theta }_{120}\}\). The forecasting performance for the target variable \({\theta }_{33}\) using the CReP framework is illustrated in Fig. 3a,b, and the average RMSE and PCC across all samples are demonstrated in Table 1. Additionally, causal inference for \({\theta }_{33}\) was conducted as shown in Fig. 3f,g, based on the computed relevance scores depicted in Fig. 3c,d. A higher relevance score to the cause representation indicates a stronger cause strength to the target variable, while a higher relevance score to the effect representation reflects a stronger effect strength to the target variable. For the true cause variables \({\theta }_{32}\) and \({\theta }_{86}\) (Fig. 3e), their cause strengths were the strongest, while the true effect variables \({\theta }_{32}\) and \({\theta }_{30}\) (Fig. 3e) exhibited prominent effect strengths compared to other variables. This fact demonstrates that causal analysis of the target variable can be effectively performed using the causal strength networks through the interpretation method \(\alpha \beta\)-LRP.

Fig. 3: The forecasting performance and causal analysis of the CReP on the power grid system.
figure 3

The time-series data were generated using the 120D Kuramoto model (Eq. (8)). We randomly selected the target variable among variables \(\{{\theta }_{1},{\theta }_{2},\cdots ,{\theta }_{120}\}\). By applying the CReP framework, we used 30 known time points (\(m=30\)) and predicted 9 future time points (\(L-1=9\)) for the target variable. The forecasting results of CReP on the system are demonstrated in (a) and (b). Additionally, (c) and (d) show the relevance scores of top 10 variables to the cause representation \(S\) and the effect representation \(Z\), respectively. As presented in the inferred causal networks in (f) and (g), the responsible causes and effects for the target variable are highlighted based on the calculated relevance scores in (c) and (d). The true causal network for the target variable is shown in (e).

Full size image

Gene regulatory network

The DREAM4 (Dialogue for Reverse Engineering Assessments and Methods) dataset63,64,65 is a benchmark for evaluating algorithms in gene regulatory network inference, featuring simulated gene expression time series data generated from known biological networks. This dataset, produced using GeneNetWeaver (GNW)66, includes various challenges, each characterized by distinct network structures, noise levels, and the number of genes. Numerous researchers utilize DREAM4 to assess the performance of causal inference methods and enhance the understanding of underlying biological mechanisms. By integrating GNW’s capabilities, DREAM4 provides a robust framework for testing and refining methodologies in systems biology.

To validate the performance of CReP, we utilize the DREAM in silico dataset with 50 nodes (\(n=50\)), which contains known gene interactions and incorporates noise to reflect biological variability. We employed the information from 40 known time points (\(m=40\)) to forecast the future values of 8 time points (\(L-1=8\)). To better demonstrate the performance of CReP, the target gene \({y}_{1}\) was selected as G18, which exhibits complex connections with other genes. The forecasting results for the target variable using CReP are visualized in Fig. 4a,b, with average RMSE of 0.0984 and PCC of 0.8894 shown in Table 1. Additionally, the true gene regulatory network for the target variable G18 is depicted in Fig. 4e, suggesting that G16, G22 and G23 are the primary causes of the dynamic change in G18, while G19, G20 and G28 are the variables mainly affected by G18. Derived from the relevance scores in Fig. 4c,d, the inferred causal strength networks of top 8 variables for the target variable are illustrated in Fig. 4f,g, highlighting that G16 and G22 exhibit prominent cause strength on G18, while G19 and G28 demonstrate significant effect strength on G18, which aligns well with the gold standard in Fig. 4e.

Fig. 4: The forecasting performance and causal analysis of the CReP on the gene regulatory network.
figure 4

We utilized the DREAM in silico dataset with 50 nodes (\(n=50\)) and applied a simple smoothing technique to reduce the noise in data. The target variable was selected due to its complex connections. Using the CReP with parameter \(m=40\) (i.e., the length of the input series is 40), we performed 8-step-ahead forecasting (\(L-1=8\)) for the target variable, as shown in (a) and (b). Additionally, the relevance scores of each gene to the causal representations were calculated and the top 10 variables are displayed in (c) and (d). The network in (e) illustrates the true causal relations of the target variable within the dataset. The cause strength network in (f) is constructed from the relevance scores in (c), while the effect strength network in (g) is derived from the relevance scores in (d). Genes with higher relevance scores indicate greater causal influence on the target variable.

Full size image

The application of the framework on real-world datasets

To better illustrate the generalizability of the CReP framework, we applied it to two real-world datasets of complex natural dynamic systems. The specific descriptions of each dataset are presented in Supplementary Note 6.

Cardiovascular inpatients forecasting

The first real-world dataset comprises a series of records on cardiovascular inpatients from major hospitals in Hong Kong, along with data on air pollutants43,44. The pollutants include the daily concentrations of nitrogen dioxide (NO2), sulfur dioxide (SO2), ozone (O3), respirable suspended particulate (Rspar), mean daily temperature, relative humidity, and other factors. The data were obtained from air monitoring stations in Hong Kong between the years 1994 and 199743,44. Based on prior research demonstrating the association between air pollutants and cardiovascular admissions67, the CReP was applied to predict daily cardiovascular disease admissions using the air pollutants data. For the 14-dimensional system (\(n=14\)), the 70 determined-state time points were used (\(m=70\)), and the 25 future values remained to be predicted (\(L-1=25\)). The forecasting performance using the CReP is demonstrated in Fig. 5a,b. Table 1 shows the average RMSE and PCC across all samples.

Fig. 5: Performance of the CReP on the two real-world datasets.
figure 5

For two periods (a) and (b), the CReP predicted the number of cardiovascular admissions using the high-dimensional time series of air pollutant indices, with an input length of \(m=70\) and a forecasting horizon of \(L-1=25\). Based on the time series of COVID-19 new cases of 47 districts, the CReP predicted the number of future new cases for Tokyo over two periods in (c) and (d), with 30 steps of known information (\(m=30\)) and 14 steps of future information (\(L-1=14\)). Additionally, the causes of cardiovascular admissions inferred by CReP, shown in (f), closely align well with the true drivers in (e). For COVID-19 transmission in Tokyo, the inferred causal strength networks are demonstrated in (g) and (h), constructed from the relevance scores. As illustrated in (i), the dominant causes and effects inferred by CReP are geographically near Tokyo, supporting the reliability of causal analysis using CReP.

Full size image

Considering the real-world causal implications, we focus on inferring the cause strength for the target variable, i.e., cardiovascular diseases, to identify the most significant factors causing the number of cardiovascular inpatients. According to the inferred cause strength network shown in Fig. 5f, respirable suspended particulates and air pollutants (e.g., NO2 and SO2), were identified as primary contributors to cardiovascular diseases. This conclusion aligns well with the causal links in Fig. 5e supported by relevant literatures11,68,69,70 that have studied the relationship between air pollutants and cardiovascular inpatients. The results enable us to understand the causal mechanisms behind the evolution process, thereby providing direction and guidance for implementing environmental protection and management to reduce the number of cardiovascular inpatients.

Japan Covid-19 transmission forecasting

The worldwide emergence of the coronavirus disease 2019 (COVID-19) pandemic has constituted a grave challenge to global public health. It is crucial to forecast the dissemination of this infectious disease in order to aid public health departments in their strategic planning endeavors. The second dataset contains a series of number representing COVID-19 daily new cases of 47 districts (\(n=47\)) in Japan. The CReP in the study helps to predict the dynamic trends of daily new cases, thereby supporting more informed decision-making. Focusing on Tokyo with severe epidemic45,71, the CReP provided a 14-step-ahead prediction (\(L-1=14\)) of COVID-19 case numbers, based on 30 known time points (\(m=30\)), as shown in Fig. 5c,d. The average forecasting performance in terms of RMSE and PCC across all samples is illustrated in Table 1.

Additionally, we analyzed the dynamic causal relationships among all districts by calculating relevance scores. The inferred cause and effect strength networks (Fig. 4g,h) indicate that Kyoto, Chiba, and Kanagawa were the primary cities influencing the dynamic changes in daily new cases in Tokyo, while Kanagawa, Saitama and Chiba were the main cities impacted by the spread of the disease in Tokyo. To better understand these causal relationships, the geographic locations around Tokyo are depicted in Fig. 5i. The proximity of Chiba and Kanagawa to Tokyo supports the rationale that these cities significantly influenced Tokyo’s COVID-19 case numbers. Although Kyoto is geographically farther from Tokyo, the frequent population flow from it to Tokyo made it a significant factor in affecting the infection rates in Tokyo. Similarly, Kanagawa, Saitama and Chiba are geographically close to Tokyo, thus explaining their susceptibility to the case dynamics originating in Tokyo. The results help to better understand the disease transmission between regions and allows for timely implementation of isolation, control, and other measures before the pandemic spreads across regions, thus effectively containing its expansion.

Ablation study on loss function

To further demonstrate the effectiveness of CReP framework, we conduct an ablation study by eliminating different loss terms from our training loss. The experiment results on the simulation datasets are presented in Table 2. The “without \({{{{\mathscr{L}}}}}_{{{\rm{REC}}}}\)”, “without \({{{{\mathscr{L}}}}}_{{{\rm{FC}}}}\)” and “without \({{{{\mathscr{L}}}}}_{{{\rm{ORTH}}}}\)” columns indicate that the reconstruction loss, the future-consistency loss and the orthogonal loss are eliminated from loss function during training CReP, respectively. Removing \({{{{\mathscr{L}}}}}_{{{\rm{REC}}}}\) prevents CReP from guaranteeing the recovery of original high-dimensional information. Without \({{{{\mathscr{L}}}}}_{{{\rm{FC}}}}\), the temporally self-constrained conditions are not enforced, and the removal of \({{{{\mathscr{L}}}}}_{{{\rm{ORTH}}}}\) means that CReP is prone to extracting overlapping or insufficient causal information from observed data.

Table 2 The ablation study results of CReP on three simulated datasets
Full size table

In this ablation study, the model performance is evaluated from two perspectives: time series forecasting and causal analysis. Forecasting performance is assessed using the root mean square error (RMSE), while causal performance requires further quantification of inferred causal strengths to enable accuracy as a metric. For the inferred causal strengths obtained through relevance scores, P-value hypothesis testing is applied to determine an appropriate threshold, enabling the identification of causes and effects associated with the target variable (Supplementary Fig. 6). This identification allows for the construction of a directed causal graph centered on the target variable, without distinctions in causal strength. By comparing the inferred causal graph to the gold standard, metrics such as accuracy and recall are computed to assess causal performance in the ablation study. The overall process to evaluate the inferred causal results are summarized as follows:

  1. 1.

    Determine an appropriate threshold using P-value hypothesis testing.

  2. 2.

    Identify the causes and effects related to the target variable.

  3. 3.

    Construct an inferred causal graph centered on the target variable.

  4. 4.

    Calculate accuracy and recall against the gold standard.

Through the evaluation process outlined above, a comparison is conducted between the predictive performance and causal analysis capability of the model after removing each component of the loss function. As presented in the Table 2, the model trained with the full loss achieves the best overall performance, indicating that all the constrains in the CReP framework contribute to producing accurate time-series forecasting and robust causal analysis. Further details regarding the ablation study are provided in Supplementary Note 7.

Discussion

Time series forecasting, which predicts future trends based on historical data, can incorporate spatial information and causal interactions to improve predictive accuracy in complex systems. In this work, we proposed the CReP framework to learn causal representations from observed data, thereby performing robust multi-step-ahead predictions. The CReP framework causally transforms high-dimensional information into temporal information of the target variable by introducing three intermediary latent representations—cause, effect, and non-causal—as bridges that capture the causal relationships with the target variable. Specifically, an autoencoder is utilized to decompose the spatiotemporal information \(X\) into the cause representation \(S\), the effect representation \(Z\) and the non-causal representation \(V\) by \(H\), and then recover these causal representations to the original information by \({H}^{-1}\). According to dynamic causation incorporating the STI transformation, the effect representation \({{{{\bf{Z}}}}}^{t}\) is mapped to the temporal vector \({{{{\bf{Y}}}}}^{t}\) by \(g\), thereby forecasting multiple future values \(\{{y}^{m+1},{y}^{m+2},\cdots ,{y}^{m+L-1}\}\), and \({{{{\bf{Y}}}}}^{t}\) is employed to recover the cause representation \({{{{\bf{S}}}}}^{t}\) by \(f\). The nonlinear functions \(H,g,f,{H}^{-1}\) are fit simultaneously in a self-supervised manner. In addition, the CReP framework implicitly uncovers underlying causal interactions by learning these causal representations, facilitating robust predictions based on causal equations. Moreover, explicit causal inference is performed through the interpretation of learned causal representations \(S\) and \(Z\) using \(\alpha \beta\)-LRP, which calculates the relevance scores of each variable to the outputs \(S\) and \(Z\). This facilitates the identification of causes and effects of the target variable. Therefore, the CReP not only achieves multi-step-ahead forecasting but also infers the causal network for the target variable, offering a comprehensive understanding of the system’s intrinsic dynamics. The applications of CReP to both simulation models and real-world datasets demonstrate its effectiveness in forecasting and causal analysis.

The CReP framework offers several advantages. Firstly, with a self-supervised training scheme, the CReP integrates multi-step time-series forecasting with implicit causal discovery by utilizing high-dimensional but short-term time series data. Secondly, the use of \(\alpha \beta\)-LRP to interpret the learned causal representations reliably reveals the causal relationships within the dynamical system, which is depicted by causal strength networks. Third, built on a solid theoretical foundation of dynamic causation and the STI transformation, the CReP presents an innovative approach for exploring spatiotemporal information in high-dimensional time series from a causal perspective, enhancing temporal prediction accuracy and showing strong potential for practical applications. However, there are still limitations in causal-oriented representation learning within CReP, particularly in finding universally applicable explanatory methods for data across all domains. In the future, we will focus on integrating different causal learning methods to enhance applicability across diverse domains. In addition, we will further explore causal detection methods through active intervention rather than mere passive observations, as they offer more intuitive causal interpretations and identify causal directions with high accuracy as well72.

Methods

Dynamic causation and generalized embedding theorem

According to the principle of dynamic causation, when the variable \(a\) acts as a cause of the variable \(b\) within a dynamical system, the temporal information of \(a\) can be reliably predicted using \(b\), as shown in Fig. 1a. Even in the presence of noise, dynamic causation is still applicable according to the stochastic version of Takens’ embedding theorem51,52 (see Supplementary Note 1). However, the mapping \(h\) in Eq. (1) is constructed within delay embedding spaces, which limits its broader applicability for detecting causality. The generalized embedding theorem37 provides a robust theoretical foundation for extending the applicability of the mapping \(h\). According to the theorem:

If \(M\) is a compact manifold with box-counting dimension \(d\), for a diffeomorphism \(\phi :M\to M\) and \(L\) smooth observation functions \({y}_{k}:M{\mathbb{\to }}{\mathbb{R}}\), then it is a generic property that the mapping described by

$$\begin{array}{c}{\Phi }_{\left(\phi , < {y}_{k} > \right)}=\left({y}_{1}\left(X\right),{y}_{2}\left(X\right),\cdots ,{y}_{L}\left(X\right)\right),\end{array}$$
(9)

is an embedding as long as \(L > 2d\).

According to the theory, the delay embedding manifold of the response variable \(b\) can be topologically conjugated to a non-delay embedding manifold53, which is summarized as the spatiotemporal information (STI) transformation8. Therefore, the mapping \(h\) in Eq. (1) can be extended to map a non-delay manifold to a delay manifold and we can obtain the generalized causal equation Eq. (2), which provides a promising perspective for causal analysis and multistep forecasting of high-dimensional but short-term time series in CReP.

Unified causal and temporal modeling with CReP

We assume that the high-dimensional observations \(X\) are generated by latent variables that support causal statements73,74. Specifically, given the observed target variable \(y\), we make the following assumptions: a) the data is generated from three type of latent variables, corresponding to the cause factors, effect factors and non-causal factors of \(y\); b) these three types of latent variables are mutually independent; and c) the latent variables are unobserved75. Accordingly, CReP employs an autoencoder to decompose \(X\) into three mutually orthogonal causal representations implicitly based on their causal relationship with \(y\) via the nonlinear function \(H\), and recover the original information using the causal representations via the conjugate mapping \({H}^{-1}\) (Eq. (4)). Furthermore, cause factors and effect factors are useful representations of the data for disentangling causal dependencies of \(y\) in the latent space based on dynamic causation76.

Assuming \(g={({g}_{1},{g}_{2},\cdots ,{g}_{L})}^{{\prime} }\) and \(f={({f}_{1},{f}_{2},\cdots ,{f}_{q})}^{{\prime} }\), we can establish the following causal equations for the target variable \(y\) according their implicit causal information based on the TCN scheme:

$$\begin{array}{c}\left(\begin{array}{c}{g}_{1}\left(\left({{{{\bf{Z}}}}}^{1}\right),{\epsilon }^{z,t}\right)\\ {g}_{2}\left(\left({{{{\bf{Z}}}}}^{1}\right),{\epsilon }^{z,t}\right)\\ \vdots \\ {g}_{L}\left(\left({{{{\bf{Z}}}}}^{1}\right),{\epsilon }^{z,t}\right)\end{array}\begin{array}{c}{g}_{1}\left(\left({{{{\bf{Z}}}}}^{1},{{{{\bf{Z}}}}}^{2}\right),{\epsilon }^{z,t}\right)\\ {g}_{2}\left(\left({{{{\bf{Z}}}}}^{1},{{{{\bf{Z}}}}}^{2}\right),{\epsilon }^{z,t}\right)\\ \vdots \\ {g}_{L}\left(\left({{{{\bf{Z}}}}}^{1},{{{{\bf{Z}}}}}^{2}\right),{\epsilon }^{z,t}\right)\end{array}\begin{array}{c}\cdots \\ \cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{g}_{1}\left(\left({{{{\bf{Z}}}}}^{m-w},\cdots ,{{{{\bf{Z}}}}}^{m}\right),{\epsilon }^{z,t}\right)\\ {g}_{2}\left(\left({{{{\bf{Z}}}}}^{m-w},\cdots ,{{{{\bf{Z}}}}}^{m}\right),{\epsilon }^{z,t}\right)\\ \vdots \\ {g}_{L}\left(\left({{{{\bf{Z}}}}}^{m-w},\cdots ,{{{{\bf{Z}}}}}^{m}\right),{\epsilon }^{z,t}\right)\end{array}\right)=\left(\begin{array}{c}{y}^{1}\\ {y}^{2}\\ \vdots \\ {y}^{L}\end{array}\begin{array}{c}{y}^{2}\\ {y}^{3}\\ \vdots \\ {y}^{L+1}\end{array}\begin{array}{c}\cdots \\ \cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{y}^{m}\\ {y}^{m+1}\\ \vdots \\ {y}^{m+L-1}\end{array}\right),\end{array}$$
(10)
$$\begin{array}{c}\left(\begin{array}{c}{f}_{1}\left(\left({{{{\bf{Y}}}}}^{1}\right),{\epsilon }^{y,t}\right)\\ {f}_{2}\left(\left({{{{\bf{Y}}}}}^{1}\right),{\epsilon }^{y,t}\right)\\ \vdots \\ {f}_{q}\left(\left({{{{\bf{Y}}}}}^{1}\right),{\epsilon }^{y,t}\right)\end{array}\begin{array}{c}{f}_{1}\left(\left({{{{\bf{Y}}}}}^{1},{{{{\bf{Y}}}}}^{2}\right),{\epsilon }^{y,t}\right)\\ {f}_{2}\left(\left({{{{\bf{Y}}}}}^{1},{{{{\bf{Y}}}}}^{2}\right),{\epsilon }^{y,t}\right)\\ \vdots \\ {f}_{q}\left(\left({{{{\bf{Y}}}}}^{1},{{{{\bf{Y}}}}}^{2}\right),{\epsilon }^{y,t}\right)\end{array}\begin{array}{c}\cdots \\ \cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{f}_{1}\left(\left({{{{\bf{Y}}}}}^{m-w},\cdots ,{{{{\bf{Y}}}}}^{m}\right),{\epsilon }^{y,t}\right)\\ {f}_{2}\left(\left({{{{\bf{Y}}}}}^{m-w},\cdots ,{{{{\bf{Y}}}}}^{m}\right),{\epsilon }^{y,t}\right)\\ \vdots \\ {f}_{q}\left(\left({{{{\bf{Y}}}}}^{m-w},\cdots ,{{{{\bf{Y}}}}}^{m}\right),{\epsilon }^{y,t}\right)\end{array}\right)=\left(\begin{array}{c}{s}_{1}^{1}\\ {s}_{2}^{1}\\ \vdots \\ {s}_{q}^{1}\end{array}\begin{array}{c}{s}_{1}^{2}\\ {s}_{2}^{2}\\ \vdots \\ {s}_{q}^{2}\end{array}\begin{array}{c}\cdots \\ \cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{s}_{1}^{m}\\ {s}_{2}^{m}\\ \vdots \\ {s}_{q}^{m}\end{array}\right).\end{array}$$
(11)

By leveraging dynamic causation with \(y\), the CReP provides the multi-step forecasting, i.e., \(\{{y}^{m+1},{y}^{m+2},\cdots ,{y}^{m+L-1}\}\), simultaneously uncovering the causal interactions for \(y\) through analyzing and interpreting the causal representations.

Optimization of CReP

Grounded in the causal equations above, the CReP effectively leverages the observed spatiotemporal information via causal decomposition, thereby improving the accuracy and robustness of multi-step forecasting. The determination of \(H,g,f,{H}^{-1}\) relies on a self-supervised learning scheme. In this study, each layer of the nonlinear mappings is followed by the LeakyReLU activation function. The optimization of our network uses a “consistently self-constraint scheme”8 which focuses on the preservation of temporal consistency for the target variable. For the delay embedding matrix \(Y\), there are \(m\) known historical values \(\{{y}^{1},{y}^{2},\cdots ,{y}^{m}\}\) and \(L-1\) to-be-predicted future values \(\{{y}^{m+1},{y}^{m+2},\cdots ,{y}^{m+L-1}\}\). The estimated delay embedding matrix \(\hat{Y}\) in each iteration is obtained through Eq. (10):

$$\begin{array}{c}\hat{Y}=\left(\begin{array}{c}{\left({\hat{y}}^{1}\right)}_{1}\\ {\left({\hat{y}}^{2}\right)}_{2}\\ \vdots \\ {\left({\hat{y}}^{L}\right)}_{L}\end{array}\begin{array}{c}{\left({\hat{y}}^{2}\right)}_{1}\\ {\left({\hat{y}}^{3}\right)}_{2}\\ \vdots \\ {\left({\hat{y}}^{L+1}\right)}_{L}\end{array}\begin{array}{c}\cdots \\ \cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{\left({\hat{y}}^{m}\right)}_{1}\\ {\left({\hat{y}}^{m+1}\right)}_{2}\\ \vdots \\ {\left({\hat{y}}^{m+L-1}\right)}_{L}\end{array}\right).\end{array}$$
(12)

We require that the estimates \({\left({\hat{y}}^{t}\right)}_{j}\) obtained from different sub-mapping functions \({g}_{j}(j\in \{{{\mathrm{1,2}}},\cdots ,L\})\) at the same time point be consistent for both historical and future information, forming \(m-1\) and \(L-2\) self-constrained conditions, respectively. In total, these \(m+L-3\) conditions regulate the network training process by enforcing temporal sequence consistency across samples.

Through the auto perception procedure, CReP is optimized through minimizing the following loss function, which comprises four weighted components:

$$\begin{array}{c}{{{\mathscr{L}}}}={\lambda }_{1}{{{{\mathscr{L}}}}}_{{{\rm{DS}}}}+{\lambda }_{2}{{{{\mathscr{L}}}}}_{{{\rm{FC}}}}+{\lambda }_{3}{{{{\mathscr{L}}}}}_{{{\rm{REC}}}}+{\lambda }_{4}{{{{\mathscr{L}}}}}_{{{\rm{ORTH}}}}.\end{array}$$
(13)

The determined-state loss \({{{{\mathscr{L}}}}}_{{{\rm{DS}}}}\) for the target variable \(y\) over time points \(\{{{\mathrm{1,2}}},\cdots ,m\}\) is calculated using the root mean squared error (RMSE), quantifying the estimation error of all historical values of \(y\). The second part \({{{{\mathscr{L}}}}}_{{{\rm{FC}}}}\) is the future consistency loss for \(y\) over time points \(\{m+1,m+2,\cdots ,m+L-1\}\) to measure the deviation between multiple estimates of \(y\) for the same future time point using RMSE. The third part \({{{{\mathscr{L}}}}}_{{{\rm{REC}}}}\) is the reconstruction loss for latent cause representation \(S\) and the original information \(X\), designed to assess the degree of information recovery. The last part \({{{{\mathscr{L}}}}}_{{{\rm{ORTH}}}}\) in Eq. (13) is the orthogonal loss between implicit causal representations for the efficient utilization of spatiotemporal information. The detailed mathematical explanations of these loss terms, along with the ablation study, are provided in Supplementary Note 7.

Multistep forecasting and causal analysis by CReP

The CReP framework is carried out to predict the future values \(\{{y}^{m+1},{y}^{m+2},\cdots ,{y}^{m+L-1}\}\) of the target variable \(y\), which is selected from \(\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\}\), and explore the causal relationships for \(y\). After training the network by minimizing the loss function in a self-supervised manner, the \(L-1\) future values \(\left\{{y}^{m+1},{y}^{m+2},\cdots ,{y}^{m+L-1}\right\}\) can be determined from the estimated delay embedding matrix \(\hat{Y}\) as follows:

$$\begin{array}{c}{y}^{m+i}={{{\rm{mean}}}}\left({\hat{y}}^{m+i}\right)=\frac{1}{L-i}{\sum }_{j=i+1}^{L}{\left({\hat{y}}^{m+i}\right)}_{j},\end{array}$$
(14)

where \(i=1,2,\cdots ,L-1\).

While generalized dynamic causation ensures that the learned representations can effectively model causal interactions, they remain too abstract to interpret directly in a practical context. To uncover the causal links associated with \(y\)—the causes and effects—\(\alpha \beta\)-LRP is employed to explain the transformation mechanism \(H\) from \(X\) to \(S\) and \(Z\). Specifically, for a multi-layer neural network, let \({c}_{i}\) and \({c}_{j}\) represent neurons in adjacent layers \(l\) and \(l+1\), respectively, where \(i\) and \(j\) denote the indices of the neurons. A common mapping from one layer to the next one can be expressed in the following form:

$$\begin{array}{c}{c}_{j}=\sigma \left({\sum }_{i:i\,\in \,K}{z}_{{ij}}\right),\end{array}$$
(15)

where \({z}_{{ij}}={w}_{{ij}}{c}_{i}\), \(\sigma\) is the activation function, and \({w}_{{ij}}\) is the weight between neurons \({c}_{i}\) and \({c}_{j}\). The set \(K\) contains all neurons in the \(l\)-th layer. LRP calculates the relevance scores of all neurons from the output \(f(X)\) backward to the input variables. Let \({R}_{i}^{(l)}\) and \({R}_{j}^{(l+1)}\) denote the relevance scores of neurons \({c}_{i}\) and \({c}_{j}\) in layers \(l\) and \(l+1\), respectively. The amount of relevance score \({R}_{j}^{(l+1)}\) that spread to neuron \({c}_{i}\) from neuron \({c}_{j}\) is denoted as \({R}_{i\leftarrow j}^{(l,l+1)}\). By posing the following constraint:

$$\begin{array}{c}{R}_{i}^{\left(l\right)}={\sum }_{j:\,{c}_{i}{{{\rm{is}}}}\, {{{\rm{input}}}}\, {{{\rm{for}}}}\, {{{\rm{neuron}}}}\,{c}_{j}}{R}_{i\leftarrow j}^{\left(l,l+1\right)},\end{array}$$
(16)

the conservation property for the relevance scores would hold between layers globally56:

$$\begin{array}{c}{\sum }_{k=1}^{n}{R}_{k}^{\left(1\right)}=\cdots ={\sum }_{i=1}^{{n}_{l}}{R}_{i}^{\left(l\right)}={\sum }_{j=1}^{{n}_{l+1}}{R}_{j}^{\left(l+1\right)}=\cdots =f\left(X\right),\end{array}$$
(17)

where \(n\) is the number of input variables, \({n}_{l}\) and \({n}_{l+1}\) are the number of neurons in layer \(l\) and \(l+1\), and the output value \(f(X)\) is the relevance score of the output neuron. The key process for LRP is to calculate the message \({R}_{i\leftarrow j}^{(l,l+1)}\), for which various rules have been proposed39,40. The adopted propagation method in this work is the \(\alpha \beta\)-rule39,40 defined as

$$\begin{array}{c}{R}_{i\leftarrow j}^{\left(l,l+1\right)}=\left(\alpha \frac{{z}_{{ij}}^{+}}{{z}_{j}^{+}}+\beta \frac{{z}_{{ij}}^{-}}{{z}_{j}^{-}}\right){R}_{j}^{\left(l+1\right)},\end{array}$$
(18)

where \({z}_{{ij}}^{+}=\max \{{z}_{{ij}},0\}\), \({z}_{{ij}}^{-}=\min \{{z}_{{ij}},0\}\), \({z}_{j}^{+}={\sum}_{i}{z}_{{ij}}^{+}\), and \({z}_{j}^{-}={\sum}_{i}{z}_{{ij}}^{-}\). The parameters α and β need to satisfy the constraint α + β = 1. By propagating relevance layer by layer, the relevance scores \({R}_{k}^{\left(1\right)}(k={{\mathrm{1,2}}},\cdots ,n)\) are obtained to evaluate the contribution of each input variable to the network’s output. Higher relevance scores indicate greater contributions of the input variables to the output.

In CReP, the relevance scores of each input variable \({x}_{k}\) to causal factors \(S\) and \(Z\), denoted by \({{RS}}_{k,S}\) and \({{RS}}_{k,Z}\), are calculated to reveal the explicit causal relationships of the target variable. A comprehensive description of \(\alpha \beta\)-LRP in CReP can be found in Supplementary Note 4. \({{RS}}_{k,S}\) quantifies the contribution of variable \({x}_{k}\) to the cause representation, while \({{RS}}_{k,Z}\) measures the contribution of \({x}_{k}\) to the effect representation. Based on the quantified contributions of all input variables to the causal representations, the inferred causal networks centered on the target variable can be constructed, where the thickness of the edges represents the strength of causal interactions. By employing the network interpretation method, the learned implicit and abstract causal information is transformed into explicit and interpretable causal relationships, thereby enhancing the understanding of the internal mechanisms of the system.