Ca²⁺ transmembrane transport enhances oscillatory growth of cancer cell invadopodia

Abstract

Invadopodia, dynamic cancer cell protrusions, deform and degrade extracellular matrix (ECM) to facilitate invasion. Intracellular calcium ions (Ca²⁺) are critical second messengers involved in cancer cells migration, proliferation, and apoptosis, but their role in invadopodia dynamics remains unclear. Here, we propose a chemo-mechanical model integrating Ca²⁺ transmembrane transport, myosin contractility, adhesion dynamics, actin polymerization, and membrane type 1 matrix metalloproteinase (MT1-MMP) hydrolysis. We find that increased invadopodia length elevates membrane tension, activating mechanosensitive channels and raising intracellular Ca²⁺ levels, aligning with experimental observations. Our model reveals that invadopodia oscillatory and monotonic dynamics are governed by actin polymerization and myosin recruitment, with Ca²⁺ transport enhancing dynamics via myosin recruitment and reciprocal effects on Ca²⁺ transport. Furthermore, by incorporating MT1-MMP-mediated ECM degradation in our model, we find that ECM degradation promotes invadopodia extension and elevates Ca²⁺ levels, which shifts the invadopodia dynamics from monotonic to oscillatory. Overall, our model offers a comprehensive theoretical framework for understanding Ca²⁺ transport and invadopodia dynamics in cancer cells.

Introduction

Calcium ions (Ca²⁺) are powerful second messengers that can regulate multiple cellular behaviors, such as cell migration, proliferation, and apoptosis^1,2,3. Ca²⁺ ions are transported across the cell membranes through Ca²⁺ channels and pumps⁴, and alterations in the individual Ca²⁺ channel or pump can affect disease progression^5,6,7. Recently, researchers have paid special attention to the Ca²⁺ oncogenic pathways^8,9 as well as the molecular mechanisms underlying the expression of associated proteins^10,11. Dysfunction in Ca²⁺ channels or pumps in cancer cells alters Ca²⁺ transmembrane transport and results in remodeling of Ca²⁺ homeostasis¹².

Cancer cells use invadopodia, actin-rich membrane protrusions, to explore the extracellular matrix (ECM) and navigate microenvironments, marking the first step in invasion. Invadopodia consist of an actin core surrounded by adhesion and scaffolding proteins^13,14,15 and exhibit dynamic protrusion-retraction cycles^16,17 driven by actin polymerization and myosin contractility¹⁸. Invadopodia play a key role in cell mechanosensing by probing ECM mechanical properties through adhesion and dynamic forces^19,20,21. Invadopodia also facilitate ECM degradation by releasing matrix metalloproteinases (MMPs)^22,23,24. Recent studies have shown that Ca²⁺ transmembrane transport regulates various cancer cell invadopodia dynamics^25,26. However, how Ca²⁺ transport interacts with mechano-transduction factors to regulate invadopodia remains unclear.

Previous theoretical studies have revealed various modes of transmembrane ion transport to maintain intracellular ion homeostasis^27,28. Jiang and Sun proposed a model for cellular volume and pressure regulation by considering the changes of intracellular ions through mechano-sensitive channels and active pumps²⁹. Building on this framework, Yang et al. investigated how cell volume and spreading dynamics respond to substrate stiffness, combining ion transport theory with experimental data³⁰. Li expanded on this by showing how ion movement at the cell’s front and rear drives migration under an electric field³¹. McEovy et al. utilized the same ion transportation framework to address the role of gap junction in cell-cell ion transportation in proliferating tumor spheroids³². Adar and Safran explored how osmotic pressure regulates cell volume through the lens of electrostatics³³. Both models and experiments highlight ions regulation of cell deformation. Despite these theoretical advances^34,35, these models mainly studied the transmembrane transport of general ions (including Potassium, Sodium, Calcium ions), without focusing on how fluctuations in Ca²⁺, crucial in mechanotransduction, influence cell dynamics. Moreover, it remains unknown how the cyclical loading induced by the protrusion and retraction of invadopodia, which periodically alters membrane tension and impacts Ca²⁺ transport.

Here, we develop a chemo-mechanical model for Ca²⁺ transmembrane transport in invadopodia with steady-state length. Our model demonstrates that longer invadopodia increase membrane tension, activating mechanosensitive channels and elevating intracellular Ca²⁺, consistent with optical tweezer experiments and ion channel-targeting treatments. By incorporating Ca²⁺ transport into our previous invadopodia dynamics model, we captured invadopodia responses to varying extracellular Ca²⁺ levels. Integrating Ca²⁺-regulated dynamics with MT1-MMP hydrolysis revealed that MT1-MMP promotes invadopodia growth, activates mechanosensitive Ca²⁺ channels, and induces oscillatory dynamics. Overall, our model highlights the interplay between Ca²⁺ homeostasis, actin polymerization, myosin recruitment, and MT1-MMP hydrolysis, offering a theoretical framework for understanding the mechanosensing and Ca²⁺ transport in cancer cells.

Results

Ca²⁺ transmembrane transport in invadopoida

Cells possess a large Ca²⁺ concentration gradient between their inside ( ~ 100 nM) and outside ( ~ 2 mM), maintained by Ca²⁺ channels⁴ (Fig. 1c–e). Ca²⁺ can be transported by passive channels along the concentration gradient³⁶, while the active pumps transport Ca²⁺ against the concentration gradient by ATP hydrolysis³⁷. The pump first binds intracellular Ca²⁺, undergoes a transformational change powered by ATP hydrolysis, and thereby performs Ca²⁺ transport. Assuming that intracellular ATP is sufficiently abundant, Ca²⁺ outflux through pumps per unit surface area can be described by the Hill equation³⁸: ${\dot{n}}_{{{\rm{pump}}}}={J}_{\max }\frac{{c}_{{{\rm{in}}}}^{2}}{{H}^{2}+{c}_{{{\rm{in}}}}^{2}}$^39,40, where ${J}_{\max }$ is the maximal pumping rate, ${c}_{{{\rm{in}}}}$ is the intracellular Ca²⁺ concentration. $H$ is the half activation concentration, which reflects Ca²⁺ affinity of the pump. The chemical potential difference between extracellular and intracellular Ca²⁺, denoted as ${X}_{{{\rm{calcium}}}}$, is given by: ${X}_{{{\rm{calcium}}}}={\mu }_{{{\rm{out}}}}-{\mu }_{{{\rm{in}}}}={R}_{{{\rm{g}}}}T{\mathrm{ln}}({c}_{{{\rm{out}}}}/{c}_{{{\rm{in}}}})$, where ${\mu }_{{{\rm{out}}}}$ and$\,{\mu }_{{{\rm{in}}}}$ are Ca²⁺ chemical potential outside and inside, respectively. ${c}_{{{\rm{out}}}}$ represents the external Ca²⁺ concentration. ${R}_{{{\rm{g}}}}$ is the gas constant and $T$ is the temperature. The ratio between the Ca²⁺ influx and outflux through passive channels is: ${\varPi }_{{{\rm{influx}}}}/{\varPi }_{{{\rm{outflux}}}}=\exp \left({X}_{{{\rm{calcium}}}}/{R}_{{{\rm{g}}}}T\right)={c}_{{{\rm{out}}}}/{c}_{{{\rm{in}}}}\gg 1$³⁸. Thus, the net Ca²⁺ influx through passive channels per unit surface area can be expressed as ${\dot{n}}_{{{\rm{passive}}}}={f}_{{{\rm{passive}}}}({c}_{{{\rm{out}}}}-{c}_{{{\rm{in}}}}){R}_{{{\rm{g}}}}T$, where ${f}_{{{\rm{passive}}}}$ is a rate constant. Invadopodia are highly dynamic structures, and the stress on the cell membrane varies continuously. Therefore, we classify passive channels into mechanosensitive (MS) and non-mechanosensitive (non-MS) channels. Ca²⁺ MS channels (Fig. 1d) like Piezo and TRPV4, respond to membrane stress, with opening probability following a Boltzmann function. We applied a piecewise linear function to describe Ca²⁺ influx through MS channels per unit surface area as ${\dot{n}}_{{{\rm{MS}}}}={f}_{{{\rm{MS}}}}(\sigma )({c}_{{{\rm{out}}}}-{c}_{{{\rm{in}}}}){R}_{{{\rm{g}}}}T$ with ${f}_{{{\rm{MS}}}}\left(\sigma \right)=\left\{\begin{array}{cc}0, & \sigma \le {\sigma }_{{{\rm{c}}}}\\ \omega \left(\sigma -{\sigma }_{{{\rm{c}}}}\right), & \,{\sigma }_{{{\rm{c}}}} < \sigma < {\sigma }_{{{\rm{s}}}}\\ \omega \left({\sigma }_{{{\rm{s}}}}-{\sigma }_{{{\rm{c}}}}\right), & \,\sigma \ge {\sigma }_{{{\rm{s}}}}\end{array}\right.,$ where $\omega$ is a rate constant, ${\sigma }_{{{\rm{c}}}}$ and ${\sigma }_{{{\rm{s}}}}$ are the threshold stress and saturating stress, respectively. Assuming the membrane is viscoelastic and modeled by Kelvin-Voigt model⁴¹, the membrane stress can be written as $\sigma ={E}_{{{\rm{m}}}}\varepsilon +{\eta }_{{{\rm{m}}}}\dot{\varepsilon }={E}_{{{\rm{m}}}}\Delta l(t)/{l}_{0}+{\eta }_{{{\rm{m}}}}\Delta \dot{l}(t)/{l}_{0}$, where ${E}_{{{\rm{m}}}}$ and ${\eta }_{{{\rm{m}}}}$ are the elastic modulus and viscosity of membrane, respectively. Here, ${l}_{0}$ is the initial length of the invadopodium and $\Delta l(t)$ is its extension length. Other than MS channels, non-MS passive channels (Fig. 1e), such as L-type, TRPV1, TRPM8, etc, also transport Ca²⁺ along the concentration gradient. We describe Ca²⁺ influx through these non-MS channels per unit surface area as ${\dot{n}}_{{{\rm{non}}}-{{\rm{MS}}}}={f}_{{{\rm{non}}}-{{\rm{MS}}}}({c}_{{{\rm{out}}}}-{c}_{{{\rm{in}}}}){R}_{{{\rm{g}}}}T$, where ${f}_{{{\rm{non}}}-{{\rm{MS}}}}$ is a rate constant. In summary, the change in Ca²⁺ number per unit surface area is: $\dot{n}={\dot{n}}_{{{\rm{passive}}}}+{\dot{n}}_{{{\rm{pump}}}}={\dot{n}}_{{{\rm{MS}}}}+{\dot{n}}_{{{\rm{non}}}-{{\rm{MS}}}}+{\dot{n}}_{{{\rm{pump}}}}.$ Considering the invadopodium as a cylinder with radius of $r$, its surface area is ${A}_{{{\rm{eff}}}}=2{{\rm{\pi }}}{rl}+{{\rm{\pi }}}{r}^{2}\approx 2{{\rm{\pi }}}{rl}$, considering $r\,\ll \,l$, where ${l=l}_{0}+\Delta l(t)$. The total Ca²⁺ number change inside the cell is expressed as: $\dot{N}={A}_{{{\rm{eff}}}}\dot{n}$.

Fig. 1: A chemo-mechanical model for invadopodia dynamics.

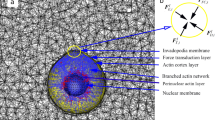
a G-actin polymerizes at the tip of F-actin with a polymerization speed ${V}_{{{\rm{p}}}}$, generating a protrusive force which is counterbalanced by cortex and ECM force. Myosin pulls F-actin toward the cell center with a retrograde flow ${V}_{{{\rm{r}}}}$, regulated by b mechanosensitive signaling pathways (Rho-ROCK pathway) and (c–e) Ca²⁺ transmembrane transport. Three types of Ca²⁺ channels are considered: c active pump, d mechanosensitive (MS) passive channel, and e non-MS passive channels. Adhesion proteins link F-actin to ECM via integrins, providing frictional resistance to retrograde flow. Invadopodia secrete MT1-MMP at their tip to degrade ECMs. f All forces are balanced in F-actin. g Open probability ${f}_{{{\rm{MS}}}}$ of mechanosensitive passive channel.

Studies have shown that Ca²⁺ diffusion between invadopodia and the cell body is locally regulated, leading to heterogeneity in Ca²⁺ concentration between invadopodia and the cell body^42,43. We investigate the impact of local calcium regulation in this study (See Supplementary Note 1) and find that variations in Ca²⁺ diffusion speed do not affect the overall conclusion. For computational simplicity, we minimize local regulation and heterogeneity, resulting in a nearly uniform Ca²⁺ concentration between the invadopodium and the cell body. Thus, Ca²⁺ concentration can be calculated as ${c}_{{{\rm{in}}}}=N/V$, where $V=\pi {r}^{2}l+{V}_{{{\rm{b}}}}$ is the total cell volume. We obtain the concentration change rate:

$$\frac{{{\rm{d}}}{c}_{{{\rm{in}}}}}{{{\rm{d}}}t}= \frac{2{{\rm{\pi }}}{{\rm{r}}}l}{{{\rm{\pi }}}{r}^{2}l+{V}_{{{\rm{b}}}}}\left[{f}_{{{\rm{MS}}}}\left(\sigma \right)\left({c}_{{{\rm{out}}}}-{c}_{{{\rm{in}}}}\right){R}_{{{\rm{g}}}}T+{f}_{{{\rm{non}}}-{{\rm{MS}}}}\left({c}_{{{\rm{out}}}}-{c}_{{{\rm{in}}}}\right){R}_{{{\rm{g}}}}T -{J}_{\max }\frac{{c}_{{{\rm{in}}}}^{2}}{{H}^{2}+{c}_{{{\rm{in}}}}^{2}}\right]-\frac{{c}_{{{\rm{in}}}}{{{\rm{\pi }}}r}^{2}}{{{\rm{\pi }}}{r}^{2}l+{V}_{{{\rm{b}}}}}\frac{{{\rm{d}}}l}{{{\rm{d}}}t}$$

(1)

Intracellular Ca²⁺ is regulated by invadopodia extension length, channels activity, and extracellular Ca²⁺ concentration

Using the above model for Ca²⁺ transmembrane transport, we can simulate the intracellular Ca²⁺ dynamics and investigate key regulating factors. For simplicity, we consider the invadopodium reaches a steady-state length, ${{\rm{d}}}l/{{\rm{d}}}t=0$. Intracellular Ca²⁺ concentration increases ${{\rm{d}}}{c}_{{{\rm{in}}}}/{{\rm{d}}}t > 0$ when the concentration below the concentration homeostasis, i.e., ${c}_{{{\rm{in}}}} < {c}_{{{\rm{inss}}}}$, and decreases (${{\rm{d}}}{c}_{{{\rm{in}}}}/{{\rm{d}}}t < 0$) when ${c}_{{{\rm{in}}}} > {c}_{{{\rm{inss}}}}$ (Fig. 2a). As the invadopodium steady-state length increases (at constant initial invadopodium length), the intersection points move towards a higher ${c}_{{{\rm{in}}}}$, indicating the elevation of intracellular Ca²⁺ concentration homeostasis (Fig. 2b). This is because of the increased membrane stress, which enhances the opening of MS channels.

Fig. 2: Multiple factors regulate intracellular Ca²⁺ concentration homeostasis.

a Relationship between intracellular Ca²⁺ concentration change rate ${{\rm{d}}}{c}_{{{\rm{in}}}}/{{\rm{d}}}t$ and the intracellular Ca²⁺ concentration ${c}_{{{\rm{in}}}}$ (red solid line); steady-state Ca²⁺ concentration ${c}_{{{\rm{inss}}}}$ (red dot); passive channel contribution (green dashed line); and active pump contribution (blue dashed line). b Changes in intracellular Ca²⁺ concentration change rate ${{\rm{d}}}{c}_{{{\rm{in}}}}/{{\rm{d}}}t$ with increasing invadopodium extension length $\triangle l$ along the arrow direction. Line colors: yellow, $1$ ${{\rm{\mu }}}{{\rm{m}}}$; pink, $3$ ${{\rm{\mu }}}{{\rm{m}}}$; purple, $5$ ${{\rm{\mu }}}{{\rm{m}}}$. c Heatmap showing how MS channels rate constant $\omega$ and non-MS channel rate constant ${f}_{{{\rm{non}}}-{{\rm{MS}}}}$ affect intracellular Ca²⁺ concentration homeostasis ${c}_{{{\rm{inss}}}}$. d Heatmap showing how maximal pumping rate ${J}_{\max }$ and the external Ca²⁺ concentration ${c}_{{{\rm{out}}}}$ regulate intracellular Ca²⁺ concentration homeostasis ${c}_{{{\rm{inss}}}}$. e The effects of Ca²⁺ chelators or Ca²⁺ blockers on simulated Ca²⁺ homeostasis.

Either a higher MS channels rate constant $\omega$ or ${f}_{{{\rm{non}}}-{{\rm{MS}}}}$ leads to the increase of the intracellular Ca²⁺ concentration homeostasis, as more Ca²⁺ is transported into the invadopodium via passive channels (Fig. 2c). In contrast, a larger maximal pumping rate ${J}_{\max }$ facilitates Ca²⁺ outflux, reducing intracellular Ca²⁺ homeostasis. A higher external Ca²⁺ concentration ${c}_{{out}}$ increases the activation energy of the active pump, reducing the inverse gradient transport (outflux) of Ca²⁺, thus increasing intracellular Ca²⁺ homeostasis (Fig. 2d). In addition to the concentration homeostasis, we also examined the timescale for Ca²⁺ concentration to reach the homeostasis (See Supplementary Note 2).

To validate the model, we referenced A.K. Efremov et al.’s work⁴⁴, which stretched filopodia while monitoring Ca²⁺ concentration changes using optical tweezer. Although invadopodia and filopodia are different, their extension and Ca²⁺ transport mechanisms are similar. The experiment showed that longer extensions led to higher intracellular Ca²⁺ concentrations, aligning with Fig. 2b. Additionally, reducing external Ca²⁺ (via EGTA), inhibiting Ca²⁺ MS channels (via GSK2193874), or blocking other passive channels (via Amlodipine) decreased intracellular Ca²⁺ homeostasis, consistent with Fig. 2c, d. In Fig. 2e, control group simulations represent Ca²⁺ homeostasis under parameter settings marked by circles in Fig. 2c, d, while drug effects correspond to crosses. Overall, the agreement between the experimental and simulation validates our model.

Kinematic of invadopodia with Ca²⁺ transmembrane transport

Next, we introduce our chemo-mechanical model for invadopodia dynamics. Actin monomers polymerize into actin filaments (F-actin), generating the protrusive force necessary for invadopodium growth²⁴. Based on the findings of Schumacher et al⁴⁵. that invadopodia elongation depends on both filopodial and lamellipodial machinery, we assumed that actin retrograde flow is driven by myosin contractility and attenuated by substrate adhesion⁴⁶. Figure 1a shows the extension speed ${{\rm{d}}}l/{{\rm{d}}}t$ is the net difference between G-actins polymerization speed ${V}_{{{\rm{p}}}}$ and retrograde flow speed ${V}_{{{\rm{r}}}}$ caused by myosin contractility, expressed as ${{\rm{d}}}l/{{\rm{d}}}t={V}_{{{\rm{p}}}}-{V}_{{{\rm{r}}}}$. As G-actin polymerizes at the invadopodium tip, the resulting protrusive force drives invadopodium extension, which is balanced by cortex tension and ECM deformation. Since the cortex exhibits viscoelastic behavior^47,48, we describe the cortex with Kelvin-Voigt model. Accordingly, the deformation resists protrusive force with ${F}_{{{\rm{c}}}}=A\left({E}_{{{\rm{c}}}}\varepsilon +{\eta }_{{{\rm{c}}}}\dot{\varepsilon }\right)$, where $A$ is the cross-sectional area, ${E}_{{{\rm{c}}}}$ and ${\eta }_{{{\rm{c}}}}$ are the elastic modulus and viscosity of cortex, respectively. The ECM resistance force is given by Hertzian contact theory ${F}_{{{\rm{e}}}}=2r{E}_{0}\Delta l$⁴⁹, where $r$ is invadopodia radius, ${E}_{0}$ is ECM elastic modulus and $\Delta l$ is invadopodia extension length. The contractile force from bound myosin, following Hill’s relation⁵⁰, is ${F}_{{{\rm{m}}}}={F}_{{{\rm{M}}}}\left(1-{V}_{{{\rm{r}}}}/{V}_{0}\right)$, where ${V}_{0}$ and ${F}_{{{\rm{M}}}}$ are the unloaded retrograde flow speed and the maximum contraction force, respectively. Adhesion proteins bind/unbind between F-actin and ECM, generating a resistance force that decreases with the retrograde flow speed⁵¹. This relationship can be expressed as ${F}_{{{\rm{a}}}}={F}_{{{\rm{amax}}}}-{\zeta }_{{{\rm{r}}}}{V}_{{{\rm{r}}}}$, where ${F}_{{{\rm{amax}}}}$ is the intercept of the relationship between ${F}_{{{\rm{a}}}}$ and ${V}_{{{\rm{r}}}}$, and ${\zeta }_{{{\rm{r}}}}$ is the friction coefficient (See Supplementary Note 3). Balancing all forces in F-actin (Fig. 1f), we obtain the force equilibrium ${F}_{{{\rm{c}}}}+{F}_{{{\rm{e}}}}+{F}_{{{\rm{m}}}}-{F}_{{{\rm{a}}}}=0$, which gives the governing equation for the extension dynamics:

$$\left(\frac{{F}_{{{\rm{M}}}}}{{V}_{0}}+\frac{A{\eta }_{{{\rm{c}}}}}{{l}_{0}}-{\zeta }_{{{\rm{r}}}}\right)\frac{{{\rm{d}}}\Delta l}{{{\rm{d}}}t}+{k}_{{{\rm{es}}}}\Delta l={F}_{{{\rm{amax}}}}-{\zeta }_{{{\rm{r}}}}{V}_{{{\rm{p}}}}-{F}_{{{\rm{M}}}}\left(1-\frac{{V}_{{{\rm{p}}}}}{{V}_{0}}\right)$$

(2)

where ${k}_{{{\rm{es}}}}=A{E}_{{{\rm{c}}}}/{l}_{0}+2r{E}_{0}$ represents the equivalent stiffness of invadopodia.

Next, myosin recruits to F-actin through phosphorylation of myosin light chain (MLC) to form phosphorylated MLC (pMLC)⁵², applying contractile force to F-actins (Fig. 1b). The number of pMLCs varies according to^53,54: ${{\rm{d}}}{m}_{{{\rm{pM}}}}/{{\rm{d}}}t={k}_{{{\rm{pM}}}}^{* }{m}_{{{\rm{M}}}}-{k}_{{{\rm{off}}}}{m}_{{{\rm{pM}}}}$, where ${k}_{{{\rm{pM}}}}^{* }$ is pMLCs formation rate, ${m}_{{{\rm{M}}}}$ is the MLCs number and ${k}_{{{\rm{off}}}}$ is pMLCs dephosphorylation rate. Rho-associated kinase (ROCK) promotes MLCs phosphorylation to generate contraction force⁵². Increased intracellular Ca²⁺ and adhesion force ${F}_{{{\rm{a}}}}$ both upregulate MLCs phosphorylation through ROCK^55,56. In contrast, Rac1 induces downregulation of Rho within the ROCK pathway through Rac-mediated reactive oxygen species (ROS)^57,58. Meanwhile, experimental results show a positive correlation between Rac1 expression and changes in invadopodia length^59,60. Assuming a linear relationship, the pMLC formation rate can be written as¹⁸: ${k}_{{{\rm{pM}}}}^{* }={k}_{{{\rm{pM}}}}^{0}+{\alpha }_{0}{F}_{{{\rm{a}}}}-{\beta }_{0}\frac{{{\rm{d}}}\Delta l}{{{\rm{d}}}t}+{\theta }_{0}{c}_{{{\rm{in}}}};$ where ${k}_{{{\rm{pM}}}}^{0}$ is the initial formation rate of pMLCs, and ${\alpha }_{0}$, ${\beta }_{0}$, and ${\theta }_{0}$ are the linear coefficients. The maximum contractile force is ${F}_{{{\rm{M}}}}={m}_{{{\rm{pM}}}}{f}_{{{\rm{pM}}}}$, and the change in ${F}_{{{\rm{M}}}}$ is:

$$\frac{1}{{k}_{{{\rm{off}}}}}\frac{{{\rm{d}}}{F}_{{{\rm{M}}}}}{{{\rm{d}}}t}+{F}_{{{\rm{M}}}}={F}_{{{\rm{M}}}0}+\alpha {F}_{{{\rm{a}}}}-\beta \frac{{{\rm{d}}}\Delta l}{{{\rm{d}}}t}+\theta {c}_{{{\rm{in}}}}.$$

(3)

Here ${F}_{{{\rm{M}}}0}=\frac{{k}_{{{\rm{pM}}}}^{0}{f}_{{{\rm{pM}}}}{m}_{{{\rm{M}}}}}{{k}_{{{\rm{off}}}}}$ is the initial force, and $\alpha =\frac{{\alpha }_{0}{F}_{{{\rm{M}}}0}}{{k}_{{{\rm{pM}}}}^{0}}$, $\beta =\frac{{\beta }_{0}{F}_{{{\rm{M}}}0}}{{k}_{{{\rm{pM}}}}^{0}}$ and $\theta =\frac{{\theta }_{0}{F}_{{{\rm{M}}}0}}{{k}_{{{\rm{pM}}}}^{0}}$ are coefficients for the signaling pathways affecting myosin recruitment.

Competition of actin polymerization and myosin recruitment drives the invadopodia oscillations

Considering that the system consisting of Eqs. (1)–(3), obtains a fixed point (${c}_{{{\rm{ins}}}},\,{F}_{{{\rm{Ms}}}},\,\Delta {l}_{{{\rm{s}}}}$) under the condition ${{\rm{d}}}{c}_{{{\rm{in}}}}/{{\rm{d}}}t=0$ ${{\rm{d}}}{F}_{{{\rm{M}}}}/{{\rm{d}}}t=0$ and ${{\rm{d}}}\Delta l/{{\rm{d}}}t=0$, where ${c}_{{{\rm{ins}}}}={c}_{{{\rm{inss}}}}$, ${F}_{{{\rm{Ms}}}}={F}_{{{\rm{M}}}0}+\alpha {F}_{{{\rm{amax}}}}-{\alpha \zeta }_{{{\rm{r}}}}{V}_{{{\rm{p}}}}+\theta {c}_{{{\rm{inss}}}}$ and $\Delta {l}_{{{\rm{s}}}}=\big[{F}_{{{\rm{amax}}}}-{\zeta }_{{{\rm{r}}}}{V}_{{{\rm{p}}}}+{F}_{{{\rm{Ms}}}}\cdot \big({V}_{{{\rm{p}}}}/{V}_{0}\,-1\big)\big]/{k}_{{{\rm{es}}}}$. Compared to invadopodium extension dynamics (with timescale ~270 s) and myosin contractility generation (with timescale ~250 s), intracellular Ca²⁺ concentration adjusts rapidly (timescale ~0.5 s). Note that the timescale $\tau$ (that is defined in the equation $\tau \frac{{{\rm{d}}}x}{{{\rm{d}}}t}=f(x,y,z)$ for sub-cellular process) represents the characteristic time required for reaching equilibrium in the system. Therefore, according to Tikhonov’s theorem, we assume that Ca²⁺ homeostasis ${c}_{{{\rm{inss}}}}$ is reached before steady states of extension and myosin recruitment. Note that the necessary conditions for Tikhonov’s theorem have been verified in the Supplementary Note 4. Next, we analyze the stability of the fixed point using linear perturbation method (see Method). By applying small perturbations $\delta {l}_{s}$ and ${\delta F}_{{Ms}}$, we obtain the eigenvalues of the Jacobian matrix:

$${\lambda }_{1,2}=\frac{{k}_{{{\rm{l}}}}}{2}\left[\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{F}}}}}-\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{l}}}}}-1\pm \sqrt{{\left(1+\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{l}}}}}-\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{F}}}}}\right)}^{2}-4\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{l}}}}}}\right]$$

where ${k}_{{{\rm{l}}}}$ is the rate of reaching $\Delta {l}_{{{\rm{s}}}}$ and ${k}_{{{\rm{F}}}}$ is the rate of signal associated myosin contraction to reaching ${F}_{{{\rm{Ms}}}}$. Here, ${k}_{{{\rm{off}}}}$ represents not only pMLCs dephosphorylation rate, but also the rate that characterizes intrinsic myosin contraction (independent of signaling feedback). Stability is determined by the real part of eigenvalues ${\mathrm{Re}}\left({\lambda }_{1,2}\right)$, and oscillations by the imaginary part ${{\rm{Im}}}\left({\lambda }_{1,2}\right)$. When ${\mathrm{Re}}\left({\lambda }_{1,2}\right) < 0$, the invadopodium exhibits stable growth (Regions I and II in Fig. 3a–c), whereas ${\mathrm{Re}}\left({\lambda }_{1,2}\right) > 0$ leads to unstable growth (Region III). Within the stable regime, if ${{\rm{Im}}}\left({\lambda }_{1,2}\right)=0$, the invadopodium exhibits monotonic growth (Region I); however, if ${{\rm{Im}}}\left({\lambda }_{1,2}\right)\ne 0$, its growth becomes oscillatory (Region II).

Fig. 3: Actin polymerization and myosin recruitment determine invadopodia dynamics.

a ${k}_{{{\rm{l}}}}$ and ${k}_{{{\rm{F}}}}$ judge the mode of invadopodia growth. Regions: I (dark blue), II (light blue), and III (pink). b Invadopodia extension dynamics in the three regions (I, II, III). c Contraction force-extension curve corresponding to region I and II. d Heatmap showing how ROCK feedback parameter $\alpha$ and adhesion proteins frictional coefficient ${\zeta }_{{{\rm{r}}}}$ regulate the oscillation period of invadopodia $T$. e Heatmap showing how pMLCs dephosphorylation rate ${k}_{{{\rm{off}}}}$ and ECM elastic modulus ${E}_{0}$ regulate the oscillation period of invadopodia $T$. f Dynamics of invadopodium extension length $\Delta l$ at stiff (red solid line) and soft (green solid line) ECM; the green dashed line indicates the average $\Delta l$ for soft ECM.

We next investigate the oscillatory growth of invadopodia and how factors such as adhesion, myosin, and ECM stiffness affect the oscillation period. Figure 3d shows a heatmap of the invadopodia oscillation period $T=2{{\rm{\pi }}}/{{\rm{Im}}}({\lambda }_{{\mathrm{1,2}}})$ as a function of the ROCK feedback parameter $\alpha$ and adhesive coefficient ${\zeta }_{{{\rm{r}}}}$. An increase in the ROCK parameter enhances pMLC formation, leading to a stronger steady-state myosin contractile force and thereby extending the oscillation period. In contrast, a higher adhesion coefficient ${\zeta }_{{{\rm{r}}}}$ weakens adhesion forces at the same instantaneous retrograde speed, resulting in a reduced oscillation amplitude. Since the polymerization rate and the maximum retrograde speed remain unchanged, the oscillation period decreases. Similarly, a heatmap of the oscillation period as a function of ECM elastic modulus ${E}_{0}$ and pMLCs dephosphorylation rate ${k}_{{{\rm{off}}}}$ (Fig. 3e) reveals that both higher ${E}_{0}$ and ${k}_{{{\rm{off}}}}$ contribute to a shorter oscillation period. A higher ${k}_{{{\rm{off}}}}$ reduces the steady-state pMLC number and myosin contraction force. A higher ${E}_{0}$ increases ECM resistance, reducing steady-state invadopodium length (see Fig. 3f). Experimental results indicate that stiffer substrates limit invadopodia extension and inhibit cancer cell invasion^61,62, aligning with our model’s prediction that higher ${E}_{0}$ results in shorter invadopodium length. Chang et al. observed that the invadopodia oscillation period is shorter in stiffer ECMs⁶¹, consistent with our model (indicated by the arrow in Fig. 3e). In short, our model explains the experimental observations of invadopodia behavior on substrates with varying stiffness.

Ca²⁺ transmembrane transportation enhances invadopodia oscillatory growth by mediating myosin recruitment

We then investigated how intracellular Ca²⁺ transmembrane transport mediates invadopodium dynamics. By integrating the Ca²⁺ transport model with invadopodium kinematics, we simulated the dynamics of invadopodium length, myosin contractile force, and intracellular Ca²⁺ concentration. Figure 4a shows that higher ${c}_{{{\rm{out}}}}$ promotes myosin contractile force, which in turn reduces the invadopodia length. To further examine the interplay between intracellular Ca²⁺ and invadopodium extension/retraction cycles, we analyzed the time evolution of invadopodium extension length, intracellular Ca²⁺ concentration, and myosin contractile force, both with and without intracellular Ca²⁺ feedback (Supplementary Fig. 4), which is further outlined as two key stages:

• (i) As the invadopodium extends, its membrane gets stretched, opening the MS channels and allowing Ca²⁺ influx and raising intracellular Ca²⁺ levels. The elevated intracellular Ca²⁺ concentration enhances myosin contraction.

• (ii) A higher myosin contractile force shortens invadopodia. This shortening reduces the membrane tension and makes MS channels closed, which lowers intracellular Ca²⁺ levels and decreases Ca²⁺ feedback.

Fig. 4: Ca²⁺ enhances invadopodia oscillatory growth by mediating myosin recruitment.

a Dynamics of invadopodium extension length $\triangle l$, myosin contraction force ${F}_{{{\rm{m}}}}$, and intracellular Ca²⁺ concentration ${c}_{{{\rm{in}}}}$ at high (red solid line) and low (green solid line) external Ca²⁺ concentrations ${c}_{{{\rm{out}}}}$; dashed lines show average $\triangle l$ and ${F}_{{{\rm{m}}}}$ for high (red) and low (green) ${c}_{{{\rm{out}}}}$. b Schematic representation of invadopodia in retraction and protrusion states. Retraction: shortened invadopodia reduce membrane tension, closing MS channels, lowering intracellular Ca²⁺ levels, and weakening Ca²⁺ feedback (thin black arrows). Protrusion: extended invadopodia stretch the membrane, opening MS channels, increasing Ca²⁺ influx and intracellular Ca²⁺ level, and enhancing Ca²⁺ feedback (thick black arrows). c Changes in intracellular Ca²⁺ homeostasis with increasing $\theta$ along the arrow direction. Line colors: orange, $1\times {10}^{4}$; green, $5\times {10}^{4}$; purple, $9\times {10}^{4}$. d By varying the parameters, invadopodia dynamic regions were divided according to theoretical calculations. The three regions correspond to the monotonical invadopodium growth (region I, dark blue), oscillatory growth (region II, light blue), and unstable growth (region III, pink).

This feedback loop weakens myosin contraction, allowing the invadopodium to re-extend and initiate a new cycle (Fig. 4b). In short, the cyclic change in the opening and closing of MS channels influences invadopodium dynamics.

Next, considering that Ca²⁺-mediated phosphorylation coefficient $\theta$ affects myosin recruitment, our model shows that a larger $\theta$ enhances myosin recruitment, decreasing steady state intracellular Ca²⁺ levels (Fig. 4c). We further varied $\theta$ and the pMLCs dephosphorylation rate ${k}_{{{\rm{off}}}}$ and repeated stability analysis using linear perturbation methods. The theoretical calculations (lines in Fig. 4d) confirm that the increased Ca²⁺-mediated phosphorylation coefficient $\theta$ promote oscillatory growth.

MT1-MMP facilitates invadopodia extension and oscillatory dynamics by softening the ECM and activating mechanosensitive Ca²⁺ channels

During cancer cell invasion, invadopodia secrete MT1-MMP to degrade surrounding ECMs, facilitating migration⁶³. MT1-MMP accumulates at invadopodia tips and degrades matrix fibers through proteolysis^{17,24,64,65,66}. We model ECM degradation as a first-order reaction with matrix density $\rho \left(t\right)$ evolving as:

$$\frac{{{\rm{d}}}\rho (t)}{{{\rm{d}}}t}=-{k}_{{{\rm{MMP}}}}\left(\rho \left(t\right)-{\rho }_{{{\rm{s}}}}\right),$$

(4)

where ${k}_{{{\rm{MMP}}}}$ is the rate constant and ${\rho }_{{{\rm{s}}}}$ is the steady state ECM density. As proposed by David Boal⁶⁷, an entropic polymer network deforms in response to external stress. Each chain in the network follows a conventional Gaussian probability distribution and undergoes affine deformation. By calculating the entropy change of the network before and after deformation, it can be shown that, under constant temperature, the microscopic polymer chain density is directly proportional to the elastic modulus. We express the elastic modulus as $E\left(t\right)={E}_{0}\rho (t)/{\rho }_{0}$ with the initial elastic modulus ${E}_{0}$ and initial ECM density ${\rho }_{0}$.

By integrating the MT1-MMP degradation process with Ca²⁺-mediated invadopodia dynamics, our model predicts MT1-MMP’s effect on invadopodia oscillation. MT1-MMP increases both invadopodia extension length and myosin contractile force at steady state (Fig. 5a). Time-dependent analysis reveals that MT1-MMP promotes longer invadopodia and higher Ca²⁺ level with more oscillations (Fig. 5b, c). Three timestamps (phases i, ii and iii) in Fig. 5d, e show that MT1-MMP degrades ECM, softening it and allowing invadopodia to extend longer. The longer invadopodia length elevates the membrane tension and further promotes the opening of MS Ca²⁺ channels, leading to a higher intracellular Ca²⁺ concentration. Meanwhile, a higher intracellular Ca²⁺ concentration promotes myosin recruitment, eventually facilitating the invadopodia oscillations (Fig. 5d). In the contrary, without MT1-MMP, invadopodia reach steady state faster (Fig. 5e). MT1-MMP hydrolysis reduces ECM density at steady state. In Fig. 5f, linear stability analysis shows that increased MT1-MMP activity softens ECM, shifting invadopodia growth from monotonic to oscillatory (black arrows in Fig. 5f).

Fig. 5: MT1-MMP degrades extracellular matrix, making invadopodia extend further and oscillate longer.

a Myosin contraction force ${F}_{{{\rm{M}}}}$ versus invadopodium extension length $\triangle l$ with MT1-MMP (light blue) and without MT1-MMP (pink). Blue and red dots indicate the steady states with and without MT1-MMP. b, c Comparison of invadopodium extension and intracellular Ca²⁺ dynamics with MT1-MMP (blue) and without MT1-MMP (red). Schematic of invadopodia and ECM at positions (i), (ii), and (iii). d With MT1-MMP: ECM degradation softens the substrate, allowing enhanced invadopodium extension, opening of MS channels, elevating intracellular Ca²⁺ levels, and promoting invadopodium oscillation. e Without MT1-MMP: no ECM degradation and unchanged substrate stiffness lead to earlier stabilization of invadopodia. f The phase diagram for monotonic (region I, dark blue) and oscillatory growth (region II, light blue) in response to ECM density change ratio ${\rho }_{{{\rm{s}}}}/{\rho }_{0}$ and reciprocals of pMLCs dephosphorylation rate $1/{k}_{{{\rm{off}}}}$.

Discussion

In this study, by proposing a chemo-mechanical model on Ca²⁺ regulated invadopodia growth, we investigate how Ca²⁺ acts as a second messenger to regulate invadopodia dynamics. Our model integrates key factors like actin polymerization, myosin recruitment, mechanosensitive signaling (Rho-ROCK pathway), Ca²⁺ transmembrane transport, and MT1-MMP secretion, offering a theoretical understanding of invadopodia dynamics. Our model indicates that increased invadopodia length elevates membrane tension, activating mechanosensitive channels and raising intracellular Ca²⁺ levels, in line with optical tweezer experiments and ion channel-targeting treatments. By integrating Ca²⁺ transport with our model of invadopodia dynamics, we captured how invadopodia adapt to variations in extracellular Ca²⁺ concentrations. Furthermore, incorporating MT1-MMP degradation into the model revealed that elevated MT1-MMP level enhances invadopodia growth and increases intracellular Ca²⁺ level, shifting growth from monotonic to oscillatory.

In contrast to previous models^29,32,68 that focused on general ion transport and volume changes, our model addressed the Ca²⁺ transport across the membrane and its associated effects on invadopodia dynamics. For Ca²⁺ transmembrane transport, passive Ca²⁺ channels allow Ca²⁺ influx along the gradient, and active Ca²⁺ pumps push Ca²⁺ outflux against the gradient. During invadopodia dynamics, protrusion and retraction cycles alter membrane tension, which triggers the opening and closing of the mechano-sensitive Ca²⁺ channels. Our model considers the active pump in terms of energy, which is released from ATP hydrolysis enabling intracellular Ca²⁺ to overcome the concentration barrier. The rate parameters of Ca²⁺ channels in our model are close in order of magnitude consistent with the rate parameters of ion channels in previous studies^29,32. In our model, Ca²⁺ transmembrane transport describes intracellular Ca²⁺ number changes caused by various Ca²⁺ channels. Importantly, our model predictions have been verified by the existing experimental results, including external Ca²⁺ concentration change and invadopodia dynamics.

For individual invadopodium, actin polymerization provides the primary driving force for invadopodia extension, while myosin recruitment pulls the invadopodium to contract. Experiments using blebbistatin or Y27632 to inhibit myosin contractility or the Rho-ROCK pathway observed monotonic invadopodia growth and significantly increased extension length¹⁸. These findings align with our model, which suggests that invadopodia dynamics, whether monotonic or oscillatory, are governed by the interplay between actin polymerization and myosin recruitment. Recent experiments have shown that actin polymerization is sensitive to the applied mechanical load^69,70, future studies can further incorporate the force sensitivity of actin polymerization into our framework to study the role of specific mechanosensitive protein in invadopodia dynamics.

To study the relationship between intracellular Ca²⁺ concentration and invadopodia more clearly, we investigate not only the role of intracellular Ca²⁺ on invadopodia steady state, but also the feedback effect of invadopodia dynamic on intracellular Ca²⁺ concentration. We first discuss intracellular Ca²⁺ concentration changes in response to a perturbation on invadopodia steady state, which is determined by passive channels and pumps. Subsequently, we focus on the whole process that considers the dynamics of invadopodia. Increasing Ca²⁺ effect on myosin recruitment $\theta$, invadopodium extension length at steady state reduce. In turn, Ca²⁺ MS channels are limited, resulting in a decrease in intracellular Ca²⁺ concentration homeostasis.

Our chemo-mechanical model demonstrates the process of matrix degradation and deformation. The growth of the invadopodia squeezes and deforms the ECM at the tip, and the MT1-MMP secreted by the invadopodia degrades the ECM. Most previous studies investigated the mechanical and chemical properties of ECM separately^16,64, indicating that both the mechanical and chemical properties of the ECM are critical for invadopodia invasion. Our simulation suggests that increasing ECM elastic modulus reduces invadopodia extension length, consistent with existing experimental observations⁶¹. By assuming a linear relationship between the ECM’s elastic modulus and matrix density, our model shows that the invadopodia extend longer and become more oscillatory for the case of MT1-MMP. We further demonstrate that MT1-MMP hydrolysis elevates intracellular Ca²⁺ concentration. Although our model simplified the ECM as a purely elastic material and considered ECM degradation as first-order reactions, our model provides a clear understanding of how the coupling of both the mechanical and chemical properties of the ECM plays a role in invadopodia dynamics. These insights underscore the need to clearly distinguish invadopodia―actin-rich cancer cell protrusions that coordinate protrusive and matrix-degrading functions―from general cell protrusions. Different experimental conditions^17,45,71 have revealed a continuum of protrusion types with diverse morphologies but overlapping functions. A better definition of invadopodia is required to separate them from other protrusions in future studies. Our model also does not consider the positive feedback loops between invadopodia and ECM degradation^72,73; however, future studies could incorporate such positive signaling feedback into our theoretical framework to systematically examine their coupling.

Alterations in Ca²⁺ transmembrane transport have been widely observed in cancer^74,75, with Ca²⁺ homeostasis linked to the regulation of calcium-sensitive oncogenic pathways and related proteins¹². Previous studies have shown that the expression of specific Ca²⁺ channels is altered in various cancers^76,77. Our model specifically addresses Ca²⁺ dynamics, showing how passive Ca²⁺ channels and active pumps maintain intracellular Ca²⁺ homeostasis during invadopodia cycles. Invadopodia facilitate ECM degradation, enabling cancer cell migration and invasion. By linking Ca²⁺ transmembrane transport to invadopodia dynamics, our model provides insights into cancer cell motility. Our Ca²⁺ transmembrane transport model can be integrated with other cell and tissue models to provide a more comprehensive understanding of complex metastatic processes. For instance, the localized regulation of Ca²⁺, including the spatial association of the Ca²⁺ channels TRPV4 and Orai1-STIM^42,43, shapes intracellular Ca²⁺ distribution and constitutes an important area of research in tumor cell invasion. Moreover, during cancer cell migration, Ca²⁺ levels are typically elevated at the trailing edge, facilitating cell movement by activating motor proteins^26,78. Future theoretical and computational models may build upon our model, which accounts for Ca²⁺ redistribution in cancer cell invasion, leading to a new insight of Ca²⁺ related targeted cancer therapy.

Method

Linear stability analysis

According to Tikhonov’s theorem, we assume that Ca²⁺ homeostasis ${c}_{{{\rm{inss}}}}$ is reached before steady states of invadopodia extension and myosin recruitment. The three ODEs (Eqs. 1–3) can be simplified as:

$$\left(\frac{{F}_{{{\rm{M}}}}}{{V}_{0}}+\frac{A{\eta }_{{{\rm{c}}}}}{{l}_{0}}-{\zeta }_{{{\rm{r}}}}\right)\frac{{{\rm{d}}}\Delta l}{{{\rm{d}}}t}+{k}_{{{\rm{es}}}}\Delta l={F}_{{{\rm{amax}}}}-{\zeta }_{{{\rm{r}}}}{V}_{{{\rm{p}}}}-{F}_{{{\rm{M}}}}\left(1-\frac{{V}_{{{\rm{p}}}}}{{V}_{0}}\right)$$

(5)

$$\frac{1}{{k}_{{{\rm{off}}}}}\frac{{{\rm{d}}}{F}_{{{\rm{M}}}}}{{{\rm{d}}}t}+{F}_{{{\rm{M}}}}={F}_{{{\rm{M}}}0}+\alpha {F}_{{{\rm{a}}}}-\beta \frac{{{\rm{d}}}\Delta l}{{{\rm{d}}}t}+\theta {c}_{{{\rm{inss}}}}$$

(6)

By setting ${{\rm{d}}}\Delta l/{{\rm{d}}}t={{\rm{d}}}{F}_{{{\rm{M}}}}/{{\rm{d}}}t=0$, we obtain the fix point (${F}_{{{\rm{Ms}}}},\,\Delta {l}_{{{\rm{s}}}}$), where ${F}_{{{\rm{Ms}}}}={F}_{{{\rm{M}}}0}+\alpha {F}_{{{\rm{amax}}}}-{\alpha \zeta }_{{{\rm{r}}}}{V}_{{{\rm{p}}}}+\theta {c}_{{{\rm{inss}}}}$ and $\Delta {l}_{{{\rm{s}}}}=\left[{F}_{{{\rm{amax}}}}-{\zeta }_{{{\rm{r}}}}{V}_{{{\rm{p}}}}+{F}_{{{\rm{Ms}}}}\cdot \right.\left.\left({V}_{{{\rm{p}}}}/{V}_{0}\,-1\right)\right]/{k}_{{{\rm{es}}}}$. Applying a small perturbation $({\delta F}_{{{\rm{Ms}}}},\,\delta \Delta {l}_{{{\rm{s}}}})$ at the fix point, we derive:

$$\left(\begin{array}{c}\frac{{{\rm{d}}}{\delta F}_{{{\rm{Ms}}}}}{{{\rm{d}}}t}\\ \frac{{{\rm{d}}}\delta \Delta {l}_{{{\rm{s}}}}}{{{\rm{d}}}t}\end{array}\right)=\left(\begin{array}{cc}\frac{-{k}_{{{\rm{es}}}}}{\frac{{F}_{{{\rm{Ms}}}}}{{V}_{0}}+\frac{A{\eta }_{{{\rm{c}}}}}{{l}_{0}}-{\zeta }_{{{\rm{r}}}}} & \frac{\frac{{V}_{{{\rm{p}}}}}{{V}_{0}}-1}{\frac{{F}_{{{\rm{Ms}}}}}{{V}_{0}}+\frac{A{\eta }_{{{\rm{c}}}}}{{l}_{0}}-{\zeta }_{{{\rm{r}}}}}\\ \frac{-{{k}_{{{\rm{off}}}}({\alpha \zeta }_{{{\rm{r}}}}-\beta )k}_{{{\rm{es}}}}}{\frac{{F}_{{{\rm{Ms}}}}}{{V}_{0}}+\frac{A{\eta }_{{{\rm{c}}}}}{{l}_{0}}-{\zeta }_{{{\rm{r}}}}} & \frac{{k}_{{{\rm{off}}}}({\alpha \zeta }_{{{\rm{r}}}}-\beta )\left(\frac{{V}_{{{\rm{p}}}}}{{V}_{0}}-1\right)}{\frac{{F}_{{{\rm{Ms}}}}}{{V}_{0}}+\frac{A{\eta }_{{{\rm{c}}}}}{{l}_{0}}-{\zeta }_{{{\rm{r}}}}}-{k}_{{{\rm{off}}}}\end{array}\right)\left(\begin{array}{c}{\delta F}_{{{\rm{Ms}}}}\\ \delta \Delta {l}_{{{\rm{s}}}}\end{array}\right)$$

The eigenvalues of the Jacobian matrix:

$${\lambda }_{1,2}=\frac{{k}_{{{\rm{l}}}}}{2}\left[\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{F}}}}}-\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{l}}}}}-1\pm \sqrt{{\left(1+\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{l}}}}}-\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{F}}}}}\right)}^{2}-4\frac{{k}_{{{\rm{off}}}}}{{k}_{{{\rm{l}}}}}}\right]$$

Here ${k}_{{{\rm{l}}}}=\frac{{k}_{{{\rm{es}}}}}{\frac{{F}_{{{\rm{Ms}}}}}{{V}_{0}}+\frac{A{\eta }_{{{\rm{c}}}}}{{l}_{0}}-{\zeta }_{{{\rm{r}}}}}$ represents the rate of approaching $\Delta {l}_{{{\rm{s}}}}$ while ${k}_{F}=\frac{{k}_{{{\rm{es}}}}}{({\alpha \zeta }_{{{\rm{r}}}}-\beta )\left(\frac{{V}_{{{\rm{p}}}}}{{V}_{0}}-1\right)}$ represents the rate of signal-associated myosin contraction to reaching ${F}_{{{\rm{Ms}}}}$. Additionally, ${k}_{{{\rm{off}}}}$ not only represents pMLCs dephosphorylation rate, but also characterizes intrinsic myosin contraction (independent of signaling feedback).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.