Quantum geometric renormalization of the Hall coefficient and unconventional Hall resistivity in ZrTe₅

Abstract

The anomalous Hall effect (AHE), conventionally associated with time-reversal symmetry breaking in ferromagnetic materials, has recently been observed in nonmagnetic topological materials, raising questions about its origin. We unravel the unconventional Hall response in the nonmagnetic Dirac material ZrTe₅, known for its massive Dirac bands and unique electronic and transport properties. Using the Kubo-Streda formula within the Landau level framework, we explore the interplay of quantum effects induced by the magnetic field (B) and disorder across the semiclassical and quantum regimes. In the semiclassical regime, the Hall resistivity remains linear in the magnetic field, but the Hall coefficient will be renormalized by the quantum geometric effects and electron-hole coherence, especially at low carrier densities where the disorder scattering dominates. In quantum limit, the Hall conductivity exhibits an unsaturating 1/B scaling. As a result, the transverse conductivity dominates transport in the ultra-quantum limit, and the Hall resistivity crosses over from B to B⁻¹ dependence as the system transitions from the semiclassical regime to the quantum limit. This work elucidates the mechanisms underlying the unconventional Hall effect in ZrTe₅ and provides insights into the AHE in other nonmagnetic Dirac materials as well.

Introduction

The anomalous Hall effect (AHE) is a key electrical transport phenomenon with significant implications for both fundamental physics and applications^{1,2,3,4,5,6,7,8,9,10}. First observed in ferromagnetic iron¹¹, the microscopic mechanisms of AHE have been debated for nearly a century^12,13,14,15. Typically, AHE requires time-reversal symmetry breaking via magnetism with Hall resistivity as ρ_xy = R₀B + R_AHM, where R₀B represents the magnetic field (B) linear ordinary Hall effect and R_AHM corresponds to the magnetization induced AHE.

ZrTe₅ is a nonmagnetic topological material characterized by massive Dirac bands, situated at the boundary between strong and weak topological insulators^{16,17,18,19,20,21,22,23}. It exhibits a paramagnetic response at low magnetic fields and no signatures of magnetic interactions^24,25. A variety of intriguing phenomena have been observed in this material, including log-periodic quantum oscillations²⁶, 3D quantum Hall effects^23,27,28, resistivity anomaly^{29,30,31,32,33,34,35}, and negative magnetoresistance^20,36. Recently, an unconventional Hall signal has been reported in ZrTe₅: the Hall resistivity ρ_xy exhibits an unconventional behavior in the high-field regime^{37,38,39,40,41,42,43,44,45,46,47,48}. This behavior, reminiscent of the AHE, is frequently attributed to the Berry curvature of the electronic bands, potentially arising from Zeeman splitting or the formation of Weyl nodes^41,42,49. However, most studies rely on a semiclassical approximation and often neglect the orbital effects of the magnetic field. This oversight is particularly significant in systems with a narrow band gap and low carrier density, where the influence of the orbital effect of the magnetic field and disorder scattering becomes pronounced. The origin of the unconventional Hall effect in paramagnetic topological materials like ZrTe₅ remains under debate, necessitating a quantitative investigation to clarify underlying mechanisms.

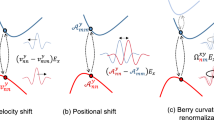
In this work, we investigate the mechanism of the unconventional Hall effect in paramagnetic Dirac materials by employing the Kubo-Streda formula within the framework of Landau levels, which deals with the quantum effect of magnetic fields and disorder on an equal footing. As shown in Fig. 1a, b, our calculations in the semiclassical regime reveal that quantum geometry effects—such as the Berry curvature (red/blue arrows) and quantum metric contributions (brown arrows)—introduce significant quantum corrections to the classical Lorentz-force-driven Hall conductivity (yellow arrows). These effects renormalize the Hall coefficient, particularly at low carrier densities where disorder scattering plays a significant role. Owing to their distinct symmetry properties under particle-hole transformation, the quantum geometry effects exhibit characteristically different behavior for electron- and hole-type carriers. In the quantum oscillation regime, the Fermi-surface contribution of the Zeeman-induced Berry curvature is suppressed by magnetic orbital effects and exhibits oscillations due to Landau level quantization, while the Fermi-sea contribution remains robust. In the quantum limit where the quasiclassical picture is entirely invalid, although the Zeeman splitting drives the formation of Weyl nodes, the Hall conductivity scales as  ~en/B without saturation, where n is the carrier density. Consequently, the transverse conductivity dominates transport in the ultra-quantum limit, causing the Hall resistivity to be inversely proportional to B. The crossover from the semiclassical regime to the quantum limit results in unconventional Hall resistivity, and we identify the critical magnetic field at which the Hall resistivity transitions from positive to negative. This study presents a unified framework to elucidate the intricate interplay of quantum geometry, magnetic fields, and disorder in paramagnetic Dirac materials, while also shedding light on the mechanisms behind anomalous transport phenomena in numerous nonmagnetic Dirac systems.

Fig. 1: Schematic illustration of Hall conductivity mechanisms in Dirac materials and three magnetic field regimes.

The Hall effect in Dirac materials arises from distinct contributions for a electron-type and b hole-type carries, where a longitudinal current I under a perpendicular magnetic field B generates a transverse voltage V. Arrows indicate carrier motion directions: yellow for the classical Lorentz force and brown for quantum geometric effects (e.g., quantum metric and orbital magnetization). Under a fixed I, the Lorentz and quantum geometric terms produce transverse velocities that are invariant under carrier sign reversal, leading to an inverted Hall voltage. Red and blue arrows denote the Berry curvature contributions from Zeeman-split majority (s = +) and minority s = − states, respectively. The Berry curvature induces opposite anomalous velocities for s = ±, creating a transverse carrier imbalance and a finite voltage. Unlike the classical and geometric terms, this contribution reverses under carrier sign change, leaving the Hall voltage unchanged. c Evolution of electronic states with magnetic field. The system progresses through three regimes: (i) semiclassical (B < χ⁻¹) (ii) quantum oscillations, and (iii) quantum limit (B > (μ² − Δ²)/(2ℏv²e)). In the semiclassical regime, disorder broadening smears out the Landau levels. In the quantum limit, all carriers occupy only the lowest Landau level. Disorder broadening (red shading) and chemical potential μ (black dashed line) are shown for reference. d Quantum geometric effect-induced Hall effect. The black arrows depict the Bloch wavefunctions at adjacent k-points, with their directional difference representing the quantum metric (state distance). The red shading indicates the emergent curvature from interband coupling.

Results

Model and Zeeman effects

The anisotropic Hamiltonian for ZrTe₅ in a finite perpendicular magnetic field B, can be written as¹⁹

$$H(k)=\Delta ({k}_{{{\rm{z}}}}){\tau }_{{{\rm{z}}}}+m{\sigma }_{{{\rm{z}}}}+{\sum}_{i=x,y}v\hslash {\Pi }_{{{\rm{i}}}}{\tau }_{{{\rm{x}}}}{\sigma }_{{{\rm{i}}}}+{t}_{{{\rm{z}}}}\sin ({k}_{{{\rm{z}}}}a){\tau }_{{{\rm{x}}}}{\sigma }_{{{\rm{z}}}}$$

(1)

with $v=\sqrt{{v}_{{{\rm{x}}}}{v}_{{{\rm{y}}}}}$ and $\Delta ({k}_{{{\rm{z}}}})=\Delta +2C(1-\cos {k}_{{{\rm{z}}}}a)$. Π = k + eA represents the kinematic momentum, A denotes the vector potential components, and a is the lattice constant along z-direction. The Zeeman effect is encoded by m = g_zμ_BB/2 with g_z = 21.3 the g-factor^42,50,51 and μ_B = 5.788 × 10⁻² meV T⁻¹ the Bohr magneton. The parameters in our model (listed in the caption of Fig. 2) are derived from first-principles calculations²³, and are consistent with magneto-infrared spectroscopy measurements¹⁹. The magnetic field has two primary effects: the orbital effect (A), which drives the formation of Landau levels, and the Zeeman effect (m), which induces spin-dependent energy splitting. In the presence of a magnetic field, the eigenstates and eigenenergies can still be solved analytically, as demonstrated in Supplementary Note 1, where we also derive the corresponding Green’s function.

Fig. 2: Zeeman splitting modifications to electronic band structure and Hall transport.

Band structure ε_sζ(k) at ∣k_⊥∣ = 0 and the Zeeman-splitting-induced Hall effect for two magnetic field strengths: a B = 4 T and b B = 12 T, below and above the field B_Δ = 2Δ/(g_zμ_B) ≈ 8.11 T required for Weyl nodes formation. The electronic structure is color-coded (red to blue) to represent the logarithmic Berry curvature, sign(Ω_z)ln∣Ω_z∣. In b k_c denotes the momentum-space separation between the Weyl nodes. The right panels of each subfigure show the Hall conductivity components: ${\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}$ (blue dashed), ${\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$ (red dashed), and their sum ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$(black solid) versus energy E. Model parameters: v_x = 9.11 × 10⁵ m .s⁻¹, v_y = 1.97 × 10⁴ m .s⁻¹, t_z = 20 meV, Δ = 5 meV, C = 100 meV, a = 1 nm, g_z = 21.3, μ_B = 5.788 × 10⁻² meV. T⁻¹.

For m = 0 and A = 0, the Hamiltonian possesses time-reversal symmetry, resulting in a vanishing Hall conductivity. For m ≠ 0 and A = 0, the energy spectrum takes the form: ${\varepsilon }_{{{\rm{s}}}\zeta }({{\bf{k}}})=\zeta \sqrt{{{{\mathcal{M}}}}_{{{\rm{s}}}}^{2}+{\hslash }^{2}{v}^{2}{{{\bf{k}}}}_{\perp }^{2}}$ where k_⊥ = (k_x, k_y), ${{{\mathcal{M}}}}_{{{\rm{s}}}}({k}_{{{\rm{z}}}})={\Delta }_{\parallel }({k}_{{{\rm{z}}}})+sm$, and ${\Delta }_{\parallel }({k}_{{{\rm{z}}}})=\sqrt{{\Delta }^{2}({k}_{{{\rm{z}}}})+{t}_{{{\rm{z}}}}^{2}{\sin }^{2}{k}_{{{\rm{z}}}}a}$. Here, s = ± represents spin index, and ζ = ± denotes the conduction and valence bands, respectively. The energy spectra for ∣k_⊥∣ = 0 are shown in Fig. 2. Zeeman splitting breaks the degeneracy of the energy levels. The Hall conductivity can be understood in terms of the nonzero Berry curvature of the occupied states, expressed as: ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}=\frac{{e}^{2}}{V\hslash }{\sum }_{{{\bf{k}}},\zeta ,{{\rm{s}}}}f({\varepsilon }_{{{\rm{s}}}\zeta }-\mu ){\Omega }_{{{\rm{z}}}}^{{{\rm{s}}}\zeta }$, where the Berry curvature is given by ${\Omega }_{{{\rm{z}}}}^{{{\rm{s}}}\zeta }=-\frac{s{\hslash }^{2}{v}^{2}{{{\mathcal{M}}}}_{{{\rm{s}}}}}{2{\varepsilon }_{{{\rm{s}}}\zeta }^{3}}$ and f is the Fermi-Dirac distribution. The momentum-space distribution of Berry curvature is visualized through color mapping of Ω_z on the electronic band structure. The superscript S indicates that this contribution arises from quantum geometry effects due to spin (S)-splitting induced by the magnetic field. When ∣m∣ increases beyond the band gap ∣Δ∣, a band crossing occurs, resulting in the creation of a pair of Weyl nodes. Particularly when μ = 0, the Hall conductivity is given by ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}=\frac{{e}^{2}{k}_{{{\rm{c}}}}}{2\pi h}$, with k_c representing the distance between the two Weyl nodes⁴. For higher Zeeman fields ∣m∣ > ∣Δ + 4C∣, two Weyl points annihilate at the Brillouin zone boundary, causing the system to become insulating again. In this situation, the Hall conductivity becomes a constant at ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}=\frac{{e}^{2}}{ha}$ with a as the lattice constant in z-direction⁵². The Hall conductivity can also be calculated by using Kubo–Streda formula^53,54, which separates Hall conductivity into two distinct contributions, ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}={\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}+{\sigma }_{xy}^{{{\rm{II}}}}$ where ${\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}$ describes the response at the Fermi surface, and ${\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$ represents a nondissipative contribution from states below the Fermi energy^55,56,57. At zero temperature, these two components of the Hall conductivity can be obtained as

$${\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}=\frac{{e}^{2}}{2h}\int_{-\pi /a}^{\pi /a}\frac{d{k}_{{{\rm{z}}}}}{2\pi }{\sum}_{s=\pm }s\Theta ({\mu }^{2}-{{{\mathcal{M}}}}_{{{\rm{s}}}}^{2})\frac{{{{\mathcal{M}}}}_{{{\rm{s}}}}}{| \mu | }$$

(2)

and

$${\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}=\frac{{e}^{2}}{2h}\int_{-\pi /a}^{\pi /a}\frac{d{k}_{{{\rm{z}}}}}{2\pi }{\sum}_{{{\rm{s}}}=\pm }s\Theta ({{{\mathcal{M}}}}_{{{\rm{s}}}}^{2}-{\mu }^{2}){{\rm{sgn}}}({{{\mathcal{M}}}}_{{{\rm{s}}}})$$

(3)

where ${{\rm{sgn}}}$ denotes the sign function, Θ is the Heaviside step function, and μ is the chemical potential. The Hall conductivity can be interpreted as a summation over each k_z slice of a two-dimensional system. We plot the chemical potential dependence of ${\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}$, ${\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$, and ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$ in Fig. 2. Figure 2a demonstrates that before Weyl point formation, all three components vanish identically within the band gap. After the Weyl points emerge (Fig. 2b), ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$ generally receives contributions from both Fermi surface and Fermi sea terms. At charge neutrality, ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$ is solely determined by the Fermi sea contribution. For small magnetic field, both ${\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}$ and ${\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$ exhibit a linear dependence on B through the Zeeman term m. To first order in the magnetic field expansion, the total Hall conductivity can be obtained as ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}=\frac{{e}^{2}}{2\pi h}\frac{{k}_{0}}{| \mu | }{g}_{{{\rm{z}}}}{\mu }_{B}B$, where k₀ is the Fermi wavevector along the z-direction in the absence of the Zeeman field, determined by Δ_∥(k₀) = ∣μ∣.

Orbital magnetic effects across semiclassical and quantum oscillation regimes

We will now address the orbital effect (m ≠ 0 and A ≠ 0). The momentum perpendicular to the magnetic field is quantized as ${{{\bf{k}}}}_{\perp }^{2}\to 2N/{l}_{B}^{2}$, where ${l}_{B}=\sqrt{\hslash /eB}$ is the magnetic length, and N = 0, 1, 2,... labels the Landau levels. The eigenenergies become ${\varepsilon }_{0{{\rm{s}}}}=s{{{\mathcal{M}}}}_{-{{\rm{s}}}}$ for the lowest Landau levels (LLLs) with N = 0 and ${\varepsilon }_{{{\rm{Ns\zeta }}}}=\zeta \sqrt{{{{\mathcal{M}}}}_{{{\rm{s}}}}^{2}+N{\eta }^{2}}$ for higher Landau levels with N ≥ 1 (gray lines in Fig. 3a), where $\eta =\sqrt{2}v\hslash /{l}_{{{\rm{B}}}}$ represents the cyclotron energy. Due to the presence of Zeeman field m, the LLLs are no longer symmetric under electron-hole transformation, while the higher Landau levels remain symmetric, although with broken degeneracy. As demonstrated in the Supplementary Note 2, we rigorously derive the Hall magnetoconductivity (σ_xy) and transverse magnetoconductivity (σ_xx) at arbitrary magnetic fields using the Kubo formula within the Landau level representation, neglecting vertex corrections. Disorder effects are incorporated by modeling the Landau levels as Lorentzians with a constant broadening width Γ, corresponding to a relaxation time τ = ℏ/(2Γ). These conductivities can be decomposed into antisymmetric (${\sigma }_{{{\rm{ab}}}}^{{{\rm{anti}}}}$) and the symmetric (${\sigma }_{{{\rm{ab}}}}^{{{\rm{sym}}}}$) terms: ${\sigma }_{{{\rm{ab}}}}={\sigma }_{{{\rm{ab}}}}^{{{\rm{anti}}}}+{\sigma }_{{{\rm{ab}}}}^{{{\rm{sym}}}}$ based on symmetry considerations. The antisymmetric Hall conductivity changes sign under carrier type reversal (${\sigma }_{{{\rm{ab}}}}^{{{\rm{anti}}}}(\mu )=-{\sigma }_{{{\rm{ab}}}}^{{{\rm{anti}}}}(-\mu )$), while the symmetric conductivity retains its sign (${\sigma }_{{{\rm{ab}}}}^{{{\rm{sym}}}}(\mu )={\sigma }_{{{\rm{ab}}}}^{{{\rm{sym}}}}(-\mu )$), where a, b = x, y. Furthermore, the system exhibits three distinct regimes based on magnetic field strength as illustrated in Fig. 1c: (i) Semiclassical regime (B ≤ χ⁻¹ with $\chi =\frac{e{v}^{2}\tau }{\mu }$ represents the mobility): The magnetic field is weak enough and disorder broadening smears the Landau levels. (ii) Quantum oscillations regimes: At higher magnetic fields, the system enters a regime characterized by quantum oscillations. (iii) Quantum limit ($B\ge \frac{{\mu }^{2}-{\Delta }^{2}}{2\hslash {v}^{2}e}$): In this regime, the magnetic field is strong enough that only the LLL is partially filled.

Fig. 3: Orbital magnetic effects on Hall conductivity.

a Landau level spectrum with orbital effects. The two lowest Landau levels ε_0s align precisely with the spin-down states in the energy spectrum of Fig. 2. k_c denotes the Fermi wavevector of the lowest Landau level at charge neutrality μ = 0. b Magnetic field dependence of the symmetric Hall conductivity ${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}}}-{\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$ at fixed chemical potential μ = 50 meV for different Γ. c Quantum oscillations in the symmetric Hall conductivity ${\sigma }_{{{\rm{xy}}}}^{{{\rm{osi,sym}}}}$ : comparison between numerical calculations and analytical results for μ = 50 meV and Γ = 6 meV. The oscillation frequency field B_f ≈ 10.74 T corresponds to the extremal Fermi surface cross-section via the Onsager relation. d The Hall conductivity σ_xy as a function of B for μ = 0. The blue line marks the value e²k_c/(2πh), corresponding to the separation of the Weyl nodes. The black squares denote the numerical results for disorder broadening Γ = 0.1 meV. The red triangles represent the result for en/B with n as the carrier density. e Antisymmetric component of σ_xy: numerical results compared with analytical expressions for different μ values with Γ = 3 meV. f Comparison between numerical calculations and the analytical model for the orbital quantum correction ${\sigma }_{{{\rm{xy}}}}^{O}$ at μ = 50 meV and Γ = 3 meV. g Analytical results for the Hall conductivity at low magnetic fields (B = 0.05 T): ${\sigma }_{{{\rm{xy}}}}^{{{\rm{LF}}}}$ (red dashed), ${\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}$(blue dashed), and ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$ (green dashed) as a function of Γ/μ. The purple line represents the summation of these contributions. The yellow line with squares corresponds to the numerical results. The chemical potential is μ = 20 meV in the simulations.

Using a small magnetic field expansion of the orbital magnetic effects and fully incorporating the Zeeman-induced band splitting, we derive the magnetoconductivities in the semiclassical regime while simultaneously capturing the background contributions that persist into the quantum oscillation regime at higher fields. The symmetric Hall conductivity ${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}}}$ is given by:

$${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}}}=\frac{{\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}}{1+{\chi }^{2}{B}^{2}}+{\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}.$$

(4)

The symmetric Hall conductivity arises from the Zeeman splitting-induced Berry curvature effect, though it is modified by orbital effects. This analytic expression is numerically validated in Supplementary Note 3. For sufficient weak fields (χB ≪ 1), where orbital effects become negligible, ${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}}}\simeq {\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$ exhibits linear field dependence. At stronger fields, orbital effects suppress Fermi surface contribution ${\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}$, while preserving Fermi sea contribution ${\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$—the topological component representing nondissipative contributions from states below the Fermi energy. Figure 3b shows the difference between the symmetric Hall conductivity and the Fermi sea contribution, ${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}}}-{\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$, plotted as a function of B for various scattering rates Γ. The difference initially increases linearly before decreasing with magnetic field, in excellent agreement with Eq. (4). At small Γ (purple line), orbital effects completely suppress ${\sigma }_{{{\rm{xy}}}}^{{{\rm{I}}}}$, causing ${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}}}$ to converge with ${\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$. By subtracting the background contribution, we isolate the quantum oscillations in the symmetric Hall conductivity:

$${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}},{{\rm{osc}}}}\approx \frac{{e}^{2}}{\sqrt{2\pi }h}{\sum}_{{{\rm{s}}}}\frac{s\Theta [{\mu }^{2}-{{{\mathcal{M}}}}_{{{\rm{s}}}}^{2}(0)]{{{\mathcal{M}}}}_{{{\rm{s}}}}(0)}{| \mu | (1+{\chi }^{2}{B}^{2})}\frac{\cos ({S}_{{{\rm{s}}}}^{(0)}{l}_{{{\rm{B}}}}^{2}-s\frac{\pi }{4})}{| {S}_{{{\rm{s}}}}^{(2)}{l}_{{{\rm{B}}}}^{2}{| }^{1/2}}\exp (-\frac{\pi }{| \chi B| })$$

(5)

where ${S}_{{{\rm{s}}}}^{(0)}$ and ${S}_{{{\rm{s}}}}^{(2)}$ are the zeroth and second order coefficients in the k_z expansion of ${S}_{{{\rm{s}}}}=\pi ({\mu }^{2}-{{{\mathcal{M}}}}_{{{\rm{s}}}}^{2})/({\hslash }^{2}{v}^{2})\approx {S}_{{{\rm{s}}}}^{(0)}+\frac{1}{2}{S}_{{{\rm{s}}}}^{(2)}{k}_{{{\rm{z}}}}^{2}$. The quantum oscillation fully comes from the Fermi surface contribution. The two bands s = ± produce two distinct Fermi surfaces as a result of Zeeman splitting, giving rise to a beating pattern in quantum oscillations due to their slightly different frequencies. At small magnetic fields, the splitting is minimal, and the symmetric component of the oscillatory Hall conductivity follows the form ${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}},{{\rm{osc}}}} \sim \cos (2\pi {B}_{{{\rm{f}}}}/B)$ with B_f ≈ (μ² − Δ²)/(2eℏv²) ≈ 10.47 T. As shown in Fig.3c, our numerical results show good agreement with the analytical expression in Eq. (5). The relation ${\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}}}\simeq {\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}$ remains valid even in the quantum limit. This is demonstrated in Fig. 3d for the case μ = 0, where an infinitesimal magnetic field drives the system into the quantum limit. Here, the Hall conductivity exhibits perfect particle-hole symmetry (${\sigma }_{{{\rm{xy}}}}={\sigma }_{{{\rm{xy}}}}^{{{\rm{sym}}}}$) and becomes nonzero for B > B_Δ, coinciding with the crossing of the zeroth Landau level through μ = 0 (Fig.3a). In this regime, ${\sigma }_{{{\rm{xy}}}}={\sigma }_{{{\rm{xy}}}}^{{{\rm{II}}}}=\frac{{e}^{2}{k}_{{{\rm{c}}}}}{2\pi h}$, as shown by the blue line.

The antisymmetric Hall conductivity can be expressed as the sum of two main contributions:

$${\sigma }_{{{\rm{xy}}}}^{{{\rm{anti}}}}=\frac{{\sigma }_{{{\rm{xy}}}}^{{{\rm{LF}}}}+{\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}}{1+{\chi }^{2}{B}^{2}}$$

(6)

where ${\sigma }_{{{\rm{xy}}}}^{{{\rm{LF}}}}$ corresponds to the classical Lorentz force response, and ${\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}$ incorporates the correction from the quantum metric, orbital magnetization, and other orbital (O) field-induced effects. Figure 3e compares numerical calculations with analytical results for the antisymmetric Hall conductivity ${\sigma }_{{{\rm{xy}}}}^{{{\rm{anti}}}}$ as a function of magnetic field B at different chemical potential μ. The analytical expressions not only match the numerical results in the classical regime but also correctly reproduce the background behavior that persists into the quantum oscillation regime at higher fields. As shown in Fig. 3f, after subtracting the classical Lorentz force contribution, ${\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}$ exhibits a linear field dependence, clearly revealing the quantum corrections arising from orbital magnetic effects. By retaining terms to linear order in the magnetic field, the explicit contributions of different mechanisms to σ_xy are listed in Table 1. We emphasize that our analytical expressions are derived in the weak scattering limit Γ → 0. When Γ is not small, this decomposition breaks down, but the full Kubo-Streda formula—evaluated using the complete Green’s function without expansion—remains rigorously valid. Fig. 3g shows the contributions to the Hall conductivity as a function of Γ/μ for a small magnetic field. ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$ (green dashed line) and ${\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}$ (blue dashed line) from quantum geometric effects are independent of τ while the classical contribution ${\sigma }_{{{\rm{xy}}}}^{{{\rm{LF}}}}$ (red dashed line) varies as τ⁻². As Γ/∣μ∣ approaches 1, the quantum geometric correction grows comparable to the classical Lorentz force contribution, driving a crossover in the total response from τ⁻² to τ⁰ scaling. The analytical results (purple line) accurately describe this crossover behavior, as confirmed by precise numerical results (yellow line with squares).

Table 1 The contributions to the Hall and transverse conductivity in the semiclassical regime and quantum limit

To analyze the magnetoresistance, we need to obtain the transverse magnetoconductivity σ_xx. The transverse magnetoconductivity is given by: ${\sigma }_{{{\rm{xx}}}}=\frac{{\sigma }_{{{\rm{xx}}}}^{0}}{1+{\chi }^{2}{B}^{2}},$ where ${\sigma }_{{{\rm{xx}}}}^{0}$ includes both electron-hole incoherent (${\sigma }_{{{\rm{xx}}},{{\rm{in}}}}^{0}$) and coherent (σ_xx, co⁰) contributions (See Supplementary Note 4 for the explicit forms of these terms). The incoherent contribution arises from the retarded-advanced channel in Kubo formula, while the coherent contribution originates from the retarded-retarded channel. As ${\sigma }_{{{\rm{xx}}},{{\rm{co}}}}^{0}/{\sigma }_{{{\rm{xx}}},{{\rm{in}}}}^{0} \sim \Gamma /\mu$, electron-hole coherence plays an important role near the band bottom (Γ ~ ∣μ∣).

In the semiclassical regime, the Hall resistivity ρ_xy ≃ σ_xy/(σ_xxσ_yy) = R_HB remains linear in B, with the Hall coefficient R_H = ∂ρ_xy/∂B given by:

$${R}_{{{\rm{H}}}}=\frac{1}{B}\frac{{\sigma }_{{{\rm{xy}}}}^{{{\rm{LF}}}}+{\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}+{\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}}{{({\sigma }_{{{\rm{xx}}},{{\rm{in}}}}^{0}+{\sigma }_{{{\rm{xx}}},{{\rm{co}}}}^{0})}^{2}}.$$

(7)

When Γ/∣μ∣ ≪ 1, ${\sigma }_{{{\rm{xx}}},{{\rm{in}}}}^{0}\simeq {\sigma }_{0}\gg {\sigma }_{{{\rm{xx}}},{{\rm{co}}}}^{0}$ and Lorentz force contribution ${\sigma}_{{{\rm{xy}}}}^{{{\rm{LF}}}}\simeq \chi B{\sigma }_{0}$ dominates σ_xy, then R_H ≃ 1/en reduces to the classical result. When Γ ~ ∣μ∣, the contribution from quantum geometric effects and electron-hole coherence can no longer be neglected. Consequently, the Hall coefficient must be modified after accounting for these effects. As shown in Fig. 4a, we plot R_H as a function of Γ/μ for a fixed carrier density n, considering both electron- and hole-type carriers. As Γ increases, R_H gradually deviates from the classical result 1/en. The analytical solution (red lines) from Table 1, derived through a Γ expansion, agrees well with numerical calculations for Γ/μ < 1. However, in the Γ/μ > 1 regime, higher-order quantum geometric corrections ( ∝ Γ²... ) become significant and must be included to accurate description. The conductivity components exhibit distinct symmetry properties: ${\sigma }_{{{\rm{xy}}}}^{{{\rm{LF}}}}$ and ${\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}$ are antisymmetric under carrier-type reversal (μ → −μ), while ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$ is symmetric. This leads to markedly different behavior for two carrier types-with increasing Γ, the hole-type R_H can vanish or even change sign when ${\sigma }_{{{\rm{xy}}}}^{{{\rm{S}}}}$ compensates or dominates the ${\sigma }_{{{\rm{xy}}}}^{{{\rm{LF}}}}$ and ${\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}$, whereas the electron-type R_H maintains its original sign throughout. By analyzing the frequency of the Shubnikov–de Haas (SdH) oscillations, which is directly proportional to the cross-sectional area of the Fermi surface, the carrier density of the system can be determined⁵⁸. By comparing the Hall coefficients obtained from Hall resistivity measurements with the carrier density extracted from SdH oscillations, one can identify the field-induced unconventional Hall effect in experiments. This approach provides a robust method to distinguish between conventional Hall effects and anomalous contributions arising from quantum geometry in the out-of-plane magnetic field configuration.

Fig. 4: Quantum geometric renormalization of Hall coefficient and nonlinear Hall resistivity.

a Hall coefficient R_H versus Γ for a fixed carrier density n = ±8 × 10¹⁶ cm⁻³ in the semiclassical regime, for both electron- and hole-type carriers. The blue dashed lines represent the classical result 1/en. The red lines show the analytical results derived from Eq. (7), while the gray squares correspond to numerical solutions obtained from the full expression. b Comparison between experimental data (black dashed line with squares) from ref. ³⁸ and theoretical simulations (red line) based on our model. The simulations use fitting parameters n = 3 × 10¹⁶cm⁻³, Γ = 6.5 meV, Δ = 5 meV, with other model parameters consistent with previous simulations. The blue and red shaded regions indicate the semiclassical regime and quantum limit, respectively. Dashed lines serve as eye guides for  ~B and en/(σ_xxσ_yy)B⁻¹. B_c ≃ 3.8 T indicates the critical field.

From a semiclassical perspective, the magnetic field modifies the conductivity through corrections to both the Berry curvature and band energy of electronic states^59,60,61,62. Using a weak magnetic field expansion of the Green’s function (See the “Methods” section and Supplementary Note 6 for details), we derive τ-independent Hall conductivity ${\sigma }_{{{\rm{xy}}}}^{(0)}={\sigma }_{{{\rm{xy}}}}^{O}+{\sigma }_{{{\rm{xy}}}}^{S}$ in terms of quantum geometric quantities. We find ${\sigma }_{{{\rm{ab}}}}^{(0)}={\sigma }_{{{\rm{ab}}}}^{(0),{{\rm{wp}}}}+{\sigma }_{{{\rm{ab}}}}^{(0){\prime} }$, where ${\sigma }_{{{\rm{ab}}}}^{(0),{{\rm{wp}}}}$ represents the previously known contribution derived from semiclassical wavepacket theory^59,60,61,62, given by ${\sigma }_{{{\rm{ab}}}}^{(0),{{\rm{wp}}}}=\frac{{e}^{2}}{\hslash }\,\int[d{{\bf{p}}}]\,[(-\frac{\partial f}{\partial \varepsilon })\left({B}_{{{\rm{c}}}}{F}_{{{\rm{cb}}}}{V}_{{{\rm{a}}}}+\frac{1}{2}{\epsilon }_{{{\rm{abc}}}}{\Omega }_{c}\right.({{\bf{m}}}\cdot {{\bf{B}}})-(a\leftrightarrow b)]$. Here, a, b, c denote Cartesian components (with Einstein summation convention), ϵ_abc is the Levi-Civita symbol, F_cb is the anomalous orbital polarizability (AOP), Ω_c the Berry curvature, and m the intraband orbital magnetic moment. The additional term ${\sigma }_{{{\rm{ab}}}}^{(0){\prime} }$ is a new correction obtained through Green’s function techniques, which contains higher-order energy derivatives of the Fermi–Dirac distribution:

$${\sigma }_{{{\rm{ab}}}}^{(0){\prime} }= \frac{{e}^{2}}{\hslash }\,\int\,[d{{\bf{p}}}]\left\{\frac{\partial f}{\partial \epsilon }\frac{1}{2}{g}_{{{\rm{ac}}}}{({{\bf{B}}}\times {\nabla }_{{{\bf{p}}}}{V}_{{{\rm{b}}}})}_{{{\rm{c}}}}-\frac{{\partial }^{3}f}{\partial {\epsilon }^{3}}\frac{1}{8}{n}_{{{\rm{ac}}}}{V}_{{{\rm{b}}}}{({{\bf{B}}}\times {{\bf{V}}})}_{c}\right.\\ \left.\left.-\frac{{\partial }^{2}f}{\partial {\epsilon }^{2}}\frac{1}{8\mu }{{\rm{Im}}}\langle \left[{\hat{V}}_{{{\rm{a}}}},{\hat{V}}_{{{\rm{b}}}}\right]\rangle ({{\bf{m}}}\cdot {{\bf{B}}})\right]-(a\leftrightarrow b)\right\},$$

(8)

where g_ac is the quantum metric tensor, and ${n}_{{{\rm{ab}}}}={{\rm{Re}}}\langle {\partial }_{{p}_{{{\rm{a}}}}}{u}_{\alpha {{\bf{p}}}}| ({\varepsilon}_{\alpha }-{\hat{H}}_{0})| {\partial }_{{p}_{{{\rm{b}}}}}{u}_{\alpha {{\bf{p}}}}\rangle$ with ϵ_α and $\left\vert {u}_{\alpha {{\bf{p}}}}\right\rangle$ as the eigenenergies and eigenstates for the band intersecting the Fermi surface. These terms are non-vanishing and essential for recovering the complete expression for ${\sigma }_{{{\rm{xy}}}}^{{{\rm{O}}}}$.

Nonlinear Hall resistivity in quantum limit

In the quantum limit, disorder has minimal impact on σ_xy, allowing us to neglect impurity effects when evaluating σ_xy. As shown in Supplementary Note 5, the total Hall conductivity can be rigorously shown to satisfy ${\sigma }_{{{\rm{xy}}}}=\frac{en}{B}$, where n is the carrier density, with the charge neutrality point defined as the midpoint between the two LLLs (see Supplementary Note 7). As demonstrated in Fig. 3d, we validate this relation by examining the case where μ = 0. Here, an infinitesimal magnetic field is sufficient to drive the system into the quantum limit. The Hall conductivity exhibits perfect particle-hole symmetry and develops a nonzero value for B > B_Δ. Our numerical results for the Hall conductivity (black squares) show excellent agreement with the analytical expression (red triangles), even when Weyl nodes form without orbital effects. This agreement persists because the carrier density can be expressed as n = eBk_c/(2πh). If the carrier density is fixed at the charge neutrality point (n = 0), the Hall conductivity vanishes identically (black dashed line). As illustrated by Fig. 1c, the leading-order conductivity σ_xx arises from the inter-band velocity and the scatterings between the 0th bands with the bands of 1, which are higher-order perturbation effects⁶³. After calculation, we find: ${\sigma }_{{{\rm{xx}}}}=\frac{{e}^{2}}{2\pi ha}\frac{\Gamma }{{t}_{{{\rm{z}}}}}{{\mathcal{F}}}$ where ${{\mathcal{F}}}$ is a dimensionless integral of order unity, weakly dependent on m/Γ and μ/Γ. For estimating ρ_xy, ${{\mathcal{F}}}$ can be approximated as a constant. σ_xx is proportional to Γ, while σ_xy is inversely proportional to B. This leads to a field-driven competition between these two conductivity components. At small field, where ${\sigma }_{{{\rm{xy}}}}^{2}\gg {\sigma }_{{{\rm{xx}}}}{\sigma }_{{{\rm{yy}}}}$, ρ_xy exhibits a classical linear dependence: ρ_xy ≃ B/en. Conversely, at larger fields, where ${\sigma }_{{{\rm{xy}}}}^{2}\ll {\sigma }_{{{\rm{xx}}}}{\sigma }_{{{\rm{yy}}}}$, ρ_xy becomes inversely proportional to B: ${\rho }_{{{\rm{xy}}}}\simeq \frac{en}{{\sigma }_{{{\rm{xx}}}}{\sigma }_{{{\rm{yy}}}}}{B}^{-1}$. The transition between these two regimes occurs at a critical magnetic field:

$${B}_{{{\rm{c}}}}=\frac{{t}_{{{\rm{z}}}}}{\Gamma }\frac{2\pi ha}{e{{\mathcal{F}}}}n.$$

(9)

For larger values of Γ and smaller carrier density n, B_c decreases, making the transition easier to observe. We apply our theory to explain the experimental data from ref. ³⁸. As shown in Fig. 4b, for a low carrier density n = 3 × 10¹⁶cm⁻³, the system enters the quantum limit at around B_QL ≈ 1T, indicated by the red shaded region. Quantum oscillations emerge in the regime where χ⁻¹ < B < B_QL = (μ² − Δ²)/(2ℏv²e), as illustrated in Fig. 1. However, when the mobility is relatively low and the carrier density is small, the quantum oscillations in the intermediate field range become difficult to observe. Using ${{\mathcal{F}}}=0.6$ and the band gap and broadening parameters provided in ref. ³⁸, the critical magnetic field is estimated to be B_c ≈ 3.8 T. Our theory accurately explains the experimental results. Additionally, it self-consistently reproduces the longitudinal conductivity, as demonstrated in Supplementary Note 8.

Conclusion

In conclusion, we propose a quantum theory for the unconventional Hall effect in paramagnetic Dirac materials, combining intrinsic band topology with field-induced quantum effects of LLs. By systematically separating the total Hall conductivity contributions based on symmetry and physical origin, we clarify how each component evolves under an applied magnetic field. In the semiclassical regime, quantum geometry effects modify the Hall coefficient, while in the quantum limit, a competition between transverse and Hall conductivities leads to the nonmonotonic field dependence of the Hall effect. This work provides a comprehensive framework for understanding the intricate interplay between quantum geometry, magnetic field, and disorder in Dirac materials, and also offers valuable insights into the origin of anomalous transport phenomena observed in other nonmagnetic Dirac materials, such as Cd₃As₂^64,65.

At last, we emphasize the fundamental distinction between our proposed mechanism and conventional multiband models. The origin of the unconventional Hall effect in our framework stems from quantum geometric effects that persist regardless of Fermi surface topology or temperature, whereas multiband models require specific band structure conditions and thermally activated carriers. If angle-resolved photoemission spectroscopy (ARPES) reveals a single Fermi surface (exclusively electron- or hole-like) without additional bands crossing the Fermi level, this would rule out multiband contributions to the unconventional Hall effect. In such a scenario, the unconventional Hall response observed at low temperatures (k_BT ≪ Δ) must arise from intrinsic quantum geometric effects, as thermally excited minority carriers are exponentially suppressed. This distinction is particularly crucial in systems like ZrTe₅, where the bandgap and Fermi level positioning are sensitive to sample stoichiometry and external perturbations. Transport measurements under controlled doping or strain could thus serve as additional tests to isolate the geometric contribution.

Methods

Eigensolutions and Green’s function for the Dirac Hamiltonian in a finite magnetic field

We perform a unitary transformation to Hamiltonian [Eq. (1)], $U={e}^{i{\tau }_{{{\rm{y}}}}{\sigma }_{z}\frac{\theta }{2}}$ with $\theta =\arctan \frac{{t}_{{{\rm{z}}}}\sin {k}_{{{\rm{z}}}}}{\Delta ({k}_{{{\rm{z}}}})}$, leading to

$$\begin{array}{rcl}{H}^{{\prime} }&=&UH{U}^{-1}\\ &=&\left[\begin{array}{llll}{\Delta }_{\parallel }+m&0&0&\eta a\\ 0&{\Delta }_{\parallel }-m&\eta {a}^{{\dagger} }&0\\ 0&\eta a&-{\Delta }_{\parallel }+m&0\\ \eta {a}^{{\dagger} }&0&0&-{\Delta }_{\parallel }-m\end{array}\right]\end{array}$$

where the ladder operators are defined as $a=\frac{v}{\eta }{\Pi }_{{{\rm{x}}}}-i\frac{v}{\eta }{\Pi }_{{{\rm{y}}}}$ and ${a}^{{\dagger} }=\frac{v}{\eta }{\Pi }_{{{\rm{x}}}}+i\frac{v}{\eta }{\Pi }_{{{\rm{y}}}}$, and ${\Delta }_{\parallel }({k}_{{{\rm{z}}}})=\sqrt{\Delta {({k}_{z})}^{2}+{({t}_{{{\rm{z}}}}\sin {k}_{{{\rm{z}}}})}^{2}}$. The Hamiltonian ${H}^{{\prime} }$ separates into two subblocks: ${H}^{{\prime} }={H}_{+}\oplus {H}_{-}$ with ${H}_{+}={{{\mathcal{M}}}}_{+}{\sigma }_{{{\rm{z}}}}+\eta a{\sigma }_{+}+\eta {a}^{{\dagger} }{\sigma }_{-},{H}_{-}={{{\mathcal{M}}}}_{-}{\sigma }_{{{\rm{z}}}}+\eta {a}^{{\dagger} }{\sigma }_{+}+\eta a{\sigma }_{-}$ and ${{{\mathcal{M}}}}_{\pm }({k}_{{{\rm{z}}}})={\Delta }_{\parallel }\pm m$. The current operator is obtained from j_a = eiℏ⁻¹[H, r_a] with a = x, y denoting the coordinates in the plane perpendicular to the magnetic field. In the subspace s with s = ± , the current operators are ${j}_{{{\rm{x}}}}^{{{\rm{s}}}}=e{v}_{{{\rm{x}}}}{\sigma }_{{{\rm{x}}}}$ and ${j}_{{{\rm{y}}}}^{{{\rm{s}}}}=se{v}_{{{\rm{y}}}}{\sigma }_{{{\rm{y}}}}$. The eigenfunctions of the 2 × 2 Hamiltonian are given by

$${\psi }_{{{\rm{ns\zeta }}}}({{\bf{r}}})=\langle {{\bf{r}}}| {\psi }_{{{\rm{ns}}}\zeta {{{\rm{k}}}}_{{{\rm{x}}}}{{{\rm{k}}}}_{{{\rm{z}}}}}\rangle =\frac{{e}^{i{k}_{{{\rm{x}}}}x+i{k}_{{{\rm{z}}}}z}}{\sqrt{{L}_{{{\rm{x}}}}{L}_{{{\rm{z}}}}}}\left[\begin{array}{l}\zeta \cos \frac{{\varphi }_{{{\rm{s}}}\zeta {{\rm{n}}}}}{2}{\phi }_{n-\frac{1+{{\rm{s}}}}{2}}(\xi )\\ \sin \frac{{\varphi }_{{{\rm{s}}}\zeta {{\rm{n}}}}}{2}{\phi }_{n-\frac{1-{{\rm{s}}}}{2}}(\xi )\end{array}\right]$$

(10)

with ξ = y/l + k_xl, $\cos {\varphi }_{{{\rm{ns\zeta }}}}=\zeta {{{\mathcal{M}}}}_{{{\rm{s}}}}/{\varepsilon }_{{{\rm{ns}}}}$, and $\sin {\varphi }_{{{\rm{s}}}\zeta {{\rm{n}}}}=\sqrt{n}\eta /{\varepsilon }_{{{\rm{ns}}}}$. ${\phi }_{{{\rm{n}}}}(\xi )=\frac{{e}^{-{\xi }^{2}/2}}{{2}^{n/2}{\pi }^{1/4}\sqrt{n!{l}_{{{\rm{B}}}}}}{H}_{{{\rm{n}}}}(\xi )$ where H_n denotes the nth Hermite polynomial. The corresponding eigenenergies are $\zeta {\varepsilon }_{{{\rm{ns}}}}=\zeta \sqrt{{{{\mathcal{M}}}}_{{{\rm{s}}}}^{2}+n{\eta }^{2}}$. The wavefunctions for the LLLs are

$${\psi }_{0+}({{\bf{r}}}) =\langle {{\bf{r}}}| {\psi }_{0+{k}_{{{\rm{x}}}}{k}_{{{\rm{z}}}}}\rangle =\frac{{e}^{i{k}_{{{\rm{x}}}}x+i{k}_{{{\rm{z}}}}z}}{\sqrt{{L}_{{{\rm{x}}}}{L}_{{{\rm{z}}}}}}\left[\begin{array}{l}0\\ {\phi }_{0}(\xi )\end{array}\right],\\ {\psi }_{0-}({{\bf{r}}}) =\langle {{\bf{r}}}| {\psi }_{0-{k}_{{{\rm{x}}}}{k}_{{{\rm{z}}}}}\rangle =\frac{{e}^{i{k}_{{{\rm{x}}}}x+i{k}_{{{\rm{z}}}}z}}{\sqrt{{L}_{{{\rm{x}}}}{L}_{{{\rm{z}}}}}}\left[\begin{array}{l}{\phi }_{0}(\xi )\\ 0\end{array}\right],$$

(11)

with the corresponding eigenenergies given by ${\varepsilon }_{0s}=-s{{{\mathcal{M}}}}_{s}$. Then, we can derive the retarded (R) and advanced (A) Green’s functions

$${G}^{{{\rm{R,A}}}}(\omega ;{{\bf{r}}},{{{\bf{r}}}}^{{\prime} })={\sum}_{{{\rm{s}}}}\frac{\langle {{\bf{r}}}| {\psi }_{0{{\rm{s}}}{k}_{{{\rm{x}}}}{k}_{{{\rm{z}}}}}\rangle \langle {\psi }_{0{{\rm{s}}}{k}_{{{\rm{x}}}}{k}_{{{\rm{z}}}}}| {{{\bf{r}}}}^{{\prime} }\rangle }{{\omega }^{{{\rm{R,A}}}}-{\varepsilon }_{0{{\rm{s}}}}}+{\sum}_{{{\rm{s}}},\zeta ,{{\rm{n}}}\ge 1}\frac{\langle {{\bf{r}}}| {\psi }_{{{\rm{ns}}}\zeta {k}_{{{\rm{x}}}}{k}_{{{\rm{z}}}}}\rangle \langle {\psi }_{{{\rm{ns}}}\zeta {k}_{{{\rm{x}}}}{k}_{{{\rm{z}}}}}| {{{\bf{r}}}}^{{\prime} }\rangle }{{\omega }^{{{\rm{R,A}}}}-{\varepsilon }_{{{\rm{ns}}}\zeta }}$$

with ω^R,A = ω ± iΓ. By substituting Eqs. (10) and (11), we can obtain

$$G(\omega ;{{\bf{r}}},{{{\bf{r}}}}^{{\prime} })={e}^{i{{\Phi }}({{{\bf{r}}}}_{\perp },{{{\bf{r}}}}_{\perp }^{{\prime} })}\widetilde{G}(\omega ;{{\bf{r}}}-{{{\bf{r}}}}^{{\prime} })$$

where the Schwinger phase as ${{\Phi }}({{{\bf{r}}}}_{\perp },{{{\bf{r}}}}_{\perp }^{{\prime} })=\int_{{{{\bf{r}}}}_{\perp }}^{{{{\bf{r}}}}_{\perp }^{{\prime} }}d{{{\bf{r}}}}_{\perp }\cdot {{\bf{A}}}({{{\bf{r}}}}_{\perp })=-\frac{(x-{x}^{{\prime} })(y+{y}^{{\prime} })}{2{l}_{{{\rm{B}}}}^{2}}$ with r_⊥ = (x, y) which breaks the translational invariance explicitly and the translational invariant part is^66,67

$${\widetilde{G}}^{{{\rm{R,A}}}}(\omega ;{{{\bf{r}}}}_{\perp }-{{{\bf{r}}}}_{\perp }^{{\prime} })= \frac{{e}^{i{k}_{{{\rm{z}}}}(z-{z}^{{\prime} })}}{2\pi {l}_{{{\rm{B}}}}^{2}}{e}^{-\frac{| {{{\bf{r}}}}_{\perp }-{{{\bf{r}}}}_{\perp }^{{\prime} }{| }^{2}}{4{l}_{{{\rm{B}}}}^{2}}}\left\{\frac{{\omega }^{{{\rm{R,A}}}}-s{{{\mathcal{M}}}}_{{{\rm{s}}}}}{{({\omega }^{{{\rm{R,A}}}})}^{2}-{\varepsilon }_{0{{\rm{s}}}}^{2}}{L}_{0}^{0}\left(\frac{| {{{\bf{r}}}}_{\perp }-{{{\bf{r}}}}_{\perp }^{{\prime} }{| }^{2}}{2{l}_{{{\rm{B}}}}^{2}}\right){P}_{-{{\rm{s}}}}\right. \\ +{\sum}_{n\ge 1}\frac{1}{{({\omega }^{{{\rm{R,A}}}})}^{2}-{\varepsilon }_{n}^{2}}\left[({\omega }^{R,A}+{{{\mathcal{M}}}}_{{{\rm{s}}}}{\sigma }_{z})\left({L}_{n-\frac{1+{{\rm{s}}}}{2}}^{0}\right.\left(\frac{| {{{\bf{r}}}}_{\perp }-{{{\bf{r}}}}_{\perp }^{{\prime} }{| }^{2}}{2{l}_{{{\rm{B}}}}^{2}}\right){P}_{+} \right.\\ +\left.{L}_{n-\frac{1-{{\rm{s}}}}{2}}^{0}(\frac{| {{{\bf{r}}}}_{\perp }-{{{\bf{r}}}}_{\perp }^{{\prime} }{| }^{2}}{2{l}_{{{\rm{B}}}}^{2}}){P}_{-}\right)+\sqrt{n}\eta \sqrt{\frac{2}{n}}\left[\begin{array}{ll}0&\frac{i(x-{x}^{{\prime} })-(y-{y}^{{\prime} })}{2{l}_{{{\rm{B}}}}}\\ \frac{i(x-{x}^{{\prime} })+(y-{y}^{{\prime} })}{2{l}_{{{\rm{B}}}}}&0\end{array}\right]\\ \left.{e}^{-\frac{| {{{\bf{r}}}}_{\perp }-{{{\bf{r}}}}_{\perp }^{{\prime} }{| }^{2}}{4{l}_{{{\rm{B}}}}^{2}}}{L}_{n-1}^{1}\left(\frac{| {{{\bf{r}}}}_{\perp }-{{{\bf{r}}}}_{\perp }^{{\prime} }{| }^{2}}{2{l}_{{{\rm{B}}}}^{2}}\right)\right\}$$

with ${L}_{n}^{\alpha }(x)$ as the generalized Laguerre polynomials. The Fourier transform of the translational invariant part $\widetilde{G}(\omega ;{{\bf{r}}}-{{{\bf{r}}}}^{{\prime} })$ can be obtained as

$${\widetilde{G}}_{{{\rm{s}}}}^{{{\rm{R,A}}}}(\omega ,{{\bf{k}}}) =\,\int\,d{{\bf{r}}}{e}^{-i{{\bf{k}}}\cdot ({{\bf{r}}}-{{{\bf{r}}}}^{{\prime} })}{\widetilde{G}}_{{{\rm{s}}}}^{{{\rm{R,A}}}}(\omega ;{{\bf{r}}}-{{{\bf{r}}}}^{{\prime} }) \\ ={e}^{-{{{\bf{k}}}}_{\perp }^{2}{l}_{{{\rm{B}}}}^{2}}{\sum }_{n=0}^{\infty }{(-1)}^{n}\frac{{S}_{{{\rm{ns}}}}^{{{\rm{R,A}}}}(\omega ,{{\bf{k}}})}{{({\omega }^{{{\rm{R,A}}}})}^{2}-{\varepsilon }_{{{\rm{ns}}}}^{2}}$$

(12)

with

$${S}_{{{\rm{ns}}}}^{{{\rm{R,A}}}}(\omega ,{{\bf{k}}})=2({\omega }^{{{\rm{R,A}}}}+{{{\mathcal{M}}}}_{{{\rm{s}}}}{\sigma }_{{{\rm{z}}}})[{L}_{{{\rm{n}}}}(x){P}_{-{{\rm{s}}}}-{L}_{{{\rm{n}}}-1}(x){P}_{{{\rm{s}}}}]-4{{{\bf{k}}}}_{\perp }\cdot {{\boldsymbol{\sigma }}}{L}_{{{\rm{n}}}-1}^{1}(x)$$

(13)

where $x=2| {{{\bf{k}}}}_{\perp }{| }^{2}{l}_{B}^{2}$ with k_⊥ = (k_x, k_y) and the projection operator is P_s = (1 + sσ_z)/2.

Kubo formula for Dirac materials in a finite magnetic field

The frequency-dependent electrical conductivity tensor is calculated using the Kubo formula: ${\sigma }_{{{\rm{ab}}}}(\Omega )=\frac{{{\rm{Im}}}{\Pi }_{{{\rm{ab}}}}^{R}(\Omega +i0)}{\Omega }$ where ${\Pi }_{{{\rm{ab}}}}^{{{\rm{R}}}}$ is the retarded current-current correlation function obtained by analytically continuing the imaginary time expression:

$${\Pi }_{{{\rm{ab}}}}(i{\Omega }_{{{\rm{m}}}}) =\frac{1}{V}\int_{0}^{\beta }d\tau {e}^{i{\Omega }_{{{\rm{m}}}}\tau }\langle {T}_{\tau }{J}_{{{\rm{a}}}}(\tau ){J}_{{{\rm{b}}}}(0)\rangle \\ =\frac{1}{\beta V}{\sum}_{{{\bf{k}}},i{\omega }_{{{\rm{n}}}},{{\rm{s}}}}{{\rm{Tr}}}[{\widetilde{G}}_{{{\rm{s}}}}(i{\omega }_{{{\rm{n}}}},{{\bf{k}}}){\hat{V}}_{{{\rm{a}}}}^{{{\rm{s}}}}{\widetilde{G}}_{{{\rm{s}}}}(i{\omega }_{{{\rm{n}}}}+i{\Omega }_{{{\rm{m}}}},{{\bf{k}}}){\hat{V}}_{{{\rm{b}}}}^{s}]$$

where ${\hat{V}}_{{{\rm{a}}}}^{{{\rm{s}}}}=\frac{1}{\hslash }\partial {H}_{{{\rm{s}}}}/\partial {k}_{{{\rm{a}}}}$ is the current operator for subblock s. By substituting Eq. (12) and performing the analytical continuation iΩ_m → Ω + i0, the magnetoconductivity can be evaluated as⁶⁶

$${\sigma }_{{{\rm{ab}}}}(\Omega )= \frac{{e}^{2}{v}^{2}}{2\pi \Omega }{{\rm{Re}}}\int_{-\infty }^{\infty }d\omega \int\frac{{d}^{3}{{\bf{k}}}}{{(2\pi )}^{3}}{e}^{-2{{{\bf{k}}}}_{\perp }^{2}{l}_{{{\rm{B}}}}^{2}}{\sum}_{{{\rm{s}}}=\pm }s{\sum }_{n,m=0}^{\infty }{(-1)}^{{{\rm{n}}}+{{\rm{m}}}}tr\left\{[{\,f}_{{{\rm{F}}}}(\omega )-{f}_{{{\rm{F}}}}({\omega }^{{\prime} })]\right.\\ \times \frac{{\sigma }_{{{\rm{a}}}}{S}_{{{\rm{ns}}}}^{{{\rm{R}}}}({\omega }^{{\prime} },{{\bf{k}}}){\sigma }_{{{\rm{b}}}}{S}_{{{\rm{ms}}}}^{{{\rm{A}}}}(\omega ,{{\bf{k}}})}{\{{[{\omega }^{{\prime} {{\rm{R}}}}]}^{2}-{\varepsilon }_{{{\rm{ns}}}}^{2}\}\{{[{\omega }^{{{\rm{A}}}}]}^{2}-{\varepsilon }_{{{\rm{ms}}}}^{2}\}}-{f}_{{{\rm{F}}}}(\omega )\frac{{\sigma }_{{{\rm{a}}}}{S}_{{{\rm{ns}}}}^{{{\rm{R}}}}({\omega }^{{\prime} },{{\bf{k}}}){\sigma }_{{{\rm{b}}}}{S}_{{{\rm{ms}}}}^{{{\rm{R}}}}(\omega ,{{\bf{k}}})}{\{{[{\omega }^{{\prime} {{\rm{R}}}}]}^{2}-{({\varepsilon }_{{{\rm{ns}}}})}^{2}\}\{{[{\omega }^{{{\rm{R}}}}]}^{2}-{({\varepsilon }_{{{\rm{ms}}}})}^{2}\}}\\ \left.+{f}_{{{\rm{F}}}}({\omega }^{{\prime} })\frac{{\sigma }_{{{\rm{a}}}}{S}_{{{\rm{ns}}}}^{{{\rm{A}}}}({\omega }^{{\prime} },{{\bf{k}}}){\sigma }_{{{\rm{b}}}}{S}_{{{\rm{ms}}}}^{{{\rm{A}}}}(\omega ,{{\bf{k}}})}{\{{[{\omega }^{{\prime} {{\rm{A}}}}]}^{2}-{({\varepsilon }_{{{\rm{ns}}}})}^{2}\}\{{[{\omega }^{{{\rm{A}}}}]}^{2}-{({\varepsilon }_{{{\rm{ms}}}})}^{2}\}}\right\}$$

where f_F represents the Fermi-Dirac distribution, ${\omega }^{{\prime} }=\omega +\Omega$, and ω^R,A = ω ± iΓ.By performing the trace while integrating out k_⊥, we can derive a more manageable form of σ_ab.

Small magnetic field expansion of the Kubo–Streda formula

In the Kubo–Streda formalism, small field corrections to conductivity can be derived from the expansion of the Green’s function in Eq. (12). To linear order in the background electromagnetic fields, the Green’s function takes the form:

$$G({{\bf{r}}},{{{\bf{r}}}}^{{\prime} })={G}_{0}({{\bf{r}}}-{{{\bf{r}}}}^{{\prime} })+{G}_{1}({{\bf{r}}},{{{\bf{r}}}}^{{\prime} })+....$$

Due to translational invariance in the absence of background fields, the zeroth-order Green’s function depends solely on the difference ${{\bf{r}}}-{{{\bf{r}}}}^{{\prime} }$, which is not true for the first-order part of the Green’s function. The Fourier transform of G₀ can be derived from the model Hamiltonian: ${G}_{0}^{{{\rm{R}}}/{{\rm{A}}}}(\mu ,{{\bf{k}}})={(\mu \pm i\Gamma -{H}_{0})}^{-1}$. The first-order correction to the Green’s function arising from the magnetic field can be expressed as⁶⁸:

$${G}_{1}({{\bf{r}}},{{{\bf{r}}}}^{{\prime} })=\,\int\,d{{{\bf{r}}}}^{{\prime\prime} }{G}_{0}({{\bf{r}}}-{{{\bf{r}}}}^{{\prime\prime} }){H}_{{{\rm{int}}}}({{{\bf{r}}}}^{{\prime\prime} }){G}_{0}({{{\bf{r}}}}^{{\prime\prime} }-{{{\bf{r}}}}^{{\prime} }).$$

where the interaction Hamiltonian H_int = J⋅A accounts for the orbital effect of the magnetic field. The spin effect of the magnetic field is fully incorporated in H₀ without any approximations. Here, we are considering only the translationally invariant part of the Green’s function, which can be obtained by

$${\widetilde{G}}_{1}=-i{\epsilon }_{{{\rm{cde}}}}\frac{{B}_{e}}{2}{G}_{0}{V}_{{{\rm{c}}}}{G}_{0}{V}_{{{\rm{d}}}}{G}_{0}$$

Thus, the first-order correction to the conductivity due to the orbital effect of the magnetic field is given by:

$${\sigma }_{{{\rm{ab}}}}^{(1)} = \frac{{e}^{2}{v}^{2}}{\pi }\int[d{{\bf{p}}}]{{\rm{Re}}}tr[{V}_{{{\rm{a}}}}{G}_{0}^{{{\rm{R}}}}{V}_{{{\rm{b}}}}{\widetilde{G}}_{1}^{{{\rm{A}}}}]\\ =\frac{{e}^{2}{v}^{2}}{\pi }{\epsilon }_{{{\rm{cde}}}}\frac{{B}_{{{\rm{e}}}}}{2}\int[d{{\bf{p}}}]{{\rm{Im}}}tr[{V}_{{{\rm{a}}}}{G}_{0}^{R}{V}_{{{\rm{b}}}}{G}_{0}^{{{\rm{A}}}}{V}_{c}{G}_{0}^{{{\rm{A}}}}{V}_{{{\rm{d}}}}{G}_{0}^{{{\rm{A}}}}]$$

with $\int[d{{\bf{p}}}]=\int\frac{{d}^{3}{{\bf{p}}}}{{(2\pi )}^{3}}$. Here, a, b, c, d,... denote the Cartesian components, and we adopt the Einstein summation convention for repeated indices. The trace can be evaluated by expressing the Green’s function in terms of the eigenenergy basis ${G}_{0}^{{{\rm{R}}}/{{\rm{A}}}}({{\bf{p}}})={\sum }_{\alpha }\left\vert {u}_{\alpha {{\bf{p}}}}\right\rangle {G}_{0,\alpha }^{{{\rm{R}}}/{{\rm{A}}}}({{\bf{p}}})\left\langle {u}_{\alpha {{\bf{p}}}}\right\vert$ where ${H}_{0}\left\vert {u}_{\alpha {{\bf{p}}}}\right\rangle ={\varepsilon }_{\alpha {{\bf{p}}}}\left\vert {u}_{\alpha {{\bf{p}}}}\right\rangle$ and ${G}_{0,\alpha }^{{{\rm{R}}}/{{\rm{A}}}}({{\bf{p}}})={(\mu \pm i\Gamma -{\varepsilon }_{\alpha {{\bf{p}}}})}^{-1}$. In the analysis of a two-band model, the first-order correction to the conductivity tensor, ${\sigma }_{{{\rm{ab}}}}^{(1)}$, can be divided into two distinct contributions:

1. Two of the band indices of the Green’s functions are identical ${\sigma }_{{{\rm{ab}}}}^{(1,{{\rm{i}}})}$:

$${\sigma }_{ab}^{(1,{{\rm{i}}})} = \frac{{e}^{2}{B}_{{{\rm{e}}}}}{2\pi }{\epsilon }_{{{\rm{cde}}}}\int[d{{\bf{p}}}]{\sum}_{\beta \ne \alpha }{{\rm{Im}}}\left[{G}_{0\alpha }^{{{\rm{R}}}}{G}_{0\alpha }^{{{\rm{A}}}}{({G}_{0\beta }^{{{\rm{A}}}})}^{2}\right.\\ \left.\times ({V}_{{{\rm{a}}}}^{\beta \alpha }{V}_{{{\rm{b}}}}^{\alpha \alpha }{V}_{{{\rm{c}}}}^{\alpha \beta }{V}_{{{\rm{d}}}}^{\beta \beta }+{V}_{{{\rm{a}}}}^{\beta \alpha }{V}_{{{\rm{b}}}}^{\alpha \beta }{V}_{{{\rm{c}}}}^{\beta \alpha }{V}_{{{\rm{d}}}}^{\alpha \beta }+{V}_{{{\rm{a}}}}^{\alpha \alpha }{V}_{{{\rm{b}}}}^{\alpha \beta }{V}_{{{\rm{c}}}}^{\beta \beta }{V}_{{{\rm{d}}}}^{\beta \alpha })\right].$$

(14)

2. Three of the band indices of the Green’s functions are identical ${\sigma }_{ab}^{(1,{{\rm{ii}}})}$ :

$${\sigma }_{{{\rm{ab}}}}^{(1,{{\rm{ii}}})} = \frac{{e}^{2}{B}_{{{\rm{e}}}}}{2\pi }{\epsilon }_{{{\rm{cde}}}}\int[d{{\bf{p}}}]{\sum}_{\beta \ne \alpha }{{\rm{Im}}}\left[{G}_{0\alpha }^{{{\rm{R}}}}{({G}_{0\alpha }^{{{\rm{A}}}})}^{2}{G}_{0\beta }^{{{\rm{A}}}}\right.\\ \left.\times ({V}_{{{\rm{a}}}}^{\beta \alpha }{V}_{{{\rm{b}}}}^{\alpha \alpha }{V}_{c}^{\alpha \alpha }{V}_{{{\rm{d}}}}^{\alpha \beta }+{V}_{{{\rm{a}}}}^{\alpha \alpha }{V}_{{{\rm{b}}}}^{\alpha \alpha }{V}_{{{\rm{c}}}}^{\alpha \beta }{V}_{{{\rm{d}}}}^{\beta \alpha }+{V}_{{{\rm{a}}}}^{\alpha \alpha }{V}_{{{\rm{b}}}}^{\alpha \beta }{V}_{{{\rm{c}}}}^{\beta \alpha }{V}_{{{\rm{d}}}}^{\alpha \alpha })\right].$$

(15)

In the weak scattering limit (Γ → 0), the product of the four Green’s functions provides the leading contribution at μ ~ ε_α or ε_β, and can be approximated using Dirac delta functions:

$${G}_{0\alpha }^{{{\rm{R}}}}{G}_{0\alpha }^{{{\rm{A}}}}{({G}_{0\beta }^{{{\rm{A}}}})}^{2}\simeq i\left[\frac{2\pi }{{\varepsilon }_{\alpha \beta }^{3}}\delta (\mu -{\varepsilon }_{\alpha })-\frac{\pi }{(2\mu -{\varepsilon }_{\alpha }-{\varepsilon }_{\beta }){\varepsilon }_{\alpha \beta }}{\delta }^{{\prime} }(\mu -{\varepsilon }_{\beta })\right] \\ +\frac{\pi }{{\varepsilon }_{\alpha \beta }^{2}\Gamma }\delta (\mu -{\varepsilon }_{\alpha })$$

(16)

and

$$ {G}_{0\alpha }^{{{\rm{R}}}}{({G}_{0\alpha }^{{{\rm{A}}}})}^{2}{G}_{0\beta }^{{{\rm{A}}}} \\ \simeq i\left[\frac{\pi }{2{\Gamma }^{2}{\varepsilon }_{\alpha \beta }}\delta (\mu -{\varepsilon }_{\alpha })-\frac{\pi }{{\varepsilon }_{\alpha \beta }^{3}}[\delta (\mu -{\varepsilon }_{\alpha })+\delta (\mu -{\varepsilon }_{\beta })]+\frac{\pi }{4{\varepsilon }_{\alpha \beta }}{\delta }^{{\prime\prime} }({\varepsilon }_{\alpha }-\mu )\right] \\ +\frac{\pi }{2{\varepsilon }_{\alpha \beta }\Gamma }{\delta }^{{\prime} }(\mu -{\varepsilon }_{\alpha })-\frac{\pi }{{\varepsilon }_{\alpha \beta }^{2}\Gamma }\delta (\mu -{\varepsilon }_{\alpha })$$

(17)

where ${\delta }^{{\prime} }(\mu -\varepsilon )=\frac{\partial \delta (\mu -\varepsilon )}{\partial \varepsilon }$, ${\delta }^{{\prime\prime} }(\mu -\varepsilon )=\frac{{\partial }^{2}\delta (\mu -\varepsilon )}{\partial {\varepsilon }^{2}}$ and ε_αβ ≡ ε_α − ε_β.

By substituting Eqs. (16) and (17) into Eqs. (14) and (15), we can obtain the current j_a = χ_abcE_bB_c in the order O(EB), where the response tensor is given by ${\chi }_{{{\rm{abc}}}}={\chi }_{{{\rm{abc}}}}^{(2)}+{\chi }_{{{\rm{abc}}}}^{(1)}+{\chi }_{{{\rm{abc}}}}^{(0)}$, which are proportional to ∝ τ², τ¹, τ⁰, respectively. The magnetoconductivity for different orders of relaxation time can be expressed as ${\sigma }_{{{\rm{ab}}}}^{({{\rm{i}}})}={\chi }_{{{\rm{abc}}}}^{({{\rm{i}}})}{B}_{{{\rm{c}}}}$ with i = 2, 1, 0.

The explicit expressions for magnetoconductivity ${\sigma }_{{{\rm{ab}}}}^{({{\rm{i}}})}$ are given by:

$${\sigma }_{{{\rm{ab}}}}^{(2)}\simeq -\frac{{e}^{2}}{4{\Gamma }^{2}\hslash }\int[d{{\bf{p}}}]\frac{\partial f}{\partial {\epsilon }_{0}}[{n}_{{{\rm{ac}}}}{V}_{{{\rm{b}}}}{({{\bf{B}}}\times {{\bf{V}}})}_{{{\rm{c}}}}-(a\leftrightarrow b)],$$

(18)

$${\sigma }_{{{\rm{ab}}}}^{(1)}\simeq -\frac{{e}^{2}}{\Gamma \hslash }\int[d{{\bf{p}}}]\{-\frac{\partial f}{\partial {\varepsilon }_{0}}\frac{1}{8}{{\rm{Re}}}\langle \{{\hat{V}}_{{{\rm{a}}}},{\hat{V}}_{{{\rm{b}}}}\}\rangle ({{\boldsymbol{\Omega }}}\cdot {{\bf{B}}}) \\ -\frac{1}{4}\frac{{\partial }^{2}f}{\partial {\varepsilon }_{0}^{2}}{B}_{{{\rm{a}}}}{V}_{{{\rm{b}}}}({{\bf{m}}}\cdot {{\bf{V}}})+(a\leftrightarrow b)\},$$

(19)

$$\begin{array}{rcl}{\sigma }_{{{\rm{ab}}}}^{(0)}&\simeq &-\frac{{e}^{2}}{\hslash }\,\int[d{{\bf{p}}}]\left\{\frac{\partial f}{\partial {\varepsilon }_{0}}[{B}_{{{\rm{c}}}}{F}_{{{\rm{cb}}}}{V}_{{{\rm{a}}}}+\frac{1}{2}{\epsilon }_{{{\rm{abc}}}}{\Omega }_{{{\rm{c}}}}({{\bf{m}}}\cdot {{\bf{B}}})-\frac{1}{2}{g}_{{{\rm{ac}}}}{({{\bf{B}}}\times {\nabla }_{{{\bf{p}}}}{V}_{{{\rm{b}}}})}_{{{\rm{c}}}}]\right.\\ &&\left.+\frac{{\partial }^{2}f}{\partial {\varepsilon }_{0}^{2}}\left[\frac{{{\rm{Im}}}\langle [{\hat{V}}_{{{\rm{a}}}},{\hat{V}}_{{{\rm{b}}}}]\rangle ({{\bf{m}}}\cdot {{\bf{B}}})}{8\mu }\right]+\frac{{\partial }^{3}f}{\partial {\varepsilon }_{0}^{3}}\frac{1}{8}{n}_{{{\rm{ac}}}}{V}_{{{\rm{b}}}}{({{\bf{B}}}\times {{\bf{V}}})}_{c}-(a\leftrightarrow b)\right\}.\end{array}$$

(20)

Here, ϵ_abc represents the Levi-Civita symbol. For a particular band with index β, the AOP is defined as ${F}_{{{\rm{ba}}}}=2{{\rm{Re}}}\frac{{{{\mathcal{M}}}}_{{{\rm{b}}}}^{\beta \alpha }{{{\mathcal{A}}}}_{{{\rm{a}}}}^{\alpha \beta }}{{\varepsilon }_{\beta \alpha }}+\frac{1}{2}{\epsilon }_{{{\rm{bcd}}}}{\partial }_{{p}_{{{\rm{c}}}}}{g}_{{{\rm{ad}}}}$ where ${{{\mathcal{A}}}}_{{{\rm{a}}}}^{\alpha \beta }=\langle {u}_{\alpha {{\bf{p}}}}| i{\partial }_{{p}_{{{\rm{a}}}}}| {u}_{\beta {{\bf{p}}}}\rangle$ is the unperturbated interband Berry connection, ${{{\mathcal{M}}}}_{{{\rm{a}}}}^{\alpha \beta }=\frac{1}{2}{\epsilon }_{abc}({V}_{{{\rm{b}}}}^{\alpha \alpha }+{V}_{{{\rm{b}}}}^{\beta \beta }){{{\mathcal{A}}}}_{{{\rm{c}}}}^{\alpha \beta }$ is the interband orbital magnetic moments, with ${V}_{{{\rm{b}}}}^{\alpha \beta }$ being the matrix elements of velocity operator, ${g}_{{{\rm{ab}}}}={{\rm{Re}}}({{{\mathcal{A}}}}_{{{\rm{a}}}}^{\alpha \beta }{{{\mathcal{A}}}}_{{{\rm{b}}}}^{\beta \alpha })$ as the quantum metric tensor, and ε_βα = ε_β − ε_α. The intraband orbital magnetic moment ${m}_{{{\rm{c}}}}=-\frac{1}{2}{\epsilon }_{{{\rm{abc}}}}{{\rm{Im}}}\langle {\partial }_{{p}_{{{\rm{a}}}}}{u}_{\beta {{\bf{p}}}}| ({\varepsilon }_{\beta }-{\hat{H}}_{0})| {\partial }_{{p}_{{{\rm{b}}}}}{u}_{\beta {{\bf{p}}}}\rangle$ and the real part of the quantity ${n}_{{{\rm{ab}}}}={{\rm{Re}}}\langle {\partial }_{{p}_{{{\rm{a}}}}}{u}_{\beta {{\bf{p}}}}| ({\varepsilon }_{\beta }-{\hat{H}}_{0})| {\partial }_{{p}_{{{\rm{b}}}}}{u}_{\beta {{\bf{p}}}}\rangle$.