Introduction

The concept of replica symmetry breaking (RSB) is one of the most fascinating aspects of the spin-glass theory for understanding the disorder or randomness of complex systems ranging from condensed matter to biophysics and social dynamics. Introduced by Parisi in the late 1970s1,2,3, RSB describes a phenomenon in which identical replicas in disordered magnetic systems under identical experimental conditions may reach distinct states, yielding different measures of observables. A typical prototype of the existence of RSB is the spin glass state in which the system exhibits many local minima in the configuration space in the free energy landscape below some critical temperature1,2. In this regime, nontrivially correlated spins “freeze” along random directions. It is worth noting that not only in spin glasses, RSB can also exist in random-bond ferromagnets in which most spins are aligned in a ferromagnetic background dominating over small frustrated spin clusters4.

The concept of RSB has been extended to nonlinear photonic systems since 20065. In photonics, the amplitude of optical modes plays the role of spins, and the pump power or current acts as the inverse temperature in spin glasses. Consequently, in the photonic-to-magnetic analogy, a spin glass RSB state exhibits strong disorder that leads to predominantly incoherent oscillation of activated modes with significant intensity fluctuations, which mirrors the frustrated spins frozen in random orientations characteristic of a spin glass state. Conversely, the RSB regime in the random-bond ferromagnet corresponds to standard passive mode-locking states, emerging under conditions of limited amount of disorder and high pump powers. In this phase, a subset of dominant modes oscillates coherently while suppressing the others through mode competition6,7,8,9 (for reviews, see, e.g., refs. 10,11,12).

Despite theoretical predictions in the last decades5,7, the first full experimental demonstration of the photonic RSB was achieved only recently13 in a random laser, an open and cavityless system with strong embedded disorder in which the emission of light depends on the random feedback in the disordered scattering medium10,11. The rich phase diagram of random lasers reveals the transition from the photonic paramagnetic replica symmetry (RS) regime below the lasing threshold to the glassy RSB regime above the threshold. To date, such photonic glassy phase with RSB has already been experimentally demonstrated in solid-state13,14,15 and colloidal random lasers16 as well as in random fiber lasers17,18,19,20,21, and even in systems without intentionally added disorder due to the competition of the active modes in the laser cavity22, and in disordered nonlinear wave propagation as well23,24.

In striking contrast to the observed photonic glassy RSB regime, the theoretically predicted RSB phase with weak disorder in the standard passive mode-locking regime has not been experimentally demonstrated so far. The first attempt to fill this gap occurred with the spontaneous mode-locking regime of a multimode Q-switched Nd:YAG laser25, in which a subset of activated longitudinal modes is excited in a nondeterministic way, but with cherent oscillation that dominates and frustrates other modes. Here, the RSB phase occurs in the aperiodic pulsating regime of a standard passive mode-locked ultrafast fiber laser with considerable degree of phase coherence26. However, we stress that the mechanism of spontaneous mode-locking of Q-switched pulses is very distinct from the standard passive mode-locking phase. Moreover, the theory of multimode disordered photonic systems put forward in refs. 5,6,7,8,9 was built taking as a starting point the Hamiltonian of standard passive mode-locking laser systems (not active mode-locking, nor spontaneous mode-locking), as discussed in the nice review9. We should remark, however, that in the presence of relevant disorder the terms in the Hamiltonian related to passive mode-locking become generic and random, and in this context mode-locking becomes a self-starting process7,27.

Ultrafast fiber lasers are favorable experimental photonic platforms for investigating complex behaviors of nonlinear systems. Depending on the balance between nonlinearity and dispersion in the presence of dissipation effects, they support many distinct regimes, including stable mode-locking (SML), pulsating mode-locking (PML), and chaotic pulses, to name a few28. Due to their rich phase diagram, besides being regarded as advanced pulsed light sources, ultrafast fiber lasers have been widely used as photonic platforms for studies of both coherent and incoherent nonlinear dynamics of light waves29,30, such as rogue waves, turbulence, and Lévy intensity statistics31,32,33,34. A recent work in a Yd-doped ultrafast fiber laser has shown that the photonic glassy RSB can also be observed in the quasi-mode-locking regime due to the optical nonlinearity and gain competition among modes35.

As is known, for a pump power above the threshold of SML, the excess of the accumulation of nonlinearity in ultrafast fiber lasers can lead to a phase transition from SML to PML naturally36,37. In the PML regime, mode-locked pulses evolve with periodical oscillation in pulse properties in terms of pulse duration, peak power, and spectral intensity. The periodicity can be either synchronized or anti-synchronized to the cavity roundtrip time, manifesting as regular or irregular intensity fluctuations38. Despite the observation of photonic glassy RSB in the pre-mode-locking phase of a mode-locked fiber laser35, it remains unclear whether the interplay of nonlinearity and gain competition among modes in the PML regime with coherent oscillations can cause the emergence of RSB, and no experimental report on this issue has been presented so far. Notably, the PML regime is essentially different from the Q-switched mode-locking regime, with full coherence among oscillating modes.

In the present work, we demonstrate the first experimental observation of RSB in the aperiodic pulsating regime of a standard passive Er-doped ultrafast fiber laser, in agreement with the standard passive mode-locking phase with RSB theoretically predicted for multimode disordered photonic systems with sufficiently large disorder5,6,7,8,9. In contrast to previous reports of the glassy RSB in random lasers or RSB in a Q-switched spontaneous mode-locking regime of multimode lasers, PML is a fully coherent mode-locking state in which all optical modes are phase-locked with manifestation of ultrashort pulses in the time domain. The emergence of the RSB is verified by calculating the intensity fluctuation overlap parameter and a Pearson correlation coefficient. Furthermore, we have employed a Michelson interferometer with a path difference of one cavity roundtrip between the arms of the device to measure the spectral interferograms of consecutive pulses, characterizing the pulse phase stability. Experimental results reveal that the onset of RSB coincides with the system’s aperiodic pulsating behavior.

Results

Experimental setup and mode-locking results

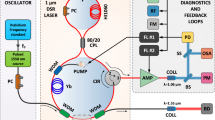
The experimental setup, shown in Fig. 1a, is an Er-doped fiber laser mode-locked by using the nonlinear polarization rotation (NPR) technology, driven by a 980 nm laser diode. The system is a standard passive mode-locked laser since no active modulator is used to mode lock the laser. The laser operates in the normal dispersion regime and details of the laser parameters can be found in the Method Section. The laser can self-initiate mode-locking at a low threshold of 42 mW once the polarization controllers (PCs) are preset.

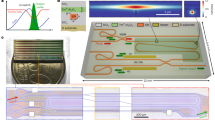
Fig. 1: Photonic regimes in the Er-doped mode-locked fiber laser.
figure 1

a Experimental setup. EDF: erbium-doped fiber. SMF: single-mode fiber. WDM: wavelength division multiplex. OC: optical coupler. PC: polarization controller. PD-ISO: polarization-dependent isolator. PD: photodetector. OSA: optical spectrum analyzer. b Output power as a function of pump power. Photonic regimes are displayed and distinguished by different colored regions. CW: continuous wave. SML: stable mode-locking. PML: pulsating mode-locking. MPML: multipulse mode-locking. c Spectra in the SML regime at a pump power of 50 mW. d Two consecutive spectra in the period-2 PML regime at a pump power of 65 mW. The legend “OSA” denotes the spectrum recorded by OSA, while “Single-shot” and “Averaged” indicate, respectively, the DFT-recorded single-shot spectrum and an averaged spectrum of DFT-recorded single-shot spectrum over 810 roundtrips. rt N (rt N + 1) denotes the Nth (N+1th) roundtrip. The red stars denote the spectral intensity at \({{{\rm{\lambda }}}}_{s}=1570\) nm.

Full size image

Different photonic regimes of the laser operation can be obtained by increasing the pump power, see Fig. 1b including continuous waves (CW), SML, PML, and multipulse mode-locking (MPML). Typical spectra in the SML (at 50 mW) and PML (at 65 mW) regimes are shown in Fig. 1c and d, respectively. The spectral evolution and corresponding pulse train in these regimes can be found in Fig. S1 of the Supplementary Information. At a pump power of 50 mW, the laser operates in the SML regime delivering pulses at a fundamental repetition rate (FRR) of 40.9 MHz, with central wavelength of 1570 nm and 189.1 fs pulse duration. The time-bandwidth-product (TBP) of pulses is calculated to be 0.501, which is close to the Fourier transform limited value of 0.441 for a Gaussian pulse with the same spectral width of 21.8 nm. The slight chirp is introduced by the fiber pigtails connected from the laser output to the autocorrelator (APE pulseCheck 150). Further enhancing the pump power to exceed a threshold to the PML regime leads to the formation of pulsating solitons via a Hopf bifurcation. In the PML regime, the excess of nonlinearity results in a larger pulse chirp, which is reflected by a wider pulse duration of 198.7 fs and bigger TBP value of 0.531 at 70 mW. A clear pedestal can be seen from the autocorrelation (AC) trace, indicating the strong nonlinearity when compared to the clean AC trace at 50 mW in the SML regime. In both regimes, although the dynamics of spectra are entirely different, there is no significant variation in the temporal pulse intensity (see Figs. S1(e) and S1(f) in the Supplementary Information). Consequently, without employing the dispersion Fourier transform (DFT) technique for real-time spectral measurements, pulsating solitons are usually unobservable. This is the first observation of such solitons exhibiting periodic pulsations in the frequency domain while maintaining unchanged pulse characteristics in the time domain in normal dispersion ultrafast lasers. These solitons have been reported in anomalous dispersion ultrafast lasers, being referred to as “invisible” pulsating solitons36.

Characterization and statistical analysis

To gain deep insight into the formation of pulsating solitons, we systematically recorded the single-shot DFT spectra over more than 100 roundtrips at varying pump powers. (Details of the DFT characterization can be found in the Method Section.) Fig. 2 presents the spectral intensity at \({{{\rm{\lambda }}}}_{s}=1570\) nm as a function of the pump power. The x-axis represents the pump power and y-axis shows the normalized intensity. For each pump power, we recorded singe-shot spectra across a minimum of 100 roundtrips and analyzed the spectral intensity at \({{{\rm{\lambda }}}}_{s}=1570\) nm. The intensity at \({{{\rm{\lambda }}}}_{s}=1570\) nm for each roundtrip was normalized to the maximum intensity value at this wavelength over 100 roundtrips. The light gray dots along the vertical axis represent the distribution of the spectral intensity over 100 roundtrips under constant pump power and the blue dots indicate the corresponding average intensity. The first bifurcation emerges at a pump power of 63 mW, marking the onset of the 2-period pulsating solitons. In ultrafast lasers, a Hopf bifurcation occurs when stable solitons lose stability for pump powers exceeding a certain threshold value, giving rise to periodic oscillations. Different from the breathing solitons that usually undergo periodic oscillations in their amplitude and width during propagation39, pulsating solitons exhibit more complex periodic or quasi-periodic variations in pulse shape and amplitude37. Specifically, while breathing solitons undergo smooth, rhythmic expansion and contraction (“breathing”), pulsating solitons can display irregular or multi-periodic structural transformations. Our observation confirms this distinction: in a range from 77 to 89 mW (Fig. 2), we identify the subsequent multi-period and aperiod pulsating solitons. At 90 mW, the system stabilizes into a stable two-soliton state, which subsequently evolves into pulsating dual solitons as evidenced by a second bifurcation at 114 mW. The bifurcation diagram in Fig. 2 unequivocally shows that the characteristics of pulsating solitons depend on the pump power. While the nonlinear Schrödinger equation (NLSE) adequately describes conservative soliton dynamics, real laser systems are dissipative and governed by the Ginzburg-Landau equation (GLE). Critical modifications in the GLE - incorporating dissipation, nonlinear gain, and/or high-order effects - break the inherent symmetry of NLSE, fundamentally altering soliton behavior. Consequently, perturbations to the gain-loss balance by changing pump power can destabilize solitons, triggering the observed pulsating states.

Fig. 2: Bifurcations of mode-locked pulses showing different photonic regimes.
figure 2

The evolution of the spectral intensity at \({{{\rm{\lambda }}}}_{s}=1570{{\rm{n}}}{{\rm{m}}}\), showing the sequence of period-N bifurcations as the pump power increases. Light gray dots along each vertical column depict the distribution of spectral intensity across 100 roundtrips under constant pump power, whereas blue dots denote the corresponding average intensity.

Full size image

To probe the underlying dynamics of pulsating solitons, we conducted a systematic statistical analysis of the laser dynamics. The spectra (“replicas”) for statistical analysis were obtained using DFT technology40. For each pump power, 810 spectra were recorded and analyzed. The identification of the emergence of photonic RSB relies on the analysis of the probability distribution of the intensity fluctuation overlap parameter between distinct replicas, i.e., successive spectra recorded at identical experimental conditions. The intensity fluctuation overlap parameter \({q}_{{{\rm{\gamma }}}{{\rm{\beta }}}}\) measures the correlation between intensity fluctuations of the spectra \({{\rm{\gamma }}}\) and \({{\rm{\beta }}}\) emitted under identical conditions, which is given by ref. 13:

$${{\mbox{q}}}_{{{\rm{\gamma }}}{{\rm{\beta }}}}=\frac{{\sum }_{{\mbox{k}}}\Delta {{\mbox{I}}}_{{{\rm{\gamma }}}}\left({{{\rm{\omega }}}}_{{\mbox{k}}}\right)\Delta {{\mbox{I}}}_{{{\rm{\beta }}}}\left({{{\rm{\omega }}}}_{{\mbox{k}}}\right)}{\sqrt{{\sum }_{{\mbox{k}}}{\left[\Delta {{\mbox{I}}}_{{{\rm{\gamma }}}}\left({{{\rm{\omega }}}}_{{\mbox{k}}}\right)\right]}^{2}}\sqrt{{\sum }_{{\mbox{k}}}{\left[\Delta {{\mbox{I}}}_{{{\rm{\beta }}}}\left({{{\rm{\omega }}}}_{{\mbox{k}}}\right)\right]}^{2}}},$$
(1)

where \({{\rm{\gamma }}},\,{{\rm{\beta }}}={\mathrm{1,2}},\ldots {N}_{R}\) are the spectrum (replica) indices and \({N}_{R}=810\) is the number of replicas; \(k\) is the wavelength index, \(\Delta {I}_{{{\rm{\gamma }}}}\left(k\right)={I}_{{{\rm{\gamma }}}}\left(k\right)-{\bar{I}}_{{{\rm{\gamma }}}}\left(k\right)\) is the intensity fluctuation, and \(\bar{I}\left(k\right)\) is the mean intensity at a wavelength indexed by \(k\), given by \(\bar{I}\left(k\right)={\sum }_{{{\rm{\gamma }}}=1}^{{N}_{R}}{I}_{{{\rm{\gamma }}}}\left(k\right)/{N}_{R}\). The probability density \(P\left(q\right)\) of the intensity fluctuation overlap parameter \({q}_{{{\rm{\gamma }}}{{\rm{\beta }}}}\), which is linked to Parisi overlap parameter in spin-glass theory (for details, see refs. 9,41), can be built, signaling a RS or a RSB regime according to the following discussion.

We start by remarking that the RSB phenomenon is intrinsically related to the presence of a rugged free-energy landscape with a large number of local minima that can trap the states of a multiequilibria complex system, either magnetic or photonic3. These states are organized in a nontrivial way that, once defined a distance, turns out to be hierarchical, also displaying nontrivial correlations. In this case, identical systems, with the same realization of disorder and initially prepared under the same conditions (the so-called replicas of the system), can eventually reach distinct states after some thermodynamic evolution, leading to different measures of observables. In the photonic context, one experimentally accessible way to measure correlations between distinct pairs of system’s replicas is through the intensity fluctuation overlap parameter \({q}_{{{\rm{\gamma }}}{{\rm{\beta }}}}\)13\(,\) given in Eq. (1). In the RSB regime of a multiequilibria photonic system, distinct pairs of replicas can display a range of different overlap values, depending on their corresponding states in the free energy landscape5,6,7,8,9. This leads to a distribution \(P\left(q\right)\) of overlap values \({q}_{{{\rm{\gamma }}}{{\rm{\beta }}}}\) that can present multiple peaks, being eventually continuous for a large number of replicas, reflecting the nontrivial correlations between intensity fluctuations. For example, in the RSB glassy regime of random lasers \(P\left(q\right)\) generally displays two side peaks near the correlated (q = 1) and anticorrelated (q = −1) overlap values, with some probability distribution of q-values in between peaks (see, e.g., Fig. 2 of ref. 14). This RSB scenario is in striking constrast with the RS regime, in which all distinct replica pairs present similar overlaps. For instance, for uncorrelated replicas with modes oscillating incoherently in the RS photonic paramagnetic regime below threshold, \(P\left(q\right)\) shows a single pronounced maximum at q = 0. Another interesting example displaying RS shall be described below in the period-2 PML phase. In this case, the period-2 oscillation in the PML regime with fully coherent modes leads the distribution \(P\left(q\right)\) to be strongly concentrated near only two overlap values, q = ±1, see below.

Another statistically relevant measure that helps to characterize the regimes of complex photonic systems is the Pearson correlation coefficient \({C}_{{ij}}\), which has been recently applied26 in the RSB regime to study the correlations between intensity fluctuations at wavelengths \({{{\rm{\omega }}}}_{{k}_{i}}\) and \({{{\rm{\omega }}}}_{{k}_{j}}\):

$${{\mbox{C}}}_{{\mbox{ij}}}=\frac{{\sum }_{{{\rm{\gamma }}}}\Delta {{\mbox{I}}}_{{{\rm{\gamma }}}}\left({{{\rm{\omega }}}}_{{k}_{i}}\right)\Delta {{\mbox{I}}}_{{{\rm{\gamma }}}}\left({{{\rm{\omega }}}}_{{k}_{j}}\right)}{\sqrt{{\sum }_{{{\rm{\gamma }}}}{\left[\Delta {{\mbox{I}}}_{{{\rm{\gamma }}}}\left({{{\rm{\omega }}}}_{{k}_{i}}\right)\right]}^{2}}\sqrt{{\sum }_{{{\rm{\gamma }}}}{\left[\Delta {{\mbox{I}}}_{{{\rm{\gamma }}}}\left({{{\rm{\omega }}}}_{{k}_{j}}\right)\right]}^{2}}},$$
(2)

where \(i,j\) denotes the wavelength index label in the same (spectrum) replica \({{\rm{\gamma }}}\), and \(\Delta {I}_{{{\rm{\gamma }}}}({{{\rm{\omega }}}}_{{k}_{i}})\) is defined as in Eq. (1), i.e., \(\Delta {I}_{{{\rm{\gamma }}}}({{{\rm{\omega }}}}_{{k}_{i}})={I}_{{{\rm{\gamma }}}}({{{\rm{\omega }}}}_{{k}_{i}})-{\bar{I}}_{{{\rm{\gamma }}}}({{{\rm{\omega }}}}_{{k}_{i}})\) is the intensity fluctuation, with \(\bar{I}({{{\rm{\omega }}}}_{{k}_{i}})\) representing the mean intensity at frequency \({{{\rm{\omega }}}}_{{k}_{i}}\), given by \(\bar{I}({{{\rm{\omega }}}}_{{k}_{i}})={\sum }_{{{\rm{\gamma }}}=1}^{{N}_{R}}{I}_{{{\rm{\gamma }}}}({{{\rm{\omega }}}}_{{k}_{i}})/{N}_{R}\). We note that in the overlap parameter \({q}_{{{\rm{\gamma }}}{{\rm{\beta }}}}\), Eq. (1), the sum is over wavelengths (or frequencies), while in the Pearson correlation coefficient \({C}_{{ij}}\), Eq. (2), the sum is over replicas. In this analysis, a positive (negative) value of \({C}_{{ij}}\) indicates that the fluctuations at a certain wavelength behave correlated (anticorrelated) to the fluctuations at a distinct wavelength of the same spectrum on average. Conversely, a nearly null \({C}_{{ij}}\) signals uncorrelated fluctuations. In the RSB regime, the distribution of \({C}_{{ij}}\) values becomes multi-modal, indicating the coexistence of distinct correlation patterns (e.g., some modes are strongly correlated while others are not). Therefore, one can identify clusters of highly correlated modes. The combined analysis of the intensity fluctuation overlap parameter (\({q}_{\gamma \beta }\)) (inter-replica correlations) and Pearson correlation coefficient \({C}_{{ij}}\) (intra-replica correlations) thus provides a powerful framework for identifying RSB in photonic systems (e.g., random lasers, complex waveguide arrays, or ultrafast lasers), manifested in the form of multiple metastable light configurations and persistent intensity fluctuations.

The evolution of the intensity profile of the recorded consecutive single-shot spectra over time is presented in the left column of Fig. 3. A single-shot spectrum captures only the instantaneous state at a given roundtrip, masking the underlying dynamical process. In contrast, analyzing a sequence of successive spectra exposes the temporal/spectral evolution of the system, unveiling soliton characteristic fluctuations.

Fig. 3: Experimental observation of replica symmetry breaking (RSB).
figure 3

a,d,g,j Evolution of consecutive single-shot spectra (replicas) recorded using DFT (top) and the change of the wavelength position of the maximum intensity of the spectra over roundtrips (bottom). b,e,h,k Distribution \(P\left(q\right)\) of values of the intensity fluctuation overlap parameter \({q}_{{{\rm{\gamma }}}{{\rm{\beta }}}}\). c,f,i,l Pearson coefficient \({C}_{i,j}\) calculated from the spectra of the Er-doped fiber laser. Each line represents a distinct regime (top to bottom): stable mode-locking (SML), period-2 pulsating mode-locking (PML), period-7 PML, and aperiodic PML.

Full size image

In the SML regime for a pump power of 50 mW, the spectra shown in Fig. 3a are stable, without relevant change in their intensity profile over time, and the wavelength position of the maximum intensity of the spectra (\(W{P}_{{I}_{max }}\)) remains unchanged. The very weak intensity fluctuations from replica to replica in the SML regime are consistent with the profile of the distribution \(P\left(q\right)\) shown in Fig. 3b, which displays a single pronounced maximum at \(q=0\) indicating RS behavior. However, unlike the photonic paramagnetic RS regime with modes oscillating incoherently and emission in the form of CW below the lasing threshold, the magnetic analog of the SML regime with RS and phase-locked modes oscillating coherently is the ferromagnetic phase, which is evidenced by the emission of femtosecond pulses in the time domain. This is corroborated by the heatmap of the Pearson coefficient \({C}_{{ij}}\) plotted in Fig. 3c, displaying a homochromatic area covering the wavelength range from 1545 nm to 1595 nm, signaling the correlated intensity fluctuations between distinct wavelengths in the same replica.

For a larger pump power of 65 mW (just above the first Hopf bifurcation at 63 mW in Fig. 2), the spectral intensity profile oscillates with a period twice the FRR (period-2 PML regime), evidenced by the change in \(W{P}_{{I}_{max }}\) in Fig. 3d. The change from replica to replica yields a double-peaked distribution \(P\left(q\right)\) in Fig. 3e that is strongly concentrated in the correlated (\(q=1\)) and uncorrelated (\(q=-1\)) overlap values. Following the above discussion, in this case all replicas present similar overlaps (either q = 1 or q = −1), with essentially null \(P\left(q\right)\) for q-values in between peaks. This characterizes a RS regime in the period-2 PML phase which is different from that of the SML phase. Accordingly, the heatmap of the Pearson correlation coefficient \({C}_{{ij}}\) shows crisscross patterns with red and green colors, indicating strong correlation and anti-correlation between wavelengths.

For an even higher pump power of 70 mW (between the first bifurcation and the onset of the aperiodic regime at 77 mW, see Fig. 2), a transition from period-2 PML to period-7 PML is observed, as shown in Fig. 3g. The corresponding distribution \(P\left(q\right)\) still presents two maxima around \(q=\pm 1\), but now we notice in Fig. 3h that q-values away from the side peaks start to occur with considerable probability. This is reasonable as the competition for gain of different modes in the spectrum is increased at higher pump powers. The larger variation of \(W{P}_{{I}_{max }}\) in this regime is captured by the somewhat less regular colored pattern of the heatmap \({C}_{{ij}}\) in Fig. 3i, if compared to Fig. 3f. This scenario is signaling that the RS regime of the period-2 PML phase is giving way to a RSB regime observed by further increasing the pump power.

Indeed, for a higher pump power of 89 mW, within the range of aperiodic PML and just below the threshold at 90 mW to the stable MPML regime, the spectral intensity profile changes drastically from roundtrip to roundtrip and the position of \(W{P}_{{I}_{max }}\) varies without periodicity, see Fig. 3j. The distribution \(P\left(q\right)\) shown in Fig. 3k still presents two maxima, although no longer strongly saturated near the extreme values q = ± 1, displaying the signature of a RSB regime. As for the Pearson coefficient \({C}_{{ij}}\), while correlated and anticorrelated regions are still evident in Fig. 3l, the emergence of larger black areas (null \({C}_{{ij}}\)) indicates a trend to the loss of correlation between intensity fluctuations at distinct wavelengths, consistent with the higher probability of small-q values in this aperiodic PML regime and the nearly random behavior of \(W{P}_{{I}_{max }}\) over time. Actually, when the system enters the stable MPML regime for even higher pump powers, the distribution \(P\left(q\right)\) becomes again single-peaked around q = 0, with RS profile as in the SML regime of Fig. 3b, and the heatmap of \({C}_{{ij}}\) becomes qualitatively similar to that of Fig. 3c.

At this stage, we can speculate that the RSB regime in the aperiodic PML phase, with phase-locked optical modes displaying full coherence, resembles a random-bond ferromagnetic state, rather than a RSB glassy phase with randomly oriented “frozen” spins. Notably, our system contains no intentional disorder. The emergence of RSB stems fundamentally from nonlinear intermodal interactions (competition for gain among modes) that generate intensity fluctuations22. In the aperiodic PML regime, the excessive nonlinearity tends to destabilize the mode-locking process, leading to pulse instability. This results in asymmetric energy transfer between modes. Some modes suppress others via gain depletion, establishing a dynamical competition in which only a subset of modes is activated at a given spectrum. Thus, each spectrum (replica) develops a distinct internal mode structure, manifesting as intensity fluctuations. The gain competition and intensity fluctuations mirror the RSB regime, in which identical experimental conditions nevertheless yield distinct pulse configurations.

We additionally show in Fig. 4 the plot of the loci \(q=\left|{q}_{max }\right|\) of points of maximum \(P\left(q\right)\) as a function of the pump power. We observe that \(\left|{q}_{max }\right|=0\) below 63 mW in the SML phase with RS, with a sharp transition to a region where \(\left|{q}_{max }\right|=1\). As discussed above, this region of pump powers between 63 mW and 89 mW corresponds in Fig. 2 to the interval between the first Hopf bifurcation to PML phases and the emergence of the stable MPML regime. According to Fig. 3, this region comprises both RS and RSB regimes. In particular, the onset of RSB at 77 mW coincides with the emergence of aperiodic pulsating solitons. A further transition to RS behavior with \(\left|{q}_{max }\right|=0\) occurs at the threshold value of 90 mW to the MPML regime, essentially a SML phase with multiple pulses. In this regime, the laser transitions to a mode-locked state supporting two pulses circulating infinitely within the cavity. Representative examples of stable two-pulse mode-locking at 100 mW and pulsating two-pulse mode-locking at 120 mW are presented, respectively, in Fig. S1c, d of the Supplementary Information. Lastly, for pump powers around 114 mW the second Hopf bifurcation takes place and the system enters a PML regime of multiple pulses in which \(\left|{q}_{max }\right|=1\), with features similar to those of the PML regime of a single pulse. The AC traces presented in Fig. 4b (for 55 mW) and 4(c) (for 70 mW) provide clear confirmation of single pulse operation.

Fig. 4: Map of the replica-symmetric (RS)-to- replica symmetry breaking (RSB) phase transition.
figure 4

a The loci \(q=\left|{q}_{\max }\right|\) of points of maximum \(P\left(q\right)\) against pump power, showing distinct photonic phases with RS or RSB regimes. b, c Autocorrelation traces (AC) in the stable mode-locking (SML) and pulsating mode-locking (PML) phases for 55 and 70 mW, respectively. In Fig. 4 a, dark-green regions denote SML regimes (single-pulse and multiple-pulses), whereas light-green regions denote PML regimes (single-pulse and multiple-pulses).

Full size image

To get insight into the physical mechanism underlying the occurrence of RSB in the PML regime, we employed a Michelson spectral interferometer to study the phase stability of the operating regimes42 (see the experimental setup in Supplementary Note 2 of the Supplementary Information). The coherence of pulses from every two consecutive roundtrips has been investigated. The superposition of two pulses with a delay time of \({{\rm{\tau }}}\) yields a spectral interference pattern, given by

$$I\left({{\rm{\omega }}}\right)=2{I}_{0}\left({{\rm{\omega }}}\right)\left[1+cos \left({{\rm{\omega }}}{{\rm{\tau }}}{{\rm{\phi }}}\right)\right],$$
(3)

where \({I}_{0}\left({{\rm{\omega }}}\right)={\left|{E}_{0}\left({{\rm{\omega }}}\right)\right|}^{2}\) denotes the optical spectrum intensity of one pulse and \({{\rm{\tau }}}\) is the pulse separation determining the period of interference fringes. A Fourier transform of \(I\left({{\rm{\omega }}}\right)\) yields the first-order AC function:

$$\Gamma \left({{{\rm{\tau }}}}^{{\prime} }\right)=2{P}_{0}+{P}_{0}{e}^{i{{\rm{\phi }}}}+{P}_{0}{e}^{-i{{\rm{\phi }}}},$$
(4)

where \({{{\rm{P}}}}_{0}\) represents the optical intensity of pulses and the second and third terms contain the information of pulse separation and relative phase difference between pulses. The procedure for extracting the pulse separation and phase difference can be found in ref. 43.

For pulses with phase coherence, spectral interferometric measurement yields the modulation on the spectrum. The validation of the DFT-based pulse-to-pulse phase coherence measurement is conducted by comparison of the modulated spectrum with the laser output spectrum in the SML regime at 50 mW, shown in Fig. S3 of the Supplementary Information. The expected spectral modulation with clear interference fringes across the whole spectrum can be identified, indicating the total pulse-to-pulse coherence in SML. We notice that the interference period is not evenly spaced due to the pulse chirp introduced in the fiber-based delay arm.

Remarkably, regardless of the operating regime, the spectral modulation fringes can be always observed in the interference spectra, as shown in the left column of Fig. 5, indicating the pulse-to-pulse coherence in both SML and PML regimes. Differences are that in the SML regime the fringes of the interference spectrum evolve stably without shifting their position, while in the case of the periodic PML regime interference spectra change from roundtrip to roundtrip, with the same periodicity as the evolution of the laser output spectra. For a clear demonstration, the middle column in Fig. 5 depicts the evolution of the AC trace and the right column shows the extracted pulse separation as a function of the roundtrips. We observe a stable evolution of the AC trace and a constant pulse separation in the photonic RS SML regime at 50 mW, a period-2 oscillation in the RS period-2 PML regime at 65 mW, and chaotic evolution at 89 mW in the aperiodic PML regime with RSB. To the best of our knowledge, these results build a connection between the emergence of RSB with the pulse interactions and explain the origin of the occurrence of RSB in the photonic aperiodic PML regime.

Fig. 5: Real-time characterization of phase stability of mode-locked pulses in different regimes.
figure 5

a–c replica-symmetric stable mode-locking (SML) at 50 mW, d–f replica-symmetric period-2 pulsating mode-locking (PML) at 65 mW, and g–i replica symmetry breaking aperiodic PML at 89 mW. Insets in (f) and (i) display the zoomed Autocorrelation traces (AC) traces for roundtrips 0–50.

Full size image

Discussion

We have performed a statistical analysis of pulsating solitons in ultrafast fiber lasers, revealing the emergence of photonic RSB behavior in a fully coherent regime – the aperiodic PML regime. The excessive accumulation of nonlinearity at high pump powers triggers a Hopf bifurcation, leading to the formation of pulsating solitons that evolve towards chaotic pulse behavior above a certain threshold value37. Unlike traditional RSB that arises from intrinsic disorder, there is no intentional disorder in the present laser system. Instead, the nonlinear interaction among modes leads to intensity fluctuations, playing a critical role in inducing the RSB22. Although experimental results have been obtained primarily by varying the pump power (suggesting deterministic behavior), we have also verified through repeated experiments that adjusting the PCs with other conditions fixed in the laser can produce qualitatively similar results as well. Indeed, altering the PC settings modifies the properties of the virtual saturable absorber and disrupts the gain-loss balance in the presence of dispersion and nonlinearity. Consequently, diverse stochastic nonlinear dynamics, including RSB, can emerge.

In addition, experimental results demonstrate the phase stability in the SML regime, periodic oscillation in the PML regime with periodic pulses, and chaotic evolution in the aperiodic pulsating regime (see also Fig. S4 in the Supplementary Information). These findings establish a connection between the dynamical evolution of the internal modes of pulses and an unobserved RSB regime in the aperiodic pulsating phase of passive mode-locked ultrafast lasers. The laser’s RS and RSB behaviors strongly depend on the dynamics of the excited modes in the replicas. In the stable SML regime the dominant modes of the mode-locked spectrum remain invariant over time, leading to a RS phase, while in the PML regime the change in the spectral intensity profile indicates the gain competition of excited modes. In particular, for stronger nonlinear interactions among modes in the chaotic aperiodic pulsating regime, the dominant modes in the replicas change from roundtrip to roundtrip, giving rise to a distribution of values of the intensity fluctuation overlap parameter with RSB profile. Also, the chirped pulses in the PML regime indicate a strong competition among modes, when compared to the pulses in the SML regime that are closer to the Fourier transform-limited pulses, contributing to the emergence of RSB in the highly nonlinear aperiodic PML regime.

To our knowledge, our work represents the first experimental report of the standard passive mode-locking regime with RSB predicted in the theoretical phase diagram of multimode photonic systems6. These findings establish a conceptual bridge between nonlinear photonics and statistical mechanics, revealing deep connections between mode-locked lasers and complex disordered systems, which opens several promising avenues for future research. For instance, the demonstration of RSB in the standard mode-locking regime implies that other driven-dissipation nonlinear systems, such as Kerr fiber resonators44, micro-resonators45,46, and spatial-temporal mode-locked lasers47, may host RSB when driven into chaotic or multimode states. Future work could leverage real-time measurement technology to uncover new RSB manifestations. Harnessing RSB in these platforms may offer a pathway to mitigate system disorder and enable precise control over coherence properties. This capability could prove invaluable for designing tailored laser sources or devices leveraging RSB with application-specific coherence requirements.

Moreover, studying RSB in the coherent pulsating regime of mode-locked lasers can also potentially deepen our understanding of complex systems physics. In lasers, pulsating regimes involve periodic or quasi-periodic intensity oscillations, sometimes exhibiting chaotic or stochastic switching. The dynamics of pulsating solitons is well described by the Ginzburg-Landau equations (GLE) or modified NLSE that incorporate additional effects, like damping, higher-order dispersion, or external potentials. Both GLE and modified NLSE apply to describe dissipative structure/pattern formation and phase transitions in other physical systems48, such as fluid dynamics, nonlinear optics, Bose-Einstein condensate, plasma physics, and magnetism. Studying such dynamics provides insights into phase transitions in these systems, linking physics to broader statistical mechanics. By bridging laser physics with statistical mechanics, research on RSB offers a pathway to uncovering universal principles governing complex systems phenomena.

In conclusion, we have reported the first experimental demonstration of the photonic RSB phenomenon in the aperiodic pulsating regime of a standard passive mode-locked ultrafast fiber laser. The identification of RSB is done by the distribution of the overlaps of pulse-to-pulse intensity fluctuations and Pearson correlation coefficient. The underlying mechanism of RSB in the aperiodic PML regime is studied by measuring the phase stability of pulses using a Michelson interferometric system, revealing a link between the internal dynamics of modes of pulses and the emergence of RSB. We hope these results can stimulate researchers to explore undisclosed novel manifestations of RSB in other classes of photonic systems, which will advance the understanding of complex systems behavior.

Methods

Details of the Er-doped ultrafast fiber laser and DFT measurements

The laser system for studying the RSB phenomenon is a standard Er-doped ultrafast fiber laser mode-locked by using the nonlinear polarization rotation (NPR) technology. It consists of a 1.42 m-long Erbium-doped gain fiber pumped by a 980 nm laser diode with a maximum power of 750 mW via a 980/1550 nm wavelength division multiplexer. The NPR is implemented by placing a polarization-dependent isolator in two PCs, providing an intensity-dependent transmission function, and acting as a virtual saturable absorber for initiating and stabilizing the mode-locking operation. Also, the isolator in the cavity ensures the unidirectional propagation of light. A 10:90 optical coupler outputs 10% of the intracavity energy for characterization and the remaining 90% of energy circulates infinitely in the cavity. The pigtails of all components are single-mode fibers (SMFs). Consequently, the laser operates in a normal dispersion regime. The net cavity dispersion is slightly normal, indicating the output pulse is similariton with a parabolic spectral intensity profile and linear pulse chirp. Details of the laser system are given in Table 1.

Table 1 Laser parameters
Full size table

Each replica considered in the RSB analysis is recorded through DFT. In principle, pulses propagating in a dispersive medium are stretched due to different group velocities for different frequency components. When the total dispersion provided by the dispersive medium is sufficient, the spectral intensity profile of the pulse is mapped to the stretched pulse intensity profile in the far field. That is to say, one pulse, one spectrum. In this way, one can detect and visualize the spectrum evolution in the temporal domain by connecting the stretched pulse signal to a digital oscilloscope via a photodetector. The spectral resolution of DFT is determined by the bandwidths of the digital oscilloscope and photodetector, as well as the total dispersion provided by the dispersive medium and the sampling rate is the frequency repetition rate of pulses. In the experiments, the bandwidths of the photodetector and oscilloscope are 35 and 20 GHz, respectively. The dispersive medium is an 18 km-meter-long SMF with a \(D\) parameter of −18 ps/km/nm. Therefore, the calculated spectral resolution of DFT is \(\Delta \lambda =\frac{1}{{DBL}}=0.16{nm}\), where \(B\) denotes the photodetector bandwidth and \(L\) is the SMF length.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.