Introduction

Transition metal dichalcogenides (TMDCs) are layered quasi-two-dimensional materials with physical properties spanning a wide range, from superconductivity to unique magnetic orders. Among them, TiSe2 stands out as an intriguing compound, exhibiting a periodic lattice distortion (PLD) characterized by a 2a × 2b × 2c superstructure below 202 K1,2,3,4,5,6. The origin of this structural transition has garnered particular attention in condensed matter physics, prompting extensive electronic structure studies through both theory and experiment7,8,9,10,11,12,13.

In its undistorted structural phase, TiSe2 is known as a semiconductor with an indirect bulk band gap between the valence and conduction bands at Γ and L-points, respectively11,12,14. The influence of PLD manifests as significant band folding between the Γ and M-points in the Brillouin zone. While a pronounced increase in the bulk band gap across the structural transition temperature is widely reported13,15,16, little to no change is observed in resistivity within the same temperature range. Instead, a broad maximum appears in the resistivity-versus-temperature curve around 165 K, superimposed on a metallic background4,17,18,19,20. This anomaly, however, remains unexplored, with only a few hypotheses proposed. Sample quality and the interplay between excitonic insulator and charge density wave phases are among the main considerations3,4,15,21. Recently, a crossover from incoherent to coherent electronic structure has also been associated with the transport anomaly, offering a new perspective on this long-standing puzzle22.

Anomalous resistivity behavior, reminiscent of that observed in TiSe₂, has also been reported in non-CDW materials such as ZrTe5 and HfTe523,24. Although these compounds lack charge density wave order, they exhibit similar temperature-dependent resistivity peaks. Band structure analyses suggest that such anomalies originate from a Lifshitz transition, wherein the Fermi surface topology changes from hole-like to electron-like as temperature decreases23,24. A comparable temperature-driven Fermi surface evolution has also been identified in ZrSiSe and WTe2, further corroborating the interpretation in terms of Lifshitz transitions25,26. By definition, a Lifshitz transition entails a topological change in the Fermi surface driven by continuous external parameters—such as temperature, pressure, or doping—without necessarily involving a symmetry-breaking phase transition27. In the case of TiSe₂, Hall effect measurements reveal a change in the dominant carrier type with temperature, supporting the presence of a Lifshitz transition3,4. More recently, theoretical modeling has successfully reproduced the resistivity anomaly in TiSe2 by invoking a crossover from electron-like carriers at low temperature to highly mobile hole-like carriers at higher temperatures28. Remarkably, this model accounts for the transport behavior without requiring the structural (CDW) transition, suggesting that the periodic lattice distortion and the resistivity anomaly may not be directly coupled.

Conventional angle resolved photoemission spectroscopy (ARPES) studies on TiSe2 are often limited by surface domain effects. Cleaved sample surfaces typically host multiple domains with slightly different crystallographic orientations, which introduce angular smearing in the photoemission signal. While this effect is minor in many cases, it becomes significant in the low-temperature distorted phase, where bands are closely spaced in energy and momentum. Resolving such subtle features—especially near the Fermi level—requires enhanced spatial resolution. This motivates the use of micro-ARPES (μ-ARPES) to obtain clearer insight into the reconstructed electronic structure.

Here, we report μ-ARPES measurements on TiSe2. At low temperatures, an electron pocket located at the Brillouin zone center dominates the density of states at the Fermi level. At higher temperatures, however, this electron-type band disappears, and hole-type valence band tip contributes non-negligible intensity to the Fermi level. Although the hole band does not fully cross the Fermi level at high temperatures, the thermally activated carriers and distinct transformation in spectral weight distribution constitute a change in Fermi surface topology consistent with a Lifshitz transition with an estimated critical temperature of 160 ± 5 K. Unlike the previous examples, the Lifshitz transition in TiSe2 results from the combined effects of band folding, temperature-induced energy shifts, and orbital-selective band renormalization—rather than a single-stage mechanism. Therefore, our observations naturally explain the resistivity anomaly in TiSe2 and deliver direct evidence of a Lifshitz transition in the electronic structure.

Results

Low temperature phase electronic structure

Fig. 1 presents series of ARPES spectra to demonstrates the folded electronic structure of TiSe2 due to PLD. For the guidance, three-dimensional Brillouin zone with high symmetry points are given in Fig. 1a. The experimental Fermi surface displays a circular feature centered at the \(\bar{M}\)-points, accompanied by small tails aligned along the \(\bar{\varGamma }\)-\(\bar{M}\) direction (Fig. 1b). A flower-shaped electron pocket, formed by folded conduction bands from \(M\)(\(L\)) to Γ(\(A\))-points, is also weakly visible at the zone center. The binding energy versus k|| data manifest the folded bands more clearly, as indicated in Fig. 1c. Highly dispersive bands below ~ 100 meV at the \(\bar{\varGamma }\)-point correspond to Se 4p-drived valence bands, which exhibit replicas at the \(\bar{M}\)-points due to PLD.

Fig. 1: Low temperature phase electronic structure.
figure 1

a Schematic representation of the hexagonal Brillouin zone with high symmetry points. b Experimental Fermi surface. c ARPES electronic structure along the \(\bar{M}\)-\(\bar{\Gamma }\) direction to experimentally illustrate the band folding. d, e ARPES electronic structures along the M-Γ-M and L-A-L directions, respectively. Orange rectangles mark the V-shape conduction band region. f ARPES electronic structure at the Γ-point, taken with a 6.3 eV laser source. g k|| versus kz map at the Fermi level. Yellow arrows indicate the two branches of V-shaped band at the opposite k|| points. h–j Photon energy and polarization dependent ARPES maps along the different k|| directions to identify components of the valence band. Black, pink, red, and dashed orange lines represents the different components of valence band to guide eyes. All the experimental data is taken at 50 K well below the structural transition temperature of 202 K.

Full size image

Additionally, a V-shaped electron type band, highlighted with dashed orange rectangles in Fig. 1d and 1e, reaches the Fermi level around the zone center. This observation is further validated by ARPES data obtained with a 6.3 eV laser source, which clearly resolves the V-shaped band (Fig. 1 f). Furthermore, this band exhibit a nearly two-dimensional nature with negligible dispersion along the kz direction, as observed in the kz versus k|| data taken at the Fermi level (Fig. 1g). Consequently, the low-temperature transport properties are expected to be controlled by this electron pocket.

To probe each component of the valence band, ARPES measurements are conducted using several photon energies with different polarization and momentum directions within the Brillouin zone. ARPES data obtained with 119 eV linearly vertical (LV) polarized light reveal two-hole bands, labeled VB2 and VB4 (Fig. 1h). Additionally, a band with a relatively flat tip, referred to as VB1, is observed using 95 eV circular left (CL) and 58 eV linearly horizontal (LH) polarized light along the M-Γ-M and \(\bar{K}\)-\(\bar{\varGamma }\)-\(\bar{K}\) directions, respectively. According to the data in Fig. 1i, VB1 exhibits a local minimum with slightly higher binding energy than VB2 at the zone center. Another band, VB3, marked with dashed orange curves in Fig. 1i and j, lies approximately 40 meV below VB2, with both bands displaying similar dispersion away from the zone center. It is important to note that kz dispersion results in slight binding energy differences between the Γ and A-points. Consequently, in the folded band structure, each band will be replicated with a small shift in binding energy. The observation of VB2 and VB3 with very similar dispersion can be attributed to this effect.

While a definitive assignment of orbital character typically requires polarization-dependent ARPES or detailed first-principles orbital projections, we infer that the VB1 band is primarily Se 4pz-derived (pz) based on two considerations: (1) photon-energy and polarization-dependent ARPES measurements that selectively enhance VB1 under conditions favorable to out-of-plane orbitals (Supplementary Fig. 1), and (2) consistency with prior DFT and experimental studies14,29,30 that identify the same feature as pz-dominated. We note that spin-orbit coupling, and spectral overlap complicate a more rigorous orbital analysis, and we emphasize the limitations of this assignment accordingly.

Temperature dependent electronic structure

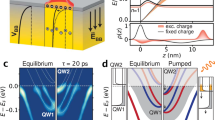
After defining the electronic structure of TiSe2 in the distorted phase, we shift our focus to temperature-dependent ARPES data. The evolution of band structure with temperature is investigated using 58 eV and 44 eV LH-polarized light along the \(\bar{K}\)-\(\bar{\Gamma }\)-\(\bar{K}\) direction (Fig. 2a and 2b), since VB1 and VB2 are well-resolved under these experimental conditions. As the temperature increases, significant band re-normalization is observed at the tip of VB1, highlighted by red curves in Fig. 2a. The flat dispersion of VB1 transitions into a downward parabolic dispersion at higher temperatures, resulting in the tip of VB1 shifting closer to the Fermi level at the \(\bar{\Gamma }\)-point. Concurrently, the V-shaped conduction bands become smeared out. The most significant changes are observed at a sample temperature of approximately 160 K. Beyond this point, the surface electronic structure remains largely stable. On the other hand, data collected with 44 eV LH-polarized light, which primarily resolves two branches of the valence band (VB2 and VB4), shows no discernible changes in dispersion character. This indicates that the observed temperature-dependent band re-normalization is orbital-selective, driving a transition from an electron-pocket to a hole-pocket Fermi surface as the sample is heated.

Fig. 2: Temperature dependence of the electronic structure.
figure 2

a, b ARPES spectra along \(\bar{K}\)-\(\bar{\Gamma }\)-\(\bar{K}\) and H-A-H directions as a function of temperature. Spectra are obtained with 58 eV LH and 44 eV LH lights, respectively. Red curves in (a) mark the band edge to guide eyes. c Temperature-dependent Fermi surface evolution at the \(\bar{\Gamma }\) point, showing the transition from an electron pocket at low temperature to hole-like spectral weight at higher temperatures, consistent with a Lifshitz transition.

Full size image

The evolution of the Fermi surface with increasing temperature is most clearly captured in the temperature-dependent Fermi surface maps (Fig. 2c). At low temperatures, the Fermi surface is characterized by a small electron pocket at the Brillouin zone center (\(\bar{\Gamma }\) point), indicative of electron-like carriers. As the temperature increases, this electron pocket progressively shrinks and eventually disappears, giving way to thermally populated states with hole-like character. This transformation reflects a qualitative change in the topology of the Fermi surface and is consistent with a temperature-induced Lifshitz transition. Furthermore, Constant energy cuts at different binding energies also reveal that when the sample temperature is below 160 K, the band structure evolves from electron pockets to hole pockets toward higher binding energies, whereas at temperatures above 160 K, only hole pocket features are observed. (Supplementary Figs. 2 and 3).

The temperature evolution of the band structure is further investigated using energy and momentum distribution curves (EDCs, MDCs). The EDCs, taken along the \(\bar{\Gamma }\) direction of the ARPES maps in Fig. 3a, show that the valence band edge is located approximately 100 meV below the Fermi level at lower temperatures. As the temperature increases, spectral weight at the Fermi level is populated by the tail of valence band, with the transition occurring around 160 K. This behavior is also corroborated by integrated MDCs around the Fermi level (Fig. 3b). The two-peaks arising from the electron pocket transitions into a single peak as the temperature increases. This observation also indicates that the Fermi level is dominated by the V-shaped conduction band at lower temperatures while it is crossed by the valence band edge at higher temperatures.

Fig. 3: Temperature evolution of electronic states at high-symmetry points.
figure 3

a Temperature dependent energy distribution curves (EDCs) taken at \(\bar{\Gamma }\) obtained from Fig. 3a. b Temperature dependent momentum distribution curves (MDCs) taken at the Fermi level from Fig. 3a. c Temperature dependent EDCs along the A-point obtained from (b).

Full size image

In contrast to visible change on the dispersion of VB1 and V-shaped conduction band, VB2 exhibits only shift of approximately 23 meV towards the Fermi level upon heating while its dispersion character remains the same (Fig. 3c). This energy shift, however, is more pronounced between 160 K and 200 K sample temperatures. On the other hand, it is insufficient to induce a significant overall change in the band structure. Thus, it can be concluded that the evolution of band structure as a function of temperature is primarily driven by the band re-normalization of VB1, which leads to the Lifshitz transition.

The observations collectively confirm that an electron pocket at the \(\bar{\Gamma }\)-point transforms into a hole-type band around 160 K upon heating. Although the hole band does not fully cross the Fermi level, thermal activation at higher temperatures allows the valence bands to dominate the transport properties28. Consequently, our temperature-dependent ARPES data reveal a Lifshitz transition occurring at the same temperature where a transport anomaly is observed in the resistivity of TiSe2 samples. Unlike previous examples, however, the band shift plays a secondary role in this transition, with orbital-selective band re-normalization serving as the primary mechanism.

Correlation between Lifshitz transition and PLD

The connection between the Lifshitz transition and periodic lattice distortion (PLD) in TiSe2 arises from the interplay between electronic correlations and structural modulations that reshape the band topology. In the normal state, ARPES measurements reveal a nearly semiconducting band structure, characterized by a narrow indirect gap between the valence band maximum at the Γ point and the conduction band minimum at the L point11,12,14. In contrast, standard DFT calculations predict a semimetallic ground state with significant band overlap (Fig. 4a).

Fig. 4: Theoretical modeling of the band structure.
figure 4

a, b Atomic orbital resolved electronic structure in the normal phase with Hubbard U term for 0 eV and 4.5 eV, respectively. c Folded band structure with U = 4.5 eV. K*, Γ*, and M* represent the high symmetry points in the Brillouin zone of the 2 ×2 x 2 distorted superstructure. d Distorted phase electronic structure as a function of U term.

Full size image

To reconcile this discrepancy, we introduce a Hubbard U term of 4.5 eV, which opens an indirect band gap of approximately 50 meV (Fig. 4b). The inclusion of on-site Coulomb interactions not only opens the gap but also increases the direct separation between conduction and valence bands at the Γ and A points, bringing the calculated dispersion into closer agreement with experiment.

Below the CDW transition temperature (~202 K), the emergence of PLD leads to Brillouin zone folding, superimposing the conduction and valence bands at high-symmetry points such as Γ and M (Fig. 4c). This folding introduces a narrow direct gap at Γ. As temperature increases, the band structure evolves: the conduction band at Γ moves below the Fermi level, while the upper branch of the valence band shifts to higher binding energies. This redistribution of spectral weight results in a change in Fermi surface topology, consistent with a Lifshitz transition.

To model this, we performed calculations across a range of U values (Fig. 4d). At U = 4.5 eV, the bulk band gap is large, and the valence band curvature at Γ resembles the experimental dispersion above 160 K, where the “Mexican-hat” profile transitions into a parabolic band. As U is reduced, the gap closes, leading to a semimetallic band structure. Notably, the upper valence band undergoes strong orbital-selective renormalization, while the lower valence states remain largely unaffected.

This variable-U approach provides a phenomenological framework to understand the temperature-dependent evolution of the experimental electronic structure within the CDW phase. At higher temperatures, thermal fluctuations suppress screening—particularly in semiconductors or poor metals—enhancing electronic localization and the effective on-site Coulomb repulsion. This leads to stronger electronic correlations and a larger effective U, consistent with the semiconducting band structure observed at elevated temperatures. As the system cools, carrier delocalization improves screening, reducing correlation effects and thereby lowering the effective U, resulting in a metallic band structure. Previous studies have also adopted finite U values to reproduce the high-temperature electronic structure of TiSe230,31. Thus, the variable U-term used here captures key elements of the insulator-to-metal crossover and supports the observed band renormalization behavior although it does not directly describe mechanism behind the evolution of the electronic structure.

These results indicate that the Lifshitz transition emerges not at the CDW onset itself, but as a consequence of PLD-enhanced correlation effects that drive a topological change in the electronic structure at lower temperatures (140–160 K). This explains why the transition is observed below the structural ordering temperature and highlights the critical role of electronic interactions in mediating the observed Fermi surface reconstruction.

Conclusion

In summary, we present a comprehensive μ-ARPES investigation of TiSe2, revealing the temperature-driven evolution of its electronic structure. Our measurements uncover a Lifshitz transition near 160 K, characterized by a transformation of the Fermi surface from an electron pocket to a hole-like feature at the zone center. This transition arises from a combination of periodic lattice distortion (PLD)-induced band folding and temperature-driven band shifts, which together lead to a progressive narrowing of the direct bulk band gap and a strong orbital-selective band renormalization.

First-principles DFT calculations incorporating a variable Hubbard U-term reproduce the key experimental trends. In particular, they show that only one component of the valence band—central to the observed Lifshitz transition—undergoes significant renormalization, evolving from a flat dispersion at low U to a pronounced upward curvature at higher U values, consistent with the experimental temperature dependence.

These findings provide a natural explanation for the anomalous behavior in transport and optical measurements around 160 K and establish a microscopic link between structural modulation, electronic correlation, and Fermi surface topology. Our work not only clarifies the origin of the resistivity anomaly in TiSe2 but also highlights the rich interplay of lattice and electronic degrees of freedom in driving emergent electronic phases.

Methods

Materials

Commercial single crystal 1T-TiSe2 samples are obtained from 2dsemiconductors.

Angle resolved photoemission spectroscopy

μ -ARPES experiments were conducted at 21-ID-1 (ESM) beamline of NSLS-II, BNL. The beamline is equipped with a DA30 Scienta electron spectrometer with deflectors enabling the Fermi surface mapping without moving the sample. Bulk TiSe2 crystals were mounted on Cu sample plate with silver epoxy and cleaved at vacuum better than 5×10-11 torr. Samples were cooled by a closed cycle He cryostat. The synchrotron radiation incidence angle was 55o. The electric field of the LV polarized light was parallel to the sample surface and analyzer slit while it was on the incident plane for LH polarized light.

The laser ARPES experiments were carried out with hv = 6.3 eV and R4000 Scienta electron spectrometer at the Research Institute for Synchrotron Radiation Science (HiSOR), Hiroshima University. The expected energy resolution was approximately 5 meV with ~10 μm incident photon beam spot diameter32.

Density functional theory

Plane-wave density functional theory as implemented in Quantum ESPRESSO package33,34 is used for electronic structure calculations, with Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation as the exchange-correlation functional35. Fullly relativistic norm-conserving pseudopotentials36,37 from Pseudo Dojo are used in the calculation. Crystal structure of the distorted TiSe2 is adopted from Reference 4. Plane wave and charge density kinetic energy cutoff of 80 and 320 Ry are used for wavefunction and charge density. 8 × 8 × 8 and 4 × 4 × 4 k mesh are used for sampling the Brillouin zone of the undistorted and distorted structure, respectively.