Electronic structures and multi-orbital models of La₃Ni₂O₇ thin films at ambient pressure

Abstract

The recent discovery of superconductivity with a transition temperature T_c exceeding 40 K in La₃Ni₂O₇ and (La, Pr)₃Ni₂O₇ thin films at ambient pressure marks a significant breakthrough in the field of nickelate superconductors. Using density functional theory (DFT), we propose a double-stacked two-orbital effective model for La₃Ni₂O₇ thin film based on the Ni − e_g orbitals. Our analysis of the Fermi surface reveals three electron pockets ($\alpha ,{\alpha }^{{\prime} },\beta$) and two hole pockets ($\gamma ,{\gamma }^{{\prime} }$), where the additional ${\alpha }^{{\prime} }$ and ${\gamma }^{{\prime} }$ pockets arise from inter-stack interactions. Furthermore, we introduce a high-energy model that incorporates O−p orbitals to facilitate future studies. Calculations of spin susceptibility within the random phase approximation (RPA) indicate that magnetic correlations are enhanced by nesting of the γ pocket, which is predominantly derived from the Ni$-{d}_{{z}^{2}}$ orbital. Our results provide a theoretical foundation for understanding the electronic and magnetic properties of La₃Ni₂O₇ thin films.

Introduction

The discovery of superconductivity in the Ruddlesden-Popper (RP) bilayer nickelate La₃Ni₂O₇ at a transition temperature T_c near 80 K under high pressure (~14 Gpa) has generated significant interest in the field of unconventional superconductivity¹. The subsequent observation of superconductivity in the trilayer nickelate La₄Ni₃O₁₀ under similar conditions further underscores the universality of superconductivity in nickelates². These discoveries have motivated extensive theoretical^{3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38} and experimental^{39,40,41,42,43,44,44,45,46} investigations into the microscopic mechanisms of unconventional superconductivity. However, the requirement of high pressure for superconductivity in La₃Ni₂O₇ and La₄Ni₃O₁₀ presents significant experimental challenges, which limit in-depth investigations. This has driven efforts to stabilize superconductivity under ambient pressure, facilitating a more comprehensive understanding of its underlying mechanisms.

Recent studies have reported superconductivity with T_c exceeding 40 K in La₃Ni₂O₇⁴⁷, (La, Pr)₃Ni₂O₇^48,49 thin films at ambient pressure, marking a significant breakthrough in nickelate superconductors. X-ray absorption spectroscopy (XAS) reveals that the Ni ions in La₃Ni₂O₇ thin film retain a mixed valence state similar to that of the bulk form⁴⁷. Furthermore, scanning transmission electron microscopy (STEM) confirms that their microscopic structure closely resembles that of the bulk phase of high pressure, adopting a tetragonal crystal structure⁴⁸. In particular, the T_c in the thin film is tunable via the in-plane lattice constant but remains relatively insensitive to the out-of-plane parameter. DFT calculation and angle-resolved photoemission spectroscopy (ARPES) measurement^50,51 suggest that Ni-${d}_{{x}^{2}-{y}^{2}}$ and Ni-${d}_{{z}^{2}}$ orbitals contribute states near the Fermi level, highlighting the similarity between the thin film and the bulk system in terms of electronic structure and superconducting properties. Despite these advances, most theoretical studies have relied on simplified half-unit-cell (Half-UC) slab model^52,53, which may not fully capture the effects of dimensionality on the electronic structure. A more comprehensive approach incorporating the full-unit-cell slab model is therefore needed to provide a more accurate description of this system.

In this paper, we employ slab models of La₃Ni₂O₇ thin films to investigate their electronic structures in various thicknesses, including three-unit-cell (Three-UC), one-unit-cell (One-UC), and Half-UC configurations. Except for the Half-UC case, each slab model retains a complete unit cell (UC), with the two bilayers denoted as Stack 1 and Stack 2, enabling a systematic exploration of the relationship between dimensionality and electronic properties. Using first-principles calculations, we propose a double-stacked two-orbital effective model for the One-UC slab structure, based on Ni −e_g orbitals. Our analysis reveals the presence of three electron pockets ($\alpha ,{\alpha }^{{\prime} },\beta$) and two hole pockets ($\gamma ,{\gamma }^{{\prime} }$) on the Fermi surface, where inter-stack interactions give rise to the additional ${\alpha }^{{\prime} }$ and ${\gamma }^{{\prime} }$ pockets. Furthermore, we extend our model by incorporating O−p orbitals into a high-energy framework to facilitate future studies. Spin susceptibility calculations within the RPA indicate pronounced magnetic correlations, primarily driven by nesting effects of the γ pocket, which is predominantly derived from the Ni$-{d}_{{z}^{2}}$ orbital. Our results provide a theoretical framework for understanding the interplay among the dimensionality, magnetism, and superconductivity in La₃Ni₂O₇ thin films, offering key insights for future theoretical and experimental investigations.

Results

Slab structures

We begin our investigation of the La₃Ni₂O₇ thin films by modeling the slab structures using DFT calculations. Bulk La₃Ni₂O₇ belongs to the n = 2 Ruddlesden-Popper phase, characterized by a UC comprising two corner-sharing NiO₆ octahedra bilayers stacking along the c axis¹. In its thin-film form, La₃Ni₂O₇ adopts a tetragonal structure similar to the high-pressure bulk phase, distinguished by an apical Ni-O-Ni bond angle approaching 180^∘47,54. To systematically explore the structural and electronic properties of La₃Ni₂O₇ thin films, we consider slab structures of varying thicknesses along the out-of-plane direction, including Three-UC, One-UC, and Half-UC slabs. To minimize interactions between periodic images, a vacuum spacing exceeding 16 Å is introduced along the c axis.

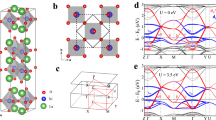
The One-UC slab consists of two stacked NiO₆ octahedra bilayers, which can adopt two distinct stacking configurations, Stack 1 and Stack 2, as illustrated in Fig. 1(a). In all slab models, we consider a free-standing geometry with a vacuum layer to eliminate inter-slab interactions. The effect of epitaxial strain from the substrate is incorporated by fixing the in-plane lattice constant to the experimentally measured value of a = 3.77Å⁴⁷. Although this approach does not capture all aspects of the experimental system—particularly in thicker films, where subtle differences between the top and bottom layers may occur—it provides a reasonable and reliable approximation for the few-layer systems considered in this study. The Ni-O bond lengths, labeled as d₁, d₂, d₃, d₄, and d₅ in Fig. 1(a), are summarized in Table 1 for different slab structures and effective Hubbard parameters (U_eff = 0 eV and U_eff = 2 eV). For clarity, only the bond distances of the middle UC are reported for the Three-UC slab structure.

Fig. 1: Slab structure and schematic illustration of the hopping parameters used in the La₃Ni₂O₇ thin-film model.

a The free-standing One-UC slab structure of La₃Ni₂O₇, where the two bilayers are labeled as Stack 1 and Stack 2. Green, gray, and red spheres denote La, Ni, and O atoms, respectively. The outer-apical (d₁ and d₄), inner-apical (d₂ and d₃), and in-plane (d₅) Ni-O bond lengths are indicated by black, red, and blue arrows, respectively. b Schematic illustration of the hopping parameters in the La₃Ni₂O₇ thin films, highlighting the Ni$-{d}_{{x}^{2}-{y}^{2}}$ (orange) and ${d}_{{z}^{2}}$ (blue) orbitals. Only nearest-neighbor hopping terms are shown.

Table 1 The Ni-O bond lengths (d) in NiO₆ octahedra of La₃Ni₂O₇ slab structures under U_eff = 0 eV and U_eff = 2 eV

For U_eff = 0 eV, the in-plane Ni-O bond (d₅) is the shortest, while the outer-apical Ni-O bonds (d₁ and d₄) are the longest, consistent with the high-pressure phase of La₃Ni₂O₇. Different slab structures yield nearly identical results in terms of bond lengths. In the Three-UC and One-UC slabs, d₁ and d₄ vary across stacking configurations, while d₂ and d₃ also exhibit stack-dependent variations, indicating symmetry breaking between different stacks. The Ni-O bond lengths in these slabs follow a specific symmetry relation: in Stack 1, d₁, d₂, d₃, d₄ correspond to d₄, d₃, d₂, d₁ in Stack 2. In contrast, the Half-UC slab exhibits a distinct structural behavior, characterized by Ni-O bond lengths that are symmetric about the central oxygen atom, differing from the asymmetric distortions observed in the other slab structures. This difference arises from the underlying structural symmetry. In Half-UC, the slab posesses m_z symmetry, with the mirror plane located between the two NiO layers. This symmetry enforces bond length equivalence with respect to the mirror plane, resulting in two nonequivalent vertical bond lengths. However, the One-UC and Three-UC slabs exhibit a different symmetry operation, $\{{m}_{z}| \frac{1}{2},\frac{1}{2},\frac{1}{2}\}$, where the mirror plane lies between two stacks. This symmetry allows for bond length variations within each individual stack, leading to distinct vertical bond lengths across the three stacks in the Three-UC slab, whereas only one stack exhibits such variations in the One-UC slab. This symmetry distinction is further reflected in the hopping parameters, influencing the electronic properties of the system.

For U_eff = 2 eV, electron correlation significantly influences the outer-apical Ni-O bond lengths (d₁ and d₄) in the Three-UC and One-UC slabs, whereas its effect is negligible in the Half-UC slab. Meanwhile, the in-plane Ni-O bond length (d₅) remains relatively stable in all configurations. These structural modifications are expected to have a pronounced impact on the electronic structures, which will be examined in detail in the following subsection. These findings highlight the critical role of interlayer interactions in determining the structural properties, which cannot be adequately captured by the Half-UC slab.

Electronic structures

We now investigate the electronic structures of La₃Ni₂O₇ thin films based on DFT calculations. For U_eff = 0 eV, the band structure and projected density of states (PDOS) of the One-UC slab exhibit a clear metallic character, as shown in Fig. 2a. The electronic states near the Fermi level (E_F) are primarily composed of Ni$-{d}_{{x}^{2}-{y}^{2}}$ and Ni$-{d}_{{z}^{2}}$ orbitals, which are well separated from the lower-energy Ni-t_2g orbitals. Moreover, these Ni−d orbitals exhibit hybridization with O−p orbitals within the energy range of  −2 eV to 2 eV. Due to interlayer hybridization, the Ni$-{d}_{{z}^{2}}$ electronic states form bonding and antibonding bands, located below and above E_F, respectively. Additionally, the La-derived states make minimal contributions to the electronic states at E_F. The electronic structures of the Three-UC slab exhibit a similar behavior to that of the One-UC slab, as shown in Supplementary Fig. 1(a). Notably, the reduced structural symmetry in thin films induces a splitting of Ni-${d}_{{z}^{2}}$ bonding bands along the M − Γ direction, leading to the formation of distinct electronic pockets near the M point [See Fig. 3(a)]. In contrast, the Half-UC slab, which retains higher structural symmetry, does not exhibit such splitting in the Ni-${d}_{{z}^{2}}$ bonding bands [see Fig. 2b].

Fig. 2: DFT-calculated band structures and partial density of states (PDOS) of La₃Ni₂O₇ thin films.

a and b correspond to calculations with U_eff = 0 eV, and c and d correspond to U_eff = 2 eV. The contributions from the Ni$-{d}_{{x}^{2}-{y}^{2}}$ and ${d}_{{z}^{2}}$ orbitals are highlighted in blue and red, respectively, while Ni − t_2g, O-p, and La states are represented in orange, green, and cyan, respectively. The Fermi level (E_F) is set to 0 eV. Here, U_eff denotes the effective hubbard parameter, and UC represents unit cell.

Fig. 3: DFT-calculated two-dimensional Fermi surfaces of La₃Ni₂O₇ thin films for different slab models.

a and c correspond to the One-UC structure, while b and d corresponds to the Half-UC structure. The upper panels show results obtained with U_eff = 0 eV, and the lower panels correspond to U_eff = 2 eV. Here, U_eff denotes the effective Hubbard parameter, and UC represents the unit cell.

For U_eff = 2 eV, the Ni$-{d}_{{z}^{2}}$ bonding bands shift downward and approach E_F. Consequently, the density of states of Ni$-{d}_{{z}^{2}}$ attains a maximum at E_F in the One-UC slab, as shown in Fig. 2c. A similar downward shift is observed in the electronic structure of the Three-UC slab, where the Ni$-{d}_{{z}^{2}}$ bonding bands move closer to E_F, as demonstrated in Supplementary Fig. 1b. This behavior corresponds to the metallization of the lower σ bonds in the high-presure phase of bulk La₃Ni₂O₇. These results indicate that the electronic structure of La₃Ni₂O₇ thin films closely resembles that of the high-pressure phase of the bulk material, which may provide insight into the emergence of high-temperature superconductivity in thin films. In contrast, the E_F in the Half-UC slab exhibits only a slight downward shift, as illustrated in Fig. 2d. Previous studies on bulk La₃Ni₂O₇ have reported that DFT calculations with U_eff = 3.5 eV yield results that are in good agreement with experimental observations³⁹. To further explore this, we also consider the case of U_eff = 3.5 eV. Under this condition, the Ni$-{d}_{{z}^{2}}$ bonding bands in the Three-UC and One-UC slabs shift further downward, moving below E_F, as shown in Supplementary Figs. 1c and 2a. However, in the Half-UC slab, E_F still crosses the Ni$-{d}_{{z}^{2}}$ bonding bands, as shown in Supplementary Fig. 2b.

Figure 3 presents the evolution of the Fermi surface in La₃Ni₂O₇ thin films under different slab configurations and Hubbard U_eff. Panels (a) and (c) correspond to U_eff = 0 eV, while panels (b) and (d) correspond to U_eff = 2 eV. For U_eff = 0 eV, the Fermi surface of the One-UC slab consists of three electron pockets ($\alpha ,{\alpha }^{{\prime} },\beta$) and two hole pockets ($\gamma ,{\gamma }^{{\prime} }$), as shown in Fig. 3a. Notably, the γ and ${\gamma }^{{\prime} }$ pockets are primarily derived from the Ni$-{d}_{{z}^{2}}$ orbital. The splitting of the Ni-${d}_{{z}^{2}}$ and Ni$-{d}_{{x}^{2}-{y}^{2}}$ states along the M − Γ and X − Γ directions gives rise to the additional ${\alpha }^{{\prime} }$ and ${\gamma }^{{\prime} }$ pockets. This splitting originates from inter-stack interactions induced by the reduced structural symmetry in thin films. In contrast, there are two electron pockets (α, β) and one hole pocket (γ) on the Fermi surface in the Half-UC slab, as shown in Fig. 3(b).

For U_eff = 2 eV, as the Ni$-{d}_{{z}^{2}}$ bonding bands in the One-UC slab shift downward and approach E_F, there is a significant reduction in the spatial extent of the hole pockets γ and ${\gamma }^{{\prime} }$ around the M point in the Brillouin zone, as shown in Fig. 3c. In contrast, the Fermi surface geometry in the Half-UC slab exhibits minimal changes, as depicted in Fig. 3d.

Two-orbital models

Based on the previous subsections, the thickness of the slab model significantly influences the Ni-O bond lengths, which in turn affect the electronic structure. Experimental samples typically have a thickness of One-UC–Three-UC, and calculations for the Three-UC slab are expected to more closely reflect the experimental conditions. However, due to the complexity of the Three-UC slab model, we have chosen to construct the tight-binding (TB) model using the One-UC slab, which captures the main features of the electronic band structure observed in the Three-UC slab. The Half-UC slab is also considered for comparison.

Building on the electronic structures obtained from our DFT calculations, we first focus on the double-stacked two-orbital model for the One-UC slab. This model incorporates the Ni$-{d}_{{x}^{2}-{y}^{2}}$ and Ni$-{d}_{{z}^{2}}$ orbitals within the framework of the maximally localized Wannier functions Hamiltonian. The total Hamiltonian is given by

$${{{\mathcal{H}}}} = {{{{\mathcal{H}}}}}_{0}+{{{{\mathcal{H}}}}}_{U},\\ {{{{\mathcal{H}}}}}_{0} = \sum\limits_{{{{\rm{k}}}}\sigma }{\Psi }_{{{{\rm{k}}}}\sigma }^{{{\dagger}} }H({{{\rm{k}}}}){\Psi }_{{{{\rm{k}}}}\sigma }.$$

(1)

Here ${{{{\mathcal{H}}}}}_{0}$ denotes the TB Hamiltonian derived from the Wannier downfolding procedure, while ${{{{\mathcal{H}}}}}_{U}$ represents the Coulomb interaction term⁵⁵.

The basis of the model is defined as ${\Psi }_{\sigma }={\left({d}_{1Ax\sigma },{d}_{1Az\sigma },{d}_{1Bx\sigma },{d}_{1Bz\sigma },{d}_{2Ax\sigma },{d}_{2Az\sigma },{d}_{2Bx\sigma },{d}_{2Bz\sigma }\right)}^{T}$, where the field operator d_sσ annihilates an electron in the state s with spin σ. The indices are assigned as follows: 1/2 label the stacked layers, A/B correspond to the bilayer sublattices, and x/z denote the ${d}_{{x}^{2}-{y}^{2}}$ and ${d}_{{z}^{2}}$ orbitals, respectively. The labeling convention is illustrated in Fig. 1(b).

The TB Hamiltonian H(k) takes the form

$$H({{{\rm{k}}}}) = \left(\begin{array}{cc}{H}^{1}({{{\rm{k}}}})&{H}^{12}({{{\rm{k}}}})\\ {H}^{12}({{{\rm{k}}}})&{H}^{2}({{{\rm{k}}}})\end{array}\right),\\ {H}^{1/2}({{{\rm{k}}}}) = \left(\begin{array}{cc}{H}_{A}^{1/2}({{{\rm{k}}}})&{H}_{AB}^{1/2}({{{\rm{k}}}})\\ {H}_{AB}^{1/2}({{{\rm{k}}}})&{H}_{B}^{1/2}({{{\rm{k}}}})\end{array}\right),\\ {H}_{A/B}^{1/2}({{{\rm{k}}}}) = \left(\begin{array}{cc}{H}_{A/B}^{1/2,x}({{{\rm{k}}}})&{H}_{A/B}^{1/2,xz}({{{\rm{k}}}})\\ {H}_{A/B}^{1/2,xz}({{{\rm{k}}}})&{H}_{A/B}^{1/2,z}({{{\rm{k}}}})\end{array}\right),\\ {H}_{AB}^{1/2}({{{\rm{k}}}}) = \left(\begin{array}{cc}{H}_{AB}^{1/2,x}({{{\rm{k}}}})&{H}_{AB}^{1/2,xz}({{{\rm{k}}}})\\ {H}_{AB}^{1/2,xz}({{{\rm{k}}}})&{H}_{AB}^{1/2,z}({{{\rm{k}}}})\end{array}\right).$$

(2)

The matrix elements are defined as follows:

$${H}_{A/B}^{1/2,x/z}({{{\rm{k}}}}) = 2{t}_{A/B,[1,0]}^{1/2,x/z}\left(\cos {k}_{x}+\cos {k}_{y}\right)\\ + 2{t}_{A/B,[2,0]}^{1/2,x/z}\left(\cos 2{k}_{x}+\cos 2{k}_{y}\right)\\ + 2{t}_{A/B,[3,0]}^{1/2,x/z}\left(\cos 3{k}_{x}+\cos 3{k}_{y}\right)\\ + 4{t}_{A/B,[1,1]}^{1/2,x/z}\cos {k}_{x}\cos {k}_{y}+{\epsilon }_{A/B}^{1/2,x/z},\\ {H}_{A/B}^{1/2,xz}({{{\rm{k}}}}) = 2{t}_{A/B,[1,0]}^{1/2,xz}\left(\cos {k}_{x}-\cos {k}_{y}\right)\\ + 2{t}_{A/B,[2,0]}^{1/2,xz}\left(\cos 2{k}_{x}-\cos 2{k}_{y}\right),\\ {H}_{AB}^{1/2,x/z}({{{\rm{k}}}}) = {t}_{AB,[0,0]}^{1/2,x/z}+2{t}_{AB,[1,0]}^{1/2,x/z}\left(\cos {k}_{x}+\cos {k}_{y}\right),\\ {H}_{AB}^{1/2,xz}({{{\rm{k}}}}) = 2{t}_{AB,[1,0]}^{1/2,xz}\left(\cos {k}_{x}-\cos {k}_{y}\right),\\ {H}_{AB}^{12,z}({{{\rm{k}}}}) = 4{t}_{AB}^{12,z}[\cos ({k}_{x}/2)\cos ({k}_{y}/2)].$$

Here ${H}_{A/B}^{1/2,x/z}({{{\rm{k}}}})$ and ${H}_{AB}^{1/2,x/z}({{{\rm{k}}}})$ describe intralayer and interlayer hopping within the same orbitals (${d}_{{x}^{2}-{y}^{2}}$ or ${d}_{{z}^{2}}$), respectively, while ${H}_{A/B}^{1/2,xz}({{{\rm{k}}}})$ and ${H}_{AB}^{1/2,xz}({{{\rm{k}}}})$ represent intralayer and interlayer hybridization between ${d}_{{x}^{2}-{y}^{2}}$ and ${d}_{{z}^{2}}$ orbitals. Additionally, ${H}_{AB}^{12,z}({{{\rm{k}}}})=4{t}_{AB}^{12,z}\cos ({k}_{x}/2)\cos ({k}_{y}/2)$ describes inter-stack hopping within the ${d}_{{z}^{2}}$ orbital, with a corresponding hopping parameter ${t}_{AB}^{12,z}=-0.025$. Hopping parameters for the One-UC slab model of La₃Ni₂O₇ thin film are summarized in Table 2.

Table 2 Hopping parameters for the One-UC slab model of La₃Ni₂O₇ thin films

For the single-stacked two-orbital model of the Half-UC slab, the system exhibits layer symmetry and the absence of inter-stack coupling, as characterized by the conditions H¹(k) = H²(k), H¹²(k) = 0, and ${H}_{A}^{1}({{{\rm{k}}}})={H}_{B}^{1}({{{\rm{k}}}})$. These conditions indicate that the Hamiltonians of the individual layers are identical, there is no direct coupling between the stacks, and the interfacial hopping parameters are equivalent for both sublattices. The corresponding hopping parameters for the Half-UC slab model of La₃Ni₂O₇ thin film are provided in Table 3.

Table 3 Hopping parameters for Half-UC slab model of La₃Ni₂O₇ thin films

Using the TB parameters listed in Tables 2 and 3, we present the resulting band structure and Fermi surface for both One-UC and Half-UC slabs. As shown in Fig. 4a, the model for the One-UC slab accurately reproduces the DFT band structure near the E_F. Notably, we observe a splitting of the Ni-${d}_{{z}^{2}}$ bonding bands along the M − Γ direction, which originates from inter-stack interaction, specifically ${t}_{AB}^{12,z}$. Regarding the Fermi surface, we identify three electron pockets $\alpha ,{\alpha }^{{\prime} },\beta$ and two hole pockets $\gamma ,{\gamma }^{{\prime} }$, as illustrated in Fig. 4c. The $\alpha ,{\alpha }^{{\prime} },\beta -{{{\rm{pocket}}}}$ exhibit mixed orbital character, while the $\gamma ,{\gamma }^{{\prime} }-{{{\rm{pockets}}}}$ are primarily dominated by the ${d}_{{z}^{2}}$ orbital state. Our results indicate that the electronic structure of La₃Ni₂O₇ thin film at ambient pressure closely resembles that of the high-pressure bulk phase. A key structural aspect is the in-plane lattice constant of the thin film, which is 3.77Å–large than the pseudo-tetragonal bulk value of 3.715Å. This lattice expansion may account for the lower T_c of the thin film compared to the bulk, suggesting that strain engineering could be a viable approach to enhancing T_c by further compressing the in-plane lattice constant. Furthermore, we note that the interlayer hopping amplitude ${t}_{AB,[00]}^{z}=-0.550$ is 1.19 times larger than the intralayer nearest-neighbor hopping ${t}_{1}^{x}=-0.462$. However, it remains 13.4% smaller than its bulk counterpart (${t}_{AB,[00]}^{z}=-0.635$). This reduction in interlayer coupling suggests a possible weakening of unconventional pairing in the thin film compared to the bulk.

Fig. 4: Band structures and Fermi surfaces of the two-obital models for La₃Ni₂O₇ thin films.

a and c correspond to the double-stacked two-orbital model for the One-UC slab, while b and d correspond to the single-stacked two-orbital model for the Half-UC slab. The color bar indicates the orbital weights, with red and blue represent ${d}_{{x}^{2}-{y}^{2}}$ and ${d}_{{z}^{2}}$, respectively. In a and b, the gray lines represent the DFT-calculated band structures with U_eff = 0 eV. The E_F is set to 0 eV. Here, U_eff denotes the effective Hubbard parameter, and UC represents the unit cell.

For the Half-UC slab model, no splitting in the Ni-${d}_{{z}^{2}}$ bonding bands (See Fig. 4b). Consequently, the Fermi surface consists of two electron pockets α, β and one hole pocket γ, as illustrated in Fig. 4d. Additionally, the interlayer hopping amplitude ${t}_{AB,[00]}^{z}=-0.503$ is 1.13 times larger than the intralayer nearest-neighbor hopping ${t}_{1}^{x}=-0.445$, yet it remains 21% smaller than its bulk counterpart. Notably, when we set ${t}_{AB}^{12,z}=0$, no splitting is observed in the band structure or the Fermi surface of the One-UC slab, as shown in Supplementary Fig. 3.

High-energy d p models

To incorporate the effects of O−p orbitals, we introduce high-energy dp models: a double-stacked eleven-orbital model for the One-UC slab (referred to as twenty-two-orbital model) and a single-stacked eleven-orbital model for the Half-UC slab (referred to as the eleven-orbital model). In both models, the basis for Stack 1 is given by $\Psi ={({d}_{Az},{d}_{Bz},{d}_{Ax},{d}_{Bx},{d}_{A{p}_{x}},{d}_{B{p}_{x}},{d}_{A{p}_{y}},{d}_{B{p}_{y}},{d}_{{p}_{z}},{d}_{{p}_{{z}^{{\prime} }}},{d}_{{p}_{{z}^{{\prime\prime} }}})}^{T}$, which includes four in-plane orbitals (p_Ax, p_Ay, p_Bx, p_By) and three apical orbitals (${p}_{z},{p}_{{z}^{{\prime} }},{p}_{{z}^{{\prime\prime} }}$), as illustrated in Supplementary Fig. 4. Here, A and B denote the bilayer sublattices.

The TB parameters of the twenty-two-orbital model are listed in Table 4, while those of the eleven-orbital model are provided in Table 5. Due to the symmetry between Stack 1 and Stack 2, only the parameters for Stack 1 are presented, and inter-stack hopping terms are not considered. Both models incorporate hopping interactions arising from pd, pp orbital overlaps. Based on the TB parameters, we present the resulting band structure and Fermi surface for both the One-UC and Half-UC slabs, as shown in Fig. 5. The resulting band structure in Fig. 5 covers an energy range akin to that of Fig. 4 and can also reproduce the main features at E_F. Furthermore, we find a hopping of 1.296 for the eleven-orbital model and of 1.304/1.105 for the twenty-two-orbital model between ${d}_{{z}^{2}}$ orbital and two apical ${p}_{{z}^{{\prime} }},{p}_{{z}^{{\prime\prime} }}$ orbitals, which are crucial in estimating effective interlayer ${d}_{{z}^{2}}$ spin exchange coupling. The high-energy models would provide a foundation for further investigations of magnetic exchange coupling and electronic correlations.

Table 4 TB parameters for Wannier downfolding of the twenty-two-orbital model

Table 5 TB parameters for the Wannier downfolding of the eleven-orbital model

Fig. 5: Band structures and Fermi surfaces of High-energy dp models including oxeygen orbitals for La₃Ni₂O₇ thin films.

a and c correspond to the eleven-orbital model for the Half-UC slab, while b and d correspond to the twenty-two-orbital model for the One-UC slab. The color bar indicates the orbital weights, with red and blue representing ${d}_{{x}^{2}-{y}^{2}}$ and ${d}_{{z}^{2}}$, respectively. In a and b, the gray lines represent the DFT-calculated band structures with U_eff = 0 eV. The E_F is set to 0 eV. Here, U_eff denotes the effective Hubbard parameter, and UC represents unit cell.

Spin susceptibility for two-orbital models

With the multi-orbital Hubbard model defined above, we investigate the magnetic response and Fermi surface nesting by calculating the spin susceptibility at the RPA level. Given that inter-stack hoppings are weak, we neglect them in our analysis. The resulting Fermi surface and energy bands in the absence of inter-stack hopping are provided in the Supplementary Fig. 3.

To better demonstrate the Fermi surface nesting relations associated with the bilayer structure, we define the even and odd magnetic susceptibilities as: χ^e/o = χ_∣∣ ± χ_⊥, with χ_∣∣ and χ_⊥ representing intralayer and interlayer contributions, respectively. The definitions and computational details are available in the Methods section. Physically, it is easily proved that the χ^e originates from nestings within the bonding (α, γ) and within the antibonding (β) bands, while χ^o originates solely from nestings between the bonding and antibonding bands⁵⁶.

Figure 6 presents the static RPA spin susceptibility χ^e/o(q, ω = 0) for the double-stacked two-orbital model, computed with U = 0.7 eV, J_H = 0.2 eV, and temperature T = 0.1K. In the even channel, we observe a strong response near the X point, indicating nesting within the γ pocket, along with additional nesting within the β pocket. In the odd channel, nesting is evident between the β and γ pockets, as well as between the α and β pockets.

Fig. 6: RPA spin susceptibilities of even and odd channel, and illustration of Fermi surfaces nesting in the double-stacked two-orbital model.

a and b show the even channel (χ^e) and odd channel (χ^o) susceptibilities for the double-stacked two-orbital model, respectively, calculated with intraorbital Coulomb interaction U = 0.7 eV and Hund’s coupling J_H = 0.2 eV at a temperature T = 0.1K. c and d depict the Fermi surfaces, where red arrows indicating the nesting vectors.

Figure 7 presents the spin susceptibility for the single-stacked two-orbital model, calculated using U = 0.8 eV, J_H = 0.2 eV and T = 0.1K. The Fermi surface nesting patterns in the odd channel closely resemble those of the double-stacked model. In the even channel, nesting primarily occurs within the γ and β pockets, whereas in the odd channel, significant nesting is observed between the γ and β pockets, as well as between the α and β pockets. The observed differences in χ^e/o between the double-stacked and single-stacked models can be attributed to their distinct Fermi surface geometries.

Fig. 7: RPA spin susceptibility of even and odd channel, and illustration of Fermi surfaces nesting in the single-stacked two-orbital model.

a and b show the even channel (χ^e) and odd channel (χ^o) susceptibilities for the single-stacked two-orbital model, respectively, calculated with intraorbital Coulomb interaction U = 0.8 eV and Hund’s coupling J_H = 0.2 eV at a temperature T = 0.1K. c and d present the Fermi surfaces, where red arrows indicate the nesting vectors.

Methods

First-principles calculations

Our first-principles calculations are performed using the DFT as implemented in the Vienna ab initio simulation package (VASP)^57,58. The exchange-correlation interactions are treated within the generalized gradient approximation (GGA) using the Perdew-Burke-Ernzerhof (PBE) functional⁵⁹. The projector augmented-wave (PAW) method⁶⁰ is employed with a plane-wave cutoff energy of 600 eV. Structural relaxation and electronic self-consistent calculations are conducted on a Γ-centered 12 × 12 × 1 k − points mesh using the Monkhorst-Pack scheme, while a denser k − points grid of 27 × 27 × 1 is used for Fermi surface calculations. The atomic positions are fully relaxed until the residual forces on each atom are less than 0.005 eV/Å, and the electronic self-consistency convergence criterion is set to 10⁻⁶ eV. The optimized atomic coordinates are provided in Supplementary Data 1 and 2 for the Half-UC structure with U_eff = 0 and 2 eV, respectively, and in Supplementary Data 3 and 4 for One-UC structure with U_eff = 0 and 2 eV, respectively.

To construct effective models, maximally localized Wannier functions are obtained using the Wannier90 code^61,62,63. For DFT  + U calculations⁶⁴, an effective Hubbard U_eff is applied to the Ni 3d orbitals.

Hamiltonian of high-energy d p models

For the twenty-two-orbital model, we do not consider the hoppings between orbitals in different stacks. So the Hamiltonian of the twenty-two-orbital model takes the same form as the one for the eleven-orbital model. Here we show the TB Hamiltonian for high-energy dp models³. The basis here is $(A{d}_{z},B{d}_{z},A{d}_{x},B{d}_{x},A{p}_{x},B{p}_{x},A{p}_{y},B{p}_{y},{p}_{z},{p}_{{z}^{{\prime} }},{p}_{{z}^{{\prime\prime} }})$. The position of these orbitals can be seen in Supplementary Fig. 4. Her,e we show the elements of Hamiltonian H(α, β)

$$\begin{array}{r}H(1,9)={t}^{A{d}_{z},{p}_{z}},H(2,9)={t}^{B{d}_{z},{p}_{z}},H(1,10)={t}^{A{d}_{z},{p}_{{z}^{{\prime} }}},H(2,11)={t}^{B{d}_{z},{p}_{{z}^{{\prime\prime} }}},\\ H(3,5)=-2{{{\rm{i}}}}{t}^{A{d}_{x},A{p}_{x}}\sin (0.5{k}_{x}),\quad H(3,7)=-2{{{\rm{i}}}}{t}^{A{d}_{x}-A{p}_{y}}\sin (0.5{k}_{y}),\\ H(4,6)=-2{{{\rm{i}}}}{t}^{B{d}_{x},B{p}_{x}}\sin (0.5{k}_{x}),\quad H(4,8)=-2{{{\rm{i}}}}{t}^{B{d}_{x}-B{p}_{y}}\sin (0.5{k}_{y}),\\ H(1,5)=-2{{{\rm{i}}}}{t}^{A{d}_{z},A{p}_{x}}\sin (0.5{k}_{x}),\quad H(1,7)=-2{{{\rm{i}}}}{t}^{A{d}_{z}-A{p}_{y}}\sin (0.5{k}_{y}),\\ H(2,6)=-2{{{\rm{i}}}}{t}^{B{d}_{z},B{p}_{x}}\sin (0.5{k}_{x}),\quad H(2,8)=-2{{{\rm{i}}}}{t}^{B{d}_{z}-B{p}_{y}}\sin (0.5{k}_{y}),\\ \hskip 9pc H(5,7)=4{t}^{A{p}_{x}-A{p}_{y}}\sin (0.5{k}_{x})\sin (0.5{k}_{y}),\\ \hskip 9pcH(6,8)=4{t}^{B{p}_{x}-B{p}_{y}}\sin (0.5{k}_{x})\sin (0.5{k}_{y}),\\ H(5,9)=-2{{{\rm{i}}}}{t}^{A{p}_{x},{p}_{z}}\sin (0.5{k}_{x}),\quad H(7,9)=-2{{{\rm{i}}}}{t}^{A{p}_{y},{p}_{z}}\sin (0.5{k}_{y}),\\ H(6,9)=-2{{{\rm{i}}}}{t}^{B{p}_{x},{p}_{z}}\sin (0.5{k}_{x}),\quad H(8,9)=-2{{{\rm{i}}}}{t}^{B{p}_{y},{p}_{z}}\sin (0.5{k}_{y}),\\ H(5,10)=-2{{{\rm{i}}}}{t}^{A{p}_{x},{p}_{{z}^{{\prime} }}}\sin (0.5{k}_{x}),\quad H(7,10)=-2{{{\rm{i}}}}{t}^{A{p}_{y},{p}_{{z}^{{\prime} }}}\sin (0.5{k}_{y}),\\ H(6,11)=-2{{{\rm{i}}}}{t}^{B{p}_{x},{p}_{{z}^{{\prime\prime} }}}\sin (0.5{k}_{x}),\quad H(8,11)=-2{{{\rm{i}}}}{t}^{B{p}_{y},{p}_{{z}^{{\prime\prime} }}}\sin (0.5{k}_{y}).\end{array}$$

(3)

The elements H(β, α) can be obtained by H(β, α) = H(α, β)^*. The diagonal elements are site energies which can be found in Tables 4 and 5.

Calculation of spin susceptibility

Upon determining the hopping parameters of the TB models and incorporating electron interactions, we construct a multi-orbital Hubbard model as Eq. (1) without considering hoppings between two stacks.

$${{{{\mathcal{H}}}}}_{U} = U\sum\limits_{is}{n}_{is\uparrow }{n}_{is\downarrow }\\ + ({U}^{{\prime} }-{J}_{H}{\delta }_{\sigma {\sigma }^{{\prime} }})\sum\limits_{i\sigma {\sigma }^{{\prime} }}({n}_{iAx\sigma }{n}_{iAz{\sigma }^{{\prime} }}+{n}_{iBx\sigma }{n}_{iBz{\sigma }^{{\prime} }})\\ + {J}_{H}\sum\limits_{i\sigma }{\sum}_{\mu }^{A,B}\left({d}_{i\mu x\sigma }^{{{\dagger}} }{d}_{i\mu z\bar{\sigma }}^{{{\dagger}} }{d}_{i\mu x\bar{\sigma }}{d}_{i\mu z\sigma }\right.\\ + \left.{d}_{i\mu x\sigma }^{{{\dagger}} }{d}_{i\mu x\bar{\sigma }}^{{{\dagger}} }{d}_{i\mu z\bar{\sigma }}{d}_{i\mu z\sigma }+h.c.\right).$$

(4)

The TB Hamiltonian ${{{{\mathcal{H}}}}}_{0}$ is expressed with the basis Ψ_σ = (d_Axσ, d_Azσ, d_Bxσ, d_Bzσ), where d_sσ is the annihilation operator for an electron in the state s = (Ax, Az, Bx, Bz) with spin σ. The interaction parameters include U (intraorbital Coulomb interaction), ${U}^{{\prime} }$ (interorbital Coulomb interaction) and J_H (Hund’s coupling). Kanamori relation is applied here, given by ${U}^{{\prime} }=U-2{J}_{H}$⁵⁵.

In general, the bare (non-interaction) susceptibility is defined as

$$\begin{array}{c}{\chi }_{\alpha \beta \gamma \delta }^{0}({{{\rm{q}}}},\omega )=-\frac{1}{{N}_{{{{\rm{k}}}}}}\sum\limits_{{{{\rm{k}}}},mn}\frac{{f}_{F}({\varepsilon }_{{{{\rm{k}}}}}^{m})-{f}_{F}({\varepsilon }_{{{{\rm{k}}}}+{{{\rm{q}}}}}^{n})}{{{{\rm{i}}}}\omega +{\varepsilon }_{{{{\rm{k}}}}}^{m}-{\varepsilon }_{{{{\rm{k}}}}+{{{\rm{q}}}}}^{n}}\\ {U}_{\delta m}({{{\rm{k}}}}){U}_{\alpha m}^{* }({{{\rm{k}}}}){U}_{\beta n}({{{\rm{k}}}}+{{{\rm{q}}}}){U}_{\gamma n}^{* }({{{\rm{k}}}}+{{{\rm{q}}}}).\end{array}$$

(5)

with the band indices m, n and the Fermi-Dirac distribution function ${f}_{F}({\varepsilon }_{{{{\bf{k}}}}})=1/({{{{\rm{e}}}}}^{{\varepsilon }_{{{{\bf{k}}}}}/T}+1)$. The matrix element U_δm(k) represents the eigenvector connecting orbital δ and band m at wave vector k. At the RPA level, the spin channel interaction vertex is defined as

$${\Gamma }_{\alpha \beta \gamma \delta }^{m}=\left\{\begin{array}{ll}U\quad &\alpha =\beta =\gamma =\delta ,\\ {U}^{{\prime} }\quad &\alpha =\delta \ne \beta =\gamma ,\\ {J}_{H}\quad &\alpha =\beta \ne \gamma =\delta ,\\ {J}^{{\prime} }\quad &\alpha =\gamma \ne \beta =\delta .\end{array}\right.$$

(6)

Here pair hopping ${J}^{{\prime} }$ satisfies ${J}^{{\prime} }={J}_{H}$. The RPA spin susceptibility is then computed in a matrix-product form as

$${\chi }_{(\alpha \beta ,\delta \gamma )}^{S}={\left[I-{\chi }^{0}{\Gamma }_{(\alpha \beta ,\delta \gamma )}^{m}\right]}^{-1}{\chi }_{(\alpha \beta ,\delta \gamma )}^{0}.$$

(7)

Considering the bilayer structure of La₃Ni₂O₇, the interlayer hopping terms in the Hamiltonian acquire a phase factor of ${{{{\rm{e}}}}}^{{{{\rm{i}}}}{k}_{z}}$ due to the k_z − dependence. Here, k_z can take values of either 0 or π. When contracting the orbital indices to compute the spin susceptibility, we define the in-plane and interlayer susceptibilities as χ_∣∣ = ∑_αβ(χ_AαAβ + χ_BαBβ) and χ_⊥ = ∑_αβ(χ_AαBβ + χ_BαAβ), where χ_αβ = χ_ααββ with orbital indices contracted. For k_z = 0, the phase factor eⁱ⁰ = 1, and the spin susceptibility is given by χ^e = χ_∣∣ + χ_⊥. Conversely, for k_z = π, the phase factor e^iπ = − 1, leading to a spin susceptibility of χ^o = χ_∣∣ − χ_⊥. In the even channel χ^e, Fermi surface nesting which occurs within the bonding/antibonding bands is evident, including the α−α, α−γ, γ−γ and β−β nesting features. In the odd channel χ^o, nesting between bonding and antibonding bands can be observed clearly, such as γ−β, α−β⁵⁶.

Discussion

Our DFT calculations of the thin-film bilayer nickelate superconductors have overall predicted that the electronic structure closely resembles the bulk one under pressure, which strongly suggests that they are all within the same superconducting mechanism. We note another key aspect to validate this idea, which is the superexchange strength. For the bulk samples, the vertical superexchange between two half-filling ${d}_{{z}^{2}}$ orbitals ${J}_{\perp }^{z}$ is widely believed to be the origin of the superconducting condensation^6,7. Here, our TB models for the La₃Ni₂O₇ thin-film also allow an estimation of the corresponding strengths, which are decreased by  ~36% and  ~24% for single-stacked and double-stacked bilayer nickelates with respect to the pressurized bulk³, assuming ${J}_{\perp }^{z} \sim {({t}^{z})}^{2}$. The asymptotic decrease of ${J}_{\perp }^{z}$ with slab number from our estimation is in line with the notable decrease of T_c from bulk to film as observed in experiments^47,48, which again reinforces the above general understanding. More profoundly, the consistency indicates an expansion of the available experimental techniques for reaching the core of the superconducting mechanism in RP nickelates. This is particularly helpful as the exploration of bulk is largely constrained by the exerted pressure. Regarding the role of pressure, on the other hand, the existing evidence on thin-film is also prone to the idea that pressure can help suppress the spin density wave, after which the superconducting order is thus exposed. Whereas for the thin-film, due to the higher stability and sniffiness of the SrLaAlO₄ substrates, ${{{{\rm{L{a}}}_{3}N{i}_{2}O}}}_{{{{\rm{7}}}}}$ the lattice is strongly confined to the I4/mmm symmetry without in-plane distortion, which can further prevent the occurrence of density waves^47,48.

On the other hand, it is worth noting that the structural differences between the One-UC and Half-UC slab models–particularly the presence of inter-stack geometry in the One-UC case–lead to more three-dimensional electronic characteristics. In particular, the enhanced interlayer coupling in the One-UC structure gives rise to noticeable out-of-plane (k_z) direction. This suggests that such k_z-dependent features may be experimentally observable in future high-resolution ARPES measurements, providing an additional means to probe the dimensionality and electronic reconstruction in La₃Ni₂O₇ thin films.

We note that both experimental and theoretical studies have reported differing results regarding the Fermi surface topology. While Ref. ⁶⁵ reports a lowering of the ${{{\rm{Ni}}}}-{{{{\rm{d}}}}}_{{z}^{2}}$ states under compressive strain, an independent group has observed a ${{{{\rm{d}}}}}_{{z}^{2}}$-derived γ-pocket at the Fermi level in La₂PrNi₂O₇ thin films, accompanied by a measurable superconducting gap on this pocket^50,51. These contrasting observations suggest that the presence or absence of the γ-pocket may be sample-dependent, potentially influenced by factors such as oxygen stoichiometry or subtle strain variations. On the theoretical side, previous studies^66,67 examined the effect of biaxial strain on bulk nickelates and found that compressive strain tends to increase the apical Ni-O-Ni bond angle toward 180^∘, consistent with structural features of the high-pressure phase. Other works^68,69, adopting the lower-pressure Amam phase as a reference and employing DFT  + U methods, reported the emergence of ${{{{\rm{d}}}}}_{{z}^{2}}$-derived pockets at the Fermi surface under tensile strain. It is well established that the calculated electronic structure of La₃Ni₂O₇ is highly sensitive to the choice of the Hubbard U_eff parameter (see Supplementary Fig. 1). We anticipate that future experimental studies will help resolve these discrepancies and clarify the microscopic origin of the observed differences.

Conclusion

In conclusion, we employ slab models for La₃Ni₂O₇ thin films that simulate the electronic structure for various thicknesses, including Three-UC, One-UC, and Half-UC. Each slab model incorporates a full unit cell, with the two bilayers referred to as Stack 1 and Stack 2, enabling a detailed examination of the interplay between dimensionality and electronic behaviors. Using density functional theory, we propose a double-stacked two-orbital effective model of La₃Ni₂O₇ thin films, based on the Ni−e_g orbitals. Our analysis reveals the presence of three electron pockets $\alpha ,{\alpha }^{{\prime} },\beta$ and two hole pockets $\gamma ,{\gamma }^{{\prime} }$ on the Fermi surface, where the additional pockets ${\alpha }^{{\prime} }$ and ${\gamma }^{{\prime} }$ emerge due to inter-stack interactions. Furthermore, we introduce high-energy models incorporating O−p orbitals to facilitate future studies. Spin susceptibility calculations within the RPA indicate pronounced magnetic correlations primarily driven by nesting effects of the γ pocket, which is predominantly contributed by the Ni$-{d}_{{z}^{2}}$ orbital state. Our results provide theoretical framework for understanding the interplay among dimensionality, magnetism, and superconductivity in La₃Ni₂O₇ thin films, offering key insights for future theoretical and experimental research.