Introduction

Skyrmions are a special type of quasiparticle that exhibit distinct vector structures and are characterized by topological protection. Proposed by the British particle physicist Tony Skyrme in the 1960s, the concept was developed to characterize the topological structure of nucleons1. Subsequently, this archetypal structure has been identified in a variety of other contexts, including magnetic materials2,3,4,5,6,7,8,9, liquid crystals10,11,12,13, quantum Hall effect systems14, acoustics15, and twistronics16. Particularly noteworthy are magnetic skyrmions due to their ultra-small dimensions and topological stability, which open new avenues for next-generation high-density magnetic storage and logic operation devices17,18,19,20.

In recent years, with the rapid development of topological photonics, optical skyrmions have been successively discovered and reported by the research teams of Tsesses21 and L. Du22. Since then, various types of two-dimensional (2D) optical skyrmions have been discovered in different optical systems, such as electromagnetic field21,22,23,24,25,26,27, spin28,29, Stokes30,31,32,33,34,35,36, pseudospin37,38,39, and Poynting vector skyrmions40. When 2D optical skyrmionic beams propagate in free space, they possess a specific type of topological stability, during which the topological structure of the vector field can evolve from a Bloch type to a Néel type while maintaining an unchanged topological number41,42. However, in the case of antiskyrmions, the vector field does not undergo changes during propagation, and the topological number remains unchanged43. This phenomenon stems from the fact that the orbital angular momentum of the two orthogonal eigenmodes remains invariant during propagation. Therefore, the polarization texture structure and the skyrmion number of the superimposed fields are preserved, which leads to the mutual transition of Bloch-type and Néel-type skyrmions with the same polarization texture structure, while anti-skyrmions and other states that have completely different skyrmion numbers cannot undergo transition upon light propagation. Optical skyrmions have demonstrated significant application potential in fields such as precision measurement44, high-security information encryption45, and optical communications46, owing to their unique topologically protected properties, subwavelength features, and topological diversity. To further advance these applications, it is crucial to address the key challenge of achieving arbitrary and dynamically configurable generation of skyrmions in free space.

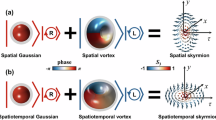
Here, we propose an approach to generate optical skyrmion beams capable of arbitrary configuration by overcoming the barrier of topological number transition during propagation in free space. Since 2D optical skyrmions are special vector projection textures from S2 Poincaré sphere to R2 plane, as shown in Fig. 1a, Bloch, Néel, and anti-type skyrmionic beams are Poincaré beams with lemon and star structured polarization patterns47, which can be achieved as a superposition of a vortex eigenmode and a non-vortex eigenmode with orthogonal polarizations. Therefore, by precisely modulating the longitudinal profiles of these components48,49, we propose and demonstrate arbitrary transitions of topological state and skyrmion number within skyrmionic beams during propagation in free space. As shown in Fig. 1b, the skyrmionic beam presents quasi-nondiffraction intensity profile, but the Stokes skyrmion orderly changes from Bloch to Néel and anti types, with the transitions of skyrmion number Q from −1 to 1. The controllability of topological number transitions provides additional degrees of freedom for information encoding and processing50,51,52.

Fig. 1: Schematic illustration of topological states and number transitions.
figure 1

a Constructing different 2D skrymions by vector projections from S2 Poincaré sphere to R2 plane. And polarization distributions of 2D skyrmionics beams corresponding to three skyrmion types, namely, the Poincaré beams. Ellipse: polarization ellipticity; Red: left hand; Blue: right hand. b The schematic of 2D Stokes skyrmion and skyrmion number transitions upon the propagation of a skyrmionic beam.

Full size image

Results and discussion

Experimental setup

We use the experimental setup shown in Fig. 2 to generate the desired 2D optical skyrmions. Linearly polarized light (λ = 532 nm) is expanded and collimated by the beam expander system composed of L1 and L2, and then passes through a half-wave plate (HWP). The horizontally polarized light transmitted through the polarizing beam splitter (PBS) illuminates the spatial light modulator (SLM1, HOLOEYE, Pluto, 1920 × 1080), which displays a computer-generated hologram (CGH) to produce the desired longitudinal modulation of the horizontal polarization component. The vertically polarized light reflected by the PBS is modulated by another HWP before illuminating SLM2, which also displays a CGH to generate the desired longitudinal modulation of the vertical polarization component. Two modulated beams are reflected back to the PBS, where they are combined coaxially. This combined beam passes through a 4 f filtering system composed of lenses L3 and L4, which filter out the +1 order. Finally, a quarter-wave plate (QWP1) is used to convert the horizontal and vertical polarizations into LCP and RCP, respectively. QWP2, polarizer, and CMOS camera constitute a Stokes parameter measurement system. A CMOS camera (Basler, acA2040, 2048 × 2048 pixels), mounted on a linear translation stage, is positioned near the back focal plane of the 4 f filtering system to observe the output field. The CGHs loaded on SLM1 and SLM2 are shown as insets.

Fig. 2: Experimental setup for generating 2D skyrmionics beams with a variant topological state and number along the propagation path.
figure 2

L, lens; HWP, half-wave plate; QWP, quarter-wave plate; PBS, polarizing beam splitter; SLM, spatial light modulator; M, mirror; P, Polarizer. Inset: computer-generated hologram; beam spectrum, the +1 order is selected by the white dashed circle; the intensity distributions of LCP and RCP.

Full size image

Transition of topological state

We first validated that the topological state undergoes a transition from a Bloch (δ = 0, β = 0) to a Néel type (δ = −π/2, β = 0), while the skyrmion number remains constant. In this case, the longitudinal wave vector component q = 0.999988k, N = 6, L = 30 cm. The two topological states are located in regions z = 0-15 cm and z = 15–30 cm, respectively. In the region of z = 0–15 cm, F1(z) = 1, F2(z)= 0, δ = 0, β = 0. While in the region of z = 15–30 cm, F1(z)= 0, F2(z) = 1, δ = -π/2, β = 0. F1(z) and F2(z) represent the longitudinal envelope functions of the first and second segment, respectively. Figure 3a shows the longitudinal light field intensity distribution of the simulated 2D optical skyrmions in the range of z = 0–30 cm. As can be seen in Fig. 3a, the longitudinal intensity distribution exhibits fringe patterns along the y-axis. The fringe patterns along the y-axis correspond to the intrinsic sidelobe structures of the Bessel beam, which are crucial for maintaining the nondiffraction character of the main lobe over long propagation distances. It can be seen that within a 30 cm range, the intensity distribution of the light field remains constant, exhibiting excellent nondiffracting propagation characteristics. Notably, the colorbar representing intensity in Fig. 3a is equally applicable to all other intensity distributions.

Fig. 3: Transition of topological state in 2D optical skyrmions.
figure 3

a Simulated longitudinal intensity distribution of 2D optical skyrmions within the range of z = 0–30 cm. b The experimental intensity, polarization, topological state and skyrmion number of 2D optical skyrmions at different longitudinal positions z = 7.5 cm, z = 15 cm, z = 22.5 cm; Purple dashed circle: The integration range of skyrmion density. c Simulated (green spherical dotted line plot) and experimental results (magenta square dotted line plot) of the skyrmion number varying with propagation distance.

Full size image

Figure 3(b) shows the experimentally measured intensity distributions in lateral planes of z = 7.5 cm, z = 15 cm, and z = 22.5 cm in the first row. The second row depicts the corresponding polarization distributions and skyrmion numbers at these positions. The skyrmion numbers are calculated by integrating the skyrmion density within the boundaries of the purple dashed circle, as defined by Eq. (1). The third row presents the topological structure distributions and skyrmion types at the corresponding positions. The polarization and topological structure distributions are derived from the experimentally measured Stokes parameters. Experimental results show that the polarization rotates clockwise during propagation, driving the topological state to transition sequentially from the Bloch to the intermediate state and finally to the Néel type. With the range of z = 0-30 cm, the topological state undergoes one transition near z = 15 cm.

Since the Bloch, intermediate, and Néel type topological states exhibit lemon-type polarization distributions, their skyrmion numbers remain stable. As shown in Fig. 3c, the simulated results and experimentally measured results of the skyrmion numbers as a function of propagation distance are presented. The green spherical dotted line plot and the magenta square dotted line plot represent the simulated and experimental results, respectively. As can be seen that the experimental results agree well with the simulated predictions. It can be observed that within a range of 30 cm, the skyrmion number remains consistently around -0.9.

It is worth noting that the numerically computed and experimentally measured skyrmion number (Q values) are both very close to the theoretically designed integer values, yet not perfectly integral. This minor deviation primarily stems from two factors. First, in our longitudinal segment modulation method, mutual coupling exists between different longitudinal segments of the beam, introducing slight perturbations in the actual light field evolution compared to the ideal case. Second, within the numerical integration region, the polarization state does not achieve ideal conditions at all positions; variations in ellipticity influence the integration result. Additionally, computational errors arising from finite sampling points and a limited integration area size also contribute to this minor discrepancy.

Transition of topological state and skyrmion number

It is noteworthy that the skyrmion number may also vary in conjunction with the transition of the topological state. In this case, the values of q, N, and L are the same as in the previous case, with the three topological states located at z = 0–10 cm, z = 10–20 cm, and z = 20–30 cm, respectively. In these three regions, longitudinal profile functions, δ and β, are orderly selected as F1(z)= (1,0,0) with δ = 0 and β = 0, F2(z)= (0,1,0) with δ = -π/2 and β = 0, and F3(z)= (0,0,1) with δ = -π/2 and β = π/2 respectively.

Figure 4a illustrates the simulated longitudinal intensity distribution of the light field over a 30 cm range, demonstrating its constant intensity and excellent nondiffracting characteristics. Figure 4b shows the simulated and experimental results of the variation of skyrmion number with propagation distance. It can be seen that experimental results are in excellent agreement with the simulated results. Initially, the skyrmion number remains constant at −0.9. Near 20 cm, the skyrmion number undergoes a transition, shifting abruptly from −0.9 to +0.9.

Fig. 4: Transition of topological state and skyrmion number of 2D optical skyrmions.
figure 4

a Simulated longitudinal intensity distribution of 2D optical skyrmions within the range of z = 0–30 cm. b Simulated (green spherical dotted line plot) and experimental (magenta square dotted line plot) results of the skyrmion number varying with propagation distance. c The experimental intensity, polarization, topological state and number of 2D optical skyrmions at different longitudinal positions z = 5 cm, z = 10 cm, z = 15 cm, z = 20 cm, z = 25 cm.

Full size image

In Fig. 4c, the first row shows the measured transverse light field intensity distributions at different longitudinal positions of z = 5 cm, z = 10 cm, z = 15 cm, z = 20 cm, and z = 25 cm. The second row displays the skyrmion numbers and polarization distributions at the corresponding positions. The third row presents the topological structure distributions of the 2D optical skyrmions at the corresponding positions and their corresponding skyrmion types. The experimental results show that within a range of 30 cm, the topological state undergoes two transitions, from the Bloch to the Néel and finally to the antiskyrmion type. These two transitions occur near z = 10 cm and z = 20 cm, respectively. The skyrmion number also changes when the transition from the Néel to the antiskyrmion type is completed.

It is noteworthy that significant variations in the intensity distribution are observed along the propagation distance, as shown in the first row of Fig. 4c. These variations are most pronounced near the critical region at z = 20 cm, where the topological number transition occurs, primarily resulting from the redistribution of optical energy during the dynamic reconstruction of the skyrmion topology. Furthermore, the multi-segment longitudinal modulation strategy employed here introduces mutual coupling effects between consecutive segments. Such coupling effects accumulate during propagation, thereby enhancing fluctuations in the intensity evolution. In addition, optical components used in the experiments, such as lenses and mirrors, introduce extraneous perturbations to the intensity profile, leading to more pronounced fluctuations over long-distance propagation.

The above experimental results verify that controllable transitions of the skyrmion number can be achieved through modulation parameters. It is noteworthy that this phenomenon is not specific to the Q = –1 to 1 pathway alone but reveals a universal physical mechanism whereby a global topological reconstruction occurs as the vector optical field reaches a critical condition during propagation, resulting in a transition of the skyrmion number. To demonstrate the ability of our method to arbitrarily modulate skyrmion topological states, we conducted systematic numerical studies. As shown in Fig. 5, a and b respectively show the skyrmion topological states at z = 7.5 cm, 15 cm, and 22.5 cm during the transition from a high-order Bloch type to different orders of anti-skyrmion types, while c and d present the corresponding simulated evolution of the skyrmion number with propagation distance for a and b. It can be seen that by designing the parameters, multiple transition pathways such as Q = –2 to 2 or Q = –2 to 1 can be realized, and sharp jumps in the skyrmion number are observed near the predicted critical point at z = 15 cm. This further establishes the universality of our method, whose significance extends beyond generating individual specific states. It provides a design rule for achieving arbitrary topological states.

Fig. 5: Arbitrary configuration of 2D optical skyrmion topological states and skyrmion numbers.
figure 5

a, b Simulated the topological state of 2D optical skyrmion at different longitudinal positions z = 7.5 cm, z = 15 cm, z = 22.5 cm. c, d The corresponding simulated results of skyrmion number variation as a function of the propagation distance for a and b.

Full size image

Our work demonstrates that the longitudinal topological state and number transition mechanism establishes a new paradigm for optical information technology. For high-security information encryption, unlike easily detectable optical field parameters such as intensity or polarization53,54, the skyrmion number serves as a hidden parameter that is challenging to detect and identify. The longitudinal topological number transition mechanism allows information to be encoded into dynamically evolving skyrmion numbers along the propagation distance45,55, thereby transforming the beam itself into a dynamic and programmable topological key. Even if the beam is intercepted at a fixed point, eavesdroppers would find it exceedingly difficult to decipher the information, greatly enhancing information security.

In terms of optical information processing46, unlike schemes using magnetic skyrmions as information carriers56,57, the longitudinal topological state transition mechanism indicates that a single physical location can multiplex and store an information sequence composed of multiple topological states along the longitudinal direction. This topological number transition architecture provides a new degree of freedom for information processing. For example, the topological number transition mechanism offers a novel perspective for photonic computing58, enabling robust integer operations without requiring the transition function of other passive optical components or external energy input. On this basis, it is even possible to achieve arbitrarily cascaded photonic computing using a single beam or a single device.

It is noteworthy that the interaction between structured spin textures of optical skyrmions and magnetic domains can enhance magneto-optical responses59. The core value of optical skyrmions lies in their ability to serve as a novel, non-invasive probe for high-resolution magnetic domain imaging. Specifically, in the presence of magnetization, alterations in the spin-orbit coupling of light allow the detection of magnetic domain structures through deformations and dynamic characteristics of topological states. Additionally, the principles proposed in this work open new avenues for generating complex topological structures, such as topological configurations with spin defects60,61, highly ordered skyrmion lattices62, and even aperiodic topological quasicrystals63. Research on such complex topological structures paves the way for applications in topologically encoded information storage, information carriers in optical communications and quantum technologies, as well as optical micromanipulation.

Conclusion

We present a method to break the topological number transition barrier by precisely controlling the longitudinal intensity profiles of vortex and non-vortex Bessel components with orthogonal polarizations, enabling arbitrary and controllable customization of the 2D optical skyrmion topological state and skyrmion number. As a demonstration, both simulated and experimental studies were conducted to explore the transition of topological state as well as the simultaneous transition of skyrmion number and state. It not only demonstrates this intrinsic phenomenon but also provides new insights into the application of 2D optical skyrmions in information storage, optical communications, etc.

Methods

Topological number

The topological properties of a skyrmion can be characterized by its skyrmion number2,64

$$Q=\frac{1}{4\pi }{\int }_{A}{{\bf{n}}}\cdot \left(\frac{\partial {{\bf{n}}}}{\partial x}\times \frac{\partial {{\bf{n}}}}{\partial y}\right)dxdy,$$
(1)

where, the vector n denotes a unit vector that enables the formation of skyrmion confined in region A, with n = [S1, S2, S3]T representing the normalized local Stokes vector, S1, S2, and S3 are Stokes parameters. The integral kernel n·(∂n/∂x × ∂n/∂y) is the skyrmion density.

Optical skyrmionic beams

The construction of optical skyrmionic beams was achieved as a superposition of a vortex eigenmode and a non-vortex eigenmode with orthogonal polarizations41,43. However, once the eigenmodes in the orthogonal polarization components are selected, they remain unchanged during propagation in free space. Consequently, the skyrmion number of the skyrmionics beam remains invariant, making it impossible to achieve the transition of the Q from -1 to 1 as illustrated in Fig. 1b. To address this issue, we employ the coaxial superposition of 2 N + 1 Bessel beams of order l to dynamically modulate the eigenmode during the beam propagation, whose electric field distribution can be expressed as48,49

$${U}_{l}(r,\varphi ,z)={{{\rm{e}}}}^{-{{\rm{i}}}\omega t}{\sum }_{j=-N}^{N}{A}_{j}{J}_{l}({k}_{jr}r){{{\rm{e}}}}^{{{\rm{i}}}{k}_{jz}z}{{{\rm{e}}}}^{{{\rm{i}}}l\varphi }$$
(2)

where, ω is the angular frequency, Jl is the l-th order Bessel function of the first kind, kjr is the transverse wave number, k2jr = k2- k2jz. kjz = q + 2jπ/L is the longitudinal wave number, q is an initial parameter related to the radius of the central spot of the Bessel beam, and L is the effective range of longitudinal intensity modulation. Aj is the weight factor corresponding to the Bessel constituent, which is determined by the longitudinal intensity envelope function F(z) as

$${A}_{j}=\frac{1}{L}{\int }_{0}^{L}F(z){{{\rm{e}}}}^{-i{{k}}_{jz}z}dz$$
(3)

The selection of F(z) allows the light field to exhibit any desired eigenmode within the selected spatial interval 0≤ z ≤ L. We construct 2D optical skyrmions from the Stokes vector fields of a set of customized vector beams, which are given by

$$\begin{array}{c}{{\bf{E}}}(r,\varphi ,z)={e}^{-i\omega t}{\sum }_{j=-N}^{N}{A}_{j}{J}_{{l}_{1}}({k}_{jr}r){e}^{i{k}_{jz}z}{e}^{i{l}_{1}\varphi }{{{\bf{e}}}}_{{{\rm{R}}}}\\ +{e}^{-i\omega t}{\sum }_{j=-N}^{N}{A}_{j}{J}_{{l}_{2}}({k}_{jr}r){e}^{i{k}_{jz}z}{e}^{i\delta }(\cos \beta {e}^{i{l}_{2}\varphi }+\,\sin \beta {e}^{-i{l}_{2}\varphi }){{{\bf{e}}}}_{{{\rm{L}}}}\end{array}$$
(4)

where, δ and β are phase constants that determine the topological structure of the optical skyrmion, eR and eL represent the unit vectors of right- (RCP) and left-handed circular polarization (LCP), respectively. We choose l1 = 0 and l2 = −1, and simultaneously apply multiple z-segmented control of L and F(z) in both RCP and LCP components. By modulating δ and β, the spatial distribution of the Stokes vector forms 2D optical skyrmions, which have a skyrmionics texture that can be controlled as Bloch (δ = 0, β = 0) with Q = −1, Néel (δ =−π/2, β = 0) with Q = −1 and antiskyrmion (δ =−π/2, β = π/2) with Q = 1.