Introduction

A major current development is the advanced and controlled connectivity of nanostructured devices to create networks and explore collective dynamics for fundamental investigations, such as chimera states1, or potential applications, such as analog Ising machines2 or artificial neural networks3,4,5. Thus, implementing such networks is based on two building blocks: the development of nanoscale oscillators and the controlled interaction between several of these oscillators. Regarding the oscillators, new developments in nonlinear dynamical effects have already been investigated based on the high photon density inside nanoscale photonic structures made of semiconductor materials. One of the major demonstrations is the self-pulsing phenomenon, where a self-sustained train of pulses is generated as output. These pulses may be induced by various underlying physical parameters, such as saturable absorption in a nanocavity laser6,7,8,9 or the thermo-optical effect10. These relaxation oscillations range from megahertz (MHz) to gigahertz (GHz), depending on the underlying physics. Self-pulsing due to two-photon absorption (TPA) and the thermo-optical effect has been extensively investigated in a single system for various applications. These include excitability experiments11 to emulate the nonlinear response of biological neurons for brain-inspired computation12; all-optical radio frequency (RF) frequency division, thanks to low phase noise performance and high compliance with external stimuli13; and modulation of radiation pressure force to excite mechanical mode lasing in opto-mechanical devices14.

Meanwhile, efforts are underway to create more complex architectures by connecting several nearly identical oscillators to form a network and explore collective dynamics. There are two main types of synchronization that can be implemented, depending on how the interaction between the oscillators is addressed and controlled15. The first, called mutual synchronization, relies on bidirectional interaction, meaning all oscillators interact with each other. This type of synchronization was initially studied by Huygens16 and has been observed in many other natural sciences, such as the blinking of fireflies17, predator-prey cycles18, and the oscillations of neuron populations19. It has also been observed in various areas of nanotechnology, such as the coupling of Josephson junctions20,21, laser arrays22,23, small clusters of opto-mechanical oscillators24, and arrays of MEMS resonators25. Currently, mutual synchronization at the nanoscale is exclusively performed via evanescent coupling. This local coupling prevents control or in situ modification of the coupling strength. The second topology, called injection locking, relies on a drive-driven mechanism. It has been observed in the adjustment of living beings’ circadian rhythms26, in the realization of pacemakers27, in GPS technology, which uses it to share time references28,29 and astronomy, to reconstruct images from telescope arrays30,31. At the nanoscale, demonstrated implementations have only been done within this framework to reduce phase noise in electro/opto-mechanical devices13,32,33,34,35. Beyond this canonical configuration, a different implementation of injection locking has been investigated, in which a laser is driven by an optical frequency comb36,37.

In this work, we experimentally demonstrate, supported by numerical simulations, the complex dynamics of the injection locking between two nearly identical self-pulsing nanoscale photonic crystal oscillators heterogeneously integrated on a single photonic circuit. First, we analyze the dynamics of a single self-pulsing oscillator triggered by an external tunable continuous-wave (CW) laser before directly injecting the modulated optical carrier as the driving signal for a second, distant self-pulsing oscillator. The overall behavior of the coupled system on a single chip is addressed by implementing optical packaging of the photonic integrated circuit (PIC), which enables improved stability and compactness. A complete and thorough study of injection locking responses and dynamics is performed depending on the system’s driving optical parameters, such as detuning and injected optical power. Within this parameter space, complex multistable dynamics with various locking values and unusual behavior are accurately reconstructed, in good agreement with numerical simulations. Additionally, a large region of injection locking is demonstrated at low injected power, even with non-identical self-pulsing photonic nano-oscillators. Furthermore, the demonstrated distant interaction is of prime importance for communications within a network and paves the way for future neural networks11,12 based on self-pulsing or other types of oscillators.

Results

Integrated photonic crystal cavities

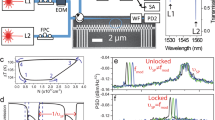
The single optical oscillator consists of a one-dimensional photonic crystal38 (PhC) cavity suspended in indium phosphide (InP), which has a thickness of 265 nm and an electronic bandgap of EG = 1.34 eV at 300 K. The PhC cavity is designed to support various optical resonances ranging from 1500 to 1600 nm. Hybrid bonding allows a single-mode silicon-on-insulator (SOI) waveguide, placed 300 nm below the structure, to transport light that is evanescently coupled to the cavity39 (see Fig. 1a, b; see the Methods section for more details). On the SOI circuitry, two arrays of 32 optical fibers each were bonded above the input and output array couplers of 32 parallel waveguides. Most of the losses originate from the grating couplers, and the fiber arrays induce almost no additional optical losses. This configuration ensures stable and easy light injection and extraction over time (see the schematic in Fig. 1c and the picture of the device under test (DUT) in Fig. 1d). It also allows two or more PhCs to be optically coupled on the same chip with a small footprint and in a simple manner.

Fig. 1: Overview of the device under test (DUT).
figure 1

a Schematic of the 265 nm thick suspended Indium Phosphide (InP) 1D photonic crystal (PhC) cavity on top of a single-mode SOI waveguide equipped with input and output grating couplers. b SEM image of suspended PhCs on top of the waveguides. c Schematic of the positioning of the input and output fiber arrays; each optical fiber (cylinders in light blue color) is aligned and glued on top of a grating coupler. d Picture of the DUT with glued fiber arrays.

Full size image

Self-pulsing in a single integrated photonic crystal cavity

The single cavity is probed by a tunable single-wavelength laser, and its output light is directly sent to the photodiode and simultaneously analyzed by an electrical spectrum analyzer (ESA) and an oscilloscope (OSC). The experimental setup used is illustrated in Fig. 2a (path #1), where polarization controllers (PC) are used to match the polarization of the light to that of the cavities.

Fig. 2: Characterization of the self-pulsing dynamic.
figure 2

a Experimental setup showing the two different paths used; path #1 (orange area) to study the dynamics of cavity 1 and path #2 (yellow area) to study the dynamics of two optically coupled self-pulsing cavities. On path #2, Erbium Doped Fiber Amplifier (EDFA) and a filter are inserted to control the optical signal. On both paths, polarization controller (PC) are inserted to efficiently coupled light into the waveguides. The output light is transduced into electrical signal by a photodiode (PD, 3.5 GHz cutoff frequency) and sent to an oscilloscope (OSC) and Electrical Spectrum Analyzer (ESA). b Low power characterization of the first (black) and second (green) cavity resonances and their respective optical Q-factors. c Normalized time-traces, recorded at λL = 1573.906 nm and 5.5 dBm input power, for one single cavity (black curve) and for the coupled cavities (orange dotted curve). The shaded areas correspond to the four phases of the self-pulsing cycle: sharp drop (yellow), low transmission (orange), sharp jump (red), and high transmission (gray). d Power Spectral Densities (PSDs) of the time traces shown in Fig. 2c for a single cavity (black curve) and for coupled cavities (orange dotted curve).

Full size image

Under a low optical input power excitation (Pin = -12 dBm), the fundamental mode of the first PhC at a resonant wavelength λres,1 = 1573.875 nm has a measured quality factor of about 40 \(\times\)103 (black curve in Fig. 2b). At higher power, starting at Pin = −3 dBm, when the laser wavelength is tuned to the resonant mode of the cavity, the photon density in the cavity is high enough to allow two concomitant and opposite effects: heating of the cavity inducing a red-shift of the resonance, resulting in the typical “sawtooth” shape of nonlinear optical resonance, and TPA. Thus, the self-pulsing effect occurs, and a modulation of the light amplitude is observed at the output. A typical time trace of the normalized transmission is shown in Fig. 2c (black curve). A self-pulsing oscillation cycle consists of four main phases10 which are highlighted in Fig. 2c: (i) the initial phase (yellow region) is a sharp drop in the transmission when λres,1 suddenly shifts from red to blue, detuned from the laser wavelength (λL) due to TPA and free-carrier absorption (FCA); (ii) the second phase (orange region) is characterized with a slower decrease in transmission when the thermo-optic (TO) effect due to the thermalization of free carriers, causing an increase in absorption while λres,1 returns to values close to λL; (iii) the third phase (red region) marks a sudden halt in absorption due to the TO effect which finally pulls back λres to its initial value red-shifted with respect to λL. This causes a sudden stop of TPA because the photon density in the cavity has decreased; and (iv) the final part (gray region) of almost zero absorption is where the thermal energy is slowly dissipated through the PhC supports into the substrate. Within a cycle, the time duration of each phases strongly depends on the relative detuning. Changes in the dynamical responses are induced by the different time scale of each physical phenomenon at play during one cycle (more details in Supplementary Note 1). Figure 2d (black curve) shows the power spectral density (PSD) curve of the normalized time trace in Fig. 2c. It evidences several peaks at integer multiple the fundamental frequency at ω1/2π = 1.6 MHz.

Figure 3a shows the evolution of the power spectral density (PSD) at a power input of 5.5 dBm as the laser wavelength is swept continuously from low to high values in 2 pm steps. The cavity begins to modulate the laser signal at 1573.8 nm, with the fundamental oscillation peak occurring at a low frequency of approximately 0.4 MHz. The frequency then increases up to 1574.05 nm, reaching a maximum of approximately 2 MHz. Then, it decreases to approximately 1 MHz at 1574.22 nm. Beyond this wavelength, the laser is no longer in resonance with the cavity mode; thus, the modulation disappears. This non-monotonic change in frequency is accompanied by an increase in absorption duration during one cycle (more details in Supplementary Note 1).

Fig. 3: Experimental evaluation of the locking ratio.
figure 3

a Power Spectral Density (PSD) of the output signal of cavity 1 as function of the laser wavelength at a 5.5 dBm input power. The fundamental peak of the modulation is observed ranging in between 0.1 MHz and 2 MHz over 420 pm. b PSD of the optical output signal of the two coupled cavities for the same input power as in Fig. 3a. Extra features appear at specific laser wavelengths where the two optical resonances overlap (width of the two resonances are highlighted with black and green rectangles on the right). The blue arrow highlights λL = 1573.88 nm, where the overlap begins. The orange arrow highlights λL = 1574 nm, the first 1:1 locking ratio. c Evolution of the locking ratio of the as function of the wavelength, it is commonly referred to as the devil’s staircase. d Arnold tongue representation of the locking values. The colored part of this graph refers uniquely to the region where the two resonances overlap. The different locking values are highlighted with different colors. The red dotted rectangle refers to the locking regions extension of (b, c).

Full size image

Optical injection locking between two self-pulsing photonic crystal cavities

Another cavity, located on an adjacent waveguide, has optical properties similar to those of the first (resonant optical mode: λres,2 = 1574.037 nm and Q-factor of 21 \(\times\)103 – shown with green curve in Fig. 2b). Although there is relatively small overlap between the two modes at low optical power, substantial red-shift of both resonances occurs at higher power inducing an overlap between the two resonances (more details in Supplementary Note 2). In this configuration, the optical output signal of the first cavity is sent to an optical amplifier (Erbium Doped Fiber Amplifier - EDFA) and filtered around the carrier to avoid introducing excessive noise due to spontaneous emission. The amplified signal is sent to the second cavity, and its output is analyzed using a photodiode (path #2 in Fig. 2a). The amplifier has an inbuilt optical isolator that prevents reflection. The light modulated by the second cavity, which is likely to return, is blocked. Thus, the behavior of the first cavity remains unaffected, guaranteeing the “drive-driven” (injection locking) nature of the experiment. The EDFA’s output power is adjusted so that the second cavity’s input power is equal to the first cavity’s input power (path #2).

Since λres,2 is at higher wavelength compared to λres,1 and λL is swept from low to high values the second cavity begins to self-pulse while the first one is already in the self-pulsing regime. Thus, at specific wavelengths and optical powers, it is possible to address the two optical resonances simultaneously. In this case, the time traces from the coupled cavities (Fig. 2c, orange dashed curve) show additional absorption spikes compared to the single cavity (black curve). The corresponding power spectral density (PSD) (Fig. 2d, orange curve) shows a fundamental peak at half the frequency of the fundamental peak for a single photonic crystal (PhC) (black curve). Peaks at even frequencies are shared with the modulation from the first cavity (the orange dotted peaks overlap the black peaks), whereas the odd multiples are exclusively due to the absorption spikes of the second cavity (the isolated orange dotted peaks in Fig. 2d). This demonstrates the impact of control on the dynamics of the second cavity.

Figure 3b shows recordings of the PSD for two cavities over a 0.42-nm wavelength range and at a fixed optical power of 5.5 dBm. Below 1573.88 nm, only the peaks corresponding to the first cavity are visible. Above 1574.22 nm, the first cavity ceases to self-pulse. The input power to the second cavity remains constant, and the second cavity freely modulates the light up to 1574.35 nm. Beyond this wavelength, λL is no longer resonant with the second cavity. From 1573.88 to 1574.22 nm (the overlap of the black and green rectangles), the dynamical response of the second cavity is strongly affected by the presence of the modulated input power.

Depending on the laser wavelength and at a fixed optical power, the self-pulsing frequency of the first cavity changes. However, the pulse frequency of the second cavity adjusts to the pulse frequency of the first cavity. The latter can therefore be seen as the carrier of a reference frequency to which the second cavity adapts. At lower powers, the amplitude of the modulated signal is low, resulting in a small overlap between the two optical resonances. Thus, the injection locking phenomenon with a ratio of 1:1 only appears when the self-pulsing frequency of the second cavity is close to that of the first. Meanwhile, the DC (Direct Current) component of the laser signal controls and increases the spectral overlap of the two cavities. Thus, the larger the DC signal, the more the injection locking phenomenon occurs over a wide wavelength range. This is accompanied by a discontinuous change in the locking ratio because the natural frequencies of each cavity change nonlinearly with wavelength (see Fig. 3c).

These adjustments result in phase and frequency locking of the second cavity to the first according to the relationship nω1 : mω2, where n and m are integer values. The ratio n:m is defined as the locking value. From each recorded power spectral density (PSD) spectrum, the frequencies of the fundamental harmonics are extracted and normalized by those of the first cavity at a given wavelength. Consequently, the ratio n/m is extracted. For a specific set of parameters where the PSD is unclear, time traces are used to identify regions of phase slip and local asynchrony. In the interaction region, different locking values are observed. At 1573.88 nm (blue arrow in Fig. 3b), the second cavity begins to self-pulse at a frequency of ω2/2π = 0.4 MHz, which is lower than the modulation of the drive, ω1/2π = 1.6 MHz. In this particular case, the second cavity is driven to modulate at a quarter of this frequency, resulting in a locking value of 1:4. Increasing the wavelength causes the modulation frequency of the second cavity to rise faster than that of the first cavity, passing through 1:4, 1:3, and 1:2 locking before finally locking at the same frequency at 1574 nm (orange arrow in Fig. 3b). This 1:1 locking is maintained up to 1574.15 nm. After this point, the modulation frequency of the first cavity decreases while the second cavity continues to modulate at high frequencies. In this section, locking values greater than one are observed (more details in Supplementary Note 2). Figure 3c shows the evolution of the n:m ratio as a function of wavelength for 5.5 dBm of input power, extracted from the recorded power spectral density (PSD) in Fig. 4b. This phenomenon is commonly referred to as the “devil’s staircase” and highlights the discretization of the frequency ratio as a function of wavelength when injection locking occurs.

Fig. 4: Numerical evaluation of the locking ratio.
figure 4

a Power Spectra Density (PSD) of the output signal of a single cavity as function of the laser wavelength (y-axis) at an input power of 5.5 dBm. The fundamental peak of the modulation is observed ranging in between ~1 and 2.1 MHz over 420 pm. Here the linear scale is preferred to have better contrast. b PSD of the two coupled cavities for the same input power as in (a). Extra peaks appear at specific laser wavelengths where the two optical resonances overlap (back and green rectangles overlap). c Evolution of the locking ratio between uncoupled (red line) and coupled cavities (black dots) as function of the wavelength. d The colored part of this graph refers uniquely to the region where the two resonances overlap (black and green rectangles overlap in (b). The red dotted rectangle refers to the locking regions extension of (b, c).

Full size image

Within this overlap region and based on the concept of Arnold tongues15, the wavelength extensions (Δλ) of each locking value can be extracted and traced over a wide range of input powers. Figure 3d shows the evolution of all Δλ as a function of laser wavelength and input power. Below −2.5 dBm, the resonances do not overlap, so no interaction is visible (shown in gray). The color code shows the different locking values. In this interaction region, for a certain set of parameters, the cavities do not lock onto a specific value, but rather exhibit more complicated behaviors, such as phase slip and local a-synchrony (more details in Supplementary Note 3 and 4).

Numerical simulations

The self-pulsing effect is described as an interaction between three time-dependent quantities: the complex amplitude of the optical field inside the cavity (ui); the free carrier density in the cavity region (Ni) originated from TPA and the temperature difference (ΔTi) between the cavity and its external environment (i = {1,2} for the first or second addressed cavity). When the photon density inside the cavity is high enough to allow TPA and the resonance is red detuned from the laser wavelength, the output optical signal evidences periodic amplitude modulation, giving rise to a limit cycle relaxation oscillator10,40,41. In the case of a single cavity, the description of this dynamic requires three coupled mode equations10,41:

$$\dot{{u}_{1}}=\left\{{{\rm{i}}}({\delta }_{1}-{K}_{{{\rm{a}}},1}\left({u}_{1};{N}_{1}\right))-{K}_{{{\rm{b}}},1}\left({u}_{1};{N}_{1}\right)\right\}{u}_{1}+\sqrt{{\Gamma }_{{{\rm{c}}}}{{{\rm{P}}}}_{{{\rm{in}}}}}$$
(1)
$$\dot{{N}_{1}}={K}_{{{\rm{c}}},1}\left({u}_{1};{N}_{1}\right)-\frac{{N}_{1}}{{{{\rm{\tau }}}}_{{{\rm{car}}}}}$$
(2)
$$\dot{{\Delta T}_{1}}={K}_{{{\rm{d}}},1}\left({u}_{1};{N}_{1}\right)-\frac{{\Delta T}_{1}}{{{{\rm{\tau }}}}_{{{\rm{th}}}}}$$
(3)

with δ1 = 2πc(1/λres,1 - 1/λL), c the speed of light and resonant wavelength λres,1 = 1573.875 nm (experimentally measured) and λL the laser wavelenght. Pin is the input power sent into the waveguide, \({\Gamma }_{{{\rm{c}}}}\) is the coupling coefficient between the waveguide and the cavity; τcar is the carrier lifetime, which we assume it does not depend on the carrier density and τth is the thermal decay time. All coefficients \({K}_{{{\rm{i}}},1}\) (with i = a, b, c, d) dependences and numerical values are discussed in the methods.

Before being solved, the coupled Eqs. (1–3) are normalized41 to avoid large parameter excursions. The numerical solution is performed to determine the output power over time as Pout(t) = Pin - Γc|u1(t)|2. The signal at the output of the first cavity (at the input of the second one) can be decomposed into a continuous laser signal Pin (which does not enter cavity 1) and a pulsed signal induced by the first cavity Γc|u1(t)|2. Note that for all the simulations, the input power was 10 times lower than in the experiments to obtain similar behavior. This difference is due to insertion and propagation losses. When the input power is set to 5.5 dBm, and the laser wavelength is swept from low to high values through the resonance, the output power as a function of time is recovered. This highlights the self-pulsation of the optical carrier. Figure 4a shows the power spectral density (PSD) of the output signal as a function of the laser wavelength, with peaks in the spectra visible from λL = 1573.86 nm to 1574.3 nm. As for the measurements, considering a single wavelength (one horizontal slice of Fig. 4a), the PSD of the output signal is composed of peaks located at integer multiples of the fundamental peak. At the ends of the resonance, the fundamental frequency approaches 1.5 MHz and reaches a maximum of 2.5 MHz near the center of the resonance (more details in Supplementary Note 2).

In the case where one cavity drives another, by assuming drive-driven mechanics (injection locking), the three coupled equations have to be doubled, and it has to be considered that the input power of the second cavity is coming from the output of the first one. Thus, the second set of coupled equations is:

$$\dot{{u}_{2}}=\left\{{{\rm{i}}}({\delta }_{2}-{K}_{{{\rm{a}}},2}\left({u}_{2};{N}_{2}\right))-{K}_{{{\rm{b}}},2}\left({u}_{2};{N}_{2}\right)\right\}{u}_{2}+\sqrt{{A\Gamma }_{{{\rm{c}}}}({{{\rm{P}}}}_{{{\rm{in}}}}-{\Gamma }_{{{\rm{c}}}}{\left|{u}_{1}\right|}^{2})}$$
(4)
$$\dot{{N}_{2}}={K}_{{{\rm{c}}},2}\left({u}_{2};{N}_{2}\right)-\frac{{N}_{2}}{{{{\rm{\tau }}}}_{{{\rm{car}}}}}$$
(5)
$$\dot{{\Delta T}_{2}}={K}_{{{\rm{d}}},2}\left({u}_{2};{N}_{2}\right)-\frac{{\Delta T}_{2}}{{{{\rm{\tau }}}}_{{{\rm{th}}}}}$$
(6)

with δ2 = 2πc(1/λres,2 - 1/λL) and resonant wavelength λres,2 = 1574.037 nm (experimentally measured). All coefficients Ki,2 (with i = a, b, c, d) dependences and numerical values are discussed in methods. In Eq. (4), Pin has been calculated from the Pout of the first cavity. The factor A refers to amplification of the signal coming out of the first cavity. It reflects the role of the EDFA in the experimental setup and so it ensures that the DC input power seen from the second oscillator is the same as the first one, hence A\(({{{\rm{\omega }}}}_{{{\rm{L}}}})\) = Pin / (Pin – RMS(|u1|2)), with RMS the root-mean-square value of the time-dependent quantity |u1|2. In the following, the two resonances are considered as identical such that all the parameters are set to be the same for both, except for their resonant wavelength which is the experimentally measured one.

The normalized Eqs. (1–6) are simulated for the coupled cavities. Setting the same input power as in the case of a single cavity allows the modulation frequency shift to be recovered while scanning the laser over the same wavelength range, as shown in Fig. 4a. Figure 4b shows the power spectral density (PSD) calculated for two cavities, where interaction can only be observed over a certain wavelength range, as in the measurements. When only the first cavity modulates the optical carrier, the peaks remain unchanged from those in Fig. 4a. However, once the laser simultaneously addresses both resonances (from 1573.96 to 1574.3 nm), more complex behaviors appear that are strongly dependent on λL. Figure 4c shows the evolution of the n:m ratio as a function of wavelength for an input power of 5.5 dBm. Addressing one cavity at a time with the same nominal optical power makes it possible to obtain the ratio between the two self-pulsing frequencies (red line in Fig. 4c). When the two cavities are optically coupled, the n:m ratio (black dots) is extracted from the numerical PSD in Fig. 4b. This demonstrates the discretization of the frequency as a function of wavelength due to the implemented optical coupling.

Similarly to what was done to construct Fig. 3d, the complete map of injection locking values can be reconstructed as a function of optical input power and laser wavelength (Fig. 4c). Only the thermal decay time (τth) and FCA coefficient (σFCA) were used as adjustable parameters to achieved results shown in Fig. 4 (more details can be found in the Methods).

Discussion

Based on three coupled equations for each self-pulsed oscillator linked by the relationship between input and output powers, a direct comparison of the numerical (Fig. 4c) and experimental (Fig. 3c) results shows good qualitative and quantitative agreement. Depending on the detuning with respect to the optical resonances and the laser, complex multistable dynamics with various locking values and behaviors consisting of regions with very high locking values, “local asynchrony” and phase slip were identified. At the lower limit of the interaction region, the input modulation frequency changes slightly, whereas the natural frequency of the second cavity increases rapidly. This means that n:m transitions from low values of 1:4 to 1:1 injection locking through intermediate values (1:3, 1:2, and 2:3). Then, for powers above 2.5 dBm, the 1:1 locking region splits into two regions: one where periodic “local asynchrony” is observed (shown in white in Figs. 3d and 4d) and one where 1:1 locking occurs. To discriminate between them, temporal dynamics are required. This phenomenon is primarily caused by the non-identical time durations of the absorption phases (gray region in Fig. 2c) for the two cavities, despite the identical overall self-pulsing cycle (more details in Supplementary Note 3). Using identical cavities is necessary to avoid this detrimental dynamic effect in future networks.

Additionally, phase slip can be identified by the black regions in Figs. 3c and 4c when transitioning from one locking region to another. In these regions, the second cavity mostly locks to a single value, resulting in a constant phase difference. However, locking can randomly be lost over time, resulting in a phase shift of 2π. This lack of perfect periodicity gives the output signal a broader spectrum, as seen in the PSD (more details in Supplementary Note 4). This feature is mainly visible in the experimental dynamics due to technical noise sources that can induce fluctuations, resulting in random phase jumps at the limits of the locking ranges.

Near the upper wavelength limit of the locking region, which corresponds to the limit of the first photonic resonance, locking values greater than one are observed for intermediate input powers. These values reach up to 6:1 for input powers between 0.5 and 2.5 dBm in the experiments (Fig. 3c) and between 0.5 and 4 dBm in the simulations (Fig. 4c). The large shift between self-pulsing frequencies results from the strong nonlinear dependence of self-pulsation frequency on laser wavelength and the wavelength shift between the involved resonances. (more details in Supplementary Note 2).

Finally, at even higher wavelengths, only the second cavity is self-pulsed, and no locking is observed. Scanning the laser wavelength backwards enables us to study the impact of optical resonance bistability on dynamics. Thus, when entering nonlinear optical resonances from the blue side, injection locking is only accessible for a smaller range of parameters, mainly on the lower wavelength side (more details in Supplementary Note 5), and only low locking ranges are accessible.

These results can be extended beyond injection locking with thermo-optically driven oscillators to multidirectional interactions where mutual couplings come into play. Achieving such coupling requires addressing the issues of optical coupling losses and nanofabrication reproducibility. Furthermore, the discussed physical principle, based on a self-pulsing thermo-optical oscillator, can be generalized to other types of oscillators with self-pulsing on different time scales, such as Josephson junctions, lasers, and opto-mechanical oscillators. This method could also be used with other types of integrated optical parametric oscillators to modulate light periodically for on-chip time reference generation42 or to implement a coherent Ising machine43. This demonstration of two coupled self-pulsing systems lays the groundwork for a potential feed-forward network topology44 and can be expanded to include multiple injection-locked oscillators to study more complex dynamics45 and achieve signal sharing across different layers of a complex network for wireless communications and mobile computing46, as a general clustering algorithm47. Controlling the relative phase between oscillators could also open new avenues in reinforcement learning48,49. These advanced on-chip architectures require precise control of the resonant wavelengths of the cavities to achieve optimal overlap. To counteract manufacturing imperfections that inevitably shift resonance frequencies, a scalable solution compatible with the presented optical conditioning could be the use of integrated heaters50,51.

Methods

Coupled mode equations

Coefficients of Eqs. 1–3:

$${K}_{{{\rm{a}}},1}=\frac{{\omega }_{{{\rm{L}}}}}{{{{\rm{n}}}}_{0}}\left[-\frac{{{{\rm{n}}}}_{2}{{\rm{c}}}}{{{{{\rm{n}}}}_{0}{{\rm{V}}}}_{{{\rm{Kerr}}}}}{\left|{u}_{1}\right|}^{2}-\left({{{\rm{\sigma }}}}_{{{\rm{r}}}1}{N}_{1}+{{{\rm{\sigma }}}}_{{{\rm{r}}}2}{N}_{1}\right)+{{{\rm{K}}}}_{{{\rm{\theta }}}}{\Delta T}_{1}\right]$$
$${K}_{{{\rm{b}}},1}=\left(\frac{{{\rm{c}}}{{\rm{\alpha }}}}{2{{{\rm{n}}}}_{0}}+\frac{{{{\rm{\beta }}}}_{2}{{{\rm{c}}}}^{2}}{2{{{{\rm{n}}}}_{0}}^{2}{{{\rm{V}}}}_{{{\rm{TPA}}}}}{\left|{u}_{1}\right|}^{2}+\frac{{{{\rm{\sigma }}}}_{{{\rm{FCA}}}}{{\rm{c}}}{N}_{1}}{{{{\rm{n}}}}_{0}}\right)$$
$${K}_{{{\rm{c}}},1}=\frac{{{{\rm{\beta }}}}_{2}{{{\rm{c}}}}^{2}}{2{{{{\rm{n}}}}_{0}}^{2}{{\hslash }}{\omega }_{{{\rm{L}}}}{{{{\rm{V}}}}_{{{\rm{FCA}}}}}^{2}}{\left|{u}_{1}\right|}^{4}$$
$${K}_{{{\rm{d}}},1}=\frac{{\left|{u}_{1}\right|}^{2}}{{{{\rm{\rho }}}}_{{{\rm{InP}}}}{{{\rm{c}}}}_{{{\rm{InP}}}}{{{\rm{V}}}}_{{{\rm{eff}}}}}\left(\frac{{{{\rm{\alpha }}}}_{{{\rm{abs}}}}{{\rm{c}}}}{{{{\rm{n}}}}_{0}}+\frac{{{{\rm{c}}}}^{2}{{{\rm{\beta }}}}_{2}{\left|{u}_{1}\right|}^{2}}{{{{{\rm{n}}}}_{0}}^{2}{{{\rm{V}}}}_{{{\rm{TPA}}}}}+\frac{{{{\rm{\sigma }}}}_{{{\rm{FCA}}}}{{\rm{c}}}{N}_{1}}{{{{\rm{n}}}}_{0}}\right)$$

Coefficients of Eqs. 4–6:

$${K}_{{{\rm{a}}},2}=\frac{{\omega }_{{{\rm{L}}}}}{{{{\rm{n}}}}_{0}}\left[-\frac{{{{\rm{n}}}}_{2}{{\rm{c}}}}{{{{{\rm{n}}}}_{0}{{\rm{V}}}}_{{{\rm{Kerr}}}}}{\left|{u}_{2}\right|}^{2}-\left({{{\rm{\sigma }}}}_{{{\rm{r}}}1}{N}_{2}+{{{\rm{\sigma }}}}_{{{\rm{r}}}2}{N}_{2}\right)+{{{\rm{K}}}}_{{{\rm{\theta }}}}{\Delta T}_{2}\right]$$
$${K}_{{{\rm{b}}},2}=\left(\frac{{{\rm{c}}}{{\rm{\alpha }}}}{2{{{\rm{n}}}}_{0}}+\frac{{{{\rm{\beta }}}}_{2}{{{\rm{c}}}}^{2}}{2{{{{\rm{n}}}}_{0}}^{2}{{{\rm{V}}}}_{{{\rm{TPA}}}}}{\left|{u}_{2}\right|}^{2}+\frac{{{{\rm{\sigma }}}}_{{{\rm{FCA}}}}{{\rm{c}}}{N}_{2}}{{{{\rm{n}}}}_{0}}\right)$$
$${K}_{{{\rm{c}}},2}=\frac{{{{\rm{\beta }}}}_{2}{{{\rm{c}}}}^{2}}{2{{{{\rm{n}}}}_{0}}^{2}{{\hslash }}{\omega }_{{{\rm{L}}}}{{{{\rm{V}}}}_{{{\rm{FCA}}}}}^{2}}{\left|{u}_{2}\right|}^{4}$$
$${K}_{{{\rm{d}}},2}=\frac{{\left|{u}_{2}\right|}^{2}}{{{{\rm{\rho }}}}_{{{\rm{InP}}}}{{{\rm{c}}}}_{{{\rm{InP}}}}{{{\rm{V}}}}_{{{\rm{eff}}}}}\left(\frac{{{{\rm{\alpha }}}}_{{{\rm{abs}}}}{{\rm{c}}}}{{{{\rm{n}}}}_{0}}+\frac{{{{\rm{c}}}}^{2}{{{\rm{\beta }}}}_{2}{\left|{u}_{2}\right|}^{2}}{{{{{\rm{n}}}}_{0}}^{2}{{{\rm{V}}}}_{{{\rm{TPA}}}}}+\frac{{{{\rm{\sigma }}}}_{{{\rm{FCA}}}}{{\rm{c}}}{N}_{2}}{{{{\rm{n}}}}_{0}}\right)$$

For most of the parameter used in Eqs. (1–6) and in their coefficients Ki,1-2, their values for InP and their meaning are listed in Table 1.

Table 1 Indium Phosphide (InP) parameters used for the solution of the coupled equations
Full size table

Furthermore, \({{{\rm{\sigma }}}}_{{{\rm{r}}}1}\),\({{{\rm{\sigma }}}}_{{{\rm{r}}}2}\) are functions of \({{{\rm{\lambda }}}}_{{{\rm{L}}}}\) that refer to the refractive index change due to carrier densities in InP:

$$\Delta n=-\left({{{\rm{\sigma }}}}_{{{\rm{r}}}1}N+{{{\rm{\sigma }}}}_{{{\rm{r}}}2}P\right)=-\left(\frac{{e}^{2}{{{{\rm{\lambda }}}}_{{{\rm{L}}}}}^{2}}{8{\pi }^{2}{c}^{2}{\epsilon }_{0}{n}_{0}}\right)\left(\frac{N}{{m}_{e}}+\frac{P}{{m}_{h}}\right)$$

Where e is the electron charge, c the light speed in vacuum, \({\epsilon }_{0}\) the vacuum permittivity, \({n}_{0}\) the InP refractive index, \({m}_{e}=0.075{m}_{0}\) and \({m}_{h}=0.42{m}_{0}\) the electron and hole effective masses, respectively, with \({m}_{0}\) the free electron mass. N and P are the electron and hole densities in CB and VB respectively which, for an undoped semiconductor are the same52.

Due to close relation between TPA and Kerr effect we can set VKerr = VTPA41. From the measured quality factor Q, the photon lifetime in the cavity is calculated as \({{{\rm{\tau }}}}_{{{\rm{ph}}}}={{\rm{Q}}}/{\omega }_{{res}}\), which allows us to calculate the overall cavity decay rate as \({{\rm{\alpha }}}\) = \({{{\rm{n}}}}_{0}/({{\rm{c}}}{{{\rm{\tau }}}}_{{{\rm{ph}}}})\)41. This parameter is composed by the sum of two terms, \({{{\rm{\alpha }}}}_{c}\) which are the coupling losses between the waveguide and the cavity and \({{{\rm{\alpha }}}}_{{cav}}\) which considers the losses taking place inside the cavity such as linear absorption losses (\({{{\rm{\alpha }}}}_{{abs}}\)), radiation losses (\({{{\rm{\alpha }}}}_{{rad}}\)) and losses due to edge roughness (\({{{\rm{\alpha }}}}_{{rough}}\)). By assuming critical coupling (in Fig. 2b the bottom of the first cavity’s Lorentzian fit is almost reaching 0 transmission) we can calculate \({{{\rm{\alpha }}}}_{c}={{{\rm{\alpha }}}}_{{cav}}={{\rm{\alpha }}}/2\)53,54. Considering the temperature variation in time (Eqs. 3 and 6), one of the pumping processes is driven by the linear absorption losses inside the cavity (\({{{\rm{\alpha }}}}_{{abs}}\)), for which we assume a ratio \({\eta }_{{lin}}={{{\rm{\alpha }}}}_{{abs}}/{{{\rm{\alpha }}}}_{{cav}}=0.1\), comparable with the literature41, since they are generally difficult to estimate precisely.

Finding the extrema (λstart - λend) of the locking regions

The extension ΔλL of each locking value has been evaluated considering the spectrum (recorded up to 20 MHz) and the time trace (recorded up to 400 μs) of the output signal at specific λL. At first, images like Figs. 2b and 4b in the main text are used to understand at which λL the overlap of the two resonances starts and ends. Then, by looking at the location of the fundamental peak of the second cavity, the starting (λstart) and ending wavelength (λend) of a locking region are guessed. At this point, the time traces for a few λL around the guessed λstart and λend are plot. The absorption pulses due to the first and second cavity are distinguished and their number are counted. By finding the lower and higher λL for which nω1:mω2 is constant, one finds the two extrema of the locking region. Whenever the relation \(n{\omega }_{1}:{m\omega }_{2}\) seems more complex, the time traces and spectra are analyzed more in details and further discussion about these regions is found in the Supplementary Notes 3-4-5.

PhC cavity design and device fabrication

The device is a one-dimensional photonic crystal cavity made of Indium Phosphide suspended 300 nm above a silicon bus waveguide where infrared light is injected and extracted through grating coupler. The 1D PhC cavity is created by drilling rectangular holes in a slab of material which is 300 nm thick, 700 nm wide. The position of the holes allows to create a cavity at the center of the beam to have the first optical mode around 1550 nm. The mirrors, on the two sides of the cavity, are created by a repetition of 10 holes with all the same dimension and the same lattice spacing designed to give the maximum confinement for the optical modes inside the cavity. Between the center of the cavity and the mirror region, a Gaussian tapering over the lattice length and the hole’s vertical dimension takes place to avoid abrupt transitions in between these two regions (gentle confinement)38,39.