Introduction

Quantum networks (QNs) hold the promise of connecting remote nodes using quantum resources1,2, enabling revolutionary applications such as secure communication3, distributed quantum computing4, and enhanced sensing5, which are beyond the capabilities of classical systems. Central to realizing large-scale QNs is the generation and sustained distribution of quantum correlations—particularly entanglement—across distant nodes6,7. The ability to “weave” entanglement throughout a QN is based on local operations and classical communication (LOCC)8, as specified by quantum resource theory9. Yet, realistic LOCC between distant nodes is severely hampered by photon loss and decoherence. To model these limitations and understand the connectivity of QNs, researchers have successfully adapted concepts from statistical physics, specifically the theory of bond percolation10. A seminal approach in this area is classical entanglement percolation (CEP)11. The CEP framework predicts the existence of a critical entanglement threshold, above which the QN can form long-distance entanglement through quantum protocols. More recently, concurrence percolation theory (ConPT) was introduced as an alternative to CEP12. While CEP employs probability as the key measure13, in ConPT the key measure becomes concurrence—an entanglement monotone14, which has the nice property of remaining scalable under deterministic protocols15. This deterministic nature eventually shows higher efficiency for distributing entanglement than traditional probabilistic protocols as used in CEP, consequently leading to a lower, more favorable entanglement threshold than what CEP predicts.

While the superiority of ConPT over CEP seems promising, it relies on a critical assumption that the network’s resources are pure states. In practice, imperfections in quantum devices mean that mixed states are unavoidable resources16,17,18. Extending entanglement percolation to networks of mixed states thus emerges as a practical, if not more significant, challenge. To address this, an early attempt by Broadfoot et al. developed a CEP-based strategy for mixed states arising from amplitude damping noise17,18. Their method, however, imposes stringent conditions: it requires that any connected pair of nodes share in parallel at least two copies of a specially structured mixed state: \({\rho }_{s}=\lambda \left|\alpha ,\gamma \right\rangle \left\langle \alpha ,\gamma \right|+(1-\lambda )\left|01\right\rangle \left\langle 01\right|\), where \(\left|\alpha ,\gamma \right\rangle =\sqrt{\alpha }\left|00\right\rangle +\sqrt{1-\alpha -\gamma }\left|11\right\rangle +\sqrt{\gamma }\left|01\right\rangle\) and 0 < λ ≤1. This requirement restricts not only the type of noise but also the network’s topology, limiting its general applicability.

To address this gap, our work investigates entanglement percolation in the presence of another important type of noise: bit-flip errors, which commonly arise from imperfect gate operations and environmental disturbances19,20,21,22,23. We demonstrate that a ConPT framework can be generalized to these resulting mixed states. We find that concurrence remains scalable under our use of protocols, allowing us to construct a mixed-state concurrence percolation model at arbitrary scale.

This generalization leads to the following initial finding: the mixed-state ConPT appears to have a lower percolation threshold than its pure-state counterpart for the same initial link concurrence. This counter-intuitive result would imply that the stochastic (bit-flip) noise we investigate is somehow less disruptive than the unitary noise that merely reduces the entanglement (but not the purity) of states. This seems to contradict the general principle in quantum information that stochastic noise is typically more detrimental than unitary noise.

We resolve this paradoxical finding by identifying a conceptual gap in our generalization: the protocols used in the mixed-state ConPT are no longer deterministic but probabilistic. Practically, this necessitates some mechanism to ensure the success of the protocols (for example, through the use of quantum memories to buffer successful events24,25,26). Otherwise, our concurrence percolation framework would be incomplete, as it must also consider the failure of protocols fundamentally rooted in this probabilistic nature. Accounting for this subtlety, we successfully show that the mixed-state ConPT threshold is no longer lower than its pure-state counterpart. This finding reinforces the understanding of the detrimental impact of stochastic noise.

Further, from a statistical physics perspective, we notice that the phase transition undergoes a qualitative shift from continuous for pure states to discontinuous for mixed states. We propose this is a consequence of our self-averaging treatment of the probabilistic protocols. This finding could pave the way for uncovering novel critical characteristics in noisy QNs.

Methods

Quantum network under bit-flip error

We consider a QN model where each link (edge) represents a bipartite entangled state shared between adjacent nodes (vertices). This entangled state is subject to bit-flip error, resulting in a mixed state:

$$\rho (F)=F\left|{\phi }^{+}\right\rangle \left\langle {\phi }^{+}\right|+(1-F)\left|{\psi }^{+}\right\rangle \left\langle {\psi }^{+}\right|,\,$$
(1)

where 1/2 < F≤1 denotes the fidelity of the state, and \(\left|{\phi }^{+}\right\rangle =(\left|00\right\rangle +\left|11\right\rangle )/\sqrt{2}\) and \(\left|{\psi }^{+}\right\rangle =(\left|01\right\rangle +\left|10\right\rangle )/\sqrt{2}\) represent the Bell states. It is straightforward to show that the mixed state ρ(F) forms a special class of the X states27,28. We denote a QN comprising n nodes by \({{\mathcal{G}}}(n)\); or by \({{{\mathcal{G}}}}_{F}(n)\) when all links in \({{\mathcal{G}}}(n)\) are characterized by an identical F.

Concurrence percolation theory

ConPT uses the entanglement measure concurrence, instead of probability, to construct a theory analogous to classical percolation theory for QNs. For pure bipartite states, the concurrence is defined as \(c=\sqrt{2(1-\,{{\rm{Tr}}}\,{\rho }_{r}^{2})}\), where ρr is the reduced density matrix of the bipartite state29. The concurrence of the mixed state in Eq. (1) is found to be27,28

$$c=2F-1.$$
(2)

ConPT employs sponge-crossing concurrence CSC as an order parameter to quantify the establishment of entanglement between boundaries of a QN12,15,30,31,32. The quantity CSC represents a weighted summation of all open paths that connect the distant boundaries, where each link’s contribution is weighted by its concurrence. In this framework, the boundaries are treated as two “mega nodes” (denoted S for source and T for target) that collectively represent all boundary nodes, and CSC measures the concurrence of the resulting entangled state established between S and T. When n → ∞, a threshold emerges:

$${c}_{{{\rm{th}}}}=\inf \{c\in [0,1]| \mathop{lim}\limits_{n\to \infty }{C}_{{{\rm{SC}}}}[{{\mathcal{G}}}(n)] > 0\},$$
(3)

such that cth is the minimum value of the weight c below which CSC becomes zero. Consequently, for any \({{{\mathcal{G}}}}_{F}(n)\) where the concurrence c exceeds the threshold value cth, long-distance entanglement transmission between the boundary nodes S and T can be achieved.

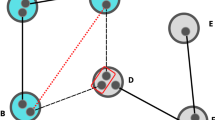
In a series-parallel network33 such as the Bethe lattice (Fig. 1a), CSC can be computed using only series and parallel rules. However, when the network includes non-series-parallel “loops”33—such as in the 2D square lattice and 2D honeycomb lattice (Fig. 1b, c), additional higher-order connectivity rules become necessary12 (Supplementary Note 3). It can be effectively approximated by employing only the series and parallel rules, similar to a local renormalization group process34.

Fig. 1: Mixed-state entanglement distribution.
figure 1

We define and apply mixed-state concurrence percolation to three network topologies, treating the boundaries as two “mega nodes"-the source (S) and target (T): (a) the Bethe lattice (S: the root; T: the outermost layer nodes); (b) the 2D square lattice (S: left boundary; T: right boundary); and (c) the 2D honeycomb lattice (S: left boundary; T: right boundary). In the framework of concurrence percolation, the distribution of entangled mixed states ρ(F) employs a combination of (d) series, (e) parallel, and (f) higher-order connectivity rules to systematically compute the distributable entanglement (concurrence) “sponge-crossing” between S and T. The series and parallel rules can be achieved by quantum operations, specifically (d) entanglement swapping and (e) purification protocols. The two rules can also be used to (f) effectively approximate higher-order connectivity rules which represent unknown quantum operations12.

Full size image

Series and parallel rules

The series rule is implemented by entanglement swapping. We first consider the scenario in which two links ρAR, ρRB are connected in series between three nodes (S–R–T), as shown in Fig. 1d, where S and R share a mixed state ρ(F1), and R and T share another mixed state ρ(F2). Performing a swapping operation on R, four probabilistic outcomes between S and T are realized via projection35,36. When a particular measurement basis is chosen for projection6,37, the link between S and T is projected onto one of the four outcome states \({\rho }_{{{\rm{ST}}}}^{{\phi }^{\pm }}\) and \({\rho }_{{{\rm{ST}}}}^{{\psi }^{\pm }}\) with the probabilities of \({p}_{{\phi }^{\pm }}=1/4\) and \({p}_{{\psi }^{\pm }}=1/4\), respectively. The final concurrences of each outcome are identical, equal to cSRcRT. Hence, the final average concurrence is \(c={\sum }_{i=1}^{4}{p}_{i}{c}_{i}={c}_{{{\rm{SR}}}}{c}_{{{\rm{RT}}}}\). Moreover, the four outcomes are locally unitary-equivalent. Hence, the swapping operation is an example of deterministic LOCC because it only yields one possible outcome, up to local unitary transform12. If the concurrence of each link is cj for j = 1, 2, …, n, and these links are connected in series by a chain, then after performing swapping at the n − 1 intermediate nodes in succession, the final concurrence is given by the formula (Supplementary Note 1):

$${{\rm{Seri}}}({c}_{1},{c}_{2},\ldots ,{c}_{n})={c}_{1}{c}_{2}\ldots {c}_{n}.$$
(4)

The parallel rule is implemented by entanglement purification. For two parallel links between S and T (Fig. 1e), the two links ρST(F1) and ρST(F2) form a tensor-product state, ρST = ρST(F1) ⊗ ρST(F2). Utilizing the purification protocol38, we can obtain a new mixed state \({\rho }_{{{\rm{AB}}}}({F}^{{\prime} })\) with \({F}^{{\prime} }=\frac{{F}_{1}{F}_{2}}{{F}_{1}{F}_{2}+(1-{F}_{1})(1-{F}_{2})}\). Since F1 > 1/2 and F2 > 1/2, we see that \({F}^{{\prime} } > {F}_{1}\) and \({F}^{{\prime} } > {F}_{2}\). If the concurrences of ρST(F1) and ρST(F2) are c1 and c2, respectively, the concurrence of the successfully purified state \({\rho }_{{{\rm{ST}}}}({F}^{{\prime} })\) is \({{\rm{Para}}}({c}_{1},{c}_{2})=\frac{{c}_{1}+{c}_{2}}{1+{c}_{1}{c}_{2}}\). One approach to implement this purification protocol is to encode the two entangled states ρST(F1), ρST(F2) into distinct modes (e.g., polarization and spatial) of one photon pair—known as the hyperentanglement mechanism—which can achieve higher efficiency than the usual two-copy entanglement purification protocols39,40,41. This hyperentanglement mechanism may also be effectively extended to other degrees of freedom in terms of photon modes, such as time bin42, frequency43, and orbital angular momentum44, which enables multi-step purification that further enhances the fidelity of entanglement. Given n links between node S and node T with concurrences c1, c2, …, cn, the parallel sum, assuming every purification operation succeeds, is given by (Supplementary Note 2):

$${{\rm{Para}}}({c}_{1},{c}_{2}\ldots ,{c}_{n})=\frac{{\prod }_{i=1}^{n}(1+{c}_{i})-{\prod }_{i=1}^{n}(1-{c}_{i})}{{\prod }_{i=1}^{n}(1+{c}_{i})+{\prod }_{i=1}^{n}(1-{c}_{i})}.$$
(5)

Table 1 summarizes the series and parallel rules for the pure-state ConPT12 and our mixed-state ConPT. Both sets of the rules are inherently scalable, as the series rule satisfies

$$\,{{\rm{Seri}}}({c}_{1},\ldots ,{c}_{n})={{\rm{Seri}}}({{\rm{Seri}}}\,({c}_{1},\ldots ,{c}_{n-1}),{c}_{n}),$$
(6)

and the parallel rule satisfies

$$\,{{\rm{Para}}}({c}_{1},\ldots ,{c}_{n})={{\rm{Para}}}({{\rm{Para}}}\,({c}_{1},\ldots ,{c}_{n-1}),{c}_{n}).$$
(7)

This scalability is critical for large-scale, versatile QN design, making QNs potentially more adaptable to experimental and technological constraints.

Table 1 Comparison of connectivity rules
Full size table

Results

A counter-intuitive low threshold

We investigate the sponge-crossing concurrence CSC and percolation threshold cth for three network topologies, including the Bethe lattice, the square lattice, and the honeycomb lattice:

Bethe lattice

The Bethe lattice represents a typical series-parallel network where each node has the same degree k. Further, it serves as an approximation for many real-world networks, as long as loops in such networks may be effectively ignored. When the number of nodes n → ∞, we can select any node as the root and subsequently establish an exact recurrence relation between the root and the subroots12,45. The behavior of CSC in Bethe lattices with k = 3 is shown in Fig. 2a. We find that the percolation threshold for mixed-state ConPT, \({c}_{{{\rm{th}}}}^{{{\rm{mixed}}}}=1/2\), is lower than that for pure-state ConPT, given by \({c}_{{{\rm{th}}}}^{{{\rm{pure}}}}=1/\sqrt{2}\). For a general degree k, we derive the threshold \({c}_{{{\rm{th}}}}^{{{\rm{mixed}}}}=1/\left(k-1\right)\) (Supplementary Note 4), which also yields \({c}_{{{\rm{th}}}}^{{{\rm{mixed}}}} < {c}_{{{\rm{th}}}}^{{{\rm{pure}}}}\) where \({c}_{{{\rm{th}}}}^{{{\rm{pure}}}}=1/\sqrt{k-1}\)12.

Fig. 2: Comparison between mixed-state and pure-state concurrence percolation.
figure 2

The concurrence of each link, c, and the sponge-crossing concurrence, CSC, are plotted on the x-axis and y-axis, respectively. The gray solid and dashed vertical lines mark the thresholds for mixed-state and pure-state concurrence percolation, respectively. a Bethe lattice with degree k = 3. The blue and orange curves represent the mixed-state and pure-state sponge-crossing concurrences CSC. The dashed orange line is unphysical. b, c 2D square and honeycomb lattices. The solid line connecting the circles represents the mixed-state CSC, while the dashed line connecting the triangles represents the pure-state CSC. Here L denotes the side length of the 2D lattices.

Full size image

Finite-size scaling analysis further shows that CSC exhibits an exponential cutoff: \({C}_{{{\rm{SC}}}} \sim {e}^{-l/{l}^{* }}\) with respect to the shortest path length l between S and T when the Bethe lattice (k = 3) has finite l layers. The characteristic length l* quantifying the cutoff diverges as a power law upon approaching the percolation threshold cth12. For both pure- and mixed-state ConPT, we identify the same critical behavior l* ~ ∣c − cth∣−1 in the Bethe lattice (Supplementary Note 5).

2D lattices

In 2D square and honeycomb lattices, all nodes on the left boundary are connected to a common “mega node” S, while all nodes on the right boundary are connected to a common “mega node” T, with these connecting links assigned a unit weight (c = 1). The value of CSC is determined not only through series and parallel rules but also by employing the SM transform. In 2D square and honeycomb lattices, where an analytical threshold cannot be derived as in the Bethe lattice case, we predict the percolation threshold in the thermodynamic limit (n → ∞) by employing finite-size scaling: the threshold is identified as the intersection point of the CSC curves across different lattice sizes. The behaviors of CSC for different lattice sizes L are presented in Fig. 2b, c. The vertical solid and dashed lines represent the thresholds predicted by mixed-state and pure-state ConPT, respectively. We again find \({c}_{{{\rm{th}}}}^{{{\rm{mixed}}}} < {c}_{{{\rm{th}}}}^{{{\rm{pure}}}}\) for both 2D lattices.

General topologies

Our results show that all mixed-state thresholds for the three different network topologies are lower than those of their pure-state counterparts (Table 2). It is straightforward to see that this observation must be rooted in the difference between the pure-state and mixed-state parallel rules (Table 1). This prompts us to define \(\delta ({c}_{1},{c}_{2},\ldots ,{c}_{n})={{\rm{Para}}}{({c}_{1},{c}_{2},\ldots ,{c}_{n})}^{{{\rm{mixed}}}}-{{\rm{Para}}}{({c}_{1},{c}_{2},\ldots ,{c}_{n})}^{{{\rm{pure}}}}.\) If δ(c1, c2, …, cn)≥0, we can demonstrate that \({C}_{{{\rm{SC}}}}^{{{\rm{mixed}}}}\ge {C}_{{{\rm{SC}}}}^{{{\rm{pure}}}}\) for any network topology \({{{\mathcal{G}}}}_{F}(n)\), which further leads to the conclusion that \({c}_{{{\rm{th}}}}^{{{\rm{mixed}}}}\le {c}_{{{\rm{th}}}}^{{{\rm{pure}}}}\) in the n → ∞ limit.

Table 2 Comparison of percolation thresholds cth between pure-state and mixed-state concurrence percolation on different lattices
Full size table

Given the scalability of the parallel rule [Eq. (7)], it is sufficient to show δ(c1, c2)≥0. We derive:

$$\delta \left({c}_{1},{c}_{2}\right)=\left\{\begin{array}{ll}g-2\sqrt{f-{f}^{2}} & f\, > \frac{1}{2},\\ g-1 \hfill & f\le \frac{1}{2},\\ \end{array}\right.$$
(8)

where \(g=\left({c}_{1}+{c}_{2}\right)/\left(1+{c}_{1}{c}_{2}\right)\) and \(f=\frac{1+\sqrt{1-{c}_{1}^{2}}}{2}\frac{1+\sqrt{1-{c}_{2}^{2}}}{2}.\) We find that the minimum value of δ(c1, c2) is equal to zero and the maximum value is close to 0.142. Thus, δ (c1, c2)≥0 holds.

Non-deterministic mixed-state concurrence percolation

The inequality \({c}_{{{\rm{th}}}}^{{{\rm{mixed}}}}\le {c}_{{{\rm{th}}}}^{{{\rm{pure}}}}\) yields the following result: it suggests that stochastic noise is less detrimental than unitary noise. The underlying reason for this is subtle: the parallel rule for our mixed-state ConPT is not deterministic LOCC. Therefore, it has a finite probability of failure—an additional complication for our mixed-state ConPT. This stands in contrast to pure-state ConPT, which implements the parallel rule via the entanglement concentration protocol46, a process that, according to Nielsen’s theorem, can be made deterministic8.

In principle, the parallel rule for mixed-state ConPT could still be rendered deterministic by using quantum memories to selectively store only successful purification outcomes. This approach would require k − 1 pairs of memories for each layer of the Bethe lattice to store the k − 1 successfully purified entangled states. However, the stringent memory capacity this demands makes the strategy experimentally challenging. In the following, we no longer assume that the purification protocol is always successful and explicitly account for the probabilistic nature of the parallel rule.

Bethe lattice

We reconsider the mixed-state ConPT for the Bethe lattice. The consideration of success probability could be effectively regarded as a “dilution” of the degree k (or more precisely, the excess degree k − 147,48) of the Bethe lattice. Specifically, we need to make the change

$$\left(k-1\right)\to {{\rm{P}}}({c}_{1},\ldots ,{c}_{k-1})\cdot \left(k-1\right),$$
(9)

where

$$\begin{array}{rl} & {{\rm{P}}}({c}_{1},\ldots ,{c}_{k-1})=\frac{{\prod }_{i=1}^{k-1}(1+{c}_{i})+{\prod }_{i=1}^{k-1}(1-{c}_{i})}{{2}^{k-1}}\end{array}$$
(10)

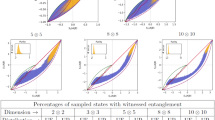
is the success probability of purifying all k − 1 links of concurrences c1, c2, …, ck−1 (Supplementary Note 2). We then calculate the sponge-crossing concurrence CSC on the diluted Bethe lattice. By exploiting the lattice’s self-similar structure, we obtain an exact solution for CSC as a function of c for various k (Fig. 3a). The physical branch of this solution reveals a discontinuous phase transition49 (Fig. 3b). This result contrasts with continuous transitions typically observed in pure-state ConPT or classical percolation. We hypothesize that the reason for this result lies in the nature of Eq. (9). This equation offers a self-averaged solution, which assumes every layer of the diluted Bethe lattice produces an identical (non-integer) number of branches. In reality, the probabilistic process of Eq. (10) implies a heterogeneous dilution, where some layers successfully generate many branches while others produce few or none. We speculate that properly accounting for this heterogeneity could restore the continuous nature of the phase transition, or even smear it out entirely50. A full analysis of such heterogeneous effects is nevertheless beyond the scope of the present work.

Fig. 3: Non-deterministic mixed-state concurrence percolation in Bethe lattices.
figure 3

The concurrence of each link, c, and the sponge-crossing concurrence, CSC, are plotted on the x-axis and y-axis, respectively. The degree of the Bethe lattice is denoted by k. a The sponge-crossing concurrence CSC with respect to c in Bethe lattices for k = 3 to k = 11. The dashed lines represent solutions that are not physical. b The physical part of CSC. The thresholds are marked by vertical dotted lines. The inset displays a magnified view of the physical part of CSC for c values in the range of 0.719 to 0.745.

Full size image

Accepting the self-averaging treatment [Eq. (9)], we can determine the percolation threshold cth precisely; the results are given in Table 3. While an exact analytical solution for the threshold as a function of k is unavailable, our numerical analysis yields an effective approximate solution (Supplementary Note 6):

$${c}_{{{\rm{th}}}}\approx \frac{2}{3}\cdot \frac{{5}^{m}+1}{{5}^{m}-1},$$
(11)

where \(m=(k-1)\left({5}^{k-1}+1\right)/{6}^{k-1}\). This nontrivial threshold demonstrates that long-distance entanglement distribution remains achievable in QNs affected by bit-flip error, even when accounting for the probabilistic nature of the parallel rule. Interestingly, the threshold shows a nonmonotonic dependence on k, in stark contrast to the strictly decreasing behavior previously observed. We find that the threshold value decreases from k = 3 until k = 6, reaching a minimum of cth ≈ 0.72 at k = 6, and then increases from k = 6 to k = 11. Most importantly, the thresholds in the diluted Bethe lattice significantly exceed those of the pure-state case, particularly for large k. This key finding reverses the previously counterintuitive inequality, yielding \({c}_{{{\rm{th}}}}^{{{\rm{mixed}}}}\ge {c}_{{{\rm{th}}}}^{{{\rm{pure}}}}\), confirming the expectation that stochastic noise is indeed more detrimental than unitary noise.

Table 3 Percolation thresholds of non-deterministic mixed-state concurrence percolation in Bethe lattices
Full size table

2D square lattice

Unlike the Bethe lattice, the 2D square lattice contains loops that place it outside the category of series-parallel networks. Although they are self-similar, we cannot apply the same method of “diluting" node degrees. Instead, we incorporate probabilistic effects by calculating the expected value of the parallel rule, replacing the deterministic version with its probabilistic expectation:

$${{\rm{Para}}}({c}_{1},\ldots ,{c}_{n})\to {{\rm{Para}}}({c}_{1},\ldots ,{c}_{n})\cdot {{\rm{P}}}({c}_{1},\ldots ,{c}_{n}).$$
(12)

The obtained threshold of 0.92(7) is higher than that of the pure-state scenario (Fig. 4). This again hints that stochastic noise is indeed more detrimental than unitary noise. Furthermore, we observe that the phase transition changes from continuous to seemingly discontinuous with increasing L, consistent with the observation for the Bethe lattices.

Fig. 4: Non-deterministic mixed-state concurrence percolation in 2D square lattices.
figure 4

The concurrence of each link, c, and the sponge-crossing concurrence, CSC, are plotted on the x-axis and y-axis, respectively. L denotes the side length of the 2D square lattices. The vertical line represents the threshold predicted by probabilistic mixed-state ConPT when L → ∞. The new threshold cth = 0.92(7) is higher than the pure-state cth = 0.62(3) (Table 2).

Full size image

Discussion

In this paper, we establish a mixed-state ConPT for QNs subject to bit-flip noise, providing a direct and efficient framework for analyzing realistic systems. Our approach simplifies practical implementation by using scalable operations on a wide class of mixed states. The analysis reveals complex physics centered on the system’s concurrence percolation threshold, informing the comparison between stochastic (bit-flip) noise versus unitary (purity-preserving) noise, which provides the first quantitative insight into the impact of different kinds of noise on entanglement percolation.

Two limitations in the current work warrant discussion. First, our final result relies on the self-averaging treatment of Eq. (9). A more complete treatment is necessary to determine if the relationship \({c}_{{{\rm{th}}}}^{{{\rm{mixed}}}}\ge {c}_{{{\rm{th}}}}^{{{\rm{pure}}}}\) is truly ubiquitous. We hypothesize that a more rigorous model must go beyond the ConPT framework to incorporate the success probability of the underlying protocols, exploring the interdependence between these two quantities—namely classical probability versus quantum entanglement. Furthermore, our analysis is specific to the class of mixed states generated by bit-flip noise. It remains an open question whether our conclusions generalize to QNs experiencing other forms of decoherence. Exploring QNs with alternative types of mixed states may present a significant challenge.

We hope that our work lays the groundwork for several critical future directions. For example, it is unknown whether scalable purification protocols that are more efficient could be found, leading to further lower thresholds. Also, we note that the probabilistic nature of purification induces a classical percolation process on the network through link removal. This insight is particularly promising because it opens the possibility of applying preprocessing strategies to the QN11. By optimizing the network’s topology before the main entanglement percolation process, such strategies could lead to different and potentially enhanced percolation thresholds.