Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Perspective
  • Published:

Physics-driven learning for inverse problems in quantum chromodynamics

Nature Reviews Physics volume 7, pages 154–163 (2025)Cite this article

Subjects

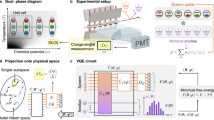
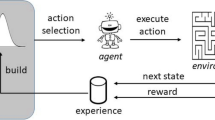
Abstract

The integration of deep learning techniques and physics-driven designs is reforming the way we address inverse problems, in which accurate physical properties are extracted from complex observations. This is particularly relevant for quantum chromodynamics (QCD) — the theory of strong interactions — with its inherent challenges in interpreting observational data and demanding computational approaches. This Perspective highlights advances of physics-driven learning methods, focusing on predictions of physical quantities towards QCD physics and drawing connections to machine learning. Physics-driven learning can extract quantities from data more efficiently in a probabilistic framework because embedding priors can reduce the optimization effort. In the application of first-principles lattice QCD calculations and QCD physics of hadrons, neutron stars and heavy-ion collisions, we focus on learning physically relevant quantities, such as perfect actions, spectral functions, hadron interactions, equations of state and nuclear structure. We also emphasize the potential of physics-driven designs of generative models beyond QCD physics.

Key points

  • Inverse problems in physical sciences determine causes or parameters from observations.

  • Physics-driven learning integrates domain-specific physical knowledge into machine learning to solve inverse problems.

  • Physics-driven learning can help to extract physical properties and build probability distributions from data.

  • In quantum chromodynamics, physics-driven learning can deduce hadron forces, dense matter equations of state, and nuclear structure.

  • Physics-driven designs can innovate the development of deep learning and generative models.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Physics-driven designs for deep learning.
Fig. 2: A lattice gauge-equivariant convolutional neural network (L-CNN).
Fig. 3: Automatic differential framework to reconstruct hadron spectral functions from observations78.
Fig. 4: The ill-posed inverse problem from observational data to theory in the context of neutron star physics.
Fig. 5: Quantum chromodynamics (QCD) transition binary classification using convolutional neural networks (CNNs) with final particle spectra from heavy-ion collisions as input.

Similar content being viewed by others

References

  1. Gross, F. et al. 50 years of quantum chromodynamics. Eur. Phys. J. C 83, 1125 (2023).

    Article  ADS  MATH  Google Scholar 

  2. Gattringer, C & Lang, C. B. Quantum Chromodynamics on the Lattice Vol. 788 (Springer, 2010).

  3. Baym, G. et al. From hadrons to quarks in neutron stars: a review. Rept. Prog. Phys. 81, 056902 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Yagi, K., Hatsuda, T. & Miake, Y. Quark-Gluon Plasma: From Big Bang to Little Bang Vol. 23 (Cambridge Univ. Press, 2005).

  5. Tanaka, A., Tomiya, A. & Hashimoto, K. Deep Learning and Physics Vol. 1 (Springer, 2021).

  6. Zhou, K., Wang, L., Pang, L.-G. & Shi, S. Exploring QCD matter in extreme conditions with machine learning. Prog. Part. Nucl. Phys. 135, 104084 (2024).

    Article  MATH  Google Scholar 

  7. Kaipio, J. & Somersalo, E. Statistical and Computational Inverse Problems Vol. 160 (Springer, 2006).

  8. Asakawa, M., Hatsuda, T. & Nakahara, Y. Maximum entropy analysis of the spectral functions in lattice QCD. Prog. Part. Nucl. Phys. 46, 459–508 (2001).

    Article  ADS  MATH  Google Scholar 

  9. Yunes, N., Miller, M. C. & Yagi, K. Gravitational-wave and X-ray probes of the neutron star equation of state. Nat. Rev. Phys. 4, 237–246 (2022).

    Article  MATH  Google Scholar 

  10. Boehnlein, A. et al. Colloquium: machine learning in nuclear physics. Rev. Mod. Phys. 94, 031003 (2022).

    Article  ADS  Google Scholar 

  11. LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).

    Article  ADS  MATH  Google Scholar 

  12. Bishop, C. M. & Bishop, H. Deep learning: Foundations and Concepts (Springer Nature, 2023).

  13. Raissi, M., Perdikaris, P. & Karniadakis, G. E. Physics informed deep learning (part I): data-driven solutions of nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Thuerey, N. et al. Physics-based deep learning. Preprint at https://doi.org/10.48550/arXiv.2109.05237 (2021).

  15. Carleo, G. et al. Machine learning and the physical sciences. Rev. Mod. Phys. 91, 045002 (2019).

    Article  ADS  MATH  Google Scholar 

  16. LeCun, Y., Chopra, S., Hadsell, R., Ranzato, M. & Huang, F. in Predicting Structured Data 191–246 (MIT Press, 2007).

  17. Jaynes, E. T. Information theory and statistical mechanics. Phys. Rev. 106, 620–630 (1957).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Sohl-Dickstein, J., Weiss, E. A., Maheswaranathan, N. & Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In ICML'15: Proc. 32nd International Conference on International Conference on Machine Learning (ICML, 2015).

  19. Müller, B, Reinhardt, J & Strickland, M. T. Neural Networks: An Introduction (Springer, 1995).

  20. Murphy, K. P. Machine Learning: A Probabilistic Perspective (MIT Press, 2012).

  21. Jin, K. H., McCann, M. T., Froustey, E. & Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 26, 4509–4522 (2017).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. Amin, G. R. & Emrouznejad, A. Inverse forecasting: a new approach for predictive modeling. Comput. Ind. Eng. 53, 491–498 (2007).

    Article  MATH  Google Scholar 

  23. Behrmann, J., Grathwohl, W., Chen, R. T., Duvenaud, D. & Jacobsen, J.-H. Invertible residual networks. In International Conference on Machine Learning 573–582 (PMLR, 2019).

  24. Qi, C. R., Su, H., Mo, K. & Guibas, L. J. PointNet: deep learning on point sets for 3D classification and segmentation. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 652–660 (IEEE, 2017).

  25. Tomiya, A. & Nagai, Y. Equivariant transformer is all you need. Proc. Sci. 453, 001 (2024).

    Google Scholar 

  26. Raissi, M., Perdikaris, P. & Karniadakis, G. E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Mattheakis, M., Protopapas, P., Sondak, D., Di Giovanni, M. & Kaxiras, E. Physical symmetries embedded in neural networks. Preprint at https://doi.org/10.48550/arXiv.1904.08991 (2019).

  28. Zhang, W., Tanida, J., Itoh, K. & Ichioka, Y. Shift-invariant pattern recognition neural network and its optical architecture. In Proc. Annual Conference of the Japan Society of Applied Physics 6p-M-14, 734 (JSAP, 1988).

  29. Geiger, M. & Smidt, T. e3nn: Euclidean neural networks. Preprint at https://doi.org/10.48550/arXiv.2207.09453 (2022).

  30. Shlomi, J., Battaglia, P. & Vlimant, J.-R. Graph neural networks in particle physics. Mach. Learn. Sci. Technol. 2, 021001 (2020).

    Article  MATH  Google Scholar 

  31. Kanwar, G. et al. Equivariant flow-based sampling for lattice gauge theory. Phys. Rev. Lett. 125, 121601 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Favoni, M., Ipp, A., Müller, D. I. & Schuh, D. Lattice gauge equivariant convolutional neural networks. Phys. Rev. Lett. 128, 032003 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  33. Cranmer, K., Kanwar, G., Racanière, S., Rezende, D. J. & Shanahan, P. E. Advances in machine-learning-based sampling motivated by lattice quantum chromodynamics. Nat. Rev. Phys. 5, 526–535 (2023).

    Article  Google Scholar 

  34. Han, M.-Z., Jiang, J.-L., Tang, S.-P. & Fan, Y.-Z. Bayesian nonparametric inference of the neutron star equation of state via a neural network. Astrophys. J. 919, 11 (2021).

    Article  ADS  MATH  Google Scholar 

  35. Shi, S., Wang, L. & Zhou, K. Rethinking the ill-posedness of the spectral function reconstruction — why is it fundamentally hard and how artificial neural networks can help. Comput. Phys. Commun. 282, 108547 (2023).

    Article  MathSciNet  MATH  Google Scholar 

  36. Karniadakis, G. E. et al. Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440 (2021).

    Article  MATH  Google Scholar 

  37. Baydin, A. G., Pearlmutter, B. A., Radul, A. A. & Siskind, J. M. Automatic differentiation in machine learning: a survey. J. Mach. Learn. Res. 18, 1–43 (2018).

    MathSciNet  MATH  Google Scholar 

  38. Cranmer, K., Brehmer, J. & Louppe, G. The frontier of simulation-based inference. Proc. Natl Acad. Sci. USA 117, 30055–30062 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Wang, H. et al. Scientific discovery in the age of artificial intelligence. Nature 620, 47–60 (2023).

    Article  ADS  MATH  Google Scholar 

  40. Jalali, B., Zhou, Y., Kadambi, A. & Roychowdhury, V. Physics-AI symbiosis. Mach. Learn. Sci. Technol. 3, 041001 (2022).

    Article  ADS  Google Scholar 

  41. Aarts, G. Introductory lectures on lattice QCD at nonzero baryon number. J. Phys. Conf. Ser. 706, 022004 (2016).

    Article  MATH  Google Scholar 

  42. Boyda, D. et al. Applications of machine learning to lattice quantum field theory. Preprint at https://doi.org/10.48550/arXiv.2202.05838 (2022).

  43. Hasenfratz, P. & Niedermayer, F. Perfect lattice action for asymptotically free theories. Nucl. Phys. B 414, 785–814 (1994).

    Article  ADS  MATH  Google Scholar 

  44. DeGrand, T. A., Hasenfratz, A., Hasenfratz, P. & Niedermayer, F. The classically perfect fixed point action for SU(3) gauge theory. Nucl. Phys. B 454, 587–614 (1995).

    Article  ADS  MATH  Google Scholar 

  45. Shanahan, P. E., Trewartha, A. & Detmold, W. Machine learning action parameters in lattice quantum chromodynamics. Phys. Rev. D 97, 094506 (2018).

    Article  ADS  MATH  Google Scholar 

  46. Nagai, Y., Tanaka, A. & Tomiya, A. Self-learning Monte Carlo for non-Abelian gauge theory with dynamical fermions. Phys. Rev. D 107, 054501 (2023).

    Article  ADS  MathSciNet  Google Scholar 

  47. Blücher, S., Kades, L., Pawlowski, J. M., Strodthoff, N. & Urban, J. M. Towards novel insights in lattice field theory with explainable machine learning. Phys. Rev. D 101, 094507 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  48. Holland, K., Ipp, A., Müller, D. I. & Wenger, U. Fixed point actions from convolutional neural networks. Proc. Sci. 453, 038 (2024).

    Google Scholar 

  49. Holland, K., Ipp, A., Müller, D. I. & Wenger, U. Machine learning a fixed point action for SU(3) gauge theory with a gauge equivariant convolutional neural network. Phys. Rev. D 110, 074502 (2024).

    Article  MathSciNet  Google Scholar 

  50. Zhou, K., Endrődi, G., Pang, L.-G. & Stöcker, H. Regressive and generative neural networks for scalar field theory. Phys. Rev. D 100, 011501 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  51. Pawlowski, J. M. & Urban, J. M. Reducing autocorrelation times in lattice simulations with generative adversarial networks. Mach. Learn. Sci. Tech. 1, 045011 (2020).

    Article  MATH  Google Scholar 

  52. Kanwar, G. Flow-based sampling for lattice field theories. In 40th International Symposium on Lattice Field Theory (Proceedings of Science, 2024); https://doi.org/10.22323/1.453.0114.

  53. Song, Y. et al. Score-based generative modeling through stochastic differential equations. In NIPS '23: Proceedings of the 37th International Conference on Neural Information Processing Systems 37799–37812 (ACM, 2020).

  54. Parisi, G. & Wu, Y. S. Perturbation theory without gauge fixing. Sci. Sin. 24, 483 (1980).

    MathSciNet  MATH  Google Scholar 

  55. Wang, L., Aarts, G. & Zhou, K. Diffusion models as stochastic quantization in lattice field theory. J. High Energy Phys. 05, 060 (2024).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  56. Wang, L., Aarts, G. & Zhou, K. Generative diffusion models for lattice field theory. In 37th Conference on Neural Information Processing Systems 21 (2023).

  57. Zhu, Q., Aarts, G., Wang, W., Zhou, K. & Wang, L. Diffusion models for lattice gauge field simulations. In 38th conference on Neural Information Processing Systems 14 (2024).

  58. Hirono, Y., Tanaka, A. & Fukushima, K. Understanding diffusion models by Feynman’s path integral. In Proc. 41st International Conference on Machine Learning (PMLR, 2024).

  59. Cotler, J. & Rezchikov, S. Renormalizing diffusion models. Preprint at https://doi.org/10.48550/arXiv.2308.12355 (2023).

  60. Müller, T., McWilliams, B., Rousselle, F., Gross, M. & Novák, J. Neural importance sampling. ACM Trans. Graph. 38, 1–19 (2019).

    Article  Google Scholar 

  61. Ron, D., Swendsen, R. H. & Brandt, A. Inverse Monte Carlo renormalization group transformations for critical phenomena. Phys. Rev. Lett. 89, 275701 (2002).

    Article  ADS  MATH  Google Scholar 

  62. Bachtis, D., Aarts, G., Di Renzo, F. & Lucini, B. Inverse renormalization group in quantum field theory. Phys. Rev. Lett. 128, 081603 (2022).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  63. Bachtis, D. Inverse renormalization group of spin glasses. Phys. Rev. B 110, L140202 (2023).

    Article  MATH  Google Scholar 

  64. Lehner, C. & Wettig, T. Gauge-equivariant neural networks as preconditioners in lattice QCD. Phys. Rev. D 108, 034503 (2023).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  65. Aronsson, J., Müller, D. I. & Schuh, D. Geometrical aspects of lattice gauge equivariant convolutional neural networks. Preprint https://doi.org/10.48550/arXiv.2303.11448 (2023).

  66. Lehner, C. & Wettig, T. Gauge-equivariant pooling layers for preconditioners in lattice QCD. Phys. Rev. D 110, 034517 (2023).

    Article  MathSciNet  MATH  Google Scholar 

  67. Cohen, T. S. & Welling, M. Group equivariant convolutional networks. In Proceedings of The 33rd International Conference on Machine Learning Vol. 48, 2990–2999 (PMLR, 2016).

  68. Cohen, T. S., Weiler, M., Kicanaoglu, B. & Welling, M. Gauge equivariant convolutional networks and the icosahedral CNN. Proc. 36th International Conference on Machine Learning Vol. 97, 1321–1330 (PMLR, 2019).

  69. Carrasquilla, J. & Melko, R. G. Machine learning phases of matter. Nat. Phys. 13, 431–434 (2017).

    Article  MATH  Google Scholar 

  70. Wetzel, S. J. & Scherzer, M. Machine learning of explicit order parameters: from the Ising model to SU(2) lattice gauge theory. Phys. Rev. B 96, 184410 (2017).

    Article  ADS  MATH  Google Scholar 

  71. Boyda, D. L. et al. Finding the deconfinement temperature in lattice Yang-Mills theories from outside the scaling window with machine learning. Phys. Rev. D 103, 014509 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  72. Lee, J. et al. Deep neural networks as Gaussian processes. Preprint at https://doi.org/10.48550/arXiv.1711.00165 (2018).

  73. Halverson, J., Maiti, A. & Stoner, K. Neural networks and quantum field theory. Mach. Learn. Sci. Tech. 2, 035002 (2021).

    Article  MATH  Google Scholar 

  74. Bachtis, D., Aarts, G. & Lucini, B. Quantum field-theoretic machine learning. Phys. Rev. D 103, 074510 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  75. Aarts, G., Lucini, B. & Park, C. Scalar field restricted Boltzmann machine as an ultraviolet regulator. Phys. Rev. D 109, 034521 (2024).

    Article  ADS  MathSciNet  Google Scholar 

  76. Aarts, G., Lucini, B. & Park, C. Stochastic weight matrix dynamics during learning and Dyson Brownian motion. Preprint at https://doi.org/10.48550/arXiv.2407.16427 (2024).

  77. Rothkopf, A. Heavy quarkonium in extreme conditions. Phys. Rept. 858, 1–117 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  78. Wang, L., Shi, S. & Zhou, K. Reconstructing spectral functions via automatic differentiation. Phys. Rev. D 106, L051502 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  79. Guo, F.-K. et al. Hadronic molecules. Rev. Mod. Phys. 90, 015004 (2018).

    Article  ADS  Google Scholar 

  80. Sombillo, D. L. B., Ikeda, Y., Sato, T. & Hosaka, A. Classifying the pole of an amplitude using a deep neural network. Phys. Rev. D 102, 016024 (2020).

    Article  ADS  Google Scholar 

  81. Sombillo, D. L. B., Ikeda, Y., Sato, T. & Hosaka, A. Model independent analysis of coupled-channel scattering: a deep learning approach. Phys. Rev. D 104, 036001 (2021).

    Article  ADS  MATH  Google Scholar 

  82. Albaladejo, M. et al. Novel approaches in hadron spectroscopy. Prog. Part. Nucl. Phys. 127, 103981 (2022).

    Article  MATH  Google Scholar 

  83. Ng, L. et al. Deep learning exotic hadrons. Phys. Rev. D 105, L091501 (2022).

    Article  ADS  MATH  Google Scholar 

  84. Keeble, J. W. T. & Rios, A. Machine learning the deuteron. Phys. Lett. B 809, 135743 (2020).

    Article  MATH  Google Scholar 

  85. Adams, C., Carleo, G., Lovato, A. & Rocco, N. Variational Monte Carlo calculations of A ≤ 4 nuclei with an artificial neural-network correlator ansatz. Phys. Rev. Lett. 127, 022502 (2021).

    Article  ADS  MATH  Google Scholar 

  86. Ishii, N., Aoki, S. & Hatsuda, T. The nuclear force from lattice QCD. Phys. Rev. Lett. 99, 022001 (2007).

    Article  ADS  MATH  Google Scholar 

  87. Aoki, S. et al. Lattice QCD approach to nuclear physics. Prog. Theor. Exp. Phys. 2012, 01A105 (2012).

    Article  MATH  Google Scholar 

  88. Aoki, S. & Doi, T. in Handbook of Nuclear Physics 1–31 (Springer, 2023).

  89. Collaboration, A. et al. Unveiling the strong interaction among hadrons at the LHC. Nature 588, 232–238 (2020).

    Article  ADS  MATH  Google Scholar 

  90. Lyu, Y. et al. Doubly charmed tetraquark \({T}_{cc}^{+}\) in (2+1)-flavor QCD near physical point. Proc. Sci. 453, 077 (2024).

    MATH  Google Scholar 

  91. Shi, S., Zhou, K., Zhao, J., Mukherjee, S. & Zhuang, P. Heavy quark potential in the quark-gluon plasma: deep neural network meets lattice quantum chromodynamics. Phys. Rev. D 105, 014017 (2022).

    Article  ADS  Google Scholar 

  92. Wang, L., Doi, T., Hatsuda, T. & Lyu, Y. Building hadron potentials from lattice QCD with deep neural networks. Preprint at https://doi.org/10.48550/arXiv.2410.03082 (2024).

  93. Fukushima, K., Mohanty, B. & Xu, N. Little-bang and femto-nova in nucleus-nucleus collisions. AAPPS Bull. 31, 1 (2021).

    Article  ADS  MATH  Google Scholar 

  94. Steiner, A. W., Lattimer, J. M. & Brown, E. F. The neutron star mass-radius relation and the equation of state of dense matter. Astrophys. J. Lett. 765, L5 (2013).

    Article  ADS  MATH  Google Scholar 

  95. Ozel, F. et al. The dense matter equation of state from neutron star radius and mass measurements. Astrophys. J. 820, 28 (2016).

    Article  ADS  MATH  Google Scholar 

  96. Brandes, L., Weise, W. & Kaiser, N. Inference of the sound speed and related properties of neutron stars. Phys. Rev. D 107, 014011 (2023).

    Article  ADS  MATH  Google Scholar 

  97. Fujimoto, Y., Fukushima, K. & Murase, K. Mapping neutron star data to the equation of state using the deep neural network. Phys. Rev. D 101, 054016 (2020).

    Article  ADS  MATH  Google Scholar 

  98. Carvalho, V., Ferreira, M., Malik, T. & Providência, C. Decoding neutron star observations: revealing composition through Bayesian neural networks. Phys. Rev. D 108, 043031 (2023).

    Article  ADS  MathSciNet  Google Scholar 

  99. Carvalho, V., Ferreira, M. & Providência, C. From NS observations to nuclear matter properties: a machine learning approach. Phys. Rev. D 109, 123038 (2024).

    Article  MATH  Google Scholar 

  100. Soma, S., Wang, L., Shi, S., Stöcker, H. & Zhou, K. Neural network reconstruction of the dense matter equation of state from neutron star observables. J. Cosmol. Astropart. Phys. 08, 071 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  101. Soma, S., Wang, L., Shi, S., Stöcker, H. & Zhou, K. Reconstructing the neutron star equation of state from observational data via automatic differentiation. Phys. Rev. D 107, 083028 (2023).

    Article  ADS  Google Scholar 

  102. Fujimoto, Y., Fukushima, K. & Murase, K. Extensive studies of the neutron star equation of state from the deep learning inference with the observational data augmentation. J. High Energy Phys. 03, 273 (2021).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  103. Bass, S. A., Bernhard, J. E. & Moreland, J. S. Determination of quark-gluon-plasma parameters from a global Bayesian analysis. Nucl. Phys. A 967, 67–73 (2017).

    Article  ADS  MATH  Google Scholar 

  104. Pang, L.-G. et al. An equation-of-state-meter of quantum chromodynamics transition from deep learning. Nature Commun. 9, 210 (2018).

    Article  ADS  MATH  Google Scholar 

  105. Du, Y.-L. et al. Identifying the nature of the QCD transition in heavy-ion collisions with deep learning. Nucl. Phys. A 1005, 121891 (2021).

    Article  Google Scholar 

  106. Steinheimer, J. et al. A machine learning study on spinodal clumping in heavy ion collisions. Nucl. Phys. A 1005, 121867 (2021).

    Article  Google Scholar 

  107. Jiang, L., Wang, L. & Zhou, K. Deep learning stochastic processes with QCD phase transition. Phys. Rev. D 103, 116023 (2021).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  108. Omana Kuttan, M., Zhou, K., Steinheimer, J., Redelbach, A. & Stoecker, H. An equation-of-state-meter for CBM using PointNet. J. High Energy Phys. 21, 184 (2020).

    Google Scholar 

  109. Pratt, S., Sangaline, E., Sorensen, P. & Wang, H. Constraining the eq. of state of super-hadronic matter from heavy-ion collisions. Phys. Rev. Lett. 114, 202301 (2015).

    Article  ADS  Google Scholar 

  110. Omana Kuttan, M., Steinheimer, J., Zhou, K. & Stoecker, H. QCD equation of state of dense nuclear matter from a Bayesian analysis of heavy-ion collision data. Phys. Rev. Lett. 131, 202303 (2023).

    Article  ADS  Google Scholar 

  111. Bernhard, J. E., Moreland, J. S. & Bass, S. A. Bayesian estimation of the specific shear and bulk viscosity of quark–gluon plasma. Nat. Phys. 15, 1113–1117 (2019).

    Article  MATH  Google Scholar 

  112. Everett, D. et al. Phenomenological constraints on the transport properties of QCD matter with data-driven model averaging. Phys. Rev. Lett. 126, 242301 (2021).

    Article  ADS  MATH  Google Scholar 

  113. Nijs, G., van der Schee, W., Gürsoy, U. & Snellings, R. Transverse momentum differential global analysis of heavy-ion collisions. Phys. Rev. Lett. 126, 202301 (2021).

    Article  ADS  Google Scholar 

  114. Li, F.-P., Lü, H.-L., Pang, L.-G. & Qin, G.-Y. Deep-learning quasi-particle masses from QCD equation of state. Phys. Lett. B 844, 138088 (2023).

    Article  MATH  Google Scholar 

  115. Cheng, Y.-L., Shi, S., Ma, Y.-G., Stöcker, H. & Zhou, K. Examination of nucleon distribution with Bayesian imaging for isobar collisions. Phys. Rev. C 107, 064909 (2023).

    Article  ADS  Google Scholar 

  116. Giacalone, G., Nijs, G. & van der Schee, W. Determination of the neutron skin of Pb208 from ultrarelativistic nuclear collisions. Phys. Rev. Lett. 131, 202302 (2023).

    Article  ADS  Google Scholar 

  117. David, C., Freslier, M. & Aichelin, J. Impact parameter determination for heavy-ion collisions by use of a neural network. Phys. Rev. C 51, 1453–1459 (1995).

    Article  ADS  MATH  Google Scholar 

  118. Bass, S. A., Bischoff, A., Maruhn, J. A., Stoecker, H. & Greiner, W. Neural networks for impact parameter determination. Phys. Rev. C 53, 2358–2363 (1996).

    Article  ADS  MATH  Google Scholar 

  119. De Sanctis, J. et al. Classification of the impact parameter in nucleus-nucleus collisions by a support vector machine method. J. Phys. G 36, 015101 (2009).

    Article  ADS  MATH  Google Scholar 

  120. Omana Kuttan, M., Steinheimer, J., Zhou, K., Redelbach, A. & Stoecker, H. A fast centrality-meter for heavy-ion collisions at the CBM experiment. Phys. Lett. B 811, 135872 (2020).

    Article  Google Scholar 

  121. Feickert, M. & Nachman, B. A living review of machine learning for particle physics. Preprint at https://doi.org/10.48550/arXiv.2102.02770 (2021).

  122. Hashimoto, K., Sugishita, S., Tanaka, A. & Tomiya, A. Deep learning and the AdS/CFT correspondence. Phys. Rev. D 98, 046019 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  123. Hashimoto, K., Sugishita, S., Tanaka, A. & Tomiya, A. Deep learning and holographic QCD. Phys. Rev. D 98, 106014 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  124. Cai, R.-G., He, S., Li, L. & Zeng, H.-A. QCD phase diagram at finite magnetic field and chemical potential: a holographic approach using machine learning. Preprint at https://doi.org/10.48550/arXiv.2406.12772 (2024).

  125. Kadambi, A., de Melo, C., Hsieh, C.-J., Srivastava, M. & Soatto, S. Incorporating physics into data-driven computer vision. Nat. Mach. Intell. 5, 572–580 (2023).

    Article  Google Scholar 

  126. Reichstein, M. et al. Deep learning and process understanding for data-driven earth system science. Nature 566, 195–204 (2019).

    Article  ADS  MATH  Google Scholar 

  127. Cichos, F., Gustavsson, K., Mehlig, B. & Volpe, G. Machine learning for active matter. Nat. Mach. Intell. 2, 94–103 (2020).

    Article  MATH  Google Scholar 

  128. Huerta, E. A. et al. Enabling real-time multi-messenger astrophysics discoveries with deep learning. Nat. Rev. Phys. 1, 600–608 (2019).

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank L. Brandes, Y. Fujimoto, S. Kamata, D. I. Müller, K. Murase, A. Tanaka and A. Tomiya for the helpful discussions and all collaborators for their contributions. The authors also thank the DEEP-IN working group at RIKEN-iTHEMS, the European Centre for Theoretical Studies in Nuclear Physics and Related Areas (ECT*), and the ExtreMe Matter Institute (EMMI) for their support in the preparation of this paper. G.A. is supported by STFC Consolidated Grant ST/T000813/1. K.F. is supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant numbers 22H01216 and 22H05118. T.H. is supported by the Japan Science and Technology Agency (JST) as part of Adopting Sustainable Partnerships for Innovative Research Ecosystem (ASPIRE), grant number JPMJAP2318. S.S. acknowledges Tsinghua University under grant number 53330500923. L.W. thanks the National Natural Science Foundation of China (number 12147101) for supporting his visit to Fudan University. K.Z. is supported by the CUHK-Shenzhen University Development Fund under grant numbers UDF01003041 and UDF03003041, and Shenzhen Peacock fund under grant number 2023TC0179.

Author information

Authors and Affiliations

  1. Department of Physics, Swansea University, Swansea, UK

    Gert Aarts

  2. Department of Physics, The University of Tokyo, Tokyo, Japan

    Kenji Fukushima

  3. Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS), RIKEN, Wako, Japan

    Tetsuo Hatsuda & Lingxiao Wang

  4. Institute for Theoretical Physics, TU Wien, Vienna, Austria

    Andreas Ipp

  5. Department of Physics, Tsinghua University, Beijing, China

    Shuzhe Shi

  6. School of Science and Engineering, The Chinese University of Hong Kong, Shenzhen, Guangdong, China

    Kai Zhou

  7. Frankfurt Institute for Advanced Studies, Frankfurt am Main, Germany

    Kai Zhou

Authors
  1. Gert Aarts
    View author publications

    Search author on:PubMed Google Scholar

  2. Kenji Fukushima
    View author publications

    Search author on:PubMed Google Scholar

  3. Tetsuo Hatsuda
    View author publications

    Search author on:PubMed Google Scholar

  4. Andreas Ipp
    View author publications

    Search author on:PubMed Google Scholar

  5. Shuzhe Shi
    View author publications

    Search author on:PubMed Google Scholar

  6. Lingxiao Wang
    View author publications

    Search author on:PubMed Google Scholar

  7. Kai Zhou
    View author publications

    Search author on:PubMed Google Scholar

Contributions

The authors contributed equally to all aspects of the article.

Corresponding author

Correspondence to Lingxiao Wang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Reviews Physics thanks Long-Gang Pang and Danilo Jimenez Rezende for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Glossary

Artificial neural networks

(ANNs). Models inspired by the structure and function of biological neural networks in human brains.

Convolutional neural networks

(CNNs). Excel with image, speech and audio inputs; they consist of three main types of layers: convolutional, pooling and fully connected layers.

Deep neural networks

Complex ANNs with multiple layers, including input, output and at least one hidden layer.

Recurrent neural networks

Bi-directional ANNs, unlike the uni-directional feedforward network; they allow outputs from nodes to influence subsequent inputs to the same nodes.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aarts, G., Fukushima, K., Hatsuda, T. et al. Physics-driven learning for inverse problems in quantum chromodynamics. Nat Rev Phys 7, 154–163 (2025). https://doi.org/10.1038/s42254-024-00798-x

Download citation

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s42254-024-00798-x

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing