Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Learning spatiotemporal dynamics with a pretrained generative model

Nature Machine Intelligence volume 6, pages 1566–1579 (2024)Cite this article

Subjects

A preprint version of the article is available at Research Square.

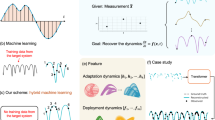
Abstract

Reconstructing spatiotemporal dynamics with sparse sensor measurement is a challenging task that is encountered in a wide spectrum of scientific and engineering applications. The problem is particularly challenging when the number or types of sensors (for example, randomly placed) are extremely sparse. Existing end-to-end learning models ordinarily do not generalize well to unseen full-field reconstruction of spatiotemporal dynamics, especially in sparse data regimes typically seen in real-world applications. To address this challenge, here we propose a sparse-sensor-assisted score-based generative model (S3GM) to reconstruct and predict full-field spatiotemporal dynamics on the basis of sparse measurements. Instead of learning directly the mapping between input and output pairs, an unconditioned generative model is first pretrained, capturing the joint distribution of a vast group of pretraining data in a self-supervised manner, followed by a sampling process conditioned on unseen sparse measurement. The efficacy of S3GM has been verified on multiple dynamical systems with various synthetic, real-world and laboratory-test datasets (ranging from turbulent flow modelling to weather/climate forecasting). The results demonstrate the sound performance of S3GM in zero-shot reconstruction and prediction of spatiotemporal dynamics even with high levels of data sparsity and noise. We find that S3GM exhibits high accuracy, generalizability and robustness when handling different reconstruction tasks.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Schematic illustration of the proposed S3GM framework.
Fig. 2: Reconstruction of KSE solutions under different types of sparse measurement.
Fig. 3: Reconstruction of Kolmogorov turbulent flow at a high Reynolds number that is not seen in training data.
Fig. 4: Reconstruction of the climate data in 2023 from incomplete and noisy observations, in which S3GM is pretrained using the historical data from 1979 to 2022.
Fig. 5: Reconstruction of the cylinder flow from different types of real-world experimental datum.

Similar content being viewed by others

Data availability

All datasets used in this work are available online. The datasets for the KSE and Kolmogorov flow are available via the Zenodo repository91 at https://doi.org/10.5281/zenodo.13925732. The ERA5 reanalysis data71 are available at https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=download. The datasets for the compressible Navier–Stokes equation and Burgers’ equation can be found in the GitHub repository of PDEBench90 at https://github.com/pdebench/PDEBench (see Supplementary Note 3 for details). Source data are provided with this paper.

Code availability

The source codes to reproduce the results in this study are available via a Code Ocean capsule at https://doi.org/10.24433/CO.6670426.v2 (ref. 92).

References

  1. Vinuesa, R., Brunton, S. L. & McKeon, B. J. The transformative potential of machine learning for experiments in fluid mechanics. Nat. Rev. Phys. 5, 536–545 (2023).

    Article  Google Scholar 

  2. Buzzicotti, M. Data reconstruction for complex flows using AI: recent progress, obstacles, and perspectives. Europhys. Lett. 142, 23001 (2023).

    Article  Google Scholar 

  3. Carrassi, A., Bocquet, M., Bertino, L. & Evensen, G. Data assimilation in the geosciences: an overview of methods, issues, and perspectives. Wiley Interdiscip. Rev. Clim. Chang. 9, e535 (2018).

    Article  Google Scholar 

  4. Kondrashov, D. & Ghil, M. Spatio-temporal filling of missing points in geophysical data sets. Nonlinear Process. Geophys. 13, 151–159 (2006).

    Article  Google Scholar 

  5. Akiyama, K. et al. First M87 Event Horizon Telescope results. III. Data processing and calibration. Astrophys. J. 875, L3 (2019).

    Article  Google Scholar 

  6. Tello Alonso, M., López-Dekker, P. & Mallorquí, J. J. A novel strategy for radar imaging based on compressive sensing. IEEE Trans. Geosci. Remote Sens. 48, 4285–4295 (2010).

    Article  Google Scholar 

  7. Fukami, K., Maulik, R., Ramachandra, N., Fukagata, K. & Taira, K. Global field reconstruction from sparse sensors with Voronoi tessellation-assisted deep learning. Nat. Mach. Intell. 3, 945–951 (2021).

    Article  Google Scholar 

  8. Chai, X. et al. Deep learning for irregularly and regularly missing data reconstruction. Sci. Rep. 10, 3302 (2020).

    Article  Google Scholar 

  9. Raissi, M., Yazdani, A. & Karniadakis, G. E. Hidden fluid mechanics: learning velocity and pressure fields from flow visualizations. Science 367, 1026–1030 (2020).

    Article  MathSciNet  Google Scholar 

  10. Hungarian, R. Hot-wire investigation of the wake behind cylinders at low Reynolds numbers. Proc. R. Soc. A 198, 174–190 (1949).

    Google Scholar 

  11. Koseff, J. R. & Street, R. L. The lid-driven cavity flow: a synthesis of qualitative and quantitative observations. J. Fluids Eng. Trans. ASME 106, 390–398 (1984).

    Article  Google Scholar 

  12. Berkooz, G., Holmes, P. & Lumley, J. L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575 (1993).

    Article  MathSciNet  Google Scholar 

  13. Everson, R. & Sirovich, L. Karhunen–Loève procedure for gappy data. J. Opt. Soc. Am. A 12, 1657–1664 (1995).

    Article  Google Scholar 

  14. Maurell, S., Boréel, J. & Lumley, J. L. Extended proper orthogonal decomposition: application to jet/vortex interaction. Flow Turbul. Combust. 67, 125–136 (2002).

    Article  Google Scholar 

  15. Borée, J. Extended proper orthogonal decomposition: a tool to analyse correlated events in turbulent flows. Exp. Fluids 35, 188–192 (2003).

    Article  Google Scholar 

  16. Arnoldi, T. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28 (2010).

    Article  MathSciNet  Google Scholar 

  17. Rowley, C. W., Mezi, I., Bagheri, S., Schlatter, P. & Henningson, D. S. Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127 (2009).

    Article  MathSciNet  Google Scholar 

  18. Schmid, P. J., Li, L., Juniper, M. P. & Pust, O. Applications of the dynamic mode decomposition. Theor. Comput. Fluid Dyn. 25, 249–259 (2011).

    Article  Google Scholar 

  19. Tu, J. H., Rowley, C. W., Luchtenburg, D. M., Brunton, S. L. & Kutz, J. N. On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1, 391–421 (2014).

    Article  MathSciNet  Google Scholar 

  20. Noack, B. R. & Eckelmann, H. A global stability analysis of the steady and periodic cylinder wake. J. Fluid Mech. 270, 297–330 (1994).

    Article  Google Scholar 

  21. Boisson, J. & Dubrulle, B. Three-dimensional magnetic field reconstruction in the VKS experiment through Galerkin transforms. New J. Phys. 13, 023037 (2011).

    Article  Google Scholar 

  22. Moin, P. Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559 (1988).

    Article  Google Scholar 

  23. Suzuki, T. & Hasegawa, Y. Estimation of turbulent channel flow at based on the wall measurement using a simple sequential approach. J. Fluid Mech. 830, 760–796 (2017).

    Article  MathSciNet  Google Scholar 

  24. Kim, H., Kim, J., Won, S. & Lee, C. Unsupervised deep learning for super-resolution reconstruction of turbulence. J. Fluid Mech. 910, A29 (2021).

    Article  MathSciNet  Google Scholar 

  25. Deng, Z., He, C., Liu, Y. & Kim, K. C. Super-resolution reconstruction of turbulent velocity fields using a generative adversarial network-based artificial intelligence framework. Phys. Fluids 31, 125111 (2019).

  26. Rao, C. et al. Encoding physics to learn reaction–diffusion processes. Nat. Mach. Intell. 5, 765–779 (2023).

    Article  Google Scholar 

  27. Karniadakis, G. E. et al. Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440 (2021).

    Article  Google Scholar 

  28. Cheng, S. et al. Machine learning with data assimilation and uncertainty quantification for dynamical systems: a review. IEEE/CAA J. Autom. Sin. 10, 1361–1387 (2023).

    Article  Google Scholar 

  29. Frerix, T. et al. Variational data assimilation with a learned inverse observation operator. Proc. Mach. Learn. Res. 139, 3449–3458 (2021).

  30. Takeishi, N. & Kalousis, A. Physics-integrated variational autoencoders for robust and interpretable generative modeling. Adv. Neural Inf. Process. Syst. 34, 14809–14821 (2021).

  31. Fukami, K., Fukagata, K. & Taira, K. Super-resolution analysis via machine learning: a survey for fluid flows. Theor. Comput. Fluid Dyn. 37, 421–444 (2023).

    Article  Google Scholar 

  32. Fukami, K., Fukagata, K. & Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 870, 106–120 (2019).

    Article  MathSciNet  Google Scholar 

  33. Güemes, A., Sanmiguel Vila, C. & Discetti, S. Super-resolution generative adversarial networks of randomly-seeded fields. Nat. Mach. Intell. 4, 1165–1173 (2022).

    Article  Google Scholar 

  34. Baddoo, P. J., Herrmann, B., McKeon, B. J., Nathan Kutz, J. & Brunton, S. L. Physics-informed dynamic mode decomposition. Proc. R. Soc. A 479, 20220576 (2023).

  35. Yin, Y. et al. PF-DMD: physics-fusion dynamic mode decomposition for accurate and robust forecasting of dynamical systems with imperfect data and physics. Preprint at https://arxiv.org/abs/2311.15604 (2023).

  36. Regazzoni, F., Pagani, S., Salvador, M., Dede’, L. & Quarteroni, A. Learning the intrinsic dynamics of spatio-temporal processes through Latent Dynamics Networks. Nat. Commun. 15, 1834 (2024).

    Article  Google Scholar 

  37. Krishnapriyan, A. S., Queiruga, A. F., Erichson, N. B. & Mahoney, M. W. Learning continuous models for continuous physics. Commun. Phys. 6, 319 (2023).

    Article  Google Scholar 

  38. Trask, N., Patel, R. G., Gross, B. J. & Atzberger, P. J. GMLS-Nets: a framework for learning from unstructured data. Preprint at https://arxiv.org/abs/1909.05371 (2019).

  39. Li, Z. et al. Fourier neural operator for parametric partial differential equations. In Proc. 9th International Conference on Learning Representations (OpenReview.net, 2021).

  40. Morra, P., Meneveau, C. & Zaki, T. A. ML for fast assimilation of wall-pressure measurements from hypersonic flow over a cone. Sci. Rep. 14, 12853 (2024).

    Article  Google Scholar 

  41. Zhao, Q., Lindell, D. B. & Wetzstein, G. Learning to solve PDE-constrained inverse problems with graph networks. Proc. 39th International Conference on Machine Learning Vol. 162, 26895–26910 (PMLR, 2022).

  42. Tang, M., Liu, Y. & Durlofsky, L. J. A deep-learning-based surrogate model for data assimilation in dynamic subsurface flow problems. J. Comput. Phys. 413, 109456 (2020).

    Article  MathSciNet  Google Scholar 

  43. Raissi, M., Perdikaris, P. & Karniadakis, G. E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019).

    Article  MathSciNet  Google Scholar 

  44. Lu, L., Meng, X., Mao, Z. & Karniadakis, G. E. DeepXDE: a deep learning library for solving differential equations. SIAM Rev 63, 208–228 (2021).

    Article  MathSciNet  Google Scholar 

  45. Jin, X., Cai, S., Li, H. & Karniadakis, G. E. NSFnets (Navier–Stokes flow nets): physics-informed neural networks for the incompressible Navier–Stokes equations. J. Comput. Phys. 426, 109951 (2021).

    Article  MathSciNet  Google Scholar 

  46. Kharazmi, E. et al. Identifiability and predictability of integer- and fractional-order epidemiological models using physics-informed neural networks. Nat. Comput. Sci. 1, 744–753 (2021).

    Article  Google Scholar 

  47. Huang, X. et al. Meta-Auto-Decoder for solving parametric partial differential equations. Adv. Neural Inf. Process. Syst. 35, 23426–23438 (2022).

    Google Scholar 

  48. Wang, S., Wang, H. & Perdikaris, P. Learning the solution operator of parametric partial differential equations with physics-informed DeepONets. Sci. Adv. 7, eabi8605 (2021).

    Article  Google Scholar 

  49. Krishnapriyan, A. S., Gholami, A., Zhe, S., Kirby, R. M. & Mahoney, M. W. Characterizing possible failure modes in physics-informed neural networks. Adv. Neural Inf. Process. Syst. 34, 26548–26560 (2021).

    Google Scholar 

  50. Wang, S., Yu, X. & Perdikaris, P. When and why PINNs fail to train: a neural tangent kernel perspective. J. Comput. Phys. 449, 110768 (2022).

    Article  MathSciNet  Google Scholar 

  51. Sohl-Dickstein, J., Weiss, E. A., Maheswaranathan, N. & Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. Proc. Mach. Learn. Res. 37, 2246–2255 (2015).

  52. Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 33, 6840–6851 (2020).

    Google Scholar 

  53. Song, Y. et al. Score-based generative modeling through stochastic differential equations. In Proc. 9th International Conference on Learning Representations (OpenReview.net, 2021).

  54. Hyvärinen, A. Estimation of non-normalized statistical models by score matching. J. Mach. Learn. Res. 6, 659–709 (2005).

    MathSciNet  Google Scholar 

  55. Song, Y. & Ermon, S. Generative modeling by estimating gradients of the data distribution. Adv. Neural Inf. Process. Syst. 32, 11918–11930 (2019).

    Google Scholar 

  56. Lugmayr, A. et al. RePaint: inpainting using denoising diffusion probabilistic models. In IEEE/CVF Conference on Computer Vision and Pattern Recognition 11451–11461 (IEEE, 2022).

  57. Chung, H., Kim, J., Mccann, M. T., Klasky, M. L. & Ye, J. C. Diffusion posterior sampling for general noisy inverse problems. In Proc. 11th International Conference on Learning Representations (OpenReview.net, 2023).

  58. Kawar, B., Ermon, S. & Elad, M. Denoising diffusion restoration models. Adv. Neural Inf. Process. Syst. 35, 23593–23606 (2022).

    Google Scholar 

  59. Song, J., Vahdat, A., Mardani, M. & Kautz, J. Pseudoinverse-guided diffusion models for inverse problems. In Proc. 11th International Conference on Learning Representations (OpenReview.net, 2023).

  60. Shu, D., Li, Z. & Barati, A. A physics-informed diffusion model for high-fidelity flow field reconstruction. J. Comput. Phys. 478, 111972 (2023).

    Article  MathSciNet  Google Scholar 

  61. Yang, G. & Sommer, S. A denoising diffusion model for fluid field prediction. Preprint at https://arxiv.org/abs/2301.11661 (2023).

  62. Lienen, M., Lüdke, D., Hansen-Palmus, J. & Günnemann, S. From zero to turbulence: generative modeling for 3D flow simulation. In Proc. 12th International Conference on Learning Representations (OpenReview.net, 2024).

  63. Cachay, S. R., Zhao, B., Joren, H. & Yu, R. DYffusion: a dynamics-informed diffusion model for spatiotemporal forecasting. Adv. Neural Inf. Processing Syst. 36, 45259–45287 (2023).

    Google Scholar 

  64. Li, T., Biferale, L., Bonaccorso, F., Scarpolini, M. A. & Buzzicotti, M. Synthetic Lagrangian turbulence by generative diffusion models. Nat. Mach. Intell. 6, 393–403 (2024).

    Article  Google Scholar 

  65. Drygala, C., Winhart, B., Di Mare, F. & Gottschalk, H. Generative modeling of turbulence. Phys. Fluids 34, 035114 (2022).

  66. Kim, J., Kim, J. & Lee, C. Prediction and control of two-dimensional decaying turbulence using generative adversarial networks. J. Fluid Mech. 981, A19 (2024).

    Article  MathSciNet  Google Scholar 

  67. Kuramoto, Y. & Tsuzuki, T. Persistent propagation of concentration waves in dissipative media far from thermal equilibrium. Prog. Theor. Phys. 55, 356–369 (1976).

    Article  Google Scholar 

  68. Chandler, G. J. & Kerswell, R. R. Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595 (2013).

    Article  MathSciNet  Google Scholar 

  69. Boffetta, G. & Ecke, R. E. Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451 (2011).

    Article  MathSciNet  Google Scholar 

  70. Kolmogorov, A. N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. A 434, 9–13 (1991).

  71. Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049 (2020).

    Article  Google Scholar 

  72. Akram, M., Hassanaly, M. & Raman, V. A priori analysis of reduced description of dynamical systems using approximate inertial manifolds. J. Comput. Phys. 409, 109344 (2020).

  73. Ronneberger, O., Fischer, P. & Brox, T. U-Net: convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015. Lecture Notes in Computer Science Vol. 9351 (eds Navab, N. et al.) 234–241 (Springer, 2015).

  74. Cao, Q., Goswami, S. & Karniadakis, G. E. Laplace neural operator for solving differential equations. Nat. Mach. Intell. 6, 631–640 (2024).

    Article  Google Scholar 

  75. Lu, L., Jin, P., Pang, G., Zhang, Z. & Karniadakis, G. E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 3, 218–229 (2021).

    Article  Google Scholar 

  76. Korteweg, D. J. & de Vries, G. XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 39, 422–443 (1895).

    Article  Google Scholar 

  77. Kochkov, D. et al. Machine learning-accelerated computational fluid dynamics. Proc. Natl Acad. Sci. USA 118, e2101784118 (2021).

    Article  MathSciNet  Google Scholar 

  78. Rombach, R., Blattmann, A., Lorenz, D. & Esser, P. High-resolution image synthesis with latent diffusion models. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition 10684–10695 (IEEE, 2022).

  79. Lu, C. et al. DPM-Solver: a fast ODE solver for diffusion probabilistic model sampling in around 10 steps. Adv. Neural Inf. Process. Systems 35, 5775–5787 (2022).

    Google Scholar 

  80. Lu, C. et al. DPM-SOLVER++: fast solver for guided sampling of diffusion probabilistic models. Preprint at https://arxiv.org/abs/2211.01095 (2022).

  81. Song, Y., Dhariwal, P., Chen, M. & Sutskever, I. Consistency models. Proc. Mach. Learn. Res. 202, 32211–32252 (2023).

  82. Kingma, D. P. & Welling, M. Auto-encoding variational bayes. Preprint at https://arxiv.org/abs/1312.6114 (2013).

  83. Ho, J. et al. Imagen video: high definition video generation with diffusion models. Preprint at https://arxiv.org/abs/2210.02303 (2022).

  84. Chan, W. & Fleet, D. J. Video diffusion models. Adv. Neurl Inf. Procss. Systems 35, 8633–8646 (2022).

    Google Scholar 

  85. Wu, Z. et al. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 32, 4–24 (2021).

    Article  MathSciNet  Google Scholar 

  86. Choy, C., Gwak, J. & Savarese, S. 4D spatio-temporal ConvNets: Minkowski convolutional neural networks. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition 3070–3079 (IEEE, 2019).

  87. Bond-Taylor, S. & Willcocks, C. G. ∞-Diff: infinite resolution diffusion with subsampled mollified states. In Proc. 12th International Conference on Learning Representations (OpenReview.net, 2023).

  88. Efron, B. Tweedie’s formula and selection bias. J. Am. Stat. Assoc. 106, 1602–1614 (2011).

    Article  MathSciNet  Google Scholar 

  89. Gong, J., Monty, J. P. & Illingworth, S. J. Model-based estimation of vortex shedding in unsteady cylinder wakes. Phys. Rev. Fluids 5, 023901 (2020).

    Article  Google Scholar 

  90. Takamoto, M. et al. PDEBench: an extensive benchmark for scientific machine learning. Adv. Neural Inf. Process. Syst. 35, 1596–1611 (2022).

    Google Scholar 

  91. Li, Z. S3GM: learning spatiotemporal dynamics with a pretrained generative model. Zenodo https://doi.org/10.5281/zenodo.13925732 (2024).

  92. Li, Z. Learning spatiotemporal dynamics with a pretrained generative model. Code Ocean https://doi.org/10.24433/CO.6670426.v2 (2024).

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (no. 11927802 to L.Y.; no. 52376090 to W.H.; no. 62325101 and no. 62031001 to Y.D.; no. 92270118 and no. 62276269 to H.S.), the National Key Research and Development Program of China (no. 2022YFF0504500 to W.H.) and the Beijing Natural Science Foundation (no. 1232009 to H.S.). W.H. and H.S. acknowledge support from the Fundamental Research Funds for the Central Universities.

Author information

Author notes

  1. These authors contributed equally: Zeyu Li, Wang Han.

Authors and Affiliations

  1. School of Astronautics, Beihang University, Beijing, China

    Zeyu Li, Wang Han, Yue Zhang, Qingfei Fu, Jingxuan Li, Lizi Qin, Ruoyu Dong, Yue Deng & Lijun Yang

  2. Gaoling School of Artificial Intelligence, Renmin University of China, Beijing, China

    Hao Sun

  3. School of Artificial Intelligence, Beihang University, Beijing, China

    Yue Deng

Authors
  1. Zeyu Li
    View author publications

    Search author on:PubMed Google Scholar

  2. Wang Han
    View author publications

    Search author on:PubMed Google Scholar

  3. Yue Zhang
    View author publications

    Search author on:PubMed Google Scholar

  4. Qingfei Fu
    View author publications

    Search author on:PubMed Google Scholar

  5. Jingxuan Li
    View author publications

    Search author on:PubMed Google Scholar

  6. Lizi Qin
    View author publications

    Search author on:PubMed Google Scholar

  7. Ruoyu Dong
    View author publications

    Search author on:PubMed Google Scholar

  8. Hao Sun
    View author publications

    Search author on:PubMed Google Scholar

  9. Yue Deng
    View author publications

    Search author on:PubMed Google Scholar

  10. Lijun Yang
    View author publications

    Search author on:PubMed Google Scholar

Contributions

L.Y., Y.D., W.H. and H.S. supervised the project. L.Y., Z.L. and W.H. conceived the idea. Z.L. carried out the numerical simulations. Z.L. and Y.Z. designed and carried out the experiments. Z.L. and W.H. performed the machine learning studies. Q.F., J.L., L.Q. and R.D. discussed the machine learning results. All authors discussed the results and assisted during manuscript preparation.

Corresponding authors

Correspondence to Hao Sun, Yue Deng or Lijun Yang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Machine Intelligence thanks Francesco Regazzoni and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Demonstration of pointwise accuracy and spectral accuracy.

a, Two samples are compared to the reference, in which sample 2 shows a lower pointwise error while failing in capturing the spectral feature. b, Another case at different parameters that shows the identical problem as in a.

Extended Data Fig. 2 Strategy for generating a longer sequence.

a, The entire sequence is divided into two subsequences according to their dependency on observation y. b, Parallel generation for subsequence depending on observation y. c, Autoregressive generation for subsequence not depending on observation y.

Extended Data Fig. 3 Schematic of PIV experimental setup.

The velocity measurement of cylinder flow is conducted using PIV technique. We use a motorized displacement stage to drive both the circular cylinder and video recorder. The aluminum cylinder with diameter of 6 mm and length of 38 mm is suspended in a glass tank filled with water, while the video recorder is also attached to the displacement stage to move synchronously with the cylinder. A beam of sectorial helium-neon laser irradiates the cylinder vertically from the downstream. To avoid severe reflection of laser, the cylinder has a matte finish all over its surface.

Supplementary information

Supplementary Information

Supplementary Notes 1–13, Figs. 1–29 and Tables 1–5.

Supplementary Video 1

Animation of the reconstruction results for Kuramoto–Sivashinsky dynamics.

Supplementary Video 2

Animation of the reconstruction results for Kolmogorov turbulent flow.

Supplementary Video 3

Animation of the reconstruction results for ERA5 climate observations.

Supplementary Video 4

Animation of the reconstruction results for cylinder flow.

Source data

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Source Data Fig. 5

Statistical source data.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Z., Han, W., Zhang, Y. et al. Learning spatiotemporal dynamics with a pretrained generative model. Nat Mach Intell 6, 1566–1579 (2024). https://doi.org/10.1038/s42256-024-00938-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s42256-024-00938-z

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics