Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Deep-learning-aided dismantling of interdependent networks

Nature Machine Intelligence volume 7, pages 1266–1277 (2025)Cite this article

Subjects

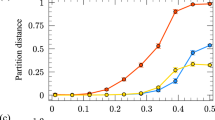
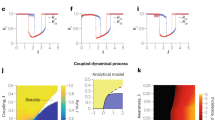
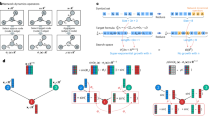
Abstract

Identifying the minimal set of nodes whose removal breaks a complex network apart, also referred as the network dismantling problem, is a highly non-trivial task with applications in multiple domains. Whereas network dismantling has been extensively studied over the past decade, research has primarily focused on the optimization problem for single-layer networks, neglecting that many, if not all, real networks display multiple layers of interdependent interactions. In such networks, the optimization problem is fundamentally different as the effect of removing nodes propagates within and across layers in a way that can not be predicted using a single-layer perspective. Here we propose a dismantling algorithm named MultiDismantler, which leverages multiplex network representation and deep reinforcement learning to optimally dismantle multilayer interdependent networks. MultiDismantler is trained on small synthetic graphs; when applied to large, either real or synthetic, networks, it displays exceptional dismantling performance, clearly outperforming all existing benchmark algorithms. We show that MultiDismantler is effective in guiding strategies for the containment of diseases in social networks characterized by multiple layers of social interactions. Also, we show that MultiDismantler is useful in the design of protocols aimed at delaying the onset of cascading failures in interdependent critical infrastructures.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: The training process of MultiDismantler.
Fig. 2: Dismantling performance of synthetic and real-world interdependent networks under the metrics AUDC and C*.
Fig. 3: The dismantling process of two real-world multiplex networks by different dismantling algorithms.
Fig. 4: Preventing disease spreading and maintaining network robustness with MultiDismantler.

Similar content being viewed by others

Data availability

All data used in this Article are publicly available. To facilitate the reproducibility of our results, all necessary data are available at https://doi.org/10.24433/CO.0638082.v1 (ref. 51).

Code availability

The code developed for this research is available at https://doi.org/10.24433/CO.0638082.v1 (ref. 51).

References

  1. Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998).

    Article  Google Scholar 

  2. Hwang, D.-U. Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006).

    Article  MathSciNet  Google Scholar 

  3. Cohen, R., Erez, K., ben-Avraham, D. & Havlin, S. Breakdown of the internet under intentional attack. Phys. Rev. Lett. 86, 3682 (2001).

    Article  Google Scholar 

  4. Morone, F. & Makse, H. A. Influence maximization in complex networks through optimal percolation. Nature 524, 65–68 (2015).

    Article  Google Scholar 

  5. Barabási, A.-L., Gulbahce, N. & Loscalzo, J. Network medicine: a network-based approach to human disease. Nat. Rev. Genet. 12, 56–68 (2011).

    Article  Google Scholar 

  6. Carreras, B. A., Lynch, V. E., Dobson, I. & Newman, D. E. Critical points and transitions in an electric power transmission model for cascading failure blackouts. Chaos 12, 985–994 (2002).

    Article  MathSciNet  Google Scholar 

  7. Bertagnolli, G., Gallotti, R. & De Domenico, M. Quantifying efficient information exchange in real network flows. Commun. Phys. 4, 125 (2021).

    Article  Google Scholar 

  8. Chen, Y., Paul, G., Havlin, S., Liljeros, F. & Stanley, H. E. Finding a better immunization strategy. Phys. Rev. Lett. 101, 058701 (2008).

    Article  Google Scholar 

  9. Braunstein, A., Dall’Asta, L., Semerjian, G. & Zdeborová, L. Network dismantling. Proc. Natl Acad. Sci. USA 113, 12368–12373 (2016).

    Article  Google Scholar 

  10. Artime, O. et al. Robustness and resilience of complex networks. Nat. Rev. Phys. 6, 114–131 (2024).

    Article  Google Scholar 

  11. Chen, W., Wang, Y. & Yang, S. Efficient influence maximization in social networks. In Proc. 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 199–208 (2009).

  12. Grassia, M., De Domenico, M. & Mangioni, G. Machine learning dismantling and early-warning signals of disintegration in complex systems. Nat. Commun. 12, 5190 (2021).

    Article  Google Scholar 

  13. Zhang, J. & Wang, B. Dismantling complex networks by a neural model trained from tiny networks. In Proc. 31st ACM International Conference on Information & Knowledge Management 2559–2568 (2022).

  14. Fan, C., Zeng, L., Sun, Y. & Liu, Y.-Y. Finding key players in complex networks through deep reinforcement learning. Nat. Mach. Intell. 2, 317–324 (2020).

    Article  Google Scholar 

  15. Bianconi, G. Multilayer Networks: Structure and Function (Oxford Univ. Press, 2018).

  16. Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).

    Article  Google Scholar 

  17. Vespignani, A. The fragility of interdependency. Nature 464, 984–985 (2010).

    Article  Google Scholar 

  18. Chen, Y., Liu, Y., Tang, M. & Lai, Y.-C. Epidemic dynamics with non-Markovian travel in multilayer networks. Commun. Phys- 6, 263 (2023).

    Article  Google Scholar 

  19. Osat, S., Faqeeh, A. & Radicchi, F. Optimal percolation on multiplex networks. Nat. Commun. 8, 1540 (2017).

    Article  Google Scholar 

  20. Baxter, G. J., Timár, G. & Mendes, J. Targeted damage to interdependent networks. Phys. Rev. E 98, 032307 (2018).

    Article  Google Scholar 

  21. Coghi, F., Radicchi, F. & Bianconi, G. Controlling the uncertain response of real multiplex networks to random damage. Phys. Rev. E 98, 062317 (2018).

    Article  Google Scholar 

  22. Han, J., Tang, S., Shi, Y., Zhao, L. & Li, J. An efficient layer node attack strategy to dismantle large multiplex networks. Eur. Phys. J. B 94, 74 (2021).

    Article  Google Scholar 

  23. Schuetz, M. J., Brubaker, J. K. & Katzgraber, H. G. Combinatorial optimization with physics-inspired graph neural networks. Nat. Mach. Intell. 4, 367–377 (2022).

    Article  Google Scholar 

  24. Khalil, E., Dai, H., Zhang, Y., Dilkina, B. & Song, L. Learning combinatorial optimization algorithms over graphs. Adv. Neural Inf. Process. Syst. 30, (2017).

  25. Wu, C. P., Lou, Y., Li, W., Xie, S. L. & Chen, G. R. A multitask network robustness analysis system based on the graph isomorphism network. IEEE Trans. Cybernetics 54, 6630–6642 (2024).

  26. Kleineberg, K.-K., Boguná, M., Ángeles Serrano, M. & Papadopoulos, F. Hidden geometric correlations in real multiplex networks. Nat. Phys. 12, 1076–1081 (2016).

    Article  Google Scholar 

  27. Boguna, M. et al. Network geometry. Nat. Rev. Phys. 3, 114–135 (2021).

    Article  Google Scholar 

  28. Kleineberg, K.-K., Buzna, L., Papadopoulos, F., Boguñá, M. & Serrano, M. Á. Geometric correlations mitigate the extreme vulnerability of multiplex networks against targeted attacks. Phys. Rev. Lett. 118, 218301 (2017).

    Article  Google Scholar 

  29. Faqeeh, A., Osat, S. & Radicchi, F. Characterizing the analogy between hyperbolic embedding and community structure of complex networks. Phys. Rev. Lett. 121, 098301 (2018).

    Article  Google Scholar 

  30. Patwardhan, S., Rao, V. K., Fortunato, S. & Radicchi, F. Epidemic spreading in group-structured populations. Phys. Rev. X 13, 041054 (2023).

    Google Scholar 

  31. Sutton, R. S. Learning to predict by the methods of temporal differences. Mach. Learn. 3, 9–44 (1988).

    Article  Google Scholar 

  32. Ren, X.-L., Gleinig, N., Helbing, D. & Antulov-Fantulin, N. Generalized network dismantling. Proc. Natl Acad. Sci. USA 116, 6554–6559 (2019).

    Article  MathSciNet  Google Scholar 

  33. Ramsey, F. P. in Classic Papers in Combinatorics 1–24 (Springer, 1987).

  34. Kivelä, M. et al. Multilayer networks. J. Complex Netw. 2, 203–271 (2014).

    Article  Google Scholar 

  35. Lou, Y., Wang, L. & Guanrong, C. Structural robustness of complex networks: a survey of a posteriori measures. IEEE Circuits Syst. Mag. 23, 12–35 (2017).

    Article  Google Scholar 

  36. Clusella, P., Grassberger, P., Pérez-Reche, F. J. & Politi, A. Immunization and targeted destruction of networks using explosive percolation. Phys. Rev. Lett. 117, 208301 (2016).

    Article  Google Scholar 

  37. Ma, Y., Wang, S., Aggarwal, C. C., Yin, D. & Tang, J. Multi-dimensional graph convolutional networks. In Proc. 2019 Siam International Conference on Data Mining 657–665 (2019).

  38. Dong, Y., Chawla, N. V. & Swami, A. metapath2vec: scalable representation learning for heterogeneous networks. In Proc. 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 135–144 (2017).

  39. Xu, S. et al. Topic-aware heterogeneous graph neural network for link prediction. In Proc. 30th ACM International Conference on Information & Knowledge Management 2261–2270 (2021).

  40. Radicchi, F. Percolation in real interdependent networks. Nat. Phys. 11, 597–602 (2015).

    Article  Google Scholar 

  41. De Domenico, M., Nicosia, V., Arenas, A. & Latora, V. Structural reducibility of multilayer networks. Nat. Commun. 6, 6864 (2015).

    Article  Google Scholar 

  42. Stark, C. et al. Biogrid: a general repository for interaction datasets. Nucleic Acids Res. 34, 535–539 (2006).

    Article  Google Scholar 

  43. Cao, X. & Yu, Y. Bass: a bootstrapping approach for aligning heterogenous social networks. In Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2016, Part I 16 459–475 (2016).

  44. De Domenico, M., Lancichinetti, A., Arenas, A. & Rosvall, M. Identifying modular flows on multilayer networks reveals highly overlapping organization in interconnected systems. Phys. Rev. X 5, 011027 (2015).

    Google Scholar 

  45. De Domenico, M. & Altmann, E. G. Unraveling the origin of social bursts in collective attention. Sci. Rep. 10, 4629 (2020).

    Article  Google Scholar 

  46. Albert, R., Jeong, H. & Barabási, A.-L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000).

    Article  Google Scholar 

  47. Celli, F., Lascio, F. M. L. D., Magnani, M., Pacelli, B. & Rossi, L. Social network data and practices: the case of Friendfeed. In International Conference on Social Computing, Behavioral Modeling and Prediction 346–353 (Springer, 2010).

  48. Radicchi, F. & Bianconi, G. Redundant interdependencies boost the robustness of multiplex networks. Phys. Rev. X 7, 011013 (2017).

    Google Scholar 

  49. Schneider, C. M., Moreira, A. A., Andrade Jr, J. S., Havlin, S. & Herrmann, H. J. Mitigation of malicious attacks on networks. Proc. Natl Acad. Sci. USA 108, 3838–3841 (2011).

    Article  Google Scholar 

  50. Wang, D., Cui, P. & Zhu, W. Structural deep network embedding. In Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 1225–1234 (2016).

  51. Gu, W., Chen, Y., Li, L. & Hou, J. Deep-learning-aided dismantling of interdependent networks. Code Ocean https://doi.org/10.24433/CO.0638082.v1 (2025).

Download references

Acknowledgements

This work was supported by grants from National Natural Science Foundation of China (grant numbers 42450183 and 72371014) and support from the Beijing University of Chemical Technology, grant number 11170044127, PY2514; partial support was also received from the Air Force Office of Scientific Research (grant numbers FA9550-21-1-0446 and FA9550-24-1-0039). The funders had no role in the study design, data collection, and analysis, the decision to publish or any opinions, findings, conclusions or recommendations expressed in the Article.

Author information

Authors and Affiliations

  1. College of Information Science and Technology, Beijing University of Chemical Technology, Beijing, People’s Republic of China

    Weiwei Gu, Chen Yang & Jinqiang Hou

  2. School of Software Enginering, University of Science and Technology of China, Hefei, People’s Republic of China

    Lei Li

  3. Center for Complex Networks and Systems Research, Luddy School of Informatics, Computing, and Engineering, Indiana University, Bloomington, IN, USA

    Filippo Radicchi

Authors
  1. Weiwei Gu
    View author publications

    Search author on:PubMed Google Scholar

  2. Chen Yang
    View author publications

    Search author on:PubMed Google Scholar

  3. Lei Li
    View author publications

    Search author on:PubMed Google Scholar

  4. Jinqiang Hou
    View author publications

    Search author on:PubMed Google Scholar

  5. Filippo Radicchi
    View author publications

    Search author on:PubMed Google Scholar

Contributions

W.W. and F.R. wrote the paper. W.W., C.Y. and F.R. designed the model and experiments. W.W., C.Y. and L.L. performed the experiments. C.Y., L.L. and J.H. plotted the figures.

Corresponding authors

Correspondence to Chen Yang or Filippo Radicchi.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Machine Intelligence thanks Roger Guimerà and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–5, Tables 1–12 and References.

Reporting Summary

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gu, W., Yang, C., Li, L. et al. Deep-learning-aided dismantling of interdependent networks. Nat Mach Intell 7, 1266–1277 (2025). https://doi.org/10.1038/s42256-025-01070-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s42256-025-01070-2

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing