Introduction

Fermi surface topology has gathered much interest in quantum materials research with the aim of understanding the intertwining of different fundamental orders such as spin, charge, and lattice1,2. Ultimately the ability to change and design the Fermi surface of a quantum material will underpin functionalities in electronic and magnetic devices. The family of layered materials including transition metal dichalcogenides (TMDs) offers significant opportunities for engineering the electronic band structure, due to the many degrees of freedom governing interlayer interactions3,4,5.

The polytypism of TMD single crystals has proven to be instrumental for the preparation of interfaces between 2D crystalline single-layers with the same chemical formula unit, but different structures6. More specifically, some group V metal disulfides and diselenides are known to form heterostructures with an alternation of 2D crystals with trigonal-prismatic (H) and octahedral (T) metal coordination (Fig. 1a)7,8. Given that H layers often exhibit superconductivity, whereas T exhibit Mott insulating states, heterostructures built from these have recently gained much interest because of the emergence of new electronic phases with exotic characteristics. A heterostructure 1T-TaS2/1H-TaS2 has been designed to demonstrate the first artificial heavy fermion material6 and been proposed for the realization of chiral superconductivity in the bulk material, known as 4Hb-TaS29. The corresponding diselenide, 4Hb-TaSe2 exhibits superconductivity with an intriguing interplay of charge density wave (CDW) order and charge transfer between the H and T layers10. One of the peculiarities of such systems arises from the proximity between a putative 2D Mott insulator, related to the well documented T layer Star-of-David (SOD) CDW11, and the metallic/superconducting H layer. The localized spins at the centres of the SOD triangular lattice are a candidate for spin liquid behaviour via Kondo coupling with the H layer12,13. While these systems host rich and fascinating phenomenology - chiral spin liquid13, heavy-Fermion physics6, Kondo lattice14, topological surface superconductivity15- details of the Fermi surface only begin to be explored16 and the crucial interlayer electronic couplings remain unaddressed.

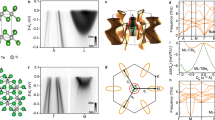
Fig. 1: Selective area ARPES of 4Hb-TaSe2.
figure 1

a Crystal structure of (normal phase) 4Hb-TaSe2, with unit cell marked by the solid line, highlighting the two possible surface terminations at the top. ARPES map at E = EF on: b a region with a mixture of H and T terminations c and d on surface areas dominated by H and T terminations, respectively. The projection of the normal phase BZ is shown with a blue hexagon, while the BZ of the \(3\,\times 3\) (green) and \(\sqrt{13}\times \sqrt{13}\quad\)(red) CDW superlattices are shown on the H and T surfaces, respectively. e Constant energy map at 450 meV below EF (same data set as d). f and g More details of the star-shaped ARPES structure illustrating the two possible orientations with the rotated \(\sqrt{13}\times \sqrt{13}\) BZ. Sample temperature 20 K.

Full size image

4Hb-TaSe2 displays two CDW transitions upon cooling the crystal; one at 410 K and a second at 75 K (ref. 8). The former is ascribed to the \((\sqrt{13}\times \sqrt{13})\)R-13.9° SOD reconstruction in the T layer, while the latter has been interpreted as quasi-commensurate ~(\(3\,\times \,3\)) in the H layer. Alone the two CDW periodicities are found in the parent compounds 1T-TaSe2 and 2H-TaSe2, respectively, but while these polytypes may appear as simpler material platforms compared to the 4Hb structure, the subtleties of the out-of-plane arrangements of the CDW can lead to a complex response to experimental probes. This is particularly relevant for the SOD stacking17,18, which has an important role in 1T-TaSe219. In fact, the \(\sqrt{13}\times \sqrt{13}\) SOD superlattice has attracted much attention, because of its peculiar electronic structure and the lack of common agreement on the nature of its gapped phases11,20, most likely linked to different interlayer configurations leading to very different couplings19. Our choice of investigating 4Hb-TaSe2 was intuitively motivated by increasing the interlayer separation of the T layer SODs and thus hoping to observe the effect of folding with the \(\sqrt{13}\times \sqrt{13}\) superlattice on the Fermi surface of a metallic system, in contrast to the gapped 1 T materials21,22. Folded bands with \(\sqrt{13}\times \sqrt{13}\) periodicity have been seen in 1T-TaS2, with a crucial role of the interlayer orbital order stacking23, but not on the Fermi surface because of the gapped nature of this compound. Overall, measuring details of the band structure and Fermi surface in the title material would help to clarify the nature of interactions, which can give rise to heavy-fermion physics, spin liquid and doped Mott insulator24.

In this work, we report detailed evidence on the folded band structure caused by the \(\sqrt{13}\times \sqrt{13}\) CDW and its pseudochiral features in 4Hb-TaSe2. Using synchrotron-based Angle Resolved Photoemission Spectroscopy (ARPES), we select areas with a predominance of T or H surface termination. ARPES maps of both terminations show that T surfaces allow to better study the rich band structure of this system which include intricate star-shaped folded bands with the presence of spectral gaps. We compare the experimental results with density functional theory (DFT) calculations, which reproduce the main features providing valuable information to interpret the interlayer interactions. Such unprecedented details on the band structure provide crucial information towards the understanding and description of the strongly correlated phases emerging in these 2D interfaces.

Results

Figure 1a shows a projection on the (11\({\bar{2}}\)0) plane of the 4Hb-TaSe2 crystal structure. Layers with H and T metal-coordination alternate along the c axis held together by van der Waals interactions. There are two symmetrically inequivalent layers per unit cell for each coordination, H, H’ and T, T’. For the rest of the paper, we will generally refer to H and T unless specified. The structure offers the possibility to achieve different surface terminations of bulk crystals upon cleaving. We have found these H and T terminations to be equally probable with randomly distributed terraces on the surface of a freshly cleaved single crystals. This is confirmed by the results of Fig. 1b, where the ARPES kx-ky map at the Fermi level combines spectroscopic characteristics similar to experiments on 2H-TaSe2 and 1T-TaSe2. A circular hole pocket centred at the \({\bar{\Gamma }}\) point together with six dog-bone shaped electron pockets around the \({\bar{{\rm{M}}}}\) points have been observed in 2H-TaSe225,26, while ARPES intensity at and surrounding \({\bar{\Gamma }}\) is typical of 1T-TaSe221,27,28. We have been able to focus the synchrotron beam on selected areas with signal dominated by H and T terminations. Figure 1c, d shows maps obtained using identical photoemission settings for two different surface locations. Panel d exhibits strong photoemission intensity at the centre of the Brillouin Zone (BZ), while panel c features a \({\bar{\Gamma }}\) centred hole pocket and intense dogbones. The ARPES map in Fig. 1c is very similar to the one extensively documented for single crystals of 2H-TaSe225,26, enabling us to identify that this surface region must be dominated by an H-type termination and exhibits signatures of \(3\times 3\) order29, although literature results indicate a slightly weakened 3 × 3 CDW in the H layers compared to 2H-TaSe28. In contrast, Fig. 1d shows characteristics often seen in 1T-TaSe2, i.e. photoemission signal at \({\bar{\Gamma }}\) from Ta bands close to the Fermi level21,28. Some features of the sub-surface H layer are still present, such as the \({\bar{\Gamma }}{{\rm{centred}}}\) hole pocket, but at low intensity due to the surface sensitivity of photoemission experiments30. Further confirmation of the two terminations, dominated by H or T, is obtained from the tantalum 4 f core levels (Supplementary Fig. 2), which are diagnostic for the two metal coordinations31. This evidence excludes that the crystal is a mosaic of 1 T and 2H domains and aligns with a 4Hb structure as X-ray diffraction confirms (Supplementary Fig. 1).

We focus our attention on the terminations dominated by the T layers. A constant energy map at 450 meV below EF in Fig. 1e shows remnants of the large elliptical pockets centred at \({\bar{M}}\) points (of the blue BZ hexagonal contour) expected for undistorted T layers21,28, as well as valence bands with Se character at \({\bar{\Gamma }}\) that are repeated according to the periodicity of the \(\sqrt{13}\times \sqrt{13}\) CDW superlattice, identified by the red miniBZ contours. Most striking, however, are the high resolution Fermi surface maps shown in Fig. 1f, g, which reveal star-shaped fine structure in a small area of momentum space surrounding \({\bar{\Gamma }}\). This fine structure is mainly within the first miniBZ of the \(\sqrt{13}\times \sqrt{13}\) CDW superlattice, as the superimposed red hexagons show with the expected rotation by 13.9° compared to the undistorted BZ. Further inspection of other crystals and domains reveal that the rotation can be counter- or clockwise, as shown in panels f and g, respectively. Such characteristics indicate that this fine structure must be related to the CDW reconstruction of the T layer. While earlier investigations on the band structure of the two prototypical materials possessing the SOD CDW, namely 1T-TaSe2 and 1T-TaS2, showed band folding effects23,32, here we find for the first time a highly structured metallic Fermi surface that emerges within the first miniBZ. Figure 2a shows a high-resolution Fermi surface map highlighting the details of the structure. A circular feature centred on the \({\bar{\Gamma }}\) point, labelled α in panel c, is surrounded by a hexagonal structure extending out to ~0.1 Å−1, indicated as β, which develops into six tips pointing close to but not exactly along \({\bar{\Gamma }}-{\bar{M}}^{* }\) directions, indicated as \({{\rm{\gamma }}}\) (we use a symbol * to distinguish high symmetry points in the folded miniBZ of the \(\sqrt{13}\,\times \,\sqrt{13}\) CDW). Photoemission intensity is also detected extending radially from the tips, constituting the δ feature and with a diffuse intensity in the \({\bar{\Gamma }}-{\bar{K}}^{* }\) direction (indicated as ε in the −20 meV map). The overall signal in the miniBZ shows pseudochirality as discussed further below.

Fig. 2: ARPES maps of 4Hb-TaSe2 on region with T termination.
figure 2

a High-resolution Fermi map. b High symmetry dispersions with Greek letters labelling of features to be compared with c panel. c ARPES maps at different energies below EF. Superimposed is the \(\sqrt{13}\times \sqrt{13}\) BZ (red hexagon) and features of interest mentioned in the main text are labelled with Greek letters. Photon energy 52 eV, polarization linear horizontal, sample temperature 43 K.

Full size image

The star shaped band structure is thus complex and comprises signal from several bands. Figure 2c shows ARPES maps at different constant energy cuts below the Fermi level. The star shape is evident down to 20 meV below the Fermi level and evolves into an intense signal in regions surrounding the tips and filling the miniBZ. Selected cuts along high symmetry directions, \({\bar{\Gamma }}-{\bar{M}}^{* }\) and \({\bar{\Gamma }}-{\bar{K}}^{* }\) are shown in Fig. 2b. The central feature α appears in both cuts as a high intensity signal extending down to ~20 meV below Fermi. Moving radially out from the \({\bar{\Gamma }}\) point, next is the signal β which corresponds to the hexagon seen in the Fermi maps and shows a small splitting in the \({\bar{\Gamma }}-{\bar{M}}^{* }\) direction. In this same symmetry direction are the tips of the star, \({{\rm{\gamma }}}\). Bands surrounding the tips, labelled ε, appear very intense at −15 meV binding energy mainly along \({\bar{\Gamma }}-{\bar{K}}^{* }\). The cuts along high symmetry points seem to suggest a complex manifold of bands, most with electron like dispersion. Normalization by a Fermi-Dirac distribution function reveals a spectral gap of ~23 meV in the \({\bar{\Gamma }}-{\bar{K}}^{* }\) direction, which mainly involves the ε bands as shown in the Supplementary Fig. 5.

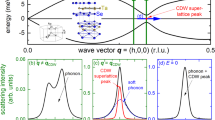
The photon energy dependence of the ARPES signal reported in Fig. 3 aims at providing insights into the three dimensional structure of the bands. Figure 3a shows the intensity at the Fermi level along a \({\bar{M}}-{\bar{\Gamma }}-{\bar{M}}\) cut as a function of photon energy. Signal from the \({\bar{\Gamma }}\) centred circular hole pocket derived from the H layer can be seen at ky = ±0.5 Å−1 and appears as two parallel lines, i.e. it does not exhibit any marked dispersion. This highlights the 2D nature of some electronic states at EF with H layer character. When looking at the bands close to the \({\bar{\Gamma }}\) point a periodic modulation in intensity is present. It involves the whole set of folded bands as can be seen in the maps of Fig. 3b for three photon energies in the interval 100 eV to 90 eV. A \(\hslash \nu\) integrated ARPES experiment is shown in Fig. 3c to offer a better overview of the whole band structure, including the deeper hole-like valence bands with selenium character centred at \({\bar{\Gamma }}\). The out-of-plane periodicity in the folded bands can be assessed in Fig. 3d, where photon energy has been converted into \({k}_{\perp }\), and presents interesting behaviour. Intensity maxima are approximately spaced by 4π/c, or equivalently 2π/(c/2), i.e. corresponding to half the periodicity of the 4-layer unit cell in real space, which suggests electrons are insensitive to the differences of T, H and T’,H’ layers (see Fig.1a), which are due to orientation of chalcogen atoms. The intensity modulation points towards a non-negligible interlayer hopping between the T and H layers, which are clearly electronically coupled. Such coupling maybe crucial for the understanding of the band structure of this material and the many observations of new emerging correlated electronic phases.

Fig. 3: ARPES photon energy dependence of 4Hb-TaSe2 on region with T termination.
figure 3

a Signal at E = EF on a cut along the \({\bar{M}}-\,{\bar{\Gamma }}-{\bar{M}}\) direction. b ARPES maps at selected photon energies indicated as dashed black lines in a. c Sum of ARPES spectra recorded for photon energies 40–130 eV. d \({k}_{z}\)-dependence at \({\bar{\Gamma }}\) in the binding energy range −1 eV to 0.2 eV (inner potential assumed to be 12.5 eV). Dashed black lines are drawn at \({k}_{z}=\frac{4\pi n}{c}\). Polarization linear horizontal, sample temperature 20 K.

Full size image

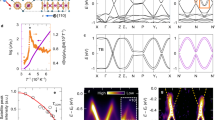
To gain further insights into this hitherto unreported band structure and to understand the nature of interlayer interactions we have performed DFT + U calculations. Figure 4a shows the calculated Fermi surface, while Fig. 4b is a series of constant energy surfaces of the electronic band structure as specified in caption. These are all seen along the [001] direction. The atomic structure has been relaxed in the presence of a SOD CDW in the T layers. The shape and symmetry of the main bands within the miniBZ is reproduced and neglecting any \(3\times 3\) charge order in the H layers does not preclude a good agreement with the experiments of Fig. 2. Literature results also indicate a lower onset temperature of the \(3\times 3\) CDW in the H layers compared to 2H-TaSe28, suggesting weakening of this charge order in the 4Hb structure. Other constant energy maps of the calculated band structure above and below Fermi are reported in Supplementary Fig. 3. The calculated Fermi surface consist of five distinct bands (Fig. 4c), which show three dimensional character. We report the band structure along high symmetry directions of the miniBZ in Fig. 4d with additional details in Supplementary Figs. 6 and 7. In Fig. 4d, we have used different hueing for the specific band contributions originating from T (blue) or H (red) layers. The folding of the normal structure bands due to the \(\sqrt{13}\,\times \,\sqrt{13}\) PLD results in a rich electronic structure. We highlight three crucial aspects: i) several bands crossing the Fermi level have mixed H-T character, i.e. they change colour from red to blue and vice-versa along the high symmetry paths, ii) there is evidence of dispersion in the kz direction as clearly seen along \({{{\Gamma }}}^{* }{-A}^{* }\), \({L}^{* }-{M}^{* }\), and \({{{\rm{H}}}}^{* }-{K}^{* }\), supporting non-negligible interlayer dispersion, iii) there are several avoided crossings and some, e.g. in the \({K}^{* }{-{{\Gamma }}}^{* }\) direction, correspond to a change in colour signifying hybridization. This theoretical result supports the picture of electronic coupling between T and H layers and is inconsistent with the heterostructure being viewed as stacked single TMD-monolayers interacting solely via charge transfer across a van der Waals interface.

Fig. 4: DFT + U simulations of 4Hb-TaSe2.
figure 4

a Calculated Fermi surface within the miniBZ, bands have been coloured differently. b Constant binding energy maps at E = EF −10 meV, E = EF − 20 meV, E = EF −50 meV, and E = EF −100 meV (left to right). c 3D representation of the bands in a within the miniBZ together with the identification of high symmetry points. d Band structure along high symmetry points of the miniBZ, hueing of bands from red to blue indicates the character in going from H dominated to T, respectively, as indicated on the vertical bar. Details of the calculations are available in the Methods section and Supplementary Table 1.

Full size image

Discussion

The ARPES signal recorded for 4Hb-TaSe2 depends on the surface termination. In the range of photon energies we have used, 40–130 eV, the escape depth of photoemitted electrons means surface top layers dominate the photoemission maps and spectra. The band topology of a single H layer, lacking strong photoemission signal at the BZ centre in the normal phase, as in 2H-TaSe232, enables the observation of the impact of the \(\sqrt{13}\,\times \,\sqrt{13}\) folding on the overall band structure. We underline that the study of 4Hb-TaSe2 is markedly different from previous attempts to observe band folding in T only crystals such as 1T-TaSe2 and 1T-TaS2 by ARPES21. While 1T-TaS2 is known to exhibit a complex charge ordering phase diagram with several incommensurate and quasi-commensurate phases, 1T-TaSe2 should provide a more defined CDW, having only a commensurate phase below room temperature. However, variability in the stacking of the SOD along the c-axis results in different local electronic structures19,33, thus making difficult the observation of a detailed folded fine structure in the bands. In 4Hb-TaSe2 the SOD are aligned along the c axis separated by a H layer34. The intercalated H layers are subjected to charge transfer from the T layers, which we estimate from Bader analysis to be 0.5 e per SOD. An estimation based on a simplified Luttinger count analysis35, reported in the Supplementary Fig. 4, gives 0.76 e per SOD. The origin of the charge transfer is the different chemical potential of the single T and H layers, as also found in 1 T/1H TaS2 bilayers24. Thus, the first important aspect to consider is that the Mott insulating T layers are essentially doped, resulting in a metallic system. This is consistent with recent ab-initio predictions on a 1 T/1H TaS2 bilayer structure24.

The information on band structure we report for the T termination is very different from an isolated monolayer of 1T-TaSe214. While it is known that reduced screening in the monolayer limit gives rise to strong correlations and the opening of a large Mott gap ~200 meV, as recently probed by scanning tunnelling microscopy (STM)11, ARPES signal at the Fermi level in all our experiments points towards a metallic system where the \(\sqrt{13}\,\times \,\sqrt{13}\) initially folds bands with T character. But then there is a finite coupling with bands from the H layer, which are also geometrically backfolded into the SOD miniBZ in calculations of the \(\sqrt{13}\,\times \,\sqrt{13}\) unit cell. The H-T hybridisation has a typical energy scale of ~10–20 meV (Supplementary Fig. 6), which is enough to perturb the bands and add in some extra complexity, yielding a multiband Fermi surface shown Fig. 4, which bears striking similarities to the experimental Fermi surface in Fig. 2. Interestingly and perhaps counter-intuitively, when taken as a whole the Fermi surface from DFT is actually predominantly constructed from bands with H character. On the other hand, upon band unfolding we find that the spectral weight associated with the H layer is mainly found outside the first miniBZ. Supplementary Fig. 8 shows this process along the \({{{\Gamma }}}^{* }{-M}^{* }{-2M}^{* }\) direction, with the weight (green circles) within the first mini-BZ maps having a considerable contribution due to the T layers. The global picture from the calculations is that the impact of the proximate metallic H layer in 4Hb-TaSe2 goes beyond a straightforward charge transfer into the T bands, but rather that hybridisations occur and modulate the overall electronic structure, with both layers contributing to the complex Fermi surface.

The absence of a full gap in this material is not only due to charge transfer, but also orbital hybridization leading to an overall metallic band structure. In comparison with tantalum disulfide, it is also worth mentioning the role of selenium bands (Fig. 3c) in contributing to screening, as in 4Hb-TaS2 early scanning tunnelling spectroscopy (STS) studies on different crystal terraces revealed a large gap ~200 meV on the T terminations36. We report that the folded bands have a relatively narrow bandwidth and exhibit quasiparticle peaks; the integrated spectral weight shown in Supplementary Fig. 9 reveals a peak towards EF. In comparison the zero bias peaks seen in recent tunnelling experiments on heterostructures of 1 T on 1H-TaS2 are only a few meV wide6, and might have a qualitatively different origin24. Thus, while our results show the presence of a folded Fermi surface derived from the SOD reconstruction in 4Hb-TaSe2, we caution against extrapolation of this result to all combinations of T and H layers in Ta-dichalcogenides. The folded bands of 4Hb-TaSe2 involve non negligible interlayer interactions as the kz data indicate. In Fig. 3d we report a periodicity consistent with half the unit cell in real space. While our kz resolution from experiments and the large unit cell along the c-axis, do not allow us to fully resolve the dispersion of bands as in calculations, the dominant spectral weight of features α β and γ is reflected in bands 1 and star-tips of band 2 being localized along the kz momentum coordinate (Fig. 4c).

A striking property of the observed Fermi surface in Fig. 2a, and indeed the constant energy maps at other energies such as Fig. 1e, is the chiral nature of these 2D projections of the ARPES intensity. It is well-understood that the commensurate SOD reconstruction breaks the in-plane mirror symmetry, and in the 4Hb structure the SOD order changes the space group from \(P{6}_{3}/{mmc}\) (no. 194) to \(P{6}_{3}/m\) (no. 176)34. However, inversion symmetry is still present, thus in a 3D and crystallographic sense, the 4Hb-TaSe2 structure is formally achiral at all temperatures. Mindful of this, as well as the presence of time-reversal symmetry, we do not describe the electronic structure as chiral, but rather pseudochiral, following the definition of Louat et al.37. The sense of rotation of the electronic structure is linked to the intrinsic rotation which occurs in the reconstructed lattice of the SOD CDW. The breaking of mirror symmetry and local selection of a sense of rotation below TCDW has elsewhere been discussed as a ferrorotational order38,39, which overlaps conceptually with pseudochirality in the case where the rotation axis is also the normal to the cleavage plane. We did not observe any preferential sense of rotation after investigation of several different positions on many single crystals. However, in structures such as bilayers 1 T/1H or 1 T/1H/1 T where a centre of inversion is effectively removed, the chirality may have crucial implications towards the understanding of other degrees of freedom such as spin and orbital currents. The recent demonstration of helical Rashba-type spin texture by spinARPES on the Fermi surface of heterostructures between H-TaSe2 and a topological insulator is remarkable40 and calls for new investigations using spin-resolved detection also on the material studied here or layers with thickness smaller than the unit cell. In addition, opportunities to control the helicity of charge order in the CDW state may arise as demonstrated in other TMDs and more recently Kagome-CDW materials41,42.

Conclusions

In conclusion, we have unveiled the intricate reconstructed Fermi surface and band structure of 4Hb-TaSe2 demonstrating how the \(\sqrt{13}\,\times \,\sqrt{13}\) CDW in the T layers results in folded bands exhibiting pseudochirality. The band structure of this metallic system shows orbital hybridization between T and H layers, which we believe is relevant for the understanding of new correlated phases in T-H heterostructures of tantalum based dichalcogenides. It is hoped that the observed Fermi surface and band structure will help to elucidate and control phenomena of current interest such as chiral superconductivity and chiral spin liquid phases. We also speculate that novel electronic phases may arise by accurate control of twisting angles in T/H Tantalum dichalcogenide heterostructures similarly to as has been observed in other 2D materials.

Methods

Crystal Growth

Single crystals were prepared following established procedures of chemical vapour transport with iodine as transport agent8,43. Stoichiometric quantities of tantalum and selenium were loaded in a quartz ampule together with a slight excess of selenium and iodine in a nitrogen glove-box. The ampule was vacuum sealed an placed in a two zone furnace to grow the 1 T polytype single crystals at 980 °C following a rapid quench in water, as in ref. 28 Following earlier studies44, the 1 T crystals with gold reflections were subsequently heated in the same ampule to reach 800 °C in 96 h. They were kept at 800 °C for two days and quenched again. Crystals with typical size 2 × 2 × 0.2 mm2 were characterised by powder x-ray diffraction as shown in Supplementary Fig. 1.

ARPES measurements

ARPES experiments were performed at the HR-branch of beam line I05 of Diamond Light Source synchrotron. Detection was performed with a R4000 electron analyzer equipped with deflectors. The beamline has energy and angular resolution of 10 meV and 0.2°, respectively. Single crystals were cleaved in-situ at low temperature (<20 K) and under ultra-high vacuum (<10−10 mbar) using the top post method. Different photon energies were used as specified in figures. A beam spot size of 50 × 50 μm2 allowed for the monitoring and selection of surface terminations dominated by H or T ARPES features.

DFT calculations

Density functional theory calculations of the atomic and electronic structure of 4Hb-TaSe2 were performed using VASP45. The \(\sqrt{13}\times \sqrt{13}\) commensurately-modulated structure was relaxed starting from the experimental geometry identified by Lüdecke et al.34. The DFT + D3 calculations used PAW potentials46 with the PBE exchange-correlation functional47 and Grimme’s dispersion correction48. An energy cut-off ENCUT = 400 eV was used and Γ-centred KPOINT sampling of 8 × 8 × 4, with atomic coordinates optimised until residual forces were less than 0.001 eV Å−1. Supplementary Table 1 lists the experimental and calculated structural parameters. Energy bands and Fermi surfaces were calculated for the optimised geometry using DFT + U49 and including spin-orbit coupling. A tantalum U value of 1.1 eV was used, estimated from calculations using the linear-response scheme performed on 2 × 2 × 1 supercells of the normal state structure containing 16 Ta atoms and including screening out to 4th nearest neighbours. A similar value is found using the 1 × 1 × 1 cell.