From localized 4f electrons to anisotropic exchange interactions in ferromagnetic CeRh₆Ge₄

Abstract

CeRh₆Ge₄ is a cerium-based ferromagnetic material exhibiting a quantum critical behavior under pressure. We derive effective exchange interactions, using the framework of density functional theory combined with dynamical mean-field theory. Our results reveal that the nearest-neighbor ferromagnetic interaction along the c axis is isotropic in spin space, leading to a formation of spin chains. On the other hand, the inter-chain coupling is highly anisotropic: The in-plane moment weakly interacts ferromagnetically in the a–b plane to stabilize the ferromagnetic state, whereas the z-component couples antiferromagnetically, contributing to its destabilization. The magnetic anisotropy of the interchain interactions as well as of the local 4f wavefunctions characterizes the magnetic properties underlying the ferromagnetic transition and the quantum critical behavior in CeRh₆Ge₄.

Introduction

Cerium based ferromagnets are materials of high fundamental interest. The highly localized 4f electrons of cerium can show Kondo lattice behavior where the localized spin is screened by conduction electrons and forms a Kondo singlet, leading to a correlated paramagnetic ground state¹. This behavior is controlled by the strength of the hybridization between the localized moment and the conduction electrons. In the case of weak hybridization, the localized 4f electrons can interact via the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction which is mediated by conduction electrons. The result can be magnetically ordered states.

A particularly interesting possibility in the case of cerium magnetism is a ferromagnetic ground state which is realized in a small but growing number of compounds such as CeRuPO², CeRu₂Al₂B³ and CePt⁴. The fact that ferromagnetic ordering temperatures T_C are typically small means that there often are experimentally accessible tuning parameters like pressure that allow suppression of T_C to zero temperature, providing access to a quantum phase transition instead of the usual thermal phase transition. The properties of materials near such a quantum critical point are highly nontrivial and interesting⁵. Ferromagnetic quantum critical points are often first order as in UGe₂⁶ or in UCoAl⁷. Here, we plan to study, CeRh₆Ge₄ which is a rare example of a Kondo lattice system with ferromagnetic order at ambient pressure and a second-order ferromagnetic quantum critical point that is accessible at elevated pressures.

CeRh₆Ge₄ exhibits a ferromagnetic transition at T_C = 2.5 K⁸. This compound has attracted significant interest due to the emergence of a ferromagnetic quantum critical point (QCP) under pressure^9,10. To realize a QCP associated with a ferromagnetic transition, magnetic anisotropy plays a key role¹⁰, as it helps to avoid a first-order transition. Theoretical investigations into the realization of a ferromagnetic QCP have subsequently explored the absence of inversion symmetry¹¹, the influence of the spin-orbit coupling¹², and the role of nonsymmorphic symmetry¹³. In this paper, we apply a recently developed first-principles method for calculating the magnetic susceptibility and derive low-energy effective interactions. We demonstrate that the exchange interactions responsible for the ferromagnetic transition are highly anisotropic, stabilizing the in-plane ferromagneitc moment of 4f electrons.

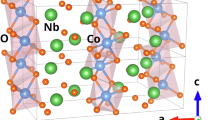
CeRh₆Ge₄ crystallizes in a LiCo₆P₄-type structure with space group $P\bar{6}m2$ (No. 187)¹⁴ as illustrated in Fig. 1. The Ce atoms occupy the 1a site with a three-fold rotational symmetry, corresponding to the point group D_3h. A clear anomaly in the specific heat indicates a phase transition at T = T_C = 2.5 K⁸. Magnetization measurements confirm the onset of ferromagnetism, with a spontaneous moment of 0.34 μ_B/Ce. Neutron scattering and μSR experiments reveal that the ordered moment lies within the a-b plane as shown in Fig. 1c¹⁵. In the paramagnetic state, the magnetic susceptibility follows the Curie-Weiss law with an effective moment of 2.35 μ_B/Ce. The electronic and magnetic properties of CeRh₆Ge₄ have been further explored using angle-resolved photoemission spectroscopy (ARPES)¹⁶, quantum oscillation measurements¹⁷, chemical substitution at the Ce site¹⁸ and the Ge site¹⁹, and thermopower measurements²⁰.

Fig. 1: The crystal structure of CeRh₆Ge₄.

a Side view showing the coordination of Ce and Rh. b View along c showing the symmetry of the Ce site. c Spin configuration proposed in neutron scattering and μSR experiments¹⁵.

Theoretically, two contrasting approaches exist for describing 4f electron magnetism, depending on whether the 4f electrons are treated as itinerant or localized. In the case of CeRh₆Ge₄, quantum oscillation measurements have shown that the Fermi surface is well described by models assuming localized 4f electrons¹⁷. Consistently, ARPES measurements have also detected signatures characteristic of a localized 4f state¹⁶. These experimental findings indicate that the localized picture provides a suitable starting point for understanding the electronic and magnetic properties of CeRh₆Ge₄.

We employ a method based on dynamical mean field theory combined with density functional theory (DFT+DMFT). Our calculation procedure which successfully reproduced the antiferro-quadrupolar ordering in CeB₆²¹ is the following. First, we perform a DFT calculation in which the 4f electrons are treated as itinerant. Based on this electronic structure, we introduce the local Coulomb repulsion among the 4f electrons via DMFT, leading to 4f electrons with localized nature. We then calculate the momentum-dependent multipolar susceptibilities associated with the local 4f degrees of freedom. By identifying the divergence in the susceptibility, we determine the transition temperature and the corresponding order parameter. Using this approach, we will demonstrate that the ferromagnetic transition in CeRh₆Ge₄ can be reproduced within the localized 4f electron framework.

Results

Electronic structure

Figure 2a shows the electronic band structure calculated with fully relativistic density functional theory calculations using the full potential local orbital (FPLO) basis²² in combination with a generalized gradient approximation exchange correlation functional²³. We used the crystal structure reported in ref. ¹⁴. The lattice parameters are a = 7.154 Å and c = 3.855 Å. The path along the high symmetry points of the hexagonal space group of CeRh₆Ge₄ is shown in Fig. 2c. Figure 2b shows the species resolved densities of states. We use projective Wannier functions within FPLO^24,25 to obtain a tight-binding model with 108 orbitals (including spin degrees of freedom) consisting of Ce 4f, Ce 5d, Rh 4d, and Ge 4p. Comparison of black and blue lines in Fig. 2a indicate that the fit is excellent in a wide energy range around the Fermi level. The maximum hybridization strengths between Ce 4f and Rh 4d and between Ce 4f and Ge 4p are 0.10 eV and 0.15 eV respectively, while the direct 4f–4f hopping is at most 2.9 meV.

Fig. 2: Electronic structure of CeRh₆Ge₄.

a Fully relativistic DFT bandstructure (blue) with a 108 band tight binding fit (black). b Corresponding density of states of CeRh₆Ge₄. The maximum of the very sharp Ce 4f density of states of 76.2 states/eV/f.u. is not shown. c Brillouin zone of CeRh₆Ge₄ with the high symmetry paths shown in (a). d Single-particle excitation spectrum A(k, ω) in DFT+DMFT calculated at T = 0.01 eV. e Corresponding k-summed spectrum A(ω).

We performed magnetic calculations within LDA and GGA. The quantization axis of the magnetic moment was chosen parallel to the a axis or the c axis. In both cases, the total energy E_tot takes minimum at m = 0. This result demonstrates that the ferromagnetic state is not reproduced within LDA and GGA.

Figure 3 compares the crystalline electric field (CEF) energy levels of 4f electrons obtained from GGA calculations and experiment. The local symmetry at the Ce site is described by the point group D_3h under which the j = 5/2 manifold splits into three Kramers doublets: $\left\vert \pm 1/2\right\rangle$, $\left\vert \pm 3/2\right\rangle$, and $\left\vert \pm 5/2\right\rangle$. Experimentally, the ground state is $\left\vert \pm 1/2\right\rangle$, with the first and second excited states being $\left\vert \pm 3/2\right\rangle$ and $\left\vert \pm 5/2\right\rangle$, respectively¹⁵. The excitation energies are Δ₁ = 5.8 meV and Δ₂ = 22.1 meV, as determined from the temperature dependence of the magnetic susceptibility. In contrast, our DFT calculations yield the opposite level ordering. Furthermore, the energy scale of the splitting is around 100 meV, which is 5 times larger than the experimental one. The CEF levels in DFT do not reproduce the experimental magnetic anisotropy. To address this discrepancy, we incorporate the experimentally determined CEF level scheme directly into our tight-binding Hamiltonian.

Fig. 3: CEF level schemes of 4f electrons in CeRh₆Ge₄.

a Scheme derived from experiment¹⁵. b CEF level scheme obtained by our DFT calculations.

We treat the Coulomb repulsion in the 4f orbitals within the DFT+DMFT framework (see Methods section for details)^26,27,28. We exclude the total angular momentum j = 7/2 states of the 4f orbitals, which lie approximately 0.3 eV above the j = 5/2 states due to the spin-orbit coupling. The DFT+DMFT calculations are therefore applied to the remaining 100 orbitals. Figure 2d shows the single-particle excitation spectrum A(k, ω) calculated with parameters U = 6.92 eV, J_H = 0.8 eV, and ϵ_f = −2.7 eV. These values were chosen to ensure consistency between our results for A(k, ω) and experiments. The Hund’s coupling J_H is adopted from ref. ²⁹. The 4f⁰ peak in A(k, ω) has been observed at ω = −Δ₋ with Δ₋ = 2.7 eV in photoemmision experiments¹⁶. The lowest excitation energy from the 4f¹ to the 4f² configurations, Δ₊ = 3.1 eV, has been reported for elemental Ce³⁰ and confirmed by BIS experiments³¹. We determined the values of U and ϵ_f to reproduce both Δ₋ and Δ₊ in our spectrum. The resultant spectrum in Fig. 2e exhibits no 4f spectral weight at the Fermi level, meaning that the 4f electrons are fully localized. The conduction band near the Fermi level primarily consists of Rh-4d and Ge-4p states.

Magnetic properties

To investigate the phase transitions in CeRh₆Ge₄, we calculate the momentum-dependent static susceptibility, defined as

$${\chi }_{{m}_{1}{m}_{2}{m}_{3}{m}_{4}}({{{\boldsymbol{q}}}})= \frac{1}{N}\sum\limits_{ij}{e}^{-i{{{\boldsymbol{q}}}}\cdot ({{{{\boldsymbol{R}}}}}_{i}-{{{{\boldsymbol{R}}}}}_{j})} \\ \times \int_{\;\;0}^{\beta }d\tau \langle {O}_{i,{m}_{1}{m}_{2}}(\tau ){O}_{j,{m}_{3}{m}_{4}}\rangle ,$$

(1)

where m = +5/2, ⋯  , −5/2 denotes the z component of j = 5/2 orbitals, N is the number of lattice sites, the argument τ indicates the imaginary-time evolution in the Heisenberg picture, and the operator ${O}_{i,mm{\prime} }$ is given by

$${O}_{i,mm^{\prime} }={f}_{im}^{{{\dagger}} }{\, f}_{i{m}^{{\prime} }}.$$

(2)

We evaluate ${\chi }_{{m}_{1}{m}_{2}{m}_{3}{m}_{4}}({{{\boldsymbol{q}}}})$ defined in Eq. (1) using the strong-coupling-limit (SCL) formula (see Methods section for details). The momentum-dependent susceptibilities in the SCL formula are given by

$$\hat{\chi }({{{\boldsymbol{q}}}})={\left[{\hat{\chi }}_{{{{\rm{loc}}}}}^{-1}-\hat{I}({{{\boldsymbol{q}}}})\right]}^{-1},$$

(3)

where all quantities with hat are matrices indexed by the combined indices (m₁m₂) and (m₃m₄). ${\hat{\chi }}_{{{{\rm{loc}}}}}$ denotes the local susceptibility calculated from the atomic system, and $\hat{I}({{{\boldsymbol{q}}}})$ represents the intersite exchange interactions.

Figure 4a shows the eigenvalues χ_λ(q) of the susceptibility matrix $\hat{\chi }({{{\boldsymbol{q}}}})$. A total of 36 eigenvalues are classified into 9 groups. The number of modes in each group and the relevant CEF levels are summarized in Table 1. We determined the symmetry of the eigenmodes by analyzing the eigenvectors. The group with the largest susceptibility corresponds to fluctuations within the CEF ground-state doublet $\left\vert \pm 1/2\right\rangle$. This Kramers doublet carries magnetic degrees of freedom, which are classified into ${A}_{2}^{{\prime} -}$ and E^″− representations in the point group D_3h. Groups with dimension 8 involve hybridization between two CEF doublets. The corresponding density operators, such as ${f}_{1/2}^{{{\dagger}} }{f}_{3/2}$, can be classified into pairs of the electric ( + ) and magnetic ( − ) multipole operators³². Groups with dimension 1 consist of the totally symmetric representation ${A}_{1}^{{\prime} +}$. Among them, the lowest fluctuation mode, which exhibits nearly zero susceptibility, corresponds to charge fluctuations. The remaining modes are higher-order electric multipoles, including quadrupole and hexadecapole.

Fig. 4: The susceptibilities in momentum space and their temperature dependence.

a The eigenvalues of the susceptibility matrix, χ_λ(q) computed at T = 0.01 eV. b The magnetic susceptibility χ_ξ(q) within $\left\vert \pm 1/2\right\rangle$ states. c The temperature dependence of the inverse of the ferromagnetic susceptibility, 1/χ_ξ(0) with ξ = x, y. The vertical dashed lines indicate the energy of the CEF level splitting Δ₁ and Δ₂ given in Fig. 3a. The solid lines show the fitting by the high-T and low-T expressions in Eqs. (9) and (11), respectively. The inset shows a zoom-up of the low-temperature region. d The temperature dependence of the inverse of the susceptibility χ_J that corresponds to experiments.

Table 1 Classification of eigenmodes χ_λ(q) of the susceptibility

We focus on the leading fluctuations, which originate from the CEF ground-state doublet $\left\vert \pm 1/2\right\rangle$. The corresponding eigenvectors of the susceptibility matrix are well described by the Pauli matrices acting within the $\left\vert \pm 1/2\right\rangle$ subspace. To capture the magnetic fluctuations, we introduce the magnetic dipole operator projected onto the $\left\vert \pm 1/2\right\rangle$ states as

$${M}_{i\xi }={\sum}_{m{m}^{{\prime} }}{f}_{im}^{{{\dagger}} }{({\hat{M}}_{\xi })}_{m{m}^{{\prime} }}{f}_{i{m}^{{\prime} }},$$

(4)

where ξ = x, y, z and the matrix ${\hat{M}}_{\xi }$ is defined by

$${\hat{M}}_{x}=\frac{1}{\sqrt{2}}\left(\begin{array}{llllll}0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&1&0&0\\ 0&0&1&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\end{array}\right),$$

(5)

$${\hat{M}}_{y}=\frac{1}{\sqrt{2}}\left(\begin{array}{llllll}0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&-i&0&0\\ 0&0&i&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\end{array}\right),$$

(6)

$${\hat{M}}_{z}=\frac{1}{\sqrt{2}}\left(\begin{array}{llllll}0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&1&0&0&0\\ 0&0&0&-1&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\end{array}\right).$$

(7)

The susceptibility corresponding to the fluctuation of M_iξ can be evaluated by

$${\chi }_{\xi }({{{\boldsymbol{q}}}})={\sum}_{{m}_{1}{m}_{2}{m}_{3}{m}_{4}}{({\hat{M}}_{\xi })}_{{m}_{1}{m}_{2}}^{* }{\chi }_{{m}_{1}{m}_{2}{m}_{3}{m}_{4}}({{{\boldsymbol{q}}}}){({\hat{M}}_{\xi })}_{{m}_{3}{m}_{4}}.$$

(8)

Figure 4b shows χ_ξ(q) on the q-path. These quantities closely follow the leading eigenvalues χ_λ(q) presented in Fig. 4a, confirming that χ_ξ(q) effectively captures the dominant magnetic fluctuations. The strongest fluctuations appear in χ_x(q) and χ_y(q) at q = 0, corresponding to ferromagnetic fluctuations of the in-plane magnetic moment M_x and M_y. The difference between χ_x(0) and χ_y(0) is small (less than 1%), and we focus on the x component hereafter. Furthermore, χ_x(q) is significantly enhanced in the q_z = 0 plane (Γ–M–K–Γ) compared to the q_z = 1/2 plane (A–L–H–A). This indicates that the c axis bond favors ferromagnetic configuration.

Figure 4c shows the temperature dependence of the inverse of the ferromagnetic susceptibility, 1/χ_x(0). In the high-temperature region (T ≫ Δ₂), the six states of j = 5/2 are effectively degenerate due to thermal fluctuations. As a result, χ_x(0) follows the Curie-Weiss law represented by

$${\chi }_{x}^{{{{\rm{high}}}}}=\frac{{C}_{6}}{T-\Theta },$$

(9)

where the Curie constant C₆ is evaluated under the assumption of no CEF splitting as

$${C}_{6}\equiv \frac{1}{6}{\sum}_{m}{({\hat{M}}_{\xi }^{2})}_{mm}=\frac{1}{6}.$$

(10)

A fit to the numerical data yields the Curie-Weiss temperature of Θ = 7.5 meV. In the low-temperature region (T ≪ Δ₁), on the other hand, only the lowest CEF doublet is thermally occupied. In this limit, χ_ξ(q) can be represented by

$${\chi }_{x}^{{{{\rm{low}}}}}=\frac{{C}_{2}}{T-{T}_{{{{\rm{C}}}}}},$$

(11)

and the Curie constant C₂ is evaluated only with the $\left\vert \pm 1/2\right\rangle$ states as

$${C}_{2}\equiv \frac{1}{2}{\sum}_{m=\pm 1/2}{({\hat{M}}_{\xi }^{2})}_{mm}=\frac{1}{2}.$$

(12)

Fitting the low-temperature data gives a ferromagnetic transition temperature of T_C = 0.28 meV ≈3.2 K. It is important to note that this first principle result for T_C is very close to the experimental value of T_C = 2.5 K. This overestimation by approximately 0.7 K or 30% is consistent with previous findings for CeB₆, where the SCL method similarly overestimated the transition temperature of the antiferro-quadrupolar ordering²¹.

We note that the magnetic susceptibility χ_ξ defined in Eq. (8) differs from the quantity measured in experiments. The experimentally measured magnetic susceptibility χ_J is defined by

$${\chi }_{J}={\frac{\partial \langle m\rangle }{\partial H}\Big| }_{H\to 0},$$

(13)

under the Zeeman field ${{{{\mathcal{H}}}}}_{Z}=-mH$. For a magnetic field parallel to the z axis, the magnetic moment operator m is given by m = −g_Jμ_Bj_z, where j_z is the z-component of the total angular momentum operator with j = 5/2 and g_J is the Landé g-factor, which is given by g_J = 6/7 for the Ce³⁺ ion. χ_J can be computed from ${\chi }_{{m}_{1}{m}_{2},{m}_{3}{m}_{4}}({{{\boldsymbol{q}}}})$ as in Eq. (2). The explicit form for χ_J is thus given by

$${\chi }_{J}= {({g}_{J}{\mu }_{{{{\rm{B}}}}})}^{2} \\ \times \sum\limits_{{m}_{1}{m}_{2}{m}_{3}{m}_{4}}{(\,{j}_{z})}_{{m}_{1}{m}_{2}}^{* }{\chi }_{{m}_{1}{m}_{2}{m}_{3}{m}_{4}}({{0}}){(\,{j}_{z})}_{{m}_{3}{m}_{4}}.$$

(14)

The cases with the magnetic field parallel to the x- and y-axes are computed in a similar manner. Figure 4d shows the temperature dependence of 1/χ_J. The overall behavior, including the anisotropy and the strong T-dependence for H∥z below T ≃ Δ₁, is consistent with the experiments¹⁵.

We now turn to the intersite interactions. To isolate the effective interaction between $\left\vert \pm 1/2\right\rangle$ states, we project the full momentum-dependent interaction ${I}_{{m}_{1}{m}_{2}{m}_{3}{m}_{4}}({{{\boldsymbol{q}}}})$ onto the dipole channel using the same transformation as in Eq. (8). The resulting quantity I_ξ(q) represents the exchange interaction within the ground-state doublet. Figure 5a shows I_ξ(q) along the representative q-path. Its q-dependence closely follows that of χ_ξ(q), in agreement with Eq. (3), which indicates that the q-dependence of χ_ξ(q) originates entirely from I_ξ(q). The magnitude of the ferromagnetic interaction is approximately 0.7 meV, which is comparable to the ferromagnetic transition temperature T_C.

Fig. 5: Effective interactions between the magnetic moments in the $\left\vert \pm 1/2\right\rangle$ states.

a The momentum-dependent effective interaction I_ξ(q). b Linear-scale plot of the effective inter-site interaction I_ξ(i, j) as a function of the distance ∣r_ij∣ = ∣R_i  − R_j∣. c A log-log plot with the line showing I_ξ(i, j) ∝ ∣r_ij∣⁻³. The vertical dashed lines show the Ce-Ce distances with the labels n₁n₂n₃ indicating r = n₁a  + n₂b + n₃c.

To gain real-space insight into the magnetic interactions, we computed I_ξ(q) over the entire Brillouin zone and performed a Fourier transform to obtain the intersite interactions I_ξ(i, j). This quantity defines the effective Heisenberg Hamiltonian for the projected dipole moments M_iξ, given by

$${{{\mathcal{H}}}}=-\frac{1}{2}{\sum}_{ij\xi }{M}_{i\xi }{I}_{\xi }(i,j){M}_{j\xi }.$$

(15)

Figure 5b shows I_ξ(i, j) as a function of intersite distance ∣R_i − R_j∣. Explicit values of I_ξ(i, j) are presented in Table 2. The strongest interaction occurs along the c axis, corresponding to the nearest-neighbor sites. This bond exhibits a sizable ferromagnetic exchange that is isotropic in spin space. The next-nearest-neighbor interactions, located in the a–b plane, exhibit pronounced spin anisotropy. Specifically, the in-plane components M_x and M_y are coupled ferromagnetically, while the out-of-plane component M_z shows antiferromagnetic coupling. Figure 5c presents a log-log plot of ∣I_ξ(i, j)∣, revealing a power-law decay I_ξ(i, j) ~ ∣R_i − R_j∣⁻³. This behavior is characteristic of the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction, confirming its role as the primary mechanism driving the magnetic ordering in CeRh₆Ge₄.

Table 2 Values of intersite interactions I_ξ(i, j) corresponding to Fig. 5b

Discussion and conclusions

The magnetic structure obtained by our calculations is illustrated in Fig. 1c. The effective interaction responsible for this structure can be described as follows. By retaining interactions up to the second nearest neighbors in Eq. (15), we obtain the effective Heisenberg model of spin S = 1/2 as

$${{{\mathcal{H}}}}\simeq -{J}_{c}\sum\limits_{\langle ij\rangle \parallel c}{{{{\boldsymbol{S}}}}}_{i}\cdot {{{{\boldsymbol{S}}}}}_{j}\\ -{J}_{ab}\sum\limits_{\langle ij\rangle \perp c}\left[{S}_{i}^{x}{S}_{j}^{x}+{S}_{i}^{y}{S}_{j}^{y}-r{S}_{i}^{z}{S}_{j}^{z}\right],$$

(16)

where the first and the second summations represent nearest-neighbor pairs along the c axis and within the a–b plane, respectively. From the numerical results in Table. 2, we obtain J_c =  0.45 meV, J_ab/J_c = 0.087, and r = 0.41 (note that J’s are twice as large as I_ξ). The first term represents the strong coupling of the Ce moments along the c axis, leading to the formation of ferromagnetic chains. These chains are aligned by weaker inter-chain interactions within the a–b plane (the second term), which collectively stabilize the ferromagnetic configuration shown in Fig. 1c. Although the in-plane components of the moment are coherently aligned, the c axis component is influenced by geometrical frustration arising from the inter-chain antiferromagnetic coupling. This frustration suppresses out-of-plane magnetic order and is reflected in the momentum dependence of the interaction I_z(q), whose maximum appears at the M point of the Brillouin zone [Fig. 5a].

In ref. ¹⁰, the strange-metal behavior around the QCP is analyzed by the Heisenberg Hamiltonian, assuming XXZ-type anisotropy with weak S^z interaction. Our microscopic derivation of the effective Heisenberg model supports their starting point, which leads to a linear dispersion of the magnetic excitations. Furthermore, the weak inter-chain coupling guarantees a second-order phase transition, enabling the emergence of the QCP under pressure¹⁰.

A direct calculation of a QCP under external pressure requires substantial computational effort. As described by the Doniach phase diagram³³, the ordering temperature is suppressed as a result of competition between long-range order induced by the RKKY interactions and the paramagnetic heavy-Fermion state driven by the Kondo effect. Our calculations using the atomic self-energy within the Hubbard-I approximation neglect the Kondo effect. Consequently, applying the present calculations under pressure simply leads to an increase in the Curie temperature associated with the reduction of the lattice constant. To estimate the Kondo temperature T_K, we employed the continuous-time quantum Monte Carlo method³⁴ as an impurity solver. While we observed signs of a low-energy quasiparticle peak emerging below T ≃ 1 meV, determining T_K and its pressure dependence with sufficient accuracy remains challenging.

Finally, we discuss the origin of the ferromagnetic transition in CeRh₆Ge₄. The q-dependence of the RKKY interaction is governed by the Fermi surface of conduction electrons. Fig. 6 displays the Fermi surface evaluated from A(k, ω) at ω = 0. As shown in Figures 6a–e, the Fermi surface is isotropic in the k_x–k_y plane. The cut at the k_y = 0 plane in Fig. 6f reveals a Fermi surface that spans the entire k_z range, indicating a deformed cylindrical shape—characteristic of two-dimensional systems. These features are consistent with a quantum oscillation measurement, which showed that the observed Fermi surface is consistent with the DFT results assuming localized 4f electrons¹⁷. It is known that the two-dimensional free electrons exhibit a plateau in the static susceptibility χ₀(q) for ∣q∣ < 2k_F, followed by a decay for ∣q∣ > 2k_F, where k_F is the Fermi wavenumber. We suggest that the weakly three-dimensional cylindrical Fermi surface gives rise to the peak at the Γ point in our numerical results.

Fig. 6: Single-particle excitation spectrum A(k, ω) of CeRh₆Ge₄ at ω = 0.

a–e The k_z = nπ/4c plane with n = 0, 1, 2, 3, 4. The hexagon indicates the Brillouin zone. f The k_y = 0 plane. A full Brillouin zone is shown.

In summary, we investigated the ferromagnetism in CeRh₆Ge₄ using the DFT+DMFT method, treating the Ce 4f electrons as localized. The intersite exchange interactions, evaluated using the strong-coupling-limit (SCL) formula, revealed dominant ferromagnetic coupling along the c axis, forming spin chains that are isotropic in spin space. In contrast, the inter-chain coupling is anisotropic: ferromagnetic for the in-plane moment and antiferromagnetic for the out-of-plane moment. These interactions give rise to a magnetic structure in which the magnetic moment is aligned within the a–b plane.

The calculated transition temperature is in reasonable agreement with the experimental value, although the mean-field nature of the intersite interaction in DMFT tends to overestimate the transition temperature. Our results provide theoretical support for anisotropic exchange interactions between localized 4f moments, offering a foundation for understanding the anomalous metallic behavior observed near the ferromagnetic QCP under pressure.

Methods

DFT+DMFT method

The DFT+DMFT method incorporates local electronic correlations within a specific shell, building upon the DFT electronic structure^26,27,28. The single-particle Green’s function matrix $\hat{G}({{{\boldsymbol{k}}}},\omega )$ is defined as

$$\hat{G}({{{\boldsymbol{k}}}},\omega )={\left[(\omega +\mu )\hat{I}-\hat{H}({{{\boldsymbol{k}}}})-{\hat{\Sigma }}_{{{{\rm{loc}}}}}(\omega )+{\hat{\Sigma }}_{{{{\rm{DC}}}}}\right]}^{-1}.$$

(17)

Here, all quantities with hats represent matrices in the Wannier-function basis. $\hat{I}$ is the identity matrix, and μ is the chemical potential. $\hat{H}({{{\boldsymbol{k}}}})$ is the tight-binding Hamiltonian obtained from DFT, where the on-site energies of the 4f orbitals are adjusted to reproduce the experimental CEF energy level scheme. ${\hat{\Sigma }}_{{{{\rm{DC}}}}}$ is the double-counting correction that accounts for correlation effects already included in DFT. Following ref. ²¹, we represent it as

$${\hat{\Sigma }}_{{{{\rm{DC}}}}}=-{\epsilon }_{f}\left\vert \, f\right\rangle \left\langle f\right\vert ,$$

(18)

where $\left\vert \, f\right\rangle \left\langle f\right\vert$ is the projection operator onto the 4f subspace. The parameter ϵ_f is determined along with the interaction parameters.

The local self-energy $\hat{\Sigma }(\omega )$ is defined on the 4f orbitals. We employ the fully rotationally invariant Slater interactions, characterized by four Slater integrals F_k with k = 0, 2, 4, 6. These are converted from two intuitive parameters: the direct Coulomb interaction U and the Hund’s exchange coupling J_H³⁵. To compute $\hat{\Sigma }(\omega )$, we solve the atomic problem within the Hubbard-I approximation, which neglects hybridization with the conduction electrons. These calculations were done using the open-source software DCore³⁶, which is implemented with TRIQS³⁷ and DFTTools³⁸ libraries. The exact diagonalization of the atomic problem was solved using pomerol³⁹. The number of k points in the DFT+DMFT calculations is 24 × 24  × 42.

SCL formula for susceptibility

We evaluate ${\chi }_{{m}_{1}{m}_{2}{m}_{3}{m}_{4}}({{{\boldsymbol{q}}}})$ defined in Eq. (1) using the strong-coupling-limit (SCL) formula, which is derived from the Bethe-Salpeter (BS) equation within DMFT^21,40. Unlike the full BS equation, the SCL formula does not require computation of the vertex function, significantly simplifying the calculation. When applied to CeB₆, the SCL formula yields quantitative agreement with the results obtained from the full BS equation²¹, demonstrating its reliability in systems with localized 4f electrons.

The momentum-dependent susceptibilities in the SCL formula are given by Eq. (3). To evaluate $\hat{I}({{{\boldsymbol{q}}}})$, we employ the two-pole approximation (SCL3)^21,40, which captures the virtual excitations around the 4f¹ configuration. We use excitation energies Δ₊ = 3.1 eV and Δ₋ = 2.7 eV, corresponding to excitations from 4f¹ states to 4f² and 4f⁰ configurations, respectively, in A(k, ω).