Introduction

Secondary organic aerosol (SOA) is the dominant type of fine-mode aerosol mass1, yet large-scale models generally underpredict the magnitude of observed organic aerosol2,3,4,5,6. These aerosols, formed from the oxidation of volatile organic compounds (VOCs), have profound impacts on the global radiation balance, either directly by scattering7 and absorbing solar radiation8, or indirectly by impacting cloud and rain formation processes9,10. Furthermore, they can boost global primary productivity up to 25% for some ecosystems via diffuse radiation fertilization11. Therefore, it is essential to understand which VOCs are emitted, how large those emissions are, and what fraction of a given VOC will ultimately be able to form SOA.

Isoprenoids are a group of biogenic VOCs (BVOC) that have been identified as the dominant sources of SOA globally1,12,13. These compounds can protect against oxidative damage at the (sub-)cellular level and can serve as signalling compounds within plant-plant and plant-insect interactions, as well as at the plant and ecosystem levels, providing protection against biotic and abiotic stress14. Isoprenoids can be emitted de novo, from recently photosynthesized carbon, like isoprene (C5) and some monoterpenes (C10) or be released from storage pools like most monoterpenes and sesquiterpenes (C15). Despite diterpenes (C20) being constituents of many plants’ essential oils15,16, they were until recently thought not to be emitted into the gas phase due to their low volatility17, and thus have never been considered relevant for atmospheric chemistry.

Diterpenes have important roles inside plants, such as growth regulators, providing an essential building block for chlorophyll (a diterpene conjugate), and playing crucial roles in ecological interactions between plants and other organisms, such as signalling and defence against herbivores in the form of oleoresins17,18. There is a wide range of diterpene molecular species (Supplementary Section 1), and some reports have found that emissions are temperature dependent19,20,21 and derived from storage pools20,22. These studies also point out that diterpenes are most likely emitted from plants with a highly active secondary metabolism20. Nevertheless, considerable gaps still exist in understanding the diterpene emissions from vegetation given the small number of plant species measured for diterpene emissions and the scarce ambient observations available up to date.

Methodological improvements in both sampling and detection have enabled observations of diterpenes in the gas phase. Ambient air mixing ratios of diterpenes have been reported from a rural site in Amazonia and two temperate forests (Landes forest in France and the Rocky mountains in the USA) ranging from 19 ppq to 2 ppt23,24. Diterpene emissions from plants have been recently detected from mosses25, temperate26 and boreal conifer trees19,27, grasses21, broadleaf trees28, Mediterranean shrubs20,29 and soil emissions from permafrost30. Additionally, diterpene emissions were observed during cooking with herbs31. In order to give a proper overview, we have performed a literature review on all available diterpene vegetation emissions measurements to date. This literature synthesis can be found in the Supplementary Information (Supplementary Section 2).

When emitted into the atmosphere, all C20 compounds are expected to impact aerosol loading simply due to their mass, similar to other large highly reactive isoprenoids such as the sesquiterpenes (C15)32,33. Very recently, kaurene (one diterpene species) ozonolysis was shown to produce a wide range of different highly oxygenated products able to condense and form SOA34. Importantly, due to its exocylic double bond35, kaurene is expected to be among the least reactive diterpenes, hence using kaurene as a representative C20 species establishes only the lower limit for the atmospheric impact of diterpenes, indicating that the cumulative impact of all diterpenes is higher. In addition, diterpenes may contribute to the so-called missing OH reactivity due to their terpenoid nature, as suggested for different environments19,36.

There is a substantial lack of data available to refine current emission models37 and aerosol formation from diterpenes. To address these knowledge gaps, we performed the first experimental SOA chamber studies of aerosol forming potential for kaurene where we were able to obtain the first kaurene SOA yield. This new result, together with the first vegetation emission estimates for diterpenes using all existing data to date, were used in the Multiscale Online Non-hydrostatic AtmospheRe CHemistry model (MONARCH)38,39,40,41,42,43,44 to assess the potential impact of diterpene emissions on the atmospheric SOA loading.

Results and discussion

SOA chamber experiments to determine the kaurene SOA formation yield

We performed chamber experiments using authentic kaurene standard (see Methods for details) to simulate the relevant atmospheric processes. Kaurene and ozone were injected into the chamber, resulting in kaurene oxidation by ozone, but to some extent also by hydroxyl radicals (OH) formed from the ozone-alkene reactions. Also in the atmosphere, kaurene will be oxidized by both O3 and OH, and therefore the conditions can be assumed roughly representative of atmospheric conditions. We added ammonium sulphate aerosols to the chamber to act as seeds for condensation of the oxidation products. Five experiments were performed, at loadings ranging from 0.11 to 11 ppb, and the observed SOA mass yields from kaurene oxidation by O3 and OH ranged from 4 to 7 % (Fig. 1), though with relatively large uncertainties, estimated as a factor of 3 (+200%/−67%), due to challenges with kaurene quantification during our experiments34. This yield was lower than anticipated based on typical values observed for other terpenes, where larger molecular sizes often correlate with higher SOA yields32,45,46,47. However, it is well known that the VOC structure plays an important role, as e.g. monoterpene SOA yields vary from negligible to several tens of percent47. Kaurene has one exocyclic double bond, which is not a favourable structure for autoxidation following ozonolysis48, which may suppress the formation of highly oxygenated organic molecules (HOM) and, consequently, the SOA yield compared to many other typical terpene functionalities. To some extent, kaurene can be compared to the monoterpene β-pinene, which also has a similar exocyclic double bond and typically shows a much lower SOA yield from ozonolysis than its counterpart α-pinene46, where the double bond is endocyclic. This comparison suggests that kaurene falls within the lower range of SOA yields for diterpenes, compared to diterpenes with endocyclic double bonds, like e.g. cembrene. Our SOA yield estimates are in agreement with reported gas-phase HOM yields of a few percent34.

Fig. 1: Measured SOA mass yield as a function of formed SOA mass.
figure 1

Colouring of the markers is based on the average kaurene concentration (range 0.11–11 ppb) and the size of markers is based on the average ammonium sulphate seed concentration (ranging from 5.8 to 42 μg m−3) in the chamber for the corresponding SOA steady state time period. Uncertainties in the yields were estimated to be +200%/−67%.

Full size image

Literature synthesis of all published plant diterpene emissions studies

In order to estimate the atmospheric impacts of diterpene emissions, we used the global chemical transport model MONARCH with BVOC emissions computed with a modified version of the Model of Emissions of Gases and Aerosols from Nature biogenic emissions (MEGANv2.04: Guenther et al.49). The MEGAN model estimates BVOC emission based on the standard emission factors (EFs, emission factors at 30 °C) for four different plant functional types (PFT), namely needle leaf trees (NL), broad leaf trees (BL), shrubs (SB) and grass/crops (HB). MEGAN includes emissions for isoprene (C5), monoterpenes (C10), and sesquiterpenes (C15) among other BVOCs, and we now added the first diterpene emissions into the model. To this end, we performed a literature synthesis on all available reports of diterpene emissions and ambient mixing ratios19,20,21,22,23,24,27,29,50,51,52, which includes a total 7 studies that report plant diterpene emissions that were used in this analysis. While this is a very limited number, fortunately these studies do cover all the four PFTs: NL with species Norway Spruce (Picea abies)19,27, Scots Pine (Pinus sylvestris)19,27, Japanese cedar (Cryptomeria japonica)50 and Japanese cypress (Chamaecyparis obtusa)50, SB with gum rockrose (Cistus Ladanifer)20,29 and rockrose (Halimium halimifolium)20, BL with downy birch (Betula Pubescens)28, and HB with fen (sedges)21 (see Supplementary Table 2.1).

Given the variability in how results were reported in the above studies, we had to use some assumptions to harmonize the diterpene emission factors. Some studies reported specific diterpene types (e.g. kaurene or cembrene), while others measured the sum of diterpenes. We converted all data to the sum of diterpenes by assuming that the studies that reported speciated diterpenes had detected the most abundant ones, and thus their sum could be taken as the total diterpenes. In addition, some of the studies reported EFs whereas for some others20,27 we needed to convert the reported emission rates to EFs using an average of empirically derived coefficients reported in the other studies that provided EFs.

Furthermore, the EFs reported exhibited significant variability of up to 4 orders of magnitude (for NL and SB). Moreover, there is very limited data available for HB and BL, with only one study reporting values for each PFT (see Supplementary Table 2.1).

Best estimates for standard emission factor EFs

The process of harmonization described above infers some uncertainties, but we expect that the largest uncertainty in our study comes from the reported emission observations, e.g. related to measurement uncertainties or the used plants not being representative for the entire PFT. For HB and BL, there were only one study each, while for NL with several observations, the EFs varied up to four orders of magnitude. For these reasons, we decided to perform several runs with varying diterpene EFs as a sensitivity analysis of the impacts of global diterpene emissions, with a primary focus on their ability to contribute to the atmospheric SOA burden.

We performed six different model runs (Table 1), where the first run (“LitData”) used the geometric mean of reported EFs values for each PFT (in cases with only one reported value, this value was then used) together with an SOA yield of 5.5% from our measurements. In the second model run (“Scaled”), the EFs for the PFTs with only one reported value available (BL and HB) were scaled to the EFs for NL using typical BL:NL and HB:NL ratios for monoterpenes (the sum of α-pinene and β-pinene). In MEGAN, these ratios are 0.36 and 0.0046, respectively, which are representative of most mono- and sesquiterpenes. However, the “LitData” BL:NL and HB:NL ratios were 0.001 and 0.22, respectively, prompting us to believe that the BL value is underestimated and the HB value overestimated. While it is possible that the diterpene emissions patterns differ so dramatically from the smaller terpenes, we opted to use the “Scaled” scenario as the base case for the last four model runs. In “ScaledMin” and “ScaledMax” we used the respective minimum and maximum NL and SB observations of EFs and obtaining the EFs for BL and HB from scaling to the NL EFs, with the exceptions that in “ScaledMin” we used the observed BL EFs and for “ScaledMax” we used the observed HB EFs. The last two runs, “ScaledHighSOA” and “ScaledLowSOA”, used the same EFs as in the “Scaled” run, but varied the SOA yield from high (17%) to low (1.8%). These values correspond to the average value multiplied or divided by 3, respectively, a factor derived from the uncertainty in kaurene concentration as discussed in Luo et al.34. For more details on the choices of each of the EFs for different runs and different PFTs, see Table 1.

Table 1 Selected basal emission factors for diterpenes for the different PFTs available in the model for diterpene emissions at a global scale
Full size table

The proportion of diterpene emission factors among the different PFTs is different than for other more known terpenes. This could be due to three reasons: 1) diterpene emissions might be fundamentally different from other terpenes, 2) the non-needle leaf tree emission factors might be highly underestimated, or 3) the needle leaf tree emission factor might be highly overestimated. In the latter case, it is important to note that the needle leaf tree emission factor is a geometric average of all measured needle leaf tree species, and this standard emission may have been overestimated for certain needle leaf tree species, such as C. Japonica and C. Obtusa, as their standard emission factors are up to three orders of magnitude higher than from other plant species. Nevertheless, a recent study reported extremely high emissions for C. Obtusa51, suggesting this species may have a very high emission capacity for diterpenes. In addition, the monitored species used for BL is downy birch (Betula Pubescens) which is known to be a low VOC emitting species, with most of its emission occurring when under stress33. This underscores the necessity for comprehensive screening of diterpene emissions across different plant species. We acknowledge the inherent uncertainty on the emission estimates derived from the scarce data available and the assumption made for the EFs for the model, which are anyhow based on values reported in literature, and exhibit equally high variability as monoterpenes53. However, our main aim was to investigate the potential impacts of diterpenes forming SOA given the currently available information and understanding, and we feel that our choice of runs allows us to make a first estimate of this.

Global simulations of diterpene emissions and the production of diterpene SOA

The global annual emission of diterpenes from the “Scaled” run is shown in Fig. 2a, being in total 11.5 Tg yr−¹ (Table 2). The global maps for the rest of the model runs can be found in Supplementary Section 3.1. This value is very close to the “LitData” result of 10.4 Tg yr−¹, which is partly due to the large contribution from NL in both runs, and partly due to compensating effect from BL (high in “Scaled”, low in “LitData”) and HB (low in “Scaled”, high in “LitData”) as can be seen from the relative contributions from PFTs in Table 2. The lower (0.10 Tg yr−¹ in “ScaledMin”) and upper (94 Tg yr−¹ in “ScaledMax”) limits for diterpene emissions in our model runs highlight the need for more emission measurements to narrow down the uncertainty. But we can contrast our model results to 424.8 Tg yr−¹ for isoprene, 90.3 Tg yr−¹ for monoterpenes or 13.5 Tg yr−¹ for sesquiterpenes (for more details see Supplementary Figs. 3.3.1., 3.3.2. and 3.3.3.). It seems feasible to assume that our maximum estimate is unrealistic, as the diterpene emissions exceed those of the smaller and more volatile monoterpenes.

Fig. 2: Annual average.
figure 2

a Diterpene emission rates [mg m−2 day−1] and b SOA diterpene surface concentration [µg m−3] estimates for 2018 for the “Scaled” run.

Full size image
Table 2 Global annual % of total emission per plant functional type, SOA burden (Tg), SOA production (Tg yr−1) for the different diterpene runs, and isoprene, monoterpenes and sesquiterpenes for the year 2018
Full size table

To derive the first estimates of the contribution of diterpenes to SOA formation, we considered 1.8–17% (average 5.5%) SOA yield for diterpenes. These values correspond to the average SOA yield scaled up/down by a factor 3 to account for the uncertainty in deriving kaurene concentrations in the chamber experiments34. The yields for isoprene12,54,55, monoterpenes46,55 and sesquiterpenes55,56,57 were approximated as 1% for isoprene, 10% for monoterpenes and 20% for sesquiterpenes given the wide range of yields reported in literature.

The global annual average aerosol mass in the atmosphere (i.e., the burden) of SOA from diterpene vegetation emission for 2018 from the “Scaled” run is 0.008 Tg (SOA production of 0.63 Tg yr−¹) (Table 2). This value is very close to the “LitData” result of 0.008 Tg (SOA production of 0.57 Tg yr−¹). The range of SOA yields caused the burden to differ from 0.003 Tg (SOA production of 0.21 Tg yr−¹) in “ScaledLowSOA” to 0.025 Tg (SOA production of 1.96 Tg yr−¹) in “ScaledHighSOA”. The effect on SOA  from varied emission factors ranges widely from a negligible effect with a 0.00007 Tg burden (SOA production of 0.005 Tg yr−¹) for the “ScaledMin” run to 0.069 Tg (SOA production of 5.19 Tg yr−¹) for the “ScaledMax” run.

Whereas the “ScaledMin” run suggests a negligible effect of diterpene emissions on SOA concentrations, the “ScaledMax” run seems unrealistic as diterpenes would have a higher impact than sesquiterpenes at a global level (SOA burden of 0.042 Tg and SOA production of 2.71 Tg yr−¹) and would correspond to half of the monoterpene SOA (burden of 0.125 Tg and production of 9.03 Tg yr−¹). Given that the experimentally derived diterpene SOA yield was for kaurene, we can expect that the average SOA yield for diterpenes could be closer to the “ScaledHighSOA” scenario, but more studies are needed to assess the SOA yields of different diterpenes, preferably under different conditions. Following the diterpene emission trends, the highest diterpene SOA surface concentration globally takes place over the tropical rainforests, with a smaller contribution from boreal and temperate forests (Fig. 2b).

The emission of diterpenes exhibits significant variability both spatially and seasonally (Figs. 2a and 3), being strongly influenced by the emission factors integrated into the model (Table 1). The diterpene SOA surface concentration seasonality follows the same seasonality as diterpene emissions (Fig. 4). Globally, peak emissions typically occur in summer. Tropical rainforests demonstrate a relatively consistent emission pattern throughout the year. Conversely, the boreal region and Southeastern US experience elevated diterpene emissions during the growing season. These emissions suggest that even if the EFs of NL is overestimated, diterpene emissions are still dominant in tropical forests, where needle leaf trees are not present or in very little abundance58. The seasonality maps of diterpene emissions for the rest of the model runs can be found in Supplementary Section 3.2.

Fig. 3: Seasonal average diterpene emission rates [mg m−2 day−1] estimates for 2018 for the “Scaled” run.
figure 3

JFM January-February-March, AMJ April-May-June, JAS July-August-September, OND: October-November-December.

Full size image
Fig. 4: Seasonal diterpene SOA surface concentration [µg g m−3] estimates for 2018 for the “Scaled” run.
figure 4

JFM January-February-March, AMJ April-May-June, JAS July-August-September, OND October-November-December.

Full size image

Given the high uncertainty involved in the selected emission factors, we have calculated the relative percentage of diterpene emission of each PFT for the different runs (Table 2). These results underscore the dominance of NL over the total global emissions. In addition, the results demonstrate how the literature data run may not be realistic given the high percentage of HB emitting diterpenes and the negligible percentage of BL emitting diterpene, which is totally different from any other isoprenoid. Furthermore, results show that the SB emissions are almost null in the “Scaled” runs, being different from the SB emissions for any other isoprenoids. Only in the “ScaledMax” run there are higher SB emissions, albeit much higher than for other isoprenoids. Despite the “ScaledMin” run seeming plausible, literature data demonstrates much higher EFs in general. Therefore, there is good reason to assume that our “Scaled” run is more realistic than the other runs, but in particular, than the “LitData” run. For a comparison of isoprene, monoterpene, and sesquiterpene emissions and associated SOA burdens from this study and previous work, see Supplementary Table 3.4 in the Supplementary Information.

The effect of varying SOA yield on the global diterpene SOA burden is lower than the effect of varying diterpene EFs (Fig. 5). This indicates that the largest uncertainty in quantifying global diterpene SOA burden is the EFs input, highlighting the need for more diterpene emission measurements. The lower sensitivity of the SOA yield is also partly explained by the fact that SOA yields for most large organic molecules range from a few percent to a few tens of percent, making it much more constrainable than EFs.

Fig. 5
figure 5

Comparison of the global diterpene SOA burden in Tg for the different SOA yield runs (left panel) and the different emission factor runs (right panel). Note the y-axis is in log scale.

Full size image

This study provides the first estimate of diterpene ozonolysis SOA yield, highlighting the diterpenes’ potential, yet previously overlooked, role in atmospheric chemistry. We estimate a range of global diterpene emissions and the associated SOA burden for 2018, although uncertainties in emission factors remain. While we demonstrate that diterpenes contribute to SOA formation, their overall significance should be further refined, as this assessment is constrained by the availability of vegetation diterpene emission factors. This constraint arises not only from the scarcity of studied plant species but also from the extremely high variability in reported emission magnitudes, with differences of up to four orders of magnitude observed among monitored species. Our work relies on all published diterpene emission data available at present, representing the best assessment of their role and associated uncertainty on atmospheric aerosol burdens. Furthermore, one of the next steps in diterpene research must be comparison of simulated diterpene concentrations to observations.

Additionally, the SOA yield was estimated only for kaurene, and its molecular structure suggests lower reactivity than other diterpenes. This indicates that some diterpenes may have an even greater atmospheric impact. These findings can also enhance our understanding of the “missing OH reactivity” and unidentified biogenic SOA, emphasizing the need for broader studies, particularly in tropical regions where emissions remain poorly quantified.

The significance of diterpenes in atmospheric processes depends on multiple factors, including emission variability, reactivity, and environmental conditions. While evidence suggests that emissions increase with temperature, further research is needed to assess their full impact on SOA formation, new particle formation, and cloud dynamics. In particular, diterpene concentrations may influence ozone and methane levels and, through aerosol loading, affect cloud properties. Future experiments should explicitly include the nucleation of diterpene oxidation products to fully understand their role in atmospheric chemistry. If diterpenes are confirmed to be a major source of SOA, current atmospheric models may be underestimating biogenic contributions, particularly in regions with high densities of diterpene-emitting vegetation. By providing the first experimental SOA yield for kaurene, this study takes an important step toward evaluating the role of diterpenes in atmospheric chemistry and their potential influence on air quality and climate.

Methods

Controlled kaurene SOA experiments

Kaurene ozonolysis experiments were conducted in a 2 m3 Teflon (FEP, supplied by Vector Foiltec, Germany) chamber, the COALA chamber at the University of Helsinki, Finland. An authentic pure solid kaurene standard was purchased from OLChemIm Ltd., Olomouc, Czech Republic. The total flow was around 36 L min−1 consisting of purified air, varying amounts of O3 and the diterpene ent-kaurene, and 80 nm inorganic seed particles comprised of ammonium sulphate (AS). The chamber was operated at room temperature (26 ± 1 °C) and under dry conditions (RH < 1%). The composition of VOCs was measured with the Vocus Proton Transfer Reaction Time of Flight mass spectrometer (Vocus PTR-ToF)59. The chemical composition of SOA was measured with a Long ToF Aerosol Mass Spectrometer (LToF-AMS)60. In addition, we had a custom-built scanning mobility particle sizer (SMPS) to measure the particle number size distribution. Based on the SMPS data, we also calculated area and volume concentrations. The SOA, ammonium sulphate (AS) and total particle mass concentrations were calculated by using the total particle volume from the SMPS combining it with the density and SOA-to-AS ratio measured with the AMS. More information on this experiment set up can be found in Luo et al.34. This approach, rather than directly using the measured mass concentrations from the AMS, was utilized since the collection efficiency of the AMS varies as a function of the ratio between organics and AS61. The details of the chamber facility, instruments, and experimental setups are found elsewhere62.

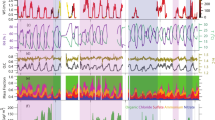
All instruments sampled the chamber air continuously, and the inputs into the chamber were varied (Fig. 3) to achieve different concentrations and ratios of kaurene and O3. The O3 concentrations ranged from ∼70 to ∼110 ppb for different experiments, and the kaurene concentration was at most ∼20 ppb. Seed aerosols were added at different times in order to initiate condensation onto aerosols rather than chamber walls, which is usually the dominant sink for low-volatility vapours. The injection of kaurene was one of the most challenging parts of the experiments due to its low volatility. Gas-phase kaurene was introduced into the chamber by flushing nitrogen (N2) through a vial containing the solid kaurene, and the flow was subsequently directed into the chamber. In addition, a heater was placed under the vial to promote the evaporation of kaurene. During the experiments, the vial’s bottom temperature stayed below 45 °C, except for the last experiment day when the vial reached a temperature around 60 °C. Already at low heating, the solid kaurene had melted to liquid form, but we did not see indications of decomposition of the kaurene from the heating in any of our mass spectra. Variable levels of kaurene in the chamber were achieved, either by turning the heater on and off or changing the flow rate of the N2 carrier gas, which was controlled with a mass flow controller (MKS, G series, Andover, MA, USA). Due to the low volatility of kaurene, residual amounts were introduced into the chamber also when no active addition was performed, presumably due to evaporation from surfaces in the tubing and chamber.

SOA yield estimation

As we used a steady state chamber, the SOA yield cannot simply be calculated by dividing the measured SOA mass with an amount of reacted VOC, as would be the case in batch-mode chambers. In addition, owing to the difficulties of injecting a constant amount of kaurene—a solid at room temperature—and the limited amount of sample available, completely stable conditions were not reached during the experiments. An example kaurene time series is shown in Fig. 6 where the concentration fluctuates in the range 0.12 ± 0.02 ppb over the initial hours of the experiment. This variation is primarily caused by fluctuations in the injection rate of kaurene into the chamber, as losses (through oxidation by ozone and through flush out) remained stable. Thus, we estimate the SOA yield using a simple box model of our chamber, employing measured kaurene, ozone, SOA, and ammonium sulphate concentrations as inputs, adjusting the effective SOA yield (as the only free parameter) to match the measured SOA. Next, a short description of the box model is presented.

Fig. 6
figure 6

Yield experiment with the particle mass concentration on the y-axis for measured SOA (in green), ammonium sulphate-seed (in red) and modelled SOA concentrations (in blue), together with the concentration of kaurene on the right-axis in cyan triangles and the concentration of ozone on the right-axis with purple triangles, from a day with \({yiel}{d}_{{SOA}}=7 \%\). The inset plot is zoomed in from the main plot to see more clearly the match between measured and modelled SOA concentrations.

Full size image

We assume that the SOA is formed from low volatility vapours (LVOCs) produced from the kaurene + ozone reactions, formed with a molar yield of \({yiel}{d}_{{LVOC}}\). The sink of these LVOCs is condensation onto the AS-seed and the chamber walls. At steady state, when the sources and sinks are equal, we can write the LVOC concentration as:

$${LVOC}=\frac{\left[{O}_{3}\right]* \left[{kaurene}\right]* {k}_{{O}_{3}+{kau}}* {yiel}{d}_{{LVOC}}}{{k}_{{wall}}+{CS}}$$

where \({k}_{O3+{kau}}\) is the reaction rate coefficient for kaurene and ozone, \({k}_{{wall}}\) is the wall loss rate of LVOC, and \({CS}\) is the condensation sink to the AS-seed. The \({CS}\) was simply estimated from the measured mass concentration, scaled linearly using the relation \({CS}=0.0015\frac{{s}^{-1}}{\frac{\mu g}{{m}^{3}}}* {m}_{{tot}}\), where \({m}_{{tot}}\) is the total particle mass concentration, based on Peräkylä et al.62 who used an identical approach in our chamber. \({k}_{{wall}}\) is estimated as 1/400 \({s}^{-1}\) for our chamber, based also on Peräkylä et al.62. The change in the SOA mass concentration is now governed by the source (condensation of LVOCs) and the sink (flush-out from the chamber):

$$\frac{\varDelta {SOA}}{\varDelta t}=\left[{LVOC}\right]* {CS}* {C}_{m,{LVOC}}-{SOA}* {k}_{{outflow}}$$

where \({k}_{{outflow}}\) is the chamber flush-out, given as the reciprocal of the average chamber residence time (~36 min), and \({C}_{m,{LVOC}}\) is a conversion factor for converting the LVOC number concentration to mass concentration. For \({C}_{m,{LVOC}},\) we assume that the mass of LVOCs to be on average 352 \({Da}\), which represents the mass of a \({C}_{20}{H}_{32}{O}_{5}\) molecule. The change in SOA can thus be modelled by:

$$\frac{\varDelta {SOA}}{\Delta t}= \left[{O}_{3}\right]* \left[{kaurene}\right]* {k}_{{{{\rm{O}}}}3+{{{\rm{kau}}}}}* {yiel}{d}_{{{{\rm{LVOC}}}}}* {C}_{{{{\rm{m}}}},{{{\rm{LVOC}}}}} \\ * \frac{{CS}}{{CS}+{k}_{{{{\rm{wall}}}}}}\,-{SOA}* {k}_{{{{\rm{outflow}}}}}$$

For every time step in the model, we used the measured kaurene, ozone and AS-seed concentrations. Therefore, once a yieldLVOC value was defined, the concentration of SOA was the only model output and this could be compared to the measured SOA, allowing us to determine yieldLVOC. A value of \(0.5\cdot 1{0}^{-15}{{cm}}^{3}{s}^{-1}\) was used for the reaction rate coefficient for kaurene + ozone, determined during these experiments, similar to other studies19. More details on how we derived such coefficient can be found elsewhere34.

The \({yiel}{d}_{{LVOC}}\) corresponds to the molar yield of condensable vapours (LVOC). In our chamber, some fraction of these LVOC condenses onto the walls (typically around 20–30%, based on calculations from Peräkylä et al.62), but in the atmosphere these would all contribute to SOA formation. The final SOA yield is normally defined as a mass yield, meaning that our molar yield needs to be multiplied by the mass increase,. \({yiel}{d}_{{{{\rm{SOA}}}}}={yiel}{d}_{{{{\rm{LVOC}}}}}* \frac{{m}_{{{{\rm{LVOC}}}}}}{{m}_{{{{\rm{kaurene}}}}}}={yiel}{d}_{{{{\rm{LVOC}}}}}* 1.29\). We note here that both \({yiel}{d}_{{LVOC}}\) and \({m}_{{LVOC}}\) could be varied to match the measured SOA, but the \({yiel}{d}_{{SOA}}\) parameter only depends on their product, which means that it is independent of the exact choice of either. As such, the SOA yield is effectively the only free parameter in the model. An example of a simulated experiment is shown in Fig. 6. The SOA yields obtained for time periods where we had a stable SOA concentration in the chamber, in total five experiments, are the ones presented in Fig. 1.

Model implementation

We used the Multiscale Online Nonhydrostatic AtmospheRe CHemistry model (MONARCH)38,39,40,41,42,43,44 to estimate emissions and SOA global burdens of diterpenes. The simulations were conducted with the MONARCH model, which was run at the global scale on a regular longitude-latitude grid of a global domain at 0.7° × 0.5° horizontal resolution and on 48 hybrid sigma-pressure vertical levels. The year 2018 was simulated driven by the meteorology of the ERA5 reanalysis63. The anthropogenic emissions applied are based on the CAMS-GLOB-ANTv4.2 database64, and the biomass-burning emissions were from the Global Fire Assimilation System v1.2 biomass-burning emissions (GFAS)65. Additionally, other meteorology-driven emissions are computed within MONARCH, such as mineral dust12 and sea salt55.

MONARCH is an on-line integrated system for mesoscale to global-scale applications developed at the Barcelona Supercomputing Center (BSC). MONARCH is designed to provide short to medium-range forecasts of atmospheric aerosols for a wide range of scales66. The model allows running both global and regional simulations with telescoping nests. As multiple choices of gas- and aerosol chemistry schemes can be selected in the model, here we describe the configuration used in this work. The gas-phase chemistry solves the carbon bond mechanism with extended chlorine chemistry (CB05)67. The model describes the lifecycle of dust, sea-salt, black carbon, organic matter (both primary and secondary), sulphate, ammonium, nitrate aerosols and non-speciated aerosols. While a sectional approach is used for dust and sea salt, a modal representation of the other aerosol species is adopted43. A simplified gas–aqueous–aerosol mechanism has been introduced in the module to account for the sulfur chemistry43 and a simple scheme is used for the formation of secondary organic aerosols68.

Organic aerosol is represented by a hydrophobic mode with atmospheric aging that transfers mass to a hydrophilic mode with a conversion lifetime of 1.15 days. Half of the primary emissions are emitted as hydrophobic species with an OM:OC (Ambient organic-mass-to-organic-carbon) ratio of 1.4, while the hydrophilic counterpart is emitted assuming an OM:OC ratio of 2.1. Marine primary organic emissions are neglected in our simulations. SOA contributions from biogenic, pyrogenic and anthropogenic sources are accounted for with fixed SOA yields adjusted to match results from more complex schemes68 (e.g., volatility basis set). Half of the biogenic SOA is emitted directly in the aerosol phase to account for the near-field formation of SOA, while the rest describes the gas-phase SOA products that partition to SOA with a conversion lifetime of 1 day68.

Biogenic emissions are computed online using the Model of Emissions of Gases and Aerosols from Nature biogenic emissions (MEGANv2.0449), which is the available version for the MONARCH set up, and provided the uncertainties on diterpene emissions, the use of this more simplified MEGAN version is suitable. A new biogenic VOC species has been added to account for diterpene emissions. From the literature review we performed on diterpene vegetation emissions (Supplementary Section 2) we have derived basal emission factors which have been separated into the four plant functional types used in MEGANv2.04 (see description in Table 1). The β-coefficient used for deriving basal emission factors was 0.13 °C−1. This value was the average β-coefficient values reported in literature (a subset of the reviewed literature). Since both kaurene and β-pinene have an exocyclic double bond and due to the lack of experimental data on diterpene oxidation, we used β-pinene as a surrogate for diterpenes for the MEGAN parameter where no information for diterpenes was available within MEGANv2.04.

To provide first global estimates of the potential significance of diterpene contribution to SOA formation from the ozonolysis of diterpenes, we extended the biogenic SOA production scheme in MONARCH68 to diterpenes adapting accordingly to the experimental data obtained by the controlled SOA formation experiments. Thus, we considered 1.8–17% SOA yield for diterpenes, 1% for isoprene, 10% for monoterpenes and 20% for sesquiterpenes. The yields for isoprene12,54,55, monoterpenes46,55 and sesquiterpenes55,56,57 were approximated in this way given the wide range of yields reported in literature.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.