Introduction

Terrestrial gross primary production refers to photosynthetic carbon fixation by vegetation canopies (GPPC in g C m−2 ground area time−1)1. This flux, marking the entry point for carbon into the terrestrial system, is currently increasing at ~3% decade−1 globally2,3. The green leaf area, over which photosynthesis happens, defined as one-sided green leaf area per unit ground area in broadleaf vegetation and one-half the total needle surface per unit ground area in needleleaf vegetation4, is also increasing at the same rate5,6,7. Several key factors contribute to these changes in GPPC and leaf area. The CO2 fertilization effect (CFE), some aspects of climate change (e.g., warming in the North), nitrogen deposition, land use and land cover changes are evidently the principal reasons for these GPPC and leaf area index (LAI) changes2,3,8,9,10,11,12,13,14. The impact of elevated atmospheric CO2 on vegetation manifests through two primary mechanisms: (1) a biochemical effect: the CO2 fertilization effect (CFE), which enhances photosynthesis and biomass accumulation, thereby altering canopy structure2; (2) a radiative effect: increased CO2 concentration leads to warming and climate change, while also modifying the light condition and nitrogen availability, all of which affect the vegetation photosynthesis15. However, not all climate change impacts are positive, particularly in arid and semi-arid regions, climate change negatively affects plant growth due to increased water stress16,17. Furthermore, intensive human land-use practices have amplified GPPC and LAI changes, particularly in China and India5.

However, spatially there is a mis-match in where and by how much GPPC and leaf area are changing. In Amazonian rainforests, it was found that leaf area decreased but vegetation canopy productivity remained constant in the 2010 drought year18,19, and that little change in leaf area was measured in contrast to substantial decreases in canopy photosynthesis in the 2015–2016 drought period20. Greening in herbaceous vegetation, for example, is much less than in woody vegetation globally, GPPC gains however are much larger in the former than the latter6. This decoupling is especially noticeable in arid and semi-arid regions. Satellite observations in these areas show minimal increases in leaf area due to persistent water limitations, yet these ecosystems experience disproportionately large surges in GPPC during occasional wet periods17.

Mounting evidence suggests that light availability limits carbon fixation in two ways: directly through incident light levels and the ratio of direct solar to diffuse sky radiation, and indirectly through changes in canopy structure, primarily via increased self-shading of leaves as leaf area expands21,22. This constraint on light availability may explain the discrepancy between vegetation greening, i.e., adding extra leaves, and GPPC changes. Consequently, this study hypothesized that greening tends to lower the average light reaching leaves in moderate to dense vegetation. This reduction can counteract the positive effects of CO2 fertilization (CFE), leading to smaller gains in GPPC. Conversely, in sparse vegetation with low leaf areas, such as arid and semi-arid regions, greening does not significantly affect light levels. In these areas, the increased leaf area will reinforce the CFE effect, resulting in substantial GPPC gains. This interaction between the CFE and light levels in vegetation has not been identified before. To understand this interaction and its implications to the carbon cycle, long-term observations and model estimates are analyzed here. Canopy scale GPP changes are separated into those resulting from leaf area changes and those from changing photosynthetic rates per unit leaf area. The latter, by normalizing for leaf area, isolate production dependency on CO2, light and water availability, and the kinetics of the process itself.

Estimates of GPPC from observations and models during the 2001–2021 period and projections for the rest of this century are discussed here. The observation-based estimates are derived from a combination of solar-induced chlorophyll fluorescence measurements of the Orbiting Carbon Observatory-2 and CO2 exchange data of flux towers (GOSIF23). The modeled GPPC estimates are – (i) an ensemble average of three Production Efficiency Models (PEMs) forced with two climate data sets, (ii) an ensemble average of 18 Dynamic Global Vegetation Models (DGVMs) of the TRENDY project24 and (iii) an ensemble average of seven Earth System Models (ESMs) of the CMIP6 project25 for the historical period (2001–2014) and projections to year 2100 based on three emission scenarios. Sections in Methods detail the three PEMs (§1), the forcing climate data (§2), parameter optimisation (§3), validation and intercomparison with peer GPPC products (§§4-6), the TRENDY DGVMs (§7) and CMIP6 ESMs (§8). Results in Supplementary Figs. 1 to 5, and also those presented here, show that modelled GPPC from simple PEMs compare well to those from process-based dynamic models (TRENDY and ESMs), peer GPPC data sets26,27,28, and observations (GOSIF and AmeriFlux). Only statistically significant (Mann-Kendall test, P ≤ 0.1) results are discussed below.

Results and Discussion

§1 Global Mis-match Between Leaf Area Expansion and Canopy Productivity Gains

Annual means of GPPC from PEMs and DGVMs are comparable to the GOSIF estimate (128 vs. 131 Pg C yr−1). They reflect an upward trend of 3.9 to 5.2 Pg C yr−1 decade−1 during the 2001–2021 period (Fig. 1a). The same from ESMs are 123 Pg C yr−1 and 3.8 Pg C yr−1 decade−1. About 44% of the 106 × 106 km2 of total vegetated area displays a positive trend, most conspicuously in China, Europe, India, North America, Sahel and abutting area, and northern Siberia. Declines are observed in only 5% of the vegetated lands, prominent only in the Brazilian Amazon. The ~ 10 Pg C of total GPPC gain is mostly from herbaceous vegetation (64%). Of note, croplands account for nearly a quarter of this gain while occupying only 11% of the total vegetated area. The more productive woody vegetation (~55% of GPPC share) contributes a third of the increase in GPPC. Overall, the modelled patterns match well with observations (Supplementary Fig. 6a) and previous studies29,30.

Fig. 1: Trends in annual gross primary production at the canopy (GPPC) and leaf (GPPL) scales.
figure 1

a Ensemble mean GPPC (g C m−2 ground area year−1) of three Production Efficiency Models (PEMs) forced with two climate data sets (§5). b GPPL is GPPC ÷ LAI (g C m−2 leaf area year−1), where LAI is the ensemble mean of two observational data sets (§9). Only statistically significant trends are colour-coded (Mann-Kendall test, P ≤ 0.1). The insets show global-scale trends from observations-based GOSIF data2 (red line is a linear fit to yearly data shown as red dots), PEMs (black line and dots), 18 TRENDY models (mean as blue line and range as blue shading; §7) and seven CMIP6 ESMs (in green; §8). The calculation of GPPL is described in §10. The ‘*’ in the inserts means that the correlation of the fitted line is significant. Analogous patterns from observations are shown in Supplementary Fig. 6. Section numbers refer to sections in Methods.

Full size image

At the same time, there have been increases in green leaf area of vegetation2,6,15,31,32,33,34. Globally, gains in leaf area and GPPC seem comparable in magnitude (3.3 vs. 3.1 to 4.6% decade−1) and extent; 44% of the vegetated lands exhibit greening, 7% browning and the rest no changes (Supplementary Fig. 7). Indeed, the same causal markers have been invoked to explain the greening and browning of lands in the satellite era2,6,15. Regions exhibiting prominent greening visually correspond to those with large GPPC increases. Numerically however, greening in herbaceous vegetation is less than that of woody vegetation (44% for herbaceous vs. 56% for woody), opposite of shares in GPPC gains (64% for herbaceous vs. 36% for woody). Croplands illustrate this disparity starkly, 23% share of GPPC gain with only 15% of greening. This mis-match in rates of change between GPPC and leaf area is delved into below.

Conceptually, the amount of photosynthate produced under prevailing conditions depends on light and dark reactions within the leaf, the availability of raw resources of light, water, nutrients and CO2, and the extent of photosynthesizing leaf area35,36,37,38. GPPC changes can be therefore separated into those resulting from leaf area changes and those from changing assimilation rates per unit leaf area. The latter, by normalising for leaf area, isolate production dependency to resource availability and kinetics of the process itself. This leaf scale photosynthetic rate can be calculated as GPPC ÷ LAI; reliable LAI data are widely available4,7,39,40,41,42 (Methods §§9 and 10). It will be denoted from hereon as GPPL (g C m−2 leaf area day−1). The accuracy and independence of GPPC (Supplementary Figs. 1, 2, and 3) and LAI7,39,42 data used to estimate GPPL imbue confidence in capturing the aggregate leaf scale dynamics, i.e., kinetics of reactions within the leaf and utilization of light, water and CO2 resources, in spite of the representation of vegetation canopy as one big leaf in PEMs.

The pattern of GPPL changes (Fig. 1b) is remarkably different than the individual patterns of changes in GPPC (Fig. 1a) and LAI (Supplementary Fig. 7b). The patterns agree well with those based on observations (Supplementary Fig. 6). At the global scale, there is little to no change in GPPL (inset Fig. 1b) contrary to a previous report based on shorter records43. However, the global numbers belie important GPPL variations regionally16,43. Leaf assimilation rates trend upward in sparsely vegetated lands in Argentina, Australia, Kazakhstan, Sahel and adjoining areas, and USA, Negative GPPL trends are seen in the more densely vegetated areas of Brazil, sub-Arctic Canada, China, northern Europe and India. Especially China and India, which exhibit large positive trends in both GPPC and LAI due to intensive land management practices5, show significant GPPL declines. The Sahel and adjoining lands, being the only exception globally, show consistent positive trends in GPPC, LAI44,45 and GPPL, in a prominent west to east swath. The reasons for this surprising pattern of GPPL gains in inhospitable climes and losses in favourable environments are explored below.

§2 Large Gains in Leaf Scale Photosynthetic Rates of Sparsely Vegetated Arid and Semi-Arid Lands

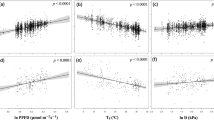
Studying the distributions of GPPC, LAI and GPPL trends reveals large gains in sparse vegetation, and these decrease with increase in growing season mean LAI (Table 1 and Fig. 2a). Sparse vegetation (~ LAI < 1), most of which is shrublands and grasslands in arid and semi-arid regions (Supplementary Fig. 7c), constitutes 41% of global vegetated area and contributes 17% of GPPC. Only in these land covers is the net change in GPPL statistically significant, reflecting a gain of 2.4% decade−1. The rest of the land covers show no changes in GPPL, although the individual trends of GPPC and LAI are statistically positive. There are, of course, significant local GPPL changes at all vegetation densities (Fig. 2a), but the only net change is a gain in sparse vegetation. The results thus inform on larger increases in GPPC relative to LAI in sparse vegetation and matching changes for the rest (Table 1), i.e., GPPC gains in vegetation with LAI < 1 are due to gains in both GPPL and LAI, while in denser canopies only due to LAI. This hints at additive impacts of causal agents in sparse vegetation and opposing impacts elsewhere, as elucidated below.

Fig. 2: Distribution of leaf scale gross primary production (GPPL) trends in different intervals of growing season average leaf area index (LAI).
figure 2

a GPPL trends in simulations with time-varying CO2 concentration, climate and fraction of vegetation-absorbed photosynthetically active radiation (FPAR) during 2001–2021 period. b GPPL trends due only to the CO2 fertilization effect (CFE). c GPPL trends due only to time-varying climate. d GPPL trends due only to time-varying FPAR. The simulations with production efficiency models (PEMs) are described in Methods §11. The growing season is defined as the period when daily GPPC > 0 and daily LAI > 0.1.

Full size image
Table 1 Distribution of trends in GPPC, LAI and GPPL in broad LAI intervals
Full size table

The trends in GPPL (Figs. 1b and 2a) can be unpacked into the individual effects of ambient CO2 concentration, climate and light on leaf photosynthate production. The fertilisation effect of increasing atmospheric CO2 concentration (CFE) on GPPL is well known2,3,12,13. The climate effect includes GPPL dependency on temperature9, vapour pressure deficit46 and soil moisture47 via precipitation. The effect of light on GPPL results from altered light distribution on leaves within the canopy due to changes in vegetation structure, including leaf area21,48. The three effects can be quantified through specialized simulations with simple PEMs forced with corresponding observations (Methods §11).

The fertilisation and climate effects represent direct and indirect effects of CO2 buildup in the atmosphere24. Changes in GPPL due only to the CFE are positive (Fig. 2b). These are large in grasses and crops (3.7% decade−1) and modest in tropical forests (2.2% decade−1). The bi-modality at LAI < 2 is due to land cover specific CFE. For example, the CFE is 2.3% decade−1 in arid shrublands where the growing season average LAI is 0.7, while it is 3.7% decade−1 in semi-arid and dry sub-humid grasslands and croplands which have a LAI of 0.9. This general pattern of higher fertilisation effect in sparse vegetation has been observed in situ49 and attributed to increased water use efficiency47. Local climate effects are both positive and negative (Fig. 2c), which closely mirrors that of total bimodal distribution, but the net change is a GPPL gain in vegetation with LAI < 3, and loss in more dense vegetation. As a result, the combined effect of atmospheric CO2 increase is a higher gain in leaf assimilation rates in sparse to moderately dense vegetation (4% decade−1) and none in tropical forests, where GPPL gains due to CFE are offset by losses due to changes in climate.

Changes in vegetation structure and leaf area alter light environment in canopies21,48. This effect is represented in PEMs through data of fraction of vegetation-absorbed photosynthetically active radiation (FPAR; Methods §1). The observations capture contemporaneous and the integral of legacy effects on structure and leaf area from CO2 concentration, climate, nutrient availability and human management13. The absolute magnitudes of FPAR effects are larger than the CO2 effects (Fig. 2dvs. b). They are negative nearly everywhere (Fig. 2d), preventing the positive influence of the CFE from entirely offsetting the overall negative GPPL distribution, with the exception of shrublands where they are net-positive. The LAI gains from greening6 (Supplementary Fig. 7b) translate to smaller FPAR gains because of the nonlinear LAI-FPAR relationship arising from increased self-shading in denser leaf canopies (Supplementary Fig. 8). Consequently, GPPC trends are smaller than leaf area trends, and hence, losses in GPPL. In sparsely vegetated shrublands, increases in LAI translate linearly to FPAR to result in GPPL gains. Thus, the effect of light on leaf assimilation rates is to offset the gains from the fertilisation effect, and climate if any, in nearly all vegetation with the exception of those with LAI < 1, i.e., the arid and semi-arid land covers of shrublands and grasslands (Fig. 2a and Table 1).

§3 Regional Divergence in Leaf Scale Photosynthetic Rates

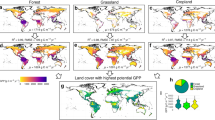
Of particular interest are two large regions, the Sudano-Sahelian zone and adjoining savanna in Africa (7 × 106 km2; “Sahel + ” from hereon) and, China and India combined (9.5 × 106 km2). Much of the population of over 3 × 109 people in these regions depends on the land for livelihood. Both display significant increases in leaf area (Supplementary Fig. 7b) and GPPC (Fig. 1a). However, GPPL gains are conspicuous only in the Sahel+ region (Fig. 1b). GPPL losses in China and India similarly stand out. This striking contrast can be understood by the effects of CO2, climate and light on GPPL.

The Sahel+ region consists of herbaceous vegetation of shrublands, grasslands and croplands to the north and savannas to the south (LAI ~ 1.2). It experienced a rebound in precipitation after severe droughts in the 1970s and early 1980s. The area has greatly greened since then44,45, settling a debate in favor of climate and against land degradation from human activities50,51. This positive climate effect on photosynthate production is further enhanced by the CO2 fertilisation effect (CFE). The resulting GPPC gain is greater than the LAI trend (10.4 vs. 6.9% decade−1 in Fig. 3a), which suggests that the negative FPAR effect is outmatched by the positive effects of fertilisation and climate (Fig. 3c). Thus, the region exhibits prominent gains in leaf assimilation rates (7.4% decade−1). Similar arguments explain the positive GPPL trends in semi-arid parts of USA, Argentina, etc. (Supplementary Fig. 9a, c).

Fig. 3: Comparison of trends in the Sahel and adjoining area and in China and India combined.
figure 3

The Sahelian region is a rectangular area spanning 4.35° N to 15° N and 17.5° W to 51.5° E showing prominent gains in GPPL (see Fig. 1b). a, b Trends in growing season average leaf area index (LAI), gross primary production at canopy scale (GPPC) and leaf scale (GPPL). c, d Trends in GPPL due only to CO2 (GPPL CFE), climate change (GPPL CC) and fraction of vegetation-absorbed photosynthetically active radiation (GPPL FPAR). The box plots show the distribution of statically significant trends (Mann-Kendall test, P ≤ 0.1). The maximum and minimum values of the colored boxes represent the 25th and 75th percentiles, respectively, and the whiskers represent the 5th and 95th percentiles. The red line represents the median (M) trend. The growing season is defined as the period when GPPC > 0 and daily LAI > 0.1.

Full size image

China and India lead in greening (Supplementary Fig. 7b) due to expanding natural forests and afforestation in the case of China and agricultural intensification in both5. China has implemented programmes to conserve and expand forests with the goal of mitigating climate change, while enhancing carbon sequestration52,53. Agricultural intensification54,55 in both countries is facilitated by heavy fertilizer use and irrigation combined with multiple cropping. Consequently, forests and croplands account for 50 and 19% of the net increase in leaf area of China, whereas croplands alone contribute 80% in the case of India. The large greening trends (Fig. 3b), however, did not enhance leaf assimilation rates because of diminished absorbed lights on per unit of leaf surfaces. In fact, the FPAR effect on GPPL is sufficiently negative that it more than offsets the positive effects of CO2 fertilisation and climate change (Fig. 3d), with resulting losses in leaf assimilation rates (−5% decade−1; Fig. 3b). This is also true in the case of Brazil and northern Europe (Supplementary Fig. 9b, d).

Conclusions

To summarize, observations and models show a consistent picture of dynamics in canopy- and leaf-scale assimilation rates and leaf area. Nearly half the vegetated lands display changes, mostly an increase, in canopy scale gross primary production (GPPC) during the 2001–2021 period. This can be traced to variations in the extent of photosynthesizing leaf area (LAI) only, assimilation rates per unit leaf area (GPPL) only, or both. Increasing trends in GPPL and LAI are seen only in the sparse vegetation of arid and semi-arid climes, the Sahel and adjoining zone being a prime example. Here, the positive trends are sustained through the CFE, higher efficiency of water use and conducive light regime. Nearly everywhere else, the negative impacts of climate and/or FPAR effects attributable to greening dominate, as in the case of China and India. Here, the residual GPPC gains are attributable to large LAI increases from intensive human land management. This largely explains the mis-match between greening and GPP changes. It also argues against conventional thinking the global greening will lead to more carbon sequestration. Earth system models project a saturation of GPPL in all scenarios (Supplementary Fig. 10), but surprisingly no declines even in an atmosphere of over 1000 ppm of CO2 concentration. Nevertheless, the current positive GPPL trends and the potential for carbon sequestration17 highlight the need for conservation and sustainable use of arid and semi-arid lands.

Methods

§1 Production Efficiency Models (PEMs)

This study included two of the most widely-used PEMs (PEMs 1 and 2 below) in addition to a more recently developed generalized PEM formulation (PEM3) to estimate the Gross Primary Production of vegetation canopies (GPPC), globally at daily time scale for the period 2001 to 2021. These models represent the current state-of-the-art for modeling GPPC based on light use efficiency while accounting for the effects of temperature, vapour pressure deficit (VPD) and atmospheric CO2. The models have the advantage of being simple while capturing tendencies seen in observations. They suffer from some well-known limitations, viz., idealizing the canopy as one big leaf, highly parameterised representation of processes, etc.

PEM1

The model used for generating GPPC product by the MODIS program56 is modified to include the CO2 fertilization effect13,57. GPPC (g C m−2 day−1) is calculated as

$${{GPP}}_{C}^{M1}={{LUE}}_{{opt}}^{M1}\times {PAR}\times {FPAR}\times {f}_{{TMIN}}^{M1}\times {f}_{{VPD}}^{M1}\times f\left({CO}2\right)$$
(1)

where \({{{{\rm{LUE}}}}}_{{{{\rm{opt}}}}}^{{{{\rm{M}}}}1}\) is the optimal light use efficiency (g C MJ−1), PAR is the incident photosynthetically active radiation (MJ m−2 day−1), FPAR is the fraction of vegetation absorbed PAR, \({{{{\rm{f}}}}}_{{{{\rm{VPD}}}}}^{{{{\rm{M}}}}1}\) is the water stress scalar (VPD) and \({{{{\rm{f}}}}}_{{{{\rm{TMIN}}}}}^{{{{\rm{M}}}}1}\) is the temperature (daily minimum) stress scalar. The CO2 fertilization effect [f(CO2)] is modelled by a relative value of \({{{{\rm{C}}}}}_{{{{\rm{s}}}}}\) (current year, \({C}_{s}^{t}\)) compared to a baseline period57 (year 2001, \({C}_{s}^{{base}}\)) as (\({{{{\rm{C}}}}}_{{{{\rm{s}}}}}\) is similar to PEM2 below)

$$f({{CO}}_{2})=\frac{{C}_{s}^{t}}{{C}_{s}^{{base}}}$$
(2)

PEM2

GPPC is calculated using the EC-LUE model57 as

$${{GPP}}_{C}^{M2}={{LUE}}_{{opt}}^{M2}\times {PAR}\times {FPAR}\times {C}_{s}\times \min ({f}_{T}^{M2},{f}_{{VPD}}^{M2})$$
(3)
$${C}_{s}=\frac{{C}_{i}-{\Gamma }^{* }}{{C}_{i}+2{\Gamma }^{* }}$$
(4)
$${C}_{i}={C}_{a}\times \chi$$
(5)

where \({{{{\rm{C}}}}}_{{{{\rm{s}}}}}\) is the effect of atmospheric CO2 concentration on GPPC35,37. \({\Gamma }^{* }\) is the CO2 compensation point in the absence of dark respiration (ppm) and Ci is the CO2 concentration in the intercellular air spaces of the leaf (ppm), which is the product of the atmospheric CO2 concentration (Ca) and the ratio of internal to ambient CO2 in the leaf (\({{{\rm{\chi }}}}\))8,58. \({{{\rm{\chi }}}}\) is calculated by

$$\chi =\frac{{\Upsilon }}{{\Upsilon }+\sqrt{{VPD}}}$$
(6)
$${\Upsilon }=\sqrt{\frac{356.51\times K}{1.6\times {\eta }^{* }}}$$
(7)
$$K={K}_{c}\times \left(1+\frac{{P}_{o}}{{K}_{o}}\right)$$
(8)
$${K}_{c}=39.97\times {e}^{\frac{79.43\times ({T}_{a}-298.15)}{298.15\times R\times {T}_{a}}}$$
(9)
$${K}_{o}=27480\times {e}^{\frac{36.38\times ({T}_{a}-298.15)}{298.15\times R\times {T}_{a}}}$$
(10)

where \({{{{\rm{K}}}}}_{{{{\rm{c}}}}}\) (Pa) and \({{{{\rm{K}}}}}_{{{{\rm{o}}}}}\) (Pa) are the Michaelis-Menten coefficient of Rubisco for carboxylation and oxygenation, respectively8. \({{{{\rm{P}}}}}_{{{{\rm{o}}}}}\) is the partial pressure of O2 (Pa). R is the molar gas constant (8.314 J mol−1 K−1), \({T}_{a}\) is air temperature, and \({{{{\rm{\eta }}}}}^{* }\) is the viscosity of water as a function of air temperature relative to its value at 25\(^\circ {{{\rm{C}}}}\)59.

PEM3

The Max Planck Institute for Biogeochemistry (MPI-BGC) model60 includes the effects of temperature, VPD, atmospheric CO2 concentration, soil moisture (W), light intensity (L), and cloudiness through an index (CI) on GPPC. It evaluates GPPC as

$${{GPP}}_{C}^{M3}={{LUE}}_{{opt}}^{M3}\times {PAR}\times {FPAR}\times {f}_{T}^{M3}\times {f}_{W}^{M3}\times {f}_{{VPD},{{{\rm{CO}}}}2}^{M3}\times {f}_{L}^{M3}\times {f}_{{CI}}^{M3}$$
(11)
$${f}_{{VPD},{{{\rm{CO}}}}2}^{M3}=\left({e}^{k\times {\left(\frac{{C}_{a0}}{{C}_{a}}\right)}^{{C}_{k}}\times {VPD}}\right)\times \left(1+\frac{{C}_{a}-{C}_{a0}}{{C}_{a}-{C}_{a0}+{c}_{m}}\right)$$
(12)

Where k is the sensitivity to VPD changes, \({{{{\rm{C}}}}}_{{{{\rm{a}}}}0}\) is the minimum optimal atmospheric CO2 concentration, Ca is the atmospheric CO2 concentration, \({{{{\rm{C}}}}}_{{{{\rm{k}}}}}\) is the sensitivity to atmospheric CO2 concentration changes, and \({{{{\rm{c}}}}}_{{{{\rm{m}}}}}\) is the CO2 fertilization intensity indicator61.

§2 input data for PEMs

Two climate data sets are used to force the PEMs – (1) GMAO MERRA-2 and (2) ECMWF ERA-5. Additional climate data required by PEM3 are obtained from GLDAS NOAH-2.1 (2001–2021). The climate data together with sensor-independent (SI) FPAR data7 are harmonised to daily and 0.05o resolutions to calculate GPPC with the three PEMs. Daily CO2 data from NOAA were used to model the fertilisation effect. The variable LUE in PEMs is land cover dependent, hence the MODIS landcover product62 is used to identify the landcover in each pixel. The rest of the variables are pixel dependent. All data are publicly available (see “Data Availability” statement).

§3 Estimation of Optimal LUE

Optimal values of light use efficiency (LUEopt) for the 11 land covers are estimated iteratively and separately for the three PEMs using annual GPPC estimates based on the average of the night-time (GPP_REF_NT_VUT) and day-time (GPP_REF_DT_VUT) partitioning approaches from the FLUXNET2015 data set63. The number of GPPC estimates for each land cover varies depending on the number of sites belonging to that land cover and the number of years for which estimates are available (Supplementary Table S1). The optimisation is done iteratively as follows.

Step 1: Model GPPC values corresponding to half the randomly selected GPPC estimates are calculated by assuming LUE = 1 and using GMAO climate and SI FPAR data. Step 2: An estimate of LUEopt is evaluated by linearly regressing modelled GPPC against measured GPPC. Step 3: Model GPPC values corresponding to the other half of GPPC estimates are calculated using LUEopt estimated in Step 2. Step 4: The RMSE is calculated by regressing the modelled GPPC values in Step 3 against the corresponding observed GPPC values. Steps 1 to 4 are repeated 10,000 times to obtain 10,000 values of LUEopt and corresponding RMSE. LUEopt values corresponding to the lowest 9,500 RMSE values are averaged to obtain LUEopt. This process is repeated separately for each landcover and for the three models – the resulting LUEopt values are given in Supplementary Table S2.

A comparison of modelled and observations-based GPPC values before and after optimisation is shown in Supplementary Fig. 1. The optimisation procedure improved performance of PEM1 and 2, but not PEM3 for the following reason. The original PEM3 contained parameters that varied at the 0.05o pixel-scale. This version agrees well with flux tower based GPPC estimates as the parameters were tuned to those estimates. It however results in global GPPC values nearly twice the other models and those reported in literature. When PEM3 is reformulated in terms of landcovers, the agreement with tower estimates degrades (Supplementary Fig. 1) but the geographical patterns and global totals match those of PEM1 and 2 (not shown for brevity).

§4 Evaluations of PEMs

The performance of PEMs is evaluated through comparisons with data from the AmeriFlux estimates. These (Supplementary Table S3) are different than the FLUXNET2015 estimates used to optimise the LUE variable of the three PEMs (§3). GPPC values from the three PEMs compare satisfactorily (R2 > 0.54 and RMSE < 483.64 g C m−2 yr−1) with tower estimates (Supplementary Fig. 2). These results are similar to those in the literature regarding the performance of PEMs in general64,65,66,67.

§5 Comparison of GPPC between PEMs

Modelled annual GPPC from the three PEMs forced with two climate data sets varies between 120 and 135 Pg C yr−1 (Supplementary Table S4). The agreement between the three PEMs at 445 BELMANIP2.1 test sites68 is good (Supplementary Fig. 3; R2 > 0.90 and RMSE between 251 to 327 gC m−2 yr−1). Average annual GPPC from this ensemble of three PEMs forced with two climate data sets is used throughout this article.

§6 Comparison of GPPC from PEMs with Peer GPPC products

The modelled ensemble average GPPC (three PEMs and two climate forcings) is compared to four other published global-scale GPPC data sets for consistency. These GPPC data sets are independent of one another. The GOSIF GPPC product is generated using relationships between satellite-measured Solar-Induced chlorophyll Fluorescence (SIF) and observed GPPC23. The Random Forest (RF) GPPC product is generated from a combination of a nested machine learning model and a theoretical photosynthesis model26. The FLUXCOM and X-BASE FLUXCOM GPPC products are a result of upscaling approaches based on machine learning methods that integrate flux tower estimates, satellite remote sensing, and meteorological data27,28. The modelled PEM ensemble average GPPC compares well to all four published data sets (Supplementary Fig. 4 and Supplementary Table S5). The comparisons at BELMANIP2.1 test sites indicate R2 > 0.91 and RMSE between 224 to 277 g C m−2 yr−1 (Supplementary Fig. 5).

§7 Dynamic Global Vegetation Models (DGVMs)

A project comprising of an international ensemble of DGVMs known as the “Trends and drivers of the regional scale terrestrial sources and sinks of carbon dioxide” (TRENDY) quantifies land biophysical exchange processes and biogeochemistry cycles24. Output at monthly resolution from TRENDYv12 simulations with varying land use change, climate, and CO2 (S3) of the following 18 models is used in this article: CABLE-POP, CLASSIC, CLM5.0, DLEM, E3SM, EDv3, IBIS, ISBA-CTRIP, JSBACH, JULES, LPJ-GUESS, LPJmL, LPX-Bern, OCN, ORCHIDEEv3, SDGVM, VISIT, and YIBs.

§8 CMIP6 Earth System Models

The sixth Coupled Model Intercomparison Project (CMIP6) is the latest to use a suite of Earth System Models (ESMs) to produce global simulations of the past, current, and future climate4,25. Monthly output from CMIP6 simulations from the following seven ESMs are used in our analyses: ACCESS-ESM1-5, CanESM5, CanESM5-CanOE, EC-Earth3-CC, GFDL-ESM4, MPI-ESM1-2-LR, and NorESM2-LM. Four of these models that included an interactive terrestrial Nitrogen cycle demonstrated improved GPPC simulations (ACCESS-ESM1-5, EC-Earth3-CC, MPI-ESM1-2-LR, and NorESM2-LM)61. All ESMs included dynamic vegetation models. These DVGMs are a subset of the TRENDY DVGMs described in §7. The representation and evaluation of the terrestrial carbon cycle in these models is described in Gier et al.69. Simulated GPPC and LAI from historical (2001 to 2014) and projection (2015−2100) periods are analysed in this study. The latter are for three emission scenarios – Shared Socio-economic Pathways (SSPs) 2-4.5, 3-7.0 and 5-8.5.

§9 Leaf Area Index Data

Two publicly available LAI data sets are used in this study: a sensor independent LAI data set7 and the GLASS LAI data set39,42. The data sets are derived independently from MODIS and other satellite-based sensors with algorithms that have been well tested over the past three decades70,71,72,73. The two LAI datasets exhibited similar spatial and trend distributions, showing no significant discrepancies in most regions7,39,42,72. The LAI data are not used in the calculation of GPPC reported in this article. LAI values from the two data sets are averaged and interpolated from 8-day to daily resolution. This mean LAI data set was used in this study to avoid large uncertainties that would arise if SI LAI/FPAR were directly used as input for GPPL calculations.

§10 Calculation of GPPL

Leaf photosynthetic carbon assimilation rate, GPPL (g C m−2 leaf area day−1), is calculated as the ratio of daily GPPC to daily LAI. In the case of PEMs, GPPL is calculated with the ensemble average GPPC from the three models (§1) forced with two climate data sets (§2) and satellite-based LAI (§9). Theoretically, the non-linear LAI-FPAR relationship has varying effects on GPPL across sparse and dense canopies, primarily by altering light distribution on leaves due to changes in vegetation structure21,22. Therefore, this study will clarify the light-related effects on GPPL changes based on this non-linear LAI-FPAR relationship. In the case of GOSIF, GPPL is calculated with GPPC from observations-based GOSIF data set23 and satellite-based LAI (§9). In the case of TRENDY models (§7) and CMIP6 ESMs (§8), GPPL is calculated with each model simulated GPPC and LAI. These SIF-based and model-based GPPL estimates can be used to independently corroborate the accuracy of GPPL obtained from the PEMs.

§11 Sensitivity Analyses with PEMs

Sensitivity simulations are performed with PEMs following the TRENDY protocol3 to quantify the contributions of the CO2 fertilisation effect (CFE), climate change and FPAR on gross primary production at canopy (GPPC) and leaf scale (GPPL). The CFE is quantified through simulation S1 by using constant climate (2001−2003 average), FPAR, and landcover from year 2001 and time-varying observed CO2 concentration for the period 2001–2021. The climate effect is quantified as the difference between simulations S2 and S1, where S2 is performed with FPAR and landcover from year 2001 and time-varying observed CO2 concentration and climate for the period 2001–2021. Finally, the effect of FPAR is quantified as the difference between simulations S3 and S2, where S3 is performed with time-varying observed CO2 concentration, climate, FPAR and landcover for the period 2001–2021. All simulations are performed with the three PEMs (§1) and two climate data sets (§2) and the ensemble average GPPC is used in further analyses. GPPL in simulations S1 and S2 is calculated as the ratio of GPPC to LAI in year 2001 at the daily scale during the growing season (GPPC > 0 and LAI > 0.1). It is calculated using time-varying LAI during 2001–2021 in simulation S3. Notably, land cover information in S3 changes only in conjunction with LAI/FPAR, and the FPAR effect implicitly incorporates land use/land cover changes. Thus, one limitation of this study is that the influence of land use/land cover changes in the PEM model cannot be directly calculated.

The coupled carbon-climate systems includes complicated linkages between various components and processes via feedbacks and lags14,74,75. The more complex dynamic models, TRENDY DGVMs (§7) and CMIP6 ESMs (§8), include some but not all of the known linkages. Sensitivity simulations similar to those described above are available from TRENDY24, however these are not used because of differences, relative to observations, in modelled LAI distribution across the entire vegetated area, both in magnitude and seasonal course. The PEMs have the advantage of incorporating measured data (CO2, Climate and FPAR) while also being simple. These models capture the direct effects of these variables on primary production. Thus, the sensitivity simulations with PEMs serve the stated goal of understanding the observed spatial patterns of GPPL to a first order.