Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Autonomous inference of complex network dynamics from incomplete and noisy data

Nature Computational Science volume 2, pages 160–168 (2022)Cite this article

Subjects

A Publisher Correction to this article was published on 29 April 2022

This article has been updated

A preprint version of the article is available at arXiv.

Abstract

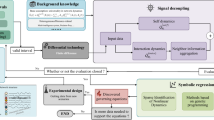
The availability of empirical data that capture the structure and behaviour of complex networked systems has been greatly increased in recent years; however, a versatile computational toolbox for unveiling a complex system’s nodal and interaction dynamics from data remains elusive. Here we develop a two-phase approach for the autonomous inference of complex network dynamics, and its effectiveness is demonstrated by the tests of inferring neuronal, genetic, social and coupled oscillator dynamics on various synthetic and real networks. Importantly, the approach is robust to incompleteness and noises, including low resolution, observational and dynamical noises, missing and spurious links, and dynamical heterogeneity. We apply the two-phase approach to infer the early spreading dynamics of influenza A flu on the worldwide airline network, and the inferred dynamical equation can also capture the spread of severe acute respiratory syndrome and coronavirus disease 2019. These findings together offer an avenue to discover the hidden microscopic mechanisms of a broad array of real networked systems.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Overview of the two-phase inference approach.
Fig. 2: Inferring FHN neuronal network dynamics on synthetic and real topologies.
Fig. 3: Inference accuracy for other four typical nonlinear network dynamics.
Fig. 4: Inferrability of network dynamics.
Fig. 5: Inference robustness against incompleteness and noises.
Fig. 6: Inference of early spreading dynamics from empirical data.

Similar content being viewed by others

Data availability

Source data are provided with this paper. The empirical network data include C. elegans connectome54,55,56, the mushroom-body region of Drosophila57, Northern Europe power grid58, the US power grid59, Advogato social network60 retrieved from https://networkrepository.com/ and worldwide airline network data retrieved from OpenFlights (https://openflights.org/data.html). The empirical data of epidemic spreading include daily reported numbers of H1N1 and SARS cases available at Kaggle (https://www.kaggle.com/lnunes/a-brief-comparative-study-of-epidemics/data) and the daily reported numbers of COVID-19 cases61.

Code availability

All the source codes are publicly available at the Code Ocean capsule62.

Change history

References

  1. Grewe, B. F., Langer, D., Kasper, H., Kampa, B. M. & Helmchen, F. High-speed in vivo calcium imaging reveals neuronal network activity with near-millisecond precision. Nat. Methods 7, 399–405 (2010).

    Article  Google Scholar 

  2. Stetter, O., Battaglia, D., Soriano, J. & Geisel, T. Model-free reconstruction of excitatory neuronal connectivity from calcium imaging signals. PLoS Comput. Biol. 8, e1002653 (2012).

    Article  MathSciNet  Google Scholar 

  3. Reuter, J. A., Spacek, D. V. & Snyder, M. P. High-throughput sequencing technologies. Mol. Cell. 58, 586–597 (2015).

    Article  Google Scholar 

  4. Levy, S. E. & Myers, R. M. Advancements in next-generation sequencing. Annu. Rev. Genom. Hum. Genet. 17, 95–115 (2016).

    Article  Google Scholar 

  5. Colizza, V., Barrat, A., Barthélemy, M. & Vespignani, A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proc. Natl Acad. Sci. USA 103, 2015–2020 (2006).

    Article  MATH  Google Scholar 

  6. Brockmann, D. & Helbing, D. The hidden geometry of complex, network-driven contagion phenomena. Science 342, 1337–1342 (2013).

    Article  Google Scholar 

  7. Chang, S. et al. Mobility network models of COVID-19 explain inequities and inform reopening. Nature 589, 82–87 (2021).

    Article  Google Scholar 

  8. Newman, M., Barabási, A.-L. & Watts, D. J. The Structure and Dynamics of Networks (Princeton Univ. Press, 2011).

  9. Barzel, B. & Barabási, A.-L. Universality in network dynamics. Nat. Phys. 9, 673–681 (2013).

    Article  Google Scholar 

  10. Harush, U. & Barzel, B. Dynamic patterns of information flow in complex networks. Nat. Commun. 8, 2181 (2017).

    Article  Google Scholar 

  11. Stankovski, T., Pereira, T., McClintock, P. V. & Stefanovska, A. Coupling functions: universal insights into dynamical interaction mechanisms. Rev. Mod. Phys. 89, 045001 (2017).

    Article  MathSciNet  Google Scholar 

  12. Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 20, 340–352 (2017).

    Article  Google Scholar 

  13. Santolini, M. & Barabási, A.-L. Predicting perturbation patterns from the topology of biological networks. Proc. Natl Acad. Sci. USA 115, E6375–E6383 (2018).

    Article  Google Scholar 

  14. Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).

    Article  Google Scholar 

  15. Yang, Y., Nishikawa, T. & Motter, A. E. Small vulnerable sets determine large network cascades in power grids. Science 358, eaan3184 (2017).

  16. Pastor-Satorras, R., Castellano, C., Van Mieghem, P. & Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 87, 925 (2015).

    Article  MathSciNet  Google Scholar 

  17. Castellano, C., Fortunato, S. & Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646 (2009).

    Article  Google Scholar 

  18. Becker, J., Brackbill, D. & Centola, D. Network dynamics of social influence in the wisdom of crowds. Proc. Natl Acad. Sci. USA 114, E5070–E5076 (2017).

    Article  Google Scholar 

  19. Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y. & Zhou, C. Synchronization in complex networks. Phys. Rep. 469, 93–153 (2008).

    Article  MathSciNet  Google Scholar 

  20. Barzel, B., Liu, Y.-Y. & Barabási, A.-L. Constructing minimal models for complex system dynamics. Nat. Commun. 6, 7186 (2015).

    Article  Google Scholar 

  21. Schmidt, M. & Lipson, H. Distilling free-form natural laws from experimental data. Science 324, 81–85 (2009).

    Article  Google Scholar 

  22. Wang, W.-X., Yang, R., Lai, Y.-C., Kovanis, V. & Grebogi, C. Predicting catastrophes in nonlinear dynamical systems by compressive sensing. Phys. Rev. Lett. 106, 154101 (2011).

    Article  Google Scholar 

  23. Brunton, S. L., Proctor, J. L. & Kutz, J. N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113, 3932–3937 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  24. Rudy, S. H., Brunton, S. L., Proctor, J. L. & Kutz, J. N. Data-driven discovery of partial differential equations. Sci. Adv. 3, e1602614 (2017).

    Article  Google Scholar 

  25. Udrescu, S.-M. & Tegmark, M. AI Feynman: a physics-inspired method for symbolic regression. Sci. Adv. 6, eaay2631 (2020).

    Article  Google Scholar 

  26. Raissi, M. & Karniadakis, G. E. Hidden physics models: machine learning of nonlinear partial differential equations. J. Comput. Phys. 357, 125–141 (2018).

    Article  MathSciNet  MATH  Google Scholar 

  27. Iten, R., Metger, T., Wilming, H., Del Rio, L. & Renner, R. Discovering physical concepts with neural networks. Phys. Rev. Lett. 124, 010508 (2020).

    Article  Google Scholar 

  28. Frishman, A. & Ronceray, P. Learning force fields from stochastic trajectories. Phys. Rev. X 10, 021009 (2020).

    Google Scholar 

  29. Brückner, D. B., Ronceray, P. & Broedersz, C. P. Inferring the dynamics of underdamped stochastic systems. Phys. Rev. Lett. 125, 058103 (2020).

    Article  Google Scholar 

  30. Shandilya, S. G. & Timme, M. Inferring network topology from complex dynamics. New J. Phys. 13, 013004 (2011).

    Article  MATH  Google Scholar 

  31. Newman, M. E. J. Network structure from rich but noisy data. Nat. Phys. 14, 542–545 (2018).

    Article  Google Scholar 

  32. Rabinovich, M. I., Varona, P., Selverston, A. I. & Abarbanel, H. D. Dynamical principles in neuroscience. Rev. Mod. Phys. 78, 1213 (2006).

    Article  Google Scholar 

  33. Marvel, S. A., Kleinberg, J., Kleinberg, R. D. & Strogatz, S. H. Continuous-time model of structural balance. Proc. Natl Acad. Sci. USA 108, 1771–1776 (2011).

    Article  Google Scholar 

  34. Strogatz, S. H. Exploring complex networks. Nature 410, 268–276 (2001).

    Article  MATH  Google Scholar 

  35. Barahona, M. & Pecora, L. M. Synchronization in small-world systems. Phys. Rev. Lett. 89, 054101 (2002).

    Article  Google Scholar 

  36. Mangan, N. M., Kutz, J. N., Brunton, S. L. & Proctor, J. L. Model selection for dynamical systems via sparse regression and information criteria. Proc. Math. Phys. Eng. Sci. 473, 20170009 (2017).

    MathSciNet  MATH  Google Scholar 

  37. Casadiego, J., Nitzan, M., Hallerberg, S. & Timme, M. Model-free inference of direct network interactions from nonlinear collective dynamics. Nat. Commun. 8, 2192 (2017).

    Article  Google Scholar 

  38. Runge, J., Nowack, P., Kretschmer, M., Flaxman, S. & Sejdinovic, D. Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 5, eaau4996 (2019).

    Article  Google Scholar 

  39. Sugihara, G. et al. Detecting causality in complex ecosystems. Science 338, 496–500 (2012).

    Article  MATH  Google Scholar 

  40. Sun, J., Taylor, D. & Bollt, E. M. Causal network inference by optimal causation entropy. SIAM J. Appl. Dyn. Syst. 14, 73–106 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  41. Kralemann, B., Pikovsky, A. & Rosenblum, M. Reconstructing effective phase connectivity of oscillator networks from observations. New J. Phys. 16, 085013 (2014).

    Article  Google Scholar 

  42. Frässle, S. et al. Regression DCM for fMRI. NeuroImage 155, 406–421 (2017).

    Article  Google Scholar 

  43. Gilson, M., Moreno-Bote, R., Ponce-Alvarez, A., Ritter, P. & Deco, G. Estimation of directed effective connectivity from fMRI functional connectivity hints at asymmetries of cortical connectome. PLoS Comput. Biol. 12, e1004762 (2016).

    Article  Google Scholar 

  44. Deco, G., Rolls, E. T. & Romo, R. Stochastic dynamics as a principle of brain function. Prog. Neurobiol. 88, 1–16 (2009).

    Article  Google Scholar 

  45. Genkin, M., Hughes, O. & Engel, T. A. Learning non-stationary Langevin dynamics from stochastic observations of latent trajectories. Nat. Commun. 12, 5986 (2021).

  46. Zhao, H. Inferring the dynamics of ‘black-box’ systems using a learning machine. Sci. China Phys. Mech. Astron. 64, 270511 (2021).

    Article  Google Scholar 

  47. Jahnke, S., Memmesheimer, R.-M. & Timme, M. Stable irregular dynamics in complex neural networks. Phys. Rev. Lett. 100, 048102 (2008).

    Article  Google Scholar 

  48. Champion, K. P., Brunton, S. L. & Kutz, J. N. Discovery of nonlinear multiscale systems: sampling strategies and embeddings. SIAM J. Appl. Dyn. Syst. 18, 312–333 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  49. Battiston, F. et al. The physics of higher-order interactions in complex systems. Nat. Phys. 17, 1093–1098 (2021).

    Article  Google Scholar 

  50. Lambiotte, R., Rosvall, M. & Scholtes, I. From networks to optimal higher-order models of complex systems. Nat. Phys. 15, 313–320 (2019).

    Article  Google Scholar 

  51. Sauer, T. Numerical solution of stochastic differential equations in finance. in Handbook of Computational Finance 529–550 (Springer, 2012).

  52. Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723 (1974).

    Article  MathSciNet  MATH  Google Scholar 

  53. Flores, B. E. A pragmatic view of accuracy measurement in forecasting. Omega 14, 93–98 (1986).

    Article  Google Scholar 

  54. White, J. G., Southgate, E., Thomson, J. N. & Brenner, S. The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci. 314, 1–340 (1986).

    Article  Google Scholar 

  55. Varshney, L. R., Chen, B. L., Paniagua, E., Hall, D. H. & Chklovskii, D. B. Structural properties of the Caenorhabditis elegans neuronal network. PLoS Comput. Biol. 7, e1001066 (2011).

    Article  Google Scholar 

  56. Yan, G. et al. Network control principles predict neuron function in the Caenorhabditis elegans connectome. Nature 550, 519–523 (2017).

    Article  Google Scholar 

  57. Scheffer, L. K. et al. A connectome and analysis of the adult Drosophila central brain. eLife 9, e57443 (2020).

    Article  Google Scholar 

  58. Menck, P. J., Heitzig, J., Kurths, J. & Schellnhuber, H. J. How dead ends undermine power grid stability. Nat. Commun. 5, 3969 (2014).

    Article  Google Scholar 

  59. Kunegis, J. KONECT: the Koblenz network collection. In Proc. 22nd International Conference on World Wide Web 1343–1350 (ACM, 2013).

  60. Rossi, R. & Ahmed, N. The network data repository with interactive graph analytics and visualization. In Twenty-Ninth AAAI Conference on Artificial Intelligence (2015).

  61. Dong, E., Du, H. & Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 20, 533–534 (2020).

    Article  Google Scholar 

  62. Gao, T.-T. & Yan, G. A two-phase approach for inferring complex network dynamics. Code Ocean https://doi.org/10.24433/CO.4774495.v1 (2022).

Download references

Acknowledgements

T.-T.G. and G.Y. are supported by the National Key Research and Development Program of China (grant no. 2021ZD0204500), National Natural Science Foundation of China (grant nos. 12161141016 and 11875043), Shanghai Municipal Science and Technology Major Project (grant no. 2021SHZDZX0100), Shanghai Municipal Commission of Science and Technology Project (grant nos. 18ZR1442000 and 19511132101) and Fundamental Research Funds for the Central Universities. We are also grateful for the helpful discussion with B. Barzel, J. Moore, X. Ru and T. Li.

Author information

Authors and Affiliations

  1. MOE Key Laboratory of Advanced Micro-Structured Materials and School of Physics Science and Engineering, Tongji University, Shanghai, People’s Republic of China

    Ting-Ting Gao & Gang Yan

  2. Frontiers Science Center for Intelligent Autonomous Systems, Tongji University, Shanghai, People’s Republic of China

    Ting-Ting Gao & Gang Yan

  3. Center for Excellence in Brain Science and Intelligence Technology, Chinese Academy of Sciences, Shanghai, People’s Republic of China

    Gang Yan

Authors
  1. Ting-Ting Gao
    View author publications

    Search author on:PubMed Google Scholar

  2. Gang Yan
    View author publications

    Search author on:PubMed Google Scholar

Contributions

G.Y. conceived the research. G.Y. and T.-T.G. designed the research. T.-T.G. performed the research. T.-T.G. and G.Y. analysed the results. G.Y. and T.-T.G. wrote the manuscript.

Corresponding author

Correspondence to Gang Yan.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Computational Science thanks Matthieu Gilson and the other, anonymous reviewer(s) for their contribution to the peer review of this work. Handling editor: Jie Pan, in collaboration with the Nature Computational Science team.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–20, Sections I–VI and Tables 1–5.

Source data

Source Data Fig. 1

True and inferred trajectories data.

Source Data Fig. 2

Unprocessed inferred results, time-series data and trajectories data.

Source Data Fig. 3

Unprocessed inferred results, time-series data and trajectories data.

Source Data Fig. 4

Statistical source data and trajectories data.

Source Data Fig. 5

Statistical source data.

Source Data Fig. 6

Raw empirical data and time-series data.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, TT., Yan, G. Autonomous inference of complex network dynamics from incomplete and noisy data. Nat Comput Sci 2, 160–168 (2022). https://doi.org/10.1038/s43588-022-00217-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s43588-022-00217-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics