Abstract
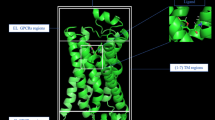
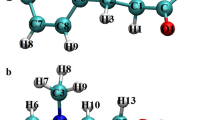
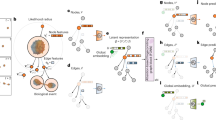
Anomalous diffusion plays a crucial rule in understanding molecular-level dynamics by offering valuable insights into molecular interactions, mobility states and the physical properties of systems across both biological and materials sciences. Deep-learning techniques have recently outperformed conventional statistical methods in anomalous diffusion recognition. However, deep-learning networks are typically trained by data with limited distribution, which inevitably fail to recognize unknown diffusion models and misinterpret dynamics when confronted with out-of-distribution (OOD) scenarios. In this work, we present a general framework for evaluating deep-learning-based OOD dynamics-detection methods. We further develop a baseline approach that achieves robust OOD dynamics detection as well as accurate recognition of in-distribution anomalous diffusion. We demonstrate that this method enables a reliable characterization of complex behaviors across a wide range of experimentally diverse systems, including nicotinic acetylcholine receptors in membranes, fluorescent beads in dextran solutions and silver nanoparticles undergoing active endocytosis.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this work are available on Code Ocean at https://doi.org/10.24433/CO.6518632.v1 (ref. 50). Source data are provided with this paper.
Code availability
Our reproduction code and the relevant documentation are available on Code Ocean at https://doi.org/10.24433/CO.6518632.v1 (ref. 50).
Change history
28 October 2024
A Correction to this paper has been published: https://doi.org/10.1038/s43588-024-00729-x
References
Kindermann, F. et al. Nonergodic diffusion of single atoms in a periodic potential. Nat. Phys. 13, 137–141 (2017).
Zhang, Y. & Hess, H. Chemically-powered swimming and diffusion in the microscopic world. Nat. Rev. Chem. 5, 500–510 (2021).
Bronstein, I. et al. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys. Rev. Lett. 103, 018102 (2009).
Rempel, A., Waddington, E., Wettlaufer, J. & Worster, M. Possible displacement of the climate signal in ancient ice by premelting and anomalous diffusion. Nature 411, 568–571 (2001).
Poletayev, A. D., Dawson, J. A., Islam, M. S. & Lindenberg, A. M. Defect-driven anomalous transport in fast-ion conducting solid electrolytes. Nat. Mater. 21, 1066–1073 (2022).
Scalas, E. The application of continuous-time random walks in finance and economics. Phys. A 362, 225–239 (2006).
Chechkin, A. V., Seno, F., Metzler, R. & Sokolov, I. M. Brownian yet non-Gaussian diffusion: from superstatistics to subordination of diffusing diffusivities. Phys. Rev. X 7, 021002 (2017).
Krapf, D. Mechanisms underlying anomalous diffusion in the plasma membrane. Curr. Top. Membr. 75, 167–207 (2015).
Weiss, M., Elsner, M., Kartberg, F. & Nilsson, T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 87, 3518–3524 (2004).
Sokolov, I. M. & Klafter, J. From diffusion to anomalous diffusion: a century after Einstein’s Brownian motion. Chaos 15, 26103 (2005).
Metzler, R., Jeon, J.-H., Cherstvy, A. G. & Barkai, E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 16, 24128–24164 (2014).
Mandelbrot, B. B. & van Ness, J. W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 10, 422–437 (1968).
Scher, H. & Montroll, E. W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 12, 2455 (1975).
Klafter, J. & Zumofen, G. Lévy statistics in a Hamiltonian system. Phys. Rev. E 49, 4873 (1994).
Lim, S. C. & Muniandy, S. V. Self-similar Gaussian processes for modeling anomalous diffusion. Phys. Rev. E 66, 021114 (2002).
Massignan, P. et al. Nonergodic subdiffusion from Brownian motion in an inhomogeneous medium. Phys. Rev. Lett. 112, 150603 (2014).
Sokolov, I. M. Models of anomalous diffusion in crowded environments. Soft Matter 8, 9043–9052 (2012).
Mangalam, M., Metzler, R. & Kelty-Stephen, D. G. Ergodic characterization of nonergodic anomalous diffusion processes. Phys. Rev. Res. 5, 023144 (2023).
Ślęzak, J., Metzler, R., & Magdziarz, M. Codifference can detect ergodicity breaking and non-Gaussianity. New J. Phys. 21, 053008 (2019).
Magdziarz, M., Weron, A., Burnecki, K. & Klafter, J. Fractional Brownian motion versus the continuous-time random walk: a simple test for subdiffusive dynamics. Phys. Rev. Lett. 103, 180602 (2009).
Li, J. Role of ergodicity, aging and Gaussianity in resolving the origins of biomolecule subdiffusion. Phys. Chem. Chem. Phys. 24, 16050–16057 (2022).
Muñoz-Gil, G. et al. Objective comparison of methods to decode anomalous diffusion. Nat. Commun. 12, 6253 (2021).
Seckler, H. & Metzler, R. Bayesian deep learning for error estimation in the analysis of anomalous diffusion. Nat. Commun. 13, 6717 (2022).
Muñoz-Gil, G., i Corominas, G. G. & Lewenstein, M. Unsupervised learning of anomalous diffusion data: an anomaly detection approach. J. Phys. A 54, 504001 (2021).
Hendrycks, D., Mazeika, M. & Dietterich, T. Deep anomaly detection with outlier exposure. In Proc. International Conference on Learning Representations (ICLR, 2019).
Hendrycks, D. & Gimpel, K. A baseline for detecting misclassified and out-of-distribution examples in neural networks. In Proc. International Conference on Learning Representations (ICLR, 2016).
Yang, J. et al. OpenOOD: benchmarking generalized out-of-distribution detection. Adv. Neural Inf. Process. Syst. 35, 32598–32611 (2022).
Zhang, H., Cisse, M., Dauphin, Y. N. & Lopez-Paz, D. Mixup: beyond empirical risk minimization. In Proc. International Conference on Learning Representations (ICLR, 2018).
Kristiadi, A., Hein, M. & Hennig, P. Being Bayesian, even just a bit, fixes overconfidence in ReLu networks. In Proc. 37th International Conference on Machine Learning 5436–5446 (PMLR, 2020).
Firbas, N., Garibo-i-Orts, Ò., Garcia-March, M. Á. & Conejero, J. A. Characterization of anomalous diffusion through convolutional transformers. J. Phys. A 56, 014001 (2023).
Elston, T. C. A macroscopic description of biomolecular transport. J. Math. Biol. 41, 189–206 (2000).
Maizón, H. B. & Barrantes, F. J. A deep learning-based approach to model anomalous diffusion of membrane proteins: the case of the nicotinic acetylcholine receptor. Brief. Bioinform. 23, bbab435 (2022).
Qu, X. et al. Semantic segmentation of anomalous diffusion using deep convolutional networks. Phys. Rev. Res. 6, 013054 (2024).
Sinai, Y. G. The limiting behavior of a one-dimensional random walk in a random medium. Theory Probab. Appl. 27, 256–268 (1983).
Uhlenbeck, G. E. & Ornstein, L. S. On the theory of the Brownian motion. Phys. Rev. 36, 823–841 (1930).
Ernst, D., Hellmann, M., Köhler, J. & Weiss, M. Fractional Brownian motion in crowded fluids. Soft Matter 8, 4886–4889 (2012).
Zaburdaev, V., Denisov, S. & Klafter, J. Lévy walks. Rev. Mod. Phys. 87, 483 (2015).
Guarnieri, D. et al. Transport across the cell-membrane dictates nanoparticle fate and toxicity: a new paradigm in nanotoxicology. Nanoscale 6, 10264–10273 (2014).
Krapf, D. et al. Spectral content of a single non-Brownian trajectory. Phys. Rev. X 9, 011019 (2019).
Balcerek, M., Burnecki, K., Thapa, S., Wyłomańska, A. & Chechkin, A. Fractional Brownian motion with random hurst exponent: accelerating diffusion and persistence transitions. Chaos 32, 093114 (2022).
Jin, H., Heller, D. A. & Strano, M. S. Single-particle tracking of endocytosis and exocytosis of single-walled carbon nanotubes in NIH-3T3 cells. Nano Lett. 8, 1577–1585 (2008).
Miller, J. How many participants? How many trials? Maximizing the power of reaction time studies. Behav. Res. Methods 56, 2398–2421 (2024).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition 770–778 (IEEE, 2016).
Daxberger, E. et al. Laplace redux-effortless Bayesian deep learning. In 35th Conference on Neural Information Processing Systems 20089–20103 (NeurIPS, 2021).
Ritter, H., Botev, A. & Barber, D. A scalable Laplace approximation for neural networks. In Proc. International Conference on Learning Representations (ICLR, 2018).
Ruff, L. et al. Deep one-class classification. In Proc. International Conference on Learning Representations Vol. 80, 4393–4402 (ICLR, 2018).
Golan, Y. & Sherman, E. Resolving mixed mechanisms of protein subdiffusion at the t cell plasma membrane. Nat. Commun. 8, 15851 (2017).
Sha, H., Li, H., Zhang, Y. & Hou, S. Deep learning-enhanced single-molecule spectrum imaging. APL Photon. 8, 096102 (2023).
Hou, S., Exell, J. & Welsher, K. Real-time 3D single molecule tracking. Nat. Commun. 11, 3607 (2020).
Xiao, F. Reliable deep learning in anomalous diffusion against out-of-distribution dynamics. Code Ocean https://doi.org/10.24433/CO.6518632.v1 (2024).
Acknowledgements
This work was supported by grants from the National Natural Science Foundation of China (grant nos. 62031023 and 62331011), and the Shenzhen Science and Technology Project (grant no. GXWD20220818170353009).
Author information
Authors and Affiliations
Contributions
X.F. conducted the experiments, analyzed the results and wrote the paper, with feedback from all authors. H.S. and S. Hou led the construction of optical system. Y.Z. and X.J. supervised the project. X.F., H.S. and Z.Y. proposed the initial idea. Y.S. took part in the experiments. Y.J. took part in the code design. S.L. and S. Han contributed to the results analysis.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Computational Science thanks Damian G. Kelty-Stephen, Diego Krapf and Gorka Muñoz-Gil for their contribution to the peer review of this work. Primary Handling Editor: Jie Pan, in collaboration with the Nature Computational Science team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–11, Tables 1–5, Algorithm 1 and Notes 1–8.
Source data
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Feng, X., Sha, H., Zhang, Y. et al. Reliable deep learning in anomalous diffusion against out-of-distribution dynamics. Nat Comput Sci 4, 761–772 (2024). https://doi.org/10.1038/s43588-024-00703-7
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1038/s43588-024-00703-7
This article is cited by
-
Effectively detecting anomalous diffusion via deep learning
Nature Computational Science (2024)