Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Everything everywhere all at once: a probability-based enhanced sampling approach to rare events

Nature Computational Science volume 5, pages 582–591 (2025)Cite this article

Subjects

A preprint version of the article is available at arXiv.

Abstract

The problem of studying rare events is central to many areas of computer simulations. We recently proposed an approach to solving this problem that involves computing the committor function, showing how it can be iteratively computed in a variational way while efficiently sampling the transition state ensemble. Here we greatly improve this procedure by combining it with a metadynamics-like enhanced sampling approach in which a logarithmic function of the committor is used as a collective variable. This procedure leads to an accurate sampling of the free energy surface in which transition states and metastable basins are studied with the same thoroughness. We show that our approach can be used in cases with the possibility of competing reactive paths and metastable intermediates. In addition, we demonstrate how physical insights can be obtained from the optimized committor model and the sampled data, thus providing a full characterization of the rare event under study.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Schematic representation of enhanced sampling framework.
Fig. 2: Müller–Brown potential.
Fig. 3: Alanine dipeptide.
Fig. 4: Asymmetric double-path potential.
Fig. 5: Chignolin folding.
Fig. 6: OAMe–G2 binding.

Similar content being viewed by others

Data availability

Training and simulation data and inputs are available on GitHub56 and on Zenodo57. Source data are provided with this paper.

Code availability

The code for the training of the NN-based committor model alongside didactic tutorials is available through the open-source mlcolvar library55, which is the preferred way to access the most updated code. To obtain the results reported in the manuscript, version 1.2.2 was used and a frozen version is also available on Zenodo57. The PLUMED58,59 interface for the application of the bias is available on GitHub56 and on Zenodo57.

References

  1. Frenkel, D. & Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, Vol. 1 (Elsevier, 2001).

  2. Hénin, J., Lelièvre, T., Shirts, M. R., Valsson, O. & Delemotte, L. Enhanced sampling methods for molecular dynamics simulations. Living J. Comput. Mol. Sci. 4, 1583 (2022).

    Article  Google Scholar 

  3. Kang, P., Trizio, E., & Parrinello, M. Computing the committor with the committor to study the transition state ensemble. Nat. Comput. Sci. 4, 451–460 (2024).

  4. Weinan, E. & Vanden-Eijnden, E. Transition-path theory and path-finding algorithms for the study of rare events. Annu. Rev. Phys. Chem. 61, 391–420 (2010).

    Article  Google Scholar 

  5. Bolhuis, P. G., Dellago, C. & Chandler, D. Reaction coordinates of biomolecular isomerization. Proc. Natl Acad. Sci. USA 97, 5877–5882 (2000).

    Article  Google Scholar 

  6. Ma, A. & Dinner, A. R. Automatic method for identifying reaction coordinates in complex systems. J. Phys. Chem. B 109, 6769–6779 (2005).

    Article  Google Scholar 

  7. Berezhkovskii, A. & Szabo, A. One-dimensional reaction coordinates for diffusive activated rate processes in many dimensions. J. Chem. Phys. 122, 014503 (2005).

    Article  Google Scholar 

  8. Peters, B. & Trout, B. L. Obtaining reaction coordinates by likelihood maximization. J. Chem. Phys. 125, 054108 (2006).

    Article  Google Scholar 

  9. Vanden-Eijnden, E. Towards a theory of transition paths. J. Stat. Phys. 123, 503–523 (2006).

    Article  MathSciNet  Google Scholar 

  10. Rotskoff, G. M., Mitchell, A. R., & Vanden-Eijnden, E. Active importance sampling for variational objectives dominated by rare events: consequences for optimization and generalization. Proc. Mach. Learn. Res. 145, 757–780 (2022).

  11. Chen, Y., Hoskins, J., Khoo, Y. & Lindsey, M. Committor functions via tensor networks. J. Comput. Phys. 472, 111646 (2023).

    Article  MathSciNet  Google Scholar 

  12. Chen, H., Roux, B. & Chipot, C. Discovering reaction pathways, slow variables, and committor probabilities with machine learning. J. Chem. Theory Comput. 19, 4414–4426 (2023).

    Article  Google Scholar 

  13. Li, Q., Lin, B. & Ren, W. Computing committor functions for the study of rare events using deep learning. J. Chem. Phys. 151, 054112 (2019).

    Article  Google Scholar 

  14. Jung, H. et al. Machine-guided path sampling to discover mechanisms of molecular self-organization. Nat. Comput. Sci. 3, 334–345 (2023).

  15. Mitchell, A. R. & Rotskoff, G. M. Committor guided estimates of molecular transition rates. J. Chem. Theory Comput. 20, 9378–9393 (2024).

    Article  Google Scholar 

  16. He, Z., Chipot, C. & Roux, B. Committor-consistent variational string method. J. Phys. Chem. Lett. 13, 9263–9271 (2022).

    Article  Google Scholar 

  17. Khoo, Y., Lu, J. & Ying, L. Solving for high-dimensional committor functions using artificial neural networks. Res. Math. Sci. 6, 1 (2019).

    Article  MathSciNet  Google Scholar 

  18. Kolmogoroff, A. Über die analytischen methoden in der wahrscheinlichkeitsrechnung. Math. Ann. 104, 415–458 (1931).

    Article  MathSciNet  Google Scholar 

  19. Bonati, L., Piccini, G. & Parrinello, M. Deep learning the slow modes for rare events sampling. Proc. Natl Acad. Sci. USA 118, e2113533118 (2021).

    Article  Google Scholar 

  20. Ray, D., Trizio, E. & Parrinello, M. Deep learning collective variables from transition path ensemble. J. Chem. Phys. 158, 204102 (2023).

    Article  Google Scholar 

  21. Laio, A. & Parrinello, M. Escaping free-energy minima. Proc. Natl Acad. Sci. USA 99, 12562–12566 (2002).

    Article  Google Scholar 

  22. Invernizzi, M. & Parrinello, M. Rethinking metadynamics: from bias potentials to probability distributions. J. Phys. Chem. Lett. 11, 2731–2736 (2020).

    Article  Google Scholar 

  23. Trizio, E., Rizzi, A., Piaggi, P. M., Invernizzi, M. & Bonati, L. Advanced simulations with PLUMED: OPES and machine learning collective variables. Preprint at https://arxiv.org/abs/2410.18019 (2024).

  24. Li, W. & Ma, A. Recent developments in methods for identifying reaction coordinates. Mol. Simul. 40, 784–793 (2014).

    Article  Google Scholar 

  25. Bonati, L., Rizzi, V. & Parrinello, M. Data-driven collective variables for enhanced sampling. J. Phys. Chem. Lett. 11, 2998–3004 (2020).

    Article  Google Scholar 

  26. Trizio, E. & Parrinello, M. From enhanced sampling to reaction profiles. J. Phys. Chem. Lett. 12, 8621–8626 (2021).

    Article  Google Scholar 

  27. Invernizzi, M. & Parrinello, M. Exploration vs convergence speed in adaptive bias enhanced sampling. J. Chem. Theory Comput. 18, 3988–3996 (2022).

  28. Vlugt, T. J. H. & Smit, B. On the efficient sampling of pathways in the transition path ensemble. PhysChemComm 4, 11–17 (2001).

    Article  Google Scholar 

  29. Borrero, E. E. & Dellago, C. Avoiding traps in trajectory space: metadynamics enhanced transition path sampling. Eur. Phys. J. Spec. Top. 225, 1609–1620 (2016).

    Article  Google Scholar 

  30. Bolhuis, P. G. & Csányi, G. Nested transition path sampling. Phys. Rev. Lett. 120, 250601 (2018).

    Article  MathSciNet  Google Scholar 

  31. Mandelli, D., Hirshberg, B. & Parrinello, M. Metadynamics of paths. Phys. Rev. Lett. 125, 026001 (2020).

    Article  MathSciNet  Google Scholar 

  32. Capelli, R., Carloni, P. & Parrinello, M. Exhaustive search of ligand binding pathways via volume-based metadynamics. J. Phys. Chem. Lett. 10, 3495–3499 (2019).

    Article  Google Scholar 

  33. Lindorff-Larsen, K., Piana, S., Dror, R. O. & Shaw, D. E. How fast-folding proteins fold. Science 334, 517–520 (2011).

    Article  Google Scholar 

  34. Schubert, E. & Lenssen, L. Fast k-medoids clustering in Rust and Python. J. Open Source Softw. 7, 4183 (2022).

    Article  Google Scholar 

  35. Pizarroso, J., Portela, J. & Muñoz, A. NeuralSens: sensitivity analysis of neural networks. J. Stat. Softw. 102, 1–36 (2022).

    Article  Google Scholar 

  36. Novelli, P., Bonati, L., Pontil, M. & Parrinello, M. Characterizing metastable states with the help of machine learning. J. Chem. Theory Comput. 18, 5195–5202 (2022).

    Article  Google Scholar 

  37. Yin, J. et al. Overview of the SAMPL5 host–guest challenge: are we doing better? J. Comput.-Aided Mol. Des. 31, 1–19 (2017).

    Article  Google Scholar 

  38. Rizzi, V., Bonati, L., Ansari, N. & Parrinello, M. The role of water in host–guest interaction. Nat. Commun. 12, 93 (2021).

    Article  Google Scholar 

  39. Limongelli, V., Bonomi, M. & Parrinello, M. Funnel metadynamics as accurate binding free-energy method. Proc. Natl Acad. Sci. USA 110, 6358–6363 (2013).

    Article  Google Scholar 

  40. Zhang, J. et al. Descriptor-free collective variables from geometric graph neural networks. J. Chem. Theory Comput. 20, 10787–10797 (2024).

  41. Dietrich, F. M., Advincula, X. R., Gobbo, G., Bellucci, M. A. & Salvalaglio, M. Machine learning nucleation collective variables with graph neural networks. J. Chem. Theory Comput. 20, 1600–1611 (2024).

    Article  Google Scholar 

  42. Zou, Z. & Tiwary, P. Enhanced sampling of crystal nucleation with graph representation learnt variables. J. Phys. Chem. B 128, 3037–3045 (2024).

    Article  Google Scholar 

  43. Aristoff, D., Copperman, J., Simpson, G., Webber, R. J. & Zuckerman, D. M. Weighted ensemble: recent mathematical developments. J. Chem. Phys. 158, 014108 (2023).

    Article  Google Scholar 

  44. Wang, Y.-G., Mei, D., Glezakou, V.-A., Li, J. & Rousseau, R. Dynamic formation of single-atom catalytic active sites on ceria-supported gold nanoparticles. Nat. Commun. 6, 6511 (2015).

    Article  Google Scholar 

  45. Wang, Y.-G. et al. CO oxidation on Au/TiO2: condition-dependent active sites and mechanistic pathways. J. Am. Chem. Soc. 138, 10467–10476 (2016).

    Article  Google Scholar 

  46. Yang, M., Raucci, U. & Parrinello, M. Reactant-induced dynamics of lithium imide surfaces during the ammonia decomposition process. Nat. Catal. 6, 829–836 (2023).

    Article  Google Scholar 

  47. Tian, J. et al. Dynamically formed active sites on liquid boron oxide for selective oxidative dehydrogenation of propane. ACS Catal. 13, 8219–8236 (2023).

    Article  Google Scholar 

  48. Perego, S., Bonati, L., Tripathi, S. & Parrinello, M. How dynamics changes ammonia cracking on iron surfaces. ACS Catal. 14, 14652–14664 (2024).

    Article  Google Scholar 

  49. Tripathi, S., Bonati, L., Perego, S. & Parrinello, M. How poisoning is avoided in a step of relevance to the Haber–Bosch catalysis. ACS Catal. 14, 4944–4950 (2024).

    Article  Google Scholar 

  50. Dill, K. A. & MacCallum, J. L. The protein-folding problem, 50 years on. Science 338, 1042–1046 (2012).

    Article  Google Scholar 

  51. Sztain, T. et al. A glycan gate controls opening of the SARS-CoV-2 spike protein. Nat. Chem. 13, 963–968 (2021).

    Article  Google Scholar 

  52. Dellago, C., Bolhuis, P. & Geissler, P. in Computer Simulations in Condensed Matter Systems: From Materials to Chemical Biology, Vol. 1 (eds Ferrario, M. et al.) 349–391 (Springer, 2006).

  53. Bolhuis, P. G., Chandler, D., Dellago, C. & Geissler, P. L. Transition path sampling: throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem. 53, 291–318 (2002).

    Article  Google Scholar 

  54. Lazzeri, G., Jung, H., Bolhuis, P. G. & Covino, R. Molecular free energies, rates, and mechanisms from data-efficient path sampling simulations. J. Chem. Theory Comput. 19, 9060–9076 (2023).

    Article  Google Scholar 

  55. Bonati, L., Trizio, E., Rizzi, A. & Parrinello, M. A unified framework for machine learning collective variables for enhanced sampling simulations: mlcolvar. J. Chem. Phys. 159, 014801 (2023).

    Article  Google Scholar 

  56. Trizio, E., Kang, P. & Parrinello, M. Supporting data for the paper: “everything everywhere all at once, a probability-based enhanced sampling approach to rare events”. GitHub https://github.com/EnricoTrizio/committor_2.0 (2025).

  57. Trizio, E., Kang, P. & Parrinello, M. Everything everywhere all at once: a probability-based enhanced sampling approach to rare events. Zenodo https://doi.org/10.5281/zenodo.15089372 (2025).

  58. Tribello, G. A., Bonomi, M., Branduardi, D., Camilloni, C. & Bussi, G. PLUMED 2: new feathers for an old bird. Comput. Phys. Commun. 185, 604–613 (2014).

    Article  Google Scholar 

  59. The PLUMED Consortium. Promoting transparency and reproducibility in enhanced molecular simulations. Nat. Methods 16, 670–673 (2019).

Download references

Acknowledgements

We are grateful to L. Bonati, A. Rizzi, J. Zhang, U. Raucci, A. Triveri and F. Mambretti for discussions and feedback about this manuscript.

Author information

Author notes

  1. These authors contributed equally: Enrico Trizio, Peilin Kang.

Authors and Affiliations

  1. Atomistic Simulations, Italian Institute of Technology, Genova, Italy

    Enrico Trizio, Peilin Kang & Michele Parrinello

Authors
  1. Enrico Trizio
    View author publications

    Search author on:PubMed Google Scholar

  2. Peilin Kang
    View author publications

    Search author on:PubMed Google Scholar

  3. Michele Parrinello
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All the authors equally contributed to the manuscript by conceptualizing the project, developing the theoretical methodologies and participating in the writing of the manuscript. Specifically, E.T. and P.K. developed the code for the training of the committor function and conducted the computational simulations.

Corresponding authors

Correspondence to Peilin Kang or Michele Parrinello.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Computational Science thanks Samik Bose, Carme Rovira, and Omar Valsson for their contribution to the peer review of this work. Primary Handling Editor: Kaitlin McCardle, in collaboration with the Nature Computational Science team.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Convergence of ΔG.

Convergence with simulation time of the estimate for the folding energy of chignolin (A) and the binding energy of the G2 ligand to the OAMe octa-acid guest (B). The average estimates from independent simulations for each system (3 for chignolin, 4 for OAMe-G2) are reported as a blue solid line, whereas the uncertainty, computed as the standard deviation over the three replicas, is depicted as a shaded blue region. The reference values are provided as gray dashed lines, and the 0.5 kBT interval around the reference is marked by gray dotted lines. For chignolin, that is the unbiased estimate from ref. 33, for the calixarene, an estimate obtained using the enhanced sampling setup of ref. 38.

Source Data

Supplementary information

Supplementary Information

Supplementary Figs. 1–9, Tables 1–6 and simulation computational details.

Reporting Summary

Peer Review File

Source data

Source Data Fig. 2

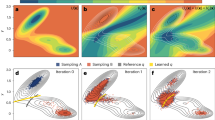
Muller–Brown potential. a, Scatter plot data, reference potential isoline data, reference and learned committor data. b, Sampling distribution data. c, Free energy surface data.

Source Data Fig. 3

Alanine. a, Free energy surface isoline data, sampling distribution data. b, Free energy surface isoline data, Kolmogorov distribution data. c, Sampling distribution data. d, Free energy surface data, reference line TSE.

Source Data Fig. 4

Double-path potential. a, Potential isoline data, learned committor data. b, Potential isoline data, Kolmogorov distribution data. c, Potential isoline data, computed free energy surface data.

Source Data Extended Data Fig. 1

a, ΔG data (time, avg, s.d., ref. value) for chingolin. b, ΔG data (time, avg, s.d., ref. value) for calixarene.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Trizio, E., Kang, P. & Parrinello, M. Everything everywhere all at once: a probability-based enhanced sampling approach to rare events. Nat Comput Sci 5, 582–591 (2025). https://doi.org/10.1038/s43588-025-00799-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s43588-025-00799-5

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics