Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Efficient modeling of ionic and electronic interactions by a resistive memory-based reservoir graph neural network

Nature Computational Science volume 5, pages 1178–1191 (2025)Cite this article

Subjects

A preprint version of the article is available at Research Square.

Abstract

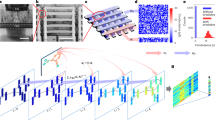
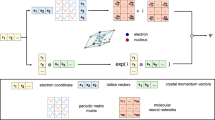
Current quantum chemistry and materials science are dominated by first-principles methodologies such as density functional theory. However, these approaches face substantial computational costs as system scales up. In addition, the von Neumann bottleneck of digital computers imposes energy efficiency limitations. Here we propose a software–hardware co-design: the resistive memory-based reservoir graph neural network for efficient modeling of ionic and electronic interactions. Software-wise, the reservoir graph neural network is evaluated for computational tasks, including atomic force, Hamiltonian and wavefunction prediction, achieving comparable accuracy while reducing computational costs by approximately 104-, 106- and 103-fold, respectively, compared with traditional first-principles methods. Moreover, it reduces training costs by approximately 90% due to reservoir computing. Hardware-wise, validated on a 40-nm 256-kb in-memory computing macro, our co-design achieves improvements in area-normalized inference speed by approximately 2.5-, 2.5- and 2.7-fold, and inference energy efficiency by approximately 2.7, 1.9 and 4.4 times, compared with state-of-the-art digital hardware, respectively.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Resistive memory-based hardware–software co-design for modeling ionic and electronic interactions.
Fig. 2: Random weights resulted from the programming randomness in resistive memory arrays.
Fig. 3: Experimental results of atomic force calculation using the co-design.
Fig. 4: Experimental results of Hamiltonian calculation using the co-design.
Fig. 5: Experimental results of ground-state wavefunction calculation using our co-design.
Fig. 6: Impact of conductance fluctuation of the resistive memory on atomic force, Hamiltonian and ground-state wavefunction computation.

Similar content being viewed by others

Data availability

The dataset used to train the deep learning model was generated through DFT and AIMD calculations. The dataset is available via Zenodo at https://doi.org/10.5281/zenodo.13346149 (ref. 63). Source data are provided with this paper.

Code availability

The code that supports the plots within this Article is available via GitHub at https://github.com/hustmeng/RGNN and via Zenodo at https://doi.org/10.5281/zenodo.15654129 (ref.64).

References

  1. Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).

    Article  Google Scholar 

  2. Marzari, N., Ferretti, A. & Wolverton, C. Electronic-structure methods for materials design. Nat. Mater. 20, 736–749 (2021).

    Article  Google Scholar 

  3. Huang, B., von Rudorff, G. F. & von Lilienfeld, O. A. The central role of density functional theory in the AI age. Science 381, 170–175 (2023).

    Article  Google Scholar 

  4. Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).

    Article  MathSciNet  Google Scholar 

  5. Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).

    Article  MathSciNet  Google Scholar 

  6. Kirkpatrick, J. et al. Pushing the frontiers of density functionals by solving the fractional electron problem. Science 374, 1385–1389 (2021).

    Article  Google Scholar 

  7. Zhang, W., Mazzarello, R., Wuttig, M. & Ma, E. Designing crystallization in phase-change materials for universal memory and neuro-inspired computing. Nat. Rev. Mater. 4, 150–168 (2019).

    Article  Google Scholar 

  8. Konstantinou, K., Mocanu, F. C., Lee, T.-H. & Elliott, S. R. Revealing the intrinsic nature of the mid-gap defects in amorphous Ge2Sb2Te5. Nat. Commun. 10, 3065 (2019).

    Article  Google Scholar 

  9. Sheng, H. W., Luo, W. K., Alamgir, F. M., Bai, J. M. & Ma, E. Atomic packing and short-to-medium-range order in metallic glasses. Nature 439, 419–425 (2006).

    Article  Google Scholar 

  10. Kolobov, A. V. et al. Understanding the phase-change mechanism of rewritable optical media. Nat. Mater. 3, 703–708 (2004).

    Article  Google Scholar 

  11. Wełnic, W. et al. Unravelling the interplay of local structure and physical properties in phase-change materials. Nat. Mater. 5, 56–62 (2005).

    Article  Google Scholar 

  12. Xu, Y. et al. Unraveling crystallization mechanisms and electronic structure of phase-change materials by large-scale ab initio simulations. Adv. Mater. 34, 2109139 (2022).

    Article  Google Scholar 

  13. Schuch, N. & Verstraete, F. Computational complexity of interacting electrons and fundamental limitations of density functional theory. Nat. Phys. 5, 732–735 (2009).

    Article  Google Scholar 

  14. Dawson, W. et al. Complexity reduction in density functional theory: locality in space and energy. J. Chem. Phys. 158, 164114 (2023).

    Article  Google Scholar 

  15. Dawson, W., Mohr, S., Ratcliff, L. E., Nakajima, T. & Genovese, L. Complexity reduction in density functional theory calculations of large systems: system partitioning and fragment embedding. J. Chem. Theory Comput. 16, 2952–2964 (2020).

    Article  Google Scholar 

  16. Rudberg, E., Rubensson, E. H. & Sałek, P. Kohn–Sham density functional theory electronic structure calculations with linearly scaling computational time and memory usage. J. Chem. Theory Comput. 7, 340–350 (2011).

    Article  Google Scholar 

  17. Zhou, Y., Zhang, W., Ma, E. & Deringer, V. L. Device-scale atomistic modelling of phase-change memory materials. Nat. Electron. 6, 746–754 (2023).

    Article  Google Scholar 

  18. Scherbela, M., Reisenhofer, R., Gerard, L., Marquetand, P. & Grohs, P. Solving the electronic Schrödinger equation for multiple nuclear geometries with weight-sharing deep neural networks. Nat. Comput. Sci. 2, 331–341 (2022).

    Article  Google Scholar 

  19. Batzner, S. et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 13, 2453 (2022).

    Article  Google Scholar 

  20. Cheng, G., Gong, X. G. & Yin, W. J. Crystal structure prediction by combining graph network and optimization algorithm. Nat. Commun. 13, 1492 (2022).

    Article  Google Scholar 

  21. Spencer, J. Learning many-electron wavefunctions with deep neural networks. Nat. Rev. Phys. 3, 458–458 (2021).

    Article  Google Scholar 

  22. Zhong, Y., Yu, H., Su, M., Gong, X. & Xiang, H. Transferable equivariant graph neural networks for the Hamiltonians of molecules and solids. npj Comput. Mater. 9, 182 (2023).

    Article  Google Scholar 

  23. Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).

    Article  Google Scholar 

  24. Deng, B. et al. CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat. Mach. Intell. 5, 1031–1041 (2023).

    Article  Google Scholar 

  25. Chen, C. & Ong, S. P. A universal graph deep learning interatomic potential for the periodic table. Nat. Comput. Sci. 2, 718–728 (2022).

    Article  Google Scholar 

  26. Li, H. et al. Deep-learning electronic-structure calculation of magnetic superstructures. Nat. Comput. Sci. 3, 321–327 (2023).

    Article  Google Scholar 

  27. Li, H. et al. Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation. Nat. Comput. Sci. 2, 367–377 (2022).

    Article  Google Scholar 

  28. Gong, X. et al. General framework for E(3)-equivariant neural network representation of density functional theory Hamiltonian. Nat. Commun. 14, 2848 (2023).

    Article  Google Scholar 

  29. Li, X., Li, Z. & Chen, J. Ab initio calculation of real solids via neural network ansatz. Nat. Commun. 13, 7895 (2022).

    Article  Google Scholar 

  30. Pfau, D., Spencer, J. S., Matthews, A. G. D. G. & Foulkes, W. M. C. Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Phys. Rev. Res. 2, 033429 (2020).

    Article  Google Scholar 

  31. Hermann, J., Schatzle, Z. & Noe, F. Deep-neural-network solution of the electronic Schrodinger equation. Nat. Chem. 12, 891–897 (2020).

    Article  Google Scholar 

  32. Schaller, R. R. Moore’s law: past, present and future. IEEE Spectr. 34, 52–59 (1997).

    Article  Google Scholar 

  33. Shin, D. & Yoo, H. J. The heterogeneous deep neural network processor with a non-von Neumann architecture. Proc. IEEE 108, 1245–1260 (2020).

    Article  Google Scholar 

  34. Zou, X., Xu, S., Chen, X., Yan, L. & Han, Y. Breaking the von Neumann bottleneck: architecture-level processing-in-memory technology. Sci. China Inf. Sci. 64, 160404 (2021).

    Article  Google Scholar 

  35. Zidan, M. A., Strachan, J. P. & Lu, W. D. The future of electronics based on memristive systems. Nat. Electron. 1, 22–29 (2018).

    Article  Google Scholar 

  36. Lin, N. et al. In-memory and in-sensor reservoir computing with memristive devices. APL Mach. Learn. 2, 010901 (2024).

    Article  Google Scholar 

  37. Tanaka, G. et al. Recent advances in physical reservoir computing: a review. Neural Netw. 115, 100–123 (2019).

    Article  Google Scholar 

  38. Han, X. & Zhao, Y. Interpretable graph reservoir computing with the temporal pattern attention. IEEE Trans. Neural Networks Learn. Syst. 35, 9198–9212 (2024).

    Article  Google Scholar 

  39. Pasa, L., Navarin, N. & Sperduti, A. Multiresolution reservoir graph neural network. IEEE Trans. Neural Networks Learn. Syst. 33, 2642–2653 (2022).

    Article  MathSciNet  Google Scholar 

  40. Micheli, A. & Tortorella, D. Designs of graph echo state networks for node classification. Neurocomputing 597, 127965 (2024).

    Article  Google Scholar 

  41. Bianchi, F. M., Gallicchio, C. & Micheli, A. Pyramidal reservoir graph neural network. Neurocomputing 470, 389–404 (2022).

    Article  Google Scholar 

  42. Sebastian, A., Gallo, M., Khaddam-Aljameh, R. & Eleftheriou, E. Memory devices and applications for in-memory computing. Nat. Nanotechnol. 15, 529–544 (2020).

    Article  Google Scholar 

  43. Ielmini, D. & Wong, H. S. P. In-memory computing with resistive switching devices. Nat. Electron. 1, 333–343 (2018).

    Article  Google Scholar 

  44. Zhang, W. et al. Neuro-inspired computing chips. Nat. Electron. 3, 371–382 (2020).

    Article  Google Scholar 

  45. Sangwan, V. K. & Hersam, M. C. Neuromorphic nanoelectronic materials. Nat. Nanotechnol. 15, 517–528 (2020).

    Article  Google Scholar 

  46. Kumar, S., Wang, X., Strachan, J. P., Yang, Y. & Lu, W. D. Dynamical memristors for higher-complexity neuromorphic computing. Nat. Rev. Mater. 7, 575–591 (2022).

    Article  Google Scholar 

  47. Kumar, S., Williams, R. S. & Wang, Z. Third-order nanocircuit elements for neuromorphic engineering. Nature 585, 518–523 (2020).

    Article  Google Scholar 

  48. Wang, Z. et al. Resistive switching materials for information processing. Nat. Rev. Mater. 5, 173–195 (2020).

    Article  Google Scholar 

  49. Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O. & Dahl, G. E. Neural message passing for quantum chemistry. Proc. 34th Int. Conf. Mach. Learn. 70, 1263–1272 (2017).

    Google Scholar 

  50. Ozaki, T. & Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 69, 195113 (2004).

    Article  Google Scholar 

  51. Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 67, 155108 (2003).

    Article  Google Scholar 

  52. Foulkes, W. M. C., Mitas, L., Needs, R. J. & Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 73, 33–83 (2001).

    Article  Google Scholar 

  53. Sun, Q. et al. PySCF: the Python-based simulations of chemistry framework. WIREs Comput. Mol. Sci. 8, e1340 (2018).

    Article  Google Scholar 

  54. Scuseria, G. E., Janssen, C. L. & Schaefer, H. F. III. An efficient reformulation of the closed‐shell coupled cluster single and double excitation (CCSD) equations. J. Chem. Phys. 89, 7382–7387 (1988).

    Article  Google Scholar 

  55. Gu, Q. et al. Deep learning tight-binding approach for large-scale electronic simulations at finite temperatures with ab initio accuracy. Nat. Commun. 15, 6772 (2024).

    Article  Google Scholar 

  56. Pfau, D., Axelrod, S., Sutterud, H., von Glehn, I. & Spencer, J. S. Accurate computation of quantum excited states with neural networks. Science 385, eadn0137 (2024).

    Article  MathSciNet  Google Scholar 

  57. Zhong, Y. et al. Accelerating the calculation of electron–phonon coupling strength with machine learning. Nat. Comput. Sci. 4, 615–625 (2024).

    Article  Google Scholar 

  58. Li, H. et al. Deep-learning density functional perturbation theory. Phys. Rev. Lett. 132, 096401 (2024).

    Article  Google Scholar 

  59. Eric, J. B., Kevin, G., Doug, B., Scott, B. B. & John, H. W. Hard scaling challenges for ab initio molecular dynamics capabilities in NWChem: using 100,000 CPUs per second. J. Phys. Conf. Ser. 180, 012028 (2009).

    Article  Google Scholar 

  60. Jacquelin, M., Jong, W. D. & Bylaska, E. Towards highly scalable ab initio molecular dynamics (AIMD) simulations on the Intel Knights Landing Manycore Processor. In 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS) 234–243 (IEEE, 2017).

  61. Held, J., Hanrath, M. & Dolg, M. An efficient Hartree–Fock implementation based on the contraction of integrals in the primitive basis. J. Chem. Theory Comput. 14, 6197–6210 (2018).

    Article  Google Scholar 

  62. Gyevi-Nagy, L., Kállay, M. & Nagy, P. R. Accurate reduced-cost CCSD(T) energies: parallel implementation, benchmarks, and large-scale applications. J. Chem. Theory Comput. 17, 860–878 (2021).

    Article  Google Scholar 

  63. Xu, M. Dataset for efficient modelling of ionic and electronic interactions by resistive memory-based reservoir graph neural network. Zenodo https://doi.org/10.5281/zenodo.13346149 (2025).

  64. Xu, M. Code for efficient modelling of ionic and electronic interactions by resistive memory-based reservoir graph neural network. Zenodo https://doi.org/10.5281/zenodo.15654129 (2025).

Download references

Acknowledgements

This research is supported by the National Key R&D Program of China (grant no. 2022ZD0117600), the National Natural Science Foundation of China (grant nos. 62122004 and 62374181), the Strategic Priority Research Program of the Chinese Academy of Sciences (grant no. XDB44000000), Beijing Natural Science Foundation (grant no. Z210006), Hong Kong Research Grant Council (grant nos. 27206321, 17205922 and 17212923). This research is also partially supported by Joint Laboratory of Microelectronics (JLFS/E-601/24), ACCESS – AI Chip Center for Emerging Smart Systems, sponsored by Innovation and Technology Fund (ITF), Hong Kong SAR.

Author information

Authors and Affiliations

  1. Department of Electrical and Electronic Engineering, University of Hong Kong, Hong Kong, China

    Meng Xu, Shaocong Wang, Yangu He, Yi Li & Xiaojuan Qi

  2. The School of Microelectronics, Southern University of Science and Technology, Shenzhen, China

    Meng Xu & Zhongrui Wang

  3. ACCESS - AI Chip Center for Emerging Smart Systems, InnoHK Centers, Hong Kong Science Park, Hong Kong, China

    Meng Xu, Shaocong Wang & Zhongrui Wang

  4. State Key Lab of Fabrication Technologies for Integrated Circuits and Key Laboratory of Microelectronic Devices and Integrated Technology, Institute of Microelectronics of the Chinese Academy of Sciences, Beijing, China

    Yi Li, Woyu Zhang, Dashan Shang & Ming Liu

  5. Department of Applied Physics, The Hong Kong Polytechnic University, Hong Kong, China

    Ming Yang

  6. School of Integrated Circuits, Huazhong University of Science and Technology, Wuhan, China

    Ming Xu & Xiangshui Miao

  7. University of Chinese Academy of Sciences, Beijing, China

    Dashan Shang

  8. Frontier Institute of Chip and System, Fudan University, Shanghai, China

    Qi Liu & Ming Liu

Authors
  1. Meng Xu
    View author publications

    Search author on:PubMed Google Scholar

  2. Shaocong Wang
    View author publications

    Search author on:PubMed Google Scholar

  3. Yangu He
    View author publications

    Search author on:PubMed Google Scholar

  4. Yi Li
    View author publications

    Search author on:PubMed Google Scholar

  5. Woyu Zhang
    View author publications

    Search author on:PubMed Google Scholar

  6. Ming Yang
    View author publications

    Search author on:PubMed Google Scholar

  7. Xiaojuan Qi
    View author publications

    Search author on:PubMed Google Scholar

  8. Zhongrui Wang
    View author publications

    Search author on:PubMed Google Scholar

  9. Ming Xu
    View author publications

    Search author on:PubMed Google Scholar

  10. Dashan Shang
    View author publications

    Search author on:PubMed Google Scholar

  11. Qi Liu
    View author publications

    Search author on:PubMed Google Scholar

  12. Xiangshui Miao
    View author publications

    Search author on:PubMed Google Scholar

  13. Ming Liu
    View author publications

    Search author on:PubMed Google Scholar

Contributions

Meng Xu, Z.W., Ming Xu and D.S. conceived the work. Meng Xu, S.W., Y.H., Y.L., W.Z. and X.Q. contributed to the design and development of the models, software and hardware experiments. Meng Xu, Z.W., M.Y., X.Q., Ming Xu, D.S., Q.L., X.M. and M.L. interpreted, analyzed and presented the experimental results. Meng Xu, Z.W., X.Q., Ming Xu and D.S. wrote the paper. All authors discussed the results and implications and commented on the paper at all stages.

Corresponding authors

Correspondence to Xiaojuan Qi, Zhongrui Wang, Ming Xu or Dashan Shang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Computational Science thanks Luca Manneschi, Ilia Valov and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Jie Pan, in collaboration with the Nature Computational Science team. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Notes 1–15, Figs. 1–42 and Tables 1–4.

Peer Review File

Source data

Source Data Fig. 2

Statistical source data.

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Source Data Fig. 5

Statistical source data.

Source Data Fig. 6

Statistical source data.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, M., Wang, S., He, Y. et al. Efficient modeling of ionic and electronic interactions by a resistive memory-based reservoir graph neural network. Nat Comput Sci 5, 1178–1191 (2025). https://doi.org/10.1038/s43588-025-00844-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s43588-025-00844-3

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing