Increasing alignment of large language models with language processing in the human brain

Abstract

Transformer-based large language models (LLMs) have considerably advanced our understanding of how meaning is represented in the human brain; however, the validity of increasingly large LLMs is being questioned due to their extensive training data and their ability to access context thousands of words long. In this study we investigated whether instruction tuning—another core technique in recent LLMs that goes beyond mere scaling—can enhance models’ ability to capture linguistic information in the human brain. We compared base and instruction-tuned LLMs of varying sizes against human behavioral and brain activity measured with eye-tracking and functional magnetic resonance imaging during naturalistic reading. We show that simply making LLMs larger leads to a closer match with the human brain than fine-tuning them with instructions. These finding have substantial implications for understanding the cognitive plausibility of LLMs and their role in studying naturalistic language comprehension.

Main

Autoregressive transformers are increasingly used in cognitive neuroscience for language processing studies, enhancing our understanding of meaning representation and composition in the human language system^1,2,3,4,5,6. For instance, Goldstein et al.² found that the probability of words given a context significantly correlates with human brain activity during naturalistic listening, suggesting that language models and the human brain share some computational principles for language processing, such as the ‘next-word prediction’ mechanism (see also refs. ^7,8). Furthermore, pre-trained transformers are essential for decoding speech or text from neuroimaging data^9,10. They provide embeddings for training encoding models that map words to neural data and generate continuations as decoding candidates¹⁰. However, those studies mostly adopted smaller pre-trained language models such GPT-2 (ref. ¹¹) and BERT (ref. ¹²), whereas recent large language models (LLMs) such as GPT-4 (ref. ¹³) and LLaMA (ref. ¹⁴) are significantly larger in terms of parameter size and training data. It has been demonstrated that as the model size, training dataset and computational resources increase, so does performance on benchmark natural language processing (NLP) tasks, following a power-law scaling^15,16,17. These newer LLMs have already been adopted in recent studies to understand language processing in the human brain^18,19, but whether they better resemble human language processing is still an ongoing debate. On the one hand, it has been demonstrated that larger models exhibit a stronger correlation with the human brain^20,21 during language comprehension, mirroring the scaling law in other deep learning contexts. On the other hand, the validity of larger models as cognitive models has been questioned due to their extensive training data and their ability to access context thousands of words long, which far exceeds human capabilities. Research has shown that surprisal values from larger transformer-based language models align less well with human reading times²², and that language model with the lowest perplexity may not result in the best model fits^23,24. Furthermore, limiting the context access of language models can improve their simulation of language processing in humans^6,25.

In addition to scaling, fine-tuning LLMs has been shown to improve performance on NLP tasks and enhance generalization to new tasks^26,27,28,29. For instance, Ouyang et al.²⁷ fine-tuned GPT-3 models of varying sizes using reinforcement learning from human feedback^30,31, and showed that the fine-tuned models with only 1.3B parameters were more aligned with human preferences than the 175B base GPT-3. Recent reasoning LLMs such as DeepSeek-R1 (ref. ³²)—which integrates chain-of-thought reasoning with reinforcement learning during fine-tuning—achieve state-of-the-art performance while using similar or fewer activated parameters than existing open-source LLMs. The superior performance of these fine-tuned LLMs over base LLMs on NLP tasks raises the question of whether scaling or fine-tuning has a greater impact on the models’ brain-encoding performance.

In this work we systematically compared the self-attention of base and fine-tuned LLMs of varying sizes against human eye movement and functional magnetic resonance imaging (fMRI) activity patterns during naturalistic reading³³. We show that as the model size increases from 774M to 65B, the alignment with human eye movement and fMRI activity patterns also significantly improves, adhering to a scaling law^20,21. By contrast, instruction tuning does not affect this alignment, consistent with past findings³⁴. Model analyses show that base and fine-tuned LLMs diverged the most when instructions were added to the stimuli sentences, suggesting that fine-tuned LLMs are sensitive to instructions in ways that naturalistic human language processing may not be.

Results

Model performance on the text stimuli

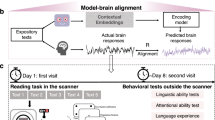
We used the publicly available Reading Brain dataset³³ from OpenNeuro to investigate the impact of scaling and instruction tuning on the alignment between LLMs and human eye movement and neural data. The dataset includes concurrent eye-tracking and fMRI data collected from 50 native English speakers (25 females, 25 males; mean age = 22.5 ± 4.1 years) as they read five English STEM articles inside an fMRI scanner. Each article contains an average of 29.6 ± 0.68 sentences, with each sentence comprising approximately 10.33 ± 0.15 words. Participants read each article sentence-by-sentence in a self-paced manner, pressing a response button to advance to the next sentence. We regressed the self-attention of base and fine-tuned LLMs of varying sizes against the eye movement and functional fMRI activity patterns of each sentence (refer to Fig. 1 for the experimental procedure and the analyses pipeline). The LLMs employed for our study include all GPT-2 models (base, medium, large, xlarge), four different sizes of LLaMA (7B, 13B, 30B and 65B), two fine-tuned versions of LLaMA (Alpaca and Vicuna) in 7B and 13B configurations, and two other fine-tuned models Gemma-Instruct 7B and Mistral-Instruct 7B (refer to Table 1 for the detailed configurations of the LLMs).

Fig. 1: Experimental procedure of the dataset and the analyses pipeline.

a, Experiment procedure. Participants read five English articles sentence-by-sentence while inside the fMRI scanner with concurrent eye-tracking. b, LLMs of different sizes with and without fine-tuning are employed in the study. c, Analysis pipeline. The attention matrices of each layer of the LLMs for each sentence in the experimental stimuli were averaged over attention heads and aligned with eye movement and fMRI activity patterns for each sentence using ridge regression.

Table 1 Configurations of the LLMs evaluated in the study

Before comparing LLMs with human behavioral and neural patterns, we first evaluated their performance on the experimental stimuli independently. To test how much the LLMs vary in predicting the next word, we calculated the averaged next-word prediction (NWP) loss of all of the LLMs on every sentence of our stimuli. The NWP loss exhibited a trend where, for the base models, an increase in model size corresponded to a decrease in mean NWP loss; however, fine-tuned models did not improve performance on NWP for our test stimuli (see Fig. 2a and Supplementary Table 1 for the mean NWP loss for each model; Supplementary Table 2 shows the t-test statistics between all model pairs).

Fig. 2: Comparison between the attention matrices of different LLMs.

a, The mean NWP loss (y-axis) of all of the LLMs for the test stimuli (N = 148). b, J–S divergence between the attention matrices of different LLMs at each layer or quarter-layer. c, The impact of scaling and fine-tuning on LLMs’ sensitivity to instructions. Shaded regions denote s.d. d, The impact of scaling and fine-tuning on LLMs’ sensitivity to trivial patterns between words in a sentence (N = 36–80). The y-axis denotes the average R² score across model layers and error bars denote s.d. Dashed lines in a and d represent groups of LLMs of same size.

Source data

Comparison of model attentions

To examine the effect of scaling and instruction tuning on LLMs’ attention matrices, we calculated the mean Jensen–Shannon (J–S) divergence (${D}_{\rm{J-S}}$) for each pair of LLM’s attention matrices over all attention heads at each model layer. We compared only the LLaMA models and their fine-tuned variants to control for potentially confounding factors such as variations in model architecture and training data. For LLMs with the same number of layers, we computed the ${D}_{\rm{J-S}}$ layerwise. For LLMs with different numbers of layers, we averaged the attention matrices for every quarter of layers and computed the ${D}_{\rm{J-S}}$ for each quarter-layer. Figure 2b shows the results of the divergence analyses. We observed that for both the base (LLaMA) and fine-tuned models (Alpaca and Vicuna), as the model size increases, the ${D}_{\rm{J-S}}$ of model attentions linearly increases from the first quarter to the last quarter of the model layers; however, when comparing the base and fine-tuned models of the same sizes, the ${D}_{\rm{J-S}}$ of model attentions remains small across all layers for most model pairs, except for Vicuna 13B and LLaMA 13B, which exhibit significantly larger divergence, particularly in the higher layers (see Supplementary Table 3 for the detailed t-test statistics). Vicuna was fine-tuned using conversational data, incorporating multi-turn dialogues that capture a wide range of conversational contexts³⁵. As a result, it provides a more natural and context-aware dialogue experience compared to Alpaca, which was fine-tuned on instruction-following examples, leading to strong performance on single-turn tasks³⁶. This distinction may account for the greater divergence observed between Vicuna 13B and LLaMA 13B.

Sensitivity of model attention to instructions

To confirm that the fine-tuned models exhibit distinct instruction-following behaviors compared with the base models, we analyzed the sensitivity of their attention to instructions. We added two instructions before each sentence in our text stimuli: ‘Please translate this sentence into German:’ and ‘Please paraphrase this sentence:’. As a control, we introduced a noise prefix composed of five randomly sampled English words, such as ‘cigarette’, ‘first’, ‘steel’, ‘convenience’, ‘champion’. We then extracted the attention matrices for the original sentence spans and calculate the ${D}_{\rm{J-S}}$ of attentions between each model pair layerwise. Our results showed a significantly larger divergence in the attention matrices for the fine-tuned models when processing plain versus instructed texts, for both the 7B and 13B sizes. By contrast, the LLaMA models did not show sensitivity to instructions at either size. No significant difference was found for the ${D}_{\rm{J-S}}$ of attentions across all layers between the base and fine-tuned models for plain versus noise-prefixed text (see Fig. 2c and Supplementary Table 4 for the detailed t-test statistics).

Sensitivity of model attention to trivial patterns

Past studies have highlighted certain patterns in LLMs’ attention matrices, such as a tendency to focus on the first word of a sentence, the immediately preceding word³⁷, or on the word itself³⁸. We consider these tendencies ‘trivial patterns’ because these behaviors are exhibited by all LLMs. As a result, it is not relevant to the effects of scaling or fine-tuning on LLMs’ brain-encoding performance, which is the primary focus of this study. To examine how scaling and fine-tuning influence the models’ sensitivity to these trivial patterns, we constructed a binary matrix for each sentence in the test stimuli, marking cells that exhibited these trivial relationships. We then regressed each model’s attention matrix for each sentence at each layer against the corresponding trivial patterns. Our findings showed that for the LLaMA series and their fine-tuned versions, as the model size increases from 7B to 65B, the average regression score for predicting the trivial patterns across layers decreases. No significant differences were observed between the LLaMA models and their fine-tuned versions (see Fig. 2d and Supplementary Tables 5 and 6). Given that similar trivial patterns were not observed in human eye movement data, we believe they do not reflect underlying human cognitive processes. As the attention weights of larger models display fewer trivial patterns compared with smaller models, this reduced sensitivity may contribute to their greater cognitive plausibility.

Effects of scaling versus fine-tuning on model–behavior alignment

Comparisons of LLMs in NWP on our test stimuli indicate an advantage for larger models, suggesting they may achieve better alignment with both behavioral and neural data. To test this hypothesis, we first regressed the attention matrices of the LLMs against the number of regressive eye saccades for all stimuli sentences. We did not include forward saccades, not only due to the unidirectional nature of LLMs, but also because regressive saccades may carry more informative value in reading. Regressive saccades occur when readers revisit earlier text, highlighting the importance of previous words in understanding the current word³⁹—similar to how attention weights function in LLMs. We extracted the lower-triangle portions (excluding the diagonal line) of the attention matrix ${n}_{\mathrm{word}}\times {n}_{\mathrm{word}}\times {n}_{\mathrm{head}}$ from all attention heads for every sentence. The attention matrices for all sentences were concatenated to create a regressor with dimensions 7,388 × ${n}_{\rm{head}}$ for each layer, where 7,388 represents the total number of elements obtained after concatenating the lower triangles of the attention matrices across all sentences in our stimuli. For the human eye saccade data, we constructed matrices for saccade number, ${{E}_{\rm{num}}{\mathbb{\in }}{\mathbb{R}}}^{{n}_{\rm{word}}{\times }{n}_{\rm{word}}}$, for each sentence. Each cell at row l and column m in ${E}_{\mathrm{num}}$ and ${E}_{\rm{dur}}$ represents the number of eye fixation moving from the word in row l to the word in column m, respectively. We then extracted the lower-triangle parts of the matrices that mark right-to-left eye movement. Similar to the models’ attention matrices, we flattened the regressive eye saccade number matrices for all sentences and concatenated them to create 7,388-length vectors for each patient. We then performed ridge regression for each model layer, using the $7,388\times {n}_{\rm{head}}$ regressor to predict each patient’s regressive eye saccade number vectors. The final ${R}_{\mathrm{model}}^{2}$ was normalized by the ${R}_{\rm{ceiling}}^{2}$, where the ceiling model represents the mean of all patients’ regressive eye saccade number vectors.

Our findings show that for the LLaMA series, as model size increases from 7B to 65B, the regression scores also increase across layers. The GPT-2 models, which has the smallest parameter size, exhibits the lowest regression scores. By contrast, base and fine-tuned models of the same sizes exhibit no difference in their regression scores when aligned with human eye movement patterns, suggesting that scaling, rather than fine-tuning, enhances the alignment between LLMs and human reading behaviors. No significant difference was found for the regression scores of controlled models of matching sizes (see Fig. 3a and Supplementary Table 7 and Supplementary Data 1). Notably, the GPT-2 models of varying sizes did not exhibit any significant differences in the fit between these models and the eye regression patterns. This may be because the size differences among these models are not as substantial as, for example, between 7B and 65B. We further plotted the maximum regression scores from all model layers against different LLMs and the logarithmic scale of parameter size, illustrating a clear scaling law of model–behavior alignment (see Fig. 3a, right panel).

Fig. 3: Effects of scaling and fine-tuning on the alignment between LLMs and human regressive eye saccade patterns during naturalistic reading.

a, Regression results of the LLMs’ best-performing layer on the regressive eye saccade patterns and their results on a logarithmic size scale (N = 51). The bar plot denotes the mean of the normalized R² score of the model best-performing layer. Error bars denote s.d. across patients. b, Regression results of different LLMs and regressive eye saccade number patterns across experimental sections (N = 51). The x-axis denotes the five consecutive sections of the stimulus, and the y-axis denotes the normalized R² score across participants. The center lines of the boxplots denote the median; the box limits denote the 25th and 75th percentiles; whiskers extend to the most extreme data points within 1.5 times the interquartile range; and outliers beyond this range are plotted individually as dots.

Source data

Given that participants answered ten comprehension questions after reading each article, there is a possibility that their reading behavior shifted from naturalistic reading to a more focused approach aimed at solving questions as the experiment progressed. This could mean that LLMs with instruction tuning might increasingly align with human behavior later in the experiment. To test this hypothesis, we performed the same regression analyses separately for each section of the experiment. Our results revealed no significant difference in the regression scores for base and fine-tuned LLMs over time, suggesting that human reading behaviors during naturalistic reading are not influenced by the subsequent comprehension questions (see Fig. 3b). Supplementary Table 8 lists the F statistics from one-way analysis of variance (ANOVA) for each base and fine-tuned LLM across the five experimental sections.

Effects of scaling versus fine-tuning on model–brain alignment

We next conducted a ridge regression using the attention matrix ${v}_{\rm{model}}^{j}$ at each layer $j$ from each LLM to predict each voxel’s blood-oxygen-level-dependent (BOLD) vector ${V}_{\rm{B}}^{i}$ in the whole brain for each patient (refer to the ‘Alignment between LLMs and fMRI data’ section in the Methods for details). As shown in Fig. 4a, the average prediction performance across patients from the best-performing layer of each LLM increases with model size. By contrast, base and fine-tuned LLMs of the same sizes did not show differences in their average prediction performance (see Supplementary Table 9 and Supplementary Data 2). We also plotted the normalized correlation coefficients from the best-performing layer of each model on a logarithmic scale, demonstrating a clear scaling effect where larger models better explained the fMRI activity patterns during naturalistic reading. Figure 4b presents significant brain clusters identified when contrasting the prediction performance (Pearson’s r maps) of larger and smaller LLMs. The results show that larger LLMs consistently exhibited significantly more activation in a bilateral temporal-parietal network compared with their smaller counterparts. Although the effect size as measured by the Cohen’s d is larger in the left hemisphere than the right hemisphere (see Table 2). We also compared the regression scores of base and fine-tuned models of same sizes, yet no significant brain cluster has been observed.

Fig. 4: Impact of scaling and fine-tuning on the alignment between LLMs and human fMRI activity patterns during naturalistic reading.

a, Regression results of the best-performing layer of different LLMs against fMRI activity patterns and their results on a logarithmic size scale. The bar plot denotes the mean of the normalized correlation coefficients of the LLMs’ best-performing layer across patients (N = 50). Error bars denote s.d. b, Significant brain clusters from the contrast of the correlation coefficients of different LLMs with smaller and larger sizes. Dashed lines in a represent groups of LLMs of same size.

Source data

Table 2 Comparison of brain-encoding results between different model pairs

Expanding the analysis to different datasets

To verify whether our findings can generalize to a broader spectrum of human language processing, we performed the same analysis on a fMRI dataset collected while participants listened to a 20 min Chinese audiobook in the scanner. We regressed the attention weights of the base and fine-tuned LLaMA3 8B, LLaMA3 70B, LLaMA3-Instruct 8B and LLaMA3-Instruct 70B models against the fMRI data matrices at the paragraph level (refer to ‘Additional results from fMRI data of naturalistic listening’ in Supplementary Section 2). We used the LLaMA3 models for their better performance in Chinese. This analysis extends beyond sentence-level comprehension to discourse-level processing and introduces both a different modality (listening versus reading) and a different language (Chinese versus English). Our findings remained consistent: model scaling had a significant effect on model–brain alignment, while fine-tuned and base models of the same size showed no difference in brain-encoding performance (see Supplementary Fig. 1a and Supplementary Tables 10–12).

We also regressed the predictions from the base and fine-tuned LLaMA3 8B and LLaMA3 70B models against the fMRI data collected while participants answered multiple-choice comprehension questions about the preceding listening session (refer to ‘Additional results from fMRI data of naturalistic listening’ in Supplementary Section 2). Our results showed LLaMA3 8B exhibited a significantly higher regression score (mean = 0.219 ± 0.004) compared with LLaMA3-Instruct 8B (mean = 0.211 ± 0.004, t = 58.073, P = 7.47 × 10⁻⁷); LLaMA3-Instruct 70B showed a higher mean regression score (mean = 0.259 ± 0.005) across participants compared to the LLaMA3 70B (mean = 0.243 ± 0.005, t = 80.528, P = 5.76 × 10⁻⁴), but no significant brain cluster has been found between the contrast of the two 70B models’ R² maps (see Supplementary Fig. 1b and Supplementary Tables 13–15).

Discussion

Two key factors driving the improvement of recent LLMs compared with their predecessors, such as BERT (ref. ¹²) and GPT-2 (ref. ¹¹), are scaling and fine-tuning. Although past work suggests that the scaling law also applies to LLMs’ brain-encoding performance with extensive fMRI data during naturalistic language comprehension^20,40, it is still unclear how effective scaling is for model–brain alignment when dealing with shorter texts. As GPT-2 has been shown to predict more variance relative to the ceiling in some neuroimaging datasets^41,42—where the ceiling is defined as the mean of the neural responses from all participants in these datasets—smaller models may have reached their performance limits on next-word prediction for simpler texts. Moreover, current LLMs far exceed human capabilities in terms of data input during training and memory resources for accessing contextual information during comprehension. It has been argued that larger models increasingly diverge from human language-processing patterns²⁵. In this study we evaluated the alignment between LLMs of varying sizes and human eye movement and fMRI activity patterns during naturalistic reading. Despite using experimental stimuli and fMRI data that are much smaller in size compared with previous studies²⁰, we observed consistent improvements in alignment as the model size increased from 774M to 65B, without any apparent diminishing returns. Similar results have also been reported for electrocorticography data during naturalistic listening²¹. This suggests that the scaling law of model–brain alignment holds even with shorter text stimuli and smaller fMRI data.

Although the largest LLMs today still do not match the human brain in terms of synapse count, training and operating such large LLMs pose significant computational challenges, especially in academic settings with limited computing resources. Fine-tuning LLMs with instructions offers a viable approach to enhance the performance and usability of pre-trained language models without expanding their size^26,27,28,29. Ouyang et al.²⁷ noted that the typical next-token prediction training objective of language models often diverges from user intentions, leading to outputs that are less aligned with user preferences. Although there is ample evidence that human language processing involves next-word prediction^2,8,43, research also showed that fine-tuning language models for tasks such as narrative summarization can enhance model–brain alignment, especially in understanding characters, emotions and motions⁴⁴. It is possible that instruction-following plays a role in human language learning and that fine-tuned models might contain richer discourse and pragmatic information beyond basic meaning representation.

However, our regression results with human behavioral and neural patterns did not reveal any significant improvement in alignment for fine-tuned LLMs compared with base models of identical size. We examined whether fine-tuned models exhibited better alignment to eye movement patterns as participants completed more comprehension questions over time, but no significant differences were found in the regression scores. We also examined predictions from the fine-tuned LLaMA3 7B and LLaMA3 70B models against the fMRI data collected while participants answered multiple-choice comprehension questions about the preceding listening session, yet we still did not find a consistent advantage of the fine-tuned model on model–brain alignment. Our results therefore highlight the greater impact of scaling over fine-tuning in model–brain alignment, contributing to the existing literature on the scaling law in brain-encoding performance^4,20,21. Similar findings have been reported by Kuribayashi et al.³⁴, who demonstrated that instruction-tuned and prompted LLMs do not provide better estimates than base LLMs when simulating human reading behavior. However, it is possible that LLMs using different fine-tuning techniques may exhibit a positive effect. Here we examined two additional fine-tuned models (Gemma-Instruct and Mistral-Instruct) and did not find any improvement over the base LLMs, but Kuribayashi et al.³⁴ reported that Falcon instruction-tuned LLMs, which use a supervised tuning approach different from reinforcement learning from human feedback, showed a moderate positive effect in simulating human reading data. Future research should further explore the impact of fine-tuning techniques on the cognitive plausibility of instruction tuning.

Our findings that scaling has a larger impact than fine-tuning on model–behavior and model–brain alignments are particularly relevant in the current landscape, where reasoning LLMs such as DeepSeek-R1 (ref. ³²) exhhibited superior performance with similar or fewer activated parameters compared with existing open-source LLMs. We acknowledge that caution is needed when interpreting these results. As instruction tuning effectively realigned the model weights in response to instructions, these realigned model weights may better fit brain activity patterns where participants performed tasks aligned with the instruction-following nature of the fine-tuning process. However, due to the lack of such openly available neuroimaging datasets, we cannot evaluated the fine-tuned LLMs on these task-specific brain data. This gap leaves the potential for future research to explore the impact of instruction tuning on model–brain alignment in controlled experimental settings.

Methods

The eye-tracking and fMRI dataset used in the analysis is publicly available³³ and does not contain sensitive content such as personal information. The adaptation and use of the dataset are conducted in accordance with its license. The model states of LLMs are used solely for research purposes, aligning with their intended use.

Eye-tracking and fMRI data

We used the openly available Reading Brain dataset³³ on OpenNeuro. This dataset includes concurrent eye-tracking and fMRI data collected from 52 native English speakers (27 females, mean age = 22.8 ± 4.7 years) as they read five English STEM articles inside an fMRI scanner. One participant’s (patient ID 21) eye-tracking data was excluded due to incomplete recording, resulting in a final sample of 51 participants (26 females; mean age = 22.6 ± 4.0 years) for the eye-tracking analysis. Two participants’ (patient IDs 21 and 52) fMRI data were excluded due to preprocessing errors, leaving 50 participants (25 females; mean age = 22.5 ± 4.1 years) for the fMRI analysis. The articles were constructed using materials from established sources such as the NASA science website, the GPS.gov website (http://www.gps.gov), and Wikipedia. These texts underwent an extensive revision process to ensure content accuracy and stylistic consistency⁴⁵. Each article contains an average of 29.6 ± 0.68 sentences, with each sentence comprising approximately 10.33 ± 0.15 words. Participants read each article sentence-by-sentence in a self-paced manner, pressing a response button to advance to the next sentence. If there was no response within 8,000 ms, the screen would automatically progress to the next sentence. The sequence in which the five texts were presented was randomized across participants to control for potential order effects. At the end of each article, participants answered ten multiple-choice questions to ensure their comprehension. The whole experiment, including preparation time, lasted for about 1 h (see Fig. 1a for the experimental procedure). The study was approved by the Pennsylvania State University Institutional Review Board (CR00003867). All participants provided written informed consent before the experiment and were compensated for their participation.

All imaging and eye-tracking data were acquired in 3 T Siemens Magnetom Prisma Fit scanner at the Center for NMR Research at the Pennsylvania State University Hershey Medical Center in Hershey, Pennsylvania. The anatomical scans were acquired using a magnetization-prepared rapid gradient-echo pulse sequence with T1 weighted contrast (176 ascending sagittal slices with A/P phase encoding direction; voxel size = 1 mm isotropic; field of view (FOV) = 256 mm; repetition time (TR) = 1,540 ms; echo time (TE) = 2.34 ms; acquisition time = 216 s; flip angle = 9°; GRAPPA in-plane acceleration factor = 2; brain coverage is complete for cerebrum, cerebellum and brain stem). The functional scans were acquired using T2*-weighted echo planar sequence images (30 interleaved axial slices with A/P phase encoding direction; voxel size = 3 mm × 3 mm × 4 mm; FOV = 240 mm; TR = 400 ms; TE = 30 ms; acquisition time varied on the speed of self-paced reading, maximal 5.1 min per run; multiband acceleration factor for parallel slice acquisition = 6; flip angle = 35°; where the brain coverage missed the top of the parietal lobe and the lower end of the cerebellum). A pair of spin echo sequence images with A/P and P/A phase encoding direction (30 axial interleaved slices; voxel size = 3 mm × 3 mm × 4 mm; FOV = 240 mm; TR = 3,000 ms; TE = 51.2 ms; flip angle = 90°) were collected to calculate distortion correction for the multiband sequences⁴⁶. fMRI preprocessing of the was conducted using fMRIPrep (v.25.0.0)⁴⁷ with all default parameters. Final resampling to Montreal Neurological Institute (MNI) space and fsaverage5 surface was performed in a single interpolation step using antsApplyTransforms and mri_vol2surf. Participants’ eye movements were simultaneously recorded using an MRI-compatible EyeLink 1,000 Plus eye tracker⁴⁸ with a sampling rate of 1,000 Hz. The eye tracker was mounted at the rear end of the scanner bore and captured eye movements via a reflective mirror positioned above the MRI’s head coil.

Large language models

To investigate the effects of scaling and instruction tuning on the alignment of LLMs with human behavior and neural data, we used the open-source LLaMA model¹⁴ and its instruction-tuned variants, Alpaca³⁶ and Vicuna³⁵, which are available in various sizes. LLaMA is a series of pre-trained causal language models trained on over one trillion publicly accessible text tokens, primarily in English. It achieved state-of-the-art performance on most LLM benchmarks¹⁴. We employed all four sizes of LLaMA: 7B, 13B, 30B and 65B. We also included all of the GPT-2 models¹¹ to represent smaller pre-trained language models (base = 124M, medium = 355M, large = 774 M, xlarge = 1.5B) as well as two other fine-tuned models, Gemma-Instruct 7B (ref. ⁴⁹) and Mistral-Instruct 7B (v.03)⁵⁰, for comparison with LLaMA 7B.

Alpaca³⁶ was fine-tuned from the 7B LLaMA model and was trained on 52K English instruction-following demonstrations generated by GPT-3 (ref. ⁵¹) using the self-instruct method⁵². We also developed a 13B version of Alpaca using the same training data and strategy. Our 13B Alpaca model achieved accuracy scores of 43.9 and 46.0 on the MMLU dataset⁵³ in zero- and one-shot settings, respectively, outperforming the original 7B model’s scores of 40.9 and 39.2. Vicuna versions 7B and 13B (ref. ³⁵) were fine-tuned from the respective 7B and 13B LLaMA models, using 70K user-shared conversations with ChatGPT¹³. This dataset includes instruction and in-context learning samples across multiple languages. Gemma-Instruct 7B was fine-tuned on a mix of synthetic and human-generated prompt-response pairs⁴⁹, and Mistral-Instruct 7B was fine-tuned on publicly available instruction datasets from the Hugging Face repository⁵⁰.

Comparison of next-word prediction loss

To examine the effects of scaling and fine-tuning model’s performance in next-word prediction, we calculated the mean NWP loss (the negative log-likelihood loss normalized by sequence lengths) of the models employed in this study on every sentence of the articles in the Reading Brain dataset. As LLMs use subword tokenization (Kudo and Richardson, 2018)⁵⁴, we aligned subwords to words by summing over the ‘to’ tokens and averaging over the ‘from’ tokens in a split word, as suggested by Clark et al.³⁸ and Manning and colleagues⁵⁵. For example, suppose the phrase ‘delicious cupcake’ is tokenized as ‘del icious cup cakes’, the attention score from ‘cupcake’ to ‘delicious’ is the sum of the attention scores from ‘del’ to ‘cup’, and ‘cake’ and ‘icious’ to ‘cup’ and ‘cake’, divided by two as there are two ‘to’ tokens (’cup’ and ‘cake’). We also removed the special tokens ‘<s>’ from the sentence beginnings. The losses for all sentences were z-scored model-wise and the contrasts of the z-scored losses for two models (for example, LLaMA 7B versus Alpaca 7B) were tested using a two-sample two-tailed related t-test. The false discovery rate (FDR) was applied to correct for multiple comparisons across layers.

Comparison of model attentions

The self-attention matrices of different LLMs given the same input were compared using their mean Jensen–Shannon (J–S) divergence across all layers. For every sentence in our stimuli, we extracted the attention matrices A and B from one attention head and one layer of two target LLMs $(A,B{\mathbb{\in }}{\mathbb{R}}^{{n}_{\rm{word}}{\times }{n}_{\rm{word}}})$, and their J–S divergence ${D}_{\rm{J-S}}(A,B)$ is computed as ${D}_{\rm{J-S}}\left(A,B\right)=\frac{1}{2}{\sum}_{i=1}^{{n}_{\rm{word}}}\left[{D}_{\rm{K-L}}\left({A}_{i}\parallel {B}_{i}\right)+{D}_{\rm{K-L}}\left({B}_{i}\parallel {A}_{i}\right)\right]$, where ${A}_{i}$ and ${B}_{i}$ are the ith rows in the two matrices and ${D}_{\rm{K-L}}$ is the Kullback–Leibler (K–L) divergence⁵⁶. The attention matrices were normalized such that each row sums to one, and the final ${D}_{\rm{J-S}}$ for each layer was averaged across attention heads. We aligned subword tokenization to words using the previously described methods for calculating NWP loss. For models with different numbers of layers, we divided their layers into four quarters and averaged the ${D}_{\rm{J-S}}$ quarter-wise. We compared each model pair’s ${D}_{\rm{J-S}}$ for each layer or each quarter-layer using a two-sided two-sample related t-test with FDR correction.

Model sensitivity to instructions

We compared the models’ attention matrices for each stimuli sentence when prefixed with two instructions: ‘Please translate this sentence into German:’, and ‘Please paraphrase this sentence:’. As a control, we introduced a noise prefix composed of five randomly sampled English words, such as ‘Cigarette first steel convenience champion.’ We then extracted the attention matrices for the original sentence spans. We calculated the ${D}_{\rm{J-S}}$ between the prefixed and original sentences across different models to assess each model’s sensitivity to instructions.

Model sensitivity to trivial patterns

Past studies have highlighted certain trivial patterns in the attention matrices within a given context, such as a tendency to focus on the first word of a sentence, the immediately preceding word³⁷, or the word itself³⁸. We consider the model’s tendencies to attend to the immediately preceding or current word ‘trivial patterns’ because these behaviors are exhibited by all LLMs. As a result, it is not relevant to the effects of scaling or fine-tuning on LLMs’ brain-encoding performance, which is the primary focus of this study. To examine whether scaling and fine-tuning will change the models’ reliance on these trivial patterns, we constructed a binary matrix for each sentence in the test stimuli, marking cells that exhibit these trivial attention relationships with a 1. We then flattened the lower-triangle parts of these matrices to create trivial pattern vectors. We then performed ridge regressions using each model’s attention vectors for each sentence at each quarter-layer to predict the corresponding trivial pattern vectors. The resulting regression scores were averaged across model layers and were z-scored and assessed for statistical significance using two-tailed one-sample t-tests with FDR corrections. We subtracted these patterns from all the attention matrices of the LLMs for the following ridge regression analyses. Given that similar patterns were not observed in human eye movement data, we believe they do not reflect underlying human cognitive processes.

We also examined results based on the original attention matrices (without subtracting the trivial patterns) from each LLM and observed a similar scaling effect, with larger models exhibiting higher model–brain alignment within a bilateral temporal-parietal network; however, no significant brain clusters were observed for the contrasts between the mid-sized LLaMA pairs 13B versus 7B and 30B versus 13B (see Supplementary Fig. 2 and Supplementary Table 16 and Supplementary Data 3). This may be due to smaller and mid-sized models being more susceptible to capturing trivial patterns, leading to similar brain responses.

Alignment between LLMs and eye movement

We input each sentence into the LLMs individually, consistent with how sentences were presented separately to participants on the screen during fMRI scanning. Furthermore, regressive eye saccade information was available only at the sentence level. As our autoregressive LLMs use right-to-left self-attention, we extracted the lower-triangle portions of the attention matrix from each layer and each attention head for every sentence. These matrices were flattened and concatenated to form the attention vector ${V}_{\rm{model}}^{\;j,k}$ for all sentences at head k in layer j. We stacked these vectors along the attention heads to create a matrix ${v}_{\rm{model}}^{\;j,k}$ for the jth layer. For the human eye saccade data, we constructed matrices for saccade number ${{E}_{\rm{num}}{\mathbb{\in }}{\mathbb{R}}}^{{n}_{\rm{word}}{\times }{n}_{\rm{word}}}$, for each sentence. Each cell at row l and column m in ${E}_{\rm{num}}$ represents the number of times of eye fixation moving from the word in row l to the word in column m, respectively. We then extracted the lower-triangle parts of the matrices which marks right-to-left regression. Like the models’ attention matrices, we flattened the regressive eye saccade number matrices for all sentences and concatenated them to get the regressive eye saccade number vector ${V}_{\rm{num}}^{i}$ for each patient i. We then conducted a ridge regression using the model attention matrix ${v}_{\rm{model}}^{\,j}$ at each layer $j$ to predict each patient’s regressive eye saccade number vector. The final dimensionality of the dependent variable X is 7,388 × N_{att_head}, where 7,388 represents the length of the concatenated vector formed by flattening the lower-triangular part of the attention matrix for each sentence at each layer, and N is the number of attention heads at that layer. We did not average across attention heads to obtain a single attention matrix per sentence, as each head is known to capture distinct relationships among words in a sentence (Manning and co-workers⁵⁵). The dependent variable (y) is a 7,388-dimensional vector, where 7,388 again reflects the length of the concatenated and flattened lower-triangular part of the regressive eye saccade matrix for each sentence.

We used ridge regression instead of ordinary least squares regression as most models have 32 attention heads, with the maximum being 64. We believe that applying ridge regression is preferable to mitigate collinearity among the regressors and enhance prediction accuracy. The penalty regularization parameter was kept as the default value of 1. The final ${R}_{\rm{model}}^{2}$ was normalized by the ${R}_{\rm{ceiling}}^{2}$, where the ceiling model represents the mean of all patients’ regressive eye saccade number vectors. At the group level, the significance of the contrast of the regression performance ${R}_{\rm{model}}^{2}$ for every model pair at every layer was examined using a two-tailed one-sample related t-test, with FDR corrections for multiple comparisons across layers.

To test this hypothesis that participants’ reading behavior shifted from naturalistic reading to a more focused approach aimed at solving questions as the experiment progressed, we performed the same regression analysis separately for each section of the experiment. We then compared the regression scores of each LLM across different times using ANOVA to assess changes in model fit over the course of the experiment.

Alignment between LLMs and fMRI data

For each voxel of the fMRI data for each patient, we constructed a BOLD matrix ${B{\mathbb{\in }}{\mathbb{R}}}^{{n}_{\rm{word}}{\times }{n}_{\rm{word}}}$ for each sentence. The value at row l and column m in B represents the sum of the BOLD signals at the timepoints where the eye fixation moves from the word in row l to the word in column m. We extracted the lower-triangle parts of the B matrices (excluding the diagonal line) for all sentences and concatenated them to form the BOLD vector ${V}_{\rm{B}}^{i}$ for each voxel of each patient i. Next, we conducted a ridge regression using each patient’s regressive eye saccade vectors ${V}_{{num}}^{i}$ to predict each patient’s BOLD vector ${V}_{\rm{B}}^{i}$ at each voxel. We then performed ridge regressions using the attention matrix ${v}_{\rm{model}}^{\;j}$ at each layer j from each LLM to predict each voxel’s BOLD vector ${V}_{\rm{B}}^{i}$ in the whole brain for each patient (see Fig. 1). The dimensionality of the independent variable is 7,388 × N_{att_head}, where 7,388 represents the length of the concatenated vector formed by flattening the lower-triangular part of the attention matrix for each sentence at each layer, and N is the number of attention heads at that layer. The dependent variable (y) is a 7,388-dimensional vector, where 7,388 again reflects the length of the concatenated and flattened lower-triangular part of the BOLD response matrix for each sentence at each voxel for each patient. As we constructed the BOLD matrix for each sentence based on the regressive eye saccade patterns, each BOLD matrix of each sentence is of size N_word × N_word, its dimension matches the dimension of model’s attention matrix for each sentence.

The penalty regularization parameter for each voxel within each patient was determined using a grid search with nested cross-validation across 20 candidate regularization coefficients (log-spaced between 10 and 1,000), following previous approach³. We adopted a train–test split method with ten-fold cross-validation, using 90% of the fMRI data (133 out of 148 sentences) to fit the ridge regression models and evaluating performance by computing the correlation between the predicted and observed time courses on the remaining 10% of the data (15 out of 148 sentences). For each voxel, a P-value for the correlation coefficient (r) was obtained by permuting the predicted time course 10,000 times and comparing the observed r to the distribution of permuted r values. Significance of the r-map contrasts was assessed using cluster-based two-sample t-tests with 10,000 permutations⁵⁷. All of our analyses and visualizations were performed using custom Python codes, making heavy use of the torch (v2.2.0)⁵⁸, MNE (v.1.6.1)⁵⁹ and scipy (v1.12.0)⁶⁰ packages.

Although most past model–brain alignment studies regressed embeddings at each model layer onto voxel-wise activity time series^3,4,18,61, this method is not feasible for the current study due to the non-linear nature of reading. Note that our task is not self-paced reading at word level where each word appears on the screen sequentially, instead, we presented the whole sentence on the screen and relied on eye-tracking to identify the timepoints for each word. We cannot directly regress the embeddings for each sentence with the fMRI data because is not strictly sequential. For example, our first participant read the sentence ‘Could humans live on Mars some day’ in the following order based their eye fixations: ‘humans humans Could humans on Mars on some some day’. We could not simply input this disordered sequence into the LLM, as it would generate meaningless representations. Similarly, we cannot directly regress embeddings from the correctly ordered sentence onto the fMRI data, as the recorded neural responses correspond to the actual reading sequence, which does not follow the original sentence structure. To the best of our knowledge, no past studies have employed this approach, probably because most previous research relied on naturalistic listening or self-paced reading paradigms at the word level, which inherently enforce sequential word processing. We hope our rationale is now clearer and that future studies incorporating concurrent eye-tracking and fMRI will consider applying our methods.

Statistics and reproducibility

We analyzed openly available eye-tracking and fMRI data from 52 participants during naturalistic sentence reading, regressing model attention matrices against their eye movement and BOLD responses. One participant (patient ID 21) was excluded in eye-tracking analysis due to incomplete recording. Two participants (patient IDs 21 and 52) were excluded in fMRI analysis due to fMRI preprocessing errors. No statistical method was used to predetermine sample size. The text order was randomized across participants, and the investigators were blinded to allocation during experiments and outcome assessment.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.