Embodied visuomotor representation

Abstract

Imagine sitting at your desk, looking at objects on it. You do not know their exact distances from your eye in meters, but you can immediately reach out and touch them. Instead of an externally defined unit, your sense of distance is tied to your action’s embodiment. In contrast, conventional robotics relies on precise calibration to external units, with which vision and control processes communicate. We introduce Embodied Visuomotor Representation, a methodology for inferring distance in a unit implied by action. With it a robot without knowledge of its size, environmental scale, or strength can quickly learn to touch and clear obstacles within seconds of operation. Likewise, in simulation, an agent without knowledge of its mass or strength can successfully jump across a gap of unknown size after a few test oscillations. These behaviors mirror natural strategies observed in bees and gerbils, which also lack calibration in an external unit.

Introduction

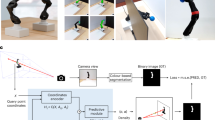
The predominant autonomy frameworks in robotics rely on calibrated 3D sensors, predefined models of the robot’s physical form, and structured representations of environmental interactions. These representations allow vision and low-level control to be abstracted as separate processes that rely on an external scale, such as the meter, to coordinate. For instance, it is common to use vision to construct a metric map scaled to the meter. Subsequently, a planning algorithm uses this geometric representation to generate a trajectory, also scaled to the meter. Finally, a pre-tuned low-level controller employs feedback to follow the metric trajectory, mapping it to motor signals. This approach is known as the sense-plan-act paradigm, and it originates from Marr’s vision framework¹. Figure 1 illustrates a block diagram of this paradigm.

Fig. 1: Architectural comparison of sense-plan-act with Embodied Visuomotor Representation.

A The classic sense-plan-act architecture used in robotics assuming visual inertial odometry (VIO) is used for state estimation. Stability depends on calibrated sensors, such as an IMU, that provide accurate knowledge of the state in an external scale. B An architecture based on Embodied Visuomotor Representation. Compared to sense-plan-act, the embodied approach includes an additional internal feedback connection (red arrow) containing the control signal u. The units of u are implied by the unknown gain b and the dynamics going from control to the state in any scale, including the meter. Embodied Visuomotor Representation leverages position-to-scale, Φ_W, obtained from vision and u to determine a state estimate $\hat{x}/b$ in the embodied scale of u. Notably, the unknown b cancels in the closed-loop system, enabling stable control without calibrated sensors. Direct methods such as Tau Theory, Direct Optical Flow Regulation, and Image Based Visual Servoing also avoid dependence on calibrated sensors by using purely visual cues (e.g., time-to-contact, optical flow, or tracked image features) for feedback. However, with few exceptions, such methods’ stability depends on tuning the control law for the expected scene distances and system velocities.

The sense-plan-act architecture allows separate teams of engineers and scientists to create equally separate vision and control algorithms tuned for particular tasks and mechanical configurations. Subsequently, alternative frameworks for vision, such as Active Vision and Animate Vision emerged^2,3,4, primarily to address the limitations of the passive role of vision in the sense-plan-act cycle. However, these frameworks consider control (action) at a high level, and so vision and control remain mostly separate fields and continue to be interfaced with external scale. This dependence leads to lengthy design-build-test cycles and, consequently, expensive systems that are available in only a few physical configurations and must be precisely manufactured. Further, it creates problems that are unobserved in biological systems. For example, it is well-known that Advanced Driver-Assistance Systems (ADAS) in modern cars, such as lane-keeping assist and collision warning, require millimeter accurate, per vehicle calibrations. Another example is the 1999 NASA Mars Climate Orbiter, whose software confused English and Metric units and crashed⁵. Finally, several billion-dollar 3D Camera and LIDAR industries aim to produce accurate 3D measurements calibrated to an external scale, and significant effort is dedicated to ensuring those calibrations do not degrade over time.

This situation is striking because biological systems do not necessarily understand distance in an external scale like the meter. Further, we know from psychology that human and other mammalian perceptual systems do not provide metric depth and shape^6,7,8,9,10. Instead, somehow, biological systems represent the world using only the signals due to their embodiment. Further, animals such as gerbils, dragonflies, and bumblebees exhibit visuomotor capabilities far in excess of robots while allowing for much broader variation in physical form and handling complex dynamics such as turbulence and muscular response^11,12,13. Similarly, humans can control augmentations to their embodiment, such as cars and airplanes, which also vary in physical form and do not maintain precise calibrations to an external scale.

One explanation is that these systems do not rely on any precise sense of distance. In support, direct approaches such as Tau Theory¹⁴, Direct Optical Flow Regulation¹⁵, and classical Image Based Visual Servoing¹⁶ offer methods to control a visuomotor system using only cues directly available from the image such as time-to-contact, optical flow, and image features. However, systems strictly limited to direct methods cannot reason about distance, a capability essential for behaviors such as the clearing maneuvers of bees¹³ and the jumping ability of gerbils¹¹. Moreover, direct methods either assume a predefined operating region for which the control system is tuned^16,17,18,19 or constrain achievable behaviors to those possible with a restricted class of feedback laws^20,21. In contrast, systems with knowledge of distance can overcome these limitations while still using direct (image space) control objectives.

Thus, a key question arises: How can a robot, without a source of external scale, use its vision and motor system to estimate a meaningful sense of distance? We refer to methods that capture this phenomenon as Embodied Visuomotor Representation and propose that its realization could drive a paradigm shift that makes robots easier to produce, more affordable, and widely accessible.

Psychologists assume humans have such representations without proposing a precise and general method for obtaining them²². Biologists argue that simple animals such as bees can develop them¹³. Computer scientists suggest that computations drive intelligence, and thus representations, as physical as the body itself²³. In particular, there is evidence that the visuomotor capabilities of animals can be attributed to well-tuned internal models closely coupled with perceptual representations. In addition to reasoning about distances, an important function of these models is prediction, which allows an animal to anticipate upcoming events, compensate for the significant time delays in their feedback loops, and, when coupled with inverse models, generate feedforward signals for other parts of the body²⁴.

However, being able to explain a phenomenon is not the same as being able to implement it. To address this, we propose Embodied Visuomotor Representation, a concrete framework that can estimate embodied, action-based distances using an architecture that couples vision and control as a single algorithm. This results in robots that can quickly learn to control their visuomotor systems without any pre-calibration to a unit of distance. In many ways, our method parallels a psychological theory of memory as embodied action due to Glenberg (who presents the idea of embodied grasping of items on a desk). Glenberg argues that the core benefit of embodied representation is that they “do not need to be mapped onto the world to become meaningful because they arise from the world” ²². Similarly, our Embodied Visuomotor Representations do not need to be pre-initalized with an external scale because they can be estimated by the robot online without sacrificing stability.

Embodied Visuomotor Representation achieves this by exchanging distance on an external scale for the unknown but embodied distance units of the acceleration affected by the motor system. As a consequence, powerful self-tuning, self-calibration, or adaptive properties emerge. At the mathematical level, the approach is similar to the Internal Model Principle, a control theoretic framework that underlies all learning-based control methods, either explicitly or implicitly²⁵. Unlike the sense-plan-act approach, which operates sequentially, the Internal Model Principle introduces a critical topological distinction: an internal feedback loop that leverages embodied motor signals to predict sensory feedback representations. This same internal feedback loop, shown in Fig. 1 enables Embodied Visuomotor Representation to integrate vision and control seamlessly, without relying on external scale, or sacrificing close-loop stability.

In what follows, we develop a general mathematical form for equality constrained Embodied Visuomotor Representation and demonstrate it on a series of experiments where uncalibrated robots gain the ability to touch, clear obstacles, and jump gaps after a few seconds of operation by using natural strategies observed in bees flying through openings and gerbils jumping gaps. For these applications, we develop specific relations between control inputs, acceleration, and observed visual features, such as lines and planes, that can be used by an uncalibrated robot to estimate state in an embodied unit. This state is used by control schemes that are guaranteed to perform a task correctly. The results suggest that Embodied Visuomotor Representation is a paradigm shift that will allow all visuomotor systems, and in particular robots, to automatically learn to control themselves and engage in lifelong adaption without relying on pre-configured 3D sensors, controllers, or 3D models that are calibrated to an external scale.

Results

First, the mathematical methodology for Embodied Visuomotor Representation will be detailed in the equality constrained case, where the results of vision and control can be set equal to each other. Next, examples of applying Embodied Visuomotor Representation to the control of a double integrator and a multi-input system with actuator dynamics are developed. Finally, algorithms that use Embodied Visuomotor Representation to allow uncalibrated robots to learn to touch, clear obstacles, and jump gaps are presented. Detailed calculations behind these applications are provided in the Methods section.

Equality constrained embodied visuomotor representation

Consider a point ${X}_{w}\in {{\mathbb{R}}}^{4}$ in homogenous coordinates corresponding to the 3D location of a point in the world coordinate frame. It is transformed by the extrinsics matrix T_cw ∈ SE(3) and projected to the homogenous pixel coordinates ${p}_{c}\in {{\mathbb{R}}}^{3}$ in the image according to an invertible intrinsics matrix $K\in {{\mathbb{R}}}^{3\times 3}$ that encodes the focal length and center pixel. The resulting well known relationship is

$${p}_{c}=\frac{1}{{X}_{c}^{z}}\left[\begin{array}{cc}K&0\end{array}\right]{T}_{cw}{X}_{w}.$$

(1)

Where ${X}_{c}^{z}$ is the third element of the product T_cwX_w. Without loss of generality, we assume that K = I.

Next, consider the warp function as known in computer vision. It has the property that

$${p}_{c}(t)=W(t,{t}_{0},{p}_{c}({t}_{0})).$$

(2)

That is, given the initial position of a world point in an image at time t₀, the warp function returns the position of the same world point in the image at another time. Note that warp functions are sometimes assumed to be linear, and this can be a good approximation when the region of interest is on a flat plane²⁶. However, in general, the warp is nonlinear because its estimation amounts to the integration of optical flow or tracking visual features such as points, lines, or patches.

Similarly to the warp function, the “flow map” from control theory, Φ_f,u, is defined as returning the solution to a system defined by f with input u as follows:

$$\begin{array}{l}\dot{x}\,=\,f(x,u),\quad x({t}_{0})\in {{\mathbb{R}}}^{n}\\ x(t)\,=\,{\Phi }_{f,u}(t,{t}_{0},x({t}_{0}))\end{array}$$

(3)

Comparing (2) to (3) reveals that W and Φ serve the same purpose. W is the solution map giving trajectories in image space, whose derivative is also called optical-flow, and Φ is the solution map for the system state, whose time derivative is driven by the system dynamics. This similarity in purpose leads to an equality constraint.

Due to W’s close relationship to position X through (1), many visual representations allow computing the position of the camera up to a characteristic scale such as the size of an object under fixation, the initial distance to a visual feature, or the baseline between two stereo cameras. We call the position to scale Φ_W and assume it can be estimated. In particular, the prominent families of computer vision algorithms, such as homography estimators, structure from motion, SLAM, and visual odometry result in such a Φ_W.

Φ_W can be related to position by a multiplicative scalar, that is the characteristic scale of the visual representation, which we call d. If the first three elements of the state are the position of a point in the camera’s frame, i.e., $x={\left[\begin{array}{cc}{X}_{c}^{T}&* \end{array}\right]}^{T}$, then Φ_W, d, and Φ_f,u are related by,

$$\begin{array}{l}{X}_{c}(t)={\Phi }_{W}(t,{t}_{0},{p}_{c}({t}_{0}))d={\Phi }_{f,u}^{1,2,3}(t,{t}_{0},x({t}_{0})),\end{array}$$

(4)

where p_c(t₀) = x^1,2(t₀)/x³(t₀) and superscripts (i.e., ${\Phi}_{f,u}^{1,2,3}$) are used to denote the individual components of a vector. Note that this formulation holds for loose and tight couplings of vision and control, where loose coupling means the vision algorithm functions independently without the knowledge of action.

The problem of visuomotor control thus becomes finding specific forms of Φ_f,u and W that possess desirable properties. In particular, we seek a transformation that reformulates the problem into a form akin to those used in linear system theory, enabling us to take advantage of the properties of linear systems. Suppose the camera is translating but not rotating. Then the world frame’s axes can be assumed to align with the camera frame’s axis. In practice, this assumption holds for durations ranging from a few to several seconds when an inexpensive Inertial Measurement Unit is mounted in the same frame as the camera sensor and is used to compensate the image so that it can be considered as coming from a camera with fixed orientation. Consequently, the rotation between the camera frame c and the world frame w can be neglected as the frames can be assumed to coincide up to a translation and so X can be used in the place of X_c.

Then Newton’s second law of motion can be applied in the fixed camera frame (within the time interval that the system can be considered rotation invariant). Let that time interval be [t₀, t₀ + T] where T ≠ 0. Then we obtain a linear system that relates the position, velocity, and acceleration components of the state X and Φ_W,

$$\begin{array}{ll}{\varPhi }_{W}(t,{t}_{0})d=X({t}_{0})+(t-{t}_{0})\dot{X}({t}_{0})+\mathop{\displaystyle\int}\nolimits_{{t}_{0}}^{t}\mathop{\displaystyle\int}\nolimits_{{t}_{0}}^{\sigma }{f}_{mech}(X({\sigma }_{2}),\dot{X}({\sigma }_{2}),{x}_{act}({\sigma }_{2}),u({\sigma }_{2}),\theta )d{\sigma }_{2}d\sigma .\end{array}$$

(5)

Here f_mech encapsulates the mechanical dynamics due to forces exerted by actuators, θ is a set of mechanical parameters (arm lengths, mass, etc.) that can be considered constant, $\dot{X}$ is the time derivative of X, and x_act is the state of the actuator dynamics. We encapsulate the actuator dynamics as a separate system

$${\dot{x}}_{act}(t)={f}_{act}({x}_{act}(t),u(t),{\theta }_{act}),$$

(6)

where θ_act are the constant parameters of the actuators.

Consider this visuomotor representation as known by an embodied agent without calibration to an external scale. Then X is the robot’s 3D position relative to the point of interest in an unknown unit, d is the characteristic scale of vision in the unknown unit, Φ_W is the unitless estimate of the position due to vision, θ and θ_act are the constant parameters of the mechanical system and the actuators in unknown units. Finally, x_act and u are the state of the actuators in unknown units.

The only quantities known in general by an uncalibrated embodied agent system are then Φ_W and u. But, because Φ_W is unitless, if the embodiment attempts to estimate X, d, θ, and θ_act so that (5) and (6) hold at all times, the units of the estimated quantities must be implicitly determined by u. For example, it can be seen that the distance units of X are determined by the distance units defined by the acceleration, that is, a distance unit over seconds squared, whose magnitude is determined from the embodied signal u transformed into acceleration by the system’s f_act and f_mech. In other words, the magnitude of X, $\dot{X}$, and d is determined by the magnitude of the the action u and thus their units are implied by u.

Consequently, the general path for employing Embodied Visuomotor Representation involves the following steps:

• Define a model that represents the physical dynamics of the agent. Both classical and learning-based models can be used.

• Ensure all quantities in the model arising from physical processes are unit-free or up to scale. For example, if gravity is to be modeled, it can be assumed the effect is non-zero, but the magnitude must not be assumed.

• Choose a visual representation Φ_W where the characteristic scale is related to a quantity of interest. For instance, in a grasping task, it may be advantageous to choose Φ_W so that d corresponds to the object’s size. Similarly, d might be the initial distance to a tracked feature, line, or object in a navigation task.

• Define a constraint between the unknowns d, X, $\dot{X}$, θ, θ_act, and x_act that enables a unique and task-relevant representation to be estimated. In what follows, we give two specific formulations.

• Construct an estimator for the chosen representation of d, X, $\dot{X}$, θ, θ_act, and x_act and incorporate these estimates into the task execution.

Closed loop control with embodied visuomotor representation

In what follows, we give two specific examples of constructing an estimator and using the resulting state for closed-loop control. In the first example, distance is estimated in units of action for a single input, single output system. In the second example, the multiple input case is considered. In that case, distance is most directly available in multiples of the characteristic scale of vision but can easily be converted to the units of action of any of the inputs. In both cases, stable closed-loop control is a consequence of the embodied representation.

For each example, we begin by constructing a model, a sliding window estimator, and a closed-loop controller which will have guaranteed stability under mild assumptions. The approach is a form of indirect-adaptive control because, first, a forward model is identified using our framework. Then, a controller is synthesized from that model²⁷.

The simplest system that can be represented in the framework of Embodied Visuomotor Representation is a robot moving along the optical axis while fixating on a nearby object. The dynamics are assumed to be that of a double integrator and the image provides the position up to the characteristic scale of vision. This system was also considered in ref. ²⁸, however, the exposition was limited. The system is given by

$$\dot{x} = \underbrace{\left[\begin{array}{ll} 0 & 1 \\ 0 & 0\end{array}\right]}_{A}x + \left[\begin{array}{l} 0 \\ b\end{array}\right] u$$

(7)

$${\Phi }_{W}(t,{t}_{0})d={x}_{1}(t).$$

(8)

Here, the observation (output) is Φ_W, and it is linearly related to the state x₁ through the unknown d. b is the unknown gain between control effort and acceleration in an external scale, such as meters per second squared. b implicitly depends on both the strength of the embodied agent’s actuators and the mass of the embodiment itself. Dimensionality analysis reveals that b is simply the unknown conversion factor between the embodied scale implied by u and the external scale. Finally, the system is observable as long as d ≠ 0. That is, the visual representation’s characteristic scale, such as the initial distance to a visual feature, size of a patch, or the baseline between two stereo cameras, is non-zero.

A sliding window estimator that considers Φ_W, and u to be known over the interval [t₀, t₀ + T], T ≠ 0 results in the problem

$$\mathop{\min }\limits_{d,x({t}_{0}),b}\mathop{\int}\nolimits_{{t}_{0}}^{{t}_{0}+T}{\left({\Phi }_{W}(t,{t}_{0})d-{x}_{1}({t}_{0})-(t-{t}_{0}){x}_{2}({t}_{0})-b\mathop{\int}\nolimits_{{t}_{0}}^{t}\mathop{\int}\nolimits_{{t}_{0}}^{\sigma }u({\sigma }_{2})d{\sigma }_{2}d\sigma \right)}^{2}dt,$$

(9)

which cannot be solved uniquely without additional constraints because a trivial solution can be realized by allowing all optimized variables to equal zero. However, dividing by b, the unknown conversion factor between external scale and embodied scale, reveals a problem that can be solved as long as acceleration is non-zero for some period during the interval [t₀, t₀ + T]

$$\mathop{\min }\limits_{\frac{\left[d,x({t}_{0})\right]}{b}}\mathop{\int}\nolimits_{{t}_{0}}^{{t}_{0}+T}{\left({\Phi }_{W}(t,{t}_{0})\frac{d}{b}-\frac{{x}_{1}({t}_{0})}{b}-(t-{t}_{0})\frac{{x}_{2}({t}_{0})}{b}-\mathop{\int}\nolimits_{{t}_{0}}^{t}\mathop{\int}\nolimits_{{t}_{0}}^{\sigma }u({\sigma }_{2})d{\sigma }_{2}d\sigma \right)}^{2}dt.$$

(10)

Since b is simply a conversion factor between units, we see that the lumped quantities d/b, x₁(t₀)/b, and x₂(t₀)/b are traditional state estimates but in the embodied units of u. Thus, we see that an embodied agent can naturally estimate state in an embodied scale by comparing what is observed with the accelerations effected through action.

In practical applications, Φ_W will be noisy because it is estimated using an image made out of discrete pixels. Even if this noise is zero mean, Eq. (10) results in a biased estimator because it uses Φ_W as an independent variable. An unbiased estimator can be realized by dividing by d/b, resulting in the problem,

$$\mathop{\min }\limits_{\frac{\left[b,x({t}_{0})\right]}{d}}\mathop{\int}\nolimits_{{t}_{0}}^{{t}_{0}+T}{\left({\Phi }_{W}(t,{t}_{0})-\frac{{x}_{1}({t}_{0})}{d}-(t-{t}_{0})\frac{{x}_{2}({t}_{0})}{d}-\frac{b}{d}\mathop{\int}\nolimits_{{t}_{0}}^{t}\mathop{\int}\nolimits_{{t}_{0}}^{\sigma }u({\sigma }_{2})d{\sigma }_{2}d\sigma \right)}^{2}dt.$$

(11)

In the new problem, Φ_W is the dependent variable because it is no longer multiplied with one of the optimized variables. Then, because the problem is linear least squares, if Φ_W is corrupted with zero mean noise, the parameter estimates will remain unbiased. On the other hand, the estimated parameters have changed. The state x is now estimated in multiples of d instead of the desired multiples of b. Further, only the reciprocal of the d/b is estimated. These estimates can be transformed back to the desired quantities with division, which will result in some bias since division does not commute with expectation. However, unlike when using Eq. (10), techniques that increase the accuracy of estimates, such as taking more measurements, will increase the accuracy of the transformed estimates. A detailed explanation is provided in the Supplemental Material.

The solution to either formulation is unique as long as the acceleration, u, is non-zero for a finite period within the sliding window. A detailed proof is given in the Supplemental Material.

Then if the control law u = K(x/b) is applied, the closed loop system dynamics become

$$\dot{x}=Ax-\left[\begin{array}{c}0\\ b\end{array}\right]K\frac{x}{b}=Ax-\left[\begin{array}{c}0\\ 1\end{array}\right]Kx.$$

(12)

Because the unknown gain b cancels out in the rightmost expression, we can say that the closed loop behavior of the system is invariant to the value of b. That is, while b is not known individually, and is only a term in the known ratios x/b and d/b, it will not affect the systems behavior. Thus, the control gains K can be chosen as if b = 1 and x itself is known. This is despite the fact that b appears individually in the dynamics model. Similarly, the characteristic scale of vision, d, does not affect the closed loop behavior despite remaining unknown.

Further, consider that once d/b is known, Φ_W(t)d/b provides a direct estimate of x₁(t) in the embodied unit. Thus, in theory, it is sufficient to solve (10) or (11) once, and subsequently treat control of (7) as a traditional output feedback problem. Finally, since the closed loop system is linear, time-invariant, controllable, and has known parameters, feedback gains K always exist and can be chosen to ensure global closed-loop stability. In particular, since this system corresponds to a PD controller applied to a double integrator, the stabilizing gains can be easily chosen.

Next, the previous example is extended to the case that the robot does not know its actuator dynamics. Typically, actuator dynamics produce a “lagging” response to control inputs. For example, they could take the form of an unknown delay or low-pass filter between the control input and its effect on acceleration. Additionally, the full 3D motion is considered.

Suppose the dynamics are fully linear, the robot can move in three dimensions, there is an unknown, stable linear system between control inputs and the 3D acceleration, and a visual process estimates the position of the robot up to the characteristic scale of vision. Then, the dynamics can be expressed as

$$\begin{array}{l}\dot{x}=\frac{d}{dt}\left[\begin{array}{c}X\\ \dot{X}\\ {x}_{act}\end{array}\right]=\left[\begin{array}{c}\dot{X}\\ Bu+{C}_{act}{x}_{act}\\ {A}_{act}{x}_{act}+{B}_{act}u\end{array}\right]\\ {\Phi }_{W}(t,{t}_{0})d=X\end{array}$$

(13)

Estimating the unknown parameters B, A_act, B_act, and C_act simplifies to satisfying the following equality constraint

$$\begin{array}{rcl}{\Phi }_{W}(t,{t}_{0})d&=&X({t}_{0})+t\dot{X}({t}_{0})\\ &&+\mathop{\displaystyle\int}\nolimits_{{t}_{0}}^{t}\mathop{\displaystyle\int}\nolimits_{{t}_{0}}^{\sigma }Bu({\sigma }_{2})+{C}_{act}\left[{\Phi }_{{A}_{act}}({\sigma }_{2},{t}_{0}){x}_{act}({t}_{0})+\mathop{\displaystyle\int}\nolimits_{{t}_{0}}^{{\sigma }_{2}}{\Phi }_{{A}_{act}}(\tau ,{t}_{0}){B}_{act}u(\tau )d\tau \right]d{\sigma }_{2}d\sigma \end{array}$$

(14)

Suppose that the actuator dynamics expressed inside the double integral are BIBO stable. Then, the impulse responses relating the inputs of the actuator’s system to this term go to zero exponentially fast. Consequently, it is sufficient in many practical applications to approximate these dynamics as a finite length convolution with the input. Then, we get the following equality constraint where G is a matrix value signal whose i,j’th entry is to be convolved with the j’th element of u to get its effect on the i’th state.

$${\Phi }_{W}(t,{t}_{0})d=X({t}_{0})+(t-{t}_{0})\dot{X}({t}_{0})+\mathop{\int}\nolimits_{{t}_{0}}^{t}\mathop{\int}\nolimits_{{t}_{0}}^{\sigma }(G* u)({\sigma }_{2})d{\sigma }_{2}d\sigma .$$

(15)

As with the previous example considering a double integrator, any problem based on this constraint has no unique solution because every term has an unknown multiplier. However, unlike the double integrator, we cannot simply divide by b to get a problem with a unique solution. Instead, we can divide by the scalar d to get a linear constraint that will be uniquely satisfied given sufficient excitation by u. A detailed proof is given in the Supplemental Material. Consider the sliding window estimator again. The full problem to be solved is

$$\mathop{\min }\limits_{\frac{[X({t}_{0}),\dot{X}({t}_{0}),G]}{d}}\mathop{\int}\nolimits_{{t}_{0}}^{{t}_{0}+T}{\left[\Phi (t,{t}_{0})-\frac{X({t}_{0})}{d}-(t-{t}_{0})\frac{\dot{X}({t}_{0})}{d}-\left(\frac{G}{d}* \mathop{\int}\nolimits_{{t}_{0}}^{{{\cdot}}}\mathop{\int}\nolimits_{{t}_{0}}^{\sigma }u(\sigma )d{\sigma }_{2}d\sigma d\sigma \right)(t)\right]}^{2}dt,$$

(16)

where the fact that the convolution with G can be brought out of the double integral has been used, and ⋅ at the top of the double integrator is the placeholder for the variable that will be convolved over.

In this case, the position of the agent is recovered in multiples of the characteristic scale of vision due to division by d. However, the units of distance can still be recovered in the embodied units of acceleration by dividing all estimated parameters by the gain of one of the actuator’s impulse responses at a particular frequency. In particular, if the DC gain of the actuator dynamics is non-zero, we can consider that

$$\left(\frac{X({t}_{0})}{d}\right)/\left(\frac{\mathop{\int}\nolimits_{0}^{\infty }{g}_{ij}(t)dt}{d}\right)=\frac{X({t}_{0})}{\mathop{\int}\nolimits_{0}^{\infty }{g}_{ij}(t)dt},$$

(17)

Where g_ij is the i, j entry of G and $\mathop{\int}\nolimits_{0}^{\infty }{g}_{ij}(t)dt$ is its scalar valued DC gain. Thus, distance in units of action is still available. Further, the distance in the units of action is different for each input, and the conversion factor between all the embodied scales is known to the agent. So, it is free to switch between units as may be convenient.

If the actuator dynamics are minimum phase, and thus an inverse impulse response G⁻¹ exists, then since G/d is known, dG⁻¹ can be determined. It is then straightforward to synthesize a reference tracking controller. Consider the control scheme given by

$$\begin{array}{l}e\,:= \,\left[\begin{array}{c}{X}_{ref}\\ {\dot{X}}_{ref}\end{array}\right]-\left[\begin{array}{c}X/d\\ \dot{X}/d\end{array}\right]\\ u\,:= \,d{G}^{-1}* Ke.\end{array}$$

(18)

Then the closed-loop dynamics are

$$\ddot{X}=G* u=G* (d{G}^{-1}* Ke)=K\left(d\left[\begin{array}{c}{X}_{ref}\\ {\dot{X}}_{ref}\end{array}\right]-\left[\begin{array}{c}X\\ \dot{X}\end{array}\right]\right),$$

(19)

where the fact that the systems G and dG⁻¹ cancel (by definition) except for the scale d has been used.

The resulting closed loop’s stability does not depend on the magnitude of the embodied scale or any external scale. Instead, the reference point is in multiples of vision’s characteristic scale, which could be the size of a tracked object, the baseline between a stereo pair, or the initial distance to an object. As before, it is straightforward to convert to the embodied units of action because d can be replaced with any actuators DC gain, $\mathop{\int}\nolimits_{0}^{\infty }{g}_{ij}(t)dt$. In that case, the closed loop dynamics become

$$\ddot{X}=K\left(\mathop{\int}\nolimits_{0}^{\infty }{g}_{ij}(t)dt\left[\begin{array}{c}{X}_{ref}\\ {\dot{X}}_{ref}\end{array}\right]-\left[\begin{array}{c}X\\ \dot{X}\end{array}\right]\right).$$

(20)

As with (12), the systems in (19) and (20) are linear, time-invariant, controllable, and all parameters are known. Thus, gains K always exist and can be selected to ensure closed loop stability ²⁹.

In practice, the inverse of the actuator dynamics should not be used in the control law because the cancellation of dynamics typically results in a control law with poor performance and robustness. Regardless, we consider the inverse dynamics above so that the final close loop control law clearly illustrates the units being employed by Embodied Visuomotor Representation. However, in general, it is now straightforward to design traditional control laws using the identified parameters. In particular, the jumping experiments avoid using inverse dynamics.

We now turn to three basic robotic capabilities: touching, clearing, and jumping, which can be accomplished by uncalibrated robots that use Embodied Visuomotor Representation.

Uncalibrated touching

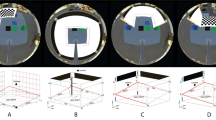
Consider an uncalibrated robot with a monocular camera that must touch a target object in front of it. The contact will occur at a non-zero speed because the robot does not know its body size and thus cannot come to a stop just as it reaches the target. Further, the robot also does not know the strength of its actuators, the size of the target, or the size of anything else in the world. In what follows, we carefully apply the five steps for using Embodied Visuomotor Representation to design an algorithm for this problem. Figure 2 outlines the resulting uncalibrated touching procedure visually.

Fig. 2: Overview of the procedure for uncalibrated touching using Embodied Visual Representation.

A The robot oscillates by applying an open loop control input $\sin (t)$ while measuring the size of the touching target in the visual field as Φ_W. B Embodied Visuomotor Representation uses the control input and visual information to estimate x₁/b and d/b, which are the size of and distance to the target in the embodied unit. C With the size of the target known, it is possible to approach the target at a desired safe contact speed, v_s, using closed-loop control. In the closed loop, the effect of the unknown embodied gain b cancels except for its interaction with the setpoint v_s. D Upon making contact with the target, the distance between the camera and the target is the size of the body w_l in the embodied unit. E The procedure can be repeated, by approaching from different directions, to approximate the convex hull of the robot.

Starting with the first step, we assume a double integrator system as in (7), that is the robot accelerates along the optical axis according to ${\ddot{x}}_{1}=bu$ where ${\ddot{x}}_{1}$ is acceleration in meters per second squared and u is a three-dimensional control input. Upon inspection, we see that the only quantity defined by the world, b, does not have a predetermined unit. Thus, the second step is complete.

To complete the third step, assume the robot is facing a planar target. The reciprocal of the target’s width in normalized pixels within the visual field can then be used as Φ_W. That is, Φ_W = Z/d, where Φ_W’s characteristic scale is the unknown width of the target, d. It should be noted that this simple visual representation is valid only for flat objects that are coplanar with the camera, making it and following experiment pedagogical in nature. However, in general, (4) demonstrates that Embodied Visuomotor Representation is agnostic to the particular visual representation or algorithm used so long as it provides position up to a characteristic scale.

The fourth step, which involves establishing a constraint between vision and control that includes the unknowns, is accomplished by recalling Eq. (8) and dividing through by b. This results in the unknowns x(t₀)/b and d/b, which correspond to the initial conditions, x(t₀), and the characteristic scale of vision, d, in the embodied units of u. Once this is done, the fifth step can be applied: estimating the unknowns using Eq. (11).

The unique estimate of d/b obtained from this formulation allows the distance between the robot and the target to be estimated at all times via the relation ${\hat{x}}_{1}/b={\Phi }_{W}(t)(d/b)$. This can be combined with the target’s position in the image to recover the target’s 3D position. Closed-loop control can then use this distance to center the robot on and approach the target along a direction in the camera frame at a constant speed, because in the closed loop, the remaining unknown, b, cancels out, as shown in Eq. (12).

To ensure safe contact without damaging the robot, the designer must specify a safe contact speed, v_s, in embodied units. This limitation mirrors biological systems, where animals often create safe environments for their young to prevent injury, ensuring that the maximum achievable speed does not cause harm. It is important to note that the robot cannot stop just before touching the target, as it does not know how where its body is relative to the camera.

In practice, the robot’s designer or a higher-level cognitive process can set v_s based on multiples of the target’s dimensions or by considering multiples of the maximum force (in embodied units) that the robot should experience upon collision. An example of this calculation is provided in the Supplemental Material. Specifically, if the designer knows the size of the target in meters and a safe speed in meters per second, they can convert the safe speed to multiples of the target’s size per second, which the robot can subsequently interpret in embodied units.

Subsequently, contact with the object can be detected either with a touch sensor or by using the visual position estimate Φ_Wd to detect that the robot has stopped getting closer to the target. Thus, the robot can approach a target at a constant safe speed in a given direction in the camera field and touch it, regardless of the embodiment and environment’s specifications.

It should be noted that it was assumed that the open-loop oscillations would not cause the robot to come in contact with the obstacles. However, this is not strictly necessary. Eq. (11) has a unique solution given any acceleration of arbitrarily small duration. Thus, in theory, it is always possible to estimate the unknowns and switch to closed loop control prior to reaching the target.

Figure 2 visually outlines the uncalibrated touching procedure. Movie 1 details the experimental procedure for both uncalibrated touching and clearing. Figure 3 shows the estimated width, distance, and velocity over time during the measurement phase of uncalibrated touching for three different control input gains, b = 0.5, 1, and 2. Since the conversion from embodied units to meters is determined by b, the embodied estimate is expected to align with the ground truth only when b = 1. Similarly, Fig. 4 shows estimated distances and control inputs as the robot approaches and touches the target while using the same three ground truth values for b. The approach velocity was fixed to the same embodied value for each trial, meaning when b = 0.5, the robot takes twice as long to reach the target compared to b = 1. Whereas when b = 2, it takes half the time. Alternatively, the methods discussed above for specifying a safe contact speed allow the robot’s designer to ensure a consistent approach speed regardless of b.

Fig. 3: Experimental data and estimated signals from the target measurement phase of uncalibrated touching for three different values of the control gain b.

The first, second, and third rows of plots show the estimated target width, distance from the target, and velocity as estimated by the sliding window formulation in Eq. (12). The bottom two rows show the inputs to the sliding window formulation, that is, the control signal u and the width of the target in the visual field in normalized pixel coordinates Φ_W. As expected, when b = 1.0, the embodied estimates are closely aligned with the ground truth distances measured in meters. However, when b = 0.5 or b = 2.0, the embodied estimates are twice as much and half, respectively, of the ground truth value in meters.

Fig. 4: Experimental data and estimated signals from the target approach phase of uncalibrated touching for three different values of the control gain b.

The methods take different amounts of time to reach the target because the approach speed was specified as a fixed value in the embodied unit while b was varied. Note that the closed loop behavior remains stable and qualitatively similar despite the control input gain varying by a factor of 4. As shown by Eq. (12) this is expected.

Additionally, two experiments were conducted to validate the accuracy of estimated embodied representations. In the first, the uncalibrated touching procedure was performed with the robot starting from an initial distance of 50, 75, 100, 150, 225, and 350 cm away from a 15 centimeter wide touch target. At each distance, the input gain b was set to 0.5, 1, and 2. When b = 1 and b = 2, the minimum initial distances were 75 cm and 150 cm, respectively, to avoid hitting the target during the open loop oscillation. In total, 70 trials were run. 350 cm was the maximum testable distance; beyond this, the procedure failed due to the limited width of the target in the field of view (<6 pixels). Figure 5 shows the resulting embodied target widths and embodied robot widths compared to ground truth. Table 1 quantifies the error in Fig. 5 as a percentage of the ground truth target and body width.

Fig. 5: Measured width of touching target and width of the robot’s body, in embodied units, as the initial distance from the target and the control input gain b are varied.

Error bars show mean, minimum, and maximum value over five trials.

Table 1 Mean absolute error in percent of the estimated target width (15 cm) and the observable robot body’s width (19.1 cm) as the initial distance from the target is increased

In the second experiment, the uncalibrated touching procedure was performed with the robot initially 150 cm from targets of ground truth width 3.75, 7.5, and 15 cm and input gain b equal to 0.5, 1, and 2. Five trials of each parameter combination were run, resulting in a total of 45 trials. Figure 6 shows the resulting embodied target widths and embodied robot widths compared to ground truth. The ground truth widths result from converting the width of the robot in meters minus the turning radius of the pan-tilt mount to the embodied distance. Table 2 quantifies the error in Fig. 6 as a percentage of the ground truth target and body width.

Fig. 6

Measured width of touching target and width of the robot’s body, in embodied units, as the width of the target and the control input gain b are varied. Error bars show mean, minimum, and maximum value over five trials.

Table 2 Mean absolute error in percent of the estimated touch target or opening width and observable robot body’s width (19.1 cm) as the target or opening width is varied

In Figures 5, 6, the blue ground truth lines result from converting the ground truth width of the target and width of the robot to meters. The plotted ground truth robot width was reduced by the turning radius of the pan-tilt mount that the camera is mounted on in embodied units.

During all trials, the robot applied an open-loop 1/3 Hz acceleration signal, resulting in positional oscillation with 25 cm of amplitude when b = 1. The sliding window estimator was configured to consider 3 seconds of data.

Uncalibrated clearing

Once a robot can touch, it can quickly determine if it can clear obstacles of initially unknown size prior to reaching them as shown in Fig. 7 and in Movie 1. In the following, the first four steps of and the estimation portion of step five are the same as in the touching application. Thus, we focus on the last portion of the fifth step, which is applying quantities estimated via Embodied Visuomotor Representation in the task.

Fig. 7: Overview of the procedure for clearing obstacles using embodied visual representation.

A The robot oscillates by applying the control input $\sin (t)$ in open loop input while using the size of the opening between two obstacles in the visual field to estimate its distance to scale, Φ_W. B Embodied Visuomotor Representation uses the control input and visual information to estimate the opening size, (X_r − X_l)/b, in the embodied units. C The size of the robot in the embodied unit, (w_r − w_l)/b, as estimated with a series of uncalibrated touches, is compared to the size of the opening in the embodied unit to determine if the robot can fit or clear the opening. D If the robot can fit, the known size of the opening can be used to determine the position of the robot, and closed-loop control can guide the robot through the opening.

Let the robot approach the touching target along direction v in the body frame; then, if the body extends further than the camera in the direction of v, the robot’s body will touch the target prior to the camera reaching the target. Let the time of contact be called t_c. At the time of contact, the vector from the camera to the point on the body that is touching the target is known and corresponds with a point on the perimeter of the robot’s body. Repeating the touching process by approaching a target from many directions allows the robot to approximate its convex hull in the scale of the embodied units.

Clearing obstacles is now as simple as measuring the distance from the robot’s camera to the object in the embodied unit and comparing that to the robot’s size in the embodied unit. In particular, as illustrated by Fig. 2, if a robot has measured its width in the embodied units as w/b = w_l/b + w_r/b, where w_l/b and w_r/b are distance from the camera to the left and right side of the robot respectively, then it only needs to measure width of the opening, as illustrated in Fig. 7, and compare it to the width of the robot. Let the positions of the left and right sides of the opening be X_l and X_r; then the robot measures their positions as X_l/b and X_r/b. Thus, the robot fits if

$$w \,<\, \parallel\!{X}_{l}-{X}_{r}\!\parallel \iff \frac{w}{b} < \left\Vert \frac{{X}_{l}}{b}-\frac{{X}_{r}}{b}\right\Vert .$$

(21)

If the robot fits, it can proceed through the opening using the same controller that was used to touch targets.

Figure 8 shows estimated distances from the opening as the robot approaches using different ground truth values for b = 0.5, 1, and 2 as before. The approach corrects a translational perturbation in the X axis in addition to approaching the target at a constant speed along the Z axis. The approach velocity was fixed to the same embodied value for each trial; thus, when b = 0.5 and b = 2, the robot takes twice and half as long, respectively, to reach the target as when b = 1.

Fig. 8: Experimental data and estimated signals from the opening approach phase of uncalibrated clearing for three different values of the control gain b.

The methods take different amounts of time to reach the target because the approach speed was specified as a fixed value in the embodied unit while b was varied. Note that the closed loop behavior remains stable and qualitatively similar despite the control input gain varying by a factor of 4. As shown by Eq. (12), this is expected.

Additionally, Fig. 9 shows the measured width of the opening as a function of the opening’s true width. Openings of size 12.5, 25, and 37.5 cm were tested with the robot’s initial distance from the opening fixed at 150 cm. Each configuration of opening size and control gain b were tested 5 times for a total of 45 trials. It should be noted that measuring an opening’s width is substantially similar to measuring a target’s width, and so Fig. 9 can be interpreted as an extension of the upper plot in Fig. 6. Table 2 quantifies the error in Fig. 9 as a percentage of the width of the opening.

Fig. 9: Measured width of opening width, in embodied units, as the width of the opening and the control input gain b are varied.

Error bars show mean, minimum, and maximum value over five trials.

Uncalibrated jumping

Suppose an uncalibrated robot with two legs, that apply force with an unknown first order response (or lag), and a monocular camera needs to jump a gap to a platform an unknown distance away but at the same height. In what follows, we carefully apply the five steps for using Embodied Visuomotor Representation. Figure 10 and Movie 2 of the Supplemental Material outline the uncalibrated jumping procedure visually.

Fig. 10: Overview of the procedure for jumping a gap using Embodied Visual Representation.

A The robot oscillates up and down using a high gain control while measuring the control input u and vertical position in the visual field Φ_W of a target line (red). The vertical acceleration achieved $\ddot{{X}}_2$ results from filtering the control input by the unknown actuator dynamics g. B, C Embodied Visuomotor Representation uses the control input and visual information to estimate the actuator dynamics g, distance to the jumping target d, and strength of gravity g_b in the embodied units ${\left(\mathop{\int}\nolimits_{0}^{\infty }g(t)dt\right)}^{-1}$. D An embodied optimal control problem is solved for the control input u_j of minimum total variation that will reach the required launch velocity v_l to jump the gap. E The jumping control input is executed in open loop after tilting the body forward.

Starting with the first step, we assume a classical model of the system. Let the legs applied force respond to inputs according to a first order low pass filter with a time constant 1/α, α > 0. That is,

$$\begin{array}{l}{\ddot{X}}_{2}\,=\,b{x}_{act}-{g}_{b}\\ {\dot{x}}_{act}=\,\alpha \left(u-{x}_{act}\right),\end{array}$$

(22)

where ${\ddot{X}}_{2}$ is acceleration in the vertical direction and g_b is an unknown gravitational bias. Then, as with the the touching example, all the quantities defined by the world, that is b, g_b, and α do not have predetermined units or magnitudes. Thus, the second step is completed.

To complete the third step, assume the robot fixates on a horizontal line that it needs to jump to and oscillates up and down. Then, the line’s height in the image in normalized pixels can be used as Φ_W. That is, Φ_W = X₂/X₃ where X₂ is the vertical position of the line and X₃ is the distance between the camera and the line. Then, the characteristic scale of vision d is equal to X₃ and is the distance to be jumped.

The fourth step of establishing a constraint between vision and control that involves the unknowns is accomplished by recalling Eq. (14), specializing it to this example’s dynamics, and adding the additional gravitational bias term. Finally, the fifth step can applied: estimating the force of gravity and the distance to the line in embodied units using Eq. (16). The full formulation is given in the methods section and specifically Eq. (23). There, a family of truncated exponential decay functions are used to represent the first order actuator dynamics, which results in a linear least squares problem and a unique solution. Subsequently, Eq. (17) can be used to recover the distance to be jumped in the embodied units as ${\hat{X}}_{3}({t}_{0})/b$. Figure 10 illustrates this procedure.

Then, given the embodied jumping distance d, embodied gravity estimate, and a predetermined launch angle θ_l, the robot can solve the projectile motion equations to determine a launch velocity, v_l, and the landing time t_f. To find control inputs that achieve this launch velocity, we pose a convex optimal control problem, (25), that solves for a non-negative control input with minimum total variation that reaches the launch velocity. The formulation of both problems is given in the methods section.

Figure 11 illustrates the results of this procedure in terms of the achieved jumping trajectory (in meters) and the applied control signal u in embodied units. Figure 12 illustrates the accuracy of the estimate of the distance to be jumped, d, and the gravitational force, g_b, in the embodied unit after completing the measurement phase. Estimates resulting from processing simulated images with color thresholding and simulating worst case pixel quantization errors are shown. The error due to finite resolution can be seen to decrease by approximately 1/resolution. A theoretical justification for this is given in the Supplemental Material. For each set of experiments, the non-varied parameter values were set to d = 3.0, 1/α = 0.1, ${\rm{res}}=200$, T = 10, g_b = 9.81, and b = 0.2.

Fig. 11: Jump trajectories and jump control signal versus experimental parameters.

The procedure can successfully jump over a wide range of unknown gaps varying from 1 to 4 meters in width. A nominal gap of 3 meters can be jumped despite variations in the unknown actuator time constant, camera resolution, oscillation period, gravitational force, and actuator gain. The jump control signals resulting from an embodied optimal control problem (25) can be seen to vary in magnitude and duration as expected given varied jump distance, actuator time constant, gravitational strength, and actuator gain.

Fig. 12: Estimated jump distance and gravitational strength in embodied units versus experimental parameters.

The blue ground truth corresponds to ground truth values. Green estimates result from using an image and color thresholding to estimate Φ_W. Blue shaded regions illustrate the maximum error achieved via simulated pixel quantization errors varied over 26 trials. Larger jump distances are estimated less accurately. Lowering the camera resolution below 200 pixels increases estimation error quickly. Increasing the oscillation period slightly improves results. Lower actuator gain, which results in less oscillation, decreases the accuracy of the estimated distance. While some variation in the estimate of gravitational bias can be observed, the error is typically on the order of 0.02 %. The effects of varying the actuator time constant and gravitational strength are included for completeness when comparing to Fig. 11.

It should be noted that performing the up and down oscillation requires a controller to compensate for the effects of gravity. For this experiment, the control gains were chosen manually, but they could easily be chosen automatically using traditional system identification and control design methods. Additionally, the mass of the robot’s legs and feet have been neglected as the effect of their mass on the jumping trajectory cannot be estimated by oscillating the body alone. For the purpose of this paper, it suffices to assume the mass of the legs and feet is small, and so does not significantly affect the achieved jumping trajectory. However, the effect of the added mass of the legs and feet can be estimated by doing a vertical test jump prior to jumping the gap. Finally, because the approach is model based, it, in theory, works for all gap sizes, gravitational strengths, and actuator time constants. However, given fixed parameters, it will fail in specific scenarios where the model’s assumptions do not hold. For example, if the strength of gravity is made very weak, the agent may fall off the jumping platform during the measurement phase unless the oscillation frequency and magnitude are also reduced.

Comparisons to Bees and Gerbils

Next, we contrast the properties of algorithms using Embodied Visual Scale with behavior observed in bees and gerbils.

Bees have been recently shown to understand the size of an opening in wingbeats during their approach to an opening. It is thought that the size of the wings is learned during early development through contact with the hive. Additionally, the bees oscillate increasingly vigorously as openings are made smaller, seemingly to determine the size of the hole more accurately¹³. Similarly, our method for uncalibrated clearing determines the size of the robot in embodied units through contact and oscillates to determine the size of the opening. Additionally, an examination of the least squares formulation admits that increased oscillation over longer periods will increase the accuracy and robustness of the estimated quantities because errors can be averaged out.

Similarly, Mongolian Gerbils vibrate their body up and down before making a jump over a gap of unknown distance. It is thought that this helps their visuomotor system determine the appropriate muscle stimulation to clear the gap¹¹. Like bees, the intensity of the oscillations increases when the gap is larger and thus is more difficult to jump over. Our approach also requires oscillation, can estimate the appropriate actuator stimulation to jump a gap, benefits from larger oscillations (which induces a larger baseline for vision), and can increase its accuracy by considering longer timer intervals.

Discussion

Embodied Visuomotor Representation is a concrete methodology that allows robots to emulate the process of estimating distance through action – a capability well established in the natural sciences. This approach simplifies implementation by allowing low-level control laws to self-tune and removing the need for detailed physical models or calibrated 3D sensors. As a result, even uncalibrated robots can reliably perform tasks such as touching, clearing obstacles, or jumping, while maintaining guaranteed stability.

Traditionally, body-length units have been proposed as a natural basis for embodied scale. However, such measurements are not directly accessible to an uncalibrated robot. Embodied Visuomotor Representation addresses this limitation by providing a mechanism through which a robot can internally estimate or re-estimate body-length units as needed. Instead of relying on external units like meters, it grounds the perception of distance using the robot’s own acceleration response to control inputs.

We further compare traditional approaches based on sense-plan-act with our approach based on Embodied Visuomotor Representation in Table 3. The table compares the main algorithmic components of traditional approaches that might be used to achieve touching, clearing, and jumping. This comparison reveals how the stability of traditional approaches becomes implicitly tied to prior knowledge of the conversion factor between an embodied scale and an external scale due to the assumption of control inputs on an external scale. Embodied Visuomotor Representation can escape this situation by using a different architecture from the traditional sense-plan-act cycle as illustrated by Fig. 1.

Table 3 Robot behaviors that can be accomplished with external scale and traditional methods, but can also be accomplished with Embodied Visuomotor Representation (EVR)

The development of Embodied Visuomotor Representation has borrowed ideas broadly from many areas, in particular the Tau Theory, Glenberg’s theory of embodiment as memory, the Internal Model Principle, and Visual Self-Models. Below, these frameworks are compared and contrasted to Embodied Visuomotor Representation. We further compare our framework to leading approaches in robotics, including Direct Optical Flow Regulation, Visual Servoing, Visual Inertial Odometry (VIO), Visual Self-Modeling, and Deep Visuomotor Control.

The Tau Theory originally proposed an embodied visuomotor relationship as the basis for how time-to-contact could be used by humans for tasks such as driving a car¹⁴. This was developed into the General Tau Theory³⁰, which aims to explain numerous behaviors using time-to-contact (tau). Later theories generalized it to motion in all directions, called looming³¹. Tau Theory does not provide a specific methodology for achieving tau trajectories and so roboticists have proposed methods ranging from direct regulation^18,32,33 to indirect estimation of position followed by regulation^28,34,35, with most relying on pre-tuned of control laws to account for the unknown embodied scale. Embodied Visuomotor Representation can use time-to-contact as the basis for a scaleless visual transition matrix Φ_W as in²⁸ without committing to any particular control law. Further, it is easy to use the framework to verify if a proposed control law is stable.

A generalization of Tau Theory is Direct Optical Flow Regulation. Here, arbitrary optical flow fields are used as the setpoint to a control loop. Such control schemes have been shown to result in striking similarities to insect flight behavior^15,36,37,38. Notably¹⁹, showed that the framework allows orientation with respect to gravity to be estimated using oscillations of orientation. Such schemes depend on pre-tuning of the control law for the expected heights and velocities³⁹. addresses this limitation by lowering the open-loop gain when oscillations occur. Embodied Visuomotor Representation can continuously estimate embodied distance without necessarily oscillating. Thus, it can be used to follow more general trajectories while simultaneously scaling the gains of a direct optical flow regulator to ensure stability.

Another approach to visuomotor control is Visual Servoing which considers objectives based on position (pose based) or image coordinates (image based)^16,17. When combined with Embodied Visuomotor Representation, pose based approaches no longer require a 3D model of known scale as demonstrated by uncalibrated touching and clearing. This situation is similar to that considered by Image Based Visual Servoing, which operates without knowledge of scale by basing the control objective on the pixel positions and mitigating the effects of unknown depth using approximations, partitioning, or adaptivity^16,17,40. Embodied Visuomotor Representation provides an estimate of depth, and so is closely related to adaptive visual servoing. However, Embodied Visuomotor Representation is also a broader framework that enables a rich set behaviors such as the examples of touching, clearing, and jumping.

Our implementation of these behaviors has strong parallels with Glenberg’s theory of embodiment as memory²². Glenberg writes, “embodied representations do not need to be mapped onto the world to become meaningful because they arise from the world” and our proposed Embodied Visuomotor Representation does just that. A core tenet of Glenberg’s theory is the “merge” operation that allows memories of different types of actions to be combined to do a new task. Our Embodied Visuomotor Representation admits a path towards realizing a general motion-based “merge” operator because it explicitly represents the system’s dynamics.

Realizing such advanced behavior requires the ability to predict. This is supported by the Internal Model Principle, that suggests an internal model of the process to be regulated must be contained within a controller if it is to succeed. This principle has analogs in psychology, where it is accepted that humans depend on internal models to control themselves^24,41. Further, recent evidence strongly suggests that even simple animals such as dragonflies have such predictive visuomotor models^12,25. In computer science, Animate Vision was proposed to explain how such visuomotor control processes can be learned through interaction with the environment^4,42. These theories are very general and do not explicitly consider the challenges introduced by the unit-less nature of vision. Thus, Embodied Visuomotor Representation can be seen as a specialization that can realize versions of these theories in robots.

An important component of predictive modeling is understanding the shape of the body. While the given examples of uncalibrated touching and clearing are the most basic way to do this, it is of interest to combine Embodied Visuomotor Representation and recent work on Visual Self-Modeling that consider neural representations of a robot’s 3D form⁴³. Similarly, it is of interest to understand Embodied Visuomotor Representations application to Deep Visuomotor Control as exemplified by⁴⁴. Recent work has considered visual navigation, where a robot must learn to navigate through a scene from visual inputs and output concrete actions to be taken by low-level controllers provided by a variety of morphologies^45,46,47.

Next, we turn to Visual Inertial Odometry (VIO), and its relation to Embodied Visuomotor Representation. VIO is the conventional approach to estimating a robot’s state from vision and calibrated inertial measurement units (IMUs). Typical approaches follow a match, estimate, and predict architecture to estimate a metric trajectory and the 3D position of tracked points^48,49,50,51. Architecturally, this is identical to sense-plan-act but in the estimation setting. In contrast, Embodied Visuomotor Representation generally considers the characteristic scale of vision, which may not be the distance to features. This encourages an object-centered visual framework where control tasks are considered with respect to individual objects. Similarly, the role of IMUs is different within Embodied Visuomotor Representation. They are useful for estimatating rotation over short periods. and their acceleration can be used up to scale to better estimate mechanical parameters. They also allow a robot to continuously estimate the conversion factor between its embodied scale and an external scale as might be needed to adhere to a safety standard or follow high level directions.

The above comparisons to existing concepts resulted in several directions for future work. However, there are many more, and so below, we outline the future work in theory and applications that we consider most important.

In terms of theory, this paper has considered only equality-constrained Embodied Visuomotor Representation. That is, the unitless quantities from vision are considered to exactly equal some operator of control inputs. Ideas from psychology, and, in particular, the Tau Theory, suggest that more qualitative processes will suffice for many applications. Thus, it is of interest to develop inequality-constrained Embodied Visuomotor Representation in hopes of realizing qualitative representations and qualitative control laws that robots can use to accomplish tasks. Similarly, it is of interest to develop Embodied Visuomotor Representation in combination with direct methods such as Direct Optical Flow Regulation, and Image Based Visual Servoing. Here, an embodied representation of distance can be used to help initialize, learn, or select direct control laws. Finally, the role of rotation has recently been found to be useful for estimating attitude from direct measurements ¹⁹. Thus, it is of interest to carefully consider the role of rotation in embodied representation.

Turning back to equality-constrained Embodied Visuomotor Representation, we have presented two types of estimation problems. The first, exemplified by (10), estimates quantities in embodied units of action. The second formulation is given by (11) and (16) which estimate quantities in units of the visual processes characteristic scale. Subsequently, these quantities can be converted to an embodied unit of action. While the latter were shown to be unbiased with respect to zero mean noise in Φ_W, it is still of interest to perform a more general and careful error analysis with the goal of constructing robust or optimal estimators for Embodied Visuomotor Representation.

Next, we discuss the representation of dynamics. The derivation of Embodied Visuomotor Representations above neglected damping and spring effects, as might be caused by friction or tendon-like attachments, respectively. However, these effects can be incorporated, assuming these naturally occurring dynamics are stable, which they almost always will be. For example, we can incorporate into an Embodied Visuomotor Representation a system’s dissipating energy due to spring and damping effects by considering velocity or position as the fundamental quantities controlled by the action instead of acceleration. In this paper, acceleration was used as the fundamental quantity controlled through action because all animals and robots must use forces.

Finally, it is interesting to consider more general dynamics than linear systems and how to control them via Embodied Visuomotor Representation. In principle, except for the use of unit-less visual feedback, this is not substantially different from existing work in robot dynamics, and we expect many techniques to port over directly. On the other hand, the linear dynamics considered in this paper should be sufficient for many applications. Thus, it is of interest to apply recent advancements in adaptive control, such as kernel methods that guarantee estimation of BIBO stable impulse responses⁵².

Next we consider future work in applications. A straightforward application that can be accomplished via Embodied Visuomotor Representation is avoiding and pursuing dynamic objects. If a position-based approach is used, the basic procedure is identical to the touching, clearing, and jumping, except that an additional model of the dynamic object must be considered. Catching is also of interest. However, it is thought that humans use direct methods (that is, they do not primarily rely on 3D position) to catch objects. The evidence is particularly strong in sports where humans achieve extraordinary performance despite sensorimotor delays^53,54. Then, since Embodied Visuomotor Representation allows for learning predictive self models that could be used for delay compensation (as is thought to be essential in biological systems^12,24), it is of particular interest to study the theoretical connections between embodied representation and direct methods in the task of robot catching.

We also consider imitation and embodied affordance estimation to be the next two most important applications. Assuming the embodied mechanical and dynamics parameters have already been estimated, imitation within Embodied Visuomotor Representation becomes a problem of determining the embodied control signals that accomplish a visually observed behavior. The characteristic scale-based representation of vision will then naturally allow robots to imitate an action using the units of their own embodiment instead of an external scale.

Finally, while this paper has exclusively considered visual processes and their connection to motor signals, the basic principles should be extended to consider multiple modalities such as tactile sensing and audio. We are particularly interested in tactile sensing because grasping is an action that results in both tactile and visual responses.

Methods

Hardware

The robot platform used for the touching and clearing experiments is a DJI RoboMaster EP. The platform features mecanum wheels, which allow it to translate omnidirectionally. The provided robot arm and camera were removed and replaced with a pan-tilt servo mount and a Raspberry Pi Camera Module 3 with a 120 degree wide-angle lens running at 1536 × 864 resolution and 30 frames per second. A Raspberry Pi 5 interpreted images and calculated control commands for the robot. The associated code is provided in the Supplemental Material.

The DJI RoboMaster does not support direct acceleration control. The lowest level supported is velocity control. To emulate the double integrator described in the touching and clearing experiments, the acceleration commands from the proposed control laws were transformed into velocity commands using a leaky integrator with a time constant of 10 seconds.

Uncalibrated touching

The touching experiment uses color thresholding to detect the pixels of a planar target and calculate Φ_W based on the assumption of a flat target parallel with the image plane. As mentioned in the results section, this visual representation was chosen as a pedagogical example and will not work for non-flat objects. In general, the theory holds without modification for any other vision algorithm that provides position to scale as per (4). The robot oscillates in open-loop by applying a 1/3 Hz sinusoidal acceleration signal over a 10 second interval. The amplitude of acceleration was set so that the positional oscillations had an amplitude of 25 cm when b = 1. Equation (11) is used to solve for the current position, velocity, and size of the touching target in embodied units using a 3 second sliding window of measurements. To do so, the outermost integral of Eq. (11) is approximated in discrete time, so that the problem can be considered as a standard linear least squares problem of the form $\mathop{\min }\nolimits_{x}\parallel\! Ax-b{\parallel }^{2}$. This problem is transformed to the normal equations A^TAx = A^Tb and x is computed using JAXopt’s⁵⁵ Cholesky decomposition based solver for linear systems. The code is available in the supplemental material.

Subsequently, the robot drives toward the target at a constant velocity of 0.3 embodied units per second using PID control and positional feedback from vision in embodied units. The approach continues for the time required to traverse the initial distance between the robot and the target. Since the robot’s body is closer to the target than the camera, the robot makes contact with the target sometime during this interval. Then, the minimum distance between the robot’s camera and the target is the horizontal distance between the robot’s camera and the edge of the robot that made contact with the target first.

The PID control loop was tuned manually and was accomplished with just a few trials because the closed-loop behavior does not depend on the units of distance or the geometry of the scene. Thus, reasonable initial values for the PID gains can be determined from a desired closed loop bandwidth.

Uncalibrated clearing

The clearing experiments consider whether the robot can fit through an opening (clear it) prior to reaching the opening. To do so, the robot determines the width of the body in the embodied unit by touching its left and right sides to a nearby object using the previously described procedure. It remains for the robot to measure the size of an opening in the embodied unit. Once again, the left and right sides of the opening are detected with color thresholding. The left and right edges of the right and left sides of the opening, respectively, are used as the characteristic scale of vision. As with the last example, this visual representation is pedagogical. The same sinusoidal acceleration and sliding window estimator used during uncalibrated touching then estimates the size of the opening in the embodied units. If the robot is smaller than the opening, it proceeds through with the same PID-based position control as used for uncalibrated touching.

Uncalibrated jumping

The jumping robot experiment was performed in a MuJoCo simulation⁵⁶. Codes for this simulation are provided in the Supplemental Material.

The robot consists of a body on two legs and feet. The legs are modeled as cylinders or pistons, with first-order activation dynamics and a time constant of 0.1 seconds. The body mass was set to 10 kg, and the mass of the legs and feet amounted to 0.22 kg. Two angular position controllers hold the legs upright during the measurement phase of the experiment and tilt the body forward approximately 20 degrees during the jumping phase.

The measurement phase of the jumping experiment consists of three parts. In the first, the minimum/maximum position of the body is estimated by recording the initial position as the bottom position, increasing the upwards force until the body begins to lift, initializing a PID controller’s integrator term with the force that overcomes gravity, and using PID control to maintain a constant upwards velocity until the top position is reached. Subsequently, the PID controller oscillates the body for 10 seconds at 1 Hz around the midpoint between the bottom and top positions with an amplitude equal to 1/4 of the distance between the top and bottom positions. While this approach introduces an assumption of a pre-tuned PID controller to control the body position, this could be eliminated by applying traditional system identification techniques in the embodied units.

During oscillation, color thresholding is used to determine the vertical normalized pixel coordinate corresponding to a red line placed in the middle of the target platform. The characteristic scale of vision then becomes the distance between the robot and the red line. Subsequently, the measurements of the control effort applied by the PID control and the vertical normalized pixel coordinate are used to solve for the leg actuator’s impulse response, the distance between the robot and the red line, and the initial velocity.

The simulated camera has a resolution of 200 × 200 pixels and a 90 degree vertical field of view and runs at 60 fps. Estimation of the maximum possible errors due to pixel quantization, as illustrated in Fig. 12, was achieved by quantifying the ground truth pixel position of the red line to integer coordinates with random quantization boundaries according to the formula p_sim = round(p_gt + Δ) − Δ and varying the value of Δ between [− 0.5, 0.5] with 26 steps.

To approximate the actuator impulse response, a linear combination of 50 first-order impulse responses truncated to 4 seconds with a DC gain of 1 and time constants ranging from 0.008 to 0.5 seconds are considered. The resulting quadratic program to estimate the distance to the line, initial velocity, and actuator dynamics is then given by:

$$\begin{array}{l}\mathop{\min }\limits_{\frac{{\dot{X}}_{2}(0),{g}_{b},c}{d}}\mathop{\displaystyle\int}\nolimits_{2}^{T}{\left({\Phi }_{W}(t)-t\frac{{\dot{X}}_{2}(0)}{d}-\frac{1}{2}\frac{{g}_{b}}{d}{t}^{2}-\frac{g}{d}* \mathop{\displaystyle\int}\nolimits_{0}^{t}\mathop{\displaystyle\int}\nolimits_{0}^{\sigma }u({\sigma }_{2})d{\sigma }_{2}d\sigma \right)}^{2}dt\\ \frac{g(t)}{d}=\sum\limits_{i}{c}_{i}{e}^{-t/{\tau }_{i}}\\ {\rm{s.t.}}\quad {c}_{i} > =0\quad \forall i\end{array}$$

(23)

where ${\dot{X}}_{2}(0)$ is the initial velocity on the robot camera’s vertical axis, g_b is the gravitational bias force, c_i are the coefficients of the basis functions for g and τ_i are the corresponding time-constants of the basis functions. The double integral and convolution are computed using a 0.001 second approximation, corresponding with the simulation’s timestep. The outermost integral is approximated with a 1/60’th of a second timestep, corresponding to the 60 fps simulated camera. The loss is evaluated over the interval [4, T] instead of [0, T] to prevent initial conditions from contributing to the actuator dynamics through the 4 second long impulse response g. Non-negativity of c_i is necessary to prevent overfitting to numerical integration errors. Similarly to the uncalibrated clearing and touching implementation, the problem is solved by approximating the outermost integral in discrete time. This results in a constrained quadratic program, which is solved using CVXOPT’s quadratic program solver⁵⁷. The code is available in the supplemental material. By solving this problem, the dynamics of the system are estimated automatically.

To convert from units of the characteristic scale to embodied units of action, we divide each estimated quantity by $\mathop{\int}\nolimits_{0}^{\infty }g(t)dt/d$. In what follows, all quantities can be assumed to be in this embodied unit.

Subsequently, the standard equations for projectile motion are combined with the estimated embodied distance and gravitational force to solve for an embodied launch velocity v_l that will jump the gap. The equations to be solved are

$$\begin{array}{l}0\,=\,{t}_{f}\sin ({\theta }_{l}){v}_{l}-\frac{1}{2}{t}_{f}^{2}g\\ d\,=\,{t}_{f}\cos ({\theta }_{l}){v}_{l},\end{array}$$

(24)

where t_f is the time of landing.

Finally, A terminally constrained optimal control problem is solved to find the control input with a minimum total variation that accelerates the body from rest to the launch velocity in 250 milliseconds over the distance oscillated over during the measurement phase. The resulting quadratic program is:

$$\begin{array}{l}\mathop{\min }\limits_{u}\mathop{\displaystyle\int}\nolimits_{0}^{T}{\left(\frac{d}{dt}u(t)\right)}^{2}dt\\ {\rm{s.t.}}\mathop{\displaystyle\int}\nolimits_{0}^{T}(g* u)(t)dt={v}_{l}\\ \mathop{\displaystyle\int}\nolimits_{0}^{T}\mathop{\displaystyle\int}\nolimits_{0}^{\sigma }(g* u)({\sigma }_{2})d{\sigma }_{2}d\sigma ={d}_{m}\\ u(0)=0,\quad u(T)=0,\quad u(t) >\!=0,\quad \forall t\in [0,T]\end{array}$$

(25)

where v_l is the necessary launch velocity in embodied units, and d_m is the distance from the start position at which the launch velocity should be achieved. d_m is necessary to ensure the launch velocity is reached prior to reaching the maximum position of the body with respect to the legs.

Non-negativity of u is required to prevent lifting the lightweight legs from the jumping platform prior to reaching the launch velocity. We formulate and solve the problem using a discrete time approximation of 0.001 seconds. Because of exponential decay, (g*u)(t) > 0 when t > T, and so the leg actuators are deactivated for t > T to prevent the body’s velocity from exceeding v_l. The resulting embodied jump control signal u is offset by the estimated gravitational bias and executed in an open loop.

Thus, by combining (23) and (25), the estimation of system dynamics and the synthesis of the jumping control input are fully automated, except for the use of a PID controller during the oscillation phase. However, this step could also be automated using existing system identification or adaptive control techniques. It is important to note that this example is pedagogical and does not account for or attempt to mitigate disturbances. Nonetheless, this does not affect the generality of the result, as Embodied Visuomotor Representation solely determines the units of distance and remains compatible with any jumping algorithm.