Introduction

The bottom-up construction of artificial nanostructures offers an exceptional framework for investigating synthetic quantum states of matter, meticulously engineered atom by atom1,2. The groundbreaking creation of the inaugural quantum corral3, enabling the visualization of confined electronic states, propelled scanning tunneling microscopy (STM) and spectroscopy (STS) into indispensable tools for crafting and customizing the electronic and magnetic characteristics of materials at the atomic level4,5,6,7,8,9,10,11,12.

Arranging atoms into chains and clusters facilitates the exploration of a rich array of quantum phenomena, including quantum-confined electrons13,14,15, Dirac bands16,17, flat bands18, and topological defects19,20. The magnetic states hosted by such nanostructures exhibit intriguing complexity influenced by underlying competing interactions21,22,23,24,25,26. Atomic impurities possess the capacity to influence the stability of large spin textures by either pinning or deflecting them27,28,29,30,31. Man-engineered nanostructures can induce chiral orbital magnetism32,33,34 and give rise to novel magnetoresistance effects35. Superlattices of adatoms can emerge through interactions mediated by surface-state electrons36,37, which are influenced by Friedel charge oscillations38,39 leading to long-range magnetic interactions known as Ruderman-Kittel-Kasuya-Yosida (RKKY) interactions40,41,42. These interactions, such as the isotropic Heisenberg interaction and the spin-orbit induced Dzyaloshinskii-Moriya interaction (DMI)43,44, oscillate and decay as a function of distance. They play a dominant role when magnetic atoms are placed directly atop a metal surface and have been quantified through measurements and electronic simulations in various diluted nanostructures45,46,47,48,49,50.

The capability to fabricate artificial atomic lattices with adjustable inter-atomic distances presents a unique opportunity to explore a vast magnetic phase diagram, a feat unattainable with conventional materials without altering their chemical compositions and structures. One remarkable example that hinges on the delicate balance of various magnetic interactions is the emergence of magnetic skyrmions51,52,53,54,55,56,57,58.

By adjusting the separation between magnetic atoms, it becomes possible to toggle the magnetic coupling from ferromagnetic (FM) to antiferromagnetic (AFM), manipulate the chirality governed by the DMI, or even access a regime where the Heisenberg magnetic interaction is eclipsed by the DMI46,47,48,49. This motivates the design of artificial lattices capable of realizing topological magnetic textures. Herein, we examine the case of Cr, Mn, or Fe adatoms deposited on a Nb(110) surface, renowned for its superconducting properties and extensively utilized in cutting-edge experiments59. These experiments aim to probe the potential emergence of topological Majorana boundary states60,61,62 or trivial ones63,64,65,66,67. Recently, it was demonstrated that two-dimensional diluted lattices comprising Cr adatoms atop a Nb(110) surface host two types of mirror-symmetry-protected topological superconductors68. Building on these findings, we now explore the case of Mn and Fe adatoms while revisiting the case of Cr adatoms using first-principles calculations and atomistic spin dynamics. We aim to investigate how various elements and lattice geometries affect the emergence of topological spin textures when interfaced with a potential superconducting surface, utilizing the design of artificial lattices.

Hinging on first-principles simulations combined with atomic spin-dynamics (ASD) (see Methods section), we unveil the emergence of diverse complex magnetic states such as domain walls, skyrmions, and antiskyrmions through the adatom-adatom magnetic interactions. The explored artificial lattices, inspired from those built experimentally in ref. 68, are illustrated in Fig. 1 and denoted as lattices (A) and (B). The presence of topological spin textures, such as skyrmions and antiskyrmions, in our artificial lattices suggests a promising platform for exploring topological superconductivity and Majorana bound states. When coupled with an s-wave superconductor like Nb(110), these non-collinear magnetic textures can induce an effective spin-orbit interaction, which, combined with superconductivity, can lead to the formation of topological superconducting phases. Specifically, theoretical studies have shown that localized Majorana modes can emerge at the cores of skyrmions when interfaced with a superconducting medium due to the breaking of time-reversal symmetry69,70. While our current study focuses on the magnetic interactions and the emergence of topological solitons, the connection to Majorana physics provides motivation for future investigations into how these textures interact with superconductivity. Incorporating superconductivity into our theoretical framework would be a natural next step to explore the potential realization of Majorana bound states in such diluted magnetic lattices.

Fig. 1: Diluted lattices.
figure 1

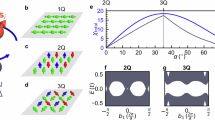
a, b Schematic representation of the magnetic adatoms positioned in both investigated lattice types, (A) the rectangular lattice with the first (second) nearest neighbors atoms separated by 0.66 nm (0.93 nm), and (B) the rhombic lattice with the first nearest neighbors set 0.87 nm apart. Note that the lattices were built experimentally as reported in ref. 68.

Full size image

Results

Magnetic interactions among the magnetic adatoms on Nb(110)

We begin by exploring the magnetic interactions among the Cr, Mn, and Fe adatoms on the Nb(110) surface and their influence on the resulting magnetic textures. Our first-principles calculations reveal that the magnetic interactions among the first nearest neighbors (n.n.), and beyond depend strongly, as shown in Fig. 2 on the types of the considered adatom lattices (A or B). The exchange interactions are mediated by the conduction electrons of Nb(110) through the RKKY mechanism40,41,42, leading to oscillatory behavior as a function of distance. This explains why some interactions are FM while others are AFM, as the sign of the interaction depends on the Fermi wave vector and atomic spacing. For Cr, the first n.n. Heisenberg exchange is AFM in both lattices but significantly weaker in lattice (B), decreasing from −5 meV in (A) to −0.3 meV in (B), see Fig. 2a–c.

Fig. 2: Magnetic interactions among magnetic adatoms on Nb(110).
figure 2

a, d, g Heisenberg exchange interactions among Cr, Mn, and Fe atoms as a function of the distance for both lattices (A) in cyan, (B) in purple, with the DMI values in inset. b, c, e, f, h, i Illustration of the simulated lattices, where each circle is colored as a function of the size of J with respect to the central atom (gray color). The positive (negative) values correspond to FM (AFM) coupling.

Full size image

For Mn based lattices, as depicted in Figure. Fig. 2 d-f, the first n.n. Heisenberg exchange interactions among Mn adatoms transition from FM coupling (J1= 2 meV) in the rectangular lattice (lattice (A)) to AFM coupling (J1= −0.43 meV) in the rhombic lattice (lattice (B)).

While the Fe adatoms experience a cancellation of the magnetic interaction, initially FM, when placing them in lattice (B) instead of (A) as shown in Fig. 2g–i. The DMI depicted in the insets of Fig. 2a, d, g, is found to be finite and can be of the same order of magnitude than the Heisenberg exchange interactions (e.g., Mn in lattice (B)). Alternatively, in the other cases, it can be one to two orders of magnitude smaller than the Heisenberg exchange interactions.

Notably, not only the Heisenberg exchange interactions and DMI vary across different adatom lattices, but the magnetocrystalline anisotropy energy (MAE) also changes, as shown in Supplementary Table 1 and Supplementary Table 2. These differences arise from variations in the electronic structures and SOC effects. The one d-electron difference between Cr, Mn, and Fe has a dramatic impact on their magnetic behavior. Their distinct configurations alter the hybridization with the Nb (110) substrate, leading to different SOC strengths and, consequently, different magnetic anisotropies. This highlights how changes in the electronic configuration and the local environment can result in significant variations in the magnetic anisotropy. These findings highlight the tunability of MAE in artificial adatom lattices and its role in shaping the resulting magnetic textures. Here, depending on the system, we observe two cases of magnetic anisotropy: either uniaxial or biaxial. In the uniaxial case, the system has one direction that differs energetically from the other two. If this unique direction has the lowest energy, it defines an easy axis; if it has the highest energy, the spins preferentially align within the plane perpendicular to it, forming an easy plane. In contrast, biaxial anisotropy is characterized by three non-degenerate directions, with the lowest-energy direction defined as the easy axis and the second as the secondary easy axis.

For Cr adatom lattices, we observe biaxial anisotropy, where the spins prefer an anisotropic in-plane (xy plane) orientation for both lattices, albeit with different energy values. In both cases, the easy axis is along the x-direction, and the secondary easy axis is along the y-direction. Conversely, for Mn adatoms, the MAE exhibits a distinct shift between lattice (A) and lattice (B). Lattice (A) shows uniaxial anisotropy with spins preferring out-of-plane (OOP) alignment, and no in-plane anisotropy is observed, unlike all other investigated cases. In lattice (B), a transition to biaxial anisotropy occurs in the xz plane, with the x-direction serving as the easy axis. Finally, for Fe-based lattices, and similarly to the Cr case, both Fe adatom lattices exhibit biaxial anisotropy, with spin alignment confined to the yz plane. The y-direction is the easy axis in lattice (A), while in lattice (B), the easy axis shifts to the z-direction. This rich set of MAE behaviors underscores the tunability of the adatom magnetic properties depending on the lattice configurations.

The observed modifications in the magnetic interactions induced by the two types of diluted lattices considered in our study impacts on the ground states and metastable states emerging spin-textures, which are discussed in the next section. It is also worth noting that the presence of adatoms on the Nb(110) surface induces a weak magnetic moment in the surrounding Nb(110) atoms, as shown in Supplementary Fig. 1.

Emerging complex magnetic states

After extracting the magnetic interactions among the adatoms for each lattice type, the next step is to investigate the underlying magnetic states.

Starting with the case of Cr adatoms, the ground states are the in-plane row-wise AFM magnetic states for both lattice (A) and (B), as depicted in the insets of Fig. 3a, b, where the spins are oriented in-plane due to the underlying in-plane MAE. AFM domain walls emerge across both types of lattices, as shown in Fig. 3a, b. Regarding the Mn-based (A) lattice case, the ground state is FM spin spirals in the absence of magnetic filed, as shown in Fig. 3c. Upon applying an OOP magnetic field of 0.4 Tesla, the spin spirals deform into elliptical FM skyrmions surrounded by an OOP FM state (Fig. 3d). In this case, the ellipse has major and minor axes of 6.4 nm and 2.5 nm. For Mn-based (B) lattices, the magnetic interactions among the adatoms do not support the stabilization of topological solitons, and only complex sets of AFM spin spirals emerge as the ground state, see Fig. 3e.

Fig. 3: Magnetic states emerging at Cr, Mn, Fe lattices.
figure 3

a, b Snapshots of the AFM domain walls forming on the in-plane (xy plane) AFM ground state with the in-plane anisotropic MAE (Kzz − Kxx, Kzz − Kyy)= −(0.31 meV, 0.15 meV), −(0.49 meV, 0.21 meV)) for Cr (A) and (B) lattices, respectively. For Mn (A) lattice, MAE favors an OOP spin alignment (Kzz − Kxx, Kzz − Kyy = 0.1 meV). The magnetic interactions, however, induce FM spin spirals as the ground state (c). The application of an OOP magnetic field of 0.4 T enables the stabilization of FM skyrmions (d). e For Mn (B) lattice, MAE prefers anisotropic spin alignment in the xz plane ((Kyy − Kxx, Kyy − Kzz) = −(0.24 meV, 0.18 meV)), and the ground state is a complex set of AFM spin spirals. f Snapshot of the FM domains forming at the FM ground state, shown in inset, for the Fe (A) lattice, where the MAE prefers anisotropic spin orientation in the yz plane ((Kxx − Kyy, Kxx − Kzz) = − (0.44 meV, 0.32 meV)). g For Fe (B) lattice the magnetic interaction among the adatoms, with an anisotropic MAE in the yz plane ((Kxx − Kyy, Kxx − Kzz) = − (0.58meV, 1.28meV)), gives rise to an irregular AFM order of spins.

Full size image

Finally, for the Fe adatoms lattices, the FM state in the yz plane is the ground state for the (A) lattice, which can host FM magnetic domain walls (see Fig. 3f and its inset). For the Fe (B) lattices, the weak magnetic interactions among the Fe adatoms (J1 = −0.03 meV) do not support the stabilization of topological solitons, and only AFM irregular (kind of arbitrary) spin alignments emerge, see Fig. 3g.

Emerging magnetic states with restored uniaxial anisotropy

To isolate the role of symmetry in shaping magnetic textures, we artificially restore uniaxial anisotropy by replacing the naturally occurring biaxial MAE. This approach enables exploration of the solitonic textures that emerge in systems with isotropic easy-axis or easy-plane energy landscapes.

Starting by Cr based lattices, in lattice (A), imposing a uniaxial in-plane MAE (K = −0.01 meV) stabilizes an in-plane AFM antiskyrmion with a size of 15.8 nm (Fig. 4a). This texture decomposes into two in-plane FM antiskyrmions on AFM-aligned sublattices (Fig. 4b, c). Similarly, when flipping the sign of the MAE while keeping the value of 0.01 meV, the OOP AFM configuration is stabilized (see Fig. 4d), which can host an elliptical AFM antiskyrmion. The major and minor axes of the elliptical AFM antiskyrmion measure 7.6 nm and 4.6 nm, respectively. The constituents of this AFM antiskyrmion are two FM antiskyrmions emerging at FM sublattices, as depicted in Fig. 4e, f. The manifestation of antiskyrmions rather than skyrmions is due to the DMI vectors that favor a directional dependence of the chirality imposed by the symmetry of the artificial lattices. The chirality is opposite sign along the x-direction than that along the y-direction.

Fig. 4: Magnetic states emerging at Cr (A) lattice by tuning the MAE.
figure 4

a Snapshot of the in-plane AFM Cr antiskyrmion when Kzz − Kxx = Kzz − Kyy = − 0.01 meV. With this MAE the spins can align isotropically in-plane, with the in-plane AFM state shown in inset being the ground state. b, c The building blocks of the in-plane AFM antiskyrmion, which are two in-plane FM antiskyrmions coupled antiferromagnetically. d Snapshot of the OOP AFM Cr antiskyrmion after flipping the sign of the MAE (Kzz − Kxx = Kzz − Kyy = 0.01 meV), which leads to an OOP AFM order. e, f The building blocks of the AFM antiskyrmion, which are two FM antiskyrmions coupled antiferromagnetically.

Full size image

The same scenario holds for the (B) lattice of Cr adatoms. Initially, with a uniaxial in-plane MAE (K = −0.2 meV), we obtain an in-plane AFM state as depicted in the inset of Fig. 5a. In this case, the DMI vectors stabilizes AFM skyrmions (Fig. 5a). This 3.9 nm sized in-plane AFM skyrmion is built up of two in-plane FM skyrmions, residing at two FM sublattices (Fig. 5b, c). Whereas upon changing the sign of the MAE to favor an OOP spin alignment, the ground state flips from the in-plane orientation to an OOP AFM state depicted in the inset of Fig. 5d. Here, an OOP AFM skyrmion emerges. This skyrmion is elliptical in shape with dimensions of (5.5 nm, 2.4 nm) as depicted in Fig. 5d, and the building blocks in this case are two elliptical FM skyrmions residing at two oppositely spin oriented FM sublattices (Fig. 5e, f).

Fig. 5: Magnetic states emerging at Cr (B) lattice by restoring the uniaxial MAE.
figure 5

a Snapshot depicting the in-plane AFM Cr skyrmion emerging when K = −0.2 meV. The latter promotes an isotropic in-plane spin orientation and therefore, the in-plane AFM order is the ground state (inset of (a)). b, c The building blocks of the in-plane AFM skyrmion, consisting of two in-plane FM skyrmions that are coupled antiferromagnetically. d The AFM Cr skyrmion when the MAE favors an OOP spin orientation (K = 0.08 meV), with the associated OOP AFM ground state shown in inset. e, f Snapshots of the constituents of the AFM skyrmion, two FM skyrmions that are antiferromagnetically coupled.

Full size image

Regarding Mn lattice (A), having originally uniaxial MAE preferring the OOP spin alignment, by flipping the sign of the MAE, and choosing it to prefer in-plane spin alignment with K = −0.5 meV, a 3.9 nm sized in-plane FM skyrmion emerges at the in-plane FM background (Fig. 6a).

Fig. 6: Magnetic states emerging at Mn and Fe adatoms (A) lattices by restoring the uniaxial MAE.
figure 6

a Snapshot of the in-plane FM skyrmion forming at Mn (A) lattice when the MAE is preferring in-plane spin alignment (K = −0.5 meV). b Snapshot of the in-plane FM antiskyrmion emerging at Fe (A) when the MAE is modified to be isotropic in the xy plane (K = −0.025 meV). Flipping the sign of the MAE (K = 0.015 meV) favors the OOP spin orientation, where the ground state is the FM state, which hosts FM antiskyrmions (c).

Full size image

Finally, for the Fe adatoms lattices, upon reducing the MAE value down to 0.025 meV, and choosing it to be uniaxial in-plane (xy plane) orientation of spins, i.e., K = −0.5 meV, a 15.1 nm sized in-plane FM antiskyrmion emerges (Fig. 6b). Whereas, when flipping the sign of the MAE, an elliptical FM antiskyrmion emerges in the OOP FM background as shown in Fig. 6c, with major and minor axes of 7.9 nm, 5.1 nm, respectively. Notably, for both Mn and Fe lattice (B) systems, even with uniaxial anisotropy, the magnetic interactions do not support the stabilization of topological magnetic textures.

To summarize, we have learned from this study that Mn-based dilute lattice (A) is the most promising case to explore the emergence of topological magnetic states. For the other cases, the complexity of the MAE tensor, which shows biaxial anisotropy, breaks magnetic rotation in the plane encompassing the spin-textures. This works against the formation of solitonic spin-textures. Restoring an isotropic in-plane rotation enables the formation of various magnetic objects such as AFM of FM skyrmions or antiskyrmions.

Discussion

In this study, we unveiled the emergence of a plethora of topological solitons on the diluted lattices of Cr, Mn, and Fe adatoms deposited on Nb(110) surface. We find potential stabilization of FM and AFM skyrmions, as well as antiskyrmions, which depend on the lattice type of the adatom structures. Motivated by recent STM experiments, demonstrating the possibility of creating diluted lattices, we assumed either a rectangular lattice (lattice (A)) or a rhombic lattice (lattice (B)).

The Heisenberg exchange interactions, DMI and MAE can be strongly modified depending on the lattice considered. For instance, the coupling between the n.n. adatoms can change from being FM to AFM such as what we observed for the case of Mn adatoms. Moreover, the DMI chirality changes across the different lattices types stabilizing for example antiskyrmions in the (A) lattices of Cr and Fe adatoms, while in the Mn (A) and Cr (B) lattices, skyrmions are formed.

In conclusion, our study provides a comprehensive understanding of the magnetic interactions and topological spin textures in diluted adatom lattices. This research opens up new possibilities for exploring synthetic quantum states of matter and their potential applications in technologies. Our investigations promote the superconducting substrate Nb for the exploration of topological superconducting states via the emergence of Majorana states expected to accompany skyrmionic states. Beyond acting as a mediator for long-range magnetic interactions, the Nb (110) substrate provides an exciting opportunity to study topological superconductivity. While our simulations focus on magnetic interactions, the presence of complex spin textures, such as skyrmions and antiskyrmions, suggests that these lattices could serve as a platform for hosting YSR states. In particular, the interplay between these spin textures and the superconducting gap could lead to the emergence of exotic bound states, including Majorana zero modes. Investigating this interplay is a natural next step, as the presence of non-trivial magnetism in a superconducting environment is a key ingredient for engineering topological superconducting phases. Future work will incorporate superconductivity into our theoretical framework to explore these effects in greater detail. Additionally, research could be extended to diluted lattices on other interfaces such as Ir(111), which might lead to more isotropic MAE.

Methods

We conducted a systematic investigation to explore the magnetic structures that can be hosted by the magnetic diluted lattices in our six layered systems. Our approach involves a two-fold procedure, combining ab initio calculations with ASD. Similarly to the experimental construction of the adatoms-based diluted structures reported in ref. 68, we consider two possible lattices denoted as (A) and (B), visually depicted in Fig. 1. We assume a slab configuration consisting of 5 Nb layers and 1 diluted adatoms-based layer. In each layer, we have 8 atoms per unit cell for lattice A and 9 atoms per unit cell for system B. We place the diluted magnetic layer (the magnetic adatoms are either Cr, Mn or Fe) such that the adatoms reside on the hollow stacking site as depicted in Fig. 1.

In the first step, we conducted detailed investigation of the magnetic properties and interactions for the different systems, using the all-electron full-potential relativistic Korringa-Kohn-Rostoker (KKR) Green function method, implemented in the JuKKR computational package71,72, in the local spin density approximation (LSDA). We employed the LSDA approximation in our calculations, as it has been extensively validated for layered magnetic systems, particularly those with itinerant 3d transition metals on metallic substrates. Previous studies have demonstrated that LSDA accurately captures exchange interactions in such systems, yielding results consistent with experimental findings27,64,65,73,74,75,76,77. In the case of Cr nanostructures on Nb (110), our predicted antiferromagnetic behavior was confirmed68. The density of states (DOS) plots for nanostructures made of Cr, Fe and Mn on Nb (110) (see Supplementary Figure 2) show no strong localization effects, supporting the suitability of LSDA without the need for a Hubbard U correction.

To perform the calculations, the momentum expansion of the Green function was truncated at \({\ell }_{\max }=3\). Self-consistent calculations were conducted using a k-mesh of 30 × 21 × 1 points for lattice A, and of 30 × 30 × 1 points for lattice B. The energy contour consisted of 32 complex energy points in the upper complex plane, and it incorporated 10 Matsubara poles. To extract the Heisenberg exchange interactions and Dzyaloshinskii-Moriya (DM) vectors43,44,78, we employed the infinitesimal rotation method79,80. For this extraction, we used a finer k-mesh of 300 × 210 × 1 points for lattice A, and of 300 × 300 × 1 points for lattice B.

After extracting the magnetic interactions characterizing the adatoms, we solve the Landau-Lifshitz-Gilbert (LLG) equation to minimize the underlying extended Heisenberg Hamiltonian:

$$\begin{array}{lll}H\;=\;{H}_{{\rm{Exchange}}}+{H}_{{\rm{DMI}}}+{H}_{{\rm{Anisotropy}}}+{H}_{{\rm{Zeeman}}}\\ \quad\;\,=\;-\sum\limits_{ < i,j > }{J}_{ij}{{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}-\sum\limits_{ < i,j > }{{\bf{D}}}_{ij}\cdot ({{\bf{S}}}_{i}\times {{\bf{S}}}_{j})-\sum\limits_{i}{{\bf{S}}}_{i}^{T}{{\mathcal{K}}}_{i}{{\bf{S}}}_{i}-\sum\limits_{i}{\mu }_{i}{\bf{B}}\cdot {{\bf{S}}}_{i}\end{array}$$
(1)

where we assign indices i and j to denote specific sites, each associated with a magnetic moment. X represents the magnetic atoms being Cr, Mn or Fe adatoms. The magnetic moment is represented by the unit vector S. J is the Heisenberg exchange coupling strength, being negative for an AFM interaction Similarly, we use the notation D for the Dzyaloshinskii-Moriya interaction vector, μiB to represent the Zeeman coupling to the atomic spin moment μ at site i, and \({\mathcal{K}}\) is the magnetocrystalline anisotropy energy tensor, whose components are calculated from the energy differences between different magnetic orientations. Taking the energy difference between the cases where the magnetization points along the x and z axis gives: εx − εz = Kzz − Kxx, while considering the magnetization along the x and y axis leads to: εx − εy = Kyy − Kxx.

To explore the magnetic properties and emerging complex states, we utilize the Landau-Lifshitz-equation (LLG) as implemented in the Spirit code81. We assumed periodic boundary conditions to model the extended two-dimensional system with cells containing 1002, 2002, and 3002 sites.