Introduction

The significance of efficient sound absorption is growing alongside with the expansion of anthropogenic activities, which contribute to increasing noise pollution in both industrial and everyday environments. Traditional noise control strategies often rely on closed panels that reflect acoustic energy back toward the source. However, these methods are fundamentally constrained by the mass law1, which dictates that achieving substantial sound transmission loss (STL) requires materials to be heavy or thick. For example, doubling the thickness of a wall results in only a 6 dB improvement in sound transmission loss (STL) at low frequencies2.

A more robust alternative involves the use of porous materials3,4,5,6, which dissipate acoustic energy due to viscous friction of air within microscopic pores7,8. The physical mechanisms responsible for sound absorption in porous materials differ significantly between low and high frequencies due to the nature of acoustic wave propagation and interaction with the material structure. At low frequencies, sound waves have longer wavelengths and tend to interact with the porous material as a bulk medium. In this regime, viscous and thermal losses dominate dissipative phenomena but require longer dimensions to be efficient. As a result, achieving effective absorption at low frequencies typically requires (i) greater material thickness to allow more interaction space, (ii) higher airflow resistivity to increase viscous losses, or (iii) resonant structures (e.g., Helmholtz resonators, membranes, etc.) embedded within the porous matrix to enhance dissipation. At high frequencies, the wavelength of sound becomes comparable to or smaller than the characteristic pore sizes. In this regime, the inertial effects owed to tortuosity and viscous boundary layers within the pores become predominantly responsible for dissipating acoustic energy; the scattering and multiple reflections within the pore network contribute to greater energy loss and, in general, the material naturally performs better without needing as much thickness or added complexity. This behavior is well described by models such as the Johnson-Champoux-Allard framework for rigid-frame porous media9,10, which capture frequency-dependent viscous and thermal dissipation mechanisms. As a result, although porous materials are a well-established solution for medium- and high-frequency sound absorption, their performance at lower frequencies is typically limited. In this context, we subsequently refer to the low- and mid-frequency ranges as those extending up to 500 Hz and from 500 to 1000 Hz, respectively, in line with common definitions found in the literature—see Figure 1.1 in ref. 11).

Significant efforts have been made in recent years to increase the sound absorption properties of porous materials in the low and mid frequency regime and, in general, in a broad frequency range, by means of structural design methods. This leads to more and more complex architectures, including: (i) incorporating local resonance mechanisms by embedding rigid inclusions12, or Helmholtz resonators13 within the porous materials13,14, (ii) adding rigid partitions into the porous media15,16, (iii) using porous materials backed with periodic17 and fractal irregularities18, (iv) combining porous media with membranes19, perforated panels20, or labyrinthine channels21,22, and (v) periodically arranging different porous material elements23, among other strategies. As a result, the absorption performance is not determined only by the properties of the material, but also by the geometric configuration of the unit cell24,25.

In addition to the studies mentioned above, the introduction of double porosity26,27 has proven to offer a relatively simple but effective approach to improve sound absorption of porous materials in a wide range of frequencies. In practical terms, the approach consists in featuring the porous materials with two scales of pores: the micro-pores, located within the porous matrix, and the meso-pores, e.g. created by perforating holes in an otherwise homogeneous porous material. The strong interaction between these two pore scales has been shown to enhance energy dissipation at low frequencies, thus promoting improved sound absorption. Specifically, Atalla et al.28 developed a code based on the finite element method (FEM) to examine the effects of meso-pore porosity, hole size, and hole distribution on sound absorption performance. Sgard et al.29 provided useful guidelines for designing double porosity materials, including a criterion to differentiate between two cases of contrast of permeability, and explored the impact of the distribution of the air cavity on sound absorption. Bécot et al.30 tested the sound absorption of foam samples with varying hole distribution patterns, diameters, and depths. The possibility of inserting another porous medium into the perforation holes of the original double porosity materials was also investigated31,32.

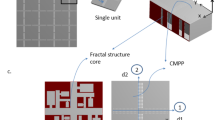
Building on these findings, this study introduces a Sierpiński-inspired double porosity design, i.e., a design where the meso-holes are arranged in a multiscale pattern based on a two-dimensional fractal geometry inspired by the Sierpiński carpet. In mathematics, a fractal is a curve or geometric figure in which each part exhibits the same statistical characteristics as the whole. A classical example is the snowflake, where similar patterns recur at progressively smaller scales. There are various methods for generating geometric fractals, the most common of which involves recursively subdividing a shape into smaller self-similar components, removing one or more of them, and repeating the process. This approach can be applied to different geometric shapes. For example, applying this method to an equilateral triangle, that is, by removing the central triangle at each iteration, produces the Sierpiński triangle, first formally described by W. Sierpiński in 1915 (see Fig. 1a). Another well-known example of a planar self-similar fractal is the Sierpiński carpet, also introduced by Sierpiński in 1916 as a two-dimensional generalization of the Cantor set. Its construction begins with a square divided into nine equal smaller squares, from which the central square is removed, leaving \(\frac{8}{9}\) of the area intact. This operation is then recursively applied to each of the remaining eight squares (see Fig. 1b). The same principle can be extended to three dimensions: when applied to cubes, it results in the Menger sponge.

Fig. 1: Rationale behind the Sierpiński carpet-inspired design.
figure 1

Illustration of four hierarchical levels for the a Sierpiński triangle and b Sierpiński carpet inspiring c our design in the sense of motivating the incorporation of self-similar (circular) voids at multiple levels within a porous medium.

Full size image

In this context, the Sierpiński triangle and the Sierpiński carpet served as inspiration for our design in the sense of motivating the incorporation of self-similar (circular) voids at multiple levels within a porous medium (see Fig. 1c). For ease of manufacturing and to match the circular cross-section of the impedance tube used in our laboratory, we chose the initial geometry to be cylindrical, as well as the cross-sections of the holes introduced at each iteration. This choice does not significantly affect the acoustic absorption performance compared to an alternative design, for example, starting from a square geometry with self-similar square holes.

The property of self-similarity has been leveraged to design acoustic metamaterials for bandgap widening and tuning33, low-frequency sound attenuation34,35,36,37,38, and near-perfect sound absorption39. In particular, Castineira et al.40,41 proposed a sonic crystal designed with a Sierpiński triangle structure, showing a wide frequency band gap resulting from the overlap of gaps corresponding to different length scales. Huang et al.42 observed multiple band gaps in a phononic crystal designed with a Sierpiński carpet structure, demonstrating that relaxing the self-similarity condition (thus, designing quasi-Sierpiński structures) endowed the system with a higher degree of tunability. Moreover, the effects of increasing hierarchical orders in the wave attenuation characteristics of Sierpiński carpet-inspired mechanical structures have been shown to be not equivalent to the superposition of the individual effects of the inclusions/voids at each level43. Enhanced low-frequency absorption has been observed in a 3D-printed Menger sponge44. Finally, randomly arranged metal fibers (with assumed transverse isotropy) were fabricated to engineer the micro-structure of porous fibrous materials, leading to significant improvements in their acoustic properties45. In this case, self-similar Sierpiński-type gaskets (triangles) were considered to model the pore areas and fractal dimension, without, however, actually realizing Sierpiński-based designs.

The literature thus seems to suggest that Sierpiński-inspired structures are potential good candidates for acoustic absorption applications. To the best of the authors’ knowledge, Sierpiński-inspired pattern designs have yet to be applied to porous materials. In this study, we aim to fill this gap by investigating the impact of incorporating multiple levels of Sierpiński-inspired fractals when introducing holes at the meso-scale. This is achieved by recursively introducing through-thickness holes at different length scales, referred to as hierarchical levels (HLs), within a cylindrical block of porous material. Using numerical calculations and impedance tube measurements, we demonstrate that the absorption coefficient improves as hierarchical Sierpiński carpet-inspired patterning is added into the porous layer. Our findings indicate that the introduction of multiple HLs can simultaneously (i) enhance absorption capacity and (ii) reduce the weight of the acoustic panel.

Results

Design strategy

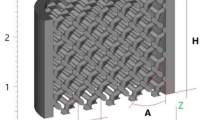
To assess the absorption performance of Sierpiński-inspired double porosity materials compared to conventional porous ones, we initially consider a rigidly backed cylinder of radius R = 96 mm and thickness H = 80 mm, called the geometry of the zero hierarchical level (0th HL). Circular through-thickness holes of different sizes are then progressively drilled into the cylinder, aligned parallel to its axis, as additional hierarchical levels are introduced. A schematic representation and photographs of the unit cells manufactured for the HLs 1st, 2nd, and 3rd used in this study are shown in Fig. 2a–c and d–f, respectively. At each additional hierarchical level n ∈ [0, 3] introduced, the circular holes are scaled down to fit within the previous level n − 1, ensuring that a minimum distance of 5 mm is maintained between adjacent holes to meet manufacturing constraints. Specifically, the 1st HL is obtained by drilling a single hole of radius a1 = 30 mm at the center of the cylinder (as reported in Fig. 2a, d). The next hierarchical level, 2nd HL, is created by drilling a set of 8 additional holes with a radius of a2 = 6 mm, arranged in an equiangular polar pattern around the single hole from the previous (first) hierarchical level. These new holes are placed at a distance of d2 = 65 mm from the center of the cylinder (see Fig. 2b, e). Finally, 3rd HL is determined by drilling 8 additional holes of radius a3 = 3 mm around each of the 8 holes of radius a2 of the previous HL. These new holes are placed at a distance of d3 = 15 mm from the center of the holes of 2nd HL (see Fig. 2c, f).

Fig. 2: Design strategy of the Sierpiński-inspired fractal meso-porosity.
figure 2

Schematic in-plane representation a–c and photographs of the manufactured samples d–f for the 1st, 2nd, and 3rd fractal levels of the proposed porous materials. The 0th fractal level, corresponding to a conventional cylinder of porous material (R = 96 mm and H = 80 mm) is not reported for the sake of brevity. Geometrical parameters are reported in the main text. Geometrical and acoustic parameters of the unit cell are provided in the text. g A schematic representation of reflection experiment and h a photograph of the impedance tube used to perform the measurements.

Full size image

This design strategy, demonstrated here for hierarchical levels up to n = 3, can be recursively extended to higher orders (n > 3), potentially enabling a bridge between micro- and macro-porosity scales. Cylindrical cavities were selected for inclusions due to their compatibility with water jet cutting technology, which facilitates precise and efficient fabrication. The continuous porous substrate is made of polyurethane foam characterized by the following nominal parameters: static airflow resistivity σ = 40,000 Pa.s/m2, porosity ϕ = 0.989, tortuosity α∞ = 1.21, viscous characteristic length \(\Lambda =\sqrt{8{\alpha }_{\infty }\eta /10\phi \sigma }=2.12\cdot 1{0}^{-5}\) m, thermal characteristic length \({\Lambda }^{{\prime} }=3\Lambda =6.36\cdot 1{0}^{-5}\) m with the viscosity of air being η = 1.839 ⋅ 10−5 kg/m. s. The properties of the porous material were selected to closely match the most influential parameter affecting absorption performance, namely the static airflow resistivity σ, targeting a value as close as possible to 40,000 Pa.s/m2 (see parametric studies in the next section). This choice ensured operation within the high-performance (red) region of the parameter space.

When we turned to commercially available materials, the closest properties were provided by a porous material made from waste produced from standard foaming processes. This porous material was obtained from the cut or lamination residues, shredded into small flakes of the desired size, and the final material is the result of the careful mix of flakes having different mass densities and a prescribed amount of binder.

Measurement and absorption mechanism

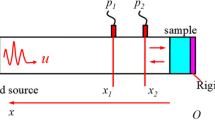
Figure 2 g and h report a schematic representation and a photograph of the experimental setup (impedance tube) used to measure the absorption coefficient of the samples described above, respectively (refer to the section “Methods: Measurements” for more details of the experimental setup).

The measured absorption coefficients for each hierarchical level are shown in Fig. 3, with black, red, blue, and green circular markers representing the HL 0th, 1st, 2nd, and 3rd, respectively. Continuous lines report the numerical absorption coefficient calculated via the Finite Element Method (refer to “Methods: Finite Element Modeling” for further details on the numerical models).

Fig. 3: Absorption and dissipation mechanisms across hierarchical levels (HLs) of the Sierpiński-inspired porous material.
figure 3

Absorption coefficients as a function of frequency for the a 0th, b 1st, c 2nd, and d 3rd hierarchical levels (HLs). Continuous lines represent numerical results for the hierarchical (multi-hole) configuration, while dashed lines correspond to single-hole configurations with equivalent total void area. Circles indicate experimental measurements. Transparent lines denote the absorption response of the preceding HL for comparison. Insets show normalized acoustic pressure fields, \(\frac{| p| }{\max | p| }\), in a one-eighth section of the geometry, where red corresponds to 1 and blue to 0. Pressure maps are displayed at the frequencies marked by black, red, blue, and green stars in the main plots, illustrating dissipation mechanisms dominated by a absorption, b wave localization, or a combination of both (c, d).

Full size image

Figure 3 illustrates the evolution of the absorption coefficient α as a function of frequency for different hierarchical levels (HL0 to HL3). Although there is a slight reduction in absorption at very low frequencies (below 200 Hz), where HL0 slightly outperforms the higher hierarchical levels, the introduction of successive hierarchical levels leads to several notable improvements:

  • Increased Peak Absorption. The maximum value of the absorption coefficient increases monotonically with each additional hierarchical level. Specifically, the peak absorption rises from α = 0.79 at 1000 Hz for the 0th level to nearly perfect absorption (α ≈ 1) at ~500 Hz for the 3rd level (highlighted by the green star in Fig. 3d).

  • Progressive Enhancement of Mid-Frequency Absorption. When frequencies above ~420 Hz are considered, structures with higher hierarchical levels consistently exhibit higher absorption values compared to lower levels.

  • Improved Low-Frequency Performance. HL1 and HL2 begin to outperform HL0 from around 210 Hz, whereas all higher-order structures (HL1 through HL3) demonstrate superior performance from ~280 Hz onward.

  • HL2 consistently outperforms HL1, which in turn outperforms HL0, throughout the entire frequency range analyzed.

These trends underscore the effectiveness of hierarchical structuring in broadening and amplifying absorption characteristics. The observed enhancements can be attributed to a redistribution of the resonance modes induced by the increased geometrical complexity. As additional hierarchical levels are introduced, the structure supports a broader range of modal interactions, which enhances broadband absorption but may redistribute energy away from very low-frequency resonances.

Normalized pressure fields \(\frac{| p| }{\max | p| }\) are shown as insets of panels a–d in Fig. 3 (with color-maps ranging from 0, blue, to 1, red). Due to symmetry conditions, one-eight of the geometry is reported, enabling us to observe the pressure fields along the longitudinal section of the cylinders (parallel to the cylinder axis), as well as the cross-section at the base of the cylinders (normal to the cylinder axis), for n ∈ [0, 3] HL. The pressure maps are taken at a single frequency in the range [400—550] Hz, corresponding to the highest absorption values for the 1st–3rd HL (marked on the curves by black, red, blue, and green stars, respectively).

The incident acoustic wave, which affects the porous material 0th HL from left to right (as shown by the black arrow in the inset), generates a pressure field that is uniformly distributed throughout the transverse cross-section of the cylinder and gradually decreases along the longitudinal axis of the cylinder (see Fig. 3a). This mechanism is similar to the one reported by Liu et al.46, where the first absorption peak indicates a pressure distribution that decreases along the depth of the medium and corresponds to a quarter-wavelength fit into the material. When 1st HL is introduced (Fig. 3b), the highest pressure levels are observed around the perforation, indicating that the primary dissipation mechanism shifts toward localization rather than absorption within the porous material, a reminiscence of the wave trapping mechanism leading to frequency-dependent localization within small spaces explained by Sornette et al.47,48,49. Finally, as additional holes are drilled (2nd and 3rd HL), the pressure field increases not only within the newly created holes but also within the porous layer itself. This indicates that, at higher HLs, both absorption and localization mechanisms take place simultaneously.

To further demonstrate the added value of higher-order hierarchical structuring, we conducted a comparative analysis showing that the observed performance gains cannot be achieved by merely tuning the radius of a single-hole design. Specifically, we computed and compared the sound absorption of the second and third hierarchical levels with that of a single-hole configuration (as used in the first HL). To ensure a fair comparison, the total perforated area between the HL and the corresponding single-hole configuration was kept constant. The resulting absorption spectra are reported as dashed lines in Fig. 3c, d for the 200–1000 Hz range, and as dashed-dotted lines for the extended 200–12,000 Hz range in Fig. 4. Introducing hierarchical structures leads to a consistent improvement in sound absorption, not only within the 200–1000 Hz band but even more significantly between 1000 and 12,000 Hz, along with sharper and more distinct absorption peaks for both HL2 and HL3 compared to their single hole counterparts. In particular, HL3 approaches near-perfect absorption (α = 1) below 1000 Hz.

Fig. 4: Comparison of the absorption efficiency of the higher HLs with a single-hole structure of the same void area.
figure 4

Absorption coefficient as a function of frequency for a 2nd-order and b 3rd-order hierarchical levels (HLs). The results for the hierarchical structures are shown as continuous lines, while the dashed lines represent single-hole configurations (analogous to the 1st HL) with an equivalent total air-filled area.

Full size image

The variation in the absorption coefficient following the increase in the hierarchical order can be explained by the double porosity theory50. The interaction between the meso-scale (in this case, the hierarchical pores) and the micro-scale (micro-pores present in the base material) leads to an additional pressure diffusion inside the micro-pores. The distribution of pressure is not uniform in the system at the meso-scale, which endows the system with increased dissipation due to the creation of secondary networks of pores29. As a result, the double porosity material exhibits a strong permeability contrast, improving sound absorption compared to its single porous counterparts (without mesopores)51. When meso-scale holes are properly designed, an increase in absorption is observed despite the reduction of volume of porous material to the hierarchical level.

To gain further insight into the observed dissipation mechanisms observed in the proposed hierarchical Sierpiński-inspired design, we implemented a “porous composite model” using the AlphaCell software product52, as described in ref. 53. This model is a generalization of the double porosity theory of Boutin et al.27,50, allowing us to represent a porous substrate with porous inclusions, which accounts for interactions between multiple scales of porosity. Figure 5 reports the results obtained, particularly for HL2, confirming that dissipation is mainly due to interaction between the different porosity scales. However, some discrepancies between the analytical predictions and both the FE simulations and the experimental results suggest that local effects around the smallest perforations (effects not captured by the homogenized analytical model) also play a role in the overall dissipation of the sound. We believe that interactions between mesoscale pores (pores introduced by the hierarchical levels in our case) and microscale pores (pores already present in the base material) lead to additional pressure diffusion within the micro-pores. This causes a non-uniform pressure distribution on the mesoscale, which improves energy dissipation through the formation of secondary pore networks29,51. As a consequence, we can conclude that the arrangement of the holes plays a key role, suggesting that the enhanced performance also stems from a more efficient meso-pore architecture enabled by the hierarchical Sierpiński-inspired design. For higher HLs the generalized theory of porous composites53 can be used to explain the dissipation mechanisms. In this context, the Sierpiński approach is a convenient tool for the design of material embedding multiple levels of porosity scales.

Fig. 5: Comparison of the results with the “porous composite model”.
figure 5

Comparison between experimental measurements and numerical results obtained using the AlphaCell software53, a generalization of the double porosity theory of Boutin et al.27,50, allowing us to represent a porous substrate with porous inclusions, which accounts for interactions between multiple scales of porosity. The solid blue line (without markers) represents the measured data, while the solid red and green lines with triangular and diamond-shaped markers correspond to numerical predictions based on the model taking into account the actual size of the perforations at HL1 and HL2 and a model single perforation with equivalent porous inclusion, respectively.

Full size image

Finally, the z-derivative of the dissipated acoustic intensity54 \(\frac{\partial I}{\partial z}\) along the line that passes through the centers of the holes is calculated and reported in Fig. 6a. We observe that dissipation is stronger around the edges of the porous material (regions of the fastest intensity decay occur near the air holes), confirming that the holes may potentially enhance the efficiency of porous material—wave interaction. Reconstruction of the \(\frac{\partial I}{\partial z}\) profiles is reported in Fig. 6b, spatially denoting the areas of the fastest intensity decay (close to air holes). Intensity derivative distributions have been extracted at the frequencies of the star-shaped markers reported in Fig. 3.

Fig. 6: Z-derivative of the absorbed intensity and its profile reconstruction.
figure 6

a Spatial derivative in the z-direction of the acoustic field intensity (\(\frac{\partial I}{\partial z}\)) along a radial line connecting the center of the cylinder to its right edge. b Reconstruction of the \(\frac{\partial I}{\partial z}\) profiles denoting the areas of fastest intensity decay (close to the air holes). Intensity derivative distributions have been extracted in correspondence of the star-like markers reported in Fig. 3.

Full size image

Dependence on the thickness of the specimen and the airflow resistivity of the porous material

It is well known that absorption properties can vary considerably depending on the thickness and JCA parameters of the porous layer. To illustrate how these classical parameters influence, and are influenced by, the introduction of hierarchical geometrical structuring, the relationships between absorption performance and (i) thickness as well as (ii) airflow resistivity of the porous layer have been calculated (and reported in Fig. 7a–c and d–f, respectively). The results are reported in terms of the difference in the absorption coefficients (α3 − α2), (α2 − α1) and (α1 − α0) relative to the HL n ∈ [0, 3] as functions of frequency.

Fig. 7: Influence of the thickness and airflow resistivity of the porous layer on the absorption coefficient.
figure 7

Maps of the difference of the absorption coefficients of successive hierarchical levels a α3 − α2, b α2 − α1, and c α1 − α0 as a function of the thickness H of the porous layer and of the frequency. The threshold of increased (regions of the plots in red) / decreased (regions of the plots in blue) performance can be easily identified by the 0-marked isolines (equal absorption performance between two successive hierarchical levels). d–f Maps of the difference of the absorption coefficients of successive hierarchical levels as a function of the airflow resistivity σ of the porous layer and of the frequency when the thickness of the porous cylinder is fixed at H = 80 mm. Similar to the previous case, most combinations of (σ, f) indicate that introducing hierarchical structures enhances absorption.

Full size image

Figure 7 a–c help identifying the minimum thickness of the porous layer at which the addition of hierarchical levels enhances performance. This threshold is frequency-dependent and can be readily recognized by the 0-marked isolines, which represent equal performance between two successive hierarchical levels. Therefore, the areas in red gradation indicate (αn − αn−1) > 0, highlighting the combinations of “cylinder thickness—frequency” with improved performance at the higher hierarchical level. In contrast, when the maps shift to blue, (αn − αn−1) < 0, and thus the introduction of additional holes proves ineffective.

The study exploring the effect on the absorption coefficient due to changes in the airflow resistivity of the porous layer was also carried out, with the results presented in Fig. 7d–f for a porous cylinder with a fixed thickness of H = 80 mm. The air flow resistivity parameter was varied within the range of 10,000–50,000 Pa.s./m2, as this encompasses typical values for porous media used in practical applications.

It is worth emphasizing here that although the JCA model is often described as a 5-parameter model, the literature (e.g., ref. 7) acknowledges that a more physically consistent representation can be achieved by accounting for the interdependence between certain parameters, particularly at high frequencies and for low airflow resistivity values (σ < 10 kPa⋅s/m2).

In our case, we considered the fact that parameters such as the viscous characteristic length Λ and the thermal characteristic length \(\Lambda^{\prime}\) are not entirely independent of the airflow resistivity σ. Empirical correlations suggest that \(\Lambda^{\prime}\) is generally about three times Λ, and both are influenced by the geometry of the pores, which is indirectly reflected in σ. To incorporate this interdependence into the model and ensure physical consistency, we adopted the following relation derived from homogenization theory and commonly used in the acoustics of porous media: 8α∞η/σϕΛ2 ≈ constant7. This expression relates the viscous characteristic length Λ to airflow resistivity σ, porosity ϕ, dynamic viscosity η, and tortuosity α∞.

The same color map as described above is applied here. Similarly to the previous case, most combinations of (σ, f) indicate that the introduction of hierarchical structures improves absorption. In particular, the overall increase in α is already more pronounced after the introduction of the first hole (1st HL).

Dependence on the angle of incidence

The angle of incidence is another parameter that can significantly affect the absorption performance of the porous layer. To evaluate the absorption of the proposed design at different angles, the geometry used for the measurements must be slightly modified from a circular to a square cross-section (to properly apply periodic Bloch-Floquet conditions), while maintaining the key characteristics of the Sierpiński carpet-inspired hierarchical patterning as outlined above. This adjustment is illustrated in Fig. 8. Specifically, Fig. 8a shows the 0th through 3rd HLs with a square cross-section of side 2R = 192 mm and a thickness of H = 80 mm. The same JCA parameters as described in the previous section are used.

Fig. 8: Unit cells and schematic of the numerical model to calculate the dependence of the absorption from the angle of incidence.
figure 8

a Modified unit cells (from circular to square cross-section) used to calculate the dependence of the absorption from the angle of incidence θ. All the hierarchical levels (0th–3rd) are reported. The side of the unit cell is 2R = 192 mm and its height H = 80 mm. b A schematic representation of the numerical model implemented to calculate the absorption coefficient for an incident plane wave at an angle θ on an infinitely periodic (in the x-direction) array of these unit cells.

Full size image

Figure 8 b presents a schematic of the numerical model used to calculate the absorption coefficient of an incident plane wave at an angle θ on an infinitely periodic (in the x-direction) array of these unit cells. The plane of incidence, along with the wave vector inclined at an angle θ, is illustrated by the transparent light brown area. Periodic Bloch-Floquet boundary conditions are applied in the domains normal to the x-axis, while Neumann conditions (\(\frac{{\rm{d}}p}{{\rm{d}}n}=0\)) are applied in the domains normal to the y-axis.

Figure 9 a–d present maps of the absorption coefficient for the four HLs in the (θ, f) plane. It is worth noticing that regions of very high absorption (α > 0.9) occur over a relatively wide range of (θ, f) combinations. At higher angles (θ > 70∘), the absorption coefficient decreases as θ increases throughout the frequency range considered.

Fig. 9: Absorption maps as a function of the angle of incidence.
figure 9

a–d Maps of the absorption coefficient in the (f, \(\theta\))-plane for all the considered HLs, i.e., 0th−3rd. e–g Comparison of the absorption coefficient maps presented above reported as α3 − α2, α2 − α1, and α1 − α0.

Full size image

For comparison, the maps of α3 − α2, α2 − α1, and α1 − α0 are shown in Fig. 9e–g. A significant increase in absorption performance (up to 20%) is observed with the introduction of the first hierarchical level, as indicated by large portions of the map (θ, f) turning red. However, at higher angles and in the low- and mid-frequency regions, the fully porous material outperforms the hierarchical designs. Similar trends are observed with the introduction of the 2nd and 3rd hierarchical levels.

Discussion

The sound absorption properties of the Sierpiński carpet inspired hierarchical patterning (through thickness holes) in porous materials have been examined both numerically and experimentally.

Although there is a slight reduction in absorption at very low frequencies (below 200 Hz), where HL0 slightly outperforms the higher hierarchical levels, the introduction of successive hierarchical levels leads to several notable improvements, namely: (i) increased peak absorption, (ii) progressive enhancement of mid-frequency absorption, and (iii) improved low-frequency performance. These trends underscore the effectiveness of hierarchical structuring in broadening and amplifying absorption characteristics.

Importantly, it has been shown that the higher absorption values cannot be obtained by using a single hole (non-hierarchical design) yielding the same void area as the distributed holes.

The increase in absorption was achieved despite a reduction in the total weight of the porous material used, with hierarchically introduced features having a significant effect on the performance. The mechanism responsible for this effect is shown to be the localization of the pressure field within the holes added by the hierarchical patterning.

A detailed parametric analysis of the absorption coefficient for the hierarchical structures, considering (i) the thickness of the sample, (ii) the airflow resistivity of the porous materials, and (iii) the angles of incidence, demonstrated a rather strong robustness of the proposed design strategy. This analysis also helped identify optimal parameter ranges to maximize absorption within the target frequency range. Numerical calculations were experimentally validated for normal incidence using impedance tube measurements, which showed excellent agreement with the theoretical predictions.

The design strategy outlined here, featuring three hierarchical levels, can be recursively extended to additional levels, with great potential applications in sound insulation engineering, where the need for higher absorption levels coincides with the demand for lighter-weight panels.

Methods

Measurements

Evaluation of the sound absorption levels is carried out in accordance to the < < two-microphone technique > > (standard ISO 10534-2)55. It consists of: (i) a laboratory-made impedance tube (see Fig. 2g, h) of 190 cm of length and 19.2 cm of diameter, (ii) four loudspeakers Visaton FRS with a diameter of 50 mm linked to (iii) an amplifier Brüel et Kjaer of type 2706, and (iv) two microphones Sennheiser MKE 2P.

For each experiment, an 80 mm thick sample is placed against the rigid backing termination. The distance between the rigid backing and the first microphone is 80 cm and the two microphones are separated by a 10 cm distance. Harmonic plane waves are swept from 200 Hz to 1 kHz (highest frequency corresponding to the plane wave cutoff frequency of the tube) with a frequency step of Δf = 15 Hz. Each harmonic wave has a duration of 1 s. Pressures at both microphone positions are recorded and then post-processed using a home-made Matlab program.

Modelling of the porous materials

The porous samples are described through the Johnson-Champoux-Allard (JCA) model considering the following five parameters: static airflow resistivity σ, high frequency limit of porosity ϕ, tortuosity α∞, viscous and thermal characteristic lengths \(\Lambda ,\Lambda^{\prime}\). These parameters are used to calculate the material’s effective density and bulk modulus as follows:

$$\begin{array}{r}{\rho }_{p}=\frac{{\rho }_{0}{\alpha }_{\infty }}{\phi }\left(1-\frac{i{\omega }_{c}}{\omega }F(\omega )\right),\\ {K}_{p}=\frac{\gamma {P}_{0}}{\phi }{\left(\gamma -(\gamma -1){\left(1-\frac{i{\omega }_{c}^{{\prime} }}{\Pr \omega }G(\Pr \omega )\right)}^{-1}\right)}^{-1},\end{array}$$
(1)

where \({\omega }_{c}=\frac{\sigma \phi }{{\rho }_{0}{\alpha }_{\infty }}\) is the Biot frequency, \({\omega }_{c}^{{\prime} }=\frac{{\sigma }^{{\prime} }\phi }{{\rho }_{0}{\alpha }_{\infty }}\), \({\sigma }^{{\prime} }=\frac{8{\alpha }_{\infty }\eta }{\phi {\Lambda }^{{\prime} 2}}\)10 is the thermal resistivity56 and the correction functions are given by9,57:

$$\begin{array}{r}F(\omega )=\sqrt{1+i\eta {\rho }_{0}\omega {\left(\frac{2{\alpha }_{\infty }}{\sigma \Lambda \phi }\right)}^{2}},\\ G(Pr\omega )=\sqrt{1+i\eta {\rho }_{0}\Pr \omega {\left(\frac{2{\alpha }_{\infty }}{{\sigma }^{{\prime} }{\Lambda }^{{\prime} }\phi }\right)}^{2}},\end{array}$$
(2)

being P0 = 101.325 kPa the atmospheric pressure. The parameters of air (which is assumed to be the fluid present in the pores) such as density ρ0, Prandtl number Pr, heat capacity ratio γ and viscosity η are calculated according to the actual ambient conditions of temperature, pressure and relative humidity. Once these parameters are determined, the wavenumber \({k}_{p}=\omega \sqrt{\frac{{\rho }_{p}}{{K}_{p}}}\) and the effective acoustic impedance \({Z}_{p}=\sqrt{{\rho }_{p}{K}_{p}}\) can be obtained.

Finite element modeling

The numerical simulations presented in this study were performed using the Finite Element Method (FEM) in the frequency domain, implemented via the COMSOL Multiphysics “Pressure Acoustics” module, which solves Helmholtz equations to simulate the “reflection experiment” performed in the impedance tube on the samples reported in Fig. 2d–f. The JCA parameters mentioned in the paper are fed into the model to describe the porous materials via the < < Poroacoustics > > node, which accounts for viscothermal losses in rigid-frame porous media. Neumann boundary conditions were applied to the lateral tube walls to mimic the physical boundaries of the experimental setup, while Perfectly Matched Layers (PML) were implemented at the inlet to suppress reflections. A harmonic plane wave is created in the air domain and is incident in the porous domain. In the perforations comprising the 1st, 2nd and 3rd HL, the Thermoviscous acoustic module is utilized. The domains are meshed with quadratic tetrahedral elements of maximum size smaller than λmin/10, where λmin is the minimum associated wavelength. We present one-eight of the geometry modeled in Comsol for the 3rd HL in Fig. 10. The abbreviations used in the figure are the following: IP, integration plane where we compute the reflected pressure, PA, poroacoustic module, and TvA, thermoviscous acoustic module.

Fig. 10: Schematic representation of the COMSOL model used to simulate the reflection experiment in the impedance tube for the samples shown in Fig. 2d–f.
figure 10

The simulations were carried out in the frequency domain using the Pressure Acoustics module of COMSOL Multiphysics, which solves the Helmholtz equation for the acoustic pressure field. Neumann boundary conditions were applied to the lateral walls to emulate the rigid boundaries of the impedance tube, while a Perfectly Matched Layer (PML) was implemented at the left end of the model to absorb outgoing waves. A harmonic plane wave was introduced in the air domain using a “background pressure field” excitation. In the perforations corresponding to the first, second, and third hierarchical levels (HL1, HL2, HL3), the Thermoviscous Acoustics (TvA) module was used to capture viscous and thermal losses within narrow channels. This figure shows one-eight of the modeled geometry for HL3. Additional labels in the figure include: IP = Integration Plane, where the reflected pressure is calculated; PA = domain where the Poroacoustics module is applied.

Full size image