Abstract
We construct two families of orthogonal product quantum states that cannot be exactly distinguished by local operation and classical communication (LOCC) in the quantum system of  2k+i ⊗
2k+i ⊗  2l+j (i, j ∈ {0, 1} and i ≥ j ) and
2l+j (i, j ∈ {0, 1} and i ≥ j ) and  3k+i ⊗
3k+i ⊗  3l+j (i, j ∈ {0, 1, 2}). And we also give the tiling structure of these two families of quantum product states where the quantum states are unextendible in the first family but are extendible in the second family. Our construction in the quantum system of
3l+j (i, j ∈ {0, 1, 2}). And we also give the tiling structure of these two families of quantum product states where the quantum states are unextendible in the first family but are extendible in the second family. Our construction in the quantum system of  3k+i ⊗
3k+i ⊗  3l+j is more generalized than the other construction such as Wang et al.’s construction and Zhang et al.’s construction, because it contains the quantum system of not only
3l+j is more generalized than the other construction such as Wang et al.’s construction and Zhang et al.’s construction, because it contains the quantum system of not only  2k ⊗
2k ⊗  2l and
2l and  2k+1 ⊗
2k+1 ⊗  2l but also
2l but also  2k ⊗
2k ⊗  2l+1 and
2l+1 and  2k+1 ⊗
2k+1 ⊗  2l+1. We calculate the non-commutativity to quantify the quantumness of a quantum ensemble for judging the local indistinguishability. We give a general method to judge the indistinguishability of orthogonal product states for our two constructions in this paper. We also extend the dimension of the quantum system of
2l+1. We calculate the non-commutativity to quantify the quantumness of a quantum ensemble for judging the local indistinguishability. We give a general method to judge the indistinguishability of orthogonal product states for our two constructions in this paper. We also extend the dimension of the quantum system of  2k ⊗
2k ⊗  2l in Wang et al.’s paper. Our work is a necessary complement to understand the phenomenon of quantum nonlocality without entanglement.
2l in Wang et al.’s paper. Our work is a necessary complement to understand the phenomenon of quantum nonlocality without entanglement.
Similar content being viewed by others
Introduction
In quantum cryptography, quantum entangled states are easily distinguished by performing global operation if and only if they are orthogonal. Entanglement has good effects in some cases, but it has bad effects in other cases such as entanglement increases the difficulty of distinguishing quantum states when only LOCC is performed1. When many global operations cannot be performed, LOCC becomes very useful. The phenomenon of quantum nonlocality without entanglement2 is that a set of orthogonal states in a composite quantum system cannot be reliably distinguished by LOCC. The study of quantum nonlocality is one of the fundamental problems in quantum information theory. LOCC is usually used to verify whether quantum states are perfectly distinguished3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23 or not. In refs 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, they focus on the local distinguishability of quantum states such as multipartite orthogonal product states can be exactly distinguished10 or how to distinguish two quantum pure states11,12. Moreover, locally indistinguishability13,14,15,16,17,18,19,20,21,22,23 of quantum orthogonal product states plays an important role in exploring quantum nonlocality.
The nonlocality problem is considered in the bipartite setting case that Alice and Bob share a quantum system which is prepared in an known set contained some mutually orthogonal quantum states. Their aim is to distinguish the states only by LOCC. Bennett et al.2 proposed a set of nine pure orthogonal product states in quantum system of C3 ⊗ C3 in 1999, which cannot be exactly distinguished by LOCC. In 2002, Walgate et al.16 also proved the indistinguishability of the nine states by using a more simple method. Zhang et al.19 extended the dimension of quantum system in Walgate et al.’s16. Yu and Oh22 give another equivalent method to prove the indistinguishability and this method is used to distinguish orthogonal quantum product states of Zhang et al.21. Furthermore, Wang et al.20 constructed orthogonal product quantum states under three quantum system cases of  2k ⊗
2k ⊗  2l,
2l,  2k ⊗
2k ⊗  2l+1 and
2l+1 and  2k+1 ⊗
2k+1 ⊗  2l+1. The smallest dimension of
2l+1. The smallest dimension of  2k ⊗
2k ⊗  2l can be constructed is
2l can be constructed is  6 ⊗
6 ⊗  6 in Wang et al.’s paper20. However, the smallest dimension of
6 in Wang et al.’s paper20. However, the smallest dimension of  2k ⊗
2k ⊗  2l can be constructed is
2l can be constructed is  4 ⊗
4 ⊗  4 in our paper. Ma et al.24 revealed and established the relationship between the non-commutativity and the indistinguishability. By calculating the non-commutativity, the quantumness of a quantum ensemble can be quantified for judging the indistinguishability of a family of orthogonal product basis quantum states. For the orthogonal product states, we firstly use a method to judge the indistinguishability of the set, the proof is meaningful. In this paper, we calculate the non-commutativity to judge the indistinguishability if and only if there exists a set to satisfy the inequality of Lemma 2.
4 in our paper. Ma et al.24 revealed and established the relationship between the non-commutativity and the indistinguishability. By calculating the non-commutativity, the quantumness of a quantum ensemble can be quantified for judging the indistinguishability of a family of orthogonal product basis quantum states. For the orthogonal product states, we firstly use a method to judge the indistinguishability of the set, the proof is meaningful. In this paper, we calculate the non-commutativity to judge the indistinguishability if and only if there exists a set to satisfy the inequality of Lemma 2.
In this paper, we construct two families of orthogonal product quantum states in quantum systems of  2k+i ⊗
2k+i ⊗  2l+j with i, j ∈ {0, 1} (i ≥ j) and
2l+j with i, j ∈ {0, 1} (i ≥ j) and  3k+i ⊗
3k+i ⊗  3l+j with i, j ∈ {0, 1, 2} and the two families of orthogonal product quantum states cannot be exactly distinguished by LOCC but can be distinguished by separable operations. Our constructions give the smaller dimension of quantum system in quantum system of
3l+j with i, j ∈ {0, 1, 2} and the two families of orthogonal product quantum states cannot be exactly distinguished by LOCC but can be distinguished by separable operations. Our constructions give the smaller dimension of quantum system in quantum system of  2k ⊗
2k ⊗  2l than Wang et al.’s20. Wang et al.’s construction can be extended, but our construction in quantum system of
2l than Wang et al.’s20. Wang et al.’s construction can be extended, but our construction in quantum system of  2k+i ⊗
2k+i ⊗  2l+j with i, j ∈ {0, 1} (i ≥ j) is a complete unextendible product bases (i.e. UPB). Therefore, our construction is trivial. The indistinguishability of a complete UPB can be directly judged by performing projective measurements and classical communication, but not Wang et al.’s20. In quantum system of
2l+j with i, j ∈ {0, 1} (i ≥ j) is a complete unextendible product bases (i.e. UPB). Therefore, our construction is trivial. The indistinguishability of a complete UPB can be directly judged by performing projective measurements and classical communication, but not Wang et al.’s20. In quantum system of  3k+i ⊗
3k+i ⊗  3l+j (i, j = 0, 1, 2), it contains not only
3l+j (i, j = 0, 1, 2), it contains not only  2k ⊗
2k ⊗  2l and
2l and  2k+1 ⊗
2k+1 ⊗  2l but also
2l but also  2k ⊗
2k ⊗  2l+1 and
2l+1 and  2k+1 ⊗
2k+1 ⊗  2l+1, so our construction in quantum system of
2l+1, so our construction in quantum system of  3k+i ⊗
3k+i ⊗  3l+j with i, j ∈ {0, 1, 2} is more generalized than Zhang et al.19 and Wang et al.20. We also use a simple method to judge the local indistinguishable by calculating the non-commutativity to quantify the quantumness of a quantum ensemble24, but not Zhang et al. and Wang et al. We also generalize the Theorem 2 in Ma et al.24 to Corollary 1 in Methods in this paper. Our work is a necessary complement to understand the phenomenon of quantum nonlocality without entanglement.
3l+j with i, j ∈ {0, 1, 2} is more generalized than Zhang et al.19 and Wang et al.20. We also use a simple method to judge the local indistinguishable by calculating the non-commutativity to quantify the quantumness of a quantum ensemble24, but not Zhang et al. and Wang et al. We also generalize the Theorem 2 in Ma et al.24 to Corollary 1 in Methods in this paper. Our work is a necessary complement to understand the phenomenon of quantum nonlocality without entanglement.
Results
LOCC indistinguishable orthogonal product quantum states in quantum system of 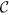 2k+i ⊗
2k+i ⊗ 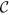 2l+j with k ≥ 1, l ≥ 1 and i, j ∈ {0, 1} (i ≥ j)
2l+j with k ≥ 1, l ≥ 1 and i, j ∈ {0, 1} (i ≥ j)
Case 1. Firstly, we construct LOCC indistinguishable orthogonal product quantum states in quantum system of  2k ⊗
2k ⊗  2l (k, l ≥ 2) (see Fig. 1(a)) and give an example in the smallest dimension (see Fig. 2(a)).
2l (k, l ≥ 2) (see Fig. 1(a)) and give an example in the smallest dimension (see Fig. 2(a)).





Here  . For example,
. For example,  .
.
Proposition 1. In quantum system of  2k ⊗
2k ⊗  2l, there are 4 kl orthogonal product quantum states |ψi〉 (in Eq. (1)) can not be exactly distinguished by LOCC whatever Alice measures firstly or Bob.
2l, there are 4 kl orthogonal product quantum states |ψi〉 (in Eq. (1)) can not be exactly distinguished by LOCC whatever Alice measures firstly or Bob.
Proof. We only discuss the case of Alice measures firstly and the same as Bob. We consider the subspace  2 ⊗
2 ⊗  m to determine POVM elements
m to determine POVM elements  . A set of general
. A set of general  2k ⊗
2k ⊗  2k POVM elements
2k POVM elements  under the basis
under the basis  can be expressed as follows
can be expressed as follows

where aij ≥ 0 and  Firstly, this selected sets {|0〉, |1〉}A, {|1〉, |2〉}A, …, and {|2k − 2〉, |2k − 1〉}A of states are of dimension
Firstly, this selected sets {|0〉, |1〉}A, {|1〉, |2〉}A, …, and {|2k − 2〉, |2k − 1〉}A of states are of dimension  2 ⊗
2 ⊗  2k, Alice cannot find appropriate basis to express them in the form of Eq. (23) in Methods according to the necessary and sufficient condition of Lemma 1.
2k, Alice cannot find appropriate basis to express them in the form of Eq. (23) in Methods according to the necessary and sufficient condition of Lemma 1.
For example, we consider the subspace {|0〉, |1〉}A, there are quantum states

The necessary and sufficiency of Lemma 1 has already been proved by Walgate in ref. 16. Now we apply the necessary and sufficiency of Lemma 1 to verify a00 = a11 and a10 = a01 = 0 in the subspace {|0〉, |1〉}A. Suppose, the form  is set up in Eq. (23), where
is set up in Eq. (23), where 
 ,
,  . The two sets
. The two sets  and
and  satisfy
satisfy  if i ≠ j. However, there also exist quantum states |0 ± 1〉A in the subspace {|0〉, |1〉}A. The reduction to absurdity is used to verify the correctness of the conclusion. Suppose there exists one POVM element that is not proportional to identity to distinguish these quantum states, the express of the POVM element is as follows
if i ≠ j. However, there also exist quantum states |0 ± 1〉A in the subspace {|0〉, |1〉}A. The reduction to absurdity is used to verify the correctness of the conclusion. Suppose there exists one POVM element that is not proportional to identity to distinguish these quantum states, the express of the POVM element is as follows

where α > β ≥ 0. For the quantum state |0〉A, it collapses into α|0〉A after measurement. For the quantum state |1〉Α, it collapses into β|1〉A after measurement. For the quantum states  , they collapse into
, they collapse into  . Hence, if and only if α = β,
. Hence, if and only if α = β,  holds. It produces contradiction between results and assumption. So it does not exist a non-trivial measurement to distinguish the orthogonal product quantum states. For the other subspaces, we have the same conclusions. After Alice performs a general measurement, the effect of this positive operator upon the following states
holds. It produces contradiction between results and assumption. So it does not exist a non-trivial measurement to distinguish the orthogonal product quantum states. For the other subspaces, we have the same conclusions. After Alice performs a general measurement, the effect of this positive operator upon the following states

is entirely specified by those elements a00, a11, a01, a10 draw from the {|0〉, |1〉}A subspace. It means that Alice cannot perform a nontrivial measurement upon the {|0〉, |1〉}A subspace. Thus, the corresponding submatrix must be proportional to the identity. Then, we obtain a00 = a11 = a, a01 = a10 = 0. For the states

and the subspace {|1〉, |2〉}A, we make the same argument. Then we get the result a11 = a22 = a, a12 = a21 = 0. For the states

and subspace {|2〉, |3〉}A, we get the result a22 = a33 = a, a23 = a32 = 0. In the same way, for the subspace {|3〉, |4〉}A, …, the subspace  , we get the result
, we get the result

Because POVM elements  is Hermitian, the equation
is Hermitian, the equation  is correct. Then we obtain
is correct. Then we obtain

Now  can be rewritten as
can be rewritten as

where a is a real number.
We now consider the states  with f = 3, i3 = 0, 2 and the subspace {|0〉, |2〉}A. After Alice measures, the result is either the states orthogonal or distinguishing them outright. If the states are orthogonal, we demand that
with f = 3, i3 = 0, 2 and the subspace {|0〉, |2〉}A. After Alice measures, the result is either the states orthogonal or distinguishing them outright. If the states are orthogonal, we demand that  . So, we get
. So, we get  . For the states
. For the states  with ib = 3, jb = 2l−2 and
with ib = 3, jb = 2l−2 and  , we get the same argument and we get
, we get the same argument and we get  . For the subspace {|0〉, |4〉}A, {|0〉, |5〉}A, … and the subspace {|2k − 3〉, |2k − 1〉}A, we get the results
. For the subspace {|0〉, |4〉}A, {|0〉, |5〉}A, … and the subspace {|2k − 3〉, |2k − 1〉}A, we get the results

Now the  is proportional to the identity. However, if Alice distinguishes the state
is proportional to the identity. However, if Alice distinguishes the state  with f = 3, if = 0, 2, we get the result
with f = 3, if = 0, 2, we get the result  . We can also have the result
. We can also have the result  , therefore a = 0. It produces contradictory with the theorem of Walgate16. So,
, therefore a = 0. It produces contradictory with the theorem of Walgate16. So,  is proportional to the identity and the 4kl orthogonal product states are indistinguishable.
is proportional to the identity and the 4kl orthogonal product states are indistinguishable.
Example 1. Now we will give 16 orthogonal product quantum states in quantum system of  4 ⊗
4 ⊗  4 (see Fig. 2(a)).
4 (see Fig. 2(a)).

where  with
with  .
.
Case 2. Secondly, we construct LOCC indistinguishable orthogonal product quantum states in quantum system of  2k+1 ⊗
2k+1 ⊗  2l+1 with k, l ≥ 1 and l ≤ l (see Fig. 1(b)) and also give an example in the smallest dimension (see Fig. 2(b)).
2l+1 with k, l ≥ 1 and l ≤ l (see Fig. 1(b)) and also give an example in the smallest dimension (see Fig. 2(b)).





Here we just give the construction for k ≤ l. When k > l, it should be rotated along the clockwise direction for Fig. 1(b) to get the construction.
Proposition 2. In quantum system of  2k+1 ⊗
2k+1 ⊗  2l+1, there are (2k + 1)(2l + 1) orthogonal product quantum states |ϕi〉 (in Eq. (13)) can not be exactly distinguished by LOCC whatever Alice measures firstly or Bob.
2l+1, there are (2k + 1)(2l + 1) orthogonal product quantum states |ϕi〉 (in Eq. (13)) can not be exactly distinguished by LOCC whatever Alice measures firstly or Bob.
Example 2. Now we will give 9 orthogonal product quantum states in quantum system of  3 ⊗
3 ⊗  3 (see Fig. 2(b)).
3 (see Fig. 2(b)).

where  with 0 ≤ i < j ≤ 2.
with 0 ≤ i < j ≤ 2.
Case 3. Thirdly, we consider the indistinguishable orthogonal product states in quantum system  2k+1 ⊗
2k+1 ⊗  2l with k ≥ 2, l ≥ 3 (see Fig. 3) and give an example in the smallest dimension (see Fig. 2(c)).
2l with k ≥ 2, l ≥ 3 (see Fig. 3) and give an example in the smallest dimension (see Fig. 2(c)).





Proposition 3. In quantum system of  2k+1 ⊗
2k+1 ⊗  2l, there are 2l(2k + 1) orthogonal product quantum states
2l, there are 2l(2k + 1) orthogonal product quantum states  (in Eq. (15)) can not be exactly distinguished by LOCC whatever Alice measures firstly or Bob.
(in Eq. (15)) can not be exactly distinguished by LOCC whatever Alice measures firstly or Bob.
Example 3. Now we will give 30 orthogonal product quantum states in quantum system of  5 ⊗
5 ⊗  6 (see Fig. 3(c)).
6 (see Fig. 3(c)).

where  with 0 ≤ i ≤ 4 and 0 ≤ j ≤ 5.
with 0 ≤ i ≤ 4 and 0 ≤ j ≤ 5.
LOCC indistinguishable orthogonal product quantum states in quantum system of 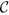 3k+i ⊗
3k+i ⊗ 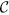 3k+j with i, j ∈ {0, 1, 2}
3k+j with i, j ∈ {0, 1, 2}
We give LOCC indistinguishable orthogonal product quantum states in quantum system of  m ⊗
m ⊗  n.
n.

In quantum system of  3k ⊗
3k ⊗  3l,
3l,  3k ⊗
3k ⊗  3l+2,
3l+2,  3k+2 ⊗
3k+2 ⊗  3l with k, l ≥ 2,
3l with k, l ≥ 2,  3k+2 ⊗
3k+2 ⊗  3l+2 with k, l ≥ 1,
3l+2 with k, l ≥ 1,  3k+1 ⊗
3k+1 ⊗  3l and
3l and  3k+1 ⊗
3k+1 ⊗  3l+2 with k, l ≥ 2.
3l+2 with k, l ≥ 2.

In quantum system of  m ⊗
m ⊗  n including
n including  3k ⊗
3k ⊗  3l+1,
3l+1,  3k+2 ⊗
3k+2 ⊗  3l+1,
3l+1,  3k+1 ⊗
3k+1 ⊗  3l+1 with k, l ≥ 2.
3l+1 with k, l ≥ 2.

In quantum system of  m ⊗
m ⊗  n including
n including  3k ⊗
3k ⊗  3l,
3l,  3k ⊗
3k ⊗  3l+2,
3l+2,  3k+2 ⊗
3k+2 ⊗  3l,
3l,  3k ⊗
3k ⊗  3l+1 and
3l+1 and  3k+2 ⊗
3k+2 ⊗  3l+1 with
3l+1 with  ,
,  3k+2 ⊗
3k+2 ⊗  3l+2 with
3l+2 with  .
.

In quantum system of  m ⊗
m ⊗  n including
n including  3k+1 ⊗
3k+1 ⊗  3l,
3l,  3k+1 ⊗
3k+1 ⊗  3l+2,
3l+2,  3k+1 ⊗
3k+1 ⊗  3l+1 with k, l ≥ 2.
3l+1 with k, l ≥ 2.

The equation k = 2ρ (or k = 2μ + 1) expresses that k is even (or odd).
Proposition 4. In quantum system of  m ⊗
m ⊗  n, there are 3(n + m) − 9 orthogonal product quantum states |θi〉 (in Eqs (17, 18, 19, 20, 21)) can not be exactly distinguished by LOCC whatever Alice measures firstly or Bob, where m = 3k + i, n = 3l + j with i, j ∈ {0, 1, 2}.
n, there are 3(n + m) − 9 orthogonal product quantum states |θi〉 (in Eqs (17, 18, 19, 20, 21)) can not be exactly distinguished by LOCC whatever Alice measures firstly or Bob, where m = 3k + i, n = 3l + j with i, j ∈ {0, 1, 2}.
For the proof of the proposition 2, 3, 4, we make the same arguments to prove the indistinguishability only by LOCC. We only need to modify some relevant places.
Example 4. Now we will give the 21 orthogonal product quantum states in quantum system of  5 ⊗
5 ⊗  5 (see Fig. 2(d)).
5 (see Fig. 2(d)).

where  with 0 ≤ i ≤ 4 and 0 ≤ j ≤ 4.
with 0 ≤ i ≤ 4 and 0 ≤ j ≤ 4.
Discussion
The orthogonal product quantum states constructed by us are indistinguishable by performing local operation and classical communication, but not separable operations25. Now, we discuss whether the separable operations can distinguish these product quantum states or not.
LOCC indistinguishable orthogonal product quantum states in quantum system of 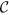 2k+i ⊗
2k+i ⊗ 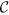 2l+j with i, j ∈ {0, 1} (i ≤ j)
2l+j with i, j ∈ {0, 1} (i ≤ j)
Obviously, these states in Eqs (1, 12, 13, 14, 15, 16) can be distinguished by separable operations. The orthogonal quantum states are not extended. Suppose, the mn quantum states are  respectively. Now, we give the measurement operations
respectively. Now, we give the measurement operations  . Because the set
. Because the set  is an orthogonal product normal base of
is an orthogonal product normal base of  m ⊗
m ⊗  n, the equation
n, the equation  satisfies the completeness and
satisfies the completeness and  is a separable measurement. Due to
is a separable measurement. Due to  , where 1 ≤ i ≤ mn, 1 ≤ j ≤ mn, if the measurement outcome is |φi〉, the quantum state is |φi〉. Therefore, the mn quantum states in Eqs (1, 12, 13, 14, 15, 16) can be distinguished by the separable operations.
, where 1 ≤ i ≤ mn, 1 ≤ j ≤ mn, if the measurement outcome is |φi〉, the quantum state is |φi〉. Therefore, the mn quantum states in Eqs (1, 12, 13, 14, 15, 16) can be distinguished by the separable operations.
Similar to Zhang et al.’s paper19, the multipartite quantum systems can be constructed when m = n = d. Such as in the quantum system  d ⊗
d ⊗  d ⊗
d ⊗  d, we give the orthogonal indistinguishable product states
d, we give the orthogonal indistinguishable product states  , where
, where  and
and  in Eqs (1, 12) of
in Eqs (1, 12) of  2k ⊗
2k ⊗  2l and
2l and  2k+1 ⊗
2k+1 ⊗  2l+1. However, Wang et al.’s construction20 cannot be extended into multipartite quantum systems because the set of orthogonal product states is extendible.
2l+1. However, Wang et al.’s construction20 cannot be extended into multipartite quantum systems because the set of orthogonal product states is extendible.
LOCC indistinguishable orthogonal product quantum states in quantum system of 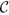 3k+i ⊗
3k+i ⊗ 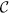 3l+j with i, j ∈ {0, 1, 2}
3l+j with i, j ∈ {0, 1, 2}
Similar to the first construction, the second construction is extendible and distinguished by separable operations. Firstly, these states in Eqs (17, 18, 19, 20, 21) all can be extended to mn orthogonal product states. Then, the proof of the process is the same as above. Finally, we construct the 3(m + n) − 9 quantum states respectively in Eqs (17, 18, 19, 20, 21) that can be distinguished by the separable operations.
Methods
In ref. 16, Walgate et al. gave a necessary and sufficient condition to prove the local indistinguishability of a set of orthogonal product states. If a quantum system which is a qubit does not exist, a uniform conclusion cannot be drawn yet. In all LOCC protocols, there must be a party to leave.
Lemma 116. Alice and Bob share a  2 ⊗
2 ⊗  n dimensional quantum system: Alice has a qubit, and Bob has an n dimensional system that may be entangled with that qubit. If Alice goes first, a set of orthogonal states {|φi〉} is exactly locally distinguishable if and only if there is a basis {|0〉, |1〉}A such that in that basis
n dimensional quantum system: Alice has a qubit, and Bob has an n dimensional system that may be entangled with that qubit. If Alice goes first, a set of orthogonal states {|φi〉} is exactly locally distinguishable if and only if there is a basis {|0〉, |1〉}A such that in that basis

where  if i ≠ j. The Lemma 1 is used to prove the indistinguishability of
if i ≠ j. The Lemma 1 is used to prove the indistinguishability of  2k+i ⊗
2k+i ⊗  2l+j quantum system with i, j ∈ {0, 1} (i ≤ j) and
2l+j quantum system with i, j ∈ {0, 1} (i ≤ j) and  3k+i ⊗
3k+i ⊗  3l+j quantum system with i, j ∈ {0, 1, 2} in Results.
3l+j quantum system with i, j ∈ {0, 1, 2} in Results.
Definition24. Let  be a set of operators. The total non-commutativity for this set is defined
be a set of operators. The total non-commutativity for this set is defined

where [A, B] = AB − BA,  is the trace norm of the operator A,
is the trace norm of the operator A,  .
.
In the Methods of Ma et al.’s24, they give the concrete calculation formula, i.e. suppose  and
and  . Denote
. Denote  with x ∈ [0, 1],
with x ∈ [0, 1],  . Hence
. Hence . When
. When  or 1,
or 1,  , when
, when  ,
,  and when
and when  ,
,  . Nextly, we give Lemma 2 as a standard of judging the indistinguishability of complete orthogonal product states.
. Nextly, we give Lemma 2 as a standard of judging the indistinguishability of complete orthogonal product states.
Lemma 224. For a complete set of  POPS,
POPS,  with
with  , the ε cannot be completely locally distinguished if and only if there exist subsets
, the ε cannot be completely locally distinguished if and only if there exist subsets  , such that
, such that  and
and  are all single sets, i.e. there exist
are all single sets, i.e. there exist  linear independent
linear independent  in
in  and
and  linear independent
linear independent  in
in  satisfying
satisfying

The quantity non-commutativity is used to quantify the quantumness of a quantum ensemble for judging the indistinguishability.
Here, we use the simply method in Lemma 2 to judge the indistinguishability of orthogonal product states in24 by calculating the non-commutativity N. The orthogonal product quantum states in Eqs (1, 13, 15) are complete. Such as the set of complete orthogonal product states in Eq. (1), we give the briefly process. Firstly, we give the sets of εA and εB.




Some duplicate items are removed in εA and εB. Nextly, we concretely calculate the non-commutativity N to quantify the quantumness of a quantum ensemble. There are 2k = (spanεA) linear independent states in εA.

For the last two non-commutativity 1.74k + 0.26 and 1.74k + 0.61, we obtain that the difference (1.74k + 0.26) −(1.74k − 0.61) = 0.87 > 0. Hence, we obtain the inequality as follows

So εA is a single set according to Lemma 2.
There are 2l = dim(spanεB) linear independent states in εB.

For the last two non-commutativity 1.74l + 0.26 and 1.74l + 0.61, we obtain that the difference (1.74l + 0.26)−(1.74l − 0.61) = 0.87 > 0. Hence, we obtain the inequality as follows

So εB is also a single set according to Lemma 2. According to the necessary and sufficient condition of Lemma 2, we make a conclusion that the set of complete orthogonal product quantum states in Eq. (1) is indistinguishable. Similarly, for the orthogonal product states in Eqs (13, 15), we obtain the same conclusion. The quantum orthogonal product states in Eqs (17, 18, 19, 20, 21) are incomplete but can be extended into a complete set, we can also judge the indistinguishability by Corollary 1. Now we will introduce the Corollary 1.
Corollary 1. For a incomplete set of orthogonal product states in quantum system of  m ⊗
m ⊗  n, it firstly should be extended into a complete set
n, it firstly should be extended into a complete set  with
with  if and only if it is completable. The indistinguishability of its complete set can be judged by Lemma 2.
if and only if it is completable. The indistinguishability of its complete set can be judged by Lemma 2.
The Corollary 1 is used to judge the indistinguishability of a set of incomplete orthogonal product states which is completable. The second family construction in quantum system of  3k+i ⊗
3k+i ⊗  3l+j with
3l+j with  is incomplete but can be completable, so we can use the Corollary 1 to judge the indistinguishability. For example, for the quantum system of
is incomplete but can be completable, so we can use the Corollary 1 to judge the indistinguishability. For example, for the quantum system of  3k ⊗
3k ⊗  3l when k, l are all even, quantum states |0〉A|0〉B, |1〉A|n1〉B with n1 = 3, 4, 5, 6, …, 3l − 3, |m〉A|n2〉B with
3l when k, l are all even, quantum states |0〉A|0〉B, |1〉A|n1〉B with n1 = 3, 4, 5, 6, …, 3l − 3, |m〉A|n2〉B with  ,
,  with
with  and |3k − 1〉A|2〉B are added into the original incomplete set. The original incomplete set becomes a complete set. And its indistinguishability can be judged by using Corollary 1.
and |3k − 1〉A|2〉B are added into the original incomplete set. The original incomplete set becomes a complete set. And its indistinguishability can be judged by using Corollary 1.
Additional Information
How to cite this article: Zhang, X. et al. LOCC indistinguishable orthogonal product quantum states. Sci. Rep. 6, 28864; doi: 10.1038/srep28864 (2016).
References
Hayashi, M., Markham, D., Murao, M. & Virmani, S. Bounds on Multipartite Entangled Orthogonal State Discrimination Using Local Operations and Classical Communication. Phys. Rev. Lett. 96, 040501 (2006).
Bennett, C. H. et al. Quantum nonlocality without entanglement. Phys. Rev. A 59, 1070–1091 (1999).
Yu, N. K., Duan, R. Y. & Ying, M. S. Any 2 ⊗ n subspace is locally distinguishable. Phys. Rev. A 84, 012304 (2011).
Ghosh, S., Kar, G., Roy, A., Sen(De), A. & Sen, U. Distinguishability of Bell States. Phys. Rev. Lett. 87, 277902 (2001).
Cohen, S. M. Local distinguishability with preservation of entanglement. Phys. Rev. A 75, 052313 (2007).
Bandyopadhyay, S. Entanglement and perfect discrimination of a class of multiqubit states by local operations and classical communication. Phys. Rev. A 81, 022327 (2010).
Bandyopadhyay, S. & Walgate, J. Local distinguishability of any three quantum states. J. Phys. A: Math. Theor. 42, 072002 (2009).
Duan, R. Y., Feng, Y., Ji, Z. F. & Ying, M. S. Distinguishing Arbitrary Multipartite Basis Unambiguously Using Local Operations and Classical Communication. Phys. Rev. Lett. 98, 230502 (2007).
Zhang, Z. C., Gao, F., Qin, S. J., Zuo, H. J. & Ying, M. S. Local distinguishability of maximally entangled states in canonical form. Quanutm Inf. Process 14, 3961–3969 (2015).
Walgate, J., Short, A. J., Hardy, L. & Vedral, V. Local Distinguishability of Multipartite Orthogonal Quantum States. Phys. Rev. Lett. 85, 4972–4975 (2000).
Virmani, S., Sacchi, M. F., Plenio, M. B. & Markham, D. Optimal local discrimination of two multipartite pure states. Phys. Lett. A 288, 62–68 (2001).
Hillery, M. & Mimih, J. Distinguishing two-qubit states using local measurements and restricted classical communication. Phys. Rev. A 67, 042304 (2003).
Yu, N. K., Duan, R. Y. & Ying, M. S. Four Locally Indistinguishable Ququad-Ququad Orthogonal Maximally Entangled States. Phys. Rev. Lett. 109, 020506 (2012).
Duan, R. Y., Xin, Y. & Ying, M. S. Locally indistinguishable subspaces spanned by three-qubit unextendible product bases. Phys. Rev. A 81, 032329 (2010).
Bennett, C. H. et al. Unextendible Product Bases and Bound Entanglement. Phys. Rev. Lett. 82, 5385–5388 (1999).
Walgate, J. & Hardy, L. Nonlocality, Asymmetry, and Distinguishing Bipartite States. Phys. Rev. Lett. 89, 147901 (2002).
Horodecki, M., De Sen, A., Sen, U. & Horodecki, K. Local Indistinguishability: More Nonlocality with Less Entanglement. Phys. Rev. Lett. 90, 047902 (2003).
Yang, Y. H., Gao, F., Tian, G. J., Cao, T. Q. & Wen, Q. Y. Local distinguishability of orthogonal quantum states in a 2 ⊗ 2 ⊗ 2 system. Phys. Rev. A 88, 024301 (2013).
Zhang, Z. C., Gao, F., Tian, G. Q., Cao, T. Q. & Wen, Q. Y. Nonlocality of orthogonal product basis quantum states. Phys. Rev. A 90, 022313 (2014).
Wang, Y. L., Li, M. S., Zheng, Z. J. & Fei, S. M. Nonlocality of orthogonal product-basis quantum states. Phys. Rev. A 92, 032313 (2015).
Zhang, Z. C., Gao, F., Qin, S. J., Yang, Y. H. & Wen, Q. Y. Nonlocality of orthogonal product states. Phys. Rev. A 92, 012332 (2015).
Yu, S. X. & Oh, C. H. Detecting the local indistinguishability of maximally entangled states. arXiv:1502.01274v1 (2015).
Zhang, Z. C., Gao, F., Cao, Y., Qin, S. J. & Wen, Q. Y. Local indistinguishability of orthogonal product states. arXiv:1509.01814v2 Phys. Rev. A 93, 012314 (2016).
Ma, T., Zhao, M. J., Wang, Y. K. & Fei, S. M. Non-commutativity and local indistinguishability of quantum states. Sci. Rep. 4, 6336 (2014).
Childs, A. M., Leung, D., Mančinska, L. & Ozols, M. A Framework for Bounding Nonlocality of State Discrimination. Commun. Math. Phys. 323, 1121–1153 (2013).
Acknowledgements
The research is funded by National Natural Science Foundation of China, under Grant Nos 61370228, 61472165 and 61502200, and Science and Technology Planning Project of Guangdong Province, China, under Grant Nos 2013B010401018 and 2015B010128008, and Natural Science Foundation of Guangdong province, China, under Grant Nos 2014A030310245 and 2016A030313090.
Author information
Authors and Affiliations
Contributions
X.Z. and X.T. proposed and wrote the main manuscript text. J.W. and Y.L. reviewed the manuscript and provided funding support.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, X., Tan, X., Weng, J. et al. LOCC indistinguishable orthogonal product quantum states. Sci Rep 6, 28864 (2016). https://doi.org/10.1038/srep28864
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep28864
This article is cited by
-
Nonlocal sets of orthogonal product states with the less amount of elements in tripartite quantum systems
Quantum Information Processing (2022)
-
Small set of orthogonal product states with nonlocality
Quantum Information Processing (2022)
-
Nonlocality without entanglement: an acyclic configuration
Quantum Information Processing (2022)
-
Novel methods to construct nonlocal sets of orthogonal product states in an arbitrary bipartite high-dimensional system
Quantum Information Processing (2021)
-
Quantum entanglement as a resource to locally distinguish orthogonal product states
Quantum Information Processing (2021)




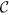 2k+i
2k+i 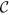 2l+j with k ≥ 1, l ≥ 1 and i, j
2l+j with k ≥ 1, l ≥ 1 and i, j 
 2k
2k  2l with k, l ≥ 2 and (b)
2l with k, l ≥ 2 and (b)  2k+1
2k+1  2l+1 with k, l ≥ 1.
2l+1 with k, l ≥ 1.
 4
4  4, (b)
4, (b)  3
3  3, (c)
3, (c)  5
5  6, and (d)
6, and (d)  5
5  5.
5.
 2k+1
2k+1  2l with k ≥ 2, l ≥ 3.
2l with k ≥ 2, l ≥ 3.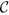 3k+i
3k+i 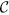 3k+j with i, j
3k+j with i, j  2k+i
2k+i  2l+j with i, j
2l+j with i, j  3k+i
3k+i  3l+j with i, j
3l+j with i, j