Abstract
In Hall’s reformulation of the uncertainty principle, the entropic uncertainty relation occupies a core position and provides the first nontrivial bound for the information exclusion principle. Based upon recent developments on the uncertainty relation, we present new bounds for the information exclusion relation using majorization theory and combinatoric techniques, which reveal further characteristic properties of the overlap matrix between the measurements.
Similar content being viewed by others
Introduction
Mutual information is a measure of correlations and plays a central role in communication theory1,2,3. While the entropy describes uncertainties of measurements4,5,6,7,8, mutual information quantifies bits of gained information. Furthermore, information is a more natural quantifier than entropy except in applications like transmission over quantum channels9. The sum of information corresponding to measurements of position and momentum is bounded by the quantity log2ΔXΔPX/ħ; for a quantum system with uncertainties for complementary observables ΔX and ΔPX and this is equivalent to one form of the Heisenberg uncertainty principle10. Both the uncertainty relation and information exclusion relation11,12,13 have been used to study the complementarity of obervables such as position and momentum. The standard deviation has also been employed to quantify uncertainties and it has been recognized later that the entropy seems more suitable in studying certain aspects of uncertainties.
As one of the well-known entropic uncertainty relations, Maassen and Uffink’s formulation8 states that

where  with
with  (k = 1, 2; j = 1, 2, …, d) for a given density matrix ρ of dimension d and
(k = 1, 2; j = 1, 2, …, d) for a given density matrix ρ of dimension d and  and
and  for two orthonormal bases
for two orthonormal bases  and
and  of d-dimensional Hilbert space
of d-dimensional Hilbert space  .
.
Hall11 generalized Eq. (1) to give the first bound of the Information Exclusion Relation on accessible information about a quantum system represented by an ensemble of states. Let M1 and M2 be as above on system A and let B be another classical register (which may be related to A), then

where  and I(Mi : B) = H(Mi) − H(Mi|B) is the mutual information14 corresponding to the measurement Mi on system A. Here H (Mi|B) is the conditional entropy relative to the subsystem B. Moreover, if system B is quantum memory, then
and I(Mi : B) = H(Mi) − H(Mi|B) is the mutual information14 corresponding to the measurement Mi on system A. Here H (Mi|B) is the conditional entropy relative to the subsystem B. Moreover, if system B is quantum memory, then  with
with  , while
, while  . Eq. (2) depicts that it is impossible to probe the register B to reach complete information about observables M1 and M2 if the maximal overlap cmax between measurements is small. Unlike the entropic uncertainty relations, the bound rH is far from being tight. Grudka et al.15 conjectured a stronger information exclusion relation based on numerical evidence (proved analytically only in some special cases)
. Eq. (2) depicts that it is impossible to probe the register B to reach complete information about observables M1 and M2 if the maximal overlap cmax between measurements is small. Unlike the entropic uncertainty relations, the bound rH is far from being tight. Grudka et al.15 conjectured a stronger information exclusion relation based on numerical evidence (proved analytically only in some special cases)

where  . As the sum runs over the d largest
. As the sum runs over the d largest  , we get
, we get  , so Eq. (3) is an improvement of Eq. (3). Recently Coles and Piani16 obtained a new information exclusion relation stronger than Eq. (3) and can also be strengthened to the case of quantum memory17
, so Eq. (3) is an improvement of Eq. (3). Recently Coles and Piani16 obtained a new information exclusion relation stronger than Eq. (3) and can also be strengthened to the case of quantum memory17

where rCP = min {rCP(M1, M2), rCP(M2, M1)},  and H(A|B) = H(ρAB) − H(ρB) is the conditional von Neumann entropy with
and H(A|B) = H(ρAB) − H(ρB) is the conditional von Neumann entropy with  the von Neumann entropy, while ρB represents the reduced state of the quantum state ρAB on subsystem B. It is clear that
the von Neumann entropy, while ρB represents the reduced state of the quantum state ρAB on subsystem B. It is clear that  .
.
As pointed out in ref. 11, the general information exclusion principle should have the form

for observables M1, M2, …, MN, where r(M1, M2, …, MN, B) is a nontrivial quantum bound. Such a quantum bound is recently given by Zhang et al.18 for the information exclusion principle of multi-measurements in the presence of the quantum memory. However, almost all available bounds are not tight even for the case of two observables.
Our goal in this paper is to give a general approach for the information exclusion principle using new bounds for two and more observables of quantum systems of any finite dimension by generalizing Coles-Piani’s uncertainty relation and using majorization techniques. In particular, all of our results can be reduced to the case without the presence of quantum memory.
The close relationship between the information exclusion relation and the uncertainty principle has promoted mutual developments. In the applications of the uncertainty relation to the former, there have been usually two available methods: either through subtraction of the uncertainty relation in the presence of quantum memory or utilizing the concavity property of the entropy together with combinatorial techniques or certain symmetry. Our second goal in this work is to analyze these two methods and in particular, we will show that the second method together with a special combinatorial scheme enables us to find tighter bounds for the information exclusion principle. The underlined reason for effectiveness is due to the special composition of the mutual information. We will take full advantage of this phenomenon and apply a distinguished symmetry of cyclic permutations to derive new bounds, which would have been difficult to obtain without consideration of mutual information.
We also remark that the recent result19 for the sum of entropies is valid in the absence of quantum side information and cannot be extended to the cases with quantum memory by simply adding the conditional entropy between the measured particle and quantum memory. To resolve this difficulty, we use a different method in this paper to generalize the results of ref. 19 in Lemma 1 and Theorem 2 to allow for quantum memory.
Results
We first consider the information exclusion principle for two observables and then generalize it to multi-observable cases. After that we will show that our information exclusion relation gives a tighter bound and the bound not only involves the d largest  but contains all the overlaps
but contains all the overlaps  between bases of measurements.
between bases of measurements.
We start with a qubit system to show our idea. The bound offered by Coles and Piani for two measurements does not improve the previous bounds for qubit systems. To see these, set  for brevity, then the unitarity of overlaps between measurements implies that c11 + c12 = 1, c11 + c21 = 1, c21 + c22 = 1 and c12 + c22 = 1. Assuming c11 > c12, then c11 = c22 > c12 = c21, thus
for brevity, then the unitarity of overlaps between measurements implies that c11 + c12 = 1, c11 + c21 = 1, c21 + c22 = 1 and c12 + c22 = 1. Assuming c11 > c12, then c11 = c22 > c12 = c21, thus

hence we get rH = rG = rCP = log2(4c11) which says that the bounds of Hall, Grudka et al. and Coles and Piani coincide with each other in this case.
Our first result already strengthens the bound in this case. Recall the implicit bound from the tensor-product majorization relation20,21,22 is of the form

where the vectors  and
and  are of size d2. The symbol ↓ means re-arranging the components in descending order. The majorization vector bound ω for probability tensor distributions
are of size d2. The symbol ↓ means re-arranging the components in descending order. The majorization vector bound ω for probability tensor distributions  of state ρ is the d2-dimensional vector ω = (Ω1, Ω1 − Ω2, …, Ωd − Ωd−1, 0, …, 0), where
of state ρ is the d2-dimensional vector ω = (Ω1, Ω1 − Ω2, …, Ωd − Ωd−1, 0, …, 0), where

The bound means that

for any density matrix ρ and  is defined by comparing the corresponding partial sums of the decreasingly rearranged vectors. Therefore ω only depends on
is defined by comparing the corresponding partial sums of the decreasingly rearranged vectors. Therefore ω only depends on  20. We remark that the quantity H(A) − 2H(B) assumes a similar role as that of H(A|B), which will be clarified in Theorem 2. As for more general case of N measurements, this quantity is replaced by (N − 1)H(A) − NH(B) in the place of NH(A|B). A proof of this relation will be given in the section of Methods. The following is our first improved information exclusion relation in a new form.
20. We remark that the quantity H(A) − 2H(B) assumes a similar role as that of H(A|B), which will be clarified in Theorem 2. As for more general case of N measurements, this quantity is replaced by (N − 1)H(A) − NH(B) in the place of NH(A|B). A proof of this relation will be given in the section of Methods. The following is our first improved information exclusion relation in a new form.
Theorem 1
For any bipartite state ρAB, let M1 and M2 be two measurements on system A and B the quantum memory correlated to A, then

where ω is the majorization bound and  is defined in the paragraph under Eq. (7).
is defined in the paragraph under Eq. (7).
See Methods for a proof of Theorem 1.
Eq. (8) gives an implicit bound for the information exclusion relation and it is tighter than log2(4cmax) + 2H(B) − H(A) as our bound not only involves the maximal overlap between M1 and M2, but also the second largest element based on the construction of the universal uncertainty relation ω21,22. Majorization approach21,22 has been widely used in improving the lower bound of entropic uncertainty relation. The application in the information exclusion relation offers a new aspect of the majorization method. The new lower bound not only can be used for arbitrary nonnegative Schur-concave function23 such as Rényi entropy and Tsallis entropy24, but also provides insights to the relation among all the overlaps between measurements, which explains why it offers a better bound for both entropic uncertainty relations and information exclusion relations. We also remark that the new bound is still weaker than the one based on the optimal entropic uncertainty relation for qubits25.
As an example, we consider the measurements M1 = {(1, 0), (0, 1)} and 
 . Our bound and log2 4cmax for ϕ = π/2 with respect to a are shown in Fig. 1.
. Our bound and log2 4cmax for ϕ = π/2 with respect to a are shown in Fig. 1.
Figure 1 shows that our bound for qubit is better than the previous bounds rH = rG = rCP almost everywhere. Using symmetry we only consider a in  . The common term 2H(B) − H(A) is omitted in the comparison. Further analysis of the bounds is given in Fig. 2.
. The common term 2H(B) − H(A) is omitted in the comparison. Further analysis of the bounds is given in Fig. 2.
Theorem 1 holds for any bipartite system and can be used for arbitrary two measurements Mi (i = 1, 2). For example, consider the qutrit state and a family of unitary matrices U(θ) = M(θ) O3M(θ)† 16,20 where

Upon the same matrix U(θ), comparison between our bound  and Coles-Piani’s bound rCP is depicted in Fig. 3.
and Coles-Piani’s bound rCP is depicted in Fig. 3.
In order to generalize the information exclusion relation to multi-measurements, we recall that the universal bound of tensor products of two probability distribution vectors can be computed by optimization over minors of the overlap matrix21,22. More generally for the multi-tensor product  corresponding to measurement Mm on a fixed quantum state, there exists similarly a universal upper bound ω:
corresponding to measurement Mm on a fixed quantum state, there exists similarly a universal upper bound ω:  . Then we have the following lemma, which generalizes Eq. (7).
. Then we have the following lemma, which generalizes Eq. (7).
Lemma 1
For any bipartite state ρAB, let Mm (m = 1, 2, …, N) be N measurements on system A and B the quantum memory correlated to A, then the following entropic uncertainty relation holds,

where ω is the dN-dimensional majorization bound for the N measurements Mm and  is the dN-dimensional vector
is the dN-dimensional vector  defined as follows. For each multi-index (i1, i2, …, iN), the dN-dimensional vector
defined as follows. For each multi-index (i1, i2, …, iN), the dN-dimensional vector  has entries of the form c(1, 2,…, N) c(2, 3, …, 1)…c(N, 1, …, N − 1) sorted in decreasing order with respect to the indices (i1, i2, …, iN) where
has entries of the form c(1, 2,…, N) c(2, 3, …, 1)…c(N, 1, …, N − 1) sorted in decreasing order with respect to the indices (i1, i2, …, iN) where  .
.
See Methods for a proof of Lemma 1.
We remark that the admixture bound introduced in ref. 19 was based upon the majorization theory with the help of the action of the symmetric group and it was shown that the bound outperforms previous results. However, the admixture bound cannot be extended to the entropic uncertainty relations in the presence of quantum memory for multiple measurements directly. Here we first use a new method to generalize the results of ref. 19 to allow for the quantum side information by mixing properties of the conditional entropy and Holevo inequality in Lemma 1. Moreover, by combining Lemma 1 with properties of the entropy we are able to give an enhanced information exclusion relation (see Theorem 2 for details).
The following theorem is obtained by subtracting the entropic uncertainty relation from the above result.
Theorem 2
For any bipartite state ρAB, let Mm (m = 1, 2, …, N) be N measurements on system A and B the quantum memory correlated to A, then

where  is defined in Eq. (10).
is defined in Eq. (10).
See Methods for a proof of Theorem 2.
Throughout this paper, we take NH(B) − (N − 1)H(A) instead of −(N − 1)H(A|B) as the variable that quantifies the amount of entanglement between measured particle and quantum memory since NH(B) − (N − 1)H(A) can outperform −(N − 1)H(A|B) numerically to some extent for entropic uncertainty relations.
Our new bound for multi-measurements offers an improvement than the bound recently given in ref. 18. Let us recall the information exclusion relation bound18 for multi-measurements (state-independent):

with the bounds  ,
,  and
and  are defined as follows:
are defined as follows:



Here the first two maxima are taken over all permutations (i1 i2 … iN): j → ij and the third is over all possible subsets  such that
such that  is a |I2|-permutation of 1, …, N. For example, (12), (23), …, (N − 1, N), (N1) are 2-permutation of 1, …, N. Clearly,
is a |I2|-permutation of 1, …, N. For example, (12), (23), …, (N − 1, N), (N1) are 2-permutation of 1, …, N. Clearly,  is the average value of all potential two-measurement combinations.
is the average value of all potential two-measurement combinations.
Using the permutation symmetry, we have the following Theorem which improves the bound  .
.
Theorem 3
Let ρAB be the bipartite density matrix with measurements Mm (m = 1, 2, …, N) on the system A with a quantum memory B as in Theorem 2, then

where the minimum is over all L-permutations of 1, …, N for L = 2, …, N.
In the above we have explained that the bound  is obtained by taking the minimum over all possible 2-permutations of 1, 2, …, N, naturally our new bound ropt in Theorem 3 is sharper than
is obtained by taking the minimum over all possible 2-permutations of 1, 2, …, N, naturally our new bound ropt in Theorem 3 is sharper than  as we have considered all possible multi-permutations of 1, 2, …, N.
as we have considered all possible multi-permutations of 1, 2, …, N.
Now we compare  with rx. As an example in three-dimensional space, one chooses three measurements as follows26:
with rx. As an example in three-dimensional space, one chooses three measurements as follows26:



Figure 4 shows the comparison when a changes and ϕ = π/2, where it is clear that rx is better than  .
.
The relationship between ropt and rx is sketched in Fig. 5. In this case rx is better than ropt for three measurements of dimension three, therefore min{ropt, rx} = min{rx}. Rigorous proof that rx is always better than ropt is nontrivial, since all the possible combinations of measurements less than N must be considered.
On the other hand, we can give a bound better than  . Recall that the concavity has been utilized in the formation of
. Recall that the concavity has been utilized in the formation of  , together with all possible combinations we will get following lemma (in order to simplify the process, we first consider three measurements, then generalize it to multiple measurements).
, together with all possible combinations we will get following lemma (in order to simplify the process, we first consider three measurements, then generalize it to multiple measurements).
Lemma 2
For any bipartite state ρAB, let M1, M2, M3 be three measurements on system A in the presence of quantum memory B, then

where the sum is over the three cyclic permutations of 1, 2, 3.
See Methods for a proof of Lemma 2.
Observe that the right hand side of Eq. (14) adds the sum of three terms

Naturally, we can also add  and
and  . By the same method, consider all possible combination and denote the minimal as r3y. Similar for N-measurements, set the minimal bound under the concavity of logarithm function as rNy, moreover let ry = minm{rmy}
. By the same method, consider all possible combination and denote the minimal as r3y. Similar for N-measurements, set the minimal bound under the concavity of logarithm function as rNy, moreover let ry = minm{rmy}  , hence
, hence  , finally we get
, finally we get
Theorem 4
For any bipartite state ρAB, let Mm (m = 1, 2, …, N) be N measurements on system A and let B be the quantum memory correlated to A, then

with  the same in Eq. (10). Since
the same in Eq. (10). Since  and all figures have shown our newly construct bound min {rx, ry} is tighter. Note that there is no clear relation between rx and ry, while the bound ry cannot be obtained by simply subtracting the bound of entropic uncertainty relations in the presence of quantum memory. Moreover, if ry outperforms rx, then we can utilize ry to achieve new bound for entropic uncertainty relations stronger than
and all figures have shown our newly construct bound min {rx, ry} is tighter. Note that there is no clear relation between rx and ry, while the bound ry cannot be obtained by simply subtracting the bound of entropic uncertainty relations in the presence of quantum memory. Moreover, if ry outperforms rx, then we can utilize ry to achieve new bound for entropic uncertainty relations stronger than  .
.
Conclusions
We have derived new bounds of the information exclusion relation for multi-measurements in the presence of quantum memory. The bounds are shown to be tighter than recently available bounds by detailed illustrations. Our bound is obtained by utilizing the concavity of the entropy function. The procedure has taken into account of all possible permutations of the measurements, thus offers a significant improvement than previous results which had only considered part of 2-permutations or combinations. Moreover, we have shown that majorization of the probability distributions for multi-measurements offers better bounds. In summary, we have formulated a systematic method of finding tighter bounds by combining the symmetry principle with majorization theory, all of which have been made easier in the context of mutual information. We remark that the new bounds can be easily computed by numerical computation.
Methods
Proof of Theorem 1
Recall that the quantum relative entropy  satisfies that
satisfies that  under any quantum channel τ. Denote by
under any quantum channel τ. Denote by  the quantum channel
the quantum channel  , which is also
, which is also  . Note that both
. Note that both  are measurements on system A, we have that for a bipartite state ρAB
are measurements on system A, we have that for a bipartite state ρAB

Note that  , the probability distribution of the reduced state ρA under the measurement M1, so
, the probability distribution of the reduced state ρA under the measurement M1, so  is a density matrix on the system B. Then the last expression can be written as
is a density matrix on the system B. Then the last expression can be written as

If system B is a classical register, then we can obtain

by swapping the indices i1 and i2, we get that

Their combination implies that

thus it follows from ref. 27 that

hence

where the last inequality has used  (i = 1, 2) and the vector
(i = 1, 2) and the vector  of length d2, whose entries
of length d2, whose entries  are arranged in decreasing order with respect to (i1, i2). Here the vector
are arranged in decreasing order with respect to (i1, i2). Here the vector  is defined by
is defined by  for each (i1, i2) and also sorted in decreasing order. Note that the extra term 2H(B) − H(A) is another quantity appearing on the right-hand side that describes the amount of entanglement between the measured particle and quantum memory besides −H(A|B).
for each (i1, i2) and also sorted in decreasing order. Note that the extra term 2H(B) − H(A) is another quantity appearing on the right-hand side that describes the amount of entanglement between the measured particle and quantum memory besides −H(A|B).
We now derive the information exclusion relation for qubits in the form of 
 and this completes the proof.
and this completes the proof.
Proof of Lemma 1
Suppose we are given N measurements M1, …, MN with orthonormal bases  . To simplify presentation we denote that
. To simplify presentation we denote that

Then we have that26

Then consider the action of the cyclic group of N permutations on indices 1, 2,..., N and take the average can obtain the following inequality:

where the notations are the same as appeared in Eq. (10). Thus it follows from ref. 27 that

The proof is finished.
Proof of Theorem 2
Similar to the proof of Theorem 1, due to I(Mm : B) = H(Mm) − H(Mm|B), thus we get

with the product  the same in Eq. (10).
the same in Eq. (10).
Proof of Lemma 2
First recall that for  we have
we have

where we have used concavity of log. By the same method we then get

with c(1, 2, 3), c(2, 3, 1) and c(3, 1, 2) the same as in Eq. (14) and this completes the proof.
Additional Information
How to cite this article: Xiao, Y. et al. Enhanced Information Exclusion Relations. Sci. Rep. 6, 30440; doi: 10.1038/srep30440 (2016).
References
Cover, T. M. & Thomas, J. A. Elements of information theory. 2nd ed. (Wiley, New York, 2005).
Holevo, A. S. Bounds for the quantity of information transmitted by a quantum communication channel. Probl. Inf. Trans. 9, 177 (1973).
Yuen, A. S. & Ozawa, M. Ultimate information carrying limit of quantum systems. Phys. Rev. Lett. 70, 363 (1993).
Wehner, S. & Winter, A. Entropic uncertainty relations a survey. New J. Phys. 12, 025009 (2010).
Bosyk, G. M., Portesi, M. & Plastino, A. Collision entropy and optimal uncertainty. Phys. Rev. A 85, 012108 (2012).
Białynicki-Birula, I. & Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Comm. Math. Phys. 44, 129 (1975).
Deutsch, D. Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631 (1983).
Maassen, H. & Uffink, J. B. M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103 (1988).
Dupuis, F., Szehr, O. & Tomamichel, M. A decoupling approach to classical data transmission over quantum channels. IEEE Trans. on Inf. Theory 60(3), 1562 (2014).
Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172 (1927).
Hall, M. J. W. Information exclusion principle for complementary observables. Phys. Rev. Lett. 74, 3307 (1995).
Hall, M. J. W. Quantum information and correlation bounds. Phys. Rev. A 55, 100 (1997).
Coles, P. J., Yu, L., Gheorghiu, V. & Griffiths, R. B. Information-theoretic treatment of tripartite systems and quantum channels. Phys. Rev. A 83, 062338 (2011).
Reza, F. M. An introduction to information theory. (McGraw-Hill, New York, 1961).
Grudka, A., Horodecki, M., Horodecki, P., Horodecki, R., Kłobus, W. & Pankowski, Ł. Conjectured strong complementary correlations tradeoff. Phys. Rev. A 88, 032106 (2013).
Coles, P. J. & Piani, M. Improved entropic uncertainty relations and information exclusion relations. Phys. Rev. A 89, 022112 (2014).
Berta, M., Christandl, M., Colbeck, R., Renes, J. M. & Renner, R. The uncertainty principle in the presence of quantum memory. Nat. Phys. 6, 659 (2010).
Zhang, J., Zhang, Y. & Yu, C.-S. Entropic uncertainty relation and information exclusion relation for multiple measurements in the presence of quantum memory. Scientific Reports 5, 11701 (2015).
Xiao, Y., Jing, N., Fei, S.-M., Li, T., Li-Jost, X., Ma, T. & Wang, Z.-X. Strong entropic uncertainty relations for multiple measurements. Phys. Rev. A 93, 042125 (2016).
Rudnicki, Ł., Puchała, Z. & Życzkowski, K. Strong majorization entropic uncertainty relations. Phys. Rev. A 89, 052115 (2014).
Friedland, S., Gheorghiu, V. & Gour, G. Universal uncertainty relations. Phys. Rev. Lett. 111, 230401 (2013).
Puchała, Z., Rudnicki, Ł. & Życzkowski, K. Majorization entropic uncertainty relations. J. Phys. A 46, 272002 (2013).
Marshall, A. W., Olkin, I. & Arnold, B. C. Inequalities: theory of majorization and its applications. 2nd ed. Springer Series in Statistics (Springer, New York, 2011).
Havrda, J. & Charvát, F. Quantification method of classification processes. Concept of structural a-entropy. Kybernetica 3, 30 (1967).
Ghirardi, G., Marinatto, L. & Romano, R. An optimal entropic uncertainty relation in a two-dimensional Hilbert space. Phys. Lett. A 317, 32 (2003).
Liu, S., Mu, L.-Z. & Fan, H. Entropic uncertainty relations for multiple measurements. Phys. Rev. A 91, 042133 (2015).
Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information. (Cambride Univ. Press, Cambridge, 2000).
Acknowledgements
We would like to thank Tao Li for help on computer diagrams. This work is supported by National Natural Science Foundation of China (Grant nos 11271138 and 11531004), China Scholarship Council and Simons Foundation grant no. 198129.
Author information
Authors and Affiliations
Contributions
Y.X. and N.J. analyzed and wrote the manuscript. They reviewed the paper together with X.L.-J.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Xiao, Y., Jing, N. & Li-Jost, X. Enhanced Information Exclusion Relations. Sci Rep 6, 30440 (2016). https://doi.org/10.1038/srep30440
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep30440

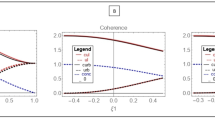



 ) is tighter than the upper blue one (Hall’s bound rH) almost everywhere.
) is tighter than the upper blue one (Hall’s bound rH) almost everywhere.
 of our bound from Hall’s bound rH for a
of our bound from Hall’s bound rH for a 
 (lower in green) is better than Coles-Piani’s bound rCP (upper in purple) everywhere.
(lower in green) is better than Coles-Piani’s bound rCP (upper in purple) everywhere.
 .
.