Supporting historic mural image inpainting by using coordinate attention aggregated transformations with U-Net-based discriminator

Abstract

Digital preservation of historic murals is essential for protecting cultural heritage. Despite centuries of damage, advances in inpainting offer new restoration possibilities. However, existing methods often distort features like color and texture, and suffer from significant pixel-level blurring. We propose a Coordinated Attention Aggregation Transformation (CAAT) GAN architecture with U-Net discriminators to address these limitations. The CAAT generator extracts contextual information from distant regions via a Coordinated Aggregation Transformation Block, expanding the receptive field and improving content inference in missing areas to restore original color and texture. The U-Net discriminator further refines results by providing both global and local confidence scores. We also introduce DunHuang-Mural, a dataset of 7983 high-resolution historical murals. Trained on 6386 images and evaluated on 1597, our CAUGAN achieves significant gains in visual fidelity and structural consistency over existing methods, demonstrating its utility for archeological mural restoration.

Introduction

In the long history of mankind, numerous mural images were left in ancient temples, palaces, caves, and other historic sites. These mural images faithfully recorded the societies, cultures, religions, landscapes, and daily lives in different human civilizations and their evolutions, which are extremely significant in the studies of archeology, sociology and history. For example, the Dunhuang mural images in the Mogao Caves (also known as the Caves of a Thousand Buddhas), constructed from 366 AD to around 1000 AD at the edge of the Taklamakan Desert, represent the historical and cultural heritage of Ancient China and transactions between China and Arabian countries on the well-known “Silk Road”.

However, the preservation of these historic murals presents significant challenges due to the degradation caused by the materials’ inherent properties and the long-term effects of environmental factors such as climate and human-induced damage. As a result, many of these murals suffer from issues like flaking, cracking, fading, and mildew. Traditional inpainting techniques, although effective in some instances, require extensive historical knowledge and specialized artistic skills, with a limited number of qualified practitioners available¹. Additionally, these methods are often time-consuming, labor-intensive, and carry the risk of secondary damage if not executed with precision. Digital inpainting allows for the accurate reconstruction of the murals’ original structure and appearance without physically intervening in the original artwork, thereby minimizing the potential for further damage². Moreover, digitization enables broader public access and interaction, offering new ways for audiences to engage with and appreciate these culturally significant works. This method not only ensures the long-term preservation of the murals but also bridges the gap between art and technology, fostering a deeper connection to cultural heritage. Through digital preservation, these invaluable works are safeguarded while also becoming accessible to a global audience, ensuring their continued relevance and appreciation³.

Traditional mural image inpainting techniques can generally be categorized into two main types: Content-based Inpainting and structure-based inpainting⁴. Content-based inpainting techniques aim to restore the visual content of a mural by replicating textures, colors, and patterns from the surrounding undamaged areas⁵. The primary objective of this method is to fill in missing or damaged sections while maintaining visual consistency, ensuring that the restored regions blend harmoniously with the original artwork. Content-based inpainting works well for murals with missing textures, colors, or patterns. One prominent content-based technique is nonparametric sampling, introduced by Efros and Leung (1999). This method synthesizes textures by directly copying pixels or blocks from a reference image, rather than using parametric models. By learning and replicating the texture patterns from surrounding areas, it effectively reconstructs missing portions of an image, such as a mural⁶. Building on this, exemplar-based inpainting fills damaged regions by sampling visually similar patches from neighboring intact areas. Criminisi et al. (2004) refined this approach by integrating structural consistency, which not only considers intensity similarity but also structural similarity between patches to ensure that the restored regions maintain the original image’s overall structure and coherence⁷. Structure-based inpainting techniques focus on restoring the structural continuity of a mural, utilizing mathematical models and algorithms to recover both its visual content and underlying geometric structure, such as lines, shapes, and overall layout. These methods aim to preserve the spatial integrity of the artwork, ensuring that both the content and composition remain true to the original mural. One key method in this category is the Fast Marching Method (FMM), proposed by Telea (2004), which offers an effective approach for image inpainting. The core principle of FMM is to initially process the pixels along the edges of the damaged area and then propagate the inpainting inward in a layer-by-layer manner until the entire region is filled. This technique is particularly effective for regions with irregular boundaries, where maintaining structural coherence is essential⁸. Another significant advancement is the work by Tschumperlé and Deriche (2005), who developed a unified framework based on partial differential equations (PDEs) for the regularization of vector-valued images. This framework enables adaptive processing of local features through anisotropic diffusion equations and locally interpreted regularization processes. By applying these techniques, it is possible to restore both the structural and textural continuity of an image, making it highly suitable for tasks such as image denoising, enhancement, and inpainting. This approach ensures that the geometric structure and fine details of the mural are preserved during the inpainting process⁹. Additionally, a texture synthesis method has been proposed that incorporates a graph cut algorithm to optimize the seams during the synthesis process. Unlike traditional methods that rely on fixed-size patches, this technique matches patches within the sample image and applies the graph cut algorithm to identify the optimal seam paths. By minimizing visible seams, this approach results in a more seamless and natural inpainting of the mural’s texture¹⁰. Traditional inpainting methods continue to play a crucial role in mural conservation due to the unique characteristics of murals. Scholars have proposed an integrated approach that begins with the automatic selection of reference mural images based on structural and texture similarity¹¹. Depth features of the murals are then extracted losslessly using a Reversible Residual Network (RRN). A channel refinement module follows, removing redundant information from the network channels. Finally, the colors of faded mural images are restored through an unbiased color transfer module, effectively recovering the original hues of the mural¹². In summary, traditional digital mural image inpainting methods primarily focus on the localized details of the mural image, aiming to restore specific damaged areas with attention to surrounding context and visual coherence.

Traditional image inpainting techniques, such as exemplar-based and structure-based methods, focus on filling missing regions by sampling from surrounding areas¹³. While these approaches are effective in certain contexts, they often face challenges in maintaining high visual fidelity in more complex scenarios¹⁴. The rise of deep learning has significantly transformed the field of image inpainting, enabling more advanced methods capable of learning intricate image features and global structures. Unlike traditional techniques, deep learning models can capture semantic information through end-to-end learning, allowing them to handle complex inpainting tasks more effectively. This advancement has solidified deep learning as a powerful tool for extracting both structural and semantic content from images. Pathak et al. (2016) introduced Context Encoders, a deep learning-based inpainting method using a CNN to predict missing image regions based on surrounding context. The model employs an encoder-decoder architecture with adversarial training, where a discriminator distinguishes real from inpainted images, guiding the generator to produce high-quality inpainting. While one of the first deep learning approaches for large-scale inpainting, it is limited by its reliance on fully connected layers, restricting its application to low-resolution images and fixed-shape missing areas¹⁵. To overcome these limitations, Iizuka et al. proposed a context attention module within a fully convolutional network (FCN), which enables the model to better identify and match relevant patches from the surrounding context, improving inpainting quality¹⁶. Building on this, Lian et al. developed a dual-feature encoder that combines both structural and texture features. By using skip connections to guide the decoder and multi-scale acceptance fields to enhance contextual and semantic consistency, this method further refines inpainting performance¹⁷. Zimu Zeng et al. utilizing convolutional neural networks, is effective in restoring small defaced areas of murals; its effectiveness significantly diminishes when applied to larger areas¹⁸.

Deep learning-based approaches have transformed mural inpainting by enabling more sophisticated restoration. Unlike traditional methods, deep learning models, such as Context Encoders and Generative Adversarial Networks (GANs), can learn intricate image features and global structures, handling complex inpainting tasks¹⁹. In GAN-based inpainting, the generator predicts the missing content, while the discriminator evaluates whether the restored image is visually authentic by distinguishing it from real images. Yeh et al. (2017) introduced the Contextual GAN, which integrates a contextual discriminator to produce more contextually accurate and visually coherent inpainting results, particularly for large missing regions, such as those found in damaged murals²⁰. However, the reliance of the local discriminator on fully connected layers restricts its ability to handle only fixed-shaped missing regions, limiting its applicability to real-world inpainting tasks. To overcome this limitation, Yu et al. introduced a modified discriminator that incorporates a contextual attention layer derived from PatchGAN. This innovation allows the model to consider distant feature blocks, improving the quality of the inpainting. Additionally, spectral normalization was applied to each layer of the discriminator to stabilize the GAN training process^21,22. Despite these improvements, PatchGAN-based models tend to overlook the regions that are common to both the natural and restored parts of the image outside of the missing areas. This can reduce the discriminator’s effectiveness, leading to suboptimal inpainting results. Expanding on this, Xu et al. (2023) developed DC-CycleGAN, an inpainting method combining Deformable Convolution (DCN), Efficient Channel Attention Network (ECANet), Residual Network (ResNet), and CycleGAN. This method was specifically designed to restore the faded and damaged frescoes of the Dunhuang Mogao Caves, which have suffered from long-term weathering and vandalism²³. Similarly, Hu et al. introduced SGRGAN, a framework for restoring traditional Chinese landscape paintings. By using sketch images as structural priors, SGRGAN reconstructs both the structural and textural components of the missing regions through a dual-stream encoder-decoder architecture²⁴. Further innovations, including Group-wise Multi-scale Self-Attention (GMSA), Encoder-Decoder Feature Interaction (EDFI), and Local Feature Enhancement Block (LFEB), have further enhanced the model’s ability to restore intricate mural details. These advancements have significantly improved the quality and effectiveness of mural inpainting, marking a clear advancement over traditional inpainting methods²⁵.GANs can be effective in restoring missing or damaged sections of murals, but several challenges remain. While the generated content may appear visually convincing, it can sometimes introduce inconsistencies, such as mismatched patterns or textures, that deviate from the original murals. Furthermore, murals often contain intricate details and culturally specific elements that are difficult for GANs to accurately replicate²⁶. Capturing and preserving these fine, contextually significant elements during the inpainting process remains a significant challenge for GAN-based approaches.

Both traditional inpainting techniques and GAN-based methods have limitations when applied to mural image restoration, as these artworks require a careful balance of both local and global features²⁷. While digital image inpainting technologies offer advanced approaches for recovering damaged or degraded images, they are not without their challenges. Many algorithms focus on larger visual elements, often neglecting finer details such as brushstrokes, textures, and subtle shading changes. Others reconstruct missing sections by relying on surrounding pixels or patterns, but murals, as unique expressions of human art, require inpainting methods that preserve the integrity of these delicate details while ensuring overall stylistic cohesion.

To address this issue, we propose a novel method for mural image inpainting using AI technologies. Concretely, a Coordinate Attention Aggregated Transformed Generative Adversarial Network (CAAT-GAN) with a U-Net discriminator is used to generate digitalized images more faithful to the original styles, which will provide support archeological workers to restore the physical mural images in the caves. Our approach consists of three key components: the Coordinate Attention Aggregated Transformation Block (CAAT), the U-Net architecture-based discriminator, and an adaptive discriminator enhancement mechanism. The CAAT module improves traditional convolution by incorporating multiple dilation rates, enabling the network to capture long-range contextual information from high-resolution images, which is essential for accurately inferring missing regions in murals. The CA attention mechanism within CAAT further enhances long-range reasoning, preserving spatial details for coherent reconstruction. The U-Net discriminator generates both global and local confidence levels for the generated image, addressing issues such as pixel-level blurring and guiding the generator to produce more accurate inpainting. Finally, the adaptive discriminator enhancement mechanism expands the dataset, stabilizes training, and ensures the authenticity of the generated images, minimizing the risk of artifacts. Together, these components allow for highly accurate and visually faithful mural inpainting, eliminating the need for post-processing.

Compared with the current literature, this paper represents a new research track for ancient mural inpainting by using artificial intelligence. It makes the following key contributions to the field of mural image inpainting: (1) Adaptation of the CAAT, which improves traditional convolution by integrating multiple dilation rates to capture long-range contextual information, thereby enhancing the accuracy of mural image and more conform to the main features of mural images. (2) A U-Net architecture-based discriminator is proposed, which generates both global and local confidence levels for the generated image. This dual-level evaluation effectively addresses pixel-level blurring and guides the generator to produce more precise and visually coherent inpainting. The implementation of an adaptive discriminator enhancement mechanism, which expands the dataset, stabilizes training, and ensures the authenticity of the generated images, minimizing the introduction of artifacts. (3) The creation of a large-scale mural dataset, DunHuang-Mural, consisting of 7983 digitalized mural images, specifically designed to support physical mural image inpainting, detection, and validation tasks, thus offering a valuable resource for future research.

The structure of the paper is as follows. Section “Methods” presents a detailed explanation of the proposed mural image restoration method, with a focus on the CAAT module and the U-discriminator. Section “Results” demonstrates the effectiveness of the method through its application to Dunhuang mural image inpainting and provides a comprehensive analysis of the experimental results. Finally, Section “Discussion” summarizes the key contributions of the work and outlines potential directions for future research.

Methods

Mural image dataset construction

The construction of comprehensive mural image datasets plays a crucial role in the successful implementation of mural image inpainting²⁸. These datasets provide the necessary data for training machine learning models, enabling them to restore damaged murals by learning from the intact portions of the images, including patterns, textures, and underlying structures. The importance of these datasets is magnified by the increasing use of advanced deep learning techniques, where high-quality datasets are essential to the successful development and validation of inpainting algorithms. Early mural datasets typically contained murals with simple degradation patterns or represented only a few selections of mural styles. This limitation makes it difficult to generalize inpainting algorithms across different regions and styles of murals. In addition, early datasets lacked annotations to label damaged areas, which is a key element in training machine learning models for tasks such as segmentation and inpainting²⁹. This paucity of data restricts the ability to conduct large-scale deep-learning training, which in turn hampers the performance and generalization capabilities of inpainting tasks. In the field of heritage science, as seen in other cultural heritage preservation studies (such as those related to ancient paintings or sculptures), a lack of sufficient data can lead to models that are unable to capture the full range of characteristics and variations within the domain.

As deep learning techniques, particularly convolutional neural networks (CNNs) and Generative Adversarial Networks (GANs), gained traction, researchers began developing more sophisticated datasets with comprehensive annotations. These datasets are designed to assist in training models for inpainting tasks, where the goal is to predict and restore missing sections of damaged murals. A notable example is the Dunhuang Murals Dataset, which contains images from the Mogao Caves in China. This dataset includes both intact and damaged portions of the murals, and provides masks of missing areas, allowing researchers to train models to restore these regions effectively³⁰. In recent years, researchers have created more specialized datasets aimed at capturing specific features of murals, such as textures, structural patterns, and geometric features. These datasets are invaluable for training deep learning models designed to recover not only missing pixels but also the fine-grained structural and artistic features of the murals. For example, Xu et al. (2024) the developed a dataset for Dunhuang mural named MuralDH which includes both intact and degraded sections along with annotations detailing the murals’ structural and texture features. This dataset comprises over 5000 high-resolution images²⁸. This dataset has been used to train models that can restore missing regions while preserving the integrity of the original artwork, both in terms of texture and structure.

Despite significant progress in the development of mural image datasets, many existing collections remain limited in their diversity. This limitation arises from the inherently finite number of murals, which span various historical periods, geographic regions, artistic styles, and iconographic traditions. As a result, current datasets often fail to represent the full scope of mural diversity. To address these shortcomings, we propose a new dataset, named DunHuang-Mural, designed to include a wide range of samples from various periods, locations, and artistic styles. By offering a more comprehensive collection, the DunHuang-Mural dataset aims to provide a richer resource for developing and evaluating mural image inpainting algorithms. Its diversity is expected to enhance the training and performance of these models, making them more adaptable to different inpainting contexts.

CAUGAN

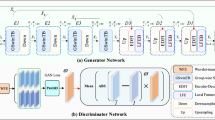
The proposed mural image inpainting method, named CAUGAN, is depicted in Fig. 1. This method comprises two main components. The first component is the Coordinated Attention Aggregate Transformation Block (CAAT), which captures rich contextual information from distant regions within the images. This allows for a more realistic inpainting of missing content in mural images. The second component is a discriminator based on the U-Net, which leverages its robust discriminative capabilities to encourage the generator to produce more realistic inpainting content, enhancing both visual quality and detail. This approach enhances both visual quality and detail. Through these innovations, our model achieves significant improvements in image inpainting quality.

Fig. 1: The framework of CAUGAN.

Note: Fig. 1 shows the architecture of the CAUGAN method for mural image inpainting. It consists of two main parts: the generator and the discriminator. The generator is responsible for inpainting the image. It includes convolution layers and Coordinated Attention Aggregate Transformation (CAAT) blocks. The CAAT blocks allow the generator to capture contextual information from distant areas of the image, helping it generate more realistic inpainting. The input to the generator is damaged and masked image, and the output is the inpainted image. The discriminator is based on the U-Net architecture and serves to evaluate the generated inpainted image. The discriminator compares the inpainted image to the original image (ground truth) and decides whether the generated content is “Real or Fake.” This adversarial process encourages the generator to improve its inpainting quality. Together, these components work to significantly enhance the visual quality and realism of the inpainted images by refining both the generated content and the evaluation process.

Coordinate attention aggregated transformations block

To ensure structural coherence during image inpainting, it is crucial to effectively infer missing information not only from the intact regions but also from spatially distant areas of the image^31,32. This allows for the preservation of both local and global patterns, ensuring that the restored regions seamlessly integrate with the surrounding content. This challenge is particularly evident in mural images, where varying scales, perspectives, and intricate details require capturing a broad range of contextual patterns to maintain the overall integrity of the artwork. The Coordinate Attention Aggregated Transformations (CAAT) module proposed in this paper tackles this issue by decomposing the standard convolution kernel into multiple sub-kernels, each operating with different dilation rates. This approach allows the model to capture contextual information at various scales, enhancing its ability to infer missing regions accurately. This enables the model to capture contextual information across multiple scales, combining fine-grained details with broader context. The features extracted from these varying receptive fields are then fused with the standard convolution outputs, ensuring a more comprehensive feature representation. This process enhances the model’s ability to restore missing regions while preserving structural and visual coherence.

As illustrated in Fig. 2(a), the conventional residual connection sums the input feature ${x}_{1}$ and the learned residual feature ${x}_{2}$ without considering spatial variation, which can result in color discrepancies in the image. To address this, we propose a modification, as illustrated in Fig. 2(b), where we integrate a Coordinate Attention (CA) mechanism into the gated residual connections. This preserves spatial information and enables the network to capture contextual details from distant regions, improving the accuracy of inferences. Initially, we aggregate the input features along the vertical and horizontal directions through two one-dimensional global pooling operations, generating direction-aware feature maps. These maps are then encoded into two attention maps that capture long-range dependencies along each spatial direction, effectively preserving location information. Additionally, removing the sigmoid function reduces feature loss during inpainting, enhancing the overall quality and coherence of the restored image. The diagram of the Coordinate Attention (CA) block used in our approach is shown in Fig. 2(b).

Fig. 2: Architectural comparison of the standard residual block and the enhanced CAAT block in the CAUGAN method.

a Standard Residual Block, b Improved CAAT Block. Note: This figure presents an architectural comparison between the Standard Residual Block and the Improved CAAT Block used in the CAUGAN method. In (a), the standard residual block processes the input feature ${x}_{1}$ through a 3 × 3 convolution and ReLU activation, then adds the result to the residual input ${x}_{2}$. While effective for general feature learning, this design lacks explicit spatial modeling, which can result in inconsistencies, such as color or texture mismatches in mural restoration. In contrast, b shows the CAAT Block, which introduces coordinate attention mechanisms and a refined structure to enhance spatial awareness. The convolution operation is divided into four sub-kernels with reduced output channels (e.g., 64 channels per sub-kernel from an original 256-channel kernel). Each sub-kernel applies a distinct dilation rate (1, 2, 4, and 8), expanding the receptive field to capture both fine details and broader contextual information. This multi-scale approach is essential for handling large or repetitive patterns often found in mural backgrounds. The outputs from these sub-kernels are concatenated and fused through an additional convolution, enabling the CAAT Block to integrate multi-scale features effectively and model spatial hierarchies. This enhanced spatial awareness helps preserve mural structure and detail, resulting in improved performance during inpainting tasks. Overall, the CAAT block outperforms the standard residual block by incorporating spatially-aware, multi-scale contextual learning, making it highly suitable for complex tasks such as mural image restoration.

The attention maps are applied to the input feature map via multiplication, enhancing the representation of relevant regions. This process is composed of two stages: coordinate information embedding and coordinate attention generation. Coordinate information embedding decomposes the global pooling operation into two one-dimensional feature encoding operations to allow the attention module to capture more precise long-range dependencies. For a given input $X$, each channel is encoded in coordinates along the horizontal and vertical directions using the pooling kernel’s two spatial ranges $\left(H,1\right)$ and $(1,W)$. Equation 1 demonstrates the decomposition of the global pooling operation into two one-dimensional feature encoding operations.

$${z}_{c}=\frac{1}{H\times W}\mathop{\sum }\limits_{i=1}^{H}\mathop{\sum }\limits_{j=1}^{W}{x}_{c}\left(i,j\right)$$

(1)

Hence, the output of the c-th channel with height h can be expressed as Eq. 2:

$${z}_{c}^{h}\left(h\right)=\frac{1}{W}\mathop{\sum }\limits_{0\le i < W}{x}_{c}\left(h,i\right)$$

(2)

Similarly, the output of c-th channel with width $w$ can be mathematically formulated as Eq. 3:

$${z}_{c}^{w}\left(w\right)=\frac{1}{H}\mathop{\sum }\limits_{0\le j < H}{x}_{c}\left(j,w\right)$$

(3)

The two transformations generate direction-aware feature maps, allowing the attention module to capture long-range dependencies in one spatial direction while preserving positional information in the other, thus improving localization accuracy.

To effectively utilize this embedded information, a second transformation, called coordinate attention generation, is introduced. This transformation concatenates the outputs of the initial steps and applies a $1\times 1$ convolutional transformation function ${F}_{1}$, as shown in Eq. 4:

$$f={\rm{\delta }}\left({F}_{1}\left(\left[{z}^{h},{z}^{w}\right]\right)\right)$$

(4)

Here, $f$ represents the feature-aware map in horizontal and vertical directions, $\delta$ is a nonlinear activation function, ${F}_{1}$ is the $1\times 1$ convolutional transform function, and $\left[{z}^{h},{z}^{w}\right]$ indicates the spatial dimension of the concatenation operation. The number of channels in ${F}_{h}$, and ${F}_{w}$ is then adjusted to match the number of channels in the input X by applying a $1\times 1$ convolutional transform, as shown in Eqs. 5 and 6:

$${g}^{h}={\rm{\sigma }}\left({F}_{h}\left({\,f}^{h}\right)\right)$$

(5)

$${g}^{w}={\rm{\sigma }}\left({F}_{w}\left({\,f}^{w}\right)\right)$$

(6)

Here, the function ${\rm{\sigma }}$ represents a Sigmoid function. Reducing the number of channels in $f$ can simplify model complexity and accelerate training. However, this reduction may lead to the loss of essential feature information, requiring careful consideration of the reduction ratio. Finally, the representation of the output of the coordinated attention block is shown in Eq. 7:

$${y}_{c}\left(i,j\right)={x}_{c}\left(i,j\right)\times {g}_{c}^{h}\left(i\right)\times {g}_{c}^{w}\left(j\right)$$

(7)

The spatially varying gate value g is computed from ${x}_{1}$ using standard convolution and CA attention mechanisms. Subsequently, the input feature ${x}_{1}$ and the learned residual feature ${x}_{2}$ are weighted and summed with g to obtain the final feature representation ${x}_{3}$, as shown in Eq. 8:

$${x}_{3}={x}_{1}\times g+{x}_{2}\times (1-g)$$

(8)

This approach of spatially varying feature aggregation updates the features within the missing region while preserving those in the intact areas. By effectively capturing contextual information from distant regions, it facilitates the accurate inpainting of the mural’s original content.

U-Net-based discriminator

To generate more realistic images, a is incorporated into the CAAT-GAN training. This enhances the generator’s ability to produce high-resolution images, reduces pixel blurring in large missing regions, and ensures clear textures in the restored images³³.

The discriminator is structured as a U-Net, with the original network serving as the encoder and a new up sampling network as the decoder^34,35. This configuration a U-Net-based discriminator, allows the decoder to provide spatially consistent feedback to the generator at the pixel level³⁶. The encoder and decoder are connected through bottleneck connections and skip links. This enhanced architecture strengthens the discriminator, making it more challenging for the generator to deceive it, thereby encouraging the generator to improve the quality of the generated samples, as shown in Fig. 3:

Fig. 3: The U-Net based discriminator architecture.

Note: The figure illustrates the architecture of the discriminator used in the CAUGAN method, which is structured as a U-Net. It is divided into two main parts: the encoder and the decoder. The encoder processes the input image, starting with a 3 × 512 × 512 image and progressively downsampling it through a series of layers with decreasing spatial dimensions. At each stage, the image is passed through convolutional layers, gradually reducing its resolution while extracting increasingly abstract features. The encoder is responsible for capturing the essential features of the input image. The decoder, on the other hand, upsamples the feature maps produced by the encoder, restoring the spatial resolution and refining the information extracted by the encoder. The decoder outputs spatially consistent feedback to the generator, helping it improve the quality of the inpainted image. The U-Net structure also includes bottleneck connections and skip links, which allow the decoder to retain important spatial information by directly connecting corresponding layers from the encoder to the decoder. This architecture enhances the discriminator’s ability to evaluate the generated inpainted images by maintaining spatial consistency at the pixel level. As a result, the generator faces a more robust challenge in trying to deceive the discriminator, pushing it to generate higher-quality, more realistic images. The feedback from the discriminator helps refine the inpainting process, improving the overall output.

This enhanced discriminator, referred to as ${D}^{U}$. differs from the original discriminator $D(x)$, by performing pixel-level classification, segmenting the image into real and fake regions rather than classifying the entire image as either true or false. Additionally, the encoder part of ${D}^{U}(x)$ retains the confidence level of the original image, enabling the discriminator to independently learn and distinguish between global and local confidence. The encoder and decoder modules are defined as ${D}_{{enc}}^{U}$ and ${D}_{{dec}}^{U}$, respectively. The learning objective of the discriminator is presented in Eq. 9:

$${{\mathcal{L}}}_{{{\mathcal{D}}}^{{\mathcal{U}}}}={{\mathcal{L}}}_{{{\mathcal{D}}}_{{\mathcal{e}}{\mathcal{n}}{\mathcal{c}}}^{{\mathcal{U}}}}+{{\mathcal{L}}}_{{{\mathcal{D}}}_{{\mathcal{d}}{\mathcal{e}}{\mathcal{c}}}^{{\mathcal{U}}}}$$

(9)

Specifically, the loss of the encoder ${{\mathcal{L}}}_{{{\mathcal{D}}}_{{\mathcal{e}}{\mathcal{n}}{\mathcal{c}}}^{{\mathcal{U}}}}$ is computed from the scalar loss of ${D}_{{enc}}^{U}$:

$${{\mathcal{L}}}_{{{\mathcal{D}}}_{\text{ec}}^{{\mathcal{U}}}}=-{E}_{x}\left[\log {D}_{\text{enc}}^{U}\left(x\right)\right]-{E}_{z}\left[\log \left(1-{D}_{\text{enc}}^{U}\left(G\left(z\right)\right)\right)\right]$$

(10)

The loss of the decoder, ${{\mathcal{L}}}_{{{\mathcal{D}}}_{{\mathcal{d}}{\mathcal{e}}{\mathcal{c}}}^{{\mathcal{U}}}}$ is calculated as the average judgment value of all pixels, as depicted in Eq. 11:

$${{\mathcal{L}}}_{{{\mathcal{D}}}_{\text{dc}}^{{\mathcal{U}}}}=-{E}_{x}\left[\mathop{\sum }\limits_{i,j}{\log \left[{D}_{\text{dec}}^{U}\left(x\right)\right]}_{i,j}\right]-{E}_{z}\left[{\sum }_{i,j}\log \left(1-{\left[{D}_{\text{dec}}^{U}\left(G\left(z\right)\right)\right]}_{i,j}\right)\right]$$

(11)

Here, ${\left[{D}_{\text{dec}}^{U}\left(x\right)\right]}_{i,j}$ and ${\left[{D}_{\text{dec}}^{U}\left(G\left(z\right)\right)\right]}_{i,j}$ represent the discriminator’s decisions at pixel $(i,j)$. The loss of the generator is described in Eq. 12:

$${{\mathcal{L}}}_{{\mathcal{G}}}=-{E}_{z}\left[\log {D}_{\text{enc}}^{U}\left(G\,\left(z\right)\right)+{\sum }_{i,j}{\log \left[{D}_{\text{dec}}^{U}\left(G\,\left(z\right)\right)\right]}_{i,j}\right]$$

(12)

Enhancements to the discriminator architecture have significantly improved its ability to distinguish real from generated images. This improvement compels the generator to focus more on both global and local structural details, leading to the production of sharper, more realistic textures in the generated images.

Loss functions

The proposed framework consists of four key loss components: adversarial loss, reconstruction loss, perceptual loss, and style loss.

Adversarial loss

The enhanced adversarial loss is formulated as:

$${{{\mathcal{L}}}_{{\rm{adv}}}={\mathcal{L}}}_{{{\mathcal{D}}}\,^{{\mathcal{U}}}}$$

(13)

Here, ${{\mathcal{L}}}_{{{\mathcal{D}}}\,^{{\mathcal{U}}}}$ is computed through a pixel-wise weighted summation of probability maps derived from the discriminator ${{\mathcal{D}}}\,^{{\mathcal{U}}}$.

Reconstruction loss

To enforce pixel-level fidelity between the generated image $\hat{x}$ and the ground-truth image the $x,$ reconstruction loss employs the L1 norm:

$${{\mathcal{L}}}_{{\rm{rec}}}={{\mathbb{E}}}_{x,\hat{x}\sim ({p}_{{\rm{data}}},G\,(z))}[\parallel x-\hat{x}{\parallel }_{1}]$$

where $G\,(z)$ represents the generator output, and ${p}_{{data}}$ is the real data distribution.

Perceptual loss

To maintain semantic consistency between the generated and ground-truth images, the perceptual loss is computed based on feature embeddings from a pre-trained VGG network (e.g., VGG16 or VGG19). The perceptual loss is defined as:

$${{\mathcal{L}}}_{\text{per}}=\sum _{i}\parallel {\phi }_{i}(x)-{\phi }_{i}(\hat{x}){\parallel }_{1}$$

where ${\phi }_{i}(\cdot )$ represents the feature map extracted at the i-th layer of the VGG network.

Style loss

To ensure the generated image matches the texture and style of the ground-truth, the style loss compares the Gram matrices $G$ of the feature activations:

$${{\mathcal{L}}}_{{\rm{style}}}=\sum _{i}\parallel G\left({\phi }_{i}(x)\right)-G\left({\phi }_{i}(\hat{x})\right){\parallel }_{1}$$

Here, $G(\bullet )$ denotes the Gram matrix computation, which captures the correlations between feature channels. For a feature map ${\phi }_{i}(x)$ of shape $H\times W\times C$, it is first reshaped into a matrix ${\phi }_{i}^{{\prime} }\in {{\mathbb{R}}}^{C\times (H\bullet W)}$. The Gram matrix is then computed as:

$$G\left({\phi }_{i}\right)={\phi }_{i}^{{\prime} }\cdot {\left({\phi }_{i}^{{\prime} }\right)}^{T}$$

The resulting $G({\phi }_{i})\in {{\mathbb{R}}}^{C\times C}$ encodes the second-order statistics of the feature maps, reflecting the style characteristics of the image.

The total loss function combines all the above components with empirically tuned weights to balance their contributions:

$${{\mathcal{L}}}_{{\rm{total}}}={\lambda }_{{\rm{adv}}}{{\mathcal{L}}}_{{\rm{adv}}}+{\lambda }_{{\rm{rec}}}{{\mathcal{L}}}_{{\rm{rec}}}+{\lambda }_{{per}}{{\mathcal{L}}}_{{\rm{per}}}+{\lambda }_{{\rm{style}}}{{\mathcal{L}}}_{{\rm{style}}}$$

The coefficients are set as ref. ³⁷: ${{\rm{\lambda }}}_{{\rm{adv}}}=0.1,{\lambda }_{{\rm{rec}}}=10{,\lambda }_{{per}}=0.1,{\lambda }_{{\rm{style}}}=250$.

Results

Datasets

In this paper, we introduce the DunHuang-Mural dataset, which consists of 7983 high-resolution images representing various types of murals. The high-resolution mural images collected from three sources: the “Chinese Dunhuang Murals Treasury” dataset (1382 murals from various Dunhuang caves), the Digital Dunhuang website (filtered and high-quality images), and search engines (via keywords like “ancient Chinese murals” and “Dunhuang murals”). The images represent different historical periods, including Northern Zhou, Sui, Tang Dynasties, and feature diverse subjects like Bodhisattvas, Buddha images, and architecture. To ensure quality, damaged murals were excluded, and images were cropped to sizes between 512 × 512 and 1200 × 1200 pixels before being resized uniformly to 512 × 512 using Python’s PIL library.

The creation of this dataset was motivated by the need to address the gap in suitable datasets for mural inpainting research, particularly for mural image inpainting. To facilitate effective model training, the dataset was divided into two subsets: a training set of 6386 images for feature learning and a test set of 1597 images for evaluating model performance and generalization.

To simulate real-world mural damage and introduce diverse deletion patterns, we incorporated the NVIDIA Irregular Mask Dataset from Liu et al.³⁸ which contains 12,000 mask images in six size categories, each with 1000 border-constrained and 1000 border-unconstrained masks. By combining this mask dataset with the DunHuang-Mural images, we exposed the network to a variety of deletion scenarios, enhancing its robustness in handling different types of damage commonly found in authentic murals. Figure 4 illustrates the original image and corresponding mask from our dataset, demonstrating the inpainting process applied to the damaged mural. The original image serves as the reference, while the mask highlights the regions with missing content, simulating real-world damage.

Fig. 4: Example of DunHuang-Mural dataset.

a DunHuang-Mural images, b Maked Image. Note: The figure shows an example from the DunHuang-Mural dataset. The Dunhuang-Mural dataset was developed from a publicly available Kaggle dataset, accessible via the following link: https://www.kaggle.com/jacobok/datasets and https://www.kaggle.com/datasets/xuhangc/dunhuang-grottoes-painting-dataset-and-benchmark. Through systematic preprocessing using Python, 7983 high-resolution images were generated. This dataset, referred to as the Dunhuang-Mural dataset, provides a critical resource for tasks such as mural image inpainting, damage detection, and validation in the field of digital heritage preservation. In (a) DunHuang-Mural images we have the original DunHuang-Mural images. These are pieces of artwork that include intricate details and colors, showcasing the rich cultural heritage of the Dunhuang murals. The images depict scenes with various figures and elements, such as a seated figure and architectural elements. In (b) Maked Image, the irregular masked images are shown. These masks are applied to the original images, simulating regions that are missing or damaged. The white areas in the mask represent the regions that are missing content and need to be inpainted or restored. The mask highlights the gaps in the images that the inpainting method, such as CAUGAN, will focus on filling to generate a complete and realistic image.

Evaluation indicator

PSNR¹⁹, SSIM³⁹, and FID⁴⁰ are well-established metrics for evaluating image quality. PSNR measures the peak signal-to-noise ratio, reflecting the accuracy of pixel-level reconstruction. SSIM assesses structural similarity, focusing on luminance, contrast, and texture, which are crucial for visual perception. FID, on the other hand, compares the distribution of generated images to real images, capturing differences in feature space and offering insights into the realism of the restored images. By utilizing these metrics, we ensure a thorough and objective evaluation of the inpainting quality achieved by our model. Therefore, in this paper, we also employ these metrics for the evaluation and comparison of our model’s performance.

Implementation details

The experiments were implemented using PyTorch⁴¹ and trained for 100 epochs with the Adam optimizer and a fixed learning rate of 0.0001 for stable convergence. We initialized the model using a pretrained VGG16 network to leverage knowledge from a large-scale dataset. All images were resized to 512 × 512 for consistency, in line with common practices in the field. The experiments were performed on a single NVIDIA V100 GPU (32 GB).

To improve the model’s performance and generalization on real-world data, we incorporate an adaptive data augmentation technique known as ADA enhancement. This method applies a variety of transformations, including 90° rotation, integer translation, geometric and color adjustments, spatial filtering, additive noise, and cutout, with each transformation being applied randomly based on an adaptive probability, p. The value of p is adjusted during training according to the model’s overfitting level, ensuring a balance between sufficient augmentation and avoiding excessive randomness. This approach enhances the model’s robustness by providing a diverse set of training examples, enabling it to better generalize across a wide range of real-world data.

The network model was implemented using the popular deep learning framework PyTorch. The training process was configured to run for 100 epochs, with the Adam optimizer being utilized to update the model’s parameters. A fixed learning rate of 0.0001 was maintained throughout the training to ensure stable convergence. To initialize the model weights, a pretrained model of VGG16 was employed, leveraging the knowledge learned from a large—scale dataset. During both the training and evaluation phases, all images were uniformly resized to 512 × 512 to maintain consistency^19,42,43. This standardization was in line with a set of commonly used settings in the field, facilitating comparisons and reproducibility of the results. All experiments were executed on a single NVidia V100 GPU (32 G), which provided the necessary computational power to handle the complex computations involved in training and evaluating the model.

To address the challenges of model overfitting and enhance its generalization ability on real—world data, we adopted an adaptive data augmentation technique known as ADA augmentation⁴⁴. This technique introduced a stochastic element to the training process by randomly selecting from a variety of augmentation operations. These operations encompassed pixel manipulations such as horizontal flipping (x—flip), 90° rotations, and integer translations, which can help the model learn invariances to these common geometric transformations. Geometric transformations, color transformations, spatial filtering, additive noise⁴⁵, and cutout⁴⁶ were also included in the augmentation repertoire. Each of these augmentations was applied to the image with a certain probability p, while with a probability of 1-p, the augmentation was skipped. Crucially, the probability p was adaptive, meaning it could be adjusted based on the degree of overfitting exhibited by the model during training. This adaptive mechanism allowed the model to receive a diverse set of training examples, thereby improving its robustness and better adapting to the characteristics of different real-world datasets.

Qualitative evaluation results

To evaluate the inpainting quality of the murals, we conducted image inpainting experiments and compared our results with those of other models. Figure 5 presents the inpainting outcomes achieved by our proposed CAUGAN model.

Fig. 5: Image inpainting results using CAUGAN model.

Note: This 3 × 3 grid illustrates the systematic workflow for mural inpainting. Each row displays three stages of the same mural segment: a Original Image—the mural with natural degradation and damage, b Masked Image—regions with structural defects highlighted by white overlays, and c Our Results–the inpainting outcomes generated using the CAUGAN model.

As demonstrated in Fig. 5(c), the model effectively restores missing regions of the mural images, demonstrating its capability to recover both fine details and large-scale structures. The restored images exhibit improved texture and color consistency, which is crucial for preserving the visual integrity of the original artwork. The model successfully handles various types of damage, including missing chunks and irregular gaps, ensuring that the restored regions seamlessly integrate with the surrounding content. These results highlight the effectiveness of our approach in addressing real-world challenges in mural inpainting.

To evaluate the performance of our proposed method, we conducted a comparative study with several state-of-the-art models, including PConv, GatedConv, and PDGAN. For a fair comparison, we used publicly available implementations of these models and ensured that all experiments were performed under identical conditions, specifically using the same masks. The results, as shown in Fig. 6, highlight significant differences in the inpainting capabilities of the models. PConv³⁸ often produced unrealistic content in the missing regions, indicating a lack of precise inpainting in certain areas. GatedConv²⁹ struggled with larger, irregular holes, leading to subpar inpainting results. Although PDGAN⁴⁷ yielded relatively reasonable inpainting, it consistently generated noticeable artifacts, which impacted the visual quality of the output. In contrast, our method demonstrated superior performance, delivering more seamless and natural inpainting with better preservation of the overall image context and finer details. The restored image using our restoration method is compared with the original image(ground truth), and the restoration is better than other models. These findings emphasize the effectiveness of our approach in addressing the challenges of mural image inpainting.

Fig. 6: Qualitative comparison with state-of-the-art methods.

We have highlighted and enlarged specific details next to each image with a red box. a Masked, (b) PConv, (c) GatedConv, (d) PDGAN, (e) Ours, (f) Ground Truth. Note: This figure compares the inpainting performance of different models for mural restoration. a shows the original image with missing sections due to natural degradation. b through (f) display the inpainting results of various models, with each panel presenting the inpainting of the same damaged region. b illustrates the result from PConv, which often produces unrealistic content in the missing areas, showing a lack of precise inpainting in certain regions. GatedConv (c) struggles with larger, irregular holes, leading to suboptimal inpainting results. While PDGAN (d) generates relatively reasonable inpainting, it consistently produces noticeable artifacts that degrade the visual quality of the restoration. In contrast, (e) shows the inpainting results from our method, which provides a significantly better output. The inpainted regions are more seamless, natural, and contextually consistent with the surrounding details. f compares the output from our method with the original (ground truth), clearly demonstrating that our approach outperforms the others in terms of quality and detail preservation.

Quantitative evaluation results

In the quantitative evaluation, we categorized the irregular mask dataset into four size ranges: 1–10%, 10–20%, 20–30%, 30–40%, and 40–50%, to assess inpainting performance under different levels of damage. Using a set of 1597 mural images, we compared the performance of our model against existing methods.

The results, as shown in Table 1, highlight the superior performance of our model compared to state-of-the-art methods across multiple evaluation metrics.

Table 1 Quantitative comparison with the state-of-the-art models

As presented in Table 1, the results demonstrate the superiority of our proposed model over existing state-of-the-art methods across multiple evaluation metrics. Specifically, in terms of PSNR, a widely used metric for assessing image quality, our model showed exceptional performance in preserving fine pixel-level details. It achieved a higher PSNR compared to other methods, indicating that the inpainted regions are more similar to the original, undamaged image content, with minimal distortion and loss of information.

The SSIM results further highlighted the effectiveness of our approach. SSIM, which considers both pixel values and structural information such as edges and textures, showed that our model was highly successful in maintaining the overall image structure. It produced colorized images with more coherent and consistent structures, thereby enhancing the visual plausibility of the inpainted regions.

In addition to PSNR and SSIM, we also evaluated the perceptual quality of the inpainted images using the Frechet Inception Distance (FID) metric. FID is known for its alignment with human visual judgment, and the results revealed that the images generated by our model were of high quality, approaching human-level perception. This suggests that our model not only produces visually appealing inpainted results but also captures the underlying characteristics and distribution of natural images, making the generated images more perceptually realistic.

In conclusion, the quantitative evaluation results clearly demonstrate that our proposed model outperforms current state-of-the-art methods in mural image inpainting. By excelling in multiple key metrics, our model proves to be highly effective in restoring missing image content while preserving both visual quality and structural integrity.

Ablation study

To investigate the impact of each component on model performance, we conducted two sets of ablation experiments using 30%-40% masks. These experiments were designed to evaluate the contributions of the CAAT module and the U-Net-based discriminator to the overall performance. To assess the impact of the CAAT module, we removed the CA attention mechanism from the residual connections, keeping all other parameters unchanged. This modified network was trained using the same protocol on our mural image dataset. Similarly, we assessed the effectiveness of the U- Net discriminator by comparing it with the original four-layer discriminator.

The quantitative results from these ablation tests are presented in Table 2, providing a clear comparison of the model’s performance with and without these components.

Table 2 The results of the ablation study

As demonstrated in Table 2, the results indicate that incorporating the CAAT module significantly improves the model’s performance across all levels of damage. Specifically, removing the CAAT module resulted in a decrease of 0.280 in PSNR, a reduction of 0.008 in SSIM, and an increase of 1.61 in FID. These findings emphasize the crucial role of the CAAT module in enhancing the model’s ability to capture contextual information, leading to more accurate and faithful inpainting of image structure and texture. Furthermore, the model with the U-Net-based discriminator consistently outperforms the one using the original discriminator architecture. Incorporating the U-Net-based discriminator improved PSNR by 0.503, SSIM by 0.015, and reduced FID by 0.89. These results highlight the effectiveness of the U-Net-based discriminator in extracting richer structural details, as evidenced by the significant improvement in SSIM. Additionally, the model demonstrated a stronger ability to capture finer pixel-level information, as reflected in the higher PSNR scores. These findings suggest that the U-Net-based discriminator is better suited to handle the complex and nuanced characteristics of the images, enabling the generator to produce more accurate and visually coherent inpainting results.

Model versatility test

To evaluate the reliability and versatility of the proposed model, additional mural images were selected for inpainting. Specifically, digital images of murals from Shanxi were chosen due to their similarity to the Dunhuang murals. Both regions of them are characterized by murals located within temples, sharing religious themes and spanning multiple Chinese dynasties with a long historical legacy. Additionally, these murals exhibit similar stylistic features, including comparable line work and color schemes. For the test, mural images from the Song Dynasty Kaihua Temple in Gaoping City, Jincheng, Shanxi, and the Yuan Dynasty Qinglong Temple in Jishan County, Yuncheng, Shanxi, were selected as the image sources for the validation dataset. The image inpainting results are presented in Fig. 7.

Fig. 7: Inpainting of a Shanxi mural using the CAUGAN model.

Note: This figure illustrates the inpainting process of a damaged Shanxi mural. The image data, originally obtained from page 29 of Volume 1 and page 7 of Volume 2 of the Shanxi Ancient Mural Masterpieces Collection, published by the Shanxi Economy Publishing House in 2016, has been digitized for subsequent analysis and research. a presents the Original Image, showing the mural with visible degradation and missing sections due to natural wear. b displays the Masked Image, where the damaged regions are highlighted and masked to prepare for restoration. c shows the Restored Result, where the inpainting has been successfully applied. As seen in (c), the damaged areas in the original Shanxi mural have been effectively reconstructed, demonstrating the CAUGAN model’s strong stability and effectiveness in restoring mural artwork. This process highlights the model’s ability to recover fine details and maintain visual coherence in complex mural restoration tasks.

Figure 7 illustrates the inpainting process: Fig. 7(a) showing the original mural, Fig. 7(b) displaying the masked image, and Fig. 7(c) presenting the restored result. As observed in Fig. 7(c), the damaged areas in the original mural have been effectively repaired. This demonstrates that the CAUGAN model exhibits strong stability in the image inpainting task.

Disscussion

In this study, we propose an image inpainting model with CAAT block and U-Net-based discriminator for restoring ancient mural paintings image. The model enhances traditional GANs by leveraging the CAAT block, which captures more information for improved image generation, and by utilizing a U-Net-based discriminator to guide the generator in producing more realistic fresco inpainting. Due to the scarcity of publicly available datasets, we created the DunHuang-Mural dataset, comprising 7983 high-resolution images. Focused on the Dunhuang murals, this dataset serves as a valuable resource for advancing research in mural inpainting and preservation, offering significant potential for furthering studies in this field.

To evaluate the effectiveness of our proposed model, we conducted a series of inpainting experiments on damaged mural images. The results demonstrate that the CAUGAN model outperforms several widely used models, including PConv, GatedConv, and PDGAN, in terms of key performance metrics such as PSNR, SSIM, and FID. This enhanced performance can be attributed to the integration of two key components: the CAAT module and the U-Net-based discriminator. The CAAT module enhances the inpainting process by preserving positional and spatial information, enabling the model to restore distant regions more accurately. This results in restored content that is both realistic and contextually coherent, significantly enhancing the quality of the restored mural images. Meanwhile, the U-Net-based discriminator contributes to improved image quality by performing both global and local assessments of image authenticity. This dual-level evaluation mechanism helps to reduce pixel-level blurriness and enhances the visual coherence of the restored regions. Together, these components enable the generation of more accurate, detailed, and visually appealing mural inpainting.

In addition to its effectiveness on the DunHuang-Mural dataset, the model also demonstrated excellent inpainting results when applied to mural images from Shanxi temples, further validating its versatility and robustness. These results highlight the potential of the CAUGAN model for broader applications in mural inpainting and cultural heritage preservation, offering a powerful tool for the inpainting of diverse types of mural artworks.

Despite the strong performance of our model, it has some limitations, particularly when dealing with large and complex missing regions in mural images. Murals often contain intricate patterns and symbolic elements, which can be difficult for the model to accurately capture, especially in areas with significant damage. This may lead to less precise inpainting in regions with significant missing content. To address this, future work should focus on improving the model’s ability to handle large-scale damage and enhance its contextual understanding for more accurate and coherent inpainting.