Introduction

In the landscape of contemporary computing, deep neural networks (DNNs) have gained prominence by enabling breakthroughs across various applications from image classification to healthcare technologies1,2,3,4,5,6. Although DNNs and their feedforward configurations have shown remarkable success in executing static tasks such as pattern recognition7,8,9,10, they are unsuitable for processing dynamic data. In this context, recurrent neural networks (RNNs), specifically analog reservoir computing (ARC) systems, have emerged as pivotal solutions11,12,13,14. An ARC system employs a dynamic reservoir that projects the input data nonlinearly into a high-dimensional feature space (Supplementary Fig. 1). This mapping, facilitated by the intrinsic short-term memory capabilities of the reservoir, enables the transformation of complex inputs into linearly separable states within the system14,15. The linearly weighted summation of these states is then processed using a trainable readout network, making ARC an efficient and robust framework for temporal data processing and prediction tasks.

However, conventional ARC systems based on complementary metal-oxide-semiconductor (CMOS) platforms suffer from a deficiency in inherent dynamic response characteristics16. This necessitates the use of complex algorithms along with large-scale integrated devices to handle nonlinear dynamic tasks, thus hindering the complete realization of the potential of ARC17. To overcome this limitation, the exploration of hardware-based ARC systems utilizing novel materials and device configurations has garnered research interest; specifically, materials and devices that exhibit distinct volatile and nonvolatile switching characteristics to implement the reservoir and readout networks, respectively. Various devices, including two-terminal memristors5,18,19,20,21,22,23,24,25,26,27, ferroelectric devices28,29,30,31,32, spintronic oscillators33, electrochemical transistors34,35,36, photonic module devices37,38,39, and quantum devices40, have been studied for the possible candidate. Despite the advantages of these hardware-based ARC systems, the full integration of the reservoir, readout network, and additional circuit components with artificial neuron functionality remains a challenge due to the utilization of different materials for each component (detailed in Supplementary Note 1). Zhong, Y. et al. presented an ARC system based on two-terminal memristors; however, the realization of the reservoir and readout network necessitated different materials–TiOx for the physical reservoir and TaOx/HfAlOy for the artificial synapse in the readout network18. Consequently, the seamless integration of these components was unattainable, promting separate fabrication of each component connected through wiring afterward. Moreover, in most studies, the integration of neuron circuitry for the readout network in ARC has not been adequately explored.

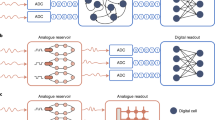
Hafnium oxide (HfO2)-based thin films present a promising solution to address these challenges by leveraging the material versatility of hafnia. HfO2 has traditionally served as a high-κ dielectric in conventional CMOS technology since the mid-2000s41. Following the discovery of its ferroelectricity originating from the orthorhombic (o)-phase in 2011, its applications have expanded to nonvolatile functionalities for memory and artificial synaptic devices42,43,44,45,46. Furthermore, through material engineering, anti-ferroelectricity, suitable for dynamic response in ARC, can also be realized. Recent advancements include the utilization of hafnium zirconium oxide (HZO) thin films near the mixed phase boundary (MPB) between the ferroelectric o-phase and tetragonal (t)-phase47,48. Although there have been no prior attempts to exploit the HZO thin films near the MPB for ARC, its volatile memory characteristics and higher polarization magnitude at lower voltages compared to anti-ferroelectric films make it suitable for both the physical reservoir and artificial neuron (Fig. 1a). Therefore, by carefully engineering HfO2-based films from ferroelectric to MPB, comprehensive integration of physical reservoir, artificial synapse, and neuron functionalities can be achieved (Supplementary Note 2a). In addition to material engineering, optimizing device configuration can further enhance the performance of ARC (Fig. 1a). While two-terminal devices are commonly employed, double-gate (DG) transistors with four terminals offer advantages in terms of enhanced controllability and reliability. Unlike two-terminal devices, which pose significant constraints in implementing neuronal functionality, DG transistors provide a broader range of design possibilities for artificial neurons. Furthermore, DG transistors facilitate a clearer differentiation between reservoir states, thereby overcoming the poor resolution and limited number of reservoir states (3 or 4 bits)16,22,28,29,49,50,51,52. Although various attempts have been made to mitigate these challenges in two-terminal devices, such as employing input encoding with various pulse intervals22,50, they require additional circuitry, inevitably increasing area and power consumption. Control of electrical characteristics utilizing additional electrodes in four-terminal transistors can improve the resolution between the states without the burden of additional circuit.

Fig. 1: Fully integrated MPBTFT-based ARC system.
figure 1

a Material-device co-optimization method for an area- and energy-efficient ARC system. HZO thin film near the MPB provides volatile memory characteristics suitable for physical reservoir and artificial neuron. Double-gate configuration of MPBTFT improves the resolution between the reservoir states and facilitates neuronal functionality. b Schematic of an MPBTFT-based ARC system utilizing c volatile MPBTFTs for physical reservoirs, d nonvolatile FeTFTs for synaptic devices in readout network, and e volatile MPBTFTs for leaky integrate-and-fire (LIF) neurons. MPBTFTs are identified as suitable candidates for physical reservoirs and LIF neurons within ARC systems, primarily owing to their inherent nonlinearity and short-term memory characteristics. FeTFTs are distinguished by their ability to represent multilevel synaptic weights with stability over time, making them ideal components for the readout network within ARC systems. By integrating these TFTs, ARC systems can harness the transient data processing capabilities of MPBTFTs with the long-term data retention properties of FeTFTs.

Full size image

In this study, we propose a material-device co-optimization method for the area- and energy-efficient ARC system utilizing HZO-based thin-film transistors (TFTs). The seamless integration of physical reservoir, readout network, and leaky integrate-and-fire (LIF) neuron is achieved by meticulously engineering the material versatility of HZO (Fig. 1b). HZO with the o-phase is utilized for nonvolatile and multilevel conductances of the ferroelectric TFT (FeTFT)-based artificial synapse, while HZO near the MPB serves as both the physical reservoir and LIF neuron (Fig. 1c–e). All these materials are integrated into the TFTs with an indium–gallium–zinc oxide (IGZO) channel. The device configuration of DG MPB-based TFT (MPBTFT) improves the performance of the ARC system by leveraging the electrical characteristics of DG to clearly distinguish between the 16 reservoir states without overlapping, and successfully demonstrates 5-bit reservoir states. For neuronal functionality, DG MPBTFT processes both excitatory and inhibitory pulses within a single device, unlike previously reported ferroelectric-based three-terminal LIF neurons53,54,55. Importantly, the adoption of similar fabrication processes for volatile and nonvolatile TFTs with HZO films enables their co-integration on a single wafer, a milestone previously unattainable. Various tasks, ranging from handwritten digit recognition tasks to waveform classification and complex time-series predictive tasks in the real world, were performed to evaluate the performance of the proposed ARC system. The integration of volatile and nonvolatile TFTs into an ARC system overcomes the limitations of previous hardware-based ARC systems and sets a new standard for energy efficiency, scalability, and versatility in ARC systems.

Results

Device Structures

Two distinct types of HZO-based TFTs were fabricated to implement an ARC system: nonvolatile FeTFT for the synaptic device in the readout network and volatile MPBTFT for the physical reservoir and LIF neuron. While both TFTs utilize HZO thin films as ferroelectric materials, variations in the material composition of the HZO thin films impart the TFTs with either volatile or nonvolatile characteristics, diversifying their functionality within the system. Both TFTs incorporate an IGZO channel within a metal–ferroelectric–metal–insulator–semiconductor (MFMIS) structure, achieving enhanced electrical characteristics (Supplementary Note 3). In particular, an MPBTFT was designed as a DG device, enabling its operation to be modulated not only by the bottom-gate (BG) but also by the top-gate (TG). TG can be utilized to refine the reservoir states of MPBTFTs and execute inhibition operations in LIF neurons. The structural similarities between FeTFT and MPBTFT facilitate the integration of both types of TFTs on a single wafer using a self-align etching process. The fabrication process for both TFTs is detailed in the Methods section and Supplementary Fig. 2.

Nonvolatile synaptic FeTFT for readout network

Figure 2a shows a schematic illustration and cross-sectional view of a nonvolatile FeTFT with an MFMIS structure. The cross-sectional transmission electron microscopy (TEM) images of the fabricated FeTFTs are shown in Fig. 2b. The structure of the FeTFT with a Mo/HZO/TiN/ZrO2/IGZO stack was examined using energy-dispersive spectroscopy (EDS) analysis (Supplementary Fig. 3). The crystallinity of the HZO (Hf:Zr = 2:1) thin films were investigated using grazing incidence X-ray diffraction (GIXRD) analysis (Supplementary Fig. 4a). Figure 2c shows the top optical images of the FeTFT array for the readout network within the ARC system. Each FeTFT functions as a synaptic device within the readout network by leveraging the inherent nonvolatile memory effects of ferroelectric materials.

Fig. 2: Device characteristics of nonvolatile FeTFT for readout network.
figure 2

a Schematic illustration and cross-sectional view of the nonvolatile FeTFT with an MFMIS structure. b Cross-sectional TEM images of the fabricated FeTFT. Magnified TEM image of the red dashed square region presents the thickness of each layer: metal (M), ferroelectric (FE), inner metal (IM), interlayer oxide (IL), and IGZO channel. c Top optical images of the FeTFT array. The FeTFT array has an AND-type array configuration, characterized by bit-lines (BLs) and source-lines (SLs) parallel to each other yet perpendicular to word-lines (WLs). The gate (G), source (S), and drain (D) electrodes of each FeTFT within the array are accessible via WL, SL, and BL, respectively. The width (W) and length (L) of a channel are both 20 μm. d Switching current and P-V hysteresis loop through the PUND measurements with 100 kHz triangular pulses. e Hysteretic transfer characteristics (ID-VGS) measured with a bidirectional direct current (DC) sweep of the gate voltage (VGS), ranging from –4.0 V to 4.0 V. A drain-source voltage (VDS) is 0.1 V. The FeTFT exhibits a wide memory window (MW) of approximately 2.2 V at a constant ID of 10 nA. f LTP and LTD characteristics of the FeTFT with the number of applied pulses. The insets show the schematics of applied PGM and ERS pulses. The FeTFT achieves multilevel synaptic weights with a highly linear conductance response. g LTP and LTD characteristics over 20 cycles, with each cycle containing 32 applied pulses. The FeTFT exhibits low cycle-to-cycle variation. h Retention characteristics of eight different conductance states at room temperature.

Full size image

Capacitors with a metal–ferroelectric–metal (MFM) structure subjected to identical fabrication processes as the FeTFTs were utilized to verify the ferroelectric properties of the FeTFTs. The ferroelectric switching current is distinguished from non-ferroelectric switching currents, such as displacement and leakage currents, through positive-up-negative-down (PUND) measurements–wherein 100 kHz triangular pulses are applied. The switching current and polarization as a function of the applied voltage are depicted in Fig. 2d. The HZO film exhibits the magnitude of remanent polarization (2Pr) of approximately 37.7 μC/cm2 in the sweep range from –3.8 V to 3.8 V. Figure 2e illustrates the hysteretic transfer characteristics of the FeTFT. The transfer characteristics demonstrate a counterclockwise hysteresis loop with a wide memory window (MW) of approximately 2.2 V at a constant drain current (ID) of 10 nA.

The nonvolatile FeTFTs can emulate the plasticity of biological synapses through the partial polarization switching of the HZO film31,32,55,56. The long-term potentiation (LTP) and long-term depression (LTD) characteristics of the FeTFT were investigated by applying program (PGM) and erase (ERS) pulses (Fig. 2f). The pulse widths were consistently maintained at 10 μs, and PGM pulse amplitudes increased from 3.5 V to 4.1 V in steps of 0.04 V, while ERS pulse amplitudes decreased from –4.35 V to –5.1 V in steps of –0.05 V. Multilevel synaptic weights were obtained through the FeTFT exhibiting a highly linear conductance response, characterized by coefficients βp = 0.04 and βd = 1.956. Figure 2g illustrates the LTP and LTD characteristics of the FeTFT over 20 cycles. Low cycle-to-cycle variation is observed (σ/μ < 0.025, σ and μ are the standard deviation and average value, respectively), indicating consistency and reliability in the operation of the FeTFT over multiple operational cycles. The retention characteristics of the FeTFT with various memory states are depicted in Fig. 2h, showing its nonvolatile memory characteristics. The FeTFT preserves the stored information for 103 s with a slight degradation, verifying the robustness and reliability of the device. The device-to-device variation, endurance characteristics, and selective PGM/ERS operations within the FeTFT array were investigated (Supplementary Figs. 5 and 6). The results confirm the suitability of the nonvolatile FeTFTs for synaptic devices. Note that by further optimizing the measurement conditions, a larger dynamic range can be obtained for enhanced system performance (Supplementary Fig. 7).

Volatile double-gate MPBTFT for physical reservoir

The distinguishing feature of the ARC system is the reservoir, which is a network of nonlinear dynamic nodes that transform input signals into a high-dimensional space, enabling the system to process temporal information. In an MPBTFT-based ARC system, these nodes are represented by volatile DG MPBTFTs, which are physical reservoirs characterized by nonlinear and dynamic responses to input stimuli. Figure 3a shows a schematic illustration and cross-sectional view of a DG MPBTFT featuring two different gates: BG and TG. The BG side operates as an MPBTFT with an MFMIS structure, while the TG side functions as a TFT with a metal–insulator–semiconductor (MIS) structure. This DG configuration affords versatile control and modulation of the electrical characteristics of the MPBTFT. Figure 3b shows the cross-sectional TEM images of the fabricated DG MPBTFTs. The structure of the DG MPBTFT with a Mo/HZO/Mo/ZrO2/IGZO/ZrO2/Mo stack was examined by EDS analysis (Supplementary Fig. 8). A GIXRD analysis was conducted for the HZO (Hf:Zr = 3:5) thin films (Supplementary Fig. 4b). Figure 3c shows the top optical images of the DG MPBTFT array for the physical reservoirs within the ARC system. The GIXRD analyses of both volatile and nonvolatile HZO thin films are detailed in Supplementary Note 2b.

Fig. 3: Device characteristics of volatile DG MPBTFT for physical reservoir.
figure 3

a Schematic illustration and cross-sectional view of the volatile DG MPBTFT. The DG MPBTFT operates as an MPBTFT with an MFMIS structure and a TFT with an MIS structure at the BG and TG sides, respectively. b Cross-sectional TEM images of the fabricated DG MPBTFT. c Top optical images of the DG MPBTFT array. The DG MPBTFT array has WL pairs (WLB and WLT) parallel to each other, each connected to the BG and TG electrodes of the DG MPBTFT within the array. The width (W) and length (L) of a channel are both 20 μm. d Switching current and P-V hysteresis loop through triangular pulses with 100 kHz. e Hysteretic transfer characteristics (ID-VBG) for various TG voltage (VTG) conditions. Bidirectional DC sweeps of the BG voltage (VBG), ranging from –2.0 V to 2.0 V, were performed at a VDS of 0.1 V. f Decay characteristics of the ID over time, subsequent to the application of a 100 μs PGM pulse. The relaxation processes are well-fitted for various VPGMs through a double exponential function (red lines). g ID response according to various VTGs when a constant pulse train (4.0 V, 100 μs) is applied to the BG. ID evolutions in response to 16 different input pulse trains (4.0 V, 100 μs) h without and i with TG utilization. Each input pulse train comprises 4 timeframes with a 3 ms time interval between successive pulses. The upper panel shows the pulse schemes for the BG and TG (e.g., input ‘1111’). By applying gradually decreasing voltage pulses across 4 timeframes to the TG, clearly distinguishable reservoir states are generated for various input data. j ID evolutions in response to 32 different input pulse trains (4.0 V, 100 μs), each comprising 5 timeframes. The upper panel shows the pulse schemes for the BG and TG (e.g., input ‘11111’). The utilization of the TG effectively expands the reservoir states.

Full size image

The capacitors featuring an MFM structure, which underwent identical fabrication processes to the DG MPBTFTs, were used to confirm the polarization properties of the DG MPBTFTs. Through triangular pulses with 100 kHz, the switching current and polarization as a function of the applied voltage are depicted in Fig. 3d. The HZO film exhibits the magnitude of saturation polarization (2Ps) of approximately 66.6 μC/cm2 in the sweep range from –2.0 V to 2.0 V. A high polarization magnitude at a relatively low voltage is obtained through the HZO film near the MPB. The switching current demonstrates a partial hysteresis of the HZO film within the DG MPBTFT. The polarization of the HZO film reverts to a non-polarized state at 0 V, indicating the capability of the HZO film to transition between the polarized and non-polarized states. The symmetric switching current peaks observed near 0 V highlight that the coercive voltage (Vc) and the energy barriers between the phases are sufficiently small to rapidly reset the polarization state. The HZO thin film near the MPB exhibits a high dielectric constant (Supplementary Fig. 9). The polarization within the HZO film is switched when an electric field is applied, whereas it returns to the initial non-polarized state in the absence of an electric field. Figure 3e presents the hysteretic transfer characteristics of the DG MPBTFT under various TG voltage (VTG) conditions. The transfer characteristics exhibit a counterclockwise hysteresis loop with a MW of approximately 0.5 V at a constant ID of 10 nA when VTG = –3.0 V. The endurance characteristics of the DG MPBTFT were investigated (Supplementary Fig. 9).

To verify the volatile memory characteristics of the DG MPBTFT, a single PGM pulse was applied to the device, followed by a read operation at a constant voltage for a specific duration. Figure 3f illustrates the dynamic response of the ID in the DG MPBTFT over time, subsequent to the application of a PGM pulse with a width of 100 μs. PGM pulses with different amplitudes were applied at the same initial state. As the amplitude of the PGM pulse (VPGM) increased, the corresponding ID increased. Following the removal of the PGM pulse, IDs decayed toward the initial state in all cases. This relaxation process fitted well with the double exponential function (red lines in Fig. 3f). The dynamic response of IDs in the DG MPBTFT to successive PGM pulses with various VPGMs was investigated (Supplementary Fig. 10). ID increases significantly as VPGM increases, while ID decays back to its initial state in the absence of a PGM pulse. The fitting parameters for these volatile memory characteristics are shown in Supplementary Fig. 11. Note that the volatile DG MPBTFTs exhibit a rapid current relaxation process, ensuring fast data processing capabilities of the ARC system.

The changes in ID when a PGM pulse is applied to the BG varies depending on the TG bias (Supplementary Fig. 12). The formation of an accumulation layer in the IGZO channel, crucial for efficiently coupling the voltage applied to the BG to the ferroelectric layer during PGM operation, is affected by the TG bias57,58. Specifically, applying a positive voltage to the TG can inhibit the formation of an accumulation layer in the IGZO channel, diminishing the PGM efficiency and the amount of change in ID. Figure 3g shows the ID response according to various TG pulse amplitudes when a constant pulse train of 4.0 V amplitude is applied to the BG. As the TG pulse amplitude increases, the amount of change in ID decreases. The dynamic interaction between the BG and TG enables modulation of the sensitivity of the physical reservoir to the input signals. This inherent flexibility in the DG configuration improves physical reservoir characteristics.

For a physical reservoir within an ARC system to function effectively, the reservoir state, manifested as the ID of the volatile DG MPBTFT, must evolve dynamically over time in response to an input signal. Distinct reservoir states for different temporal inputs are essential for transforming and expanding input signals across the high-dimensional state space of the reservoir5,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40. Figure 3h demonstrates the ID evolutions of the DG MPBTFTs in response to 16 different input pulse trains, each comprising 4 timeframes. For each timeframe, a pulse with an amplitude of 4.0 V and a width of 100 μs was applied to the BG, while a fixed voltage of 0 V was applied to the TG. The time interval between successive pulses is 3 ms (see Supplementary Fig. 13 for ID evolutions over various time intervals). The device-to-device variations of the DG MPBTFTs were further investigated (Supplementary Fig. 14). The results verify the capability of the DG MPBTFT to effectively distinguish input pulse trains. Nevertheless, some input pulse train configurations exhibit similar final conductance states. To address this states overlap issue, the TG of DG MPBTFT is utilized in this study.

Figure 3i illustrates the ID evolutions of the DG MPBTFTs in response to various input pulse trains with TG utilization. The proposed pulse scheme for TG is depicted in the upper panel of Fig. 3i. The utilization of TG enhances the distinctness between reservoir states compared to the case in which TG is not employed and clearly distinguishes each state. The enhanced distinction between reservoir states is attributed to PGM efficiency affected by VTG. Gradually decreasing VTG across 4 timeframes augments the influence of the input data in the latter timeframe (see Supplementary Note 4 for details). Supplementary Fig. 15 contrasts the normalized difference between the reservoir states of the DG MPBTFT with and without TG utilization. Note that the final reservoir states can be further optimized by adjusting the pulse scheme for TG (see Supplementary Fig. 16 for ID evolutions with different TG pulse scheme). The utilization of TG in DG MPBTFTs not only clearly distinguishes reservoir states but also enables the expansion of reservoir states. A demonstration of 32 distinct reservoir states (5 bits) in response to input pulse trains with 5 timeframes is shown in Fig. 3j. The proposed strategy effectively leverages the TG to modulate the electrical characteristics of DG MPBTFTs, thereby enhancing the performance and area/energy efficiency of the ARC system by ensuring sufficiently distinct reservoir states or expanding the states.

Volatile double-gate MPBTFT for leaky integrate-and-fire neuron

Within the ARC system, the versatility of volatile DG MPBTFTs extends to their application as LIF neurons, facilitating the seamless integration of physical reservoirs, readout networks, and LIF neurons. DG MPBTFTs utilize the inherent polarization volatility and partial polarization switching capabilities of the HZO film to implement the leaky effect and integrate-and-fire function of LIF neurons. Figure 4a shows a schematic of the DG MPBTFT-based LIF neuron, which eliminates the need for capacitors and complex circuits that are typically associated with larger footprints. The DG MPBTFT-based LIF neuron exhibits high area efficiency and functional versatility. Moreover, the DG MPBTFT can process both excitatory and inhibitory pulses through BG and TG, respectively, within a single device. This characteristic negates the necessity for additional devices or connections, streamlining the composition of the neuron53,54,55. The pulse schemes for the BG and TG are shown on the right side of Fig. 4a. The implementation and measurement setup for the DG MPBTFT-based LIF neuron are detailed in Supplementary Fig. 17.

Fig. 4: Characteristics of volatile DG MPBTFT-based LIF neuron.
figure 4

a Schematic of the volatile DG MPBTFT-based LIF neuron (left panel) and excitatory/inhibitory pulse schemes for the BG/TG (right panel). The DG MPBTFT-based LIF neuron exhibits high area efficiency and functional versatility as it can process both excitatory and inhibitory pulses within a single device. Excitatory pulses applied to the BG increase the ID of the DG MPBTFT, whereas inhibitory pulses applied to the TG decrease the ID. The voltage of the excitatory pulses ranges from Vbase to Vhigh, while the voltage of the inhibitory pulses ranges from –3.0 V to Vinh. Every neuronal behavior was investigated under a VDS of 0.1 V. b Demonstration of the neuronal behavior with self-reset characteristics of the DG MPBTFT when excitatory pulses are applied. The neuron can still fire in response to the excitatory pulses after the self-reset. Modulation of neuronal behavior through the c Vbase and d Vhigh. As the Vbase increases, the leaky effect of the neuron is decelerated, and the integration function is strengthened. An increase in Vhigh leads to more significant polarization switching in the HZO film and increases the ID change. On the contrary, insufficient Vhigh degrades the integration function of the neuron. Neuronal behaviors in response to the application of both excitatory and inhibitory pulses with various e Vinh, f inhibitory pulse width (twidth,inh), and g the number of inhibitory pulses (N). The inhibitory efficiency of the neuron is enhanced as Vinh, twidth,inh, and N increase. h Neuronal behavior of DG MPBTFT-based LIF neuron. The inset represents the input pulse train. The neuron demonstrates three primary functions: integration, firing, and resetting functions.

Full size image

Figure 4b illustrates the ID response of the DG MPBTFT when excitatory pulses are applied to the BG. During this time, a fixed voltage of –3.0 V is applied to the TG. The DG MPBTFT demonstrates neuronal behavior with self-reset characteristics. The application of excitatory pulses to the BG induces gradual polarization switching of the HZO film, increasing ID. When ID exceeds a specific threshold current (Ith) required for the neuron to fire, the neuron self-resets to its initial state, which is attributed to the inherent leaky effect. This characteristic eliminates the necessity for an external reset circuit. Neuronal behaviors with various reset times are shown in Supplementary Fig. 18. The roles of base voltage (Vbase) and high voltage (Vhigh) in modulating neuronal behavior are further investigated. As Vbase increases, the polarization of the HZO film is preserved, thereby decelerating the leaky effect (Fig. 4c). A high Vbase maintains the polarization of the HZO film during the delay between pulses, thus strengthening the integration function of the neuron. In addition, even if the same reset time is given, the neuronal behavior varies distinctly with Vbase. The neuron is completely reset to its initial state under low Vbase conditions. By contrast, under higher Vbase conditions, the neuron cannot be reset to its initial state within the same reset time, thus requiring an extended reset time for complete initialization. Figure 4d shows the neuronal behavior as a function of Vhigh. An increase in Vhigh results in more significant polarization switching in the HZO film and increases the ID change. However, an insufficient Vhigh (e.g., Vhigh = 1.0 V) barely switches the polarization of the HZO film, thus impairing the integration function of the neuron. These results highlight the critical roles of Vbase and Vhigh in modulating neuronal behavior. The impact of the delay between pulses on neuronal behavior is depicted in Supplementary Fig. 19.

Figure 4e–g show the neuronal behavior when inhibitory pulses are applied after a sequence of excitatory pulse trains. Notably, even with a shorter reset time (1.0 ms) compared to Fig. 4b–d, the application of sufficient inhibitory pulses facilitates the complete reset of the neuron to its initial state. This is particularly evident as the inhibitory voltage (Vinh) intensifies, enhancing the inhibitory efficiency of the neuron and requiring a greater number of excitatory pulses for the neuron to fire (Fig. 4e). These results highlight the potent inhibitory efficiency of higher Vinh levels. Furthermore, modulation of the width or quantity of inhibitory pulses significantly influences the inhibitory efficiency of neurons. Inhibitory pulses with extended pulse widths inhibit the neuron (Fig. 4f). The application of numerous inhibitory pulses also inhibits the neuron, leading to a complete reset to its initial state (Fig. 4g). These results verify the suitability of volatile DG MPBTFTs as LIF neurons, emphasizing their ability to finely modulate neuronal behavior in response to varying excitatory or inhibitory pulses (see Supplementary Note 5 for details). Figure 4h depicts the neuronal behavior of DG MPBTFT-based LIF neurons, demonstrating its three primary functions: integration, firing, and resetting functions. As input pulses are applied to the neuron, the voltage at node A increases, mimicking the integration function of the neuron. When the voltage at node A exceeds a certain threshold voltage (3.0 V), the neuron fires and generates an output spike. Following neuron firing, the neuron spontaneously resets to its initial state when no further input pulses are applied.

While the DG MPBTFT-based LIF neurons are not completely similar to the ideal behavior of LIF neurons, which reset to their initial state following a single firing action, they are well-suited for applications addressed in this work. This is because the digit corresponding to the output neuron that fires first is identified as the correct answer since a binary input pulse train is used in the digit recognition tasks (see Methods section). Enhancing the spontaneous reset speed of LIF neurons could significantly improve the latency of ARC systems.

MPBTFT-based analog reservoir computing system for digit recognition

An ARC system utilizing volatile DG MPBTFTs and nonvolatile FeTFTs is shown in Fig. 5a. Volatile DG MPBTFTs are employed as physical reservoirs and LIF neurons, while nonvolatile FeTFTs constitute the readout network. The MPBTFT-based ARC system operates through unique interactions between the physical reservoir, readout network, and LIF neurons, as detailed in Supplementary Note 6.

Fig. 5: MPBTFT-based ARC system for handwritten digit recognition.
figure 5

a Schematic of the ARC system utilizing volatile DG MPBTFTs and nonvolatile FeTFTs. In the system, input pulses are applied to the DG MPBTFT-based physical reservoirs. The generated reservoir states are fed into the readout network, which is comprised of FeTFT-based synaptic devices. Subsequently, the output currents from the readout network are transmitted to the DG MPBTFT-based LIF neurons, which produce the final outputs of the ARC system. b Preprocessing step of the MNIST dataset. Input images are cropped and encoded into input pulse trains. The image divided into five distinct sections along the row direction, each comprising 4 pixels, is shown as an example. Each of these encoded input pulse trains is then applied to the DG MPBTFT-based physical reservoirs. The obtained reservoir states from both the DG MPBTFT- and linear resistor-based physical reservoirs are depicted on the right side. c Classification accuracy for the MNIST dataset utilizing several different device-based physical reservoirs. Each result signifies the average accuracy derived from performing the task five times, ensuring a robust performance evaluation by mitigating the influence of outliers and variability. The DG MPBTFT-based physical reservoirs achieve the highest accuracy, particularly when utilizing the TG. d Average accuracies achieved for various physical reservoirs. e Confusion matrix for the MNIST digit recognition task. The MPBTFT-based ARC system accurately distinguishes ten types of handwritten digits.

Full size image

A handwritten digit recognition task was performed using the MNIST dataset to evaluate the performance of the MPBTFT-based ARC system. The images are preprocessed prior to their introduction into the reservoir (see Fig. 5b and Methods section). The encoded input pulse trains are applied to the volatile DG MPBTFT-based physical reservoir. The state of each physical reservoir evolves over time, and the state in the last timeframe is transmitted to the readout network. The reservoir states in the last timeframe are shown for the physical reservoirs based on DG MPBTFTs and linear resistors (right side of Fig. 5b). The response of the linear resistor is solely contingent on the magnitude of the input pulse applied at any given instant, thereby lacking the capacity to retain information regarding previous states. The absence of memory effects in linear resistors leads to an inability to distinguish between similar images. By contrast, the DG MPBTFTs exhibit well-distinguishable reservoir states. This attribute significantly enhances the ability of the system to discern subtle differences in inputs, thereby facilitating accurate pattern recognition. Note that the configuration of the size and number of sections in the input encoding process can be adjusted. A comprehensive explanation of the input encoding process is detailed in the Methods section.

Figure 5c shows the results of performing a digit recognition task utilizing several different device-based physical reservoirs: volatile DG MPBTFTs, nonvolatile FeTFTs, and linear resistors. Linear resistor-based physical reservoirs, limited by their capacity to retain information solely from the last timeframe of the input signal, demonstrate the lowest level of accuracy (~83.63%). When FeTFTs are utilized as physical reservoirs, the system lacks the capacity to process temporal information. However, these FeTFT-based physical reservoirs exhibit different responses depending on the number of input pulses applied. This characteristic results in a slight enhancement in accuracy (~85.45%) over linear resistors, which is attributable to the increased number of reservoir states (five states per reservoir). In contrast, DG MPBTFT-based physical reservoirs facilitate temporal information processing. This allows 16 reservoir states (4 bits) for each physical reservoir, significantly increasing the accuracy (~89.42%). In particular, the highest accuracy (~90.23%) is achieved when utilizing TG, which effectively differentiates between the reservoir states without any overlap. This distinct advantage demonstrates the suitability of the DG MPBTFT as a physical reservoir, highlighting its potential for accurately handling complex computing tasks through enhanced reservoir state discrimination. The system utilizing 32 reservoir states (5 bits) significantly enhances the area efficiency (~20% enhancement) with a slight degradation in accuracy (~88.25%). This enhancement is attributed to the reduction in the number of physical reservoirs required for input encoding and the subsequent number of synaptic devices that constitute the readout network. The flexibility of the MPBTFT-based ARC system enables for a significant reduction and optimization of hardware resources with slight accuracy adjustments. The average accuracies achieved for the various physical reservoirs are shown in Fig. 5d. Figure 5e shows the confusion matrix obtained using the MPBTFT-based ARC system. The system accurately distinguishes ten types of handwritten digits. These results substantiate the proficiency of DG MPBTFTs utilizing TG to distinguish each reservoir state with remarkable distinction and even expand reservoir states. The MPBTFT-based physical reservoir consumes ~22.5 pJ per input, while the FeTFT-based synaptic device consumes ~0.2 pJ per input (Supplementary Note 7). Benchmarking analysis against previous studies is presented in Supplementary Table 1.

MPBTFT-based analog reservoir computing system for waveform classification and time-series prediction

In addition to the handwritten digit recognition task, where the original static image data are converted to temporal data, waveform classification and time-series prediction tasks were performed to further evaluate the capabilities of the MPBTFT-based ARC system for processing temporal signals59. The quintessential applications of ARC systems lie in their proficiency in processing temporal data59,60. In an MPBTFT-based ARC system, the implementation of the waveform classification and time-series prediction tasks relies heavily on masking techniques. This technique augments input information and increases the number of virtual nodes within the temporal domain, enhancing the computational capabilities18,19,21,28,29,30. A comprehensive explanation of the masking process is detailed in the Methods section.

Through the masking process, each DG MPBTFT creates M virtual nodes in response to the application of an M-timeframe input pulse train. The state of each virtual node is characterized by the ID response of the DG MPBTFT within each corresponding timeframe. These virtual nodes of the DG MPBTFTs effectively expand the reservoir size from N to N × M, significantly enhancing the computational density without requiring additional hardware. The expanded reservoir states are subsequently fed into an (N × M) × 1 fully connected single-layer readout network. The readout network is trained using a linear regression method and outputs the classification or prediction results through a linear combination of all the reservoir states. A detailed description of the linear regression method can be found in the Methods section. An MPBTFT-based ARC system that utilizes the masking process is illustrated in Fig. 6a.

Fig. 6: Demonstration of waveform classification and time-series prediction.
figure 6

a Schematic of the MPBTFT-based ARC system utilizing the masking process. Following the masking process, the virtual node states created by each volatile DG MPBTFT are fed into the readout network and generate outputs. The time interval (τ) indicates the total duration of each input pulse train consisting of M timeframes. The weights (wout) of the readout network are trained through a linear regression method. b Inputs and c classification results of sine and square waveforms obtained from the MPBTFT-based ARC system. Each waveform is composed of eight-time steps. The input data with the initial 300-time steps are used for training, while the rest are used for testing. d Time-series prediction results obtained from the MPBTFT-based ARC system. The initial 300 data points are used for training, while the rest are used for testing. The system successfully predicts the time-series dataset, achieving a low NRMSE of 0.035. e Two-dimensional (2D) representation of the Hénon map. The results exhibit excellent consistency between the target and predicted values. f Results of complex real-world predictive task: the number of confirmed COVID-19 cases prediction. The black and red lines represent the actual and predicted number of confirmed cases, respectively. The data from January 2020 to February 2022 are used for training, while the rest are used for testing. The MPBTFT-based ARC system demonstrates an ability to forecast the future number of confirmed COVID-19 cases by leveraging historical data on previously confirmed cases.

Full size image

In the waveform classification task, the input data contain randomly arranged sine and square waveforms (Fig. 6b). The target output is a binary sequence of 0 and 1, representing sine and square waveforms, respectively. The MPBTFT-based ARC system classified the waveforms with a normalized root mean squared error (NRMSE) of 0.0044 (Fig. 6c). This indicates a sufficiently low classification error, demonstrating the proficiency of the system in handling classification tasks.

In addition to the waveform classification task, a time-series prediction task was performed to comprehensively assess the performance of the MPBTFT-based ARC system in handling temporal signals. A benchmark task is focused on Hénon map prediction, which is a typical discrete-time dynamic chaotic system prediction61. A detailed description of the Hénon map prediction task can be found in the Methods section. Figure 6d shows the target values (black line) and outputs of the MPBTFT-based ARC system after training (red line). The ARC system predicts a time-series dataset and achieves a low NRMSE of 0.035. Figure 6e shows a two-dimensional (2D) representation of the Hénon map, which exhibits excellent consistency between the target and predicted values. This result demonstrates that the ARC system can effectively reconstruct strange attractors of the Hénon map.

In this study, complex real-world data that extend beyond theoretical models are addressed to further evaluate the applicability and effectiveness of the MPBTFT-based ARC system in practical scenarios. The number of confirmed coronavirus disease 2019 (COVID-19) cases from January 2020 to March 2023, provided by Johns Hopkins University, was used for the evaluation62. The MPBTFT-based ARC system forecasts the future number of confirmed COVID-19 cases based on the historical data of previously confirmed cases. Figure 6f shows the actual number of confirmed cases (black line) and the predicted number of confirmed cases (red line). The remarkable concordance between the predicted and actual numbers of confirmed cases verifies the exceptional precision of the system in forecasting outbreak progression. Despite the complexity of real-world predictive tasks, a low NRMSE of 0.28 is achieved. The impressive system performance is primarily attributed to the polarization dynamics inherent in DG MPBTFTs, which result in a robust ability to process temporal features. This result demonstrates the potential of the MPBTFT-based ARC system in public health analytics and response strategies, providing a valuable tool for predictive modeling in epidemiology by leveraging its sophisticated temporal data processing capabilities.

Discussion

In this study, we demonstrated an ARC system by leveraging volatile DG MPBTFTs and nonvolatile FeTFTs with an IGZO channel and MFMIS structure, which can be easily integrated on a single wafer using a similar fabrication process. The synaptic characteristics of the nonvolatile FeTFTs were validated, showcasing their suitability as synaptic devices within the readout network. The volatile DG MPBTFTs successfully demonstrated the generation of 32 distinct reservoir states (5 bits), verifying their suitability as physical reservoirs for processing temporal information. The strategic utilization of the TG in DG MPBTFTs enhances the differentiation of the reservoir states and expands the states, thereby significantly enhancing the performance and area efficiency of the MPBTFT-based ARC system. The DG MPBTFT-based LIF neuron demonstrated the integrate-and-fire function with self-reset characteristics while processing both excitatory and inhibitory pulses with a single device. The performance evaluation of the MPBTFT-based ARC system was conducted using a handwritten digit recognition task, which achieved a high classification accuracy (~90.23%). Moreover, the system successfully predicted the future number of confirmed COVID-19 cases, which is complex real-world data, thereby ensuring the temporal data processing capability of the system. The ability to accurately process and predict temporal data highlights the potential of the MPBTFT-based ARC system, which could open new avenues for the development of advanced computing technologies.

Methods

Fabrication process of volatile DG MPBTFTs and nonvolatile FeTFTs

Volatile MPBTFTs and nonvolatile FeTFTs were fabricated on a buffer oxide (SiO2, 300 nm). A 40 nm Mo layer was deposited as the BG via DC sputtering and patterned using dry etching. Initially, a thin film with nonvolatile memory characteristics, 8 nm HZO (Hf:Zr = 2:1), was deposited via thermal atomic layer deposition (ALD). Subsequently, 20 nm TiN was deposited via plasma-enhanced ALD (PEALD) and patterned to serve as a floating gate (FG). The FG acted as a mask during the subsequent wet etching process using a DHF solution, isolating the nonvolatile thin film. Following the isolation step, a volatile thin film, 6.5 nm HZO (Hf:Zr = 3:5), was deposited via thermal ALD. Subsequently, 20 nm Mo was deposited via DC sputtering, and the FG of the volatile transistor was patterned and isolated using the same method. Through the process, transistors with thin films of different characteristics were formed. Note that BG and FG have a proportional area ratio (AR) to control capacitance matching between the ferroelectric layer and insulator.

The subsequent fabrication processes for both TFTs were performed without any distinction. To induce crystallinity in the deposited thin film, rapid thermal annealing (RTA) was performed at 500 °C under N2 ambient conditions. Subsequently, an 8 nm ZrO2 layer was deposited via thermal ALD as the insulator layer. For the channel material, 30 nm of amorphous IGZO was deposited via PEALD and subjected to a wet etching process using a diluted HCl solution. The width (W) and length (L) of the formed channels were both 20 µm. Ti and Al were deposited using a DC sputtering process and patterned as source (S) and drain (D) using dry etching. Both TFTs were annealed at 350 °C for 1 h under O2 ambient conditions to induce conduction in the IGZO channels by forming oxygen vacancies. Additionally, some of the oxygen vacancies formed in this process moved to the interface between IGZO and the metal of the S/D, thereby reducing the contact resistance. Finally, an 8 nm ZrO2 layer was deposited via thermal ALD to form a DG for the volatile transistor. Following isolation, the Mo TG was deposited using DC sputtering and patterned via dry etching. Refer to Supplementary Fig. 2 for more details.

Electrical measurements

A probe station and a semiconductor parameter analyzer (Keithley 4200-SCS) were used to investigate the ferroelectricity of the fabricated volatile and nonvolatile FeTFTs. The direct current (DC) ID-VGS measurements were performed using a semiconductor parameter analyzer (Keysight B1500A). A B1500A equipped with a waveform generator/fast measurement unit (WGFMU) module was used for the pulse measurements. To evaluate the electrical characteristics of the devices within the array, a probe station, custom-made probe card, semiconductor parameter analyzer (Keysight 4156B), and pulse generator (Keysight 81110 A) were used. The inputs from each source were distributed on the probe card using a switching matrix (Keysight E5250A). All the electrical measurements and characterizations were performed in ambient air at room temperature. Detailed experimental setup for electrical measurements are shown in Supplementary Fig. 20.

To evaluate the retention characteristics of fabricated FeTFTs, the device was initially erased completely. Subsequently, a PGM pulse with an amplitude of VPGM and a width of 10 μs was applied, followed by a read operation performed at VGS = 0 V and VDS = 0.1 V conditions. The VPGMs applied for each conductance state are 2.0, 2.4, 2.8, 3.2, 5.3, 5.65, 6.0, and 6.35 V, increasing from the lowest to the highest conductance state. The retention characteristics for a broad range of conductance states ensure reliable operations across the full spectrum of LTP/LTD characteristics along with a potentially wider range of conductance states. The eight conductance states shown in Fig. 2h are equally spaced on a logarithmic scale and encompass all the conductance states in the LTP/LTD characteristics (Fig. 2f), demonstrating that the retention characteristics are sufficiently reliable for employing FeTFTs as synaptic devices.

Handwritten digit recognition task

(1) Preprocessing step of the MNIST dataset: The images were preprocessed before being fed into the reservoirs (Fig. 5b). The original grayscale images were transformed into a binary format with superfluous border regions trimmed away, resulting in a streamlined 22 × 20 pixel representation. This conversion and cropping process retains the essence of the image, while optimizing it for subsequent reservoir processing. The preprocessed image, now structured into 22 rows, each containing 20 pixels, was further segmented into five distinct sections along the row direction, each comprising 4 pixels. Each section is encoded into an input pulse train with 4 timeframes and applied to a volatile DG MPBTFT-based physical reservoir.

(2) Input encoding process: The size and number of sections play pivotal roles in the input encoding process, which determines the performance and efficiency of the ARC system. Decreasing the number of sections results in each section comprising a greater number of pixels, which exponentially increases the number of states that each physical reservoir should represent. This can make it difficult to distinguish between each state of the physical reservoir, potentially degrading the system performance. Nevertheless, this modification can enhance the area efficiency of an ARC system by reducing the total number of physical reservoirs and the readout network size. Conversely, increasing the number of sections reduces the number of pixels per section, making it easier to accurately identify the individual states of the physical reservoirs. However, this modification requires an increase in the total number of physical reservoirs and readout network size to accommodate a larger number of sections, thereby degrading the area efficiency of the ARC system. Therefore, the input encoding process must be meticulously designed, including setting an appropriate number of sections for an efficient and effective ARC system.

(3) ARC system architecture: The ARC system, which utilizes 16 reservoir states (4 bits), requires input pulse trains with 4 timeframes alongside 110 (22 × 5) physical reservoirs. A 110 × 10 fully connected single-layer readout network was used. When the system utilizes 32 reservoir states (5 bits), 5-timeframe input pulse trains and 88 (22 × 4) physical reservoirs are required. Therefore, an 88 × 10 readout network is used, reducing the required number of synaptic devices. Similar to the other neural networks, the performance of the ARC system improves when a large-scale readout network is used (see Supplementary Fig. 21 for the performance of the ARC system for different readout network sizes)16,22,63,64.

During ARC system operations, a pulse train encoded from binarized input image pixels is applied to the BG of the DG MPBTFT-based physical reservoir, while a consistent sequential pulse train is repeatedly applied to the TG independent of the input image (see Fig. 3i and j). Despite the necessity for additional circuitry to generate the sequential pulse train with decreasing amplitude for the TG, the overall hardware demand is minimized because only one such circuit is required globally. This is feasible since the same pulse train is repeatedly applied to all TGs for each input image, regardless of the image. This results in a relatively minor hardware burden compared to the circuitry typically required for individual BGs, which encode the binarized input image pixels.

Input neurons are activated at the last timeframe for each input image through a clock signal, following the approach used in previous studies18,22,28,29,50. They gather the ID response from each DG MPBTFT-based physical reservoir at the last timeframe and transmit it to the readout network. Output neurons receive the BL current from the readout network through a current mirror and switch the polarization of DG MPBTFTs. Subsequently, ten output neurons generate distinct outputs, and the digit corresponding to the output neuron that fires first is identified as the correct answer. Note that different methods are required to identify the digits depending on the utilized encoding method, such as rate coding, temporal coding, and phase coding.

For the handwritten digit recognition task, the simulation incorporates various experimental data crucial for different layers of the system. In the reservoir layer, the final reservoir states of the DG MPBTFT-based physical reservoir at the last timeframe of the input pulse train are utilized. In the readout layer, the multilevel synaptic weights of the FeTFT-based readout network are utilized. Lastly, for neuron activation, the integrate-and-fire function and the reset/leaky characteristics of the DG MPBTFT-based LIF neuron are utilized. These components are crucial for accurately performing the digit recognition task.

Masking process

The initial step of the masking process involves the application of a predefined mask to the input data, thereby effectively expanding the dimensionality of the data. The input data are multiplied by the mask, which is typically a random but fixed one-dimensional (1D) binary vector of length M. N masks are utilized to diversify the input data, ensuring that the system can generate a wide array of reservoir states from simple inputs29,50. Therefore, each input data point is converted into N input pulse trains with M timeframes and fed into N parallel volatile DG MPBTFTs. Both the number (N) and length (M) of masks employed in the input encoding process should be optimized to enhance the system performance19,21,29. The amplitude of the input pulse train is linearly scaled proportional to the input data and ranges from 3.5 V to 5.0 V. The masking process expands the dimensions of the input data, thereby enhancing the richness and diversity of the data fed into the reservoir. For the waveform classification task, parameters M and N are set to 6 and 8, respectively. For the number of confirmed COVID-19 cases prediction tasks, parameters M and N are optimized to 3 and 15, respectively.

Time-series prediction task

The Hénon map represents a nonlinear 2D mapping that converts a point (x(n), y(n)) on a plane into a new point (x(n + 1), y(n + 1)) following the equations below61,65:

$$x\left(n+1\right)=y\left(n\right)-1.4{x(n)}^{2}$$
(1)
$$y\left(n+1\right)=0.3x\left(n\right)+w(n)$$
(2)

where w(n) represents Gaussian noise with a mean value of zero and a standard deviation of 0.05. The task is to predict the point (x(n + 1), y(n + 1)) at the subsequent time step n + 1, given the points (x(n), y(n)) up to the time step n. By combining the Eqs. (1) and (2), the Hénon map is reformulated into a 1D representation as follows:

$$x\left(n+1\right)=0.3x\left(n-1\right)+w(n-1)-1.4{x(n)}^{2}$$
(3)

Consequently, the task is refined to predict the value of x(n + 1) based on the known values of x(n) and x(n − 1). For Hénon map prediction, a dataset with a length of 500 consisting of x(n) following the above equations was utilized.

The masking process generates N input pulse trains, each consisting of M timeframes, for both input x(n) and x(n − 1). Therefore, a total of 2 N volatile DG MPBTFT-based physical reservoirs generate 2 N × M virtual node states. These virtual node states are fed into a (2 N × M) × 1 fully connected single-layer readout network. The readout network outputs a predicted value of x(n + 1) by linearly combining all the reservoir states. The parameters M and N are set to 3 and 15, respectively.

Readout network training

The readout network establishes effective mapping between high-dimensional reservoir states and outputs. The readout network within the ARC system was trained using the stochastic gradient descent (SGD) method for handwritten digit recognition tasks. For waveform classification and time-series prediction tasks, a linear regression method was used to train the readout network. The weight matrix (Wout) of the readout network was obtained using the following equation66:

$${{{\bf{W}}}}_{{{\bf{out}}}}={{\bf{Y}}}{{{\bf{X}}}}^{{\dagger} }={{\bf{Y}}}{{{\bf{X}}}}^{{{\bf{T}}}}{({{\bf{X}}}{{{\bf{X}}}}^{{{\bf{T}}}})}^{-{{\bf{1}}}}$$
(4)

where X and Y represent the input and target matrices, respectively. The symbol † represents the Moore–Penrose pseudo-inverse. In handwritten digit recognition, waveform classification, and time-series prediction tasks, pre-trained synaptic weights are transferred to the conductance of FeTFTs within the readout network and remain unchanged throughout system operations.

Error analysis

The error in the output results obtained using the FeTFT-based ARC system was calculated using the NRMSE function65 defined as follows:

$${{\rm{NRMSE}}}=\sqrt{\frac{{\sum }_{k}{\sum }_{i}{({p}_{i}(k)-{y}_{i}(k))}^{2}}{{\sum }_{k}{\sum }_{i}{{y}_{i}}^{2}(k)}}$$
(5)

where \({p}_{i}(k)\) and \({y}_{i}(k)\) represent the predicted outputs of the ARC system and the target output, respectively.