Neuronal diversity and stereotypy at multiple scales through whole brain morphometry

Liu, Yufeng; Jiang, Shengdian; Li, Yingxin; Zhao, Sujun; Yun, Zhixi; Zhao, Zuo-Han; Zhang, Lingli; Wang, Gaoyu; Chen, Xin; Manubens-Gil, Linus; Hang, Yuning; Gong, Qiaobo; Li, Yuanyuan; Qian, Penghao; Qu, Lei; Garcia-Forn, Marta; Wang, Wei; De Rubeis, Silvia; Wu, Zhuhao; Osten, Pavel; Gong, Hui; Hawrylycz, Michael; Mitra, Partha; Dong, Hongwei; Luo, Qingming; Ascoli, Giorgio A.; Zeng, Hongkui; Liu, Lijuan; Peng, Hanchuan

doi:10.1038/s41467-024-54745-6

Download PDF

Article
Open access
Published: 26 November 2024

Neuronal diversity and stereotypy at multiple scales through whole brain morphometry

Nature Communications volume 15, Article number: 10269 (2024) Cite this article

10k Accesses
12 Citations
20 Altmetric
Metrics details

Subjects

Abstract

We conducted a large-scale whole-brain morphometry study by analyzing 3.7 peta-voxels of mouse brain images at the single-cell resolution, producing one of the largest multi-morphometry databases of mammalian brains to date. We registered 204 mouse brains of three major imaging modalities to the Allen Common Coordinate Framework (CCF) atlas, annotated 182,497 neuronal cell bodies, modeled 15,441 dendritic microenvironments, characterized the full morphology of 1876 neurons along with their axonal motifs, and detected 2.63 million axonal varicosities that indicate potential synaptic sites. Our analyzed six levels of information related to neuronal populations, dendritic microenvironments, single-cell full morphology, dendritic and axonal arborization, axonal varicosities, and sub-neuronal structural motifs, along with a quantification of the diversity and stereotypy of patterns at each level. This integrative study provides key anatomical descriptions of neurons and their types across a multiple scales and features, contributing a substantial resource for understanding neuronal diversity in mammalian brains.

A Multi-Scale Neuron Morphometry Dataset from Peta-voxel Mouse Whole-Brain Images

Article Open access 23 April 2025

Morphological diversity of single neurons in molecularly defined cell types

Article Open access 06 October 2021

Connectivity of single neurons classifies cell subtypes in mouse brains

Article Open access 21 March 2025

Introduction

Neurons are the fundamental units of the nervous system, and their morphological analysis is crucial to understand neural circuits¹. One salient feature of mammalian neurons is their extensive, long-range axonal projections across brain regions². However, our understanding of neuronal morphology and function is limited by the incomplete digital representation of neuron patterns^3,4. Recent studies have focused on full neuronal morphology, including both dendrites and axons, using genetic and viral techniques that label neurons sparsely^5,6,7,8. In combination of these labeling techniques, various imaging modalities, such as serial two-photon tomography (STPT)⁹, light-sheet fluorescence microscopy (LSFM)^10,11 and fluorescence micro-optical sectioning tomography (fMOST)^12,13, have been employed. These techniques have produced an extensive volume of imaging data, primarily hosted by the Brain Research through Advancing Innovative Neurotechnologies (BRAIN) Initiative - Cell Census Network (BICCN) community¹⁴.

Recent studies emphasize the importance and advances of generating complete neuron morphology reconstructions, particularly long projecting axons^15,16,17,18. However, analyses of the complex arborization patterns of axons in mammalian brains are still limited. Analysis of the dendritic arborization has also been limited to traditionally defined morphological features, but is largely missing the overlay with brain anatomy to yield rich spatial information. Additionally, there has been little work on integrating information from neuronal populations, individual neurons, and sub-neuronal structures¹⁹.

In our effort to analyze morphological patterns of neurons at different scales, we consider the statistical distributions that quantify both the diversity and stereotypy of morphological patterns^16,20. Across different “types” or “classes” of morphological patterns, a diversity metric describes the variety among different types of morphological patterns and their respective degrees, while a stereotypy metric quantifies the level of conservation of patterns within each type. Neurons may differ greatly in their morphological, physiological and molecular attributes^2,21,22,23. Despite previous efforts to study the diversity and stereotype of various neuron types, such as hippocampal interneurons²⁴, striatal neurons²⁵, and cortical neurons¹⁶, a systematic analysis at a whole brain level and across multiple scales is still missing.

Our study makes an initial effort in describing the diversity of conserved morphological patterns of neurons at various anatomical and spatial scales in the context of whole mouse brains. Using a massive number of light-microscopic images of mouse brains generated by the community of Brain Research through Advancing Innovative Neurotechnologies (BRAIN) Initiative - Cell Census Network (BICCN), we performed an analysis of 3.7 peta-voxels of images with which we also reconstructed thousands of annotated neurons, and developed one of the largest available multi-morphometry datasets. By analyzing patterns of neurons at six structural scales, we discovered conserved morphological modules (collections of brain anatomical regions) and motifs (sub-neuronal structures) distributed throughout entire brain. This effort allows us to characterize the mouse brain anatomy based on a detailed, multi-scale description of neuron morphologies. Furthermore, we also attempted to establish a model explaining how features of different scales have complementary effects on morphological characterization. By combining the diversity and stereotypy scores at different scales, we visualized and identified the modularized structure of brain regions or neuron types, which were defined based on soma location, projection, or lamination information, at single-neuron resolution.

Results

Brain mapping of multi-morphometry data generated from peta-voxels of neuron images

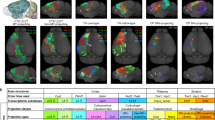
Our collaborative effort with BICCN and partners has led to the assembly of one of the largest collections of single-neuron morphology data in mice. This 3.7 peta-voxels dataset included 204 whole-brain images captured at micrometer and sub-micrometer resolutions using fMOST, STPT, and LSFM techniques (Fig. 1A; and the meta information including transgenic lines, main targeted neuronal types, and many other information are summarized in Supplementary Data 1). We call this image dataset IMG204 to simplify the subsequent description. We analyzed these images captured by different modalities to investigate the modular organization of brains and associated patterns across anatomical scales. To facilitate an objective comparison of morphological patterns across different imaging modalities and experimental conditions, we registered all IMG204 images to the Allen Common Coordinate Framework version 3 (CCFv3) atlas²⁶, using the cross-modality registration tool mBrainAligner^27,28 (Fig. 1A, Methods). Indeed, the sparsely labeled populations of neurons in different brains could be accurately aligned to study the colocalization relationship of their patterns (Fig. 1A).

**Fig. 1: Multiscale morphometry analysis from mouse brain images.**

To demonstrate the utility of our data analysis framework, we produced quantitative descriptors of patterns at various morphological scales, from the entire brain to the resolution of individual synapses. To do so, we developed a cloud-based Collaborative Augmented Reconstruction (CAR) platform²⁹, which is a software package with multiple computational tools for high-throughput generation of multi-morphometry. We performed semi-automatic annotation of a total of 182,497 neuronal somas from 122 fMOST brains (Fig. 1B; Supplementary Data 1; Supplementary Data 2) using an initial automatic soma detection, followed by collaborative annotation through a mobile application CAR-mobile, available on the CAR platform. We call this soma dataset SEU-S182K, including detailed information of brain ID, soma-location in 3-D, and registered brain region (Supplementary Data 3). As neurons were often labeled with different degrees of sparsity in these brains, we captured the large variation of soma distribution across various brain samples. We achieved this by annotating both brains with very sparsely labeled neurons and also brains with densely labeled neurons. Overall, in 72% (88/122) of the brains in SEU-S182K, there are more than 100 annotated somas. Spatially, among 314 non-fiber-tract regions in CCFv3 (CCF-R314; Methods), 296 regions contain annotated soma (Fig. 1B). For specific brain regions, such as the caudoputamen (CP) and the main olfactory bulb (MOB), We identified over 20,000 somas and high densities of up to 1710 and 2576 somas/mm³ respectively.

We then traced both the dendritic and axonal morphologies of individual neurons with annotated somas. For dendrites, we constructed a database, called SEU-D15K, which contains 15,441 automatically reconstructed 3D dendritic morphologies. We cross-validated the brain-wide reconstructions in SEU-D15K with the dendrites of 1876 manually curated neurons and found similar distributions of morphological features (Supplementary Fig. S1A; Methods) and Topological Morphology Descriptor (TMD) scores (Supplementary Fig. S1B). Overall, SEU-D15K dendrites showed consistent morphological features, with exemplar tracings for various projection subtypes aligning well with visualized neurite signals (Supplementary Fig. S14). We observed distinct morphologies for representative tracings for the brain stem, cerebellum, forebrain, and neuromodulatory centers (Supplementary Fig. S15). However, dendrites with somas in proximity, particularly those in the same brain regions, usually clustered closely (Supplementary Fig. S1C). To derive a spatially tuned dendritic feature vector with high discrimination power, here we extended our recent spatial tensor analysis of dendrites for human neurons³⁰ to analyze these mouse dendrites in SEU-D15K. Subsequently, we developed a dendritic microenvironment representation to characterize local neighborhood information around a target dendrite (Fig. 1C; Methods). Due to the higher precision of location information available in mouse brains compared to human surgical tissues³⁰, we were able to construct the dendritic microenvironment could also be constructed to describe the spatially tuned dendrite structures (Methods). In this way, we produced 15,441 dendritic microenvironments corresponding to SEU-D15K and used this approach to quantify the dendritic diversity and stereotypy as described below.

Using our framework of multiscale morphometry (Fig. 1D; Methods) that spans resolution levels from centimeters to micrometers, we analyzed morphological patterns of labeled neurites from 191 mouse brains that containing detectable neurites on low resolutions (Fig. 1A, D), as well as accordingly generated dendritic microenvironments (Fig. 1C) and fully reconstructed neuron morphologies. We extended our analysis to the SEU-A1876 dataset, which contains fully traced 3-D morphologies of 1876 neurons, including their complete dendrites, proximal axonal arbors, and distal axon arbors (Fig. 1D). The dataset primarily consists of projection neurons, mainly located in the Thalamus (37.2%), Cortex (24.1%), and CP (16.8%), with 702, 455, and 317 neurons, respectively. We specifically extracted 3776 densely branching axonal arbors, 1876 dendritic arbors, as well as the primary projection tracts connecting such arbors (Fig. 1D). We also identified axonal bundle motifs as diverging, converging or parallel projecting patterns. Additionally, we detected 2.63 million axonal varicosities from the axonal arbors, and accordingly pinpointed the respective synaptic patterns (Fig. 1D).

Our analytics framework covers six major scales of morphological patterns (Fig. 1D): Neuronal populations, dendritic microenvironments, single-cell full morphology, sub-neuronal dendritic and axonal arborization, structural motifs, detected axonal varicosities, along with quantitative characterizations of the diversity and stereotypy of patterns at each level. We quantified a number of morphological features to characterize properties of brain regions as well as individual neurons whenever possible (Fig. 1E). Cross-scale feature maps demonstrate high potential for cell typing and subtyping, with anatomically similar regions generally exhibiting analogous morphology throughout the whole brain (Supplementary Fig. S2A). Moreover, lamination and projection patterns emerge as prominent factors in grouping subtypes of cortical neurons, based on cross-scale features (Fig. 1E, Supplementary Fig. S2). Our analyses also revealed that broadly distributed yet highly discriminating features across multiple scales could be integrated (Supplementary Fig. S2). We have outlined the key novelties of our approach and related findings pertaining to the six morphological scales (Supplementary Data 8).

Inferring brain modules using multiplexed brains

For morphological patterns visible in the range of millimeters to centimeters, we analyzed the diversity and stereotypy of neuron populations labeled in IMG204 (Fig. 1D). Quantifying the conservation or reproducibility of morphological patterns (stereotypy), in functionally established anatomical regions helps define whether these patterns are sufficiently consistent to make biological inferences. On the other hand, capturing the diversity of these patterns not only confirms expected variations across brain regions, but also validates the accuracy in aligning images during brain multiplexing.

We developed an algorithm to segment the neurites in IMG204 (Methods), and used the co-occurrence of these neurites over the entire set of image samples to infer the diversity and stereotypy of the respective neuron populations. We grouped all 314 brain regions defined in CCFv3 into 13 larger regions (compound areas, CAs). Each CA corresponds to sets of functionally related brain regions within the CCFv3 taxonomy (Fig. 2A). We found that several CAs, such as isocortex, cerebellar cortex (CBX) and cerebellar nuclei (CBN), have more tightly correlated intra-areal neurite patterns compared to other CAs (Fig. 2A). Within each CA, the positively correlated neuron populations (Fig. 2A) imply covarying brain patterns in IMG204.

**Fig. 2: Modules inferred from multiplexed brains.**

We sought to identify highly correlated brain regions for each of the 314 CCFv3 regions (“target”), resulting in the discovery of 313 sets of individual regions that exhibit a Spearman correlation no less than 0.5 with their respective target regions (Supplementary Fig. S13; Supplementary Data 4). For each of these sets, we identified one or more matching brain regions whose neurite patterns correlate most strongly with the patterns in the target (Fig. 2B, Supplementary Data 4). 11 sets involve regions in the same CAs (intra-CA), while the remaining 302 involve regions from different CAs (cross-CA). Regions in most of these 313 sets, however, turn out to be immediate neighbors that share region borders (Fig. 2B; Supplementary Fig. S13). Examples include the pair of caudoputamen (CP) and globus pallidus – external segment (GPe) for which we previously reported single neuron level projection¹⁶. These results suggest that stereotyped “connections” of neurites exhibit a noteworthy degree of consistency with the brain anatomy delineated in existing brain atlases like CCFv3.

The observation above motivated us to further search for modules of brain regions that share similar co-occurring neurite-patterns as tight clusters (Fig. 2C). We identified 18 non-overlapping, intercorrelated, tight modules from the hierarchical dendrogram (Methods). 16 of which are cross-CA, composed of neighboring regions from multiple compound areas (Fig. 2C, Supplementary Fig. 13, Supplementary Data 5, Methods), which highlight hubs of co-occurring neurites. For example, the M3* module includes the medial preoptic nucleus (MPN) that closely associated with various regions, including the anterior, intermediate, and preoptic parts of the periventricular hypothalamic nucleus (PVa, PVi, PVpo)³¹. M5* encompasses four auditory cortical regions and five somatosensory regions, suggesting possible associations between auditory and somatosensory functions in mice³². The M7* module contains regions linked to the primary motor area (MOp) circuit, either as input (gustatory area, GU; dorsal part of the agranular insular area, AId) or output (GU; AId; ventral and posterior parts of the agranular insular area, AIv, AIp; orbital areas, ORBm, ORBl, ORBvl)³³. In the M8* module, regions such as the dorsal tegmental nucleus (DTN), laterodorsal tegmental nucleus (LDT), and raphe regions like dorsal nucleus raphe (DR) are known to play roles in the regulation of sleep and circadian rhythms^34,35. In the M10* module, we found the intergeniculate leaflet of the lateral geniculate complex (IGL), dorsal and ventral parts of the lateral geniculate complex (LGd, LGv), olivary pretectal nucleus (OP), superior colliculus (SCm, SCs), nucleus of the optic tract (NOT), and anterior pretectal nucleus (APN). These regions are part of the projection circuit from thalamic GABAergic neurons involved in circadian responses to light³⁶. In the M14* module, regions are either involved in the basal ganglia circuits, including CP, GPe, and GPi, or they are part of the projection from the amygdaloid to CP³⁷. The majority of regions in the M15* module are associated with glutamatergic and GABAergic regulation³⁸.

Discovering brain parcellation using dendritic microenvironments

We used the diversity and stereotypy of single neuron morphological patterns to further delineate brain modules. We first examined the dendritic patterns of individual neurons within SEU-D15K (Fig. 1C). In this dataset, each local dendrite was reconstructed within a soma-centered cuboid approximately 28.52 million μm³ in volume (Methods), ~57 times of the larger volume compared to a recent study delineating local dendrites in cortical L4 neurons³⁹. Our dendritic reconstructions are distributed in the majority of CCFv3 regions (222/314). To characterize the neuronal architecture in local neighborhoods, we extracted a 24-dimensional feature vector for each dendritic microenvironment. This vector aggregated both the dendritic morphology of individual neurons and the spatial relationship of neurons in a small neighborhood (Methods). Next, we used a minimum-Redundancy-Maximum-Relevance (mRMR) algorithm⁴⁰ to select the top three discriminating features. We mapped those to the CCFv3 atlas to produce a 3-D brain-wide RGB-coded microenvironment map, where each channel corresponds to one feature (Fig. 3A). This RGB-coded representation facilitates the visualization of spatial variability in microenvironment features across the entire brain.

**Fig. 3: Feature distributions of dendritic microenvironments across the whole brain.**

Whether dendritic features can be leveraged to distinguish cell types is debated^41,42. However, without complete and accurate dendrite reconstructions we are limited in these efforts. Unfortunately, existing labeling techniques pose challenges to reconstruct error-free entire dendrite arborization. For pyramidal neurons, reconstructing precisely both basal and apical parts of dendrites is difficult, as apical dendrites can extend substantially. Neuron partition methods such as G-Cut⁴³ cannot avoid loss of information, either. In our dendritic microenvironment approach, we mitigated these problems by prioritizing accuracy over completeness, focusing on precisely reconstructed local dendrites surrounding somas to improve classification.

One remarkable observation is that despite the limitations of the approach, the microenvironment map shows clear boundaries that align with the primary CCFv3 region borders (Fig. 3A). For example, CP neurons are clearly distinct from cortical neurons. Cortical layers can also be discriminated based on these features, adding on observations from conventional soma-density method^26,44, axon projections¹⁶, or a full description of the apical-basal dendrites of cortical neurons. Indeed, while each of the three color-coding features has a different distribution (Supplementary Fig. S4D–F), they jointly define a number of anatomical details that are consistent with the CCF parcellation.

Based on the diversity of brain regions indicated by the dendritic microenvironments, we identified six major clusters of regions (Fig. 3B). In the shown example, most laminated cortical neurons share similar feature patterns, placing them in one of the major clusters, although they could be further clustered hierarchically. Hippocampal neurons in CA1 and CA3 are clustered away from cortical, striatal, and thalamic neurons (Fig. 3B). Indeed, the hippocampal neurons have similar average straightness and Hausdorff dimensions like most other cortical neurons but differ in variance percentages (Supplementary Fig. S4D–F). CP neurons, instead, have a distinct pattern compared to other striatal neurons (Fig. 3A, B).

Within each microenvironment cluster, however, neurons show clear stereotypy. To measure the conservation and transition of these features within or across brain regions, we took an approach guided by the definition of four axial projection paths (Fig. 3C). The first path follows the tangential direction along the lamination of cortical layers. Cortical neurons share relatively stable features until entering the entorhinal area, lateral part, layer 5 (ENTl5) (Fig. 3D – Path1). The second path, orthogonal to the first one, clearly reveals reduced “variance-percentage” and “straightness” when entering and leaving CP (Fig. 3D – Path2). The third path following inner side of the border of CP and nearby regions shows the different distributions for the three features, which means that local dendrites along this path have strong heterogeneity. Thus, along the third path, there is a high likelihood that a variety of cell types can be encountered (Fig. 3D – Path 3). The fourth path, from the inner side to the outer side of CP, indicates a linear gradient of the “variance-percentage” and “straightness” features for CP, albeit with opposite trends (left and middle of Fig. 3E).

As the CCF anatomy was essentially developed using expert-annotation of an averaged brain of registered individual brain-images to determine the boundary of anatomical regions²⁶, we also generated the CCF-space average of all 191 brains to measure the visible contrast of previously defined brain regions or subregions compared to what we could observe using the microenvironment approach (Supplementary Fig. S16). The microenvironment features are able to identify more variation across and within brain regions compared to the average brain. We quantified this in the profiled features along the four exemplar paths (Fig. 3C–E). Indeed, the intensity profile in the average map along the first three paths does not correlate with the straightness and Hausdorff-dimension features. However, it resembles the “variance-percentage” feature of the microenvironment (Fig. 3D), with Pearson correlation coefficients of 0.86, 0.67, and 0.71 for Paths 1, 2, and 3, respectively. The top-3 microenvironment features complement each other in characterizing brain anatomy, with small average Pearson correlation coefficients of 0.013, 0.207, and −0.015 for the three paths. Our microenvironment representation appears to be discriminative for brain parcellation. Similarly, the intensity profile along the radial path of the CP region in the average brain (Path 4) exhibited a linearly increasing trend, aligning with the “variance-percentage” feature of the microenvironment. However, it differs from the decreasing trend observed in the feature straightness of microenvironment (Fig. 3E).

The whole-brain dendritic microenvironments could facilitate the exploration of both inter-regional and intra-regional organization across various brain areas, in addition to the four exemplar paths. Interesting examples include but are not limited to the stereotypy discovered in analyzing the middle sagittal and coronal sections (Supplementary Fig. S4), and the left-right symmetry of feature patterns in two hemispheres of the brain (Supplementary Fig. S4, Figure S5). Overall, the microenvironment analysis is consistent with established brain parcellation in CCFv3, offering finer detail with respect to the dendritic characteristic within each brain region.

Detecting primary distributions and key morphological variables of fully reconstructed neurons

We next analyzed the fully reconstructed neurons with meticulously annotated axons and dendrites in SEU-A1876. While the neuron reconstructions were manually edited by multiple annotators to ensure the correctness of branching patterns, the limited precision of spatial (3-D) pinpointing in manual annotation caused the skeleton of almost every neuron to deviate slightly from the center of the image voxels of the neurites. To address this, we developed an automatic approach⁴⁵ that precisely centered neuron skeletons, facilitating the subsequent analyses of axonal varicosities.

The entire set of SEU-A1876 neurons exhibits a brain-wide distribution, projecting across most major brain regions, with cell bodies in 92 brain regions, primarily located in cortex, thalamus, and striatum (Supplementary Data 6). These neurons span dozens of millimeters (Fig. 4). It has been often observed that different neuron classes are poorly discriminated by global morphology features such as length and branching number^16,46. To overcome this limitation, we registered the dataset to the CCFv3 using mBrainAligner. The standardization of these neurons’ coordinates allowed us to use the spatial adjacency of neurons to augment morphological features, inspired by previous studies³⁰ and the microenvironment representation (Figs. 1C and 3).

**Fig. 4: Anatomical characterization of fully reconstructed neurons.**

Specifically, we generated a similarity matrix of 47 morphological features of the 1876 neurons, and used the spatial adjacency of neurons as a coefficient matrix to finetune the morphology similarity (Methods, Supplementary Fig. S6). This approach reduced the likelihood of clustering together as the result of potentially incorrect matching of morphological features. Indeed, we were able to produce 4 clusters of full neuron morphologies (Fig. 4A), even if the locations of their somas did not appear visibly separated in 3-D space (Fig. 4C). Visual inspection of examples of neurons in distinct clusters confirmed their difference in appearance (Fig. 4B). Each cluster exhibited intra-cluster diversity, prompting a detailed analysis of subcellular structures as discussed in the subsequent sections. The soma-distribution of the neurons in each cluster indicates that C1 consists of cortical neurons; C2 and C4 contain mostly thalamic neurons and a few cortical neurons; and, most C3 neurons are located in the striatum (Fig. 4C). However, we also noticed that 6%, 25%, 31%, and 11% of neurons innervate from non-dominant brain areas for clusters C1, C2, C3, and C4, respectively. Interestingly, when comparing each pair of the four clusters, the two clusters being compared appeared to be separable even with only three morphological features selected using the mRMR algorithm, although these characterizing features were different in each case (Fig. 4C – lower triangle).

The overall consistency between our de novo clustering outcomes and established primary cell types in the mammalian brain prompted a detailed exploration of the most discriminating features of each cluster (Fig. 4D). We found the most discriminating features vary among clusters (Fig. 4C). At the whole-brain scale, the most prominent features were the “bifurcation distance to the soma” (“bif_EucDist2soma”), and “remote tilt angles” (“tilt_remote_std” and “tilt_remote_mean”, Methods). Importantly, no single feature could separate these four clusters (Fig. 4E), emphasizing that a combination of the top features (Fig. 4D) is necessary to characterize neuron clusters. On average, C1 neurons have a smaller likelihood to have large distal arbors, but typically project over long distances (Fig. 4E, F). Bifurcations of C2 neurons tend to be in close proximity to somas, and a smaller variance of “remote tilt angles” (Fig. 4E). In contrast, C3 neurons rarely have distal arbors, and have a larger variance of “remote tilt angles” (Fig. 4E, F). While C4 neurons correlate with C2 spatially, with comparable branching patterns, they have a substantially greater bifurcation-to-soma distance (Fig. 4C, E and F). Note that C2 and C4 primarily consist of thalamic neurons, the substantial difference between them indicates the potential existence of two major neuron subtypes in these thalamic regions.

Conserved neuron arborization encodes cortical anatomy

Based on the evidence that fully reconstructed neuronal morphology aligns with neuron class (Fig. 4), we further investigated neurons innervating multiple brain regions. This exploration was twofold: based on (a) the arborization patterns for both dendrites and axons (Fig. 5), and (b) the fiber-projecting patterns that connect these arbors (Fig. 6).

**Fig. 5: Morphological stereotypy and diversity in neuronal arbors.**

**Fig. 6: Projection patterns and anatomical insights from primary axonal tracts.**

We define sub-neuronal arbors as dense branching sub-trees of full neuron morphologies. Practically the diameter of an arbor can range from about 100 micrometers to millimeters (Fig. 1D). The tight packing in space may indicate putative structural units. Profiling the level of arbor stereotypy provide additional insights to those inferred from full morphologies. We decomposed a single neuron into a series of arbors to obtain the sub-neuronal representation. Manually annotated dendrites were treated as independent arbors due to their obvious layout. We used the AutoArbor algorithm¹⁶ (Methods) to divide axons into multiple internally connected arbors. To facilitate comparison, axons of neurons within the same brain region were decomposed to have the same number of arbors, determined using the majority-vote method for all neurons in the region. Two kinds of arbors, proximal and distal, were defined based on distance from the soma using a threshold of 750 μm (Fig. 5A). The arbors were sequentially ordered by their Euclidean distances to soma (e.g., A1, A2, A3). This method detected 3,776 axonal arbors and 1,876 dendritic arbors. We considered various morphological features (Methods) tailored for the arbor structures, including arbor type (proximal or distal), the volume of the rotated 3-D bounding box of the arbor (μm³), the number of branches, and the Euclidean distance to the soma (dist2soma).

We analyzed arbor features in three brain areas: thalamus, cortex, and striatum. Quantitative assessments across 20 CCFv3 regions highlighted morphological diversity and stereotypy, particularly in axonal arbors (Fig. 5A). Overall, neurons in the cortex and striatum have around 50% proximal arbors, while thalamic regions have an apparently smaller number of proximal arbors. The extent of proximal arbors is also considerably variable in the thalamus, i.e., ventral posterolateral and posteromedial nucleus of the thalamus (VPL and VPM) neurons have more proximal arbors than other thalamic regions. The branching number and the respective maximum density features differ from arborization patterns revealed mostly by the arbor-volume feature, which indicates that several neurons originating in multiple cortical regions have very large arbors. Overall, cortical neurons show larger axonal arbors, and AId and MOs neurons have a clearly larger axonal arbor A2 than neurons in other regions. MOp have smaller axonal arbors A2 than MOs. By contrast, supplemental somatosensory area (SSs) and primary visual area (VISp) neurons have one large axonal arbor A1, which also has a chance to position beyond or below the 750 μm threshold to be either a distal or a proximal arbor. Remarkably, brain regions in the primary somatosensory area (SSp) display dramatically contrasting and indeed combinatorial arborization patterns. SSp-ul and SSp-ll have comparable arbors A1, A2, and A3; however, SSp-m, SSp-n and SSp-bfd have large A2 arbors.

These arborization patterns of cortical neurons, particularly SSp neurons, seem to define a “codebook” that we sought to further examine. We compared arbors within two major cortical projection classes-extratelencephalic (ET) and intratelencephalic (IT) neurons (Fig. 5B; Supplementary Fig. 17). Differences between projection classes are evident in dendritic features. Indeed, ET neurons have both larger dendrites than IT neurons in the same brain regions. However, IT neurons have higher maximum compartment densities for dendrites. For axonal arbors, ET neurons have smaller A1-arbors, but a greater chance to have a larger A2 than the respective IT counterparts, consistent with the categorization of these ET-IT neurons.

We also examined the features of neurons in six regions of the primary somatosensory cortex across cortical layers (Fig. 5C). Neurons in the unsigned regions (SSp-un) have large proximal axonal arbors projecting mainly to cortical layer 6 (L6), but not to layer 1 (L1), layer 2/3 (L2/3), and layer 4 (L4), and distal arbors mainly projecting to L5 and L6. Subdividing neurons by laminar position reveals distinct attributes in the projection patterns of proximal and distal arbors, with some overlaps. Axonal arbors of L2/3 neurons primarily project to L2/3 and L5, while L4 neurons reach mostly L2/3. Instead, L5 neurons project mostly to L5 and L6, and L6 neurons extend projections preferentially to L5 (Fig. 5C). The circular visualization provides a detailed view with soma regions and cortical layer information displayed (Fig. 5C – circular view). It is important to note that this codebook may evolve as more neuron reconstructions become available.

As we observed that thalamic neurons have a variety of arborization patterns (Fig. 5A), we clustered both the morphological features of arbors (8-dimensional) and projection distributions (108-dimensional) of neurons originating from each brain region (Methods). Thalamic core and matrix neurons have similar projection volumes overall (Supplementary Fig. S18). In detail, matrix neurons from nucleus of reuniens (RE), lateral dorsal nucleus of thalamus (LD) and ventral medial nucleus of the thalamus (VM) have greater variability in projection volume than neurons from other regions. Morphologically, axonal arbors of thalamic matrix neurons are generally larger and more complex, exhibiting a greater diversity than thalamic core neurons (Supplementary Fig. S18). Indeed, arbors of thalamic core neurons, except LGd, are more conserved in volume. In terms of projections, thalamic core neurons have a higher concentration of arbors in mostly cortical and midbrain areas, which are responsible for sensory and motor control. On the other hand, thalamic matrix neurons have a wide range of projection targets, covering 108 regions.

Characterizing motifs of primary axonal tracts

To complement the analysis of neuronal arborization, we further studied the projecting axons connecting major arbors (Fig. 6A). Understanding the diversity and stereotypy of axonal tracts may help to understand the global structure of the brain. We focused on primary axonal tracts, obtained by iteratively pruning short branches off the longest axonal path (Fig. 6A; Methods), and identified three projection patterns, i.e., convergent, divergent, and parallel (Fig. 6B).

In 19 major brain regions with fully reconstructed neurons SEU-A1876, we found different projection patterns (Fig. 6C). First, striatal and thalamic neurons showed opposite projecting tendencies. SNr-projecting CP neurons (CP_SNr) and GPe-projecting CP neurons (CP_GPe) have convergent patterns, with widely distributed somas but tightly packed primary projection targets. The cross-sectional radii tended to decrease from 1.5 mm to sub-millimeters. In contrast, both the thalamic matrix neurons (TH_matrix) and thalamic core neurons (TH_core) show an evident divergent pattern, with somas concentrated in each of the eight thalamic regions, i.e., lateral posterior nucleus of the thalamus (LP), VM, LGd, medial geniculate complex (MG), submedial nucleus of the thalamus (SMT), VPL, parvicellular part of VPL (VPLpc), and VPM, but projection targets wide spread. The cross-sectional radii extended from sub-millimeter to about 1.5 millimeters for TH_core and VM neurons, and reached to the range of 2 ~3 millimeters for LP neurons.

Different from the striatum and thalamus, cortical neurons showed more complex patterns (Fig. 6C). IT-projecting cortical neurons (CTX_IT) display divergent projections, expanding the cross-sectional radii by about 3 times or more along the primary axonal tracts. However, ET-projecting cortical neurons (CTX_ET) have have a much more conserved axonal trajectories to target brain regions, with deviations only occurring near target regions. Interestingly, the majority of cortical neurons, irrespective of ET or IT projection types, showed a converging pattern at the initial part of the projection pathway, as illustrated by decreased radii immediately after the somas (Fig. 6C).

We also analyzed the topographical organizations for the ET-projecting and IT-projecting cortical neurons, GPe-projecting CP neurons, and VPM neurons, based on the primary axonal tracts (Supplementary Fig. 19). Notably, the termini of primary axonal tracts of ET neurons exhibit a high degree of dispersion within each subtype (Supplementary Fig. S19). However, these termini are conserved across all ET projecting neurons, despite their diverse soma locations (Supplementary Fig. S19). In contrast, IT projecting neurons display distinct topographical organizations, with the termini locations being more closely correlated to their respective soma locations (Supplementary Fig. S19).

We mapped these conserved projection motifs onto CCFv3, with both soma regions and the project target regions highlighted (Fig. 6D). Based on our current data, the brain-wide axonal projects are heavily divergent, regardless of the locations of somas, except for specific cases like CP-SNr and CP-GPe. However, it is also remarkable to see that the divergent CTX_ET projections can be further factorized in terms of clustered target brain regions (Fig. 6C – CTX_ET row). For instance, CTX_ET SSp-m neurons have divergent projections, but their targets can be grouped into three clusters (Fig. 6E, Supplementary Fig. S7). The projection of neurons from each of the three clusters showed a nearly parallel pattern. In other words, the cortical neurons may have a strongly stereotyped, target-dependent projection pattern although overall the diversity is visibly dominant. In this way, these stereotyped projection motifs provide a high-level description of neuronal arbors across the entire brain.

Cross-scale topography of axonal varicosities

After estimating axonal and dendritic arborizations, we sought to identify putative synaptic sites. As we had analyzed and modeled dendritic spines in a previous study⁴⁷, we used IMG204 to study putative axonal varicosities. Axonal varicosities may be classified as terminaux (TEB) and en passant (EPB)⁴⁸ (Fig. 7A). Using the complete axons in SEU-A1876 neurons, we identified both types of varicosities. To maximize accuracy, we refined manually annotated neuron skeletons with an automated skeleton de-skewing algorithm⁴⁵, followed by approximating varicosities using a Gaussian distribution model (Methods; Supplementary Fig. S8). We identified 2.63 million axonal varicosities from all axonal reconstructions (SEU-A1876), averaging 1,404 varicosities per neuron. The identification exhibited high robustness for independently traced but morphologically similar neurons (Supplementary Fig. S21). The high correlation between detected varicosities from such independent sources would not be possible if these varicosities were merely noise without any biological consistency (Supplementary Fig. S21). Benchmark on 1450 manually annotated varicosities showed a high accuracy (99% precision and 91.7% recall). Additionally, EPB ratios of four manually annotated hippocampal CA1 neurons in our dataset are 98.9%, 97.1%, 96.4%, and 97.6%, aligning with electron microscopy-based detection⁴⁹. We also categorized axonal branches into varicosity-branches or null-branches, based on the presence or absence of detected varicosities (Fig. 7A).

**Fig. 7: Spatial patterns of axonal varicosities distribution at various scales.**

We studied the spatial distributions of varicosities at several scales. At the whole-neuron level, we calculated varicosity densities against their distances to somas in 16 brain regions (Fig. 7B). Varicosities of thalamic neurons are predominantly located on the distal axons. Claustrum (CLA) and AId neurons have very broad varicosity distributions. Olfactory tubercle (OT) and RT neurons have high varicosity density along intermediate ranges of axon extensions. Neurons in the other brain regions, including 5 cortical regions and the striatal region CP which has large local axons (Supplementary Fig. S22), have enriched varicosities in local axons (Fig. 7B).

We also generated a varicosity-feature topography for different neurons (Fig. 7C). In each of three major categories of brain areas (cerebral nuclei (CNU), thalamus, and cortex), varicosity feature distributions are typically stereotyped, exception for reticular nucleus of the thalamus (RT) neurons, which have a different feature map from other thalamic neurons. CNU neurons, particularly CP and OT neurons, showed much higher TEB ratios. However, the average patterns across these three brain areas are diverse, offering more detail than the one-dimensional radial distributions (Fig. 7B) that are summarized as the third varicosity feature F3 (Fig. 7C).

In our data, neurons from cortical and thalamic regions have on average 271.1 and 233.8 varicosity-branches, significantly larger than striatal neurons (151.3; Fig. 7D). Notably, the ratios between varicosity-branches and null-branches remain consistently around a value of approximately 3 across neurons from various brain areas (Fig. 7D). Higher varicosity-branch ratios were found in terminal branches than in bifurcating branches such as 81% of the former containing varicosities versus only 71% of the latter. Interestingly, the average lengths of varicosity-branches and null-branches are indistinguishable (Fig. 7D). On average, varicosity-branches of striatum neurons are slightly more curved than null-branches (Fig. 7D). At the branch level, we categorized bifurcating varicosity-branches into three types depending on the type of children branches (Fig. 7E), with a dominance of consecutive varicosity-containing branches (B0 and B1 types, Fig. 7E). These observations suggest that varicosities may aggregate in close-packing axonal arbors. We also found clear differences in the number of varicosities at the individual branch level for various neuron types (Fig. 7D). Furthermore, varicosities are preferentially located at the branch terminal ends (Fig. 7F). Overall, our data suggest that varicosity distribution strongly depends on the scale of analysis: varying dramatically at the full neuron level (global diversity), but sharing analogous patterns at lower structural levels (local stereotypy).

Characterizing whole-brain diversity and stereotypy using cross-scale features

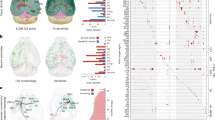
In observing substantial diversity across different morphometry scales, we questioned whether such diversified patterns across scales could be combined to characterize neurons. To do so, for each neuron, n_i, we first concatenated its features across resolution scales (microenvironment, full morphology, arbors, motifs, and varicosities) into a feature vector f_i. For two neurons n_i and n_j, we obtained Pearson correlation of the concatenated features of two neurons, c_ij, to measure the similarity. Next, for neurons innervated from two brain regions U and V, i.e., two soma-types (s-types), we averaged the correlation coefficients of all inter-region neuron pairs to produce an overall cross-scale feature similarity score s_UV in these two regions. A s_UV score close to 0 indicates minimal commonality between neurons in the two regions, while scores approaching 1 or -1 indicates high similarity or dissimilarity, respectively. When U and V are the same region, the score becomes s_UU (or s_U for simplicity), which measures the intra-region averaged similarity, or “intra-type” stereotypy. In this way, we constructed a Diversity-and-Stereotypy (DS) matrix S, where each entry is s_UV, for all pairs of brain regions to quantify the distribution of morphological patterns (Fig. 8A).

**Fig. 8: Quantitative diversity and stereotypy analyses based on cross-scale features.**

We found that cross-scale features were able to discriminate between different neuron types. Indeed, the DS matrix of all soma-types showed three clear modules, which correspond to the majority of cortical, thalamic, and striatal neurons (Fig. 8A – top-left), except for the thalamus reticular nucleus (RT) neurons, which are distinguishable from other thalamic neurons in terms of neurotransmitters and connectivity⁵⁰. In addition, the DS submatrix of cortical neurons correlates negatively with that of the thalamic neurons, but exhibits weak correlation with the striatal neurons. Thalamic neurons also correlate weakly but also negatively with striatal neurons. Within each module, DS values are relatively large with small variations, indicating that neurons are remarkably conserved in these brain regions. This modular grouping of brain regions based on cross-scale features is also consistent with our alternative analyses, e.g., microenvironment analysis (Fig. 3).

We focused on the diagonal of the DS matrix (Fig. 8A – EX_d) to examine the distribution of features for the five resolution scales (Fig. 8A, – intra-region correlations, Supplementary Fig. S9). Although overall cortical, thalamic, and striatal neurons have similar average DS scores within each brain region (mean-values = 0.34, 0.47, and 0.52, respectively, as shown as the diagonal values in Fig. 8A – DS matrix of s-type), they have different degrees of stereotypy with respect to morphological scales. For instance, for microenvironment features, the average correlation value of thalamic neurons (0.29) is much larger than that of cortical neurons (0.07) (Fig. 8A – Intra-region correlations), indicating that microenvironment features are more discriminating for thalamic neurons. Similarly, certain cortical neurons, like CLA neurons, display high conservation in full morphology and varicosity features, indicated by high mean correlation values (0.8 and 0.7, respectively) (Fig. 8A - Intra-region correlations).

We also used the DS matrix to examine subtypes of neurons. We focused on two subtypes, i.e., neuron-projection subtypes (Fig. 8A - EX_p) and soma-lamination subtypes (Fig. 8A - EX_I) for cortical regions that contain at least 10 fully reconstructed neurons. Specifically, our analyses included 1513 neurons for s-type, 1350 neurons for projection subtypes, and 431 neurons for lamination-based subtypes of cortical neurons. For projection subtypes (Fig. 8A - EX_p), most DS scores among ET neurons are larger than 0.3, which also holds true for IT neurons. However, the majority of ET neurons correlate weakly with IT neurons, even when they are located in the same brain regions (e.g., SSp-n-ET vs SSp-n-IT neurons). Interestingly, several projection subtypes such as MOp-IT, MOs-IT, SSs-IT, and SSs-ET neurons show considerable correlations with all neuron subtypes. The DS matrix also highlights an interesting submodule composed of six SSp ET projecting subtypes, with pairwise correlations higher than 0.4 in most cases.

We observed modularity for cortical laminar subtypes (Fig. 8A - EX_I). L2/3 and L4 neurons are inter-correlated with each other, but exhibit weak correlation with other layers, with clear module boundaries. In the module of L2/3-L4 neurons, a sub-module consisting of five L4 subtypes, SSp-bfd-4, SSp-m-4, SSp-n-4, SSs-4, and VISp-4, also stands out, with a DS score around 0.4. L5 subtypes also appear stereotyped in the DS matrix, but inter-region correlations tend to be weak, in the 0.15 range. The two L6 subtypes, AId-6 and SSs-6, highly resemble each other but have slightly different correlation profiles with other subtypes. Interestingly, VISp-5 neurons show negative correlations with most of the L5 neurons and all L6 neurons, but correlate considerably with L4 and L2/3 neurons. In addition, neurons from the same brain region but in different layers are not necessarily correlated. For instance, the L5 subtypes of SSp neurons and the respective L4 subtypes are negatively and weakly correlated.

We also attempted to understand the relationship among features of different scales. To do so, we calculated the “distance” between each pair of scales (Fig. 8B, Methods), along with the statistics of these features for different brain regions (Fig. 8C). We found that microenvironment and motif features were far away from features of other scales. Instead, varicosity features had small distances to both full morphology and arbor features (Fig. 8B). Therefore, microenvironment and motif features have relatively little redundancy when combined with other scales to categorize neurons and brain regions. The two separate pairs of scales, i.e. {full morphology and varicosity} and {arbor and varicosity}, could be used to cross-validate whether or not data analyses are consistent across scales.

Our analysis above, especially the DS matrices of the projection and lamination subtypes of cortical neurons, indicate that neuronal types can be well defined by their axonal projections and soma location (Fig. 8A). This suggests an underlying relationship between spatial distribution and morphogenesis, indicating proximal neurons sharing more similar morphologies. We tested this hypothesis by evaluating the correlation between morphological correlation of neurons and soma-to-soma distance. The morphological similarity between neurons was negatively correlated with both the soma-to-soma distance, within a scale of 4 millimeters, comparable to the sizes of brain regions (Fig. 8D, E). This correlation aligns with the morphological similarity observed among neurons within the same region (Figs. 3, 5–7, and 8A). Simultaneously, it reinforces the inclusion of spatial adjacency in microenvironment construction (Fig. 3) and single neuron clustering (Fig. 4).

Another approach to integrating cellular morphometry across scales involves iterative modularization of neuromorphometry. To illustrate, we examined the relationship between projection patterns (represented by “Delta Radius” (Supplementary Fig. S23), the difference in radius between the termini of primary axonal tracts and their somas) and dendritic arbor features of different cortical neurons. Both the “volume” and “max_density” features demonstrated a linear correlation with the radius difference for both ET and IT neurons, with the absolute values of Pearson correlation (R) greater than 0.5 (Supplementary Fig. S23). Specifically, the dendritic arbor volumes in ET neurons showed a strong positive correlation with “Delta Radius” (R = 0.94, P = 0.0019), suggesting that ET neurons with larger dendrites tend to have more divergent projections. In contrast, dendritic arbor volumes in IT-projecting neurons were negatively correlated with “Delta Radius”, indicating that larger dendritic arbors are associated with more convergent projections. Additionally, both ET and IT neurons displayed positive correlations (R = 0.66 and 0.51, respectively) between the “max_density” feature and the radius difference (Supplementary Fig. S23). To underscore cellular diversity across the detected modules, we also provided visual examples (Supplementary Fig. S24). Notably, neurons in modules M10 and M12 lack significant local axonal arbors, unlike in modules M5, M6, and M7, where local axonal arbors are present. Moreover, neurons in module M5 exhibit larger volumes compared to those in other modules (Supplementary Fig. S24).

Discussion

We studied the morphological patterns of neurons in the context of whole mouse brains at multi-scales, from centimeters to sub-microns, with specific focus on the quantification of the diversity and stereotypy of neuronal structures (Supplementary Fig. S25). We leveraged the collaborative effort of the BICCN community to collect and standardize one of the largest mammalian brain imaging databases to the latest Allen Common Coordinate Framework, followed by systematic extraction of morphological features from whole brain level to axonal varicosity level. Subsequently, we categorized morphological patterns in the cortex, striatum, and thalamus, in conjunction with their soma-distribution, projection trajectories and targets, and more detailed arborization and detected varicosities when applicable. Using rich representations of morphological data, we discovered brain modules and morphology motifs across scales, and identified the suitable spatial scales for quantifying the diversity and stereotypy of morphological patterns.

Our multi-scale analysis attempts to complement a number of previous efforts in generating macroscale, mesoscale, and microscale morphometry in the mouse brain and other model systems^{51,52,53,54,55,56}. At the neuron-population level, we analyzed the modular organization of brain regions based on neurite distribution patterns. Previously, modules of mammalian brains have been studied in macroscale, primarily using functional Magnetic Resonance Imaging⁵⁷, and in mesoscale, such as the brain-wide neuronal population based projecting-networks using whole-brain optical imaging^53,54,58. Our analysis confirmed several previous observations such as neighboring regions being more likely in the same module^54,57. We also additionally estimated modularization from large-scale analysis at the micron and even sub-micron resolutions. This study represents a notable advancement beyond our previous work on single-scale, straightforward neuron morphology screening for mouse brains¹⁶ and other model systems⁴. These earlier studies did not analyze the vast array of patterns observable at and across different scales. In contrast, this study expands the scope and delves deeper into the complex interplay of neuronal patterns at multiple scales, offering a more complete picture of neuronal morphology.

We constructed dendritic microenvironments to enhance the ability to discriminate the structure of local dendrite arborization. Historically, the morphological features of local dendrites were thought to offer limited power for discriminating neuronal classes^59,60. These observations have also motivated recent studies that rely on fully reconstructed long axons to differentiate neuron classes^15,16,17. Nonetheless, the cost to produce long axons or full neuron morphology is still high, and sometimes is exceedingly expensive for large mammalian brains such as primates⁶¹. We have recently proposed aggregating the spatial neighboring information of local dendrites of human cortical neurons with their 3-D morphology, and thus have obtained superior classification performance of neurons³⁰. In this study, we followed the same principle to formulate dendritic microenvironments that offer a valid alternative to integrate spatial information of neurons and their morphology. The microenvironment representation of a large set of dendrites allows for the visualization of the covarying morphological features of neighboring neurons, thus providing a greater chance to differentiate neurons that have limited dendritic features to discriminate each region. This aligns with the finding that neurons in different cortical regions of the human brain share cell types but in different proportions⁶². Meanwhile, the ensemble nature of it helps alleviate the possible imperfections of reconstructions. It provides a balanced compromise between the scarcity of available single morphologies and the limited discriminatory capacity of soma density. Our approach has allowed visualization of more anatomical detail for several brain regions compared to what had been documented in the CCFv3 atlas²⁶ and the Mouse Brain in Stereotaxic Coordinates⁶³.

In addition to introducing dendritic microenvironments, we were able to identify critical, minimally redundant factors that contribute to the different categorizations of individual neurons, for their full morphologies. We found that the clustering of cortical, striatal and thalamic neurons into broadly recognizable clusters, each with a specific fingerprint, could emerge with little a priori knowledge. The key features could be identified in the least redundant subspace of spatially tuned morphology features. This finding also complements the conventional parcellation of brain regions in anatomical atlases primarily based on cell densities. Future studies in this direction, potentially combined with the microenvironment analysis of neurites, might suggest alternative approaches to investigate the murine brain anatomy using morphological, physiological, molecular and connectional properties of neurons^2,23.

Individual neurons have traditionally been studied by analyzing their overall morphology^64,65. However, it is intriguing to explore the variability of arborization and projection patterns within neurons, as they naturally constitute interconnected sub-trees and projecting neurite tracts. We note that this aspect has not been extensively investigated to date. To address this, we undertook a decomposition of single-neuron morphologies into densely packed sub-trees, referred to as arbors. These arbors serve as structural foundations for potential neuronal functions. Additionally, we categorized the arbors according to their proximity to the respective somas. Furthermore, we extracted the primary projecting tracts of neurons originating from different brain regions and examined their spatial divergence and convergence patterns. This approach simplifies the comparison of different neuron types while retaining crucial morphological information. Moreover, it facilitates the quantification of the diversity of conserved patterns, denoted as “motifs” of arbors and neurite tracts. Our work complements previous endeavors aimed at characterizing sub-neuronal structures, such as branching topologies^66,67.

The investigation of synaptic connectivity is a contemporary and critical topic. While electron microscopy remains the gold standard for synapse identification, its limited range (~1 mm³) currently prevents its applicability to mammalian brain-wide axonal projections. Previous studies have thus focused on detecting and analyzing potential synaptic sites collected by optical microscopy^68,69,70 using various labeling techniques, including genetic or antibody labeling for presynaptic and/or postsynaptic sites, as well as a combination of both^47,71,72. This study aims to expand on existing synapse-detection research in three ways. First, the full morphologies of nearly 2,000 neurons were used to provide a high-quality dataset for analysis. Second, whole-brains, encompassing a number of cortical, striatal, and thalamic regions, were used to provide a complete picture of the distribution of putative synaptic sites. Third, we explored a wide range of features associated with putative synapses. In this way, we have characterized the patterns of brain-wide varicosity-distributions across various cell types that complement previous studies. Of note, while the biological validation of the predicted axonal varicosities is beyond the scope of this resource study, we have utilized statistics from independent yet morphologically similar neurons in the same brain regions (Supplementary Fig. S21). The distributional consistency demonstrates that it is highly unlikely for the predicted varicosities and their patterns to lack biological relevance.

The knowledge gathered from investigating various spatial scales prompted us to develop an integrated model of neuron morphometry and brain anatomy. As an initial effort, we introduced a DS matrix to measure the degree of diversity across neurons with respect to the stereotypy of neuron types. We observed interesting hierarchical and modularized organization of neurons in cortical, striatal and thalamic regions emerging in a quantifiable way, even without explicit clustering. This finding has two valuable implications. First, it confirms complex neuron morphology strongly correlates with existing brain anatomy in the established mouse brain atlases such as CCFv3. Second, and more importantly, it allows us to hypothesize that for a more complicated mammalian brain such as those of primates, an effective way to explore and understand the brain anatomy and even the associated brain functions could take a similar multi-scale approach, instead of relying solely on anatomists’ manual drawing of brain structures. The present study highlights the power of large scale systematically mapped neuronal data in elucidating detailed cell type structure and morphology. Our cross-scale integration of information may also extend to incorporate in the future other data modalities such as single-cell transcriptomic data^59,73,74.

Many of our observations align well with previous studies, including the similarity between the projection patterns calculated from primary axonal tracts (Fig. 6) and those estimated from single neuron morphologies¹⁶. The regions in most detected modules (Fig. 2; Supplementary Data 5) is consistent with experiments^33,38, and the proportion of EPB varicosities is similar to that observed in electron microscopy studies⁴⁹. On the other hand, there are many previously unexplored findings (Supplementary Data 8). One such example is the discovery of three subtypes for the L5 neurons in the primary somatosensory area - mouth region (Fig. 6E, Supplementary Fig. S7), based on the clustering of primary axonal tract termini. Another finding is the identification of four primary clusters for all single neuron morphologies. We introduced spatial adjacency into feature comparison, allowing unambiguous identification of four large, primary clusters with clear separation (Fig. 4). Within each cluster, neurons exhibit substantial diversity, quantified in this work to measure stereotypy and separation between clusters. These in-cluster variance motivates the identification of sub-neuronal conserved structures for characterizing neurons at finer scales.

These data-driven findings, resulting from correlation analyses, warrant dedicated experiments to unravel functional mechanisms. As a resource paper providing morphometry data and analytical tools, the verification of these findings is beyond its scope. Nevertheless, these insights offer valuable directions for future biological experiments, making the resources in this work a valuable mining-and-validation protocol for the neuroscience community. In our ongoing exploration of these resources, we aim to delve deeper into the morphological diversity between different scales, as well as adapt to a broad range of neurons. For example, while our current dataset primarily comprises projection neurons (Supplementary Data 6), we acknowledge the importance of exploring interneurons, which constitute 20%–30% of the neocortex in the human brain⁷⁵. We plan to incorporate public-domain reconstructions of interneurons⁷⁶ mapped to the CCF, enabling a joint analysis with our datasets. Additionally, we aim to investigate correlations between conserved patterns at various scales, exploring aspects such as cellular diversity across different modules and the relationship between axonal arbors and projection patterns.

Methods

Nomenclature

The nomenclature of brain regions follows the CCFv3²⁶, which categorizes a mouse brain into 671 regions. Each region, except for the direct tectospinal pathway (tspd), comprises two mirroring subregions in the left and right hemispheres. A higher level of granularity consisting of 314 regions (CCF-R314) is used by merging highly homogeneous regions, such as the lamination-differentiated cortical subregions. All brain regions used in this work are from the CCF-R314 regions. We have spelled out the full names of the regions in the manuscript whenever we refer to them for the first time. The CCFv3 atlas can be found at https://connectivity.brain-map.org/3d-viewer?v=1.

Super-regional anatomical entities, such as brain areas, are sets of functionally related regions that are continuous in space. While the definitions of brain areas are similar, they differ in granularity. In this paper, we discussed a higher granularity consisting of 4 areas: cortex (CTX), cerebellum (CB), cerebral nuclei (CNU), and brain stem (BS). We also discussed 13 compound areas, which are CBN: cerebellar nuclei, CBX: cerebellar cortex, CTXsp: cortical subplate, HPF: hippocampal formation, HY: hypothalamus, isocortex, MB: midbrain, MY: medulla, OLF: olfactory areas, P: pons, PAL: pallidum, STR: striatum, and TH: thalamus.

To facilitate understanding, specific terms describing multi-scale morphometry and morphological patterns are detailed in Supplementary Data 7.

Image acquisition and processing

We collected 204 whole mouse brains at submicron or micron resolutions from 4 BICCN projects within the BICCN community and another collaboration project. Of these, 180 fMOST brains came from a U19 project (1U19MH114830-01). The other 10 fMOST brains and 10 STPT brains were obtained from another U19 project (1U19MH114821-01) and 1 LSFM brain from a U01 project (1U01MH114829-01). These brains were downloaded from the Brain Image Library (BIL, http://www.brainimagelibrary.org). 3 LSFM mouse brains were provided by P.O. (n = 2) and Z.W. (n = 1), who were granted from another U01 project (1U01MH114824-01). The brain images exhibit anisotropic resolutions, primarily ranging from 0.2 to 0.35 μm in the xy plane and 1 μm in the z direction. The fMOST images were labeled using sparse viral-like transgenic lines. The primary reporters include TIGRE-MORF (Ai166), GFP-expressing TIGRE2.0 (Ai139 or Ai140), and TIGRE1.0 (Ai82). These reporters were paired with various drivers, such as Cre expression lines, which target distinct yet specific neuronal types¹⁶. Detailed information regarding brain IDs, modalities, sources, resolutions, downloadable links, transgenic labeling and the primary targeted neuronal types is summarized in Supplementary Data 1.

The brain datasets, totaling 3.7 peta-voxels, are managed via MorphoHub⁷⁷. To get fast access to both fine-grained details and a global overview, we restructure each brain into hierarchical TeraFly⁷⁸ format.

Registration

Brain images were registered to the 25 μm CCFv3 template using the cross-modal registration tool mBrainAligner^27,28. We employed a similar pipeline consisting of image standardization and preprocessing, global registration, and deep learning enhanced local registration, with a minor update on the landmark searching strategy which improved overall registration accuracy for the hippocampal and striatal neurons. Registration channels were leveraged whenever possible. The brains were down-sampled to approximately 25 μm resolution through even-folds linear interpolation prior to registration. Non-brain tissues were semi-automatically removed with Vaa3D^79,80,81 and mBrainAligner. Anatomical regions of the brains were automatically labeled based on the CCFv3 atlas and the deformation matrices obtained during registration. The multi-morphometry including full morphologies, local morphologies, arbors, and varicosities, were reverse-mapped to the CCFv3 space using the inverse deformation matrix. We estimated the robustness of the registration by computing the average registration offsets and intensity variance across 191 analyzed brains for 2213 landmarks (Supplementary Fig. S10), sampled homogeneously from the regional boundaries of CCFv3 atlas. For each landmark, the intensity variance was normalized by the average offset. The CCF-space average brain was generated by computing the mean voxel value for each voxel on the CCFv3 atlas across all 191 brains.

Soma identification

The SEU-S182K soma dataset comprises two parts. The first part consists of 45,664 somas manually annotated using the Vaa3D-TeraFly platform, most of which were reported in a previous study⁷⁷. An additional 136,833 somas were semi-automatically annotated using the Collaborative Augmented Reconstruction (CAR) platform²⁹, which is updated from our Vaa3D-TeraFly and immersive annotation system Vaa3D-TeraVR⁸².

The semi-automatic soma identification protocol involves two major steps. Firstly, we filtered out the TeraFly image blocks (~256 voxels in each dimension, ~59 × 59 × 256 μm³) with maximal intensities less than 250 (unsigned 16-bit image), standardized the remaining blocks through a Z-score normalization, and converted them to the unsigned 8-bit range. Next, the blocks were binarized using their 99th percentile as thresholds, and the resulting images were transformed using the gray-scale distance transform (GSDT) algorithm. Candidates were identified as voxels with intensities in the range of 5 to 30 on the transformed image, followed by a Non-Maximal-Suppression (NMS)-like strategy to eliminate redundant candidates.

In the second step, we cropped 128 × 128 × 128-sized image blocks on the second-highest resolution images (~59 × 59 × 256 μm³) centered at the position of putative somas. These blocks were then distributed to remote users on the mobile application CAR-mobile. Using this protocol, we identified 179,115 somas within weeks, involving 23 trained annotators and 7 fresh annotators without any prior knowledge.

The soma locations were then optimized by applying the mean-shift algorithm bound with Vaa3D after zero-clipping of voxels with intensity lower than μ + σ, where μ and σ are the mean and standard deviation of the image block. A window size of 15 voxels was used for the mean-shift soma location optimization. Possible duplicates were removed when two somas are within 15 voxels and their center point intensity was lower than the average intensity of the two somas. Somas outside of CCF-R314 regions were excluded.

Neurite detection

Neurite voxels were segmented using an automatic algorithm and then summarized the number of voxels by brain regions to produce a region-wide vector consisting of 314 values. Each value represented the total number of detected neurite voxels in the corresponding brain region, normalized by the total number of neurite voxels in the brain. The algorithm segments neurite in 191 out of the 204 brains on low resolution images, averaging at approximately 1 μm (x) × 1 μm (y) × 4 μm (z), for a trade-off between accuracy and efficiency. Among these, 183 brains were from 34 genetically labeled driver genes (Supplementary Fig. S3). Consequently, each of the 314 regions was represented by a brain-wide neurite distribution vector, resulting in a neurite density matrix (M_d) with dimensions of 314×191. The neurite density for each region was computed as the total number of detected neurite voxels within that region divided by the total number of neurite voxels detected in the entire brain. Using the matrix, we estimated a pair-wise regional correlation map (M_c) with dimensions of 314×314, among which each value was the Spearman correlation coefficient between the normalized 191-dimensional vectors of the corresponding region. To counteract the imbalance in the number of brains across different transgenic lines, we employed normalization during the estimation of correlation coefficients using the “wCor” package in R, where each brain was assigned a weight that corresponds to the reciprocal of the number of brains from the respective transgenic line. In cases where brains without transgenic labeling information, we used the average of all weights.

Based on the correlation map (M_c), we assessed the intra-compound area consistency as the distribution of correlations between all pairs of regions within the compound area. In this way, the distributions for all 13 compound areas were calculated (Fig. 2A).

The neurite detection algorithm is an efficient pipeline without utilizing deep learning models. The procedure can be summarized in 6 steps:

1.
Estimation of an empirical foreground threshold for each brain. This step involved finding an empirical threshold value (thresh) to distinguish between the foreground (neurite voxel) and background (non-neurite voxels) on the lowest-resolution image. The threshold was estimated based on the mean and standard deviation of all voxels: $0.9\times \min (\max (\mu+1.5\sigma,400),1000)$, where μ and σ were the mean and standard deviation of all voxels of the brain (16-bit image).
2.
Split the brain into non-overlapping image blocks. In this step, the third lowest resolution brain images were split into small non-overlapping blocks for subsequent memory-affordable processing. We utilized the image blocks of Vaa3D-TeraFly files at the specific resolution of approximately 256 voxels in each dimension.
3.
Pre-filtering. This step involves filtering out blocks that are unlikely to contain neurite. Image block files (in compressed TIFF format) that were smaller than a certain size (1.7 MB) or had a maximum pixel value lower than 300 were considered neurite-free blocks and were excluded.
4.
Calculation of the salient map. An image block was firstly denoised by an adaptive filter similar to the “ada_threshold” plugin on Vaa3D. At the same time, an anisotropic salience map was estimated through block-wise PCA analysis on 16 × 16 × 16 voxels-sized cuboids which were upsampled from 16 × 16 × 4 cuboids of the original image, as the resolution in z axis of the image is about 3 times smaller than that in x and y axes. The anisotropy score of each cuboid is defined as $\frac{{S}_{1}-{S}_{2}}{{S}_{1}+{S}_{2}}\cdot \frac{{S}_{1}-{S}_{3}}{{S}_{1}+{S}_{3}}$, where S₁, S₂, and S₃ are the eigenvalues of first, second, and third principal components of the cuboid, similar to the content index Q in previous studies⁸³. The final salient map was calculated by multiplying the denoised image and anisotropy map.
5.
Thresholding. The salient map was thresholded using 0.1 × thresh calculated in step 1. thresh may be manually adjusted based on the segmentation results if it was inappropriate.
6.
Mapping neurite voxels to CCFv3 atlas. Finally, the identified neurite voxels were mapped to the CCFv3 space and summarized by regions to obtain a region-wide neurite voxel vector in the shape of 314. The vector was then normalized by dividing it by the total number of neurite voxels, resulting in a neurite density vector for the brain.

Our neurite detection algorithm was qualified by the good linearity between the number of annotated somas and the total number of detected neurite voxels of each brain and in each region (Supplementary Fig. S3C). The considerable variety of sparse labeling and a large number of transgenes (n = 34) and brains (n = 191) provide a minimal-redundant neurite matrix, laying the foundation of a reliable neurite detection. A large set of diverse labeling genes and brains down-weights the co-expression patterns and highlights possible morphological relationships. When two regions show a high correlation between their distributions across 191 brains, it may indicate a possible connection. To estimate the possibility of mislabeling neighboring regions, we calculated correlation coefficients between the number of annotated somas in neighboring regions for the 10 brains with the highest annotated somas. The coefficients were small, ranging from 0.001 to 0.2797 (Supplementary Fig. S12). Neurite detections on image blocks were presented in Supplementary Fig. S3A and Supplementary Fig. S11A. An example of the neurite connections and corresponding detections between the regions CP and GPi/GPe was illustrated in Supplementary Fig. S11B.

Target-correlated regions detection

We considered each region as the target region and extracted regions having a Spearman correlation coefficient of no less than 0.5 with it, thereby forming its highly correlated region set. Out of the 314 regions, 313 regions have highly correlated regions based on this criterion. A detailed list of these region sets is provided in Supplementary Data 4. We classified the region sets into two categories: intra-compound area (intra-CA) and cross-compound area (cross-CA), based on whether the regions were within the same compound area.

Regional module detection

We classified all regions into 18 non-overlapping subsets or initial modules, based on the dendrogram produced by applying hierarchical clustering to the correlation map (M_c). The module detection process begins by finding a seed branching point, which is the cluster with the lowest level (i.e., the first diverging cluster) in the dendrogram, followed by checking the number of all its subsidiary region leaves. If a cluster contains no less than 3 regions and no more than 30 regions, it is defined as an initial module. Otherwise, we merge the current cluster with the most closing cluster or split it into modules. The process repeats until all regions are categorized into a module, resulting in a total of 18 non-overlapping initial modules.

For all the initial modules, we removed any region that occurred less than twice in the target-correlated region sets (Supplementary Fig. S13; Supplementary Data 4). If a module had at least two regions remaining, it was considered a tight module. Otherwise, it was deleted. Using these criteria, we identified 18 tight modules (Fig. 2B, Supplementary Data 5), each with a high consistency score of no less than 0.42, where the consistency score was calculated as the average Spearman correlation coefficient of the cross-brain neurite density distribution for all pairs in that module.

Tracing local morphology

The local reconstructions were generated using the somas of SEU-S182K. To avoid highly interweaved neurons, somas with more than five neighboring somas within a radius of approximately 128 μm were eliminated. For each soma, a block measuring 512 × 512 × 256 voxels was cropped from the second highest resolution images, with the soma located at the center of the block. This block size corresponds to an approximate diameter of 236 μm in each of the x and y axes, and 512 μm in z axis around the soma, encompassing most of the basal dendrites (98% of total compartments in manual annotations), a portion of the apical dendrite (63%).

We combined two automatic tracing algorithms, All-Path-Pruning (APP2)⁸⁴, and the tubular fitting-based algorithm neuTube⁸⁵, to trace each image block. Default parameters were used for both algorithms except that the background threshold in APP2 was set to an automatically determined threshold of μ + 0.5σ, where μ and σ are the mean and standard deviation of the input image. Reconstructions from APP2 and neuTube were combined to get an initial reconstruction. Specifically, neuTube reconstructions were used to prune the APP2 reconstructions, and nodes in APP2 reconstructions that did not have corresponding nodes within 5 voxels (~2.3 μm) in neuTube reconstructions were pruned. Images were enhanced using a signal-background contrast enhancement method⁸⁶ before being subjected to tracing algorithms.

The generated reconstructions were subjected to a segment-pruning pipeline, rectifying possible loops, erratic branches, and intersections with other neurons. Each pruning step operates as an independent filter that takes in the raw neuron tree, and the resulting tree is the intersection of all filtered reconstructions. The detailed pipeline can be summarized as follows:

1.
Firstly, a branch pruning was performed to remove any branch that had an excessive angle to its parent ( < 80 degrees) or had an excessive increase in radius (1.5 times the parent branch’s radius).
2.
Secondly, a crossover pruning step was carried out to expunge branches from putative crossover structures. To do that, we detected all putative crossover structures, including multifurcating nodes containing more than two child nodes and consecutive bifurcating nodes within five voxels. For each of the crossover structures, we checked all connections between the current branch and its child branches. In specific, branches with small angles (< 80 degrees) were marked as removable. Then, we evaluated branches with mediocre turning angles (80–100 degrees) to confirm if another branch with a large enough angle existed between them (> 150 degrees). If such a branch existed, we removed the other branches.
3.
Then, a soma pruning strategy was applied to remove branches originating from any other putative somas. A soma candidate was identified when the total area of a candidate node or a set of nearby candidate nodes is large (> 500 pixel² on the maximum intensity projection on the xy plane, corresponding to ~105 μm²). A candidate node here is a reconstructed node with a radius larger than five pixels (~2.3 μm) on the xy-plane. Nodes within 50 pixels (~23 μm) to the current soma - were not checked. For each detected soma, an integration of deviation angle along the neurite path in between the detected soma and the target soma was estimated, to locate the best cutting position. The deviating angle is the angle between a single local branch and the radial line connecting the soma and the nearer end of the same branch, similar to the G-Cut⁴³. We then calculate the integral of deviation angles at both sides, that is, from the current branch to the current soma and the current branch to the putative soma respectively, by weighting the deviation angle with the branch length. Branches with a lower deviation angle integral leading to the putative soma were subsequently removed.
4.
Next, a winding pruning was performed to remove any branch that followed a circuitous path to the soma, defined as the ratio between path distance and Euclidean distance being greater than three.
5.
Finally, all subsequent nodes of a pruned branch or nodes identified in the previous steps were removed, and reconstructions with fewer than 20 nodes were discarded.

We reconstructed 15,441 local morphologies following this protocol. The morphologies were then mapped to the CCFv3 atlas and automatically labeled the regions of the somas.

Dendritic microenvironment construction

A dendritic microenvironment was defined as the spatial-tuned fusion of a local morphology and its top five most similar morphologies within a sphere of radius 249 μm. The radius corresponds to the 50th percentile distance among the distances between the 5th closest neuron and the target neuron for all neurons in SEU-D15K. The similarity between two neurons was calculated as the Euclidean distance of their standardized (Z-score normalized) morphological feature vectors.

Each neuron was represented using a 24-dimensional feature vector consisting of 18 L-Measure^Vaa3D features⁸⁷ (except for the “Nodes”, “SomaSurface”, “AverageDiameter”, and “Surfaces” features of the 22 features described in the “Morphology features” section in the Methods), the explained variance ratios of three principal components (variance percentages of PC_1, PC_2, and PC_3), and sum-normalized values of the first principal component (PC_11, PC_12, and PC_13). The principal components (PC_1, PC_2, PC_3) were calculated using principal component analysis (PCA) for all nodes in isotropic space. The variance percentage of a principal component represents the ratio of its variance among that of all principal components. The microenvironment feature is a spatial proximity weighted averaging of features derived from all six neurons constituting the microenvironment. Specifically, the spatial weight for a neuron is the exponential of negatively normalized distance. Therefore, for each microenvironment, its feature was calculated as:

$${F}_{M}={\sum}_{i=1}^{6}{w}_{i}\times {F}_{i}$$

(1)

where

$${w}_{i}=\frac{\exp (-{d}_{i}/D)}{{\sum }_{i=1}^{6}\exp (-{d}_{i}/D)}$$

(2)

where F_M and F_i are the feature vectors of the microenvironment and neuron i. d_i is the distance between the soma of the target neuron and its neighboring neuron i. Here, D is the sphere radius (249 μm).

To intuitively visualize the data, we used the max-relevant min-redundancy (mRMR) algorithm to reduce the 24-dimensional microenvironment feature vector to the three most discriminating features. The identified top three features were straightness, Hausdorff dimension, and variance percentage of the third principal component (PC_3), which represent the branch bending, the fractal dimension of the morphology, and the explained variance ratio of PC_3, respectively. The automatically selected mRMR features may be replaced by other user-chosen features in the 24-dimensional feature-space. To generate the whole-brain microenvironment map, we initialized an empty image of the same size as the 25 μm resolution CCFv3 atlas and assigned each neuron’s three features to the three color-channels (R, G, B) of its soma location in the image. The resulting map contained 15,441 data points that clearly represented the three most discerning microenvironment feature values. Data points located in the right hemisphere were mirrored to the left hemisphere, based on the widely accepted left-right symmetry assumption, which was also validated in this work (Supplementary Fig. S4, Supplementary Fig. S5). Each feature underwent min-max normalization and linearly mapped to a range between 0 and 255 for consistent comparison. Microenvironments located within 1 mm of the middle sections along the axial, sagittal, and coronal views were mapped to the corresponding middle sections using the maximum intensity projection (MIP). The resulting maps were superimposed with the boundary outlines of the CCFv3 atlas to facilitate the semantic analysis of the feature distribution. We employed KMeans clustering to classify regions based on the concatenation of the mean and variance feature vectors of all microenvironments in that region.

Refining single neuron reconstructions and skeletons

We manually annotated 140 single neurons in their entirety from 19 fMOST mouse brains from the 1U19MH114830-01 project at submicron resolutions. The annotations were carried out with the CAR platform²⁹. Together with refined versions of previously released 1736 neurons¹⁶ we aggregated a total of 1876 single-neuron morphologies (SEU-A1876). Each neuron-reconstruction should meet the following criteria: (1) A neuron-reconstruction must have a single soma. (2) A neuron-reconstruction must be a single connected piece (graph). (3) A neuron-reconstruction cannot have any loop. (4) A neuron-reconstruction cannot contain duplicated reconstructed compartments. (5) A neuron-reconstruction can have only bifurcating branches except at the soma. (6) A neuron-reconstruction should have consistently annotated dendritic and axonal segments.

The morphologies annotated at low resolutions frequently lead to image-morphology mismatch in the highest resolution space. To overcome this issue, we developed a retracing strategy to refine the skeleton skewness⁴⁵. This involved a two-step process. First, the skeletons were split into fragments of 50 μm, and every two consecutive middle points of the fragments were connected using the graph-augmented deformable model (GD)⁸⁸. The GD algorithm automatically fits the skeleton to the nearest salient neurite with the constraints of the original skeleton priors. In the second step, an additional step of GD tracing was applied to the middle points of two consecutive refined fragments.

L-Measure^Vaa3D features

We used L-Measure features to characterize microenvironment, full morphology, and local morphology. We calculated 22 features implemented in the “global_neuron_feature” plugin of Vaa3D: “Nodes”, “SomaSurface”, “Stems”, “Bifurcations”, “Branches”, “Tips”, “OverallWidth”, “OverallHeight”, “OverallDepth”, “AverageDiameter”, “Length”, “Surface”, “Volume”, “MaxEuclideanDistance”, “MaxPathDistance”, “MaxBranchOrder”, “AverageContraction”, “AverageFragmentation”, “AverageParent-daughterRatio”, “AverageBifurcationAngleLocal”, “AverageBifurcationAngleRemote”, “HausdorffDimension”.

Note that while the meaning of the L-Measure^Vaa3D features are the similar to these defined in L-Measure server⁸⁷ (http://cng.gmu.edu:8080/Lm), some of them slightly differ in implementation. For instance, in Vaa3D, features like “OverallWidth”, “OverallHeight”, and “OverallDepth” represent the span of all nodes or compartments along the x (anterior-posterior), y (dorsal-ventral), and z (left-right) axes, respectively. However, the 5% extreme values were excluded in L-Measure server.

Full morphology analysis

We leveraged L-Measure^Vaa3D features (22 dimensions) but excluded five inaccessible features such as soma surface and total surfaces for the manually annotated neurons, resulting in 7 global features and 10 local features for each fully reconstructed neuron. Each of the local features was represented by four statistical characteristics: minimum, maximum, mean, and standard deviation, resulting in a total of a 47-dimensional feature vector. The seven global features are “Stems”, “Branches”, “OverallWidth”, “OverallHeight”, “OverallDepth”, “OverallVolume”, and “Length”. The ten local features are “br_length” (path length of a branch), “br_order” (branch order), “br_contraction” (contraction of a branch in L-Measure), “bif_EucDist2soma”, “bif_PathDist2soma”, “asymmetry” (“Partition Asymmetry” in L-Measure), “ampl_local”, “ampl_remote”, “tilt_local”, and “tilt_remote” (Supplementary Fig. S6). We standardized all the features using Z-score normalization, and evaluated neuronal similarity as the cosine distances between these features. We also considered the spatial relationships between neurons by calculating the Euclidean distance (d) of each soma in CCFv3 space. We then computed the exponential of -d for these two somas after normalization. We defined the similarity of neurons as the product of feature similarity and spatial distance. Spectral clustering was utilized to classify neurons into different clusters. Specifically, we treated the entire dataset as a graph, where the neurons in the dataset served as individual nodes, and the weights of the connections between nodes were defined by the similarities between the neurons.

The silhouette scores between soma locations were estimated with the “metrics.silhouette_score” method of the scikit-learn package, using default parameters, which are calculated as (b - a) / max(a, b), where (a) is the mean intra-cluster distance of a sample, and (b) is the distance between the sample and the cluster not containing the sample

Arbor detection and analysis

An arbor in this work is a dense-packing sub-tree. The dendritic arbors are the complete dendrites. For axons, we utilized spectral clustering to subdivide them into arbors. This was done by creating an undirected graph composed of vertices that represent nodes in the original tree, while the weights of edges between vertex pairs were represented by the exponential of the negative distances between nodes. To facilitate comparison, we utilized the dominant auto-clustering arbor number of neurons in the same brain region using the majority-vote principle. Regional features were calculated by taking the average of the features of all neurons in that region.

We employed the number of branches (“#branch”), total arbor volume (“volume”), and maximal spatial density (“max_density”) - the latter being defined as the number of axonal nodes located within a 20 μm radius for every node - as three features to characterize arbor morphology. We differentiated between proximal and distal arbors based on whether or not the Euclidean distance from the maximal density node to the soma exceeded 750 μm. All values of the same feature were min-max normalized to the range of 0 to 1. The arbors of each neuron were sorted by the Euclidean distance-to-soma and designated as “A1”, “A2”, and “A3” (if present). For the classification of thalamic axonal arbors, we utilized agglomerative clustering by combining 4 features (the 3 aforementioned features and “distance-to-soma”) alongside the average projection of the axonal arbors.

Detect primary axonal tract motifs

The primary axonal tract for a neuron is the longest axonal path without short branches at the terminal side. The process of identifying the primary axonal tract begins by determining the longest axonal path and then iteratively removing all branches shorter than the second-longest axonal branch from the tip of the path towards its soma. The resulting path is the primary axonal tract, and its direction is defined as soma to the terminal.

We then mapped primary tracts to the standardized CCFv3 space, grouping them according to projection subtypes, and estimated the radius profile of each group. To this end, we sub-sampled each tract with 200 uniformly-spaced nodes and calculated the cross-sectional radii of points with corresponding percentiles. In specific, for a given set of points, we computed the distance of every point to their center in the reduced 2-dimensional space generated by principal component analysis (PCA), and extracted the 75th percentile as the radius. Based on the comparison of somas and terminal radii, projection patterns were defined as convergent, divergent, and parallel.

Detect axonal varicosities

We updated the approach reported previously⁷⁷ by combining both intensity and radius profiles along the axonal shafts. We standardized the neuronal images by applying an enhancement pipeline⁸⁶ designed to enhance the signal-to-background contrast. The detection process starts with partitioning the axonal skeletons into 20 μm length fragments, along which we calculated the intensity and radius profiles, leading to the identification of initial candidates for varicosities, which exhibit overlapped peaks in the intensity and radius profiles. False positive results in the initial candidates were filtered out through heuristic criteria that a varicosity should be 1.5 times larger than its surrounding axonal nodes similar to the weight threshold in previous studies^69,89 and have an image intensity value above 120 in 8-bit images (maximum intensity 255). Finally, we remove any possible duplicates by deleting candidates that were closer than five voxels in highest-resolution images, a distance roughly equivalent to the size of a typical varicosity (1–2 μm). All detected varicosities were registered to the CCFv3 atlas along with their morphologies using mBrainAligner. To evaluate the varicosity detection, two independent experts manually annotated 235 image blocks (~59 × 59 × 256 μm³) using CAR-mobile, yielding 1,450 annotated varicosities. This manual annotation dataset was utilized to evaluate the accuracy of the automatic varicosity detection method.

Cross-scale feature generation

We obtained a 75-dimension cross-scale feature vector (Fig. 1E) for each neuron in SEU-A1876, by concatenating features derived from five distinct morphological scales, including microenvironment, full morphology, arbor, varicosity, and primary axonal tract (motif). The microenvironment features for each neuron were acquired by extracting the microenvironment features of the neuron in the same soma region in SEU-D15K that had the most similar L-Measure^Vaa3D features. For microenvironment and full morphology, we utilized 18 L-Measure^Vaa3D features, such as “Bifs”, “Branches”, and “Tips”, as those in “Dendritic microenvironment construction” (Methods). The arbor features consisted of a concatenation of dendritic and axonal arbor features. For comparative reasons, the axons of each neuron were arborized to two arbors. All features were standardized to a normal distribution and concatenated. Features of a region were estimated by averaging all neurons within that region.

We introduced a metric, called the DS matrix, to calibrate the diversity among cell types, encompassing both intra-type and inter-type similarities. Each value (DS value) in the matrix indicates the average correlation coefficient between all neuron pairs for the respective two regions (neuron types). The correlation of two neurons is determined by calculating the Pearson correlation coefficient between their cross-scale features. A higher value in the matrix signifies greater stereotypy, while a lower value signifies greater diversity. The axon-axon “distance” was the Euclidean distance between the projection vectors of the neuron pair, which was released in our previous work (Peng et al.¹⁶).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

All morphometry data are accessible from both Zenodo (https://doi.org/10.5281/zenodo.13944322) and Google Drive (https://drive.google.com/drive/folders/1NwwTe840_0KQhv-zVLhw58LU9nntkb-F?usp=sharing). Documentation and video demonstrations for the dataset are available at https://sd-jiang.github.io/full_spectrum/. All brain images are generated from projects within the BICCN initiative, with most of them publicly accessible through the Brain Image Library (BIL) at https://www.brainimagelibrary.org/. The remaining 28 brain images will be made available shortly after compilation and uploading. Source data are provided with this paper.

Code availability

The source codes are available via https://doi.org/10.5281/zenodo.13979929. Dependencies are summarized in the requirement.txt, which can be easily installed using the Python package manager, PIP. Detailed documentation and step-by-step instructions are provided in the repository. Video instructions showing how to use the package is available at https://sd-jiang.github.io/full_spectrum/. Vaa3D (version 4.001) and Vaa3D-x (version 1.1.2) are available on the Vaa3D GitHub repository (https://github.com/Vaa3D) in both source code and released binary forms. Every version of Vaa3D encompasses core bindings such as TeraFly and TeraVR, plugins that include “Simple_Adaptive_Thresholding” filter, “global_neuron_feature”, Grayscale Image Distance Transform (GSDT), and auto-tracing algorithms like APP2, neuTube, and GD. The updated version of mBrainAligner can be found at https://github.com/Vaa3D/vaa3d_tools/tree/master/hackathon/mBrainAligner. MorphoHub is available at https://github.com/SD-Jiang/MorphoHub. Source codes for varicosity detection can be found at https://github.com/Vaa3D/vaa3d_tools/tree/master/hackathon/shengdian/BoutonDetection. The collaborative augmented reconstruction system (CAR) is available through https://github.com/neurogeom/CAR. The codes for full morphological feature extraction are accessible at https://github.com/Vaa3D/vaa3d_tools/blob/master/hackathon/shengdian/NeuroMorphoLib. Clustering and other machine learning algorithms, including K-Means, spectral clustering, HDBSCAN, and Principal Component Analysis (PCA), come from the third-party package scikit-learn (version 1.2.2) of Python (version 3.10). The Python derivative of mRMR (pymrmr, version 0.1.11, https://github.com/fbrundu/pymrmr) is used in this paper to select the most discriminating features. Hierarchical clustering in module detection and arbor analysis utilizes the hclust library from the stats package (version 4.2.2) in R (version 4.2.2).

References

Luo, L. Architectures of neuronal circuits. Science 373, eabg7285 (2021).
Article CAS PubMed PubMed Central Google Scholar
Zeng, H. & Sanes, J. R. Neuronal cell-type classification: challenges, opportunities and the path forward. Nat. Rev. Neurosci. 18, 530–546 (2017).
Article CAS PubMed Google Scholar
Peng, H. et al. BigNeuron: Large-Scale 3D neuron reconstruction from optical microscopy images. Neuron 87, 252–256 (2015).
Article CAS PubMed PubMed Central Google Scholar
Manubens-Gil, L. et al. BigNeuron: a resource to benchmark and predict performance of algorithms for automated tracing of neurons in light microscopy datasets. Nat. Methods 20, 824–835 (2023).
Article CAS PubMed Google Scholar
Ghosh, S. et al. Sensory maps in the olfactory cortex defined by long-range viral tracing of single neurons. Nature 472, 217–220 (2011).
Article ADS CAS PubMed Google Scholar
Kuramoto, E. et al. Two types of thalamocortical projections from the motor thalamic nuclei of the rat: a single neuron-tracing study using viral vectors. Cereb. Cortex 19, 2065–2077 (2009).
Article PubMed Google Scholar
Lin, R. et al. Cell-type-specific and projection-specific brain-wide reconstruction of single neurons. Nat. Methods 15, 1033–1036 (2018).
Article CAS PubMed Google Scholar
Luo, W. et al. Supernova: a versatile vector system for single-cell labeling and gene function studies in vivo. Sci. Rep. 6, 35747 (2016).
Article ADS CAS PubMed PubMed Central Google Scholar
Ragan, T. et al. Serial two-photon tomography for automated ex vivo mouse brain imaging. Nat. Methods 9, 255–258 (2012).
Article CAS PubMed PubMed Central Google Scholar
Keller, P. J. & Ahrens, M. B. Visualizing whole-brain activity and development at the single-cell level using light-sheet microscopy. Neuron 85, 462–483 (2015).
Article CAS PubMed Google Scholar
Silvestri, L. et al. Micron-scale resolution optical tomography of entire mouse brains with confocal light sheet microscopy. J. Vis. Exp. 80, 50696 (2013).
Gong, H. et al. High-throughput dual-colour precision imaging for brain-wide connectome with cytoarchitectonic landmarks at the cellular level. Nat. Commun. 7, 12142 (2016).
Article ADS CAS PubMed PubMed Central Google Scholar
Zhong, Q. et al. High-definition imaging using line-illumination modulation microscopy. Nat. Methods 18, 309–315 (2021).
Article CAS PubMed Google Scholar
Hawrylycz, M. et al. A guide to the BRAIN Initiative Cell Census Network data ecosystem. PLoS Biol. 21, e3002133 (2023).
Article CAS PubMed PubMed Central Google Scholar
Winnubst, J. et al. Reconstruction of 1,000 projection neurons reveals new cell types and organization of long-range connectivity in the mouse brain. Cell 179, 268–281.e13 (2019).
Article CAS PubMed PubMed Central Google Scholar
Peng, H. et al. Morphological diversity of single neurons in molecularly defined cell types. Nature 598, 174–181 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Gao, L. et al. Single-neuron projectome of mouse prefrontal cortex. Nat. Neurosci. 25, 515–529 (2022).
Article CAS PubMed Google Scholar
Qiu, S. et al. Whole-brain spatial organization of hippocampal single-neuron projectomes. Science 383, eadj9198 (2024).
Article CAS PubMed Google Scholar
Parekh, R. & Ascoli, G. A. Quantitative investigations of axonal and dendritic arbors: development, structure, function, and pathology. Neuroscientist 21, 241–254 (2015).
Article CAS PubMed Google Scholar
Peng, H. et al. BrainAligner: 3D registration atlases of Drosophila brains. Nat. Methods 8, 493–498 (2011).
Article CAS PubMed PubMed Central Google Scholar
Compston, A. Texture of the nervous system of man and the vertebrates by Santiago Ramon y Cajal. J. Neurol., Neurosurg. Psychiatry 70, 421c–4421c (2001).
Article Google Scholar
The Petilla Interneuron Nomenclature Group (PING). Petilla terminology: nomenclature of features of GABAergic interneurons of the cerebral cortex. Nat. Rev. Neurosci. 9, 557–568 (2008).
Article Google Scholar
Miller, J. A. et al. Common cell type nomenclature for the mammalian brain. eLife 9, e59928 (2020).
Article CAS PubMed PubMed Central Google Scholar
Booker, S. A. & Vida, I. Morphological diversity and connectivity of hippocampal interneurons. Cell Tissue Res. 373, 619–641 (2018).
Article CAS PubMed PubMed Central Google Scholar
Surmeier, D. J., Carrillo-Reid, L. & Bargas, J. Dopaminergic modulation of striatal neurons, circuits, and assemblies. Neuroscience 198, 3–18 (2011).
Article CAS PubMed Google Scholar
Wang, Q. et al. The allen mouse brain common coordinate framework: A 3D Reference Atlas. Cell 181, 936–953.e20 (2020).
Article CAS PubMed PubMed Central Google Scholar
Li, Y. et al. mBrainAligner-Web: a web server for cross-modal coherent registration of whole mouse brains. Bioinformatics 38, 4654–4655 (2022).
Article CAS PubMed Google Scholar
Qu, L. et al. Cross-modal coherent registration of whole mouse brains. Nat. Methods 19, 111–118 (2022).
Article CAS PubMed Google Scholar
Zhang, L. et al. Collaborative augmented reconstruction of 3D neuron morphology in mouse and human brains. Nat. Methods 21, 1936–1946 (2024).
Article CAS PubMed PubMed Central Google Scholar
Han, X. et al. Whole human-brain mapping of single cortical neurons for profiling morphological diversity and stereotypy. Sci. Adv. 9, eadf3771 (2023).
Article ADS PubMed PubMed Central Google Scholar
Simerly, R. B. & Swanson, L. W. Projections of the medial preoptic nucleus: A Phaseolus vulgaris leucoagglutinin anterograde tract‐tracing study in the rat. J. Comp. Neurol. 270, 209–242 (1988).
Article CAS PubMed Google Scholar
Godenzini, L. et al. Auditory input enhances somatosensory encoding and tactile goal-directed behavior. Nat. Commun. 12, 4509 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Muñoz-Castañeda, R. et al. Cellular anatomy of the mouse primary motor cortex. Nature 598, 159–166 (2021).
Article ADS PubMed PubMed Central Google Scholar
Herkenham, M. & Nauta, W. J. H. Efferent connections of the habenular nuclei in the rat. J. Comp. Neurol. 187, 19–47 (1979).
Article CAS PubMed Google Scholar
Saper, C. B., Scammell, T. E. & Lu, J. Hypothalamic regulation of sleep and circadian rhythms. Nature 437, 1257–1263 (2005).
Article ADS CAS PubMed Google Scholar
Brock, O. et al. A Role for Thalamic Projection GABAergic Neurons in Circadian Responses to Light. J. Neurosci. 42, 9158–9179 (2022).
Article CAS PubMed PubMed Central Google Scholar
Mcdonald, A. J. Topographical organization of amygdaloid projections to the caudatoputamen, nucleus accumbens, and related striatal-like areas of the rat brain. Neuroscience 44, 15–33 (1991).
Article CAS PubMed Google Scholar
An, S. et al. A Whole-Brain Connectivity Map of VTA and SNc Glutamatergic and GABAergic Neurons in Mice. Front. Neuroanat. 15, 818242 (2021).
Article CAS PubMed PubMed Central Google Scholar
Motta, A. et al. Dense connectomic reconstruction in layer 4 of the somatosensory cortex. Science 366, eaay3134 (2019).
Article CAS PubMed Google Scholar
Peng, H., Long, F. & Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 27, 1226–1238 (2005).
Article PubMed Google Scholar
DeFelipe, J. et al. New insights into the classification and nomenclature of cortical GABAergic interneurons. Nat. Rev. Neurosci. 14, 202–216 (2013).
Article CAS PubMed PubMed Central Google Scholar
Polavaram, S., Gillette, T. A., Parekh, R. & Ascoli, G. A. Statistical analysis and data mining of digital reconstructions of dendritic morphologies. Front. Neuroanat. 8, (2014).
Li, R. et al. Precise segmentation of densely interweaving neuron clusters using G-Cut. Nat. Commun. 10, 1549 (2019).
Article ADS PubMed PubMed Central Google Scholar
Kim, Y. et al. Brain-wide maps reveal stereotyped cell-type-based cortical architecture and subcortical sexual dimorphism. Cell 171, 456–469.e22 (2017).
Article CAS PubMed PubMed Central Google Scholar
Li, Y., Jiang, S., Ding, L. & Liu, L. NRRS: a re-tracing strategy to refine neuron reconstruction. Bioinforma. Adv. 3, vbad054 (2023).
Article Google Scholar
Liu, L. & Qian, P. Manifold classification of neuron types from microscopic images. Bioinformatics 38, 4987–4989 (2022).
Article CAS PubMed Google Scholar
Iascone, D. M. et al. Whole-neuron synaptic mapping reveals spatially precise excitatory/inhibitory balance limiting dendritic and somatic spiking. Neuron 106, 566–578.e8 (2020).
Article CAS PubMed PubMed Central Google Scholar
Anderson, J. C. & Martin, K. A. C. Does bouton morphology optimize axon length? Nat. Neurosci. 4, 1166–1167 (2001).
Article CAS PubMed Google Scholar
Turégano-Lopez, M. et al. Tracing nerve fibers with volume electron microscopy to quantitatively analyze brain connectivity. Commun. Biol. 7, 796 (2024).
Roy, D. S., Zhang, Y., Halassa, M. M. & Feng, G. Thalamic subnetworks as units of function. Nat. Neurosci. 25, 140–153 (2022).
Article CAS PubMed PubMed Central Google Scholar
Shapson-Coe, A. et al. A petavoxel fragment of human cerebral cortex reconstructed at nanoscale resolution. Science 384, eadk4858 (2024).
Article CAS PubMed Google Scholar
Cabral, J., Fernandes, F. F. & Shemesh, N. Intrinsic macroscale oscillatory modes driving long range functional connectivity in female rat brains detected by ultrafast fMRI. Nat. Commun. 14, 375 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Oh, S. W. et al. A mesoscale connectome of the mouse brain. Nature 508, 207–214 (2014).
Article ADS CAS PubMed PubMed Central Google Scholar
Harris, J. A. et al. Hierarchical organization of cortical and thalamic connectivity. Nature 575, 195–202 (2019).
Article ADS CAS PubMed PubMed Central Google Scholar
Whitesell, J. D. et al. Regional, layer, and cell-type-specific connectivity of the mouse default mode network. Neuron 109, 545–559.e8 (2021).
Article CAS PubMed PubMed Central Google Scholar
Witvliet, D. et al. Connectomes across development reveal principles of brain maturation. Nature 596, 257–261 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Bertolero, M. A., Yeo, B. T. T. & D’Esposito, M. The modular and integrative functional architecture of the human brain. Proc. Natl Acad. Sci. Usa. 112, E6798–E6807 (2015).
Article ADS CAS PubMed PubMed Central Google Scholar
Benavidez, N. L. et al. Organization of the inputs and outputs of the mouse superior colliculus. Nat. Commun. 12, 4004 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Gouwens, N. W. et al. Integrated morphoelectric and transcriptomic classification of cortical GABAergic cells. Cell 183, 935–953.e19 (2020).
Article CAS PubMed PubMed Central Google Scholar
Kozareva, V. et al. A transcriptomic atlas of mouse cerebellar cortex comprehensively defines cell types. Nature 598, 214–219 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Ascoli, G. A., Huo, B.-X. & Mitra, P. P. Sizing up whole-brain neuronal tracing. Sci. Bull. 67, 883–884 (2022).
Article Google Scholar
Siletti, K. et al. Transcriptomic diversity of cell types across the adult human brain. Science 382, eadd7046 (2023).
Article CAS PubMed Google Scholar
Paxinos, G. & Franklin, K. B. J. Paxinos and Franklin’s The Mouse Brain in Stereotaxic Coordinates (Academic Press, an imprint of Elsevier, London, 2019).
Wan, Y. et al. BlastNeuron for automated comparison, retrieval and clustering of 3D neuron morphologies. Neuroinform 13, 487–499 (2015).
Article MathSciNet Google Scholar
Gao, L. et al. Single-neuron analysis of dendrites and axons reveals the network organization in mouse prefrontal cortex. Nat. Neurosci. 26, 1111–1126 (2023).
Article CAS PubMed Google Scholar
Gillette, T. A. & Ascoli, G. A. Topological characterization of neuronal arbor morphology via sequence representation: I - motif analysis. BMC Bioinforma. 16, 216 (2015).
Article Google Scholar
Lin, C., Huang, Y., Quan, T. & Zhang, Y. Modelling brain-wide neuronal morphology via rooted Cayley trees. Sci. Rep. 8, 15666 (2018).
Article ADS PubMed PubMed Central Google Scholar
Hallock, C. A. et al. Axonal bouton modeling, detection and distribution analysis for the study of neural circuit organization and plasticity. In 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro 165–168 (IEEE, Paris, France, 2008).
Gala, R. et al. Computer assisted detection of axonal bouton structural plasticity in in vivo time-lapse images. eLife 6, e29315 (2017).
Article PubMed PubMed Central Google Scholar
Xie, Q. et al. An automated pipeline for bouton, spine, and synapse detection of in vivo two-photon images. BioData Min. 10, 40 (2017).
Article PubMed PubMed Central Google Scholar
Micheva, K. D. & Smith, S. J. Array tomography: a new tool for imaging the molecular architecture and ultrastructure of neural circuits. Neuron 55, 25–36 (2007).
Article CAS PubMed PubMed Central Google Scholar
Kim, J. et al. mGRASP enables mapping mammalian synaptic connectivity with light microscopy. Nat. Methods 9, 96–102 (2012).
Article ADS CAS Google Scholar
Yao, Z. et al. A taxonomy of transcriptomic cell types across the isocortex and hippocampal formation. Cell 184, 3222–3241.e26 (2021).
Article CAS PubMed PubMed Central Google Scholar
Allen, W. E., Blosser, T. R., Sullivan, Z. A., Dulac, C. & Zhuang, X. Molecular and spatial signatures of mouse brain aging at single-cell resolution. Cell 186, 194–208.e18 (2023).
Article CAS PubMed Google Scholar
Markram, H. et al. Interneurons of the neocortical inhibitory system. Nat. Rev. Neurosci. 5, 793–807 (2004).
Article CAS PubMed Google Scholar
Jiang, X. et al. Principles of connectivity among morphologically defined cell types in adult neocortex. Science 350, aac9462 (2015).
Article PubMed PubMed Central Google Scholar
Jiang, S. et al. Petabyte-scale multi-morphometry of single neurons for whole brains. Neuroinform 20, 525–536 (2022).
Article Google Scholar
Bria, A., Iannello, G., Onofri, L. & Peng, H. TeraFly: real-time three-dimensional visualization and annotation of terabytes of multidimensional volumetric images. Nat. Methods 13, 192–194 (2016).
Article CAS PubMed Google Scholar
Peng, H., Ruan, Z., Long, F., Simpson, J. H. & Myers, E. W. V3D enables real-time 3D visualization and quantitative analysis of large-scale biological image data sets. Nat. Biotechnol. 28, 348–353 (2010).
Article CAS PubMed PubMed Central Google Scholar
Peng, H., Bria, A., Zhou, Z., Iannello, G. & Long, F. Extensible visualization and analysis for multidimensional images using Vaa3D. Nat. Protoc. 9, 193–208 (2014).
Article CAS PubMed Google Scholar
Liang, J. et al. Vaa3D-x for cross-platform teravoxel-scale immersive exploration of multidimensional image data. Bioinformatics 39, btac794 (2023).
Article CAS PubMed PubMed Central Google Scholar
Wang, Y. et al. TeraVR empowers precise reconstruction of complete 3-D neuronal morphology in the whole brain. Nat. Commun. 10, 3474 (2019).
Article ADS PubMed PubMed Central Google Scholar
Liang, H., Acton, S. T. & Weller, D. S. Content-aware neuron image enhancement. In 2017 IEEE International Conference on Image Processing (ICIP) 3510–3514 (IEEE, Beijing, 2017).
Xiao, H. & Peng, H. APP2: automatic tracing of 3D neuron morphology based on hierarchical pruning of a gray-weighted image distance-tree. Bioinformatics 29, 1448–1454 (2013).
Article CAS PubMed PubMed Central Google Scholar
Feng, L., Zhao, T. & Kim, J. neuTube 1.0: A new design for efficient neuron reconstruction software based on the SWC format. eNeuro 2, (2015).
Guo, S., Zhao, X., Jiang, S., Ding, L. & Peng, H. Image enhancement to leverage the 3D morphological reconstruction of single-cell neurons. Bioinformatics 38, 503–512 (2022).
Article CAS PubMed Google Scholar
Scorcioni, R., Polavaram, S. & Ascoli, G. A. L-Measure: a web-accessible tool for the analysis, comparison and search of digital reconstructions of neuronal morphologies. Nat. Protoc. 3, 866–876 (2008).
Article CAS PubMed PubMed Central Google Scholar
Peng, H., Ruan, Z., Atasoy, D. & Sternson, S. Automatic reconstruction of 3D neuron structures using a graph-augmented deformable model. Bioinformatics 26, i38–i46 (2010).
Article CAS PubMed PubMed Central Google Scholar
Cheng, S. et al. DeepBouton: automated identification of single-neuron axonal boutons at the brain-wide scale. Front. Neuroinform. 13, 25 (2019).
Article PubMed PubMed Central Google Scholar

Download references

Acknowledgements

We thank Yong Yao and NIH for coordination of the BICCN effort in data collection and synergized analysis, Brain Image Library (BIL, www.brainimagelibrary.org) for public sharing of the BICCN database, Josh Huang for sharing raw image data, Yuanyuan Song and Lulu Yin for assistance of the single-neuron annotation, Jiangshan Liang, Luchen Deng, Shize Chen, Fei Xing, Yihang Zhu, Lei Huang and Kaixiang Li for help in tool development, Xuan Zhao, Ye Zhong, Jingzhou Yuan, and another 7 anonymous users for help in soma-annotation, and Yiwei Li for assistance of optimizing soma locations. This work was mainly supported by a Southeast University (SEU) initiative of neuroscience and a New Cornerstone grant awarded to H.P.; The Southeast University team was also supported by a MOST (China) Brain Research Project, “Mammalian Whole Brain Mesoscopic Stereotaxic 3D Atlas” (2022ZD0205200 and 2022ZD0205204) awarded to L.L.; L.L. and Y.Liu were also supported by “the Fundamental Research Funds for the Central Universities of China” (No. 2242023K5005); G.A.A. was supported in part by NIH grants R01NS39600 and RF1MH128693. H.Z. was supported by BRAIN Initiative grant U19MH114830. P.M. was supported in part by the Crick-Clay Professorship (Cold Spring Harbor Laboratory) and BRAIN Initiative grant U19MH114821. Q.L. and H.G., were supported by STI2030-Major Projects Grant No. 2021ZD0201001, National Natural Science Foundation of China Grants No. 81827901. Research reported in this publication was also supported by the National Institute of Mental Health under Award Number R01MH131537 to S.D.R. and Z.W., U01MH114824 from National Institute of Mental Health to P.O. and Z.W., the Friedman Brain Institute under a Research Award by the Fascitelli Family to S.D.R. and Z.W., the Mindich Child Health and Development Institute under a pilot grant to S.D.R. and Z.W., and M.G.F. was also supported by the Beatrice and Samuel A. Seaver Foundation and the Fundacio Martin Escudero.

Author information

These authors contributed equally: Shengdian Jiang, Yingxin Li.

Authors and Affiliations

New Cornerstone Science Laboratory, SEU-ALLEN Joint Center, Institute for Brain and Intelligence, Southeast University, Nanjing, Jiangsu, China
Yufeng Liu, Shengdian Jiang, Yingxin Li, Sujun Zhao, Zhixi Yun, Zuo-Han Zhao, Lingli Zhang, Gaoyu Wang, Xin Chen, Linus Manubens-Gil, Yuning Hang, Qiaobo Gong, Penghao Qian, Lei Qu, Lijuan Liu & Hanchuan Peng
School of Computer Science and Engineering, Southeast University, Nanjing, Jiangsu, China
Shengdian Jiang & Zhixi Yun
School of Biological Science & Medical Engineering, Southeast University, Nanjing, Jiangsu, China
Yingxin Li, Sujun Zhao, Lingli Zhang & Lijuan Liu
Ministry of Education Key Laboratory of Intelligent Computation and Signal Processing, Information Materials and Intelligent Sensing Laboratory of Anhui Province, School of Electronics and Information Engineering, Anhui University, Hefei, Anhui, China
Yuanyuan Li & Lei Qu
Seaver Autism Center for Research and Treatment, Icahn School of Medicine at Mount Sinai, New York, NY, USA
Marta Garcia-Forn & Silvia De Rubeis
Department of Psychiatry, Icahn School of Medicine at Mount Sinai, New York, NY, USA
Marta Garcia-Forn, Wei Wang & Silvia De Rubeis
The Mindich Child Health and Development Institute, Icahn School of Medicine at Mount Sinai, New York, NY, USA
Marta Garcia-Forn, Wei Wang & Silvia De Rubeis
Friedman Brain Institute, Icahn School of Medicine at Mount Sinai, New York, NY, USA
Marta Garcia-Forn & Silvia De Rubeis
Alper Center for Neural Development and Regeneration, Icahn School of Medicine at Mount Sinai, New York, NY, USA
Marta Garcia-Forn & Silvia De Rubeis
Appel Alzheimer’s Disease Research Institute, Feil Family Brain and Mind Research Institute, Weill Cornell Medicine, New York, NY, USA
Zhuhao Wu
Department of Cell, Developmental & Regenerative Biology, Icahn School of Medicine at Mount Sinai, New York, NY, USA
Zhuhao Wu
Department of Neuroscience, Icahn School of Medicine at Mount Sinai, New York, NY, USA
Zhuhao Wu
Cold Spring Harbor Laboratory, Cold Spring Harbor, NY, USA
Pavel Osten & Partha Mitra
HUST-Suzhou Institute for Brainsmatics, JITRI, Suzhou, China
Hui Gong
Allen Institute for Brain Science, Seattle, WA, USA
Michael Hawrylycz & Hongkui Zeng
Center for Integrative Connectomics, Department of Neurobiology, David Geffen School of Medicine at UCLA, Los Angeles, CA, USA
Hongwei Dong
State Key Laboratory of Digital Medical Engineering, School of Biomedical Engineering, Hainan University, Haikou, China
Qingming Luo
Key Laboratory of Biomedical Engineering of Hainan Province, One Health Institute, Hainan University, Haikou, China
Qingming Luo
Volgenau School of Engineering, George Mason University, Fairfax, VA, USA
Giorgio A. Ascoli

Authors

Yufeng Liu
View author publications
Search author on:PubMed Google Scholar
Shengdian Jiang
View author publications
Search author on:PubMed Google Scholar
Yingxin Li
View author publications
Search author on:PubMed Google Scholar
Sujun Zhao
View author publications
Search author on:PubMed Google Scholar
Zhixi Yun
View author publications
Search author on:PubMed Google Scholar
Zuo-Han Zhao
View author publications
Search author on:PubMed Google Scholar
Lingli Zhang
View author publications
Search author on:PubMed Google Scholar
Gaoyu Wang
View author publications
Search author on:PubMed Google Scholar
Xin Chen
View author publications
Search author on:PubMed Google Scholar
Linus Manubens-Gil
View author publications
Search author on:PubMed Google Scholar
Yuning Hang
View author publications
Search author on:PubMed Google Scholar
Qiaobo Gong
View author publications
Search author on:PubMed Google Scholar
Yuanyuan Li
View author publications
Search author on:PubMed Google Scholar
Penghao Qian
View author publications
Search author on:PubMed Google Scholar
Lei Qu
View author publications
Search author on:PubMed Google Scholar
Marta Garcia-Forn
View author publications
Search author on:PubMed Google Scholar
Wei Wang
View author publications
Search author on:PubMed Google Scholar
Silvia De Rubeis
View author publications
Search author on:PubMed Google Scholar
Zhuhao Wu
View author publications
Search author on:PubMed Google Scholar
Pavel Osten
View author publications
Search author on:PubMed Google Scholar
Hui Gong
View author publications
Search author on:PubMed Google Scholar
Michael Hawrylycz
View author publications
Search author on:PubMed Google Scholar
Partha Mitra
View author publications
Search author on:PubMed Google Scholar
Hongwei Dong
View author publications
Search author on:PubMed Google Scholar
Qingming Luo
View author publications
Search author on:PubMed Google Scholar
Giorgio A. Ascoli
View author publications
Search author on:PubMed Google Scholar
Hongkui Zeng
View author publications
Search author on:PubMed Google Scholar
Lijuan Liu
View author publications
Search author on:PubMed Google Scholar
Hanchuan Peng
View author publications
Search author on:PubMed Google Scholar

Contributions

H.P. conceptualized and managed this study. H.Z., P.O., H.D., Z.W., and S.D.R. provided brain images. M.G.F. prepared several viral labeled brains and W.W. processed the samples and did the LSFM imaging for several brains supplied by Z.W. and S.D.R. S.J. collected and preprocessed brain images. L.L. and X.C. led the single-neuron annotation. L.Z. and Y.H. led the development of tools for soma annotation and neuron reconstruction. S.J. developed the tools for data management, co-developed the skeleton refinement, and detected varicosities. Y.Liu and Z.Z. implemented neurite segmentation. Z.Z. and G.W. reconstructed the local dendrite morphologies. Y.Liu coordinated data analysis and conducted analysis on microenvironments, projection patterns, and cross-scale features, and implemented algorithms for neurite segmentation and arbor feature extraction. S.J. conducted analysis on full morphology and varicosities. Y.Li performed analysis on regional modularization and multi-morphometry visualization. S.Z. and Y.Liu analyzed neuron arbors. Z.Y. conducted the image registration and morphometry mapping to CCF. Yuanyuan L. and L.Q. evaluated the registration robustness. P.Q. assisted with the validation of varicosity detection. Y.Liu and Q.G. reviewed and refactored the source codes. H.G. and Q.L. produced fMOST imaging. H.P. and Y.Liu wrote the manuscript with assistance of all authors, including L.M.G, G.A.A., P.M., M.H., Z.W., S.D.R., who reviewed and revised the manuscript. These authors contributed equally: S.Z., Z.Y., Z.Z.

Corresponding authors

Correspondence to Lijuan Liu or Hanchuan Peng.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Minmin Luo and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Files

Supplementary Data 1

Supplementary Data 2

Supplementary Data 3

Supplementary Data 4

Supplementary Data 5

Supplementary Data 6

Supplementary Data 7

Supplementary Data 8

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this article

Cite this article

Liu, Y., Jiang, S., Li, Y. et al. Neuronal diversity and stereotypy at multiple scales through whole brain morphometry. Nat Commun 15, 10269 (2024). https://doi.org/10.1038/s41467-024-54745-6

Download citation

Received: 11 June 2024
Accepted: 18 November 2024
Published: 26 November 2024
DOI: https://doi.org/10.1038/s41467-024-54745-6

This article is cited by

A Multi-Scale Neuron Morphometry Dataset from Peta-voxel Mouse Whole-Brain Images
- Shengdian Jiang
- Sujun Zhao
- Hanchuan Peng
Scientific Data (2025)
NeuroXiv: AI-powered open databasing and dynamic mining of brain-wide neuron morphometry
- Shengdian Jiang
- Lijun Wang
- Hanchuan Peng
Nature Methods (2025)
Reconstruction of a connectome of single neurons in mouse brains by cross-validating multi-scale multi-modality data
- Feng Xiong
- Lijuan Liu
- Hanchuan Peng
Nature Methods (2025)