Dendritic excitations govern back-propagation via a spike-rate accelerometer

Park, Pojeong; Wong-Campos, J. David; Itkis, Daniel G.; Lee, Byung Hun; Qi, Yitong; Davis, Hunter C.; Antin, Benjamin; Pasarkar, Amol; Grimm, Jonathan B.; Plutkis, Sarah E.; Holland, Katie L.; Paninski, Liam; Lavis, Luke D.; Cohen, Adam E.

doi:10.1038/s41467-025-55819-9

Download PDF

Article
Open access
Published: 04 February 2025

Dendritic excitations govern back-propagation via a spike-rate accelerometer

Pojeong Park ORCID: orcid.org/0000-0002-5574-6104¹^na1^nAff5,
J. David Wong-Campos¹^na1,
Daniel G. Itkis¹,
Byung Hun Lee¹,
Yitong Qi¹,
Hunter C. Davis¹,
Benjamin Antin²,
Amol Pasarkar²,
Jonathan B. Grimm ORCID: orcid.org/0000-0003-0331-4200³,
Sarah E. Plutkis ORCID: orcid.org/0009-0003-1822-0466³,
Katie L. Holland³,
Liam Paninski²,
Luke D. Lavis³ &
…
Adam E. Cohen ORCID: orcid.org/0000-0002-8699-2404^1,4

Nature Communications volume 16, Article number: 1333 (2025) Cite this article

8943 Accesses
9 Citations
2 Altmetric
Metrics details

Subjects

Abstract

Dendrites on neurons support electrical excitations, but the computational significance of these events is not well understood. We developed molecular, optical, and computational tools for all-optical electrophysiology in dendrites. We mapped sub-millisecond voltage dynamics throughout the dendritic trees of CA1 pyramidal neurons under diverse optogenetic and synaptic stimulus patterns, in acute brain slices. Our data show history-dependent spike back-propagation in distal dendrites, driven by locally generated Na⁺ spikes (dSpikes). Dendritic depolarization created a transient window for dSpike propagation, opened by A-type K_V channel inactivation, and closed by slow Na_V inactivation. Collisions of dSpikes with synaptic inputs triggered calcium channel and N-methyl-D-aspartate receptor (NMDAR)-dependent dendritic plateau potentials and accompanying complex spikes at the soma. This hierarchical ion channel network acts as a spike-rate accelerometer, providing an intuitive picture connecting dendritic biophysics to associative plasticity rules.

An astrocytic signaling loop for frequency-dependent control of dendritic integration and spatial learning

Article Open access 24 December 2022

Dendritic excitability controls overdispersion

Article 27 December 2023

Neuromorphic dendritic network computation with silent synapses for visual motion perception

Article 06 June 2024

Introduction

Dendrites exhibit many nonlinearities and distinct regenerative excitations, such as sodium^1,2, calcium^3,4, and NMDA spikes. While these events have been characterized in detail by patch clamp studies^{5,6,7,8,9,10,11,12}, their functional significance remains unclear^6,13,14. A key challenge in studying dendritic excitability is that the spatial structures of dendritic excitations are not well characterized. Patch clamp measurements can probe dendritic voltages at most at a few discrete points^15,16, and voltage imaging measurements have only probed the voltage in at most a few dendritic branches^17,18,19,20. Thus it is not known how broadly shared dendritic excitations are across the dendritic tree, to what extent these excitations show branch-specific dynamics, or how the footprint of an excitation depends on the spatial structure of the synaptic inputs. To understand information flow and processing in dendrites, one would like to inject signals in arbitrary patterns of space and time and to record the resulting global voltage dynamics.

Here we introduce molecular, optical, and computational tools for large-area, high-speed, voltage imaging and targeted optogenetic stimulation in dendritic trees. We apply these tools to study CA1 pyramidal neurons in acute brain slices. Our measurements reproduce many of the classic results in CA1 pyramidal cell dendritic biophysics, including history-dependent back-propagation modulated by dendritic sodium and potassium channels^{21,22,23,24,25,26,27,28}, and initiation of NMDA spikes by collision of distal synaptic inputs with back-propagating action potentials (bAPs)^{9,29,30,31,32}.

Our measurements reveal the spatial structures of dendritic excitations. By mapping the spatial footprints of these events under a wide range of optogenetic, synaptic, and pharmacological conditions, we construct a holistic picture of how the different excitations interact. Under conditions where integration is dominated by passive cable properties, back-propagation is still strongly modulated by dendritic excitations. Specifically, bAPs successively inactivate A-type potassium channels, then activate dendritic sodium channels, calcium channels, and, in the presence of synaptic inputs, NMDA receptors. The net effect is that conjunction of distal synaptic inputs with an acceleration in the somatic spike rate (e.g. a period of silence followed by a pair or trio of closely spaced somatic spikes) leads to dendritic plateau potentials. Sustained high-frequency somatic spiking, however, drives dendritic sodium channel inactivation, and suppresses initiation of NMDA spikes.

The molecular, optical, and computational tools developed here open a door to mapping biophysical properties of dendrites across cell types, brain regions, and developmental stages, in models of health and disease.

Results

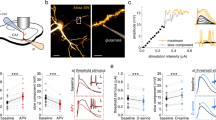
We probed dendritic excitability by combining targeted optogenetic stimulation and high-speed structured illumination voltage imaging (Fig. 1). We modified a blue-shifted channelrhodopsin, CheRiff ³³, and a chemigenetic voltage indicator, Voltron2³⁴, to improve dendritic expression by attaching an N-terminal Lucy-Rho tag³⁵ and C-terminal ER export and TS trafficking motifs^36,37. We expressed both constructs from a bicistronic vector at very low density in mouse hippocampal CA1 pyramidal neurons, prepared acute brain slices, and stained with a red-shifted HaloTag ligand dye, JFX₆₀₈ (Methods). We designate this Voltron-based tool for all-optical dendritic electrophysiology, Optopatch-V.

**Fig. 1: Mapping dendritic voltages with all-optical electrophysiology.**

Using patch clamp recordings, we verified that Optopatch-V did not perturb neuronal resting properties or excitability, in comparison to neighboring non-expressing neurons (Fig. S1). We then performed simultaneous patch clamp and fluorescence recordings and validated that the recordings measured voltage changes with sub-millisecond kinetics, ~1 mV precision, sensitivity of ~12% ΔF/F per 100 mV, and perfect spike-detection fidelity over thousands of spikes at spike rates up to the maximum tested, 100 Hz (Figs. S2, S14).

The blue light used for optogenetic stimulation also excited fluorescence of the eYFP expression tag in CheRiff-eYFP. Thus the spatial pattern of eYFP fluorescence was a direct measure of the strength of optogenetic drive of CheRiff (Fig. S3, Methods). We tested the specificity of the patterned 1-photon optogenetic stimulation by comparing evoked responses for stimuli targeted directly to an in-focus dendrite vs. the same stimuli laterally offset by differing amounts (Fig. S4). Dendritic optogenetic stimuli could be localized within a ~30 μm region.

Finally, we quantified how well the structured illumination voltage imaging rejected out-of-focus signals. Maps of -ΔF_spike, the voltage-induced action potential amplitude, clearly showed the structure of the in-focus components of the dendritic tree, confirming that voltage signals from in-focus dendrites were readily distinguishable from out-of-focus background and light scatter (Fig. S5).

After functional recordings, we made high-resolution, three-dimensional structural images via 2-photon (2 P) microscopy. We mapped the functional recordings onto the independently measured cell morphology via a fit to a forward model of the microscope blurring function (Methods, Fig. S6). We further used PCA-based denoising similar to Ref. ³⁸ (Methods, Fig. S7) to reduce the effect of pixel-wise shot noise. Together, these techniques produced simultaneously high spatial and temporal resolution two-dimensional (Supplementary Movie 1, Fig. 1c–e) and three-dimensional (Supplementary Movie 2) voltage maps which accounted for > 93% of the variance in the raw data, confirming that the procedure captured most of the underlying dynamics. We then applied the Sub-Nyquist action potential timing (SNAPT)³³ technique to map bAP wavefront motion with 25 μs time resolution (Supplementary Movie 3, Fig. 1f, Methods). While the above image-processing steps were helpful for visualizing the voltage response maps, the biophysical analyses below were performed on the raw fluorescence to ensure fidelity to the underlying dynamics.

Distal dendritic depolarization favors dendritic spikes (dSpikes)

In well-isolated neurons expressing Optopatch-V, we optogenetically stimulated a small cluster of proximal oblique dendrites (20 ms duration, 5 Hz, 54 repeats) and mapped the bioelectrical responses (Fig. 2). Each stimulus evoked two spikes at the soma, and dichotomous responses in the distal apical dendrites: in most trials the dendrites showed a low-pass filtered and strongly attenuated copy of the somatic activity; but in some cases (8 of 54 trials), the dendrites produced a single rapid spike (Fig. 2a). A histogram of event amplitudes in the soma and dendrites showed a unimodal distribution at the soma and a clearly bimodal distribution in the distal dendrites (Fig. 2b). A histogram of event times showed that in this experiment the dendritic excitations always emerged from the second somatic spike, never the first (Fig. 2c). We refer to these dendritic excitations as dSpikes.

**Fig. 2: Spatial and temporal maps of dendritic spikes (dSpikes).**

We then examined the spatial structures of the neuronal voltages in detail. The eYFP fluorescence in CheRiff-eYFP showed the stimulus profile (Fig. 2d). We calculated a stimulus-triggered average of the subthreshold depolarization prior to the onset of the first somatic spike. This voltage had greatest amplitude in the directly stimulated dendrites, and decayed smoothly away from the stimulus region (Fig. 2d), suggestive of passive dendritic integration.

We then divided the trials into those that did or did not evoke a dSpike. To map event amplitudes, we calculated the spike-triggered average of the peak depolarization. In the -dSpike trials the bAP was primarily confined to the soma and proximal apical and basal dendrites (Fig. 2e). In the +dSpike trials, the depolarization was amplified in the distal dendrites (Fig. 2f).

To study the spatiotemporal structure of the voltage dynamics, we plotted a kymograph of the voltage along the main apical trunk (i.e., a heatmap of voltage with one space axis and one time axis; space axis shown by red line in Fig. 2d). The kymograph showed that upon stimulus onset, the depolarization rose first where the stimulated dendrites joined the trunk (Fig. 2g). This subthreshold depolarization propagated diffusively along the trunk in both the apical and basal directions. When the subthreshold depolarization reached the soma, it triggered a spike (we did not resolve the axon so we could not determine the precise initiation zone). The kymograph showed the finite velocity of spike back-propagation into the dendrites. Plots of the peak spike amplitude along the apical trunk showed exponential decay of the -dSpike events (length constant 255 ± 10 μm, mean ± s.e.m., n = 93 spikes) and distal amplification of the +dSpike events (Fig. 2h), very similar to theoretical predictions²⁴.

We then repeated these experiments and analyses with optogenetic stimuli delivered either to one of several dendritic branches (Fig. 3a, S8–11), the soma (Fig. 3b), or the soma and a distal dendrite simultaneously (Fig. 3c). Experiments were repeated in n = 17 neurons from 15 animals. We noted several consistent features of the dendritic voltage responses:

**Fig. 3: Distal dendritic depolarization favors dendritic spikes (dSpikes).**

First, the subthreshold voltage profile moved with the stimulus location and decayed smoothly outside the stimulated zone (Fig. 3d–f, S10–11). We only observed diffusive-like propagation of the subthreshold voltages, never dSpikes that initiated in the dendrites. Some prior dendritic patch clamp studies reported that strong current injection (e.g., 2 nA for 5 ms) triggered local dendritic sodium spikes¹, while others did not observe these events^21,39. Highly synchronous and spatially clustered synaptic inputs have also been reported to evoke local dSpikes in radial oblique dendrites⁴⁰ and the apical trunk and tuft⁴¹ of CA1 pyramidal cells, though more gradual depolarization via asynchronous inputs did not evoke localized dSpikes. Based on the cumulative eYFP fluorescence evoked by our dendrite-targeted optogenetic stimulation, we estimate dendritic CheRiff currents of ~130 pA, much smaller than the injected currents previously reported to trigger local sodium spikes. We performed numerical simulations of a conductance-based CA1 model (details below) and found that the absence of dendrite-initiated dSpikes in our experiments was likely due to the more gradual, weaker, and spatially distributed nature of optogenetic vs. patch clamp stimuli (Fig. S20a, b). Dendritic integration under our conditions appeared to be dominated by passive cable properties.

Second, the neurons produced precisely two kinds of excitations: perisomatic bAPs and bAP-driven distal dSpikes—and, surprisingly, neither spatial profile depended on the location of the driving stimulus. All spikes had similar waveforms at the soma, and then either decayed exponentially along the apical trunk or were amplified distally (Fig. S9), leading to a bimodal distribution of amplitudes in distal apical dendrites (Fig. S10). bAPs reliably engaged all perisomatic and proximal dendrites and failed along the distal trunk, while dSpikes reliably engaged distal apical dendrites too (Fig. S11). Neither bAPs nor dSpikes showed a preference for (or exclusion from) the stimulated dendritic branch. The amplitude of dSpikes relative to the first bAP (i.e., ∆F_max/∆F₁) was maximum in the distal dendritic trunk (313 ± 41 µm from the soma, mean ± s.d., n = 22 stimulated regions (soma or proximal branch), 17 neurons, 15 animals; Fig. 3g, h). Mean propagation velocity of bAPs along the apical trunk was 141 ± 30 µm/ms (mean ± s.d., n = 17 neurons, 15 animals; Fig. S12). Propagation speeds were slightly faster in the apical trunk than in distal branches (Fig. S12), but we did not quantify this effect because the timescales were at the edge of our 1 ms time resolution. We did not observe differences in conduction speed between dendritic branches.

Third, the probability that a bAP became a dSpike depended on the stimulus location and spike timing. Proximal stimuli ( < 200 μm from the soma) almost never evoked dSpikes on the first bAP, but sometimes evoked dSpikes on the second or third bAP (Figs. 2c, 3e, f, S8). In contrast, distal stimuli ( > 250 μm from the soma) reliably evoked dSpikes on the first bAP (Fig. 3d). Pooled data from 35 branch stimulations (n = 13 cells from 11 animals) revealed that the probability of evoking a dSpike with the first bAP followed a sigmoidal distance dependence, with a plateau of ~80% success rate for stimuli > 300 µm from the soma (Fig. 3i).

These seemingly complex dSpike dynamics could be described with a simple rule. dSpikes arose if and only if the distal dendrites had been depolarized for at least 15 ms prior to arrival of a bAP. Distal stimuli took approximately 15 ms to depolarize the soma enough to elicit a spike. As a result, stimulation at a distal dendrite (D2) usually produced dSpikes on the first bAP (Fig. 3d). In contrast, stimuli at the soma or proximal dendrites evoked rapid somatic spikes before the distal dendrites were depolarized. These bAPs incrementally depolarized the distal dendrites, opening a window for dSpikes triggered by subsequent bAPs.

This rule is illustrated by comparing Fig. 3d–f. Stimulation of the soma alone never evoked dSpikes on the first two bAPs, and occasionally evoked a dSpike on the third bAP (6 of 54 trials), which came 13 – 17 ms after stimulus onset (Fig. 3e). Stimulation of distal dendrite D2 alone evoked dSpikes on the first bAP, with 65% probability (35 of 54 trials, Fig. 3d). These bAPs came 14 – 21 ms after stimulus onset. Simultaneous stimulation at soma and D2 produced two quick bAPs which failed to evoke dSpikes, and then the third bAP (12 – 17 ms after stimulus onset) triggered a dSpike with 100% probability (54 of 54 trials, Fig. 3f).

Prior work in cortical neurons had suggested that evoking apical dendritic spikes required either a somatic spike rate above a critical frequency^42,43 or pairing of individual somatic spikes with synaptically evoked distal depolarization³. Our results show that in CA1 pyramidal cells the somatic spike rate is not the key variable, but rather the dendritic depolarization. An isolated bAP (which does not have a frequency) can become a dSpike if the distal dendrites are pre-depolarized. Consistent with this notion, under a gradual optogenetic ramp stimulus delivered to the soma or proximal dendrites ( < 150 µm from the soma), the subthreshold depolarization permeated the dendritic tree before the first spike. For this stimulus waveform, the first somatic spike almost always evoked a dSpike (92%, 188 ramps, 56 cells, 44 animals; Fig. S13). As the stimulus amplitude further increased, bAP amplitude in the distal dendrites then decreased, sometimes gradually and sometimes abruptly, a phenomenon previously attributed to dendritic sodium channel inactivation²¹.

Dendritic spike-rate accelerometer, period-doubling, and stochastic back-propagation

Step-wise optogenetic stimuli to the soma or proximal dendrites ( > 200 ms duration) evoked sustained spiking at the soma and a biphasic pattern of bAP propagation. For example, a step stimulus to a proximal apical dendrite evoked a bAP without a dSpike, then two bAPs with dSpikes, then a series of bAPs without dSpikes (Fig. 4a). Pooled data (n = 43 stimulated branches, 16 cells, 13 animals) showed that upon onset of step-wise optogenetic stimulation, dSpikes failed for the first 18 ± 7 ms (mean ± s.d.), then there was a period where dSpikes succeeded which lasted until 83 ± 47 ms after stimulus onset, followed by subsequent dSpike failures (Fig. 4b). Sustained spiking at the soma led to very few dSpikes later than 100 ms after stimulus onset, regardless of stimulus strength or location. The net effect of this window for dSpike formation was that the dendrites acted as a spike-rate accelerometer: a step-wise increase in the spike rate at the soma led to a transient increase in the dSpike rate in the distal apical dendrites.

**Fig. 4: Dendritic excitations implement a spike-rate accelerometer.**

We observed a similar accelerometer-like pattern in bAP propagation when using patch clamp injection of current pulses at the soma. At low frequencies (e.g., 3 Hz), membrane depolarization did not accumulate sufficiently to trigger dSpikes; instead, we observed a progressive attenuation of bAP amplitudes in the distal dendrites, consistent with the slow Na_V inactivation as previously reported (Fig. S14d)^21,26,28. At frequencies ≥ 80 Hz, however, we observed a characteristic motif of bAP failure, then a series of dSpikes, and then failures again (Fig. S14), similar to previous reports in L5 pyramidal cells⁴². The fluorescence and patch clamp recordings at the soma showed excellent correspondence (Fig. S14b, c), further confirming the validity of our voltage imaging data.

We then used a wide-field optogenetic stimulus to test whether stronger depolarization could extend the dSpike time-window. To our surprise, this stimulus reliably evoked a period-doubling bifurcation: bAPs alternately succeeded and failed to evoke dSpikes (n = 9 cells from 9 animals, Fig. 4c, d). The dSpike window persisted to ~180 ms after stimulus onset, but, despite the stronger stimulus, all bAPs after ~180 ms failed to evoke dSpikes (Fig. 4e). Even stronger stimuli evoked an epoch of seemingly random interplay of bAPs and dSpikes (Fig. S15), followed by sustained dSpike failures. The random dynamics appeared similar to previously reported stochastic backpropagation in L5 cortical pyramidal cells¹⁷, and were reminiscent of the transition from alternans to arrhythmia in overdriven heart tissue⁴⁴, and also to the onset of chaos in linear chains of excitable HEK cells⁴⁵.

We used pharmacology and numerical simulations to study the biophysical origins of the dendritic spike-rate accelerometer function and of the period-doubling bifurcation. Motivated by prior studies of dendritic excitability^22,46, we hypothesized that opening of the dSpike window was driven by inactivation of A-type K_V channels. These transient K⁺ channels are expressed at a ~ 6-fold higher level in distal dendrites than in soma²². Subthreshold depolarization closes these channels with a voltage-dependent time constant between 6 ms (at -25 mV) and 27 ms (at +55 mV)²².

To test the involvement of A-type K_V channels, we applied the potassium channel blockers, 4-AP (5 mM) or BaCl₂ (150 µM), and applied brief optogenetic stimuli at the soma (20–30 ms duration, 5 Hz, 59 repeats). Both blockers significantly increased dSpike probability compared to the baseline (BaCl₂: 11 ± 2% before to 64 ± 10% after, mean ± s.e.m., n = 9 cells from 6 animals, p < 0.001, paired t-test; 4-AP: 19 ± 4% before to 92 ± 4% after, mean ± s.e.m., n = 4 cells from 3 animals, p < 0.001, paired t-test; Fig. S16). These results are consistent with previous literature suggesting that A-type K_V channel inactivation opens the dendritic spike window in distal dendrites^22,47.

We hypothesized that the dSpikes were primarily driven by fast Na⁺ currents. To test the involvement of Na_V channels, we applied the Na_V channel blocker TTX at very low concentration (20 nM), which has been shown not to interfere with synaptic transmission⁴⁸. We stimulated a relatively large area to increase the baseline dSpike probability ( ~ 100 µm diameter across the soma and proximal dendrites, 20 ms duration, 5 Hz, 59-118 repeats). This low TTX dose did not affect spiking at the soma, but the mean dSpike probability was significantly decreased (control: 44 ± 15%, TTX: 11 ± 8%, mean ± s.e.m., n = 4 cells from 3 animals, p = 0.008, paired t-test; Fig. S17a–d). In some experiments, a higher concentration of TTX (100 nM) eliminated all dSpikes at distal dendrites, while preserving somatic spiking (Fig. S17e).

We further tested the role of VGCC-dependent Ca²⁺ currents in mediating the dSpikes. The dSpikes were not affected by addition of the Ca_V blocker Ni²⁺ (100-500 µM; Fig. S18a–e), suggesting that they are not mediated by VGCCs. Under strong optogenetic drive, dSpikes occasionally triggered broader ( > 20 ms duration) dendritic spikes which we hypothesized were Ca²⁺ spikes (Fig. S18f). Addition of Ni²⁺ (500 μM) eliminated these broad spikes, confirming their dependence on VGCC activation. Addition of K_V blocker Ba²⁺ (150 µM) to otherwise untreated neurons increased the prevalence of putative Ca²⁺ spikes, and subsequent addition of Ni²⁺ (500 µM) eliminated these events while preserving dendritic Na⁺ spikes (Fig. S18g, h). Together, these results imply that dendritic Na⁺ spikes could trigger dendritic Ca²⁺ spikes, and that dendritic potassium channels typically supressed Ca²⁺ spikes.

These data confirmed that dSpikes were primarily mediated by Na⁺ currents, and suggested that the closing of the dSpike window was driven by dendritic Na_V channel slow inactivation²¹. Dendritic Na_V slow inactivation time constants have been reported to range from 216 ms at 10 Hz spike rate to 58 ms at 50 Hz²⁷, broadly consistent with our measurement of a 100–180 ms dSpike window (Fig. 4b, e).

We simulated a multi-compartment conductance-based model of a CA1 pyramidal neuron, using biophysically realistic ion channels, modified from Ref. ⁴⁹ (Methods, Fig. S19, Supplementary Software 1). To reproduce our data, we added a slow inactivation gate to the dendritic Na_V channels; and we adjusted the spatial distributions of dendritic A-type and Na_V channels. After tuning the model, a simulated step-wise optogenetic stimulation at the soma led to a dSpike motif of failure, success, success, failures (Fig. 4f), which closely matched our observations of a dendritic spike-rate accelerometer (Fig. 4a). Simulated wide-field optogenetic stimulation with the same model parameters evoked a period-doubling bifurcation with alternating dSpike successes and failures, followed by repeated failures (Fig. 4g), matching our observations with wide-field stimulation (Fig. 4c). We conclude that the numerical model accurately captured the dynamics of a CA1 pyramidal dendritic tree.

The simulations reported the contributions of each channel type to the dynamics, confirming that the dSpike window was plausibly opened by A-type K_V inactivation and closed by slow Na_V inactivation. Together, these two channels converted a step-wise increase in spike rate at the soma into a transient burst of dSpikes, i.e. implementing a spike-rate accelerometer. The simulations also explained the period-doubling: Under simultaneous distal and proximal stimulation, the absolute refractory period of the distal dendrites slightly exceeded the refractory period of the soma. Consequently, after a successful dSpike, the dendrites were still recovering when the next bAP arrived.

To characterize the robustness of the simulations, we systematically varied the dendritic Na_V density, amount of Na_V slow inactivation, A-type K_V density, and stimulus strength. While the precise number of bAP failures and bAP-evoked dSpikes depended on these parameters (consistent with the variable number of dSpikes in our experiments), the spike-rate accelerometer motif of bAP failure, dSpikes, and then failure persisted over a wide range of parameters (Fig. S20). This robustness highlights the biological plausibility of the mechanisms identified in our simulations.

Motivated by the parsimonious explanation of the seemingly complex dendritic phenomenology, we also developed a coarse-grained two-compartment Izhikevich-type model (Supplementary Software 2) which also captured the opening and closing of the dSpike window (i.e. spike-rate accelerometer) and the period-doubling under simultaneous distal and proximal stimulation (Fig. S21). Such a model may be useful for computationally efficient large-scale simulations of neural dynamics with semi-realistic dendrites.

Plateau potentials are evoked by collision of synaptic inputs and dSpikes

The experiments with patterned optogenetic stimulation raised a perplexing question: Since bAP and dSpike spatial footprints were each largely insensitive to the stimulus location, then where is the eligibility trace which determines the specific synapses to potentiate during long-term potentiation? Our voltage imaging experiments ruled out membrane voltage as a primary carrier of the eligibility trace.

Optogenetic stimulation provides a pure depolarization to the dendrites, bypassing the ligand-gated channels which are engaged during synaptic transmission. In particular, NMDA receptors show voltage-dependent gating only if first bound to glutamate⁵⁰. To determine how glutamatergic inputs affected dendritic electrophysiology, we performed experiments combining synaptic stimulation, optogenetic stimulation, and dendritic voltage imaging.

We used electric field stimulation (EFS; 0.1 ms, single pulses, 10–40 V) to activate presynaptic axon terminals in the temporoammonic pathway that synapses onto the distal apical dendrites. We sequentially applied optogenetic stimulation to the soma alone (30 ms), EFS alone, or EFS and optogenetic stimulation. As before, the optogenetic stimulation alone evoked bAPs. EFS alone evoked a distal depolarization which propagated diffusively toward the soma. Remarkably, combining optogenetic and electrical stimuli evoked a long-lasting ( ~ 120 ms) plateau potential in the dendrites and a burst of spikes on top of a strong subthreshold depolarization at the soma, resembling a complex spike (Fig. 5a). Similar dynamics have been observed in vivo, wherein conjunction of basal inputs from CA3 and apical inputs from entorhinal cortex induced dendritic plateau potentials and somatic complex spikes^51,52,53. This behavior was qualitatively different from the combined soma + distal dendrite optogenetic stimulation (Fig. 3c, f), pointing to a critical role of glutamate-gated channels in the process. Fig. S23 shows a gallery of kymographs of responses to optogenetic, EFS, and combined stimulation in n = 9 neurons (7 animals).

**Fig. 5: Collision of synaptic inputs and bAP-induced dSpikes triggers plateau potentials.**

We compared the area under the curve (AUC) for the waveforms at distal dendrites ( > 200 µm from the soma) induced by optical, electrical, and combined stimulation. The average AUC_combined was 3.1 ± 0.7-fold greater than AUC_optical + AUC_electrical (mean ± s.e.m.) and for more than half of the cells studied (15 of 28 cells from 12 animals), AUC_combined was more than twice AUC_optical + AUC_electrical (Fig. 5b). We characterized in detail the response properties of the cells that showed > 200% nonlinearity. The nonlinear amplification was greatest when the optical and electrical stimuli overlapped in time (n = 8 cells from 7 animals; Fig. 5c, d, S22). The amplification was an asymmetric function of the time offset: For ‘EFS before bAPs’, the amplification followed a sigmoidal profile, decaying by half in 87 ms. For ‘EFS after bAPs’, the amplification decayed exponentially with a time constant of 35 ms. These findings are consistent with prior results showing that when presynaptic inputs are paired with postsynaptic bursts, hippocampal LTP can occur for either relative timing of pre- and post-synaptic activity^31,52.

We then tested how the number of optogenetically evoked bAPs affected the nonlinear amplification. Triggering a single bAP by a 10 ms optogenetic stimulus targeted to the soma did not evoke a nonlinear dendritic response, regardless of timing relative to the EFS (n = 5 cells from 4 animals; Fig. 5c, d). We conclude that at least one bAP-evoked sodium dSpike was necessary to create a plateau potential.

In our model, Na_V-mediated dSpikes are a necessary trigger for plateau potentials. This model makes a counterintuitive prediction: if there is a sustained train of somatic spikes, and a distal synaptic input arrives after the dSpike window has closed ( > 180 ms after spike-train onset), then this synaptic input will not be able to trigger a plateau potential despite coincidence with somatic spikes. We tested this prediction by stimulating the soma with gradual (3 s) optogenetic stimulus ramps, and delivering EFS at the beginning (0.5 s after ramp start) and end (2.5 s after ramp start) of the ramps (Fig. 5e). The early EFS reliably evoked plateau potentials (AUC 5.6 ± 3.6, mean ± s.d.), whereas the late EFS, which occurred when the average spike rate was 24 ± 4 Hz (mean ± s.d.), did not (AUC 1.6 ± 1.0, mean ± s.d., n = 7 cells from 5 animals, p = 0.01, paired t-test, Fig. 5f). These experiments illustrate the important contribution of the dendritic spike-rate accelerometer to formation of plateau potentials: coincidence of distal synaptic inputs with somatic spikes alone was not sufficient to induce a plateau potential; rather, distal synaptic inputs had to coincide with onset of rapid somatic spiking.

As a control experiment, we delivered a weak 3 s optogenetic step stimulus to the soma, too small to drive dendritic Na_V inactivation on its own (Fig. 5g). In this case EFS at 0.5 s and at 2.5 s were equally effective at inducing plateau potentials (0.5 s: AUC 4.5 ± 2.0, mean ± s.d., 2.5 s: AUC 4.0 ± 2.0, mean ± s.d., p = 0.19, n = 7 cells from 5 animals, paired t-test; Fig. 5h).

We applied channel blockers to investigate the molecular mechanisms underlying dendritic plateau potentials. Block of NMDARs by D-AP5 (50 µM) reduced the plateau area to 42 ± 7% of baseline (n = 6 cells from 5 animals, mean ± s.e.m.) compared to vehicle control (107 ± 5% of baseline, n = 11 cells from 8 animals; p < 0.001, one-way ANOVA with Bonferroni’s post hoc test; Fig. 6a, b). Block of voltage-gated Ca²⁺ channels (VGCCs) by Ni²⁺ (100 µM) largely eliminated the plateau potential (AUC 18 ± 5% of baseline, n = 4 cells from 4 animals, mean ± s.e.m.; Fig. 6a, b), implying that VGCC currents were necessary for the initiation of the plateau potential.

**Fig. 6: Contribution of dendritic ion channels to plateau potentials.**

The relatively smaller effect of D-AP5 on the plateau potential compared to the effect reported by Takahashi et al.⁹ is likely due to differences in the induction protocol. Takahashi et al. used high-frequency EFS pulses (5 trains of 5 stimuli delivered at 100 Hz with a 200 ms interval between trains), likely driving strong enough synaptic stimulation to directly release local Mg²⁺ block from NMDA receptors. In contrast, we used only a single EFS pulse, combined with optogenetic stimulation at the soma. We speculate that this protocol increased the relative contribution of VGCC currents compared to NMDAR currents in driving plateau potentials.

Block of dendritic Na_V channels by TTX (20 nM) also eliminated plateau potentials (AUC 26 ± 8% of baseline, n = 4 cells from 3 animals, mean ± s.e.m.; Fig. 6a, b), implying that Na_V currents were also necessary to trigger plateau potentials. None of these drugs substantially affected somatic spiking or synaptic transmission at the concentrations used. The drug effects on the plateau were much larger than their effects on the AUC for EFS or optogenetic stimulation alone (Fig. S24), confirming that the drug effects were selective to the regenerative currents directly involved in producing plateau potentials.

While we have focused on how somatic spiking activates distal dendrites, dendritic excitations can also drive a current along the apical trunk into the soma, an effect first simulated in cortical pyramidal cells by Mainen and Sejnowski⁵⁴. To visualize this “ping-pong” effect, we subtracted the soma fluorescence signal from the signal in the dendritic region where the plateau potential was largest. This procedure revealed the slowly rising and falling dendritic depolarization (presumably dominated by VGCC and NMDAR currents) which persisted for up to ~300 ms after the end of the optogenetic stimulus to the soma (Fig. S23). This feedback from dendrites to soma drove the high-frequency somatic firing which accompanied dendritic plateau potentials.

Discussion

Dendrites carry information in two directions: they integrate synaptic inputs to determine spike times at the soma^55,56,57, and they combine back-propagating action potentials (bAPs) with synaptic inputs to modulate synaptic strength^46,58. Given the distinct functions of integration and back-propagation (real-time information processing vs. slower changes in neuronal input-output functions), it is hard to imagine how a single set of dendritic excitability rules could facilitate both processes.

Previous studies had shown that dendritic excitations can be activated either by strong local current injection^1,40,41,59 or by bAPs^39,42,60. Prior experimental work in cortical neurons had suggested an important role of dendritic excitations in mediating synaptic plasticity^61,62. Simulation studies have proposed computational roles of dendritic excitations in integration^63,64,65, but there are also studies arguing for roles in regulating back-propagation and ultimately plasticity^66,67,68,69. Our experiments showed that under conditions where integration appears primarily linear and passive, bAPs nonetheless can drive strong dendritic excitations. These findings suggest a primary role for dendritic excitations in mediating plasticity, but this hypothesis will need to be tested in vivo.

Our high-resolution voltage imaging and optogenetics experiments revealed the spatial structure and probed the biophysical origin of plateau potentials in CA1 pyramidal cells (Fig. 6c). In a polarized dendrite, A-type K_V channels shunt the voltage, suppressing bAP propagation. The 6-27 ms time-constant for A-type channels to inactivate²² is slow enough that distal inputs usually trigger a spike at the soma before the dendrites become directly excitable. One or two closely spaced bAPs, direct distal depolarization, or gradual subthreshold somatic depolarization, transiently inactivates this shunt, opening a path for subsequent bAPs to activate Na_V channels, evoking dSpikes. The dSpikes then activate VGCC channels, leading to distal Ca²⁺ spikes. Together, the Na_V and VGCC currents activate the NMDAR receptors, leading to plateau potentials. Under sustained spiking, Na_V inactivation returns the dendrites to a non-excitable state. Simulations showed that the rate constant for slow Na_V inactivation governed the duration of the dSpike window.

These biophysical dynamics imply that plateau potentials are not simply due to conjunction of distal synaptic inputs and somatic spikes, but rather from conjunction of distal inputs and an onset of somatic spiking, i.e. a spike-rate accelerometer. During sustained high-frequency firing, distal synaptic inputs do not evoke plateau potentials (Fig. 5e-h).

Under targeted optogenetic stimulation, bAP spatial profiles were highly stereotyped, comprising only two motifs: bAPs alone, or bAPs with broadly distributed dSpikes. Thus dSpikes appeared as a broadcast signal, covering the apical dendritic tree and carrying precise spike timing information but little spatial information. This idea had been proposed previously, but not directly observed⁷⁰. In contrast, the pattern of glutamate-bound NMDA receptors carried precise spatial information on the identities of the activated synapses, but little temporal information. The conjunction of these electrical and chemical signals drove spatiotemporally precise NMDA receptor activation.

NMDAR-mediated plateau potentials are effective triggers for synaptic plasticity in acute brain slices, and can trigger synaptic plasticity⁷¹ and the formation of CA1 place cells in vivo via behavioral timescale synaptic plasticity (BTSP)⁵². Our data provide a biophysical basis for the “triplet learning rule”⁷², which has been shown to tame instabilities of simple Hebbian plasticity and to capture many aspects of plasticity experiments^73,74. The loss of dendritic excitability at sustained high spike rates suggests a mechanism for Bienenstock-Cooper-Munroe (BCM)-style metaplasticity, i.e. suppression of LTP at sustained high spike rates to avoid runaway plasticity⁷³. The dendritic spike-rate accelerometer provides an intuitive biophysical mechanism for a multiplet-based plasticity rule in CA1 pyramidal cells.

Our findings also suggest that neurons may have two distinct plasticity modes. If synaptic activation is sparse, then conjunction of dSpikes with synaptic activation may drive local NMDAR activation, calcium influx, and plasticity, without triggering a plateau potential^29,48,75. If synaptic activation in apical dendrites is sufficiently dense, then cooperative NMDAR and VGCC activation drives broadly distributed plateau potentials and somatic complex spikes, which may potentiate all synapses that are active within a broad time window surrounding the plateau potential. This second mode of plasticity resembles BTSP⁵². This second plasticity mode implies an associative plasticity rule in which inputs from entorhinal cortex on distal dendrites gate, via plateau potentials, plasticity of inputs from CA3, which primarily synapse onto basal and proximal apical dendrites⁷⁶.

Dynamics in vivo might differ from our observations in acute slices, but some in vivo experiments suggest that the overall picture is similar. Early extracellular recordings from CA1 pyramidal neurons of behaving rats found that spike bursts (indicative of complex spikes) were most likely to occur following 0.1 – 1 s of silence and were suppressed during epochs of sustained fast spiking⁷⁷. Furthermore, bursts of dendritic activity and putative Ca²⁺ spikes were always preceded by a large-amplitude fast dendritic spike, which we associate with a dSpike⁵¹. It is not known how the patterns of synaptic bombardment in vivo will affect the conditions for evoking a dSpike. We recently performed simultaneous voltage imaging in soma and apical dendrites of Layer 2/3 pyramidal cells in vivo and observed highly correlated voltages across the dendritic tree, and a biphasic trend in bAP propagation amplitude during sustained somatic spiking, similar to our observations here (e.g. Fig. 4b)⁷⁸.

In vivo calcium imaging experiments have reported localized dendritic signals, which are thought to arise from subthreshold calcium influx through VGCCs and NMDARs^12,79,80. It is important to appreciate that the spatial structures of dendritic calcium and voltage signals may differ substantially. Whereas Ca²⁺ ions diffuse ~2 μm during a typical 100 ms subthreshold event (effective buffered diffusion coefficient of calcium in dendrites is D < 20 μm²/s)^81,82, electrical length constants are typically > 100 μm and so electrical events are much more homogeneous across space. Simultaneous voltage and calcium imaging experiments will be crucial for determining the quantitative relations between these two modalities.

Neurons in vivo receive inhibitory and neuromodulatory inputs that could modify the simple picture presented here. Branch-specific inhibition, local NMDAR activation, or modulation of other ion channels might lead to more branch-to-branch variability in voltage dynamics. It remains to be determined whether excitatory inputs in vivo are sufficiently strong and clustered to overwhelm the A-type suppression mechanism and to directly drive dendrite-initiated excitations without first initiating a bAP. Further study is required to map dendritic integration and back-propagation in CA1 pyramidal cells in live animals.

Methods

Genetic constructs

We used Voltron2, an improved chemigenetic voltage indicator³⁴, and co-expressed it with a blue-shifted channelrhodopsin, CheRiff by a self-cleaving p2a linker. To optimize expression and dendritic membrane trafficking we designed the construct CAG::LR-Voltron2-TS-ER2-p2a-LR-CheRiff-TS-eYFP-ER2 (Addgene: #203228). In this construct, LR is the membrane localization signal from Lucy-Rho³⁵, TS is the trafficking sequence from K_ir2.1³⁶, and ER2 is the endoplasmic reticulum export signal FCYENEV³⁶. In some experiments, we used a Cre recombinase-dependent DIO (double-floxed inverse open reading frame) construct, CAG::DIO-LR-Voltron2-TS-ER2-p2a-LR-CheRiff-TS-eYFP-ER2 (Addgene: #203229), and co-expressed it with CAG::Cre (Addgene: #13775) plasmid wt/wt = 30:1 for in utero electroporation. As both approaches yielded sparse hippocampal expression and similar data, the data were pooled.

The genes were cloned into an adeno-associated virus (AAV) backbone with a synthetic CAG promoter using standard Gibson Assembly. Briefly, the vector was linearized by double digestion using restriction enzymes (New England Biolabs) and purified by the GeneJET gel extraction kit (ThermoFisher). DNA fragments were generated by PCR amplification and then fused with the backbones using NEBuilder HiFi DNA assembly kit (New England Biolabs). All plasmids were verified by sequencing (GeneWiz).

In utero electroporation (IUE)

All animal procedures adhered to the National Institutes of Health Guide for the care and use of laboratory animals and were approved by the Harvard University Institutional Animal Care and Use Committee (IACUC). Mice were kept in the vivarium under a reversed 12-hour light/dark cycle and maintained at 23 °C and 40% relative humidity. The IUE surgery was performed as described previously⁸³. Briefly, timed-pregnant female CD1 mice (embryonic day 15.5, E15.5; Charles River) were deeply anesthetized and maintained with 2% isoflurane. The animal body temperature was maintained at 37 °C. Uterine horns were exposed and periodically rinsed with warm phosphate-buffered saline (PBS). Plasmid DNA was diluted in PBS (2 μg/μL; 0.05% fast green), and 1 µL of the mixture was injected into the left lateral ventricle of the embryos. Electrical pulses (40 V, 50 ms duration) targeting the hippocampus were delivered five times at 1 Hz using tweezers electroporation electrodes (CUY650P5; Nepa Gene). Injected embryos were returned to the abdominal cavity, and the surgical incision was closed with absorbable PGCL25 sutures (Patterson).

Slice preparation

Coronal slices (300 µm) were prepared from CD1 mice of either sex between 2-4 postnatal weeks. This age range was within the age range used in prior studies on dendritic electrophysiology^27,42,60. Most prior dendritic electrophysiology studies were conducted in rats (see e.g^9,16,21.), which have longer dendrites and somewhat different membrane properties from mice^84,85.

Animals were anesthetized with isoflurane and euthanized by decapitation. The brain was then removed and placed in ice-chilled slicing solution containing (in mM): 210 sucrose, 3 KCl, 26 NaHCO₃, 1.25 NaH₂PO₄, 5 MgCl₂, 10 D-glucose, 3 sodium ascorbate, and 0.5 CaCl₂ (saturated with 95% O₂ and 5% CO₂). Acute slices were made using a Vibratome (VT1200S, Leica) while maintained in the slicing solution. Slices were recovered at 34 °C for 10 min in the imaging solution (artificial cerebrospinal fluid, ACSF) containing (in mM): 124 NaCl, 3 KCl, 26 NaHCO₃, 1.25 NaH₂PO₄, 2 MgCl₂, 15 D-glucose, and 2 CaCl₂ (saturated with 95% O₂ and 5% CO₂). Slices were then incubated in ACSF containing JFX₆₀₈-HaloTag ligand⁸⁶ (0.5-1 µM) for 30 min at room temperature, and moved to a fresh ACSF for another 30 min to wash out excess dye. Slices were maintained at room temperature until recordings were made.

Functional recordings were performed at 34 °C. We found that at 24 °C the dendritic excitability dynamics were significantly different (Fig. S25). After a sample had been recorded at 34 °C, the in-line solution heater was switched off for at least 10 min, with the bath temperature continuously monitored using a thermistor probe. We observed a significant increase in dSpike probability at 24 °C (0% vs. 29 ± 16% by the first bAP, p = 0.09; 16 ± 3% vs. 50 ± 12% by any bAP, p = 0.02; mean ± s.e.m., n = 6 cells from 4 animals, paired t-test). This temperature effect could explain the difference between our results and prior measurements at room temperature of bAP propagation into distal dendrites²¹. Previously published simulations that accounted for the different temperature sensitivities of A-type K_V channels and Na_V channels^87,88 predicted temperature-sensitive back-propagation dynamics¹⁷.

Electrophysiology

Somatic whole-cell recordings were acquired from hippocampal CA1 pyramidal neurons using a custom upright microscope. All experiments were performed at 34 °C, and continuously perfused at 2 mL/min with ACSF. Patch pipettes (2–4 MΩ) were filled with an internal solution containing (in mM): 8 NaCl, 130 KmeSO₃, 10 HEPES, 5 KCl, 0.5 EGTA, 4 Mg-ATP, and 0.3 Na₃-GTP. The pH was adjusted to 7.3 using KOH and osmolality was adjusted to 285–295 mOsm/L with water. Signals were amplified using a Multiclamp 700B (Molecular Devices), filtered at 10 kHz with the internal Bessel filter, and digitized at 100 kHz using a PCIe-6323 (National Instruments) A/D board. After entering the whole-cell configuration, membrane capacitance and membrane resistance were measured under voltage-clamp mode (Fig. S1). Resting membrane potential, rheobase and spike rates were measured under current-clamp mode. Rheobase was defined as the minimum amplitude of a current step (500 ms duration) to evoke at least one spike. To induce a rapid, isolated single spike, 2 nA current (2 ms duration) was injected into the soma in current-clamp mode (Fig. 1b and Fig. S14).

For the experiments in Figs. 5–6, we applied electric field stimulation (EFS) to the temporoammonic (TA) pathway to evoke synaptic responses. We used a concentric bipolar electrode (CBAPB50, FHC) with stimuli of 10-40 V (0.1 ms duration). Stimulus intensity was adjusted to be high enough to obtain plateau potentials when combined with optogenetic stimulation at the soma (30 ms duration). ACSF contained picrotoxin (50 µM) to prevent GABA_A receptor-mediated currents, and MgCl₂ concentration was lowered to 1 mM from 2 mM to enhance NMDA receptor-mediated currents, a standard modification in synaptic plasticity experiments⁹.

Voltage imaging in custom upright microscope

Voltage imaging experiments were conducted on a previously described home-built epifluorescence microscope³⁷. The instrument was controlled by Luminos Microscopy software (https://www.luminosmicroscopy.com/). Briefly, blue (488 nm) light was patterned by a digital micromirror device (DMD) and used for targeted channelrhodopsin stimulation. Stimulated regions were confirmed by fluorescence of the eYFP marker in LR-CheRiff-eYFP. Orange (594 nm) illumination was also patterned by a separate DMD and used for structured illumination voltage imaging and post hoc HiLo reconstruction of dendritic morphology⁸⁹. Typical laser intensity for 594 nm was typically 15 mW/mm². Intensity for 488 was typically 0.3 mW/mm². The fluorescence excitation coefficient of JFX₆₀₈ is ~83-fold greater at 594 nm than at 488 nm. Combined with the ~50-fold greater light intensity at 594 vs. 488 nm (15 mW/mm² vs. 0.3 mW/mm²), the crosstalk of blue light into the Voltron2 fluorescence signal was typically ~0.02% ΔF/F, much smaller than the voltage-dependent signals (1 – 10% ΔF/F). Thus, optical crosstalk was negligible.

Laser lines from a blue laser (488 nm, 150 mW, Obis LS) and orange laser (594 nm, 100 mW, Cobolt Mambo) were combined by a dichroic (IDEX, FF506-Di03-25×36) and sent through an acousto-optic modulator (TF525-250-6-3-GH18A, Gooch and Housego) for amplitude control. After the modulator, blue and orange lines were split with a dichroic mirror (IDEX, FF506-Di03-25×36), expanded, and sent to two independent DMDs for spatial modulation; one for the blue (Lightcrafter DLP3000, Texas Instruments) and the other for the orange (V-7000 VIS, ViALUX). The DMD planes were recombined via a dichroic mirror and re-imaged onto the sample via a tube lens (U-TLU, Olympus) and a 10x water-immersion objective, NA 0.60 (Olympus XLPLN10XSVMP). Fluorescence was collected by the objective and separated from the excitation by a multi-band dichroic mirror (IDEX, Di01-R405/488/594-25×36, three bandpasses). The fluorescence was then imaged onto a sCMOS camera (Hamamatsu Orca Flash 4.0) with the appropriate emission filter for the orange (Chroma, ET645/75 m, bandpass) and blue (Chroma, ET525/50 m, bandpass). Voltage-imaging recordings were acquired at a 1 kHz frame rate unless stated otherwise.

To enhance the spatial resolution of the high temporal resolution movies, we mapped the timing data onto a static 2 P structural image of either eYFP (from the LR-CheRiff-eYFP fusion, λ_exc = 920 nm) or JFX₆₀₈ HaloTag ligand (λ_exc = 820 nm, targeting the ²S transition). Sometimes we made a structural image using 1 P HiLo imaging (e.g., Fig. 4a)⁸⁹. A 25x water-immersion objective, NA 1.05 (Olympus XLPLN25XSVMP2) was used to increase the spatial resolution. Maximum intensity projections of z-stacks were used to form images of the dendritic arbor. The distance for each recording site is a slight underestimate of the true on-path distance from the soma because we ignored changes along the z-axis.

Optogenetic stimuli require an overlap of blue light and CheRiff molecules. Since the eYFP was fused to the CheRiff, the map of eYFP fluorescence was a direct measure of the strength of the CheRiff stimulation. We manually defined a polygon around a target dendrite, and then used the DMD to create this pattern of blue illumination. After the experiment, we took an image in the eYFP channel to quantify the distribution of CheRiff stimulation, which we used in post-processing to estimate the stimulus strength (Fig. S3).

For the experiments in Fig. S4, we created the DMD pattern by outlining a region of interest (ROI) around the soma or a single dendritic branch. This pattern was then sequentially shifted by 10 µm increments, up to a total of 100 µm from the original ROI. The shifting of the DMD pattern was triggered with digital clock pulses, cycling through the pre-defined set of patterns three times. The responses from these three cycles were averaged.

Pharmacology

Drugs were prepared as frozen stock solutions (stored at -20 °C). Drugs were: picrotoxin (Abcam), D-(-)-2-Amino-5-phosphonopentanoic acid (D-AP5, Tocris), tetrodotoxin (TTX, Abcam), NiCl₂ (Sigma), BaCl₂ (Sigma), and 4-Aminopyridine (4-AP, Abcam). Ni²⁺ is considered a non-selective VGCC blocker, but T-type (Ca_V3.x) and R-type (Ca_V2.3) are sensitive at the used concentration of Ni²⁺ (100 µM; Fig. 6a, b)⁹⁰. We chose Ni²⁺ over SNX-482 due to reports that SNX-482 also inhibits A-type K⁺ channels⁹¹. Drugs were mixed with ACSF and perfused over the slice for at least 15 min prior to measurements.

Statistics

All treatment groups were interleaved with control experiments. Statistical significance was assessed using (two-tailed) paired or unpaired Student’s t-tests or one-way ANOVA with Bonferroni’s post hoc test as appropriate; the level of significance is denoted on the figures as follows: *p < 0.05, **p < 0.01 and ***p < 0.001. The experiments were not randomized, and the investigators were not blinded to the experimental condition. Sample size was based on reports in related literature and was not predetermined by calculation.

Image analysis

All analysis was performed in MATLAB, as described below.

Mapping functional data onto structural data

We reconstructed voltage in three dimensions by combining 2P anatomy scans and 1P voltage imaging functional datasets.

Image registration

A high-resolution two-photon z-stack of the cell was acquired with z-spacing of 2 μm (Fig. S6). A wide-field epifluorescence image was also acquired and used to define a DMD mask to restrict the 594 nm illumination to the cell and its immediate neighborhood. Patterned illumination substantially decreased background autofluorescence and increased the contrast of the dendrites. We then registered the 2P z-stack to the 1P image. First we performed registration in the x-y plane. We manually defined control points on in-focus parts of the 1P image, and on corresponding structures on a maximum-intensity projection of the 2P z-stack. We used a second-order polynomial fit to map the 2P z-stack onto the 1P image. We then used a cross-correlation approach to find the z-planes in the 2P z-stack which best matched the region around each in-focus control point on the 1P image. We used these coordinates to define rotations and translations out of the image plane, to register the 2P z-stack to the in-focus parts of the 1P image.

Determining the microscope model, M

We then built a forward model to simulate the 1P image from the 2P z-stack. We assumed a Gaussian beam point-spread function (PSF) with width at focus w₀ and confocal parameter b (while the Gaussian beam approximation is not strictly correct for the high NA objective, we found that in the presence of tissue light scattering this parameterization of the PSF was adequate). We convolved each plane of the registered 2P z-stack with the corresponding PSF to create a stack 2P_blur, where each slice was blurred in accordance with its distance from the focal plane. Summing these blurred 2P images with a depth-dependent weight (to account for signal attenuation) reproduced the 1P image. The depth-dependent PSF and weighting comprised the microscope model M.

Mapping 2D images to 3D voltages

To enforce the biophysical constraints of continuity and smoothness in the dendritic voltage, we approximate the voltage along the entire tree by linearly interpolating between a small number (a few hundred) of nodes. For the results in Fig. S6 and Supplementary Movie 2, we used 106 nodes, with a maximum spacing between nodes of 50 μm. Nodes were placed at each branch point and end point of the segmented dendritic tree, to ensure that the model could capture voltage differences between branches.

The assumption of low-dimensional voltage dynamics (e.g. 106 dimensions in Fig. S6) is analogous to the assumptions made when using matrix factorization methods^38,92,93 to denoise calcium or voltage imaging movies, and allows us to solve the challenging inverse problem of inferring 3D voltages given 2D measurements (Fig. S6a). Below, we describe a simplified version of the method and refer the reader to Ref. ⁹⁴ for details.

We preprocessed the voltage movie to remove changing baselines by fitting a b-spline to each pixel, and subtracting this baseline estimate³⁸. We then segmented the anatomy stack using Ilastik⁹⁵ to yield a 3D voxelized model of the apical dendrite and soma (our segmentation did not resolve the axon or basal dendrites).

We then skeletonized this 3D model of the dendritic tree into a set of nodes and edges using the NeuTube tracing software⁹⁶. Edges exist only between nodes which are connected on the dendritic tree. Combined, the nodes and edges form a tree-structured graph that will be used when solving the voltage inference problem. Crucially, the number of nodes is far fewer than the number of voxels in the tree, thus implementing our assumption of low dimensionality.

Let Q be the number of voxels in the segmented neuron and P be the number of nodes in the skeletonized graph. We define the Q × P basis matrix B to map from node weights to voxel voltages. The columns of B have a simple interpretation: they are smooth basis functions used to reconstruct the voltage. The node weights in a given frame, w_t, control the relative intensities of these basis functions (Fig. S6b). Using W to refer to the P ×T matrix of node weights across all frames, we have $\hat{v}={BW}$, where the Q ×T matrix $\hat{v}$ represents our three-dimensional voltage estimate across all frames.

To account for the blurring and attenuation created by the 1 P microscope, we pass the 3D voltage estimate through the microscope model M. The microscope model performs a depth-dependent blur and summation (Fig. S6e). A simplified version of the model is therefore:

$${f}_{t}={MB}{w}_{t}+{noise}$$

where f_t is a (preprocessed) voltage imaging frame (f standing for fluorescence), and w_t are the (unknown) node weights.

To infer the node weights w_t, we use the graph of nodes to solve a regularized inverse problem (Fig. S6a). The regularizer is given by:

$$R({w})={\sum}_{(i,j)\in E:i < j}{({{w}}_{i}-{w}_{j})}^{2}={w}^{{\rm T}}Lw$$

where L is the graph-Laplacian. This regularizer encourages adjacent nodes to have similar weights. With this regularizer, the (simplified) optimization problem used to infer node weights is:

$${{minimize}\atop{w}_{t}}\left|\left|{MB}{w}_{t} - {f}_{t} \right|\right|_{2}^{2}+\lambda {{w}_{t}^{{\rm T}}}{Lw_{t}}\cdot$$

We use generalized cross validation (GCV⁹⁷) to select the penalty parameter λ which best describes the data.

For brevity, we have omitted some complexities of the model in this summary. The full details of our voltage reconstruction can be found in ref. ⁹⁴. In practice, we found it helpful to include gain and offset terms to account for non-uniform indicator expression and baseline fluorescence. The full model jointly estimates these parameters along with the node voltages. We fit the model iteratively, alternating between estimating voltages and optimizing gains and offsets. This approach yields 3D voltage estimates $\hat{v}$ for each frame (Fig. S6f, h). We then passed these estimates through the microscope model M to create the reconstructed frame shown in Fig. S6g.

PCA-based filtering

Electrical length constants extended over many pixels, so we used Principal Component Analysis (PCA)-based filtering to remove pixel-wise shot noise, similar to the approach in Ref. ³⁸. We found that > 96% of the variance in the recordings was contained within the first three principal components, whose spatial footprints broadly corresponded to the soma-proximal region, the dendritic trunk, and the distal dendrites, supporting the use of PCA to remove high spatial-frequency noise (Fig. S7). The first five temporal components contained signals related to neural activity and were used to resynthesize a denoised movie; the remaining components represented uncorrelated shot noise. To verify that the PCA filtering did not distort the underlying AP waveforms, we compared mean AP waveforms in subcellular compartments before and after the filtering steps. We observed no systematic deviations in the AP waveforms in the soma or dendrites (Fig. S7).

Extracting fluorescence from movies

Fluorescence values were extracted from raw movies in one of two ways. One approach used the maximum-likelihood pixel-weighting algorithm described previously³³. Briefly, the fluorescence at each pixel was correlated with the whole-field average fluorescence. Pixels that showed stronger correlation to the mean were preferentially weighted. This algorithm automatically found the pixels carrying the most information, and de-emphasized background pixels. Alternatively, a user defined a region comprising the soma and dendrites and calculated fluorescence from the unweighted mean of pixel values within this region. These two approaches gave similar results. Photobleaching was corrected by dividing the frames by a regression fit to the mean fluorescence.

Spike-triggered average (STA) movies

A simple threshold-and-maximum procedure was applied for spike detection. Fluorescence traces were first high-pass-filtered, and a threshold was manually selected. Once spike times were determined, movie segments surrounding each spike were averaged together. To calculate stimulus-triggered averages, traces or movies were aligned to the optogenetic stimulus onset.

Sub-Nyquist action potential timing (SNAPT)

Spike propagation delay was calculated using the SNAPT subframe interpolation algorithm as described previously³³. In brief, spike-triggered average (STA) movies were used as a template and fit with a quadratic spline interpolation of the spike waveform, pixel-by-pixel. For each pixel, we calculated the sub-frame interpolated time that the spike reached 50% of local maximum, to create a map of the spike delay. The fits were then converted into movies. Spike timing at each pixel was represented by a brief flash, which followed a Gaussian time-course with duration equal to the cell-average time resolution, σ.

The pixel matrix of the subframe interpolated movie was expanded to match the dimensions of the high-resolution image, and the amplitude at each pixel was then set equal to the mean brightness at that pixel. For assembly of the color movies, the timing signal was assigned to a color map that was overlaid on a grayscale image of mean fluorescence. The optically stimulated region of the cell was highlighted in blue.

Normalization to reference signal (∆F/F_ref)

To account for sub-cellular variations in voltage sensitivity (likely due to variations in Voltron2 trafficking), we normalized the fluorescence signal associated with a spike, ∆F, by the amplitude of the change in fluorescence during the passive return to baseline after a stimulus (i.e., ∆F/F_ref; Fig. 1d). ∆F/F_ref was used for all spike amplitude heatmaps and kymographs unless stated otherwise. By comparing two voltage-sensitive signals, this measure was insensitive to background and protein trafficking.

Kymographs

We manually drew a line along the apical dendrite and then determined the mean fluorescence time-course in equal-length segments along the line. Typical segment size was 10 pixels (6.5 µm with 10x objective). The fluorescence waveforms were assembled into a kymograph matrix showing signal amplitude as a function of linear position and time. Example waveforms were calculated by averaging responses from 5 segments ( ~ 33 μm contour length) and plotted on top of the kymographs.

Counting bAPs and dSpikes

All spikes at the soma were counted as back-propagating action potentials (bAPs). The timing of each bAP was estimated relative to the optogenetic stimulation onset. Dendritic spikes (dSpikes) were detected by high-pass-filtering and simple threshold-and-maximum in a user-defined region (typically > 300 µm from soma). We defined dSpikes as a large and narrow discharge (typically <5 ms in full width at half maximum). Dspike successes and failures were clearly distinguished in the fluorescence traces (e.g., Fig. 2a and Fig. S10).

Period doubling bifurcation

We typically observed period doubling during wide-field optogenetic stimulation (Fig. 4c–e). Overly strong stimulation frequently led to the failure of all spikes, likely due to incomplete recovery of Na_V channels (i.e. depolarization block). In preliminary experiments, we determined a stimulation intensity approximately halfway between rheobase and depolarization block. The frequency of bAPs was estimated by measuring the time interval between bAP peaks, while the amplitude was normalized to the average of the final 5 bAPs in a stimulus epoch (Fig. 4e).

Normalization of plateau potential area

The cumulative area under the curve (AUC) was determined by integrating fluorescence changes, ∆F, with respect to time (Fig. S22). In Fig. 5b, the normalized area (% sum) was calculated as AUC for combined stimulation (AUC_combined), divided by the sum of the AUC for optogenetic stimulation alone (AUC_optical) and the AUC for EFS alone (AUC_electrical). In Fig. 5d, the normalized area (% peak) was calculated by mapping the AUC for combined stimulus for each cell vs. ∆Time to the range [0, 1] (Fig. S22b-c). In Fig. 6b, the normalized area (% baseline) was determined as the ratio of AUC to baseline AUC prior to any vehicle or drug treatment.

Biophysical modeling

Simulating a CA1 pyramidal cell in NEURON

Morphologically realistic simulations were carried out on an AMD64-Windows computer using NEURON⁹⁸ through its Python interface (Python 3.11, NEURON 8.2) and exported into MATLAB to analyze and compare with experimental data. Model specifications and simulation code are available as Supplementary Files.

Model properties

We adapted an existing CA1 pyramidal cell model (ModelDB accession number: 116084)⁴⁹. Our model uses the same morphology as Ref. ⁴⁹. We added a slow inactivation gate to the Na_V channels, varied the distributions of Na_V channels and A-type K_V channels, added a gradient in the maximal Na_V inactivation from soma to the distal dendrites, and introduced channelrhodopsin in the somatic and dendritic compartments. The distribution of delayed rectifier K_DR channels was homogeneous throughout the cell, as in Ref. ⁴⁹. We sought to replicate the voltage profiles under pure optogenetic stimulation, so our model did not contain VGCC or NMDAR conductances. Table 1 shows values of the model parameters.

Table 1 Ion channel densities in a model CA1 pyramidal cell. Channel models were adapted from Ref. ⁴⁹

Full size table

For voltage-gated channels, the maximum channel conductance densities were modeled as sigmoidal functions of the contour distance, d, from the soma. These sigmoid distributions take the general form shown in Eq. 1, with asymptotic densities g_Prox and g_Distal, a half-way distance d_1/2 (where the density is (g_Prox + g_Distal)/2) and a steepness parameter z.

$$g\left(d\right)={g}_{{Prox}}+\left[{g}_{{Distal}}-{g}_{{Prox}}\right]\cdot {\left[1+\exp \left(\frac{d-{d}_{1/2}}{z}\right)\right]}^{-1}$$

(1)

The g parameters were selected to agree with literature values²², while the other parameters were adjusted to match our data. Fig. S19a–c show channel densities of Na_V and A-type K_V across the neuron morphology after tuning to match our data. For temperature-dependent channel gating parameters, we used a temperature of 35 °C.

In the axonal compartments channel densities and membrane capacitance were set separately to account for differences in channel targeting, myelination, and clustering of Na_V channels at the axon initial segment (AIS) and nodes of Ranvier. Table 1 summarizes the model parameters.

A-type K_V

A-type potassium channels are present in the soma and dendrites, with approximately six-fold higher density in the distal apical dendrites than the soma⁹⁹. Proximal (d < 100 μm) and distal (d > 100 μm) channels differed slightly in the kinetics and voltage dependence of the activation variable, to reproduce measured channel properties in CA1 pyramidal dendrites^22,62. The detailed kinetic properties of the two types of A-type K channels are given below, where v is in mV, I_KA is in µA/cm² and time constants τ in ms. Kinetic scheme for proximal A-type K_V channels (d < 100 μm):

$${I}_{{KA}}={g}_{{KA}}\left(d\right)\cdot n\cdot l\cdot \left(v+90\right)$$

(2)

$${n}_{\infty }=\frac{1}{1+{\alpha }_{n}};\,{\tau }_{n}=\frac{4{\beta }_{n}}{1+{\alpha }_{n}}$$

$${\alpha }_{n}=\exp \left(-0.038\left(1.5+\frac{1}{1+\frac{\exp \left(v+40\right)}{5}}\right)\cdot \left(v-11\right)\right)$$

$${\beta }_{n}=\exp \left(-0.038\left(0.825+\frac{1}{1+\frac{\exp \left(v+40\right)}{5}}\right)\cdot \left(v-11\right)\right)$$

$${l}_{\infty }=\frac{1}{1+{\alpha }_{l}};{\tau }_{l}=0.26\cdot (v+50)$$

$${\alpha }_{l}=\exp \left(0.11\left(v+56\right)\right)$$

Time constants are constrained to τ_n ≥ 0.1 ms and τ_l ≥ 2 ms. For distal A-type K_V channels (d > 100 μm) the kinetic scheme is similar, with the replacements:

$${n}_{\infty }=\frac{1}{1+{\alpha }_{n}};{\tau }_{n}=\frac{2{\beta }_{n}}{1+{\alpha }_{n}}$$

(3)

$${\alpha }_{n}=\exp \left(-0.038\left(1.8+\frac{1}{1+\frac{\exp \left(v+40\right)}{5}}\right)\cdot \left(v+1\right)\right)$$

$${\beta }_{n}=\exp \left(-0.038\left(0.7+\frac{1}{1+\frac{\exp \left(v+40\right)}{5}}\right)\cdot \left(v+1\right)\right)$$

Voltage-gated sodium channel, Na_V

To capture the loss of dendritic excitability after several dSpikes, we used a Hodgkin-Huxley-type model with a slow inactivation variable, s, and assumed that a fraction, a_r2, of Na_V channels could undergo slow inactivation (e.g. a_r2 = 70% means that at most 70% of Na_V channels can undergo slow inactivation). We further assumed that a_r2 followed a sigmoid function of d of the form of Eq. 1, with a_r2 = 0 (i.e. no slow inactivation) at the soma. Fig. S19d shows the steady state value of s, as a function of membrane voltage and a_r2. Steady-state Na_V inactivation is thus modeled as a mixture of inactivating and persistent currents as s_∞ (V, a_r2) = a_r2 · s_∞ (V, 100%) + (1 – a_r2), where s_∞ (V, 100%) is the voltage dependent equilibrium value of the fully inactivating channels.

Kinetic scheme for Na_V channels with slow inactivation:

$${I}_{Na}={g}_{NaV}(d)\cdot {m}^{3}\cdot h\cdot s\cdot (v-55)$$

(4)

$${m}_{\infty }=\frac{{\alpha }_{m}}{{\alpha }_{m}+{\beta }_{m}};{\tau }_{m}=\frac{0.5}{{\alpha }_{m}+{\beta }_{m}}$$

$${\alpha }_{m}=\frac{0.4\left(v+30\right)}{1-\exp \left(-\frac{v+30}{7.2}\right)}$$

$${\beta }_{m}=\frac{0.124\left(v+30\right)}{\exp \left(\frac{v+30}{7.2}\right)-1}$$

$${h}_{\infty }=\frac{1}{1+\exp \left(\frac{v+50}{4}\right)}$$

$${\tau }_{h}=\frac{0.5}{{\alpha }_{h}+{\beta }_{h}}$$

$${\alpha }_{h}=\frac{0.03\left(v+45\right)}{1-\exp \left(-\frac{v+45}{1.5}\right)}$$

$${\beta }_{h}=\frac{0.01\left(v+45\right)}{\exp \left(\frac{v+45}{1.5}\right)-1}$$

$${s}_{\infty }=\frac{\left(1+{a}_{r2}\left(d\right)\cdot \exp \left(\frac{v+58}{2}\right)\right)}{\left(1+\exp \left(\frac{v+58}{2}\right)\right)}$$

$${\tau }_{s}=\frac{3300{\beta }_{s}}{1+{\alpha }_{s}}$$

$${\alpha }_{s}=\exp \left(0.45\left(v+60\right)\right)$$

$${\beta }_{s}=\exp \left(0.09\left(v+60\right)\right)$$

Na_V time constants are constrained to τ_m ≥ 0.02 ms, τ_h ≥ 0.5 ms and τ_s ≥ 10 ms.

Delayed rectifier potassium, K_DR

Delayed rectifier K_V channels are uniformly distributed across the neuron as in Ref. ⁴³

$${I}_{KDR}={g}_{KDR}\cdot n\cdot (v+90)$$

(5)

$${n}_{\infty }=\frac{1}{1+{\alpha }_{n}};{\tau }_{n}=\frac{50{\beta }_{n}}{1+{\alpha }_{n}}$$

$${\alpha }_{n}=\exp \left(-0.11\left(v-13\right)\right)$$

$${\beta }_{n}=\exp \left(-0.08\left(v-13\right)\right)$$

The K_DR time constant is constrained to τ_n ≥ 2 ms.

Passive properties

The passive leak conductance (V_rev = –66 mV) was uniform across the soma and dendritic arbor. Dendrites were modeled as smooth cylinders. To account for the excess surface area due to dendritic spines, the effective membrane capacitance was set to 1.50 μF/cm², larger than the geometrical membrane capacitance of ~1 μF/cm² ¹⁰⁰.

Channelrhodopsin

Optogenetic stimulation was implemented using distributed time-dependent conductances with reversal potential 0 mV. The conductance was proportional to the simulated blue light illumination profile.

Parameter fitting

The nonlinear interactions of Na_V, K_DR and K_A channels produce a rich variety of subthreshold and spiking patterns, even in models with one or a few compartments. Also, a given electrical response pattern can often arise from multiple combinations of ion channel parameters. As our model uses realistic neuronal morphology, the parameter space grows exponentially as each compartment can have different channel parameters.

To reduce the size of the parameter search space we introduced constraints from literature data wherever possible, and reduced the number of spatially dependent parameters by imposing the parameter distributions of Eq. 1.

Parameter space was mapped using sweep searches, varying optogenetic stimulus intensity, somatic and distal Na_V densities and the level of Na_V slow inactivation. The voltage traces were then classified based on the patterns of bAP successes and failures and arranged as phase diagrams (Fig. S20c–e). The threshold to distinguish bAP successes from failures was whether the voltage at a compartment at 500 μm from the soma reached a peak voltage above or below -40 mV.

Model validation

The model was originally used to simulate responses to patch clamp and synaptic stimulation⁴⁹. To validate our version of the model, we first compared a localized current-clamp stimulus at the soma vs. distributed channelrhodopsin conductance at the soma (g_Distal = 0, d_1/2 = 40 μm, z = 10 μm). For similar net currents, these two stimulation methods yield similar spiking and bAP patterns, which also matched our experimental results (Fig. 4f–g). Under strong somatic or weaker widefield stimulation, the model also recreated the dendritic period doubling behavior observed experimentally.

To further validate the model, we compared simulation results to data on patch clamp current injection in oblique dendrites¹. We simulated 2 nA current injections and observed dendrite-localized dSpikes similar to experimental observations (Fig. S20a). Turning off the dendritic Na_V channels mimicked the effect of adding TTX in the experiments. We then simulated the same dendrite under optogenetic stimulation (d_1/2 = 50 μm, z = 10 μm, g_distal = 0, g_oblique = 1 mS/cm² centered on an oblique dendrite as shown in Fig. S20b). The optogenetic stimulation resulted in AP starting at the soma and backpropagating into the dendritic arbor, with a bAP amplitude pattern consistent with our experimental results for stimulation of an oblique dendrite.

Defining channel reserve

To determine the biophysical basis of our experimentally observed dSpike time window, we defined channel reserves for Na_V and A-type K_V channels. The channel reserve is the fraction of ion channels that could transition to the open state due to a bAP. For Na_V channels, the slow inactivation variable s measures the channel reserve. For example, at s = 0.6, only 60% of Na_V channels could participate in amplifying a bAP. In A-type K_V channels, the inactivation variable l plays a similar role. Tracking the channel reserves for these two channels indicated that a depleted A-type reserve and un-depleted Na_V reserve were necessary for dSpikes to occur.

Simplifications and omissions

CA1 pyramidal cells contain diverse Na_V channels due to different genes, subunit compositions, and post-translational modifications¹⁰¹, whereas we used a single Na_V with a gradient in slow inactivation. The mechanism of slow inactivation and the factors driving a spatial gradient in this parameter have not been fully elucidated but post-translational modification by protein kinase C has been implicated¹⁰². The sigmoidal channel distribution of Eq. 1 may miss effects from finer-grained subcellular variations in channel density. Our channelrhodopsin model does not include the light-dependent opening kinetics of CheRiff, the conductance sag under continuous illumination, or finite closing kinetics.

Several classes of ion channels were omitted from our model, including calcium-activated potassium channels (K_CA), VGCCs, NMDARs and hyperpolarization-activated cyclic nucleotide-gated (HCN) channels. The omission of these channels is justified because we focused on the short-time dynamics of bAP filtering under pure optogenetic drive (Fig. 2-4), and the model accurately captured the observed dynamics under these conditions. VGCCs and NMDARs drive apical calcium plateaus and initiate complex spikes under synaptic inputs. HCN-channels are preferentially targeted to the dendritic tuft and could play a role similar to the A-type K_V channels in gating back-propagation¹⁰³. These channels may also be important in mediating neuromodulatory effects, a variable not explored in this work.

Coupled two-compartment Izhikevich model

As a complement to the morphologically and physiologically detailed CA1 model, we introduced a two-stage resistively coupled Izhikevich model (Fig. S21, Supplementary Software 2). Despite its simplicity, this model broadly reproduced the bAP filtering characteristics of the CA1 dendrites. The classical Izhikevich model is a computationally efficient spiking neuron model consisting of a voltage variable v and a slow adaptation variable u, and is capable of reproducing a wide variety of neuronal behaviors observed in mammalian brains¹⁰⁴. These characteristics made it an attractive starting point for a simplified CA1 model.

Model specifications and simulation code are available as Supplementary Files. The model equations were

Soma:

$$\frac{d{v}_{s}}{dt}= (0.04{v}_{s}^{2}+5{v}_{s}+140-{u}_{s})+{g}_{s}{v}_{s}+{g}_{c}\Delta v\\ \frac{d{u}_{s}}{dt}= 0. \\ {{\rm{If}}}\,{v}_{s} > {v}_{{{\rm{ts}}}}:{{\rm{set}}}\,{{{\rm{v}}}}_{{{\rm{s}}}}\to {{{\rm{v}}}}_{{{\rm{rs}}}}.$$

(6)

Dendrites:

$$\frac{d{\nu }_{D}}{{dt}}= \left(0.04\,{\nu }_{D}^{2}+5\,{\nu }_{D}+140-{u}_{D}\right)+{{g}_{D}\nu }_{D}-{g}_{c}\Delta \nu \\ \frac{d{u}_{D}}{{dt}}= a\left(b{\nu }_{D}-{u}_{D}\right) \\ {{\rm{If}}}\,{{\rm{v}}}_{{\rm{D}}} \, > \, {{\rm{v}}}_{{{\rm{tD}}}}:{{\rm{set}}}\,{{{\rm{v}}}}_{{{\rm{D}}}}\to {{{\rm{v}}}}_{{{\rm{rD}}}},{{\rm{u}}}_{{\rm{D}}} \to {{\rm{u}}}_{{\rm{D}}}+{{\rm{d}}}$$

(7)

Here $\Delta v={v}_{D}-{v}_{s}$. The parameter values used in the simulations were: a = 0.0025, b = 0.01, c = -55, d = 1, v_ts = 30, v_tD = 0, g_c = 0.325. Initial values were: v_s = -75, v_D = -75, u_s = -13, u_D = -13. For soma-only stimulation, we used g_s = 0.16, g_D = 0. For wide-field stimulation we used g_D = 0.05, g_s = 0.3.

In our adaptation of the Izhikevich model, the soma was tuned to exhibit regular spiking without adaptation. The soma was resistively coupled to the dendrite compartment that featured an adjusting spiking threshold. Optogenetic-like stimulation was implemented as variable conductances with 0 mV reversal potential at the soma or dendrites. When the model was driven by optogenetic stimulation at the soma only, it replicated the behavior seen in Fig. 4f. A single spike from the soma did not depolarize the dendrites enough to trigger a spike, but a spike train from the soma was able to evoke dendritic spikes. The spike-threshold adaptation in the dendrites mimicked the effect of Na_V inactivation, causing the dendrites to lose excitability after several successful spikes. The distal dendrites thereby acted as a high-pass filter or accelerometer, selectively responding to a small number of somatic spikes following a step increase in somatic firing rate. Simultaneous stimulation of soma and dendrites recreated the experimentally observed period-doubling bifurcation shown in Fig. 4g.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

The voltage imaging data generated in this study are on the DANDI archive under accession code 001266 and are available at https://dandiarchive.org/dandiset/001266. Source data are provided with this paper.

Code availability

Codes for numerical simulations of dendritic excitability are provided with this paper. Instrument control software is available at: https://www.luminosmicroscopy.com/

References

Golding, N. L. & Spruston, N. Dendritic sodium spikes are variable triggers of axonal action potentials in hippocampal CA1 pyramidal neurons. Neuron 21, 1189–1200 (1998).
Article CAS PubMed Google Scholar
Magee, J. C. & Johnston, D. Characterization of single voltage‐gated Na⁺ and Ca²⁺ channels in apical dendrites of rat CA1 pyramidal neurons. J. Physiol. 487, 67–90 (1995).
Article CAS PubMed MATH PubMed Central Google Scholar
Larkum, M. E., Zhu, J. J. & Sakmann, B. A new cellular mechanism for coupling inputs arriving at different cortical layers. Nature 398, 338–341 (1999).
Article ADS CAS PubMed Google Scholar
Golding, N. L., Jung, H., Mickus, T. & Spruston, N. Dendritic calcium spike initiation and repolarization are controlled by distinct potassium channel subtypes in CA1 pyramidal neurons. J. Neurosci. 19, 8789–8798 (1999).
Article CAS PubMed PubMed Central Google Scholar
Johnston, D., Magee, J. C., Colbert, C. M. & Cristie, B. R. Active properties of neuronal dendrites. Annu. Rev. Neurosci. 19, 165–186 (1996).
Article CAS PubMed MATH Google Scholar
Hausser, M., Spruston, N. & Stuart, G. J. Diversity and dynamics of dendritic signaling. Science 290, 739–744 (2000).
Article ADS CAS PubMed MATH Google Scholar
Spruston, N. Pyramidal neurons: dendritic structure and synaptic integration. Nat. Rev. Neurosci. 9, 206–221 (2008).
Article CAS PubMed Google Scholar
Major, G., Larkum, M. E. & Schiller, J. Active properties of neocortical pyramidal neuron dendrites. Annu. Rev. Neurosci. 36, 1–24 (2013).
Article CAS PubMed MATH Google Scholar
Takahashi, H. & Magee, J. C. Pathway interactions and synaptic plasticity in the dendritic tuft regions of CA1 pyramidal neurons. Neuron 62, 102–111 (2009).
Article CAS PubMed MATH Google Scholar
Brandalise, F., Carta, S., Helmchen, F., Lisman, J. & Gerber, U. Dendritic NMDA spikes are necessary for timing-dependent associative LTP in CA3 pyramidal cells. Nat. Commun. 7, 13480 (2016).
Article ADS CAS PubMed PubMed Central Google Scholar
Schiller, J., Major, G., Koester, H. J. & Schiller, Y. NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature 404, 285–289 (2000).
Article ADS CAS PubMed MATH Google Scholar
Grienberger, C., Chen, X. & Konnerth, A. NMDA receptor-dependent multidendrite Ca²⁺ spikes required for hippocampal burst firing in vivo. Neuron 81, 1274–1281 (2014).
Article CAS PubMed Google Scholar
Larkum, M. E. Are dendrites conceptually useful? Neuroscience 489, 4–14 (2022).
Article CAS PubMed Google Scholar
Häusser, M. & Mel, B. Dendrites: bug or feature? Curr. Opin. Neurobiol. 13, 372–383 (2003).
Article PubMed MATH Google Scholar
Davie, J. T. et al. Dendritic patch-clamp recording. Nat. Protoc. 1, 1235–1247 (2006).
Article CAS PubMed MATH PubMed Central Google Scholar
Magee, J. C. & Carruth, M. Dendritic voltage-gated ion channels regulate the action potential firing mode of hippocampal CA1 pyramidal neurons. J. Neurophysiol. 82, 1895–1901 (1999).
Article CAS PubMed MATH Google Scholar
Short, S. M. et al. The stochastic nature of action potential backpropagation in apical tuft dendrites. J. Neurophysiol. 118, 1394–1414 (2017).
Article PubMed MATH PubMed Central Google Scholar
Canepari, M., Vogt, K. & Zecevic, D. Combining voltage and calcium imaging from neuronal dendrites. Cell. Mol. Neurobiol. 28, 1079 (2008).
Article CAS PubMed PubMed Central Google Scholar
Holthoff, K., Zecevic, D. & Konnerth, A. Rapid time course of action potentials in spines and remote dendrites of mouse visual cortex neurons. J. Physiol. 588, 1085–1096 (2010).
Article CAS PubMed MATH PubMed Central Google Scholar
Roome, C. J. & Kuhn, B. Simultaneous dendritic voltage and calcium imaging and somatic recording from Purkinje neurons in awake mice. Nat. Commun. 9, 1–14 (2018).
Article CAS MATH Google Scholar
Spruston, N., Schiller, Y., Stuart, G. & Sakmann, B. Activity-dependent action potential invasion and calcium influx into hippocampal CA1 dendrites. Science 268, 297–300 (1995).
Article ADS CAS PubMed Google Scholar
Hoffman, D. A., Magee, J. C., Colbert, C. M. & Johnston, D. K⁺ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature 387, 869–875 (1997). 869-875.
Article ADS CAS PubMed MATH Google Scholar
Gasparini, S., Losonczy, A., Chen, X., Johnston, D. & Magee, J. C. Associative pairing enhances action potential back-propagation in radial oblique branches of CA1 pyramidal neurons. J. Physiol. 580, 787–800 (2007).
Article CAS PubMed PubMed Central Google Scholar
Golding, N. L., Kath, W. L. & Spruston, N. Dichotomy of action-potential backpropagation in CA1 pyramidal neuron dendrites. J. Neurophysiol. 86, 2998–3010 (2001).
Article CAS PubMed MATH Google Scholar
Pan, E. & Colbert, C. M. Subthreshold inactivation of Na⁺ and K⁺ channels supports activity-dependent enhancement of back-propagating action potentials in hippocampal CA1. J. Neurophysiol. 85, 1013–1016 (2001).
Article CAS PubMed MATH Google Scholar
Colbert, C. M., Magee, J. C., Hoffman, D. A. & Johnston, D. Slow recovery from inactivation of Na⁺ channels underlies the activity-dependent attenuation of dendritic action potentials in hippocampal CA1 pyramidal neurons. J. Neurosci. 17, 6512–6521 (1997).
Article CAS PubMed MATH PubMed Central Google Scholar
Mickus, T., Jung, H. & Spruston, N. Properties of slow, cumulative sodium channel inactivation in rat hippocampal CA1 pyramidal neurons. Biophys. J. 76, 846–860 (1999).
Article CAS PubMed PubMed Central Google Scholar
Jung, H.-Y., Mickus, T. & Spruston, N. Prolonged sodium channel inactivation contributes to dendritic action potential attenuation in hippocampal pyramidal neurons. J. Neurosci. 17, 6639–6646 (1997).
Article CAS PubMed PubMed Central Google Scholar
Golding, N. L., Staff, N. P. & Spruston, N. Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature 418, 326–331 (2002).
Article ADS CAS PubMed Google Scholar
Inglebert, Y., Aljadeff, J., Brunel, N. & Debanne, D. Synaptic plasticity rules with physiological calcium levels. Proc. Natl Acad. Sci. 117, 33639–33648 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Wittenberg, G. M. & Wang, S. S. H. Malleability of spike-timing-dependent plasticity at the CA3-CA1 synapse. J. Neurosci. 26, 6610–6617 (2006).
Article CAS PubMed MATH PubMed Central Google Scholar
Pike, F. G., Meredith, R. M., Olding, A. W. A. & Paulsen, O. Postsynaptic bursting is essential for ‘Hebbian’ induction of associative long-term potentiation at excitatory synapses in rat hippocampus. J. Physiol. 518, 571–576 (1999).
Article CAS PubMed PubMed Central Google Scholar
Hochbaum, D. R. et al. All-optical electrophysiology in mammalian neurons using engineered microbial rhodopsins. Nat. Methods 11, 825–833 (2014).
Article CAS PubMed MATH PubMed Central Google Scholar
Abdelfattah, A. S. et al. Sensitivity optimization of a rhodopsin-based fluorescent voltage indicator. Neuron 111, 1547–1563 (2023).
Article CAS PubMed MATH PubMed Central Google Scholar
Shepard, B. D., Natarajan, N., Protzko, R. J., Acres, O. W. & Pluznick, J. L. A cleavable N-terminal signal peptide promotes widespread olfactory receptor surface expression in HEK293T cells. PloS One 8, e68758 (2013).
Article ADS CAS PubMed PubMed Central Google Scholar
Gradinaru, V. et al. Molecular and cellular approaches for diversifying and extending optogenetics. Cell 141, 154–165 (2010).
Article CAS PubMed MATH PubMed Central Google Scholar
Adam, Y. et al. Voltage imaging and optogenetics reveal behaviour-dependent changes in hippocampal dynamics. Nature 569, 413–417 (2019).
Article ADS CAS PubMed MATH PubMed Central Google Scholar
Buchanan, E. K. et al. Penalized matrix decomposition for denoising, compression, and improved demixing of functional imaging data. arXiv 1807.06203 (2018).
Stuart, G., Spruston, N., Sakmann, B. & Häusser, M. Action potential initiation and backpropagation in neurons of the mammalian CNS. Trends Neurosci. 20, 125–131 (1997).
Article CAS PubMed MATH Google Scholar
Losonczy, A. & Magee, J. C. Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron 50, 291–307 (2006).
Article CAS PubMed MATH Google Scholar
Gasparini, S., Migliore, M. & Magee, J. C. On the initiation and propagation of dendritic spikes in CA1 pyramidal neurons. J. Neurosci. 24, 11046–11056 (2004).
Article CAS PubMed MATH PubMed Central Google Scholar
Larkum, M. E., Kaiser, K. M. M. & Sakmann, B. Calcium electrogenesis in distal apical dendrites of layer 5 pyramidal cells at a critical frequency of back-propagating action potentials. Proc. Natl Acad. Sci. USA 96, 14600–14604 (1999).
Article ADS CAS PubMed MATH PubMed Central Google Scholar
Larkum, M. E., Waters, J., Sakmann, B. & Helmchen, F. Dendritic spikes in apical dendrites of neocortical layer 2/3 pyramidal neurons. J. Neurosci. 27, 8999–9008 (2007).
Article CAS PubMed PubMed Central Google Scholar
Mines, G. R. On dynamic equilibrium in the heart. J. Physiol. 46, 349–383 (1913).
Article CAS PubMed MATH PubMed Central Google Scholar
McNamara, H. M. et al. Geometry-dependent arrhythmias in electrically excitable tissues. Cell Syst. 7, 359–370 (2018).
Article CAS PubMed MATH PubMed Central Google Scholar
Magee, J. C. & Johnston, D. A Synaptically controlled, associative signal for hebbian plasticity in hippocampal neurons. Science 275, 209–213 (1997).
Article CAS PubMed MATH Google Scholar
Chen, X. et al. Deletion of Kv4.2 gene eliminates dendritic A-type K⁺ current and enhances induction of long-term potentiation in hippocampal CA1 pyramidal neurons. 26, 12143–12151 (2006).
Kim, Y., Hsu, C.-L., Cembrowski, M. S., Mensh, B. D. & Spruston, N. Dendritic sodium spikes are required for long-term potentiation at distal synapses on hippocampal pyramidal neurons. eLife 4, 372 (2015).
Article Google Scholar
Jarsky, T., Roxin, A., Kath, W. L. & Spruston, N. Conditional dendritic spike propagation following distal synaptic activation of hippocampal CA1 pyramidal neurons. Nat. Neurosci. 8, 1667–1676 (2005).
Article CAS PubMed Google Scholar
Kampa, B. M., Clements, J., Jonas, P. & Stuart, G. J. Kinetics of Mg²⁺ unblock of NMDA receptors: implications for spike-timing dependent synaptic plasticity. J. Physiol. 556, 337–345 (2004).
Article CAS PubMed PubMed Central Google Scholar
Kamondi, A., Acsády, L. & Buzsáki, G. Dendritic spikes are enhanced by cooperative network activity in the intact hippocampus. J. Neurosci. 18, 3919–3928 (1998).
Article CAS PubMed MATH PubMed Central Google Scholar
Bittner, K. C., Milstein, A. D., Grienberger, C., Romani, S. & Magee, J. C. Behavioral time scale synaptic plasticity underlies CA1 place fields. Science 357, 1033–1036 (2017).
Article ADS CAS PubMed PubMed Central Google Scholar
Bittner, K. C. et al. Conjunctive input processing drives feature selectivity in hippocampal CA1 neurons. Nat. Neurosci. 18, 1133–1142 (2015).
Article CAS PubMed MATH PubMed Central Google Scholar
Mainen, Z. F. & Sejnowski, T. J. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382, 363–366 (1996).
Article ADS CAS PubMed MATH Google Scholar
Turner, R., Meyers, D., Richardson, T. & Barker, J. The site for initiation of action potential discharge over the somatodendritic axis of rat hippocampal CA1 pyramidal neurons. J. Neurosci. 11, 2270–2280 (1991).
Article CAS PubMed PubMed Central Google Scholar
Magee, J. C. Dendritic integration of excitatory synaptic input. Nat. Rev. Neurosci. 1, 181–190 (2000).
Article CAS PubMed MATH Google Scholar
Stuart, G. J. & Spruston, N. Dendritic integration: 60 years of progress. Nat. Neurosci. 18, 1713–1721 (2015).
Article CAS PubMed MATH Google Scholar
Markram, H., Lübke, J., Frotscher, M. & Sakmann, B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215 (1997).
Article CAS PubMed Google Scholar
Svoboda, K., Helmchen, F., Denk, W. & Tank, D. W. Spread of dendritic excitation in layer 2/3 pyramidal neurons in rat barrel cortex in vivo. Nat. Neurosci. 2, 65–73 (1999).
Article CAS PubMed Google Scholar
Stuart, G. J. & Sakmann, B. Active propagation of somatic action potentials into neocortical pyramidal cell dendrites. Nature 367, 69–72 (1994).
Article ADS CAS PubMed MATH Google Scholar
Gambino, F. et al. Sensory-evoked LTP driven by dendritic plateau potentials in vivo. Nature 515, 116–119 (2014).
Article ADS CAS PubMed MATH Google Scholar
Caya-Bissonnette, L., Naud, R. & Béïque, J.-C. Cellular substrate of eligibility traces. bioRxiv 2023.06.29.547097 (2023).
Beniaguev, D., Segev, I. & London, M. Single cortical neurons as deep artificial neural networks. Neuron 109, 2727–2739.e3 (2021).
Article CAS PubMed Google Scholar
Boahen, K. Dendrocentric learning for synthetic intelligence. Nature 612, 43–50 (2022).
Article ADS CAS PubMed Google Scholar
Poirazi, P. & Papoutsi, A. Illuminating dendritic function with computational models. Nat. Rev. Neurosci. 21, 303–321 (2020).
Article CAS PubMed Google Scholar
Bliss, T. V. P. et al. Active dendrites, potassium channels and synaptic plasticity. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 358, 667–674 (2003).
Article MATH Google Scholar
Sjöström, P. J., Rancz, E. A., Roth, A. & Häusser, M. Dendritic excitability and synaptic plasticity. Physiol. Rev. 88, 769–840 (2008).
Article PubMed MATH Google Scholar
Sacramento, J., Ponte Costa, R., Bengio, Y. & Senn, W. Dendritic cortical microcircuits approximate the backpropagation algorithm. arXiv 1810.11393v1 https://arxiv.org/abs/1810.11393 (2018).
Payeur, A., Guerguiev, J., Zenke, F., Richards, B. A. & Naud, R. Burst-dependent synaptic plasticity can coordinate learning in hierarchical circuits. Nat. Neurosci. 24, 1010–1019 (2021).
Article CAS PubMed Google Scholar
Colbert, C. M. Back-propagating action potentials in pyramidal neurons: a putative signaling mechanism for the induction of Hebbian synaptic plasticity. Restor. Neurol. Neurosci. 19, 199–211 (2001).
CAS PubMed MATH Google Scholar
Fan, L. Z. et al. All-optical physiology resolves a synaptic basis for behavioral timescale plasticity. Cell 186, 543–559.e19 (2023).
Article CAS PubMed MATH PubMed Central Google Scholar
Pfister, J.-P. & Gerstner, W. Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 26, 9673–9682 (2006).
Article CAS PubMed MATH PubMed Central Google Scholar
Gjorgjieva, J., Clopath, C., Audet, J. & Pfister, J.-P. A triplet spike-timing–dependent plasticity model generalizes the Bienenstock–Cooper–Munro rule to higher-order spatiotemporal correlations. Proc. Natl Acad. Sci. 108, 19383–19388 (2011).
Article ADS CAS PubMed PubMed Central Google Scholar
Toyoizumi, T., Pfister, J.-P., Aihara, K. & Gerstner, W. Generalized Bienenstock–Cooper–Munro rule for spiking neurons that maximizes information transmission. Proc. Natl Acad. Sci. 102, 5239–5244 (2005).
Article ADS CAS PubMed MATH PubMed Central Google Scholar
Lisman, J. & Spruston, N. Postsynaptic depolarization requirements for LTP and LTD: a critique of spike timing-dependent plasticity. Nat. Neurosci. 8, 839–841 (2005).
Article CAS PubMed MATH Google Scholar
Magee, J. C. & Grienberger, C. Synaptic plasticity forms and functions. Annu. Rev. Neurosci. 43, 95–117 (2020).
Article CAS PubMed MATH Google Scholar
Harris, K. D., Hirase, H., Leinekugel, X., Henze, D. A. & Buzsáki, G. Temporal interaction between single spikes and complex spike bursts in hippocampal pyramidal cells. Neuron 32, 141–149 (2001).
Article CAS PubMed MATH Google Scholar
Wong-Campos, J. D. et al. Voltage dynamics of dendritic integration and back-propagation in vivo. bioRxiv 2023.05.25.542363 (2023).
Sheffield, M. E. J. & Dombeck, D. A. Calcium transient prevalence across the dendritic arbour predicts place field properties. Nature 517, 200–204 (2015).
Article ADS CAS PubMed Google Scholar
Beaulieu-Laroche, L., Toloza, E. H. S., Brown, N. J. & Harnett, M. T. Widespread and highly correlated somato-dendritic activity in cortical layer 5 neurons. Neuron 103, 235–241.e4 (2019).
Article CAS PubMed PubMed Central Google Scholar
Soler-Llavina, G. J. & Sabatini, B. L. Synapse-specific plasticity and compartmentalized signaling in cerebellar stellate cells. Nat. Neurosci. 9, 798–806 (2006).
Article CAS PubMed Google Scholar
Allbritton, N. L., Meyer, T. & Stryer, L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science 258, 1812–1815 (1992).
Article ADS CAS PubMed Google Scholar
Landau, A. T. et al. Dendritic branch structure compartmentalizes voltage-dependent calcium influx in cortical layer 2/3 pyramidal cells. eLife 11, e76993 (2022).
Article CAS PubMed PubMed Central Google Scholar
Beaulieu-Laroche, L. et al. Allometric rules for mammalian cortical layer 5 neuron biophysics. Nature 600, 274–278 (2021).
Article ADS CAS PubMed Google Scholar
Vitale, P. et al. Different responses of mice and rats hippocampus CA1 pyramidal neurons to in vitro and in vivo-like inputs. Front. Cell. Neurosci. 17, 1281932 (2023).
Lin, D. et al. Time-tagged ticker tapes for intracellular recordings. Nat. Biotechnol. 41, 631–639 (2023).
Article CAS PubMed MATH PubMed Central Google Scholar
Yang, F. & Zheng, J. High temperature sensitivity is intrinsic to voltage-gated potassium channels. eLife 3, e03255 (2014).
Article PubMed PubMed Central Google Scholar
Kriegeskorte, S. et al. Cold and warmth intensify pain-linked sodium channel gating effects and persistent currents. J. Gen. Physiol. 155, e202213312 (2023).
Article CAS PubMed PubMed Central Google Scholar
Lim, D., Chu, K. K. & Mertz, J. Wide-field fluorescence sectioning with hybrid speckle and uniform-illumination microscopy. Opt. Lett. 33, 1819 (2008).
Article ADS PubMed MATH Google Scholar
Avery, R. B. & Johnston, D. Multiple channel types contribute to the low-voltage-activated calcium current in hippocampal CA3 pyramidal neurons. J. Neurosci. 16, 5567–5582 (1996).
Article CAS PubMed MATH PubMed Central Google Scholar
Kimm, T. & Bean, B. P. Inhibition of A-type potassium current by the peptide toxin SNX-482. J. Neurosci. 34, 9182–9189 (2014).
Article PubMed MATH PubMed Central Google Scholar
Pnevmatikakis, E. A. et al. Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron 89, 1–15 (2016).
Article MATH Google Scholar
Charles, A. S. et al. GraFT: Graph filtered temporal dictionary learning for functional neural imaging. IEEE Trans. Image Process 31, 3509–3524 (2022).
Article ADS PubMed MATH PubMed Central Google Scholar
Antin, B., Pasarkar, A., Park, P., Cohen, A.E., & Paninski, L. 3D econstruction of dendritic voltage using functional imaging and structural data. In prep. (2024).
Berg, S. et al. ilastik: interactive machine learning for (bio)image analysis. Nat. Methods 16, 1226–1232 (2019).
Article CAS PubMed MATH Google Scholar
Feng, L., Zhao, T. & Kim, J. neuTube 1.0: A New design for efficient neuron reconstruction software based on the SWC format. eNeuro 2, 0049–14 (2015).
Article Google Scholar
Golub, G. H., Heath, M. & Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 21, 215–223 (1979).
Article MathSciNet MATH Google Scholar
Hines, M. L. & Carnevale, N. T. The NEURON simulation environment. Neural Comput 9, 1179–1209 (1997).
Article CAS PubMed MATH Google Scholar
Johnston, D. et al. Dendritic potassium channels in hippocampal pyramidal neurons. J. Physiol. 525, 75–81 (2000).
Article CAS PubMed MATH PubMed Central Google Scholar
Sterratt, D., Graham, B., Gillies, A., Einevoll, G. & Willshaw, D. Principles of Computational Modelling in Neuroscience. (Cambridge University Press, 2023).
Lorincz, A. & Nusser, Z. Molecular identity of dendritic voltage-gated sodium channels. Science 328, 906–909 (2010).
Article ADS CAS PubMed MATH PubMed Central Google Scholar
Colbert, C. M. & Johnston, D. Protein kinase C activation decreases activity-dependent attenuation of dendritic Na⁺ current in hippocampal CA1 pyramidal neurons. J. Neurophysiol. 79, 491–495 (1998).
Article CAS PubMed MATH Google Scholar
Tsay, D., Dudman, J. T. & Siegelbaum, S. A. HCN1 channels constrain synaptically evoked Ca²⁺ spikes in distal dendrites of CA1 pyramidal neurons. Neuron 56, 1076–1089 (2007).
Article CAS PubMed PubMed Central Google Scholar
Izhikevich, E. M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572 (2003).
Article CAS PubMed MATH Google Scholar

Download references

Acknowledgements

We thank A. Preecha and S. Begum for technical assistance, F. P. Brooks for assistance with software, and B. Sabatini, M. Triplett, D. Peterka, and N. Altunkeser for helpful discussions. This work was supported by Chan Zuckerberg Initiative Dynamic Imaging grant 2023-321177 (A.E.C. and L.P.), a Vannevar Bush Faculty Fellowship (A.E.C.), a Brain Research Foundation Scientific Innovations Award BRF-SIA−2022-02 (A.E.C.), NIH grants R01-NS126043 (A.E.C.), R01-NS133755 (A.E.C.), and R01-MH117042 (A.E.C.), DoD OUSD (R&E) under Cooperative Agreement PHY−2229929 (The NSF AI Institute for Artificial and Natural Intelligence, L.P.), the Kavli Foundation and the Gatsby Charitable Foundation grant GAT3708 (L.P.), and Harvard Brain Science Initiative Postdoc Pioneers Grant (P.P.). J.D.W.-C. is a Merck Awardee of the Life Sciences Research Foundation. J.B.G., S.E.P. and L.D.L. are supported by the Howard Hughes Medical Institute. Figs. 1a, 2(a,g), 5(a,e), 6c, S18(f, g), S23a contain elements generated in BioRender.

Author information

Pojeong Park
Present address: Department of Brain Sciences, DGIST, Daegu, Republic of Korea
These authors contributed equally: Pojeong Park, J. David Wong-Campos.

Authors and Affiliations

Department of Chemistry and Chemical Biology, Harvard University, Cambridge, MA, USA
Pojeong Park, J. David Wong-Campos, Daniel G. Itkis, Byung Hun Lee, Yitong Qi, Hunter C. Davis & Adam E. Cohen
Departments of Statistics and Neuroscience, Columbia University, New York, NY, USA
Benjamin Antin, Amol Pasarkar & Liam Paninski
Janelia Research Campus, Howard Hughes Medical Institute, Ashburn, VA, USA
Jonathan B. Grimm, Sarah E. Plutkis, Katie L. Holland & Luke D. Lavis
Department of Physics, Harvard University, Cambridge, MA, USA
Adam E. Cohen

Authors

Pojeong Park
View author publications
Search author on:PubMed Google Scholar
J. David Wong-Campos
View author publications
Search author on:PubMed Google Scholar
Daniel G. Itkis
View author publications
Search author on:PubMed Google Scholar
Byung Hun Lee
View author publications
Search author on:PubMed Google Scholar
Yitong Qi
View author publications
Search author on:PubMed Google Scholar
Hunter C. Davis
View author publications
Search author on:PubMed Google Scholar
Benjamin Antin
View author publications
Search author on:PubMed Google Scholar
Amol Pasarkar
View author publications
Search author on:PubMed Google Scholar
Jonathan B. Grimm
View author publications
Search author on:PubMed Google Scholar
Sarah E. Plutkis
View author publications
Search author on:PubMed Google Scholar
Katie L. Holland
View author publications
Search author on:PubMed Google Scholar
Liam Paninski
View author publications
Search author on:PubMed Google Scholar
Luke D. Lavis
View author publications
Search author on:PubMed Google Scholar
Adam E. Cohen
View author publications
Search author on:PubMed Google Scholar

Contributions

P.P. developed the genetic constructs, performed IUE surgeries, and performed all experiments and data analysis. J.D.W.C. developed the optical system. D.G.I. performed numerical simulations. B.H.L. helped with the experimental design. Y.Q. identified and characterized the dye and opsin combination for in vivo Optopatch-V (Voltron-based Optopatch). H.C.D. developed the instrument control software. J.B.G., S.E.P., K.L.H., and L.D.L. provided HaloTag dyes and guidance on their use. B.A., A.P., and L.P. developed methods to fuse functional and structural recordings. A.E.C. supervised the project, helped with data analysis and wrote the manuscript along with P.P.

Corresponding author

Correspondence to Adam E. Cohen.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Janos Fuzik, Amelie Bergs and the other, anonymous, reviewer for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Peer review File

Description of Additional Supplementary Files

Supplementary Movie 1

Supplementary Movie 2

Supplementary Movie 3

Supplementary Software 1

Supplementary Software 2

Reporting Summary

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Park, P., Wong-Campos, J.D., Itkis, D.G. et al. Dendritic excitations govern back-propagation via a spike-rate accelerometer. Nat Commun 16, 1333 (2025). https://doi.org/10.1038/s41467-025-55819-9

Download citation

Received: 30 August 2024
Accepted: 31 December 2024
Published: 04 February 2025
DOI: https://doi.org/10.1038/s41467-025-55819-9

This article is cited by

All-optical voltage interrogation for probing synaptic plasticity in vivo
- Jacques Carolan
- Michelle A. Land
- Michael Häusser
Nature Communications (2025)