Abstract
Accelerating the discovery of novel crystal materials by machine learning is crucial for advancing various technologies from clean energy to information processing. The machine-learning models for prediction of materials properties require embedding atomic information, while traditional methods have limited effectiveness in enhancing prediction accuracy. Here, we proposed an atomic embedding strategy called universal atomic embeddings (UAEs) for their broad applicability as atomic fingerprints, and generated the UAE tensors based on the proposed CrystalTransformer model. By performing experiments on widely-used materials database, our CrystalTransformer-based UAEs (ct-UAEs) are shown to accurately capture complex atomic features, leading to a 14% improvement in prediction accuracy on CGCNN and 18% on ALIGNN when using formation energies as the target, based on the Materials Project database. We also demonstrated the good transferability of ct-UAEs across various databases. Based on the clustering analysis for multi-task ct-UAEs, the elements in the periodic table can be categorized with reasonable connections between atomic features and targeted crystal properties. After applying ct-UAEs to predict formation energy in hybrid perovskites database, we realized an improvement in accuracy, with a 34% boost in MEGNET and 16% in CGCNN, showcasing their potential as atomic fingerprints to address the data scarcity challenges.
Similar content being viewed by others
Introduction
The development of deep learning (DL) and machine learning (ML) has created research methods for kinds of research fields1,2,3,4. In materials science, this development is leading to discoveries of the material properties, which may be a challenging task for traditional methods5,6,7,8. Many DL algorithms and models have been proposed, such as the Crystal Graph Convolutional Neural Network (CGCNN)9, MatErials Graph Network (MEGNET)10, Atomistic Line Graph Neural Network (ALIGNN)11, improved Crystal Graph Convolutional Neural Networks (iCGCNN)12, OrbNet13, and so on14,15,16,17,18,19,20,21,22,23,24. They have achieved success in kinds of applications, such as learning properties from multi-fidelity data25, discovering stable lead-free hybrid organic-inorganic perovskites26, mapping the crystal-structure phase27, designing material microstructures28, and etc.
In the solid-state theory, the features and spatially topological arrangements of the constituent atoms in crystals or other condensed systems determine their properties, which are intricately encapsulated into the entity of “atomic embedding”29,30 in the DL algorithms. Specifically, the atomic embedding is the process of inputting the properties of atoms into crystal model digitally, and this idea is originated from the natural language processing technique, in which the word embeddings transform the way textual data is represented31,32,33. An appropriate atomic embedding can accelerate the training of model, improve the accuracy of prediction, and some explainable information can be derived from it34,35,36,37,38. Currently, most attention in the field of materials informatics has been focused on the designing of crystal model architecture, for improving the accuracy of property prediction, while the studies on the atomic embedding are rare. Typically, it is common to simply adopt 0–1 embedding as the atomic embedding algorithm9,10, which generally generates a sparse embedding matrix not conducive to the information extraction of models.
In recent years, a large number of Transformer-based training methods39 and predictive models, such as OrbNet40, 3D-Transformer41, and so on, have been developed in the field of chemical molecular property and structure prediction, which are believed to be able to fully leverage the advantages of the Transformer architecture in processing atomic interactions and capturing the three-dimensional structures, enabling efficient representation of the complex interactions between atoms. Motivated by these advancements, we developed the home-made CrystalTransformer model to generate universal atomic embeddings called ct-UAEs based on transformer architecture, which learns a unique “fingerprint” for each atom, capturing the essence of their roles and interactions within the materials. The obtained embeddings are then transferred to different DL models. After using the clustering method of the Uniform Manifold Approximation and Projection (UMAP) clustering42, we categorized atoms into different groups, analyzing the connection between the embeddings and the real atoms.
Results and discussions
Universal atomic embeddings
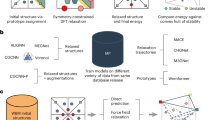
Generally, when predicting the properties such as formation energy and bandgap of a material in deep-learning models, each atom is first embedded as features. This embedding process is the intrinsic process of GNNs models such as CGCNN, ALIGNN, and MEGNET. Then the deeper feature extraction processes, including information transmission and aggregation, node feature updating, etc., are conducted to predict the crystal properties. In this context, these GNNs are denoted as back-end models, while the methods for obtaining atomic embeddings are denoted as front-end models. Essentially, the parameter of atomic embeddings can be transferred using pretrained parameters or constructed based on predefined properties, which is realized in the front-end model of methods (I, II, III), as shown in Fig. 1b, c.
aThe workflow of front-end and back-end model using atomic embeddings. Atomic Embedding is derived from the front-end models while graph neural networks (GNN) serve as back-end models trained for different properties. b The process and principles of Method (I, II) which use deep learning to train on large database and generate atomic embeddings. Method I uses Crystaltransformer to produce universial atomic embeddings (UAE), while Method II uses the traditional GNN model to produce ordinary atomic embedding. c The process and principles of Method III, which artificially constructs atomic embeddings using query databases or mapping known atomic properties to a 0–1 vector or one-hot vector in most cases.
As shown in Fig. 1a, for the front-end model, we used our proposed CrystalTransformer to generate atomic embeddings (Method I). Other pretrained atomic embeddings used GNN models (Method II shown in Fig. 1b). While some used artificially constructed features based on known atomic properties like the autoencoder-based approach43(Method III shown in Fig. 1c). The CrystalTransformer model learns atomic embeddings directly from chemical information in crystal databases. Compared to Method III, which generates atomic embeddings by processing on a predefined set of atomic properties, our proposed ct-UAE can adapt to any desired material property without relying on predefined atomic attributes.
To examine the atomic embeddings tensors obtained from different models, we used MP and MP* dataset for formation energy (Ef) and PBE bandgap (Eg), which are key properties for evaluating their chemical stabilities and electronic performances. MP stands for the 2018.6.1 version for MP44 dataset, which contains 69,239 materials with properties. MP* denotes the 2023.6.23 version, which contains 134,243 materials. For training, validation, and testing splits, we followed the distribution of 60,000 (training), 5000 (validation), and 4239 (testing) for the MP dataset as used in previous works. While the MP*44, and their properties are split into 80% training, 10% validation, and 10% testing sets. It is worthy to note that, as discussed in Supplementary 1, the gaps in the band structures of solids in materials databases such as the MP, which are defined as the difference between the eigenvalues of the conduction-band minimum (CBM) and valence-band maximum (VBM), were obtained by solving the Kohn-Sham (KS) equation with exchange-correlation (xc) in the Perdew-Burke-Ernzerhof (PBE) parametrization45. In semiconductors and insulators, these PBE bandgaps \({E}_{g}^{PBE}\) are not equal to their fundamental gaps EG, but differ by a term called derivative discontinuity of the xc energy Δxc46, leading to the substantial underestimation of \({E}_{g}^{PBE}\) compared to EG as large as 40–50%47,48. However, since the KS equation is constructed based on the kinetic energy and Coulomb potentials between charged particles (electrons and ions), when specific exchange-correlation functionals are used, the eigenvalues of the KS equation should capture the major physical interactions within the interacting systems. Therefore, if the PBE bandgaps are used as target in the deep learning model, the derived atomic embedding should involve the atomic properties and the structural information, since \({E}_{g}^{PBE}{{\rm{s}}}\) have involved such information when constructing the KS Hamiltonian using the PBE-type xc functional.
Front-end models as CrystalTransformer, CGCNN, ALIGNN, and MEGNET are first pre-trained on the expanded MP* dataset, focusing on the bandgap energy Eg and formation energy Ef predictive tasks. Subsequently, the extracted atomic embeddings are integrated into a CGCNN back-end model and trained on the original MP dataset, which results in CT-CGCNN, CG-CGCNN, ALI-CGCNN, and so on. Table 1 shows a comparative MAE analysis to evaluate the relative performance enhancements attributable to the front-end atomic embeddings, denoted as N-CGCNN in Table 1 (N means the front-end model described above). As listed in Table 1, among the atomic embeddings pre-trained by different models, those who use ct-UAEs (CT-CGCNN) perform the best, with 14% and 7% reduction in MAE for Ef and Eg, also outperforming the best GNN front-end embeddings (CG-CGCNN in this context) by 4% and 5% for both properties, respectively. The predicted formation energy versus target formation energy for those models are listed in Fig. 2a–c.
Ef is the formation energy. MAE refers to the Mean Absolute Error. R2 is the R-squared value in predicting each property. None means trained from scratch with no front-end model, and CT indicates CrystalTransformer or ct-UAE. a–c Plots of predicted formation energy versus target formation energy for CGCNN9, MEGNET10, and ALIGNN11 models on the MP dataset. The upper part and the right part denotes target and prediction data distribution respectively. The MAE and R2 for None-CGCNN are 0.083 eV/atom and 0.982, respectively, while for CT-CGCNN, the MAE and R2 are 0.073 eV/atom and 0.986 respectively. The MAE and R2 for None-MEGNET are 0.051 eV/atom and 0.994, respectively, while for CT-MEGNET, the MAE and R2 are 0.049 eV/atom and 0.994 respectively. The MAE and R2 for None-ALIGNN are 0.022 eV/atom and 0.997, respectively, while for CT-CGCNN, the MAE and R2 are 0.018 eV/atom and 0.997 respectively. d The distribution curve for the formation energy across the entire dataset. Source data are provided as a Source Data file.
Furthermore, as listed in Table 1, performances of GNN models like CGCNN, MEGNET, and ALIGNN were enhanced by using the CrystalTransformer-generated atomic embeddings (ct-UAEs) evaluated on the MP dataset. The CGCNN model transferred with CrystalTransformer-generated embeddings (ct-UAEs), denoted by CT-CGCNN in Table 1, shows a significant reduction in MAE values for formation energy Ef, decreasing from 0.083 eV/atom to 0.071 eV/atom, a reduction of 14%, and for bandgap Eg, decreasing from 0.384 eV to 0.359 eV, a reduction of 7%. A similar reduction can be observed for MEGNET, denoted by CT-MEGNET in Table 1, with Ef decreasing from 0.051 eV/atom to 0.049 eV/atom, a 4% reduction, and for bandgap Eg, decreasing from 0.324 eV to 0.304 eV, a reduction of 6%. ALIGNN also exhibits an improvement in Ef prediction accuracy, denoted by CT-ALIGNN in Table 1, decreasing from 0.022 eV/atom to 0.018 eV/atom, a reduction of 18%, and for bandgap Eg, decreasing from 0.276 eV to 0.256 eV, a 7% reduction.
Transferability of ct-UAEs
To further investigate the performance of the ct-UAEs on different properties, task-generated embeddings are transferred to different tasks. For example, Ef-task-generated atomic embeddings are applied to bandgap prediction and Eg-task-generated embeddings to formation energy task. The results are listed in Table 2, denoted as \({{{\rm{CT}}}}^{{E}_{f}}\)-CG and \({{{\rm{CT}}}}^{{E}_{g}}\)-CG. Embeddings trained on bandgap tasks, when transferred to the formation task, lead to a measurable improvement in accuracy with the MAE decreasing from 0.083 to 0.078 eV/atom, a 6% reduction. Further, although trained on a simple task such as formation energy, the embedding reduces MAE on the more challenging bandgap prediction by 0.2%.
Further experiments focus on multi-task-generated embeddings (MT). As listed in Table 2, the embeddings trained from two properties (formation energy and bandgap), denoted as MT@2p, yield better performance compared to single-task-generated embeddings. When transferred to the CGCNN model (CTMT@2p-CGCNN), the model achieves an MAE of 0.068 eV/atom for Ef and 0.357 eV for Eg, outperforming the baseline CGCNN (by an 18% reduction in Ef and a 7% reduction in Eg) as well as the CGCNN variants using single-task embeddings, with a 4% reduction in Ef and 0.5% for bandgap.
Additional multi-task variants (MT@3p and MT@4p) incorporating total energy and total magnetization are introduced. When introducing MT@3p with an additional property of total energy, a 0.2% reduction in bandgap MAE is achieved, with formation energy almost unchanged. However, the introduction of magnetization in MT@4p leads to a slight increase in the MAE for bandgap prediction from 0.357 to 0.367 eV, which is probably due to the physical differences between these two properties.
Then, different training strategies are used to evaluate the performance of the model, and the results are listed in Table 3. The CTfreeze-CGCNN, which employs frozen pre-trained embeddings from the CrystalTransformer or ct-UAEs, achieves an MAE of 0.073 eV/atom for formation energy Ef and 0.358 eV for bandgap Eg. However, when integrating the coordinate embeddings together with ct-UAEs (chemistry information) into the CGCNN framework (CTchem+coords-CGCNN), the MAE increases from 0.071 eV/atom in the atom-embedding-only model to 0.085 eV/atom. Similarly, the MAE worsens from 0.359 eV to 0.395 eV for bandgap Eg.
The ability and transferability of the universal atomic embedding are further tested on different databases and tasks. Each is cut into 8:1:1 for training, validation, and testing. Details on the dataset can be found in Supplementary 2A. As for the Jarvis dataset49, the result is shown in Table 1. The CT-CGCNN model demonstrates an improvement in predicting both formation energy Ef and bandgap energy Eg. The MAEs for formation energy and bandgap are reduced from 0.080 eV/atom to 0.066 eV/atom by 17.5% and from 0.531 eV to 0.463 eV by 12.8%, respectively.
The embedding is further evaluated on the MC3D dataset. Properties such as total energy (E) are chosen as the task, and the result is shown in Table 1. The MAE of CGCNN is reduced from 5.558 eV to 5.341 eV, indicating a 3.9% improvement. For the ALIGNN model, the MAE remains nearly unchanged. While for the MEGNET model, the MAE decreases from 5.029 eV to 4.687 eV, showing a 6.8% improvement.
Additionally, we also investigated the suitability of ct-UAE on energy-conserving interatomic potential (IAP) models, which are trained based on the MPtrj dataset50. As demonstrated in Supplementary 4, we trained ct-UAE on vectorial and scalar targets, i.e., force, stress, and energy. To benchmark, we re-trained CHGNet50, M3GNet51, and MACE52 models on the MP-RELAX dataset proposed by M3GNet51. Remarkably, adding ct-UAEs to CHGNet resulted in a significant reduction in force loss, from 0.284 to 0.242 (a 14.8% decrease), along with a reduction in stress loss from 1.496 to 1.437 and a slight decrease in energy loss from 0.460 to 0.457. For M3GNet, ct-UAE led to a slight reduction in total loss (energy, force, stress) from 2.1236 to 2.1234 and in energy loss from 0.3597 to 0.3595, indicating a minor performance improvement. However, for MACE, the ct-UAE did not lead to a reduction in loss.
Interpretability
This investigation leverages straightforward clustering algorithms to conduct an in-depth analysis of ct-UAEs. Here, the UMAP clustering method42 is employed to project these ct-UAEs into a two-dimensional space, thereby offering a means to intuitively understand atomic characteristics in a reduced dimensional setting. Consequently, the dimensionality of the ct-UAEs is reduced from the original 89 × 128 to 89 × 2, and through the application of the K-means clustering method53 in the two-dimensional space, atoms are further categorized into three distinct groups as shown in Fig. 3a. The t-SNE clustering method54 is used as an additional supplementary comparison, as shown in Fig. S1. Furthermore, the community detection method55 is also used to directly cluster ct-UAEs into three categories without dimension reduction, as an additional method to investigate the interpretability of ct-UAEs, which is shown in Fig. S2.
a UMAP (Uniform Manifold Approximation and Projection) maps ct-UAEs into two dimensions denoted as Component 1 and 2, while K-means method clusters them into three categories denoted by three colors. The shadow background reflects the number of elements in the cluster in the region. The darker shadow indicates a higher number of elements in that cluster region. b, c Elbow plot and silhouette score graph for optimal cluster number. The dashed line in (b) is located at 3, representing the silhouette score being at a relatively high level. So is the dashed line in (c), indicating that the slope of the Sum of Squared Error (SSE) curve is relatively steep when the number of clusters is 3. Five random seeds are used to get averaged results. d–f The violin plots of formation energy, bandgap, and total magnetization of oxide compounds and oxygen allotropes from the Materials Project dataset, categorized into Classes A, B, and C using MT@4p embedding with UMAP. The total numbers of samples for Class A, Class B and Class C shown in (d–f) are 2197, 2719, and 7752, respectively. Parameters like outliers or center for violin plots are listed in the Source data. Source data are provided as a Source Data file.
To determine the best number of clusters for atoms, the elbow plots56 and siltouette coefficient graphs56 are needed, with quantitative analysis shown in Fig. 3b, c. Both elbow plot and silhouette coefficient graph demonstrate that 3 or 4 clusters’ solution is the best choice for the classification of atoms. In this work, the CrystalTransformer model can be trained with 2, 3 or 4 different properties, (but these atomic embeddings all show the same best number of clusters of 3 or 4 clusters).
Based on the clustering results, most of the elements in the periodic table can be categorized, as shown in Fig. 3a. This example divides all elements into 3 classes, called as Class A (the green cluster), Class B (the yellow cluster), and Class C (the blue cluster). And individual elements that don’t appear in datasets are colored with gray. Essentially, this clustering scheme based on ct-UAEs differs from the traditional classification rules of elements in the periodic table arranged based on the atomic number of elements, but for the clarity and convenience, we also presented the results using the periodic table scheme as well. The detailed result of the UMAP clustering shown in the periodic-table scheme is demonstrated in Fig. S3 in Supplementary 5.
To further interpret the element classification and without loss of generality, we chose oxide compounds from the Materials Project, which yielded a total of 62,068 retrieved materials. From these, we filtered for those that contain data on formation energy, bandgap, and total magnetization. We then categorized the filtered materials into three groups according to the previously determined element classification Classes A, B, and C clustered by MT@4p embedding using UMAP. Each group contains only elements from the corresponding class and oxygen, with no inclusion of elements from other classes. The analysis resulted in 2197 compounds containing oxygen and Class A elements, 2719 compounds containing oxygen and Class B elements, and 7752 compounds containing oxygen and Class C elements. Violin plots for each of the three properties are shown in Fig. 3d–f.
As illustrated in Fig. 3d, the formation energy of oxide compounds for the three classes of elements shows significant differences. the formation energy of Class A is concentrated between −2.5 eV/atom and −4.0 eV/atom, indicating a relatively high chemical stability for oxides containing A-class elements. Class B exhibits the widest range of formation energies, from near 0 eV/atom to −4 eV/atom. The formation energy of oxides containing C-class elements is concentrated between −1.0 eV/atom and −2.5 eV/atom, also indicating their relatively good chemical stability, albeit with generally lower stability compared to Class A. Specifically, the Class A includes Group IIA, IIIB, and IVB elements, and their similar characteristics is the tendency that valence electrons participate in metallic bonding, contributing to the more compact lattice structure57,58,59. The Class B includes most of Groups VB to VIIIB, with their d-orbital electrons possessing close energy levels, which distinguishes them from the main group elements dominated by s-orbital electrons and lanthanides and actinides influenced by f-orbital electrons. Previous studies reported that these elements can participate the formation of crystals with unique electrical and thermal conductivity properties, as well as distinctive catalytic capabilities60,61,62,63,64. The Class C includes Group IA, IB, and IIB elements, along with main group metals and nonmetals. These elements show electronic exchange and sharing abilities in solid states. Among them, the alkali metals and halogen tend to participate in the electron sharing to form the most stable structure. Group IB and IIB metals have relatively stable d-orbital electrons, but can provide additional electron density during the formation of crystals, resulting in high melting points and good electrical conductivity65.
As illustrated in Fig. 3e, the bandgap distribution of oxide compounds for the three classes of elements also reveals distinct behaviors. The bandgaps of oxides containing A-class elements are concentrated between 3 eV and 6 eV, indicating that they are primarily wide-bandgap semiconductors. The bandgap for Class B is concentrated between 0.5 eV and 2.5 eV, reflecting narrow-bandgap semiconducting behavior. The bandgap for Class C is concentrated between 1 eV and 4 eV, which fall within the typical semiconductor range.
Lastly, Fig. 3f shows the distribution of magnetization across the three classes of elements. The magnetization of most elements across all three classes is concentrated near 0 μB, indicating that, most oxides exhibit very low net magnetic moments, characteristic of paramagnetic or diamagnetic materials. Specifically, the magnetization of Class A is almost entirely centered at 0 μB. For Class B, the distribution of magnetization is broader, and a substantial number of elements have magnetization values greater than 5 μB, demonstrating notable ferromagnetic behavior. Also, Fe and Co are in class B. The magnetization of Class C is primarily distributed between 0 μB and 5 μB.
To further investigate the intrinsic information of the embeddings, we conduct reverse training experiments, which involves taking a series of important elemental properties, including atomic radius, boiling temperature, melting temperature, electrical conductivity, first ionization energy as training targets to train a Catboost model66. 80% of atomic embeddings are selected randomly as training data, while the rest serves as validation to calculate R2 (coefficient of determination). The R2 for the model in predicting each property is calculated, with the best results listed in Table 4, which reveals that, the Catboost model exhibits high values of R2 larger than 0.78. So even with small-set data, the ct-UAEs are able to establish a robust connection with the physical and chemical properties of atoms. We further employed the SHAP67 algorithm to determine the most important dimensions contributing to the final results. The outcome is averaged over multiple random seeds to maintain stability. While the results shown in Table 4 reveal that certain properties correspond to specific dimensions, which acts like genes. The calculated SHAP value is shown in Fig. S4.
To further understand the difference between embeddings derived from different multi-tasks properties. We use the Dynamic Time Warping (DTW)68 method to measure the similarity between mean embedding from MT@2p, MT@3p and MT@4p. Averaging and window smoothing of size 5 are first conducted to reduce noise information and uncover the inner trends. The threshold of 0.013 is used to distinguish periods of high similarity from those with divergence, which was further shown by the inverse DTW distance in Fig. 4b, and the reference line at 0.26 × 103 is served as a benchmark to underscore the distinction between embeddings. Our analysis revealed a pronounced alignment as shown in Fig. 4, suggesting similar feature evolution despite the introduction of more tasks related to total energy and total magnetization.
MT@np demotes embeddings trained with muti-task learning on n properties. MT@2p is trained using formation energy and bandgap, while MT@3p adds total energy, and MT@4p further includes total magnetization. DTW is the Dynamic Time Warpin method. a Multi-task embedding comparison for MT@2p, MT@3p, and MT@4p, highlighting DTW similarity regions (max distance < 0.013). The average standard deviation of MT@2p, MT@3p and MT@4p across different dimensions are 0.0358, 0.0397, and 0.0481 respectively. Similar standard deviations denote similar magnitude of variance per atom. b Inverse DTW distances, with notable variance and a reference line at 0.26 (scaled by 103). This value is determined to cover the curves with similar trends in (a) and distinguish between similar and dissimilar trend regions. Source data are provided as a Source Data file.
As shown in Fig. 4a, the blue region indicate that the coresponding embeddings share some similarity, which also equals to the values in Fig. 4b being above the threshold. The observation indicates that although the target properties is diverse, the basic trends of the embeddings remain largely the same. Of particular note is the high similarity between the embeddings of the MT@3p and MT@2p models, which only differ by one total energy task. In contrast, the introduction of magnetic properties in the MT@4p model led to al disagreements but still contained relatively sufficient similarities. The fact that the average standard deviation of each embedding is 0.0358, 0.0397, and 0.0481 shows that the average variance of the embeddings are close to each other. Further, we calculate the variance of each embeddings’ standard Deviation (std), the result is 0.016, 0.014, and 0.017, which implies that the std of the 128 dimensions is stable.
Application in hybrid organic-inorganic perovskite crystals
Hybrid organic-inorganic perovskite (HOIP) materials are gaining tremendous attention for their outstanding optoelectronic properties. However, studying on the HOIP materials is hindered due to the scarcity of training data69,70. Contrary to other materials, HOIP crystals lack a large and high-quality database because of their complex synthesis. Such scarcity of data presents a significant challenge for traditional deep learning models.
After merging two distinct datasets of HOIP materials69,70, we created a more diverse dataset containing 2103 HOIP crystals, which is still small compared to other material databases such as the MP dataset44. Figure 5a shows the workflow for applying ct-UAEs to predict properties of HOIP materials, with the results presented in Fig. 5. The MAE of CGCNN model for predicting formation energy (Ef) of HOIP materials was reduced significantly, from 0.054 eV/atom to 0.046 eV/atom by a 16% improvement. Similarly the MAE of MEGNET reduces from 0.032 eV/atom to 0.021 eV/atom, by nearly 34.38%. For ALIGNN, the MAE values are not in the same magnitude as the aforementioned models. Figure 5b, c shows the plot of predicted formation energy versus the target formation energy for the MEGNET and CGCNN models.
Ef is the formation energy. MAE is the Mean Absolute Error. R2 is the R-squared value in predicting each property. The prefix None- denotes models that do not use ct-UAE. The prefix CT- indicates models that use ct-UAE. The perfix CTMT@np is models that use ct-UAE trained by n properties. a Schematic representation of the workflow for applying ct-UAEs to predict properties of perovskite materials. When the back-end model is MEGNET10, the MAE for UAE-free case is 0.32 eV/atom. Using the transfer learning strategy with ct-UAE results in an MAE of 0.030 eV/atom, while the MAE for the transfer learning strategy with ct-UAE trained using multi-task learning is 0.021 eV/atom. b, c Predicted formation energy versus target formation energy for the MEGNET10 and CGCNN9 models. The upper part and the right part denotes target and prediction data distribution respectively.
Methods
The crystaltransformer model
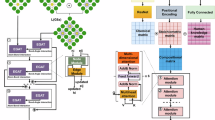
To construct universal atomic embeddings, the vanilla transformer algorithm is introduced as the main part of the model, resulting in the home-made model named CrystalTransformer, whose architecture is shown in Fig. 6. When given an atom input in a batch of size batch for N-atom with L features per atom (L denotes a one-hot encoding of the atomic species) and the coordinate input with batch × N × D size (Here D indicates the spatial dimension (equals 3 in this context)), the model first topologically augments the coordinates input using translation and rotation transformation. The details of the augmentation are described in Supplementary 6. After that, both inputs are applied by linear transformation to embed features to a dimension of C.
where A denotes the one-hot initialization for atom input features, with the dimension of batch × N × L. Tensor X denotes the atom position coordinates, with the dimension of batch × N × D. WA and WX denote the weight matrices for atom features and position coordinates respectively, while bA and bX denote their corresponding biases. \({A}^{{\prime} }\) and \({X}^{{\prime} }\) have the same dimension of batch × L × C. It should be noted that the WA and bA matrix or the AWA + bA output (A is one-hot input) are the embedding matrix of the atomic information, which is the most important part of the CrystalTransformer model. The transformed atoms and position features are then concatenated along the feature dimension by,
where M is the concatenated feature matrix with the shape of batch × N × 2C. Then, the Multihead Transformer’s encoder is applied to M, which consists of multiple layers of multihead-self-attention and feed-forward neural networks, written as,
where Z(0) = M and l indexes the layer of the encoder. Each Multihead Transformer encoder layer processes the input sequence and updates it through multihead self-attention mechanisms and point-wise feed-forward networks, as described in the Supplementary 2B section. After processing the crystal structure features through the Transformer encoder, the CrystalTransformer model selects the first token from the output sequence for downstream prediction tasks, which is passed through a linear layer to produce the network’s predicted material properties as,
where \({Z}_{1}^{(L)}\) denotes the first token of the final encoder layer’s output, and ypred is the material properties predicted by the network.
a The main part of CrystalTransformer model. InputA and InputX denote atom (chemistry) and structure (coordinates) information respectively. After passing through the information extraction layers, the inputs are transformed into the A matrix and X matrix. These two matrices are then concatenated and processed through the Transformer layers which include multi-head self-attention, feedforward layers, and other components, to produce the output target. b Chemical information extraction layer. InputA is first passed through an embedding layer, followed by a linear transformation. c Coordinates information extraction layer. InputX undergoes data augmentation followed by a linear transformation.
The Transformer’s multihead-self-attention mechanisms allow the model to learn representations that can capture the underlying mechanisms for material properties. It not only processes the chemical part, but also incorporates the coordinates part. To further investigate the role of the coordinates part of CrystalTransformer in model performance, an ablation study and qualitative analysis are conducted as described in Supplementary 7, which shows that the coordinates part encapsulates important geometric characteristics of crystal systems and is important in training the embeddings. Without the coordinates part, the training MAE will increase, with MAE from 0.395 eV to 0.458 eV when trained on the MP bandgap dataset. By comparison of the definition of attention weights αij in Transformer as shown in Eq (S16), and the general expression describing physical interaction between atoms V(rij) as shown in Eq (S17), it is straightforward that the attention weight αij is analogous to the physical interaction coefficients between atoms V(rij), which suggests that the attention mechanism can learn spatial relationships and interaction properties in real physical systems.
The CrystalTransformer method exhibits a theoretical complexity primarily driven by the self-attention mechanism in its Transformer layers. For a crystal with n atoms, the self-attention mechanism computes pairwise correlations with a complexity of \({{\mathcal{O}}}({n}^{2}\cdot d)\), where d is the dimensionality of atomic features. Traditional Graph Neural Networks (GNNs), by contrast, typically operate with a lower theoretical complexity of \({{\mathcal{O}}}(n\cdot {d}^{2})\) due to their localized edge-based interactions. Despite this, the manageable scale of n in conventional crystal structures results in a feasible runtime for both approaches. Real runtime experiments show CrystalTransformer required 21 seconds for 100 batches with 512 crystals per batch, while CGCNN needed 10 seconds, which is evenly matched. Further details are available in Supplementary 3.
In order to test the CrystalTransformer model’s performance on crystal datasets, we conducted performance assessments against established graph neural network models. These models were evaluated on the MP and MP* dataset for formation energy (Ef) and PBE bandgap (Eg), As listed in Table 1, the None-CrystalTransformer, None-CGCNN, None-MEGNET, None-ALIGNN, denote the models trained from scratch without any front-end model, which is the traditional method. It is clear that, despite lacking the prior inputs of atomic features and edge information of crystals, the None-CrystalTransformer demonstrates competitive accuracy in predicting material properties, i.e., only 1–4 times larger in Ef and 1–3 times larger in Eg compared to the traditional GNNs models on MP/MP* datasets. The increase in MAE is partly because it does not strictly rely on predefined graph structures and inductive bias. The lack of certain inductive biases compels the model to acquire this knowledge independently. Although diminishing its predictive capabilities, it does encourage the model’s parameters to assimilate additional information, leading to more informative embeddings, as described in Table 1.
Crystal-symmetry restrictions and data augmentation
The ct-UAE method accounts for the rotational and translational invariance through its architecture and data augmentation strategy as described in Supplementary 6. While the ct-UAE front-end indeed does not explicitly enforce rotational and translational invariance, the back-end GNN model is designed to ensure this restriction of symmetries. Actually, the front-end model can easily learn and maintain symmetries through data augmentation. To validate this assertion, firstly we used a stronger data augmentation method to train the MT@3p model on the MP* dataset. Then a group of crystals are randomly selected, and subjected to random augmentations through rotations and translations. The consistency of the output vectors from these augmented samples was assessed using pairwise cosine similarity and Euclidean distance. The trained MT@3p model achieved an average cosine similarity of 0.998 and an average Euclidean distance of 0.275, indicating that the output vectors were nearly identical across augmentations. Notably, a recent study employing a similar method of data augmentation demonstrated that, unconstrained model architectures like transformers can be trained to achieve a high degree of invariance such as rotational invariance by learning these symmetries from data71, and this unconstrained architecture can, in fact, lead to improved performance, which is essentially consistent with the rationale behind our proposed front-end model of CrystalTransformer.
Multi-task learning method
MTL72,73,74 (multi-task learning) is a learning method. The model is trained simultaneously on different tasks, while the parameter is optimized toward the trend that all tasks improve. This training method enhances generalization. In the context of CrystalTransformer, MTL stands for different properties for materials. The loss function is a weighted sum of the loss for each task:
where Lossi could be MSE or MAE, wi are the task weights, and i indexes the task. MTL is capable of ensuring the universality of atomic embeddings, rather than developing an UAE that is specially optimized on a single task.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The embeddings generated by our ct-UAEs are available on Github (https://github.com/fduabinitio/ct-UAE) under MIT license. ct-UAEv1.075(https://doi.org/10.5281/zenodo.14557908) contains all the embeddings used in this work. Source data are provided with this paper as a Source Data file. Source data are provided with this paper.
Code availability
The ct-UAE source code used in this study is publicly available on GitHub (https://github.com/fduabinitio/ct-UAE) under MIT license. ct-UAEv1.075 (https://doi.org/10.5281/zenodo.14557908) was used to generate all embeddings in this work.
References
Jumper, J. et al. Highly accurate protein structure prediction with alphafold. Nature 596, 583–589 (2021).
Davies, A. et al. Advancing mathematics by guiding human intuition with AI. Nature 600, 70–74 (2021).
Kirkpatrick, J. et al. Pushing the frontiers of density functaionals by solving the fractional electron problem. Science 374, 1385–1389 (2021).
Zhou, J. et al. Graph neural networks: a review of methods and applications. AI open 1, 57–81 (2020).
Zhuo, Y., Mansouri Tehrani, A. & Brgoch, J. Predicting the band gaps of inorganic solids by machine learning. J. Phys. Chem. Lett. 9, 1668–1673 (2018).
Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O. & Walsh, A. Machine learning for molecular and materials science. Nature 559, 547–555 (2018).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Wu, Z. et al. A comprehensive survey on graph neural networks. IEEE Transact. Neural Netw. Learn. Syst. 32, 4–24 (2020).
Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).
Chen, C., Ye, W., Zuo, Y., Zheng, C. & Ong, S. P. Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 31, 3564–3572 (2019).
Choudhary, K. & DeCost, B. Atomistic line graph neural network for improved materials property predictions. npj Comput. Mater. 7, 185 (2021).
Park, C. W. & Wolverton, C. Developing an improved crystal graph convolutional neural network framework for accelerated materials discovery. Phys. Rev. Mater. 4, 063801 (2020).
Qiao, Z., Welborn, M., Anandkumar, A., Manby, F. R. & Miller, T. F. Orbnet: deep learning for quantum chemistry using symmetry-adapted atomic-orbital features. J. Chem. Phys. 153, 124111 (2020).
Gasteiger, J., Groß, J. & Günnemann, S. Directional message passing for molecular graphs. In Proc. International Conference on Learning Representations (ICLR, 2020).
Gasteiger, J., Giri, S., Margraf, J. T. & Günnemann, S. Fast and uncertainty-aware directional message passing for non-equilibrium molecules. In Machine Learning for Molecules Workshop at NeurIPS (NIPS, 2020).
Shui, Z. & Karypis, G. Heterogeneous molecular graph neural networks for predicting molecule properties. In 2020 IEEE International Conference on Data Mining (ICDM), pages 492–500. (IEEE, 2020).
Schütt, K. T., Arbabzadah, F., Chmiela, S., Müller, K. R. & Tkatchenko, A. Quantum-chemical insights from deep tensor neural networks. Nat. Commun. 8, 13890 (2017).
Anderson, B., Hy, T.-S. & Kondor, R. Cormorant: covariant molecular neural networks. In Proc. 33rd International Conference on Neural Information Processing Systems (NIPS, 2019).
Zhang, S., Liu, Y. & Xie, L. Molecular mechanics-driven graph neural network with multiplex graph for molecular structures. In Machine Learning for Molecules Workshop at NeurIPS (NIPS, 2020).
schuett, K. T. et al. Schnetpack: a deep learning toolbox for atomistic systems. J. Chem. Ther. Comput. 15, 448–455 (2018).
Jha, D. et al. Elemnet: deep learning the chemistry of materials from only elemental composition. Sci. Rep. 8, 17593 (2018).
Westermayr, J., Gastegger, M. & Marquetand, P. Combining schnet and sharc: the schnarc machine learning approach for excited-state dynamics. J. Phys. Chem. Lett. 11, 3828–3834 (2020).
Wen, M., Blau, S. M., Spotte-Smith, E. W. C., Dwaraknath, S. & Persson, K. A. Bondnet: a graph neural network for the prediction of bond dissociation energies for charged molecules. Chem. Sci. 12, 1858–1868 (2021).
Isayev, O. et al. Universal fragment descriptors for predicting properties of inorganic crystals. Nat. Commun. 8, 15679 (2017).
Chen, C., Zuo, Y., Ye, W., Li, X. & Ong, S. P. Learning properties of ordered and disordered materials from multi-fidelity data. Nat. Comput. Sci. 1, 46–53 (2021).
Lu, S. et al. Accelerated discovery of stable lead-free hybrid organic-inorganic perovskites via machine learning. Nat. Commun. 9, 3405 (2018).
Chen, D. et al. Automating crystal-structure phase mapping by combining deep learning with constraint reasoning. Nat. Machine Intell. 3, 812–822 (2021).
Lee, X. Y. et al. Fast inverse design of microstructures via generative invariance networks. Nat. Comput. Sci. 1, 229–238 (2021).
Zhang, X., Zhou, J., Lu, J. & Shen, L. Interpretable learning of voltage for electrode design of multivalent metal-ion batteries. npj Comput. Mater. 8, 175 (2022).
Ju, S. et al. Exploring diamondlike lattice thermal conductivity crystals via feature-based transfer learning. Phys. Rev. Mater. 5, 053801 (2021).
Devlin, J., Chang, M. W., Lee, K. & Toutanova, K. BERT: pre-training of deep bidirectional transformers for language understanding. In Proc. 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (Long and Short Papers) 4171–4186 (ACL, 2019).
Kim, D., Saito, K., Saenko, K., Sclaroff, S. & Plummer, B. Mule: multimodal universal language embedding. Proc. AAAI Conference on Artificial Intelligence. 34, 11254–11261 (2020).
Li, Y. & Yang, T. Word embedding for understanding natural language: a survey. Guide Big Data Appl. 26, 83–104 (2018).
Lee, J. & Asahi, R. Transfer learning for materials informatics using crystal graph convolutional neural network. Comput. Mater. Sci. 190, 110314 (2021).
Feng, S., Zhou, H. & Dong, H. Application of deep transfer learning to predicting crystal structures of inorganic substances. Comput. Mater. Sci. 195, 110476 (2021).
Yamada, H. et al. Predicting materials properties with little data using shotgun transfer learning. ACS Central Sci. 5, 1717–1730 (2019).
Kim, J., Jung, J., Kim, S. & Han, S. Predicting melting temperature of inorganic crystals via crystal graph neural network enhanced by transfer learning. Comput. Mater. Sci. 234, 112783 (2024).
Jha, D. et al. Enhancing materials property prediction by leveraging computational and experimental data using deep transfer learning. Nat. Commun. 10, 5316 (2019).
Choukroun, Y. & Wolf, L. Geometric transformer for end-to-end molecule properties prediction. In Proc. Thirty-First International Joint Conference on Artificial Intelligence, IJCAI-22 2895–2901 (IJCAI, 2022).
Qiao, Z., Welborn, M., Anandkumar, A., Manby, F. R. & Miller, T. F. Orbnet: deep learning for quantum chemistry using symmetry-adapted atomic-orbital features. J. Chem. Phys. 153, 124111 (2020).
Wu, F. et al. 3d-transformer: molecular representation with transformer in 3d space. (2021).
Healy, J., McInnes, L. Uniform manifold approximation and projection. Nat. Rev. Methods Primers 4, 82 (2024).
Herr, J. E., Koh, K., Yao, K. & Parkhill, J. Compressing physics with an autoencoder: creating an atomic species representation to improve machine learning models in the chemical sciences. J. Chem. Phys. 151, 084103 (2019).
Jain, A. et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Perdew, J. P. & Levy, M. Physical content of the exact kohn-sham orbital energies: band gaps and derivative discontinuities. Phys. Rev. Lett. 51, 1884 (1983).
Borlido, P. et al. Large-scale benchmark of exchange–correlation functionals for the determination of electronic band gaps of solids. J. Chem. Ther. Comput. 15, 5069–5079 (2019).
Borlido, P. et al. Exchange-correlation functionals for band gaps of solids: benchmark, reparametrization and machine learning. npj Comput. Mater. 6, 1–17 (2020).
Choudhary, K. et al. The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design. npj Computational Materials 6, 173 (2020).
Deng, B. et al. Chgnet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat. Machine Intell. 5, 1031–1041 (2023).
Chen, C. & Ong, S. P. A universal graph deep learning interatomic potential for the periodic table. Nat. Comput. Sci. 2, 718–728 (2022).
Batatia, I., Kovacs, D. P., Simm, G., Ortner, C. & Csányi, G. Mace: Higher order equivariant message passing neural networks for fast and accurate force fields. Adv. Neural Inform. Process. Syst. 35, 11423–11436 (2022).
Ahmed, M., Seraj, R. & Islam, S. M. S. The k-means algorithm: a comprehensive survey and performance evaluation. Electronics 9, 1295 (2020).
van der Maaten, L. & Hinton, G. Visualizing Data using t-SNE. Journal of Machine Learning Research 9, 2579–2605 (2008).
Traag, V. A., Waltman, L. & Van Eck, N. J. From louvain to leiden: guaranteeing well-connected communities. Sci. Rep. 9, 1–12 (2019).
Saputra, D. M., Saputra, D. & Oswari, L. D. Effect of distance metrics in determining k-value in k-means clustering using elbow and silhouette method. In Sriwijaya international conference on information technology and its applications (SICONIAN 2019), pages 341–346. (Atlantis Press, 2020).
Heaven, M. C., Bondybey, V. E., Merritt, J. M. & Kaledin, A. L. The unique bonding characteristics of beryllium and the group iia metals. Chem. Phys. Lett. 506, 1–14 (2011).
Zhang, Y., Liu, W. & Niu, H. Native defect properties and p-type doping efficiency in group-iia doped wurtzite aln. Phys. Rev. B 77, 035201 (2008).
Ri, S.-R., Ri, J.-E., Ri, N.-C. & Hong, S.-I. One way for thermoelectric performance enhancement of group iiib monochalcogenides. Solid State Commun. 339, 114485 (2021).
Liu, W.-S., Zhang, B.-P., Zhao, L.-D. & Li, J.-F. Improvement of thermoelectric performance of cosb3−xxtex skutterudite compounds by additional substitution of ivb-group elements for sb. Chem. Mater. 20, 7526–7531 (2008).
Yin, Y., Yi, M. & Guo, W. High and anomalous thermal conductivity in monolayer msi2z4 semiconductors. ACS Appl. Mater. Interfaces 13, 45907–45915 (2021).
Song, J. et al. Performance enhancement of perovskite solar cells by doping tio2 blocking layer with group vb elements. J. Alloys Compounds 694, 1232–1238 (2017).
Patsalas, P. et al. Conductive nitrides: growth principles, optical and electronic properties, and their perspectives in photonics and plasmonics. Mater. Sci. Eng. R Rep. 123, 1–55 (2018).
Awadallah, A. E., Aboul-Enein, A. A., El-Desouki, D. S. & Aboul-Gheit, A. K. Catalytic thermal decomposition of methane to cox-free hydrogen and carbon nanotubes over mgo supported bimetallic group viii catalysts. Appl. Surf. Sci. 296, 100–107 (2014).
Chattopadhyay, S., Mani, B. K. & Angom, D. Triple excitations in perturbed relativistic coupled-cluster theory and electric dipole polarizability of group-IIB elements. Phys. Rev. A 91, 052504 (2015).
Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A. V. & Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. Proceedings of the 32nd International Conference on Neural Information Processing Systems, 6639–6649 (Curran Associates Inc., 2018).
Lundberg, S. M. & Lee, S.-I. A Unified Approach to Interpreting Model Predictions. Proceedings of the 31st International Conference on Neural Information Processing Systems, 4768–4777 (2017).
Müller, M. Dynamic Time Warping. Information Retrieval for Music and Motion 69–84 (Springer Berlin Heidelberg, 2007).
Kim, C., Huan, T. D., Krishnan, S. & Ramprasad, R. A hybrid organic-inorganic perovskite dataset. Sci. Data 4, 1–11 (2017).
Nakajima, T. & Sawada, K. Discovery of pb-free perovskite solar cells via high-throughput simulation on the k computer. J. Phys. Chem. Lett. 8, 4826–4831 (2017).
Langer, M. F., Pozdnyakov, S. N. & Ceriotti, M. Probing the effects of broken symmetries in machine learning. Machine Learn. Sci. Technol. 5, 04LT01 (2024).
Sanyal, S. et al. Mt-cgcnn: Integrating crystal graph convolutional neural network with multitask learning for material property prediction. arXiv:1811.05660 (2018).
Thung, K.-H. & Wee, C.-Y. A brief review on multi-task learning. Multimedia Tools Appl. 77, 29705–29725 (2018).
Zhang, Y. & Yang, Q. A survey on multi-task learning. IEEE Transact. Knowledge Data Eng. 34, 5586–5609 (2022).
Luo, J. ct-UAE (GitHub, 2025). https://doi.org/10.5281/zenodo.14557909 (2025).
Acknowledgements
The authors thank G. F. Zheng and H. Y. Yu for helpful discussions. This work is supported by the National Key R&D Program of China (2023YFA1608501), Shanghai Municipal Natural Science Foundation under Grant No. 24ZR1406600, and Natural Science Foundation of Shandong Province under grants no. ZR2021MA041. L.J. and Z.D. also want to acknowledge the support of FDUROP (Fudan’s Undergraduate Research Opportunities Program) (24052, 23908).
Author information
Authors and Affiliations
Contributions
H.Z. conceived the project and contributed to securing funding. H.Z. and Y.C. supervised the research. L.J. and Z.D. developed and trained the neural networks and analyzed the results. L.J. and Z.D. wrote the original manuscript. L.J., Z.D., L.S., Y.X., Y.M., Y.C., and H.Z. contributed to the discussion of results and manuscript preparation and revision.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Jin, L., Du, Z., Shu, L. et al. Transformer-generated atomic embeddings to enhance prediction accuracy of crystal properties with machine learning. Nat Commun 16, 1210 (2025). https://doi.org/10.1038/s41467-025-56481-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-56481-x