Striatal arbitration between choice strategies guides few-shot adaptation

Abstract

Animals often exhibit rapid action changes in context-switching environments. This study hypothesized that, compared to the expected outcome, an unexpected outcome leads to distinctly different action-selection strategies to guide rapid adaptation. We designed behavioral measures differentiating between trial-by-trial dynamics after expected and unexpected events. In various reversal learning data with different rodent species and task complexities, conventional learning models failed to replicate the choice behavior following an unexpected outcome. This discrepancy was resolved by the proposed model with two different decision variables contingent on outcome expectation: the support-stay and conflict-shift bias. Electrophysiological data analyses revealed that striatal neurons encode our model’s key variables. Furthermore, the inactivation of striatal direct and indirect pathways neutralizes the effect of past expected and unexpected outcomes, respectively, on the action-selection strategy following an unexpected outcome. Our study suggests unique roles of the striatum in arbitrating between different action selection strategies for few-shot adaptation.

Introduction

Common reinforcement learning (RL) models explain that animals gradually learn to take specific actions to maximize the reward. This also allows them to adapt to a changing environment. Several neural substrates, including the prefrontal cortex (PFC)¹, hippocampus², and striatum³, have been implicated in adaptive behavior.

Various reversal learning tasks are used to study adaptive behavior⁴. In a probabilistic reward learning task, subjects learn to associate action with a specific reward probability determined by the task context, which remains constant for several trials. Then action-reward probability is reversed without explicit cues, necessitating adaptation to a new context.

During an experiment, rational subjects make choices they believe will lead to rewards based on their estimated context. Receiving an actual reward confirms their belief about the current context. However, the absence of an expected reward does not necessarily invalidate their context estimation. This unexpected outcome suggests at least two possibilities: first, the context estimation remains valid, and the lack of reward is simply a noisy event due to environmental uncertainty. In this case, there’s no need to change the choice behavior. Second, the context has actually changed, necessitating rapid adaptation through inferring a new context and adjusting associated choices. This thought experiment suggests that unexpected outcomes may initiate complex behavioral dynamics associated with context adaptation, which cannot be adequately explained by conventional few-shot learning. We term this the unexpected event-driven few-shot adaptation hypothesis.

As a means to explore behavioral evidence of few-shot adaptation guided by unexpected events, we designed measures, specifically, behavioral dynamics profiles that differentiate between trial-by-trial dynamics after an unexpected event and those after an expected one. The analyses using the proposed measures on the behavioral data, collected from rats during the two-step task⁵, demonstrated that various reinforcement learning (RL) models’ predictions fail to explain choice behavior after an unexpected event, compared to an expected one. It strongly supports our hypothesis that animals often exhibit abrupt and rapid changes in choice behavior depending on whether the last event was expected.

To better understand complex behavioral dynamics of rapid adaptation guided by expected and unexpected events, we propose a computational model that learns two decision variables; the support-stay bias and conflict-shift bias, called the support-stay, conflict-shift (SSCS) model. The SSCS model successfully replicates the behavioral patterns following both an unexpected and an expected event, qualitatively and quantitatively better than various RL models. The prediction of the SSCS model is also confirmed by the multi-trial history regression analysis, which explains the choice behavior after an unexpected event as a function of past expected and unexpected events, across different forms of reversal tasks (two-step task⁵, two-armed bandit task^6,7, and T-maze task⁸) and species (rat^5,8 and mouse^6,7).

Using electrophysiological data from rats⁸, we found two pools of medium-spiny neurons (MSNs) in the dorsomedial and ventral striatum encoding the trial-by-trial changes of support-stay and conflict-shift bias. Another behavioral data analysis on mice data under inactivation of D1R- and D2R-expressing MSNs⁷ revealed that the respective inactivation substantially affects the effect of past expected and unexpected outcomes on choice behavior after unexpected ones, elucidating the dissociable roles of different MSN types in conveying the associations between past outcomes and the action-selection strategy after unexpected outcomes.

Results

Unexpected event-driven few-shot adaptation hypothesis

In a context-switching environment with binary choices and probabilistic reward (Fig. 1a left), a subject who infers the current task context as T₁ (p₁ > p₂; marked as a red square in the reward probability plot) is likely to choose the action A₁ since it leads to the outcome state S₁ with a higher reward probability (p₁). Suppose a reward is not offered, contrary to its expectation. Although this unexpected outcome can be regarded as a noisy event due to the probabilistic nature of the reward function, it could also indicate the context switching to T₂ (p₂ > p₁; marked as a blue square in the reward probability plot). This cognitive process might urge action A₂ at the trial right after, which can lead to highly rapid adaptation. Such contextual behavior patterns contradict the prediction of the conventional RL models that choices are made based on values of decision variables accumulated over several past trials.

Fig. 1: Specialized action-selection strategy after experiencing the unexpected event.

a Alternative role of the unexpected event. Left for an example reversal learning task with two contexts and two actions. p₁/p₂ is the probability of receiving a reward after arriving at the outcome state S₁/S₂, respectively. Right for the reward probability plot depicting the context reversal. At the task context T₁, p₁ > p₂. On the other hand, in the task context T₂, p₁ < p₂. b, c Key terminology for behavioral measures. b The definition of action support/conflict events. c The two-step task⁵; Left for the definition of positive/negative actions with the task diagram. Here, the current task context is T₁ (p₁ > p₂). Right for the summary table of 4 event types.

Based on this thought experiment, we hypothesize that the occurrence of an expected and unexpected event triggers a distinctly different action-selection strategy. To examine this, we proposed behavioral measures that can differentiate between trial-by-trial dynamics after an unexpected event and those after an expected event. As a prerequisite for our measures, for each context, we defined an action typically leading to a positive (or negative) outcome as the positive (or negative) action. For example, in the task shown in Fig. 1a, if the current task context is T₁, then A₁ and A₂ are positive and negative actions, respectively. The subject’s action is followed by transitioning to a specific outcome state according to a certain transition probability. The outcome state is associated with a specific reward probability. The event where the actual outcome matches (or mismatches) the subject’s expectation is defined as a support (or conflict) event (Fig. 1b). Here, the subject interprets A₁/A₂ as a positive/negative action, assuming the current context as T₁. If a reward is received after choosing A₁, this event is classified as a support event. This is because the actual outcome matches the subject’s expectation that A₁ will lead to a reward.

Reframing choice behavior from an event-type perspective

To examine whether animal choice behavior after support/conflict events can be explained by the RL model, we analyzed the rat behavior during the two-step task⁵ using various RL models (model-free (MF), model-based (MB), and latent-state models). The two-step task is a paradigm commonly used to distinguish between the influences of MF and MB reinforcement learning on animal behavior.

In each trial, the subject chooses between two actions, A₁ and A₂, associated with the outcome state S₁ or S₂ (Fig. 1c left). Each action leads to one outcome state with high probability (e.g., A₁ leads to S₁ with probability 0.8, a “common” transition) and to another outcome state with low probability (e.g., A₁ leads to S₂ with probability 0.2, an “uncommon” transition). S₁ and S₂ have different probabilities of yielding a reward: p₁ for S₁ and p₂ for S₂, which is determined by the task context at the current trial. The task context remains constant for several trials before changing unpredictably and without explicit cues, called “reversal.” When it occurs, the values of p₁ and p₂ become switched.

Suppose the current task context is T₁, where p₁ > p₂ (Fig. 1c left). Here, A₁ is defined as the “positive” action (the 1^st column of Table in Fig. 1c) because this action leads to a reward with a higher probability. When a subject chooses a positive action (e.g., “I am making this choice because I think the current context is T₁.”), the “positive support” event (S+ of Table in Fig. 1c) refers to the outcome confirming one’s prediction about the context (e.g., “After the common transition, the reward is given exactly as I expected, suggesting that current context is T₁”), whereas the “positive conflict” event (C+ of Table in Fig. 1c) is the outcome contradicting one’s prediction (e.g., “After the common transition, the reward was omitted contrary to my expectation, suggesting that the context has switched to T₂, where p₁ < p₂”).

In the same context T₁, A₂ it is defined as the “negative” action (the 2^nd column of table in Fig. 1c) as it is less likely to lead to a reward. When the subject chooses a negative action for a certain reason, (e.g., “I am making this choice because I suspect the context has switched from T₁ to T₂.”), the “negative support” event (S− of table in Fig. 1c) refers to the outcome confirming one’s context prediction (e.g., “After the common transition, the reward is given exactly as I expected, reinforcing my prediction of T₁ → T₂.”), whereas the “negative conflict” event (C− of table in Fig. 1c) means that the outcome is not what one predicted (e.g., “After the common transition, the reward was omitted contrary to my expectation, suggesting the current context is still T₁.”)

This terminology enables us to classify all possible action-state transitions of the two-step task (table in Fig. 1c). The episodes of (1) being rewarded after a common transition (Common-Rewarded) and (2) reward omission after an uncommon transition (Uncommon-Omission) can be classified as support events (the 1^st row of table in Fig. 1c). Likewise, the episodes of (1) reward omission after a common transition (Common-Omission) and (2) being rewarded after an uncommon transition (Uncommon-Rewarded) are classified as conflict events (the 2^nd row of table in Fig. 1c).

RL models fail to predict animals’ choice behavior after an unexpected event

To evaluate how much the animal’s actual behavior confirms the predictions of RL theory, an MB model was fitted to the rat’s behavioral data since it was shown to be the most dominant behavior component on this task following the analyses in ref. ⁵. After each trial, the model first updates the outcome value V using the Rescorla-Wagner (RW) learning rule:

$$V\leftarrow V+\alpha (r-V),$$

where r is a binary variable indicating reward delivery, and α is a learning rate. RW learning rule⁹, derived from the RW model¹⁰, has been widely utilized to estimate the action values for the MF RL^{8,11,12,13,14,15,16} and the state values for the MB RL^17,18,19.

The MB model computes the action value by multiplying the transition matrix with the outcome value. This implies that the event types (S+ or C+) affect the outcome value updates, which subsequently affects the relative action value of the positive action, defined as a positive action value minus a negative action value (relative action value hereinafter)²⁰.

Specifically, the S+ event leads to an increase in the relative action value, whereas the C+ event decreases it. For instance, the model chooses a positive action A₁ in the current task context T₁ and receives the reward after a common transition (S+ event). The model increases the outcome value V of the outcome state S₁ by α(1 − V), resulting in an increase in the action value of A₁ that commonly leads to S₁. Consequently, the relative action value increases. Likewise, when the reward was omitted after an uncommon transition (S+ event), the outcome value V of the outcome state S₂ decreases to V + α(0 − V). This decreases the action value of the negative action A₂ that commonly leads to S₂. As a result, the relative action value increases.

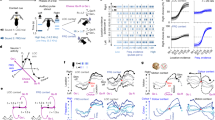
First, to examine the dynamics behind rats’ choices when they experienced S+ events consistently, we used the choice inconsistency (CI; Fig. 2a), defined as the probability of choosing the negative action (at trial t, marked as a blue rectangle) as a function of the number of S+ repetitions (N_S), when the subject experienced S+ events N_S times until the last trial (from trial t − N_S to t − 1, marked as a blue bold line on the trial axis). The CI quantifies how often rats make a choice that contradicts the supporting evidence provided by preceding trials (prior S+ events), even when the context remains unchanged.

Fig. 2: RL models fail to predict animal behavior after the conflict event.

a–c Behavioral dynamics profiles. Left for the conceptual diagram of the individual profile, middle for the result from the fitted model-based RL model behavior, and right for the result from rat behavior. In the conceptual diagram, each event is depicted as a rectangle above the trial axis, indicating when it happened (trial index). S+ and C+ events are marked in gray and white, respectively. Each profile consists of two components: (1) the event sequence leading up to the last t − 1^th trial, represented by a bold line on the trial axis, and (2) the probe trial at the current t^th trial, where the probability of choosing the negative action is assessed; a Choice inconsistency (CI). b Effect of conflict event (CE). c Conditional effect of conflict event (Conditional CE). Decreases in behavioral dynamics profiles and their finite differences were assessed using paired two-sample permutation tests. The difference between CE-C and CE-S was examined using a linear mixed-effects model, with the number of S+ repetitions (N_S) and type (CE-C or CE-S) as fixed factors and subject as a random effect. The main effects were tested using paired two-sample permutation tests. d Multi-trial history regression analysis; Left for the regression weights estimated from the fitted model-based RL model behavior, and right for the regression weights estimated from rat behavior. Regression weights were tested against zero using paired two-sample permutation tests. e Support-stay index (SSI); Left for conceptual diagram, and right for SSI computed from the fitted model-based RL model behavior and rat’s behavior. f Conflict-shift index (CSI); Left for conceptual diagram, and right for CSI computed from the fitted model-based RL model behavior and rat’s behavior. SSI and CSI were tested against zero using paired two-sample permutation tests. All statistical tests were two-sided and corrected for multiple comparisons using the Benjamini–Yekutieli procedure. All panels show data from n = 21 rats. Error bars indicate mean ± s.e.m. ***P < 0.001. See Supplementary Table 2 for full statistical information. Source data are provided as a Source Data file.

The MB model predicts that CI(N_S) will decrease as N_S increases. Experiencing S+ events consecutively increases the relative action value, reducing the probability of choosing the negative action (CI). Further, the MB model estimates that its finite difference, CI(N_S) − CI(N_S − 1), will also decrease as N_S increases. The above theoretical predictions of the MB model are confirmed by the CI profile measured from the simulated behavior of the fitted MB model (Fig. 2a, middle). Both the CI and its finite difference continually decrease significantly until N_S = 5.

These trends are also observed in the rats’ profile (Fig. 2a, right) until N_S = 2. The lack of a significant decrease in other N_S can be attributed to the limited number of trials, both in the model’s simulated behavior and the animal’s actual behavior. These results imply that the RW learning rule can reliably describe the rats’ action selection after they have experienced a sequence consisting solely of S+ events.

Next, we introduced a behavioral profile called the effect of conflict event (CE) to examine the dynamics behind rats’ action-selection strategy when a C+ event takes place following multiple S+ events (Fig. 2b). The CE quantifies how often rats perceive a noisy event (C+ event), which is caused by a probabilistic transition or reward delivery, as the evidence suggesting context-switching, even though the context does not change. It is defined as the probability of choosing the negative action (at trial t, marked as an orange rectangle) immediately after the C+ event (at trial t − 1, marked as red on the trial axis) as a function of N_S, where N_S(≥0) is the number of successive S+ events (from trial t − N_S − 1 to t − 2, marked as an orange bold line on the trial axis) preceding the C+ event (at trial t − 1, marked as red on the trial axis). N_S = 0 means no S+ event occurred before the C+ event happened at trial t.

The MB model predicts that, similar to CI, both the CE and its finite difference will decrease as N_S increases. These predictions are confirmed by the CE profile measured from the simulated behavior of the fitted MB model (Fig. 2b, middle). The CE and its finite difference decrease significantly until N_S = 3. These trends are also observed in the rats’ profile (Fig. 2b, right) until N_S = 2.

The action-selection strategy after the conflict event can be understood by analyzing its interaction with events in multiple past trials, rather than the most recent trial only. For this, we defined a more detailed behavioral profile based on CE, called conditional effect of conflict event (Conditional CE; Fig. 2c). The conditional CE is divided into two cases, depending on whether the event sequence of CE (Fig. 2b, marked as an orange bold line on the trial axis) is preceded by a C+ event (CE-C; Fig. 2c left top) or an S+ event (CE-S; Fig. 2c left bottom) at trial t − N_S − 2 (marked as red on the trial axis), where N_S is the number of successive S+ events (from trial t − N_S − 1 to t − 2, marked as a bold line on the trial axis) preceding the C+ event (at trial t − 1).

The MB model predicts the following about conditional CE: for the same N_S, CE-C will be higher than CE-S. The event sequence of CE-S (Fig. 2c left bottom, marked as an orange bold line on the trial axis) contains one more S+ event than the event sequence of CE-C (Fig. 2c left top, marked as a yellow bold line on the trial axis). This additional S+ event further increases the relative action value. Consequently, the relative action value after experiencing the event sequence of CE-S will be larger than that after CE-C. Thus, the probability of choosing the negative action in the former case (CE-S) will be lower than in the latter case (CE-C).

Furthermore, as N_S increases, the difference between CE-C and CE-S (ΔCE) will be more reduced. The more successive S+ events that occur, the greater the accumulated increase in the relative action value. Here, in the context of this cumulative growth of the relative action value, the effect of different initial events (C+ or S+ event, marked as red on the trial axis) on the choice probability becomes more negligible as N_S increases (Fig. 2c middle).

The above theoretical predictions of the MB model are confirmed by the conditional CE profiles measured from the simulated behavior of the fitted MB model (Fig. 2c middle). ΔCE is significantly positive and shows a decreasing trend at any N_S.

These two predictions made by the MB model are in sharp contrast with those of rat data (Fig. 2c right). First, the rats’ CE-C was not significantly higher than their CE-S at any N_S. Second, ΔCE decreases significantly only when N_S changes from 0 to 1. Specifically, ΔCE is insignificantly different from 0 at N_S = 0, but becomes significantly negative at N_S = 1. To dismiss any potential biases, we balanced CE-S with CE-C by excluding cases where the event sequence for CE-C is preceded by the S+ event. Despite such adjustment, observed discrepancies between the MB model and rats were consistent (Supplementary Fig. 1).

Event-type-specific behavioral dynamics underlying few-shot adaptation

Such behavioral patterns show defining characteristics of rats’ few-shot adaptation: unexpected event-guided confirmation bias. At the trial t − N_S − 2 (Fig. 2c left, marked as red on the trial axis), rats become more affected by the S+ event following their decision to stay with the same action after a C+ event (affirming their belief despite the noisy event), compared to when they decided to simply stay after a S+ event. This effect lasts until when rats experience the C+ event again, leading to CE-C ≤ CE-S at N_S ≥ 1.

The following example scenario can capture this explanation: At trial t − N_S − 2 (Fig. 2c left, marked as red on the trial axis), rats may still choose the same action after experiencing a C+ event that signals a potential context reversal. If it is followed by an S+ event, rats interpret this sequence of events as evidence that the context does not change. Thereafter, the unexpected event-guided confirmation bias weakens the association between the conflict event and action switch. Rats are less likely to interpret a following C+ event as a sign of the context switch. Instead, they attribute it to the inherent randomness in reward delivery and transition, decreasing the probability of switching to negative action in response to future C+ events. This collectively suggests that the action-selection strategy after the conflict event should be described by not only the effect of the latest trial but also the interaction effect between the latest and past trials.

We also investigated the MF model alongside the MB model by analyzing how different conflict events influence the action-selection strategy, finding that the MF model fails to replicate animal behavior after the conflict event (Supplementary Fig. 2).

To further examine the behavioral dynamics underlying action-selection strategy after a conflict event (Fig. 2b, c) in a more generalized setting that accommodates both positive and negative actions, we employed a multi-trial history regression analysis based on ref. ⁵. We used a logistic regression model that approximates the action-selection strategy after the conflict event, the conditional probability of choosing the positive action (a₊) given that the subject experienced the conflict (C) event in the previous trial (P(a_t = a₊∣e_t−1 ∈ C)). The regression model represents this action-selection strategy as a parametric function of recent trials and their event types (Fig. 2d top and Supplementary Fig. 3).

Trials from the past are indexed by the variable τ. An event that occurred τ trials ago can be one of two types: support (S) and conflict (C) event. For each τ, each of these trial types is assigned a corresponding weight (β_S(τ) and β_C(τ), respectively). A positive weight indicates a greater likelihood that the subject will make the same choice. For example, β_S(2) > 0 indicates that the subject is more likely to choose the same action that was made two trials ago, in which the support event occurred. Conversely, a negative weight indicates a higher likelihood that the subject will make the opposite choice to the one made τ trials ago. Note that there is no β_S(1) term in the logistic regression model (Fig. 2d top), as the model focuses exclusively on the effect of past events on the action-selection strategy when a conflict event, rather than a support event, occurred one trial ago.

In terms of β_S(τ), the MB model predicts that it will be positive at any τ. After experiencing a support event, the MB model increases the relative action value of the corresponding action, which increases the probability of choosing the same action in the future. These predictions are confirmed by the β_S computed from the simulated behavior of the fitted MB model (Fig. 2d, bottom left, blue curve). These trends are also observed in the rats’ profile (Fig. 2d, bottom right, blue curve) until τ = 4. To quantify the general effect of past support events (τ > 1) on choosing the same action, we defined the support-stay index (SSI) as the average of regression weights β_S(τ > 1) (Fig. 2e left). We confirmed that SSIs computed from both the MB model and the rat are significantly positive (Fig. 2e right). The MB model also predicts that β_C(τ) will be negative at any τ, which is confirmed by the β_C measured from the simulated behavior of the fitted MB model (Fig. 2d, bottom left, orange curve). This prediction, however, does not at all match with the rat data (Fig. 2d, bottom right, orange curve) showing significantly negative β_C only at τ = 1 and positive otherwise. This result implies that the effect of past conflict events on action-selection strategy after the conflict event depends on when this past event occurred. A conflict event 1 trial ago after choosing one action leads rats to switch to the alternative action (β_C(τ = 1) <  0). In contrast, a conflict event more than 1 trial ago leads them to repeat the same action (β_C(τ > 1) > 0). Note that the MB model does not accommodate this effect. The effects of past conflict events are also consistent with our interpretation of the discrepancies observed at conditional CE, CE-C ≤ CE-S at N_S ≥ 1.

To quantify the general effect of past conflict events (τ > 1) on choosing the alternative action, we defined the conflict-shift index (CSI) as the average of regression weights β_C(τ > 1) multiplied by −1 (Fig. 2f left). The CSI computed from the MB model is significantly positive, whereas the CSI of the rat is significantly negative (Fig. 2f right). This result corroborates our finding that the past conflict events (τ > 1) guide rats to stay on this action, which cannot be explained by the MB model.

Taken together, we found behavioral evidence that support and conflict events guide animal action-selection strategies differently, contradicting the predictions of conventional RL models. This motivates us to design a dual-process model to accommodate support and conflict events in a distinctly different manner (Fig. 3a).

Fig. 3: Computational accounts of event-type-dependent action-selection strategies.

a The mechanisms of the support-stay, conflict-shift (SSCS) model. After each trial, the model performs (1) conflict bias update, (2) event-type-dependent action selection, (3) support bias update, and (4) setting a flag for the conflict bias update in the next trial. Each variable’s superscript indicates the trial index, e.g. e^t represents the event type (support or conflict event) the model experienced at the t^th trial. f^t represents the flag at the t^th trial. b The rat’s choice behavior after the reversal and representations of the SSCS model; Left for the choice behavior after reversal of rat (Black) and the SSCS model (Gray). The x-intercept and time constant of the exponential curve fitted to rat behavior and SSCS model behavior were compared using paired two-sample permutation tests and Spearman correlation analysis. Right for the modulation of decision variables, the support bias difference ${b}_{{{\rm{S}}}}^{+}-{b}_{{{\rm{S}}}}^{-}$ (Top) and the conflict bias difference ${b}_{{{\rm{C}}}}^{+}-{b}_{{{\rm{C}}}}^{-}$ (Bottom). The positive and negative actions are determined by the context after the reversal. The dotted lines indicate the trial when the context reversal occurs, the trial when the quantity of interest exceeds 0, and the time constant of the exponential curve fitted to the quantity of interest after the context reversal from the left. b shows data from n = 21 rats. All statistical tests were two-sided. Error bars indicate mean ± s.e.m. See Supplementary Table 2 for full statistical information. Source data are provided as a Source Data file. SSCS, support-stay, conflict-shift model.

Computational model for event-type-dependent action-selection strategy

We designed a support-stay, conflict-shift (SSCS) model to understand how support and conflict events guide action-selection strategy differently. In the SSCS model, each action is associated with two decision variables: support-stay bias (support bias hereinafter) and conflict-shift bias (conflict bias hereinafter). The first and the second variables accommodate the patterns of CI (Fig. 2a) and conditional CE/β_C (Fig. 2c, d), respectively.

The support bias is defined as the likelihood of taking the same action following a support event, encoding the association between the support event and the chosen action. The conflict bias is defined as the likelihood of switching to the other action following a conflict event, encoding the association between the conflict event and the chosen action.

In each trial, the model updates the conflict bias (g_C: ${b}_{{{\rm{C}}}}^{t}\to {b}_{{{\rm{C}}}}^{t+1}$, Process 1 in Fig. 3a), based on the support/conflict event (e^t) and the flag (f^t). The flag is a simple gating function to determine whether the model repeats the same action despite a previous conflict event. Note that this update reflects behavioral patterns of conditional CE (Fig. 2c) and the effect of past conflict events (β_C of Fig. 2d). The model then chooses the next action (a^t+1, Process 2 in Fig. 3a) based on the support bias (${b}_{{{\rm{S}}}}^{t}$) or the conflict bias (${g}_{{{\rm{C}}}}({b}_{{{\rm{C}}}}^{t})$) following a support or conflict event, respectively. The model then updates the support biases (g_S: ${b}_{{{\rm{S}}}}^{t}\to {b}_{{{\rm{S}}}}^{t+1}$, Process 3 in Fig. 3a), specifically increasing the support bias of the chosen action (a^t+1) and decreasing that of the alternative action. Finally, a flag (f^t+1, Process 4 in Fig. 3a) is set to indicate whether the model repeats the same action in the next trial despite a conflict event. The flag serves as a mental note to bet on the possibility that there was no context change.

To investigate how the SSCS model represents animal behavior, we first measured the rat’s choice behavior during the trials around the context reversal and compared it with those from the simulated behavior of the SSCS model. After the context reversal, rats rapidly adapt to a new context. After 3 trials, the choice probability of the positive action P(+) is significantly higher than that of the negative action P(−). The exponential curve fitted to their difference (choice bias), P(+) − P(−), converges to the upper asymptote with the average time constant of 5 trials (Fig. 3b left black line). The SSCS model accurately describes this adaptation (Fig. 3b left gray line). Both the x-intercepts and the time constants from rat behavior and the SSCS model were insignificantly different and showed a significant positive correlation.

Among the two decision variables, the support bias was the one that showed a faster response to the context reversal. After 4 trials, the support bias of the positive action ${b}_{{{\rm{S}}}}^{+}$ becomes significantly higher than the support bias of the negative action ${b}_{{{\rm{S}}}}^{-}$, and their difference ${b}_{{{\rm{S}}}}^{+}-{b}_{{{\rm{S}}}}^{-}$ converges to the upper asymptote with the average time constant of 6 trials (Fig. 3b right top).

On the other hand, the conflict bias exhibited slower dynamics. After 8 trials, the conflict bias of the positive action ${b}_{{{\rm{C}}}}^{+}$ becomes significantly lower than the conflict bias of the negative action ${b}_{{{\rm{C}}}}^{-}$, and their difference ${b}_{{{\rm{C}}}}^{+}-{b}_{{{\rm{C}}}}^{-}$ converges to the lower asymptote with the average time constant of 12 trials (Fig. 3b right bottom).

The SSCS model explains rat’s few-shot adaptation

The SSCS model was compared against the six other models; (1) the model-free RL (MF) model²¹, (2) the model-based RL (MB) model²², (3) the latent-state (LT) model²³, (4) the meta-learning (MTL) model²⁴, (5) the asymmetric Bayesian learning (ABL) model²⁵, and (6) the reduced (RD) model⁵.

The MF model selects the next action based on the action value updated following the RW learning rule. The MB model is based on the MF model, except that its action value prediction incorporates the model of the environment. The LT model selects the next action based on the most probable task context, while its probability is inferred by the Bayesian update rule. The MTL model builds upon the MB model but modulates RPE magnitude and negative outcome learning rate based on expected and unexpected uncertainty. The ABL model is extended from the LT model by assuming that the task context inference is asymmetrically influenced by the receipt and omission of rewards. The RD model adopts a mixture-of-agents approach, where the action value is calculated by a weighted average of several different ’agents’ implementing different behavioral strategies, including model-based planning, novelty preference, bias, and perseveration.

Baseline models were chosen to ensure a comprehensive and fair comparison by incorporating a broad spectrum of computational perspectives. First, we grounded our selection in empirical evidence, choosing models that have been recognized as the “best" in previous studies for specific tasks analyzed in our work. In the two-step task, we adopted the reduced model as detailed in ref. ⁵. Next, considering that the two-step task incorporates the transition uncertainty between the chosen action and the arrived outcome state, we considered different action-selection strategies used in popular value-based decision-making tasks. The models include model-free²¹, model-based²², Bayesian ideal observer^23,25, meta-learning²⁴, and mixture-of-agents approaches⁵.

Each model was fitted to the behavioral data of each animal individually. The normalized BIC score and the normalized cross-validation likelihood were used to compare the different models’ predictability. We confirmed that all models showed significantly higher scores than the chance level in both measures. The RD and SSCS models showed the highest scores, followed by the ABL, MTL, MB, LT, and MF models (Fig. 4a top for normalized cross-validation likelihood, Supplementary Fig. 4 for normalized BIC score).

Fig. 4: Event-type-dependent action-selection strategies explain rat’s few-shot adaptation.

a Model predictability comparison using normalized cross-validation likelihood and time constant of the choice bias. In the normalized cross-validation likelihood, a white bar indicates a significantly lower value than the highest model (P < 0.05). In the time constant, a white bar indicates a significantly different value than the rat’s time constant (P < 0.05). b Comparison of behavioral dynamics profiles between animal and top 2 models. Filled dots indicate significantly different model predictions from rat behavior (P < 0.05), while blank dots indicate insignificant differences (P > 0.05). c–f Model explainability comparison in multi-trial history regression analysis by measuring similarity measures computed from rat behavior and simulated behavior of the fitted model. c β_S. β_S of the RD model, β_S of the SSCS model, and the comparison of cosine similarity across baseline models. d Model explainability comparison by measuring the RMSE and Spearman correlation coefficient between SSI computed from rat’s behavior and simulated behavior of the fitted model. e β_C. β_C of the RD model, β_C of the SSCS model, and the comparison of cosine similarity across baseline models. f Model explainability comparison by measuring the RMSE and Spearman correlation coefficient between CSI computed from rat’s behavior and simulated behavior of the fitted model. In RMSE, a white bar indicates significantly higher values than the lowest model (P < 0.05). In cosine similarity and Spearman correlation coefficient, a white bar indicates significantly lower values than the highest model (P < 0.05). Model comparisons were performed using paired two-sample permutation tests and Dunn and Clark’s Z tests. All statistical tests were two-sided and corrected for multiple comparisons using the Benjamini–Yekutieli procedure. All panels show data from n = 21 rats. Error bars indicate mean ± s.e.m., while for the Spearman correlation coefficient, they represent mean ± bootstrap standard error. See Supplementary Table 2 for full statistical information. Source data are provided as a Source Data file. MF, model-free RL model²¹; MB, model-based RL model²²; LT, latent-state model²³; MTL, meta-learning model²⁴; ABL, asymmetric Bayesian learning model²⁵; RD, reduced model⁵; SSCS, support-stay, conflict-shift model.

To measure the adaptation speed of the animal or the fitted model, we computed the choice bias (Fig. 3b left) and fitted the exponential curve to it. The comparison between the time constant of the exponential curve between the animal and fitted models (Fig. 4a bottom) showed that the models following the MB strategy exhibited significantly smaller time constants than that of the rat (MB, LT, RD models), compared to other types of RL models (ABL, MF, MTL models).

It implies that conventional models capable of adaptation predict unrealistically fast adaptation compared to animal behavior. Notably, our SSCS model has nearly the same time constants as the one from animal behavior. This result underscores the capability of the SSCS model to accurately reflect the temporal dynamics of behavioral adaptation in a manner that closely approximates the natural processes observed in animal behavior.

We also ran behavioral recoverability tests, in which we computed behavioral dynamics profiles (CI, CE, and conditional CE) from the simulated behavior of the fitted models and compared them with those of rats. Our model showed the most similar behavioral dynamics profiles to rats (Supplementary Figs. 5 and 6). Specifically, the SSCS model exhibited a quantitatively better prediction than the RD model, especially in CI and ΔCE profiles (Fig. 4b). The results suggest that the two key variables of our model serve to predict rapid context-switching behavior, above and beyond the predictions made by previously known variables of the RD model, including novelty preference, bias, and perseveration.

Next, we conducted behavioral recoverability tests, in which we computed β_S and β_C from the simulated behavior of fitted models and compared them with those of rats. We found that various models replicate β_S with similar accuracy (Fig. 4c, and Supplementary Fig. 7a). By and large, the SSCS model and various baseline models exhibit similar explainability of SSI (Fig. 4d and Supplementary Fig. 7c). On the other hand, the SSCS model replicates β_C (Fig. 4e, and Supplementary Fig. 7b) most accurately. The direct comparison of CSI between rats and the fitted models showed that the SSCS model explains CSI most accurately (Fig. 4f and Supplementary Fig. 7d).

In addition to these cognitive models, we considered two types of biologically plausible neural networks implementing the PFC-basal ganglia function^25,26. In both models, PFC recurrent networks learn to infer the hidden task context by predicting an upcoming state, while basal ganglia rectified linear units learn the corresponding value and appropriate action using the RL mechanism. In one network model (NN model with direct input), the PFC network received full information, the preceding state, and action²⁶. On the other hand, the PFC network of another model (NN model with gated input) received only the information about the preceding state, gated by whether the reward was given²⁵.

After training these models to maximize their reward, we conducted additional analyses computed from the simulated behavior. First, we examined whether the behavioral dynamics profiles of the two trained neural network models can replicate the trends shown in rats’ profiles (Supplementary Fig. 8a–c). Although the model’s predictions are by and large aligned with the rats’ behavioral profiles, the NN model with direct input shows that [CE-C]>[CE-S] significantly at N_S = 0 and 1 (Supplementary Fig. 8c middle), which does not match with the rats’ profile, [CE-C] ≤ [CE-S] at every N_S (Supplementary Fig. 8c left).

Second, to validate whether two events (CO and UR events) in the C+ category differently affect the action-selection strategy, we compared the behavioral dynamics profiles from the trained models. Here, in every profile of the NN model with gated input, we observed that there are significant differences between CO and UR events (Supplementary Fig. 8d–f right), which do not align with the rat behavior (Supplementary Fig. 8d–f left).

Furthermore, when we compared β_C and CSI, both NN models do not replicate the rat’s result (Supplementary Fig. 8h). Taken together (Supplementary Fig. 8), we found that two NN models could not replicate the animal behavior in the two-step task, especially in terms of representing the action-selection strategy after the conflict event.

In conclusion, we introduced the SSCS model, a computational framework that captures how animals leverage support and conflict events to guide their action-selection strategies. The SSCS model outperformed existing models in explaining animal behavior, particularly while describing the animal’s action-selection strategy after the conflict event (Fig. 3b and 4a–b, e–f). These findings strongly support our hypothesis that animals differentiate their action-selection strategies following conflict events compared to those following support events, especially within a context-switching environment.

The SSCS model characterizes the behavior of different species in simpler tasks

To test whether our findings are replicated in another experiment, we conducted the same analyses on an independent dataset where mice perform a two-armed bandit task with context reversal⁶. In each trial, the mouse chooses between two actions, A₁ and A₂. A₁ and A₂ have different probabilities of yielding a reward: p for A₁ and 1 − p for A₂, which is determined by the task context at the current trial. When the context reversal happens, the reward probabilities allocated to each action become switched. The same mice performed several sessions with different values of higher reward probability p, fixed to one of three values (0.7, 0.8, 0.9) during each session (Fig. 5a). In this task, we also classified possible events into four categories. After choosing the positive action, we classified the event when the reward was given or omitted as an S+ event and a C+ event, respectively.

Fig. 5: Mouse behavior in a two-armed bandit task⁶.

a Task structure description. b Model explainability comparison by measuring the RMSE between behavioral dynamics profiles computed from mouse behavior and simulated behavior of the fitted model. CI, CE, CE-C, CE-S, and ΔCE from the left. Comparison of MF and SLRP models with respect to the SSCS model from the top. c–f Model explainability comparison in multi-trial history regression analysis by measuring similarity measures computed from mouse behavior and simulated behavior of the fitted model. In RMSE and cosine similarity, comparison of MF and SLRP models with respect to the SSCS model from the left. c Cosine similarity between β_S. d Model explainability comparison with respect to SSI. Left for RMSE between SSI. Right for repeated-measures correlation coefficient⁹¹ between SSI. e Cosine similarity between β_C. f Model explainability comparison with respect to CSI. Left for RMSE between CSI. Right for repeated-measures correlation coefficient⁹¹ between CSI. RMSE and cosine similarity comparisons between models were performed using a linear mixed-effects model, with reward probability (p) and model type as fixed factors and subject as a random effect. Estimated marginal means were compared with degrees of freedom adjusted by the Satterthwaite method for main effects and simple main effects tests. SSI and CSI computed from mouse and model behavior across different p were compared using repeated-measures correlation analysis. All statistical tests were two-sided and corrected for multiple comparisons using the Benjamini–Yekutieli procedure. b–f show data from n = 6 mice. Error bars indicate mean ± s.e.m., while for the repeated-measures correlation coefficient, they represent mean ± bootstrap standard error. *P < 0.05, **P  < 0.01, ***P  < 0.001. See Supplementary Table 2 for full statistical information. Source data are provided as a Source Data file. MF, model-free RL model²¹; SLRP, stochastic logistic regression policy model⁶; SSCS, support-stay, conflict-shift model.

From analyses of behavioral data, we found that mice also showed behavioral patterns observed in the two-step task consistently across different values of p; consecutive decreases in CI (Supplementary Fig. 9a) and reversal of the sign of the difference between CE-C and CE-S (Supplementary Fig. 9c).

In the two-armed bandit task⁶, we considered the stochastic logistic regression policy (SLRP) model as the best model based on the BIC score comparison detailed in the original study⁶. Unlike the two-step task, this task does not involve transition uncertainty from the chosen action to the outcome state, confining ourselves with models that do not utilize transition information, such as the MF model²¹.

As a result, we compared our SSCS model with two other models: (1) the MF model²¹, which selects the next action based on action values updated using the RW learning rule, and (2) the SLRP model⁶, which uses a logistic regression model incorporating choice and choice-reward interaction terms to capture mice’s stochastic and efficient action-switching behavior after context reversal.

All the models were fitted to the behavioral data of each animal in different values of p individually. Detailed comparisons showed that the SSCS model most accurately predicts various profiles (CE, ΔCE, SSI, β_C) in every value of p (Fig. 5b–f and Supplementary Fig. 10). These results support that our model, which is based on the policy arbitrates between support and conflict bias, better describes the animal behavior in context reversal consistently across different species, task complexity, and environmental parameters.

The SSCS model explains the activity of medium-spiny neurons

After confirming that the SSCS model accurately replicates the event-type-dependent action-selection strategy across species and task complexity (Figs. 4 and 5, Supplementary Figs. 1, 4–7, 10), we sought to investigate its neural substrates. During value-based decision-making, the striatum is known to integrate reward-related information⁸, evaluate the value of different options¹⁶, and execute appropriate actions based on expected rewards⁷. Especially dorsomedial striatum (DMS) has been traditionally implicated in action selection in context-changing environments^7,8, and it is known to be associated with flexible behavior during value-based decision-making²⁷.

Various RL models, such as the model-free RL (MF) model²¹, and the differential forgetting Q-learning (DFQ) model²⁸, are frequently employed to investigate whether neurons encode the decision variables, such as action value or state value, during reversal learning tasks^{11,15,20,27,29,30}. However, these models have not been tested for their ability to replicate the animal’s event-type-dependent action-selection strategies. We hypothesized that the striatum guides the event-type-dependent action-selection strategy. To examine this, we reanalyzed previously published datasets of rat behavior during a T-maze task with context reversal, a spatial navigation task that resembles the previous two-armed bandit task (Fig. 5)⁸. In this experiment, the activities of medium-spiny neurons (MSNs) in the DMS were simultaneously recorded (Fig. 6a left).

Fig. 6: Neural representation of the support-stay, conflict-shift model.

a Task configuration⁸. The numbered S marks within the T-maze indicate the position of photo-beam sensors, which represent the boundaries between different sections within a single trial. b Distribution of neurons encoding decision and task variables (n = 201 neurons from 3 rats). c Behavioral dynamics profiles from rats and fitted SSCS model (n = 3 rats). CI, CE, and Conditional CE from the left. The difference between CE-C and CE-S was examined using a linear mixed-effects model, with the number of S+ repetitions (N_S) and type (CE-C or CE-S) as fixed factors and subject as a random effect. Estimated marginal means were compared with degrees of freedom adjusted by the Satterthwaite method for main effects and simple main effects tests. d Regression weights from the multi-trial history regression analysis from rats and fitted SSCS model (n = 3 rats). β_S and β_C from the left. Regression weights were tested against zero using a linear mixed-effects model, with the trials in the past (τ) as the fixed factor and the subject as a random effect. Estimated marginal means were compared with degrees of freedom adjusted by the Satterthwaite method for post-hoc tests. e, f Example temporal dynamics sorted and colored by the value of the corresponding decision variable, Modulations of firing rates are listed in the order of prepare, action, reward, and update section from the left; e Normalized firing rate of support bias neurons. f Normalized firing rate of conflict bias neurons. All statistical tests were two-sided and corrected for multiple comparisons using the Benjamini–Yekutieli procedure. Error bars indicate mean ± s.e.m. See Supplementary Table 2 for full statistical information. Source data are provided as a Source Data file.

To validate this hypothesis at the behavioral level, we conducted behavioral dynamics profiles and multi-trial history regression analyses. We classified possible events into four categories identical to those used in the two-armed bandit task. For the T-maze task with context reversal⁸, we considered the differential forgetting Q-learning (DFQ)²⁸ model as the best model, in accordance with the BIC score comparison conducted in the original study⁸. Similar to the two-armed bandit task⁶, this task does not involve transition uncertainty from the chosen action to the outcome state, for which case models that do not account for probabilistic transition are suitable, such as the MF model²¹ for comparative purposes.

Therefore, our SSCS model was compared with: (1) the MF model²¹, which uses the RW learning rule to update action values, and (2) the DFQ model²⁸, which extends the MF model by incorporating a forgetting rate for the unchosen action and applying distinct update rules to the chosen action based on whether it was rewarded.

The analysis of the rat’s behavioral dynamics profiles revealed that CE-C is significantly lower than CE-S (Fig. 6c top, 3^rd column). The SSCS model is the only model that successfully replicates this trend (Fig. 6c bottom, 3^rd column), unlike the MF (Supplementary Fig. 11b top, 3^rd column) and DFQ (Supplementary Fig. 11c top, 3^rd column) models, which exhibited that CE-C is significantly higher than CE-S at every N_S. Second, from multi-trial history regression analyses, we observed that rat’s β_C significantly fluctuates, crossing zeros, across different τ values. It was significantly negative only at τ = 1, but became significantly positive from τ = 2 onward (Fig. 6d top right). Once again, only the SSCS model accurately replicates this finding (Fig. 6d bottom right), in contrast to the MF (Supplementary Fig. 11f right) and DFQ models (Supplementary Fig. 11g right).

These results (Fig. 6c, d and Supplementary Fig. 11) demonstrate that rats utilized the event-type-dependent action-selection strategy. The RL models, including the MF and DFQ models that are widely used to decode the neural representation of decision variables, failed to replicate the action-selection strategy after the conflict event. In contrast, our SSCS model successfully replicated these behavior patterns.

We then examined MSN activity to determine whether the striatum represents the event-type-dependent action-selection strategy by analyzing their correlations with the key decision variables of the SSCS model, the support, and conflict biases. The entire T-maze was divided into four sections; prepare, action, reward, and update (Fig. 6a right). The average firing rates of MSNs were computed during each trial. For each trial and each section, the average firing rates of MSNs were also computed while rats were passing over the corresponding section.

To accommodate temporal correlations for identifying striatal representation³¹, we employed the autoregressive exogenous (ARX) model, a mathematical framework for time series analysis and system identification. The ARX model explains such correlations by adding the autoregressive term inside the fitting model³². This approach has been validated in³⁰ for effectively mitigating false identifications related to temporal correlations.

For each neuron, we fit an ARX model to evaluate how much the average firing rates of neural data are explained by the decision variables (support and conflict bias) of the SSCS model and task variables (choice and reward as confounding variables) on a trial-by-trial basis. A neuron was considered to represent a specific variable if the ARX regression coefficient associated with that variable was significantly different from zero, as determined using a block-wise permutation test⁸.

As well as choice and reward-encoding neurons previously reported, we found two sets of neurons encoding trial-by-trial changes of support bias (Fig. 6b, 6e and Supplementary Fig. 12a) or conflict bias (Fig. 6b, f, and Supplementary Fig. 12b). We observed that distinct sets of neurons representing either support or conflict biases were consistently identified in each section of the T-maze (Fig. 6b, e, f, and Supplementary Fig. 12a, b). Notably, we also found that a proportion of MSNs in the ventral striatum (VS) also represent the support bias or conflict bias (Supplementary Fig. 12c, d).

Taken together, these findings demonstrate that the striatum represents the event-type-dependent action-selection strategy, captured by the SSCS model. Especially, the striatum represents the distinct action-selection strategy after the conflict event, the behavior dynamics overlooked by the other models.

Mice exhibit event-type dependent action-selection strategy, independent from MSN inactivations

We further examined the possibility the different types of MSNs could provide a more detailed account of the striatal representation of the event-type-dependent action-selection strategy. We considered two types of MSNs, D1 receptor-expressing MSNs (D1-MSNs) and D2 receptor-expressing MSNs (D2-MSNs), distinguished by their connectivity and expression profile of dopaminergic receptors³³. D1-MSNs are part of the direct pathway, facilitating desired actions and selecting actions that lead to positive outcomes. On the other hand, D2-MSNs are part of the indirect pathway, associated with inhibiting competing actions and suppressing actions linked with negative outcomes^34,35,36. The balance between the direct and indirect pathway activity is crucial for flexible behavior and adaptive decision-making since it helps to optimize the behavior in response to changing environments^7,35,36.

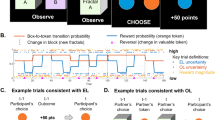
These functional segregations could be related to the action-selection strategy after the conflict event, a key process underlying flexible behavior in a context-switching environment. This motivated us to investigate another behavioral study in which mice performed a two-armed bandit task with context reversal (Fig. 7a left) while they were under reversible inactivation of D1-MSNs or D2-MSNs in DMS, respectively (Fig. 7a right)⁷. The analysis aimed to assess if MSN inactivation leads to deficits in this strategy, as well as to explore the differential contributions of D1-MSNs and D2-MSNs to this process.

Fig. 7: Effect of type-specific inactivation of MSNs to event-type-dependent action-selection strategy.

a Description of the two-armed bandit task with reversal task and reversible inactivation used in the experiment⁷. b–d Behavioral dynamics profile comparisons between the mice in the control condition and fitted MF model (n = 39 mice). Left for results from simulated behavior of fitted MF model. Right for results from mice behavior in control condition; b Choice inconsistency (CI). c Effect of conflict event (CE). d Conditional effect of conflict event (Conditional CE). e–g Behavioral dynamics profiles from mice behavior in inactivation condition. Left for results from mice behavior in D1-MSN inactivation (n = 20 D1R-Cre mice). Right for results from mice behavior in D2-MSN inactivation (n = 19 D2R-Cre mice). e CI. f CE. g Conditional CE. Decreases in behavioral dynamics profiles and their finite differences were assessed using paired two-sample permutation tests. The difference between CE-C and CE-S was examined using a linear mixed-effects model, with the number of S+ repetitions (N_S) and type (CE-C or CE-S) as fixed factors and subject as a random effect. The main effects were tested using paired two-sample permutation tests. All statistical tests were two-sided and corrected for multiple comparisons using the Benjamini–Yekutieli procedure. Error bars indicate mean ± s.e.m. See Supplementary Table 2 for full statistical information. Source data are provided as a Source Data file. MF, model-free RL model²¹.

In the two-armed bandit task with MSN inactivation⁷, we considered the MF model as the best model based on the BIC score comparison performed in the original study⁷. Additionally, previous studies employing this task^8,37 have demonstrated that the DFQ model outperforms the MF model, prompting us to also include the DFQ model for comparison.

Our model was evaluated against: (1) the MF model²¹, which updates action values through the RW learning rule, and (2) the DFQ model²⁸, which extends the MF model by incorporating a forgetting mechanism for the unchosen action and separate update rules for the chosen action depending on whether it was rewarded. All the models were fitted to the behavioral data of each animal individually and separately for different pharmacological conditions.

To investigate whether mice employ different action-selection strategies after a conflict event compared to after a support event, we applied the behavioral dynamics profiles to the mouse behavior under the control condition. We classified possible events into four categories identical to those used in the two-armed bandit task (Fig. 7a middle). Unlike the two-step task incorporating the probabilistic transition from a chosen action to an outcome state, the two-armed bandit task with context reversal does not have such uncertainty. Therefore, we selected the MF model as a baseline. The MF model increases the relative action value after experiencing an S+ event and decreases it after a C+ event. Also, after each trial, the MF model updates its action values based on the RW learning rule. Therefore, the MF model yields the same predictions as those demonstrated by the MB model in the two-step task (Fig. 2).

First, the MF model predicts that CI(N_S) and its finite difference will decrease as N_S increases. These predictions are confirmed by the CI profile measured from the simulated behavior of the fitted MF model. Both CI and its finite difference continually decrease significantly until N_S = 5 (Fig. 7b left). These trends are also observed in the mice profile until N_S = 2 (Fig. 7b right).

Second, the MF model predicts that CE(N_S) and its finite difference will decrease as N_S increases. These are confirmed by the CE profile measured from the simulated behavior of the fitted MF model. Both CE and its finite difference continually decrease significantly until N_S = 4 (Fig. 7c left). These trends are also observed in the mice profile until N_S = 1 (Fig. 7c right).

Third, the MF model predicts that CE-C(N_S) will be higher than CE-S(N_S) for any N_S. These predictions are confirmed by the conditional CE profile measured from the simulated behavior of the fitted MF model. CE-C is significantly higher than CE-S until N_S = 2 (Fig. 7d left). But in the mice profile, CE-C and CE-S were insignificantly different (Fig. 7d right).

The alignment observed in CI/CE (Fig. 7e, f) and discrepancies observed in conditional CE (Fig. 7g) also manifested in mice behavior during the inactivation of D1-MSNs or D2-MSNs. Especially, after D1- or D2-MSN inactivation, CE-C becomes significantly lower than CE-S. Furthermore, the direct comparison of mice behavioral dynamics profiles between control and inactivation conditions revealed that D1-MSN inactivation significantly increases CI (Supplementary Fig. 13a left), CE (Supplementary Fig. 13b left), and CE-S (Supplementary Fig. 13d left). Importantly, D1-MSN inactivation did not significantly alter CE-C (Supplementary Fig. 13c left), demonstrating the specificity of the observed effects. D2-MSN inactivation did not significantly influence any of the assessed behavioral dynamics profiles (Supplementary Fig. 13a–d right).

The findings suggest that mice exhibit a different action-selection strategy after the conflict event (Fig. 7), consistent with our previous analyses involving various tasks (Figs. 2, 4–6). Moreover, it is noteworthy that such utilization also appears after D1-MSNs or D2-MSNs are inactivated (Fig. 7e–g). However, only the inactivation of D1-MSNs specifically increases some behavioral dynamics profiles, thereby implying the distinct roles of D1- and D2-MSNs in the event-type-dependent action-selection strategy of mice (Supplementary Fig. 13).

The SSCS model replicates type-specific contributions of MSNs to the action-selection strategy after the conflict event

To further investigate the dissociable contributions of D1-MSNs and D2-MSNs to the event-type-dependent action-selection strategy, we examined how past events influenced the action-selection strategy following a conflict event and how these relationships were altered by MSN inactivation.

First, to investigate the effect of past support events, we computed the regression weights β_S and SSI from the actual behavior of mice under control and inactivation conditions. β_S showed continual decay, regardless of inactivation (Fig. 8a).

Fig. 8: Effect of type-specific inactivation of MSNs to the association between past events and the action-selection strategy after the conflict event.

a–c Effect of type-specific inactivation to the regression weight β_S and SSI; a, b Effect of type-specific inactivation to the regression weight β_S. β_S before and after D1-MSN inactivation, and β_S before and after D2-MSN inactivation from the left; a β_S from mouse actual behavior. b β_S from simulated behavior of fitted SSCS model. c The effect of inactivation on SSI and replications of the SSCS model. d–f Effect of type-specific inactivation to the regression weight β_C and CSI; d, e Effect of type-specific inactivation to the regression weight β_C. β_C before and after D1-MSN inactivation, and β_C before and after D2-MSN inactivation from the left; d β_C from mouse actual behavior. e β_C from simulated behavior of fitted SSCS model. f The effect of inactivation on CSI and replications of the SSCS model. g, h Model explainability comparison by measuring the Spearman correlation coefficient between the measure computed from the mouse behavior and simulated behavior of the fitted model. D1+, D1−, D2+, and D2− from the left. g Model explainability comparison on SSI. h Model explainability comparison on CSI. In the Spearman correlation coefficient, white bars indicate significantly lower values than the highest model (P < 0.05). SSI and CSI comparisons between control and inactivation conditions were evaluated using paired two-sample permutation tests. Spearman correlation coefficients between models were compared using Dunn and Clark’s Z tests. All statistical tests were two-sided and corrected for multiple comparisons using the Benjamini–Yekutieli procedure. Panels show data from n = 20 D1R-Cre mice (D1+/D1−) or n = 19 D2R-Cre mice (D2+/D2−). Error bars indicate mean ± s.e.m., while for the Spearman correlation coefficient, they represent mean ± bootstrap standard error. *P  < 0.05, **P < 0.01, ***P < 0.001. See Supplementary Table 2 for full statistical information. Source data are provided as a Source Data file. MF, model-free RL model⁵; DFQ, Q-learning with different forgetting model²⁸; SSCS, support-stay, conflict-shift model; D1+, D1-MSN control; D1−, D1-MSN inactivation; D2+, D2-MSN control; D2−, D2-MSN inactivation.

After the inactivation of D1-MSNs, the SSI from mice behavior decreases significantly (Fig. 8c 1^st column). In contrast, the effect of D2-MSN inactivation on SSI was marginal (Fig. 8c 2^nd column). This implies that the effect of past support events on choosing the same action becomes attenuated after D1-MSN inactivation specifically.

Second, to investigate the effect of past conflict events, we computed the regression weights β_C and CSI from mouse behavior under control and inactivation conditions. Regardless of targeted types (D1-MSN or D2-MSN) and conditions (control or inactivation), mice’s β_C starts from a value nearby 0, increases significantly at τ = 2, and continuously decays as τ increases (Fig. 8d).

After the inactivation of D1-MSNs, the change in CSI from mouse behavior was insignificant (Fig. 8f 1^st column). On the other hand, after the inactivation of D2-MSNs, the CSI from mouse behavior decreases significantly (Fig. 8f 2^nd column). This implies that the effect of past conflict events on choosing the same action increases after D2-MSN inactivation specifically.

To investigate whether the SSCS model can replicate these findings, we performed multi-trial history regression analyses on the simulated behavior of the fitted SSCS model. We found that the SSCS model accurately replicated (1) similar trends in β_S (Fig. 8b) and β_C (Fig. 8e) regardless of conditions (D1+, D1−, D2+, and D2−), (2) a specific decrease in SSI after D1-MSN inactivation (Fig. 8c 3^rd column), and (3) a selective decrease in CSI after D2-MSN inactivation (Fig. 8f 4^th column). Furthermore, the SSI and CSI values from the SSCS model showed significant positive correlations with those of the mice (Fig. 8g for SSI, Fig. 8h for CSI) across different conditions (D1+, D1−, D2+, and D2−).

Collectively, these results suggest neural substrates conveying the associations between past events and the action-selection strategy after the conflict event. D1-MSNs selectively transfer the effect of past support events, whereas D2-MSNs specifically transfer the effect of past conflict events.

To validate whether the observed deficits following MSN inactivations are specifically attributed to impairments in the event-type-dependent action-selection strategy represented by the SSCS model, we conducted model explainability comparisons. Specifically, we performed multi-trial history regression analyses on simulated behaviors of different models and compared these regression results with those derived from actual mouse behavior.

First, we computed the regression weights β_S and SSI from the simulated behavior of the fitted models under control and inactivation conditions. All models exhibited a continual decay in β_S regardless of inactivation (Supplementary Fig. 15a for D1-MSN, Supplementary Fig. 15f for D2-MSN), mirroring the trends observed in mice. Consistent with this, the cosine similarity of β_S between mice and the fitted models did not differ significantly across the different models (Supplementary Fig. 15b for D1-MSN, Supplementary Fig. 15g for D2-MSN).

A selective decrease in SSI following D1-MSN inactivation (Supplementary Fig. 15c), but not D2-MSN inactivation (Supplementary Fig. 15h), was observed across simulations of all three models. Comparing model explainability for SSI under D1-MSN manipulation (Supplementary Fig. 14a, c), the models showed similar performance in terms of RMSE (Supplementary Fig. 15d) and Spearman correlation coefficient (Supplementary Fig. 15e), regardless of inactivation. This pattern was also observed for D2-MSN manipulations (Supplementary Fig. 15i for RMSE, and Supplementary Fig. 15j for Spearman correlation coefficient).

Second, we computed the regression weights β_C and CSI from the simulated behavior of the fitted models under control and inactivation conditions. Across all targeted MSN types (D1-MSN or D2-MSN) and conditions (control or inactivation), the SSCS model most accurately replicated the β_C trends (Supplementary Fig. 16a 4^th column for D1-MSN, Supplementary Fig. 16f 4^th column for D2-MSN) observed in mice (Supplementary Fig. 16a 1^st column for D1-MSN, Supplementary Fig. 16f 1^st column for D2-MSN). This was supported by significantly higher cosine similarity of β_C between mice and the fitted SSCS model relative to the other models across conditions (Supplementary Fig. 16b for D1-MSN, Supplementary Fig. 16g for D2-MSN).

A selective decrease in CSI following D2-MSN inactivation (Supplementary Fig. 16h), but not D1-MSN inactivation (Supplementary Fig. 16c), was also consistent with simulations from the SSCS model. When comparing the model explainability of CSI for D1-MSN manipulations (Supplementary Fig. 14b, d), the SSCS model demonstrated significantly lower RMSE under inactivation condition (Supplementary Fig. 16d right) and higher Spearman correlation coefficient across both conditions (Supplementary Fig. 16e) compared to the other models. Furthermore, the SSCS model exhibited significantly lower RMSE (Supplementary Fig. 16i) and higher Spearman correlation coefficient (Supplementary Fig. 16j) for both D2-MSN control and inactivation conditions.

These results indicate that the observed behavioral changes in mice following striatal inactivation are specifically linked to impairments in the event-type-dependent action-selection strategy, providing causal evidence for its essential role. Given this causal evidence and our findings that the striatum represents the event-type-dependent action-selection strategy (Fig. 6), these results underscore that the striatum encodes the event-type-dependent action-selection strategy. This highlights its critical function in guiding flexible, context-driven behavior.

Discussion

This study demonstrated how rodents achieve flexible behavior at the behavioral, computational, and neural levels. We hypothesized that the animal achieves this by operating different action-selection strategies after experiencing support and conflict events, respectively. Using behavioral dynamics profiles to track the trial-by-trial dynamics of the action-selection strategy after one type of event, we showed that conventional RL models fail to explain the action-selection strategy after the conflict event (Fig. 2). On the other hand, the computational model, which implements our inferred learning rules from behavioral dynamics profiles, makes quantitatively successful predictions about flexible behavior patterns in the four independent datasets^5,6,7,8 (Figs. 3–7 and Supplementary Figs. 1, 4–7, 10–11, 14–16). Interestingly, MSNs in both DMS and VS were found to encode not only choice and reward information but also the two key decision variables of our computational model, suggesting a possibility that the striatum serves as the information hub of flexible behavior (Fig. 6 and Supplementary Fig. 12). Moreover, our model explains the exclusive contributions of different MSN types on the action-selection strategy after the conflict event; D1-MSNs selectively transfer the effect of past support events (Fig. 8c and Supplementary Fig. 14a, c), whereas D2-MSNs specifically transfer the effect of past conflict events (Fig. 8f and Supplementary Fig. 14b, d).

Previously, several regression-based behavioral profiles^5,38,39 have been proposed, but they mainly targeted to distinguish between MF and MB RL^5,39 and have several limitations^23,40. The proposed behavioral dynamics profiles can characterize the trial-by-trial dynamics of the action-selection strategy following events that support or conflict with the subject’s inferred task context. Moreover, these profiles reflect how one model updates its decision variable, such as action value, outcome value, or belief. Therefore, these profiles can compare the update rules between different models and evaluate whether the model’s update rule reflects the animal behavior. Using these measures, we found that the animals’ action-selection strategy following an unexpected event does not match conventional RL models; this result corroborates an alternative view that the animals might have different action-selection strategies to handle the support event and conflict event. Furthermore, our behavioral measures can serve as complementary tools along with traditional methods, such as likelihood-based model comparison.

Another significant contribution of our work is that we generalized the idea of behavioral flexibility, which earlier discussions have mainly focused on discrimination tasks^41,42,43,44. To understand this, we investigated the dynamics of the action-selection strategy after the conflict event, which is vital to achieving behavioral flexibility. In general, it is hard to evaluate whether two measures quantify different aspects of the same behavioral policy, potentially leading to multicollinearity^45,46,47. To explain the action-selection strategy after the conflict event better without such issues, we introduced multi-trial history regression, which discriminated between the effect of past support events and conflict events on the action-selection strategy after the conflict event. Notably, our model consistently replicated the effect of past support events and past conflict events computed from animal behavior of independent datasets across different species and task complexities^5,6,7,8.

Our support-stay, conflict-shift model underpinning the animal behavior in reversal learning tasks has been evaluated at the behavioral, computational, and neural levels. Specifically, a proportion of MSNs in both DMS and VS reflects the gain control effect of the two decision variables of our computational model, support and conflict bias, and the striatal direct and indirect pathways are shown to contribute to maintaining flexible behavior differentially.

The robust neural evidence solidly supports our conclusions regarding the striatum’s pivotal role in the action-selection strategy following the conflict event. The results from behavioral and neural analyses in rats (Fig. 6 and Supplementary Figs. 11 and 12) reinforce the idea that the striatum encodes the distinct action-selection strategy after the conflict event, which previous models had overlooked. Through analyses of mice behavior that assessed the impact of selective inactivation of D1- and D2-MSNs, we have clarified the striatal association with the action-selection strategy after the conflict event (Figs. 7 and 8). Collectively, these findings strongly support the hypothesis that the striatum engages in the action-selection strategy after the conflict event, as evidenced across different species (rat for MSN recording, mouse for MSN inactivation), methodologies (electrophysiology for MSN recording, pharmacogenetics for MSN inactivation), and tasks (T-maze task for MSN recording, two-armed bandit task for MSN inactivation).

Previously, numerous studies had related different types of dopamine receptors with behavioral flexibility^36,48,49,50 respectively, but they mainly focused on manipulating neurons and examining simple behavioral effects. On the contrary, we linked the neuron/circuit level activities with our model implementing support and conflict bias with their update rules inferred from animal behavior. This could provide an integrative framework capable of producing more viable predictions. For example, our model can explain the recent finding investigating the role of striatal direct and indirect pathways in goal-directed behavior in updating action selection³⁵, including a pathway-specific association of task variables to neuronal signals and results of optogenetic stimulation. In the long run, the support-stay, conflict-shift model can help us deepen the understanding of how the striatal dopaminergic system manages flexible behavior.

It would be interesting to show that our model can generalize to situations accommodating various choices and a hierarchical structure between adjacent states. Recently, several papers have discussed the generalization of binary choices to multiple ones by incorporating the Bayesian ideal observer model⁵¹. However, such inductive reasoning requires an assessment by objective behavioral measures to preclude any hasty generalization fallacy. In this regard, one experiment⁵² showed that the Bayesian ideal observer model could not explain captured discrepancies in a three-alternative visual categorization task.

There are two major directions to which insights from our findings can be extended. What neurons encode depends on both the brain region they locate and how much experience accumulated inside the task environment. First, since dorsal and ventral striatum receive and send different inputs^53,54,55 and outputs^56,57 respectively, it is necessary to investigate how the distribution of neurons encoding decision variables modulates across the dorsoventral axis^58,59,60 and how their dynamics are changing throughout training^61,62.

Second, without explicit cues indicating different contexts, subjects must actively infer the task structure^63,64,65 based on their past experiences^66,67,68,69. After continual evaluations to determine whether the inferred structure can explain underlying variances^{17,70,71,72,73,74}, this reasoning may lead to the true task structure^26,75. While the SSCS model fits the broader definition of model-based RL models by utilizing task structure, it can be viewed as a form of meta-learning, as it learns to choose between contexts/tasks and associated actions simultaneously. Furthermore, our model advances the concept of biological meta-RL by providing detailed computational principles underlying event-type-dependent action-selection for rapid animal adaptation¹⁵.

Overall, our support-stay, conflict-shift model can provide an expanded interpretation of the action-selection strategy after the conflict event guiding behavioral flexibility and shed light on the multi-dimensional role of the striatum and related dopaminergic control in driving flexible behavior.

Methods

Terms for behavioral analyses

Our study considers behavioral datasets derived from various research^5,6,7,8. These tasks share five key components:

• Action: The task contains two possible actions.

• Transition: Each action leads to an outcome state according to the state-action-state transition probability.

• Outcome state: Each action leads to one of two potential outcome states.

• Reward: After reaching an outcome state, a reward is allocated based on a probabilistic schedule.

• Task context: The task consists of two distinct contexts, each favoring a different, non-overlapping outcome state by allocating a higher reward probability to it.

During a given session, only one context is active at a time and controls the reward system. However, the active context can switch randomly during the session, a process we refer to as a “reversal". We define a sequence of trials where the context remains unchanged as a “block".

Within a block, where the task context remains constant, there are some inherent stochastic elements. These include (1) the transition between action and outcome state and (2) the reward probability. Given these uncertainties, we categorize an action leading to a reward with a higher probability as a “positive action" (a₊) and one leading to a reward with a lower probability as a “negative action" (a₋).

The event is the sequence, which consists of the action chosen (positive or negative), the transition type from the chosen action to the arrived outcome state (common or uncommon), and the actual outcome (rewarded or omission). After choosing one action X, the set of events when the actual outcome matches the subject’s outcome expectation is defined as a “support event" of the action X, S^X. For example, suppose that the subject experiences a common transition after choosing the action X. It will predict that there will be a reward because it chooses the best action based on its assumed task context and arrives at the outcome state that has a higher probability of receiving a reward under the context. If there is an actual reward, this event belongs to the support event of action X, S^X. On the contrary, after choosing one action X, the set of events when the actual outcome mismatches the subject’s outcome expectation is defined as a “conflict event" of action X, C^X.

For several analyses, we defined two terms, the “task variable" and the “decision variable". A task variable is an observable object in animal behavior, such as what choice the subject made or whether the subject was rewarded or not. On the contrary, a decision variable is a latent object, often assumed to explain the animal behavior, such as action value or state value.

Summary of datasets and sources

Table 1 provides clarity on the datasets analyzed in this study, confirming that the results are based on a comprehensive reanalysis of existing datasets from previous research^5,6,7,8. The table summarizes each dataset, its corresponding section in the manuscript, and the figures representing the analyzed data.

Table 1 Summary of datasets utilized in the analyses

Experiment details

The two-step task (Figs. 2–4)

The experimental procedures described below were adopted from the original study⁵ where the dataset was first published and made publicly available.

Subjects

All subjects (n = 21) were adult male Long-Evans rats (Taconic Biosciences, NY), placed on a restricted water schedule to motivate them to work for water rewards. Some rats were housed on a reverse 12-h light cycle and others on a normal light cycle; in all cases, rats were trained during the dark phase of their cycle. Rats were pair-housed during behavioral training. Animal use procedures were approved by the Princeton University Institutional Animal Care and Use Committee and carried out in accordance with NIH standards.

Task design

In this experiment, rats performed the task in a behavioral chamber outfitted with six nose ports arranged in two rows of three ports each. Choice ports were located on the left and right sides of the top row, and reward ports were located on the left and right sides of the bottom row.

In the first step of the task, rats initiated each trial by entering the center port on the top row and then indicated their choice by entering one of the choice ports. Each choice port led to one reward port with an 80% probability (common transition, Fig. 1c) and to another reward port with a 20% probability (uncommon transition, Fig. 1c). Such transitions were guided by an auditory stimulus that indicated which reward port became available.

In the second step, rats first entered the center port on the bottom row, followed by entering the reward port. After visiting the reward port, rats either received (reward) or did not receive (omission) a bolus of water. Reward probabilities were allocated differently for each reward port, and this allocation was determined by the context of the current block (Fig. 1a). The number of trials in each block was 10 plus a random number drawn from a geometric distribution with a mean of 50.

The two-armed bandit task with context reversal (Fig. 5)

The experimental procedures described below were adopted from the original study⁶ where the dataset⁷⁶ was first published and made publicly available.

Subjects

Wild-type mice (n = 6, C56BL/6N from Charles River and bred in-house) aged 6–10 wk were water restricted to 1–2 mL per day prior to training and maintained at >80% of full body weight. All training sessions were conducted in the dark or under red-light conditions. Experimental manipulations were performed in accordance with protocols approved by the Harvard Standing Committee on Animal Care, following guidelines described in the NIH Guide for the Care and Use of Laboratory Animals.

Task design

In each session, the mouse had the freedom to move around in a chamber that had three ports (Fig. 5a). These ports allowed the mouse to interact with the task by poking its nose into them. One of the side ports, called the high port, had a reward probability of p, while the other side port, called the low port, had a reward probability of 1 − p. There were three different task conditions, with p values of 0.7, 0.8, and 0.9, representing different reward probabilities for the high port. The value of p remained constant within a session but changed across different sessions.

At the beginning of each trial, an LED above the center port was activated, indicating to the mouse that it could start a trial by poking its nose into the center port at any time. This action triggered the activation of LEDs above the two side ports, prompting the mouse to choose between the left or right port. The mouse had 2 s to make its selection. After entering a side port, the decision to deliver a water reward or not was determined by the corresponding port’s reward probability. The trial ended when the mouse withdrew from the side port, and a new trial began after a 1-s inter-trial interval (ITI). During the ITI, there was a 0.02 probability of a context reversal, which determined whether the high and low ports would switch positions. This random process resulted in blocks of consecutive trials where the position of the high port remained the same, with an average block length of 50 trials. After the ITI, the LED above the center port turned on. Each behavior session lasted for 40 min.

The T-maze task with context reversal (Fig. 6)

The experimental procedures described below were adopted from the original study⁸ where the dataset⁷⁷ was first published and made publicly available.

Subjects

Young male Sprague Dawley rats (n = 3, 9–11 weeks old, 250–330 g) were used. Initially, they had unlimited access to food and water. With the start of behavioral training, water access was limited to 30 min post-session daily. Experiments took place during the dark phase of a 12-h light/dark cycle. The experimental protocol was approved by the Ethics Review Committee for Animal Experimentation of the Ajou University School of Medicine.

Task design

Each trial began as the subject returned to the central stem of a modified T-maze. Inside the maze, there were photo-beam sensors that alarmed the moment when the subject entered the corresponding spot. By the intervals between sensors, we divided a single trial into four different sections: prepare, action, reward, and update (Fig. 6a).

After a delay of 2–3 s, the central bridge was lowered (action offset), allowing the subject to navigate forward and choose freely between the two goal locations to obtain a water reward. The beginning of the reward section was the time when the animal broke the photo-beam that was placed 6 cm ahead of the water-delivery nozzle. The central connecting bridge was raised at the onset of the reward section. The beginning of the update section was the time when the animal crossed an invisible line 11 cm away from the water-delivery nozzle. The beginning of the prepare section in the next trial was when the animal broke the central photo-beam that was placed 13 cm from the proximal end of the maze.

The neural activity of each rat was recorded for a total of 4–18 sessions, and each session consisted of four blocks of trials. Each block was associated with one of four different reward probability pairs (left:right = 0.72:0.12, 0.63:0.21, 0.21:0.63, or 0.12:0.72). The sequence of blocks was randomly determined with the constraint that the higher probability target changes its location at the beginning of each block. The number of trials in each block was 35 plus a random number drawn from a geometric distribution with a mean of 5, while the maximum number of trials was set at 45.

Unit recording

Single unit activities were recorded from the left (n = 1) or right (n = 2) DS and VS. For the DS recording, unit activity was recorded from the dorsomedial striatum, and for the VS recording, activity was mostly recorded from the core of the nucleus accumbens. A microdrive array loaded with 12 tetrodes was lowered aiming the dorsomedial striatum (1.2 mm anterior, 1.7 mm lateral from bregma) with six tetrodes implanted in the DS [3.0 mm ventral (V) from the brain surface] and the other six implanted in the VS (6.0 mm V from the brain surface) under deep anesthesia. The identity of unit signals was determined based on the clustering pattern of spike waveform parameters, averaged spike waveforms, baseline discharge frequencies, autocorrelograms, and interspike interval histograms. For those units that were recorded for two or more days, the session in which the units were most clearly isolated from background noise and other unit signals was used for analysis.

Single units were isolated by examining various two-dimensional projections of spike waveform parameters, and manually applying boundaries to each subjectively identified unit cluster using custom software (MClust 3.4). Only those clusters that were clearly separable from each other and from background noise throughout the recording session were included in the analysis. Unit signals were recorded with the animals placed on a pedestal (resting period) for 10 min before and after experimental sessions to examine the stability of recorded unit signals. Unstable units were excluded from the analysis. Post-recording, marking lesions confirmed recording sites histologically.

Unit classification

Units were categorized as either putative medium-spiny neurons (MSNs) or interneurons based on their firing rates and spike widths. The majority of the analyzed units were putative MSNs. were MSNs. We analyzed the activity of MSNs only.

The two-armed bandit task with MSN inactivation (Figs. 7 and 8)

In our study, we used the behavioral data⁷⁸ during the two-armed bandit task, described as the dynamic TAB task in the original study⁷. Therefore, in this section, we only introduced the subject information and manipulation related to our analyses. The full experimental procedures are detailed in the original study⁷ where the dataset⁷⁸ was first published and made publicly available.

Subjects

C57BL/6J BAC transgenic mouse lines expressing Cre recombinase under the control of dopamine D1R or D2R (Drd1-EY217 and Drd2-ER44, respectively) were obtained from Gene Expression Nervous System Atlas. The animals were extensively handled and then water-deprived so that their body weights were maintained at 80% of ad libitum levels throughout the experiments. Each mouse was housed in an individual home cage, and all experiments were performed in the dark phase of a 12 h light/dark cycle. 21 D1R-Cre and 20 D2R-Cre mice were used for expression of h4DMi-mCherry in the striatum. Only male mice were used in the present study and all were 10–15 wk old at the time of virus injection surgery. All animal care and experimental procedures were performed in accordance with protocols approved by the directives of the Animal Care and Use Committee of Korea Advanced Institute of Science and Technology (approval number KA2018-08).

Virus injection

Mice were anesthetized with isoflurane (1.0–1.2% [vol/vol] in 100% oxygen), and two burr holes were made bilaterally at 0.3 mm anterior and 2.0 mm lateral to bregma. AAV8-based, modified human M4 muscarinic receptor (AAV8-hSyn-DIO-hM4Di-mCherry) expression construct was injected bilaterally at a depth of 3.0 mm from the brain surface at a rate of 0.05 ml/min (total volume, 2 ml). The injection needle was held in place for 15 min before and after the injection.

Task design

At the beginning of each trial, an LED in the center port was activated. A nose poke in the central port turned off the central LED and turned on the LEDs in the both left and right ports. The animal was free to choose between the two lit nose-poke ports at this stage. A nose poke in either the left or right port turned off the both left and right LEDs and turned on the center LED. After entering one port, the decision to deliver a water reward (30 ml) or not was determined by the corresponding port’s reward probability.

In this task, one session consisted of four blocks of trials, each of which consisted of 35–50 trials (one session per day; 24 h apart); The block length for one block was determined randomly among 35, 40, 45, or 50 trials. In each block, one port delivered water with a relatively high probability (72%), and the other port delivered water with a relatively low probability (12%). The reward probabilities in the first block were determined randomly and were reversed across block transitions (Fig. 7a). Before the experiment with inactivation started, all mice had been trained extensively in the same task 3 weeks beforehand.

Pharmacogenetic intervention

To examine the effects of inactivating D1R- or D2R-expressing striatal neurons, mice were intraperitoneally injected with dimethyl sulfoxide (DMSO, 2.5−3%, 0.5 ml/kg, control) and clozapine-N-oxide (CNO, 5 mg/kg, inactivation) on alternate days 40 min prior to daily sessions. The behavioral data under control or inactivation conditions were collected for 10 sessions each. The order of drug injection was counterbalanced across animals.

Determination of steady-state

To account for the potential influence of variable learning rates caused by increased uncertainty immediately following a reversal^79,80, we established a criterion for determining the steady-state while investigating the decision variable and its update rule through behavioral dynamics profiles. This steady-state period represents the phase where the subject shifts toward exploitation over exploration and stabilizes its tendency to choose the positive action rather than the negative action consistently.

First, we estimated the binomial probability of repeating positive action p₊ and negative action p₋ at trial index t. Here, the trial index is the counter variable that resets to 0 when the reversal occurs.

$$\begin{array}{l}{p}_{+}\left(t\right)=P\left({a}_{t-1}={a}_{t}={a}_{+}| t\right)\\ {p}_{-}\left(t\right)=P({a}_{t-1}={a}_{t}={a}_{-}| t)\end{array}$$

Then, we fitted g, the exponential function with linear asymptote to represent p₊ and p₋ as functions of the trial index,

$$\begin{array}{l}{p}_{+}\left(t\right)\approx {g}_{+}\left(t\right)={A}_{+}\exp \left({B}_{+}t\right)+{C}_{+}t+{D}_{+}\\ {p}_{-}\left(t\right)\approx {g}_{-}\left(t\right)={A}_{-}\exp \left({B}_{-}t\right)+{C}_{-}t+{D}_{-}.\end{array}$$

We defined the “steady-state" using a plateau detection method^81,82. First, for each fitted curve g₊ and g₋, we drew a line l connecting the initial point and the endpoint (Supplementary Fig. 17b, Bold lines). The endpoint (or asymptotic point) is defined as t = t_∞, where t_∞ is the 95th percentile of the block length distribution for each subject’s data.

Next, for the stay probability of the positive action, we defined the positive steady-state criterion ${t}_{S}^{+}$ (Supplementary Fig. 17b left, Vertical, dotted line) as the point where the derivative of the function g₊ (Supplementary Fig. 17b left, Diagonal, dotted line) is closest to s₊, the slope of the line l drawn on g₊.

$${t}_{S}^{+}={{{\rm{argmin}}}}_{\tau \in \left[0\,{t}_{\infty }\right]}\left\vert {g}_{+}^{{\prime} }\left(\tau \right)-{s}_{+}\right\vert,\quad {s}_{+}=\frac{{g}_{+}\left({t}_{\infty }\right)-{g}_{+}\left(0\right)}{{t}_{\infty }-0}.$$

Likewise, we defined the negative steady-state criterion ${t}_{S}^{-}$ (Supplementary Fig. 17b right, dotted lines).

$${t}_{S}^{-}={{{\rm{argmin}}}}_{\tau \in \left[0\,{t}_{\infty }\right]}\left\vert {g}_{-}^{{\prime} }\left(\tau \right)-{s}_{-}\right\vert,\quad{s}_{-}=\frac{{g}_{-}\left({t}_{\infty }\right)-{g}_{-}\left(0\right)}{{t}_{\infty }-0}.$$

Finally, for each subject, we computed the steady-state criterion t_S as the average of ${t}_{S}^{+}$ and ${t}_{S}^{-}$. The steady-state period is defined as a set of trials with indices greater than t_S.

Behavioral dynamics profile

We designed behavioral dynamics profiles to achieve two main objectives: (1) to characterize the animal’s action-selection strategy after a specific event type in detail and (2) to compare it with the prediction of different models. When defining these measures, we denoted the action that subjects chose and the event subjects experienced at trial t as a_t and e_t, respectively.

Behavioral dynamics profiles are defined as the conditional probability of choosing the negative action at trial t (probe trial) given the sequence of past events until trial t − 1 (event sequence). Since all the data analyzed in this work has only the discrete binary choice data indicating whether the subject chose a negative action after experiencing the corresponding event sequence up to the last trial, we estimated this action probability value from the binary choice data.

To reduce the influence of variable learning rate due to uncertainty^79,80, we considered the subject behavior during the steady-state and estimated the binomial probabilities from the trials included in the steady-state. We focused on the trial in which subjects chose the negative action during the steady-state because it implies that subjects might suspect the context change even if the actual context does not change.

Choice inconsistency (CI, Fig. 2a)

The choice inconsistency at length k, denoted as CI(k), is defined as the conditional probability of choosing the negative action given that the subject had experienced the positive support (S+) events k times in a row, most recently.

$${{\rm{CI}}}(k)=P\left({a}_{t}={a}_{-}| {e}_{t-k:t-1}\in {{\rm{S}}}+\right)$$

Effect of conflict event (CE, Fig. 2b)

The effect of conflict event at length k, denoted as CE(k), is defined as the conditional probability of choosing the negative action given that the subject experienced the positive conflict (C+) event most recently after it had experienced the positive support (S+) events k times in a row.

$${{\rm{CE}}}(k)=P\left({a}_{t}={a}_{-}| {e}_{t-k-1:t-2}\in {{\rm{S}}}+,\, {e}_{t-1}\in {{\rm{C}}}+ \right)$$

Conditional effect of conflict event (conditional CE, Fig. 2c)

There are two types of conditional effects of conflict event to quantify the effect of past events on the action-selection strategy after the conflict event. First, CE-C at length k is given by

$$\,{\mbox{CE-C}}\,(k)=P\left({a}_{t}={a}_{-}| {e}_{t-k-2}\in {{\bf{C}}}{{\boldsymbol{+}}} ,\,{e}_{t-k-1:t-2}\in {{\rm{S}}}+,\,{e}_{t-1}\in {{\rm{C}}}+\right).$$

Second, CE-S at length k is given by

$$\,{\mbox{CE-S}}\,(k)=P\left({a}_{t}={a}_{-}| {e}_{t-k-2}\in {{\bf{S}}}{{\boldsymbol{+}}} ,\,{e}_{t-k-1:t-2}\in {{\rm{S}}}+,\,{e}_{t-1}\in {{\rm{C}}}+\right).$$

Filtering behavioral dynamics profiles

To address the inherent limitations of binomial probability estimation with small sample size data, we implemented a robust filtering process for analyses using behavioral dynamics profiles. Consider a behavioral dynamics profile X at length k, denoted as X(k), where X can be any behavioral dynamics profile, such as CI, CE, CE-C, and CE-S. For each subject, we estimated the value of X(k), representing the binomial probability of choosing the negative action, while varying k. To filter out unreliable estimates, we utilized the confidence interval as a criterion, as it is known to be a reliable measure of the estimation’s uncertainty.

Suppose that a subject chooses the negative action m times out of n trials, following an event sequence of X(k). A common approach to calculating the confidence interval involves using the normal approximation to the binomial distribution. However, this approximation requires that both m and n are sufficiently large, typically m > 10 and n > 20⁸³.

As k increases, it becomes hard to meet this condition since the event sequence of X(k) must contain k consecutive S+ events. This creates two specific issues:

• 1. Decrease in n: The probability that a subject experiences k consecutive S+ events decreases, leading to a decrease in n.

• 2. Decrease in m: After experiencing k consecutive S+ events, subjects generally refrain from choosing the negative action, resulting in a decrease in m.

Therefore, we cannot resort to the normal approximation for calculating the confidence interval since it becomes invalid for large k due to unmet assumptions. To address this issue, we can use f(p), the posterior probability distribution of p = X(k), given the observed data m and n⁸⁴.

Derivation of f(p)

Assuming that the choice behavior follows a Bernoulli process, the likelihood of observing m negative actions in n trials, given p is:

$$\Pr \left[m| p\right]=\left(\begin{array}{c}n\\ m\end{array}\right){p}^{m}{\left(1-p\right)}^{n-m}\propto {p}^{m}{\left(1-p\right)}^{n-m}.$$

Since we are only interested in p and the binomial coefficient $\left(\begin{array}{c}n\\ m\end{array}\right)$ is constant with respect to p, we can omit it in the likelihood function (as it will cancel out in the posterior distribution).

We do not have any prior knowledge about p; therefore, the prior distribution of p is the uniform distribution over the interval $\left[0,1\right]$, i.e., $\Pr \left[p\right]=1$. Applying Bayes’ theorem, the posterior distribution of p given m and n is:

$$\Pr \left[p| m\right]=\frac{\Pr \left[m| p\right]\cdot \Pr \left[p\right]}{\Pr \left[m\right]}=\frac{{p}^{m}{\left(1-p\right)}^{n-m}}{\int_{0}^{1}{p}^{m}{\left(1-p\right)}^{n-m}dp}.$$

The denominator is the normalization constant, which is the integral of the numerator over $p\in \left[0,1\right]$.

$$\Pr \left[m\right]=\int_{0}^{1}{p}^{m}{\left(1-p\right)}^{n-m}dp=\int_{0}^{1}{p}^{(m+1)-1}{\left(1-p\right)}^{(n-m+1)-1}dp={{\rm{B}}}(m+1,n-m+1),$$

where B denotes the beta function. Therefore, the posterior distribution f(p) is a beta distribution with parameters α = m + 1 and β = n − m + 1:

$$f\left(p\right)=\frac{{p}^{m}{\left(1-p\right)}^{n-m}}{{{\rm{B}}}(m+1,n-m+1)}.$$

Recall that f(p) is the posterior probability distribution of p = X(k), given the observation that the subject chooses the negative action m times our of n trials. Based on  f(p), we can calculate the most probable value of X(k), which is the expectation.

Calculating ${\mathbb{E}}\left[p\right]$

The expectation of p is:

$${\mathbb{E}}\left[p\right]=\int_{0}^{1}p\cdot f\left(p\right)dp=\int_{0}^{1}p\cdot \frac{{p}^{m}{\left(1-p\right)}^{n-m}}{{{\rm{B}}}(m+1,n-m+1)}dp=\frac{\int_{0}^{1}{p}^{m+1}{\left(1-p\right)}^{n-m}dp}{{{\rm{B}}}(m+1,n-m+1)}.$$

The numerator is the beta function with parameters m + 2 and n − m + 1:

$$\int_{0}^{1}{p}^{m+1}{\left(1-p\right)}^{n-m}dp=\int_{0}^{1}{p}^{(m+2)-1}{\left(1-p\right)}^{(n-m+1)-1}dp={{\rm{B}}}(m+2,n-m+1).$$

Then, the expectation ${\mathbb{E}}\left[p\right]$ becomes:

$${\mathbb{E}}\left[p\right]=\frac{\int_{0}^{1}{p}^{m+1}{\left(1-p\right)}^{n-m}dp}{{{\rm{B}}}(m+1,n-m+1)}=\frac{{{\rm{B}}}(m+2,n-m+1)}{{{\rm{B}}}(m+1,n-m+1)}.$$

Using the property of the beta function,

$${{\rm{B}}}(m,n)=\frac{\left(m-1\right)!\left(n-1\right)!}{\left(m+n-1\right)!}.$$

We can simplify:

$${{\rm{B}}}(m+2,n-m+1)=\frac{\left(\left[m+2\right]-1\right)!\left(\left[n-m+1\right]-1\right)!}{\left(\left[m+2\right]+\left[n-m+1\right]-1\right)!}=\frac{\left(m+1\right)!\left(n-m\right)!}{\left(n+2\right)!}.$$

$${{\rm{B}}}(m+1,n-m+1)=\frac{\left(\left[m+1\right]-1\right)!\left(\left[n-m+1\right]-1\right)!}{\left(\left[m+1\right]+\left[n-m+1\right]-1\right)!}=\frac{\left(m\right)!\left(n-m\right)!}{\left(n+1\right)!}.$$

Thus,

$${\mathbb{E}}\left[p\right]=\frac{{{\rm{B}}}(m+2,n-m+1)}{{{\rm{B}}}(m+1,n-m+1)}=\frac{\left(m+1\right)!}{\left(n+2\right)!}\cdot \frac{\left(n+1\right)!}{\left(m\right)!}=\frac{m+1}{n+2}.$$

Calculating the confidence interval for X(k)

The confidence interval of X(k) can be derived from the cumulative density function (CDF) of the distribution f(p). Since f(p) is a beta distribution, the CDF is the regularized incomplete beta function ${I}_{p}\left(m+1,n-m+1\right)$. The c × 100% confidence interval $T=\left[{p}_{L},{p}_{U}\right]$ for X(k) is determined by:

$${I}_{{p}_{L}}\left(m+1,n-m+1\right)=\frac{\left(1-c\right)}{2},\qquad {I}_{{p}_{U}}\left(m+1,n-m+1\right)=\frac{\left(1+c\right)}{2}.$$

To find p_L and p_U, we use the inverse of the regularized incomplete beta function I⁻¹:

$${p}_{L}={I}_{\left(1-c\right)/2}^{-1}\left(m+1,n-m+1\right),\qquad {p}_{U}={I}_{\left(1+c\right)/2}^{-1}\left(m+1,n-m+1\right).$$

Therefore, the c × 100% confidence interval T for X(k) is:

$$T=\left[{p}_{L},{p}_{U}\right]=\left[{I}_{\left(1-c\right)/2}^{-1}(m+1,n-m+1),{I}_{\left(1+c\right)/2}^{-1}(m+1,n-m+1)\right].$$

The width ℓ(T) of the confidence interval T is determined by the difference between the upper and lower bounds of the interval T:

$$\ell (T)={I}_{\left(1+c\right)/2}^{-1}(m+1,n-m+1)-{I}_{\left(1-c\right)/2}^{-1}(m+1,n-m+1).$$

By using the Bayesian approach with the beta distribution, we can accurately estimate the confidence intervals for X(k) even when m and n are small. This method addresses the limitations of the normal approximation in the context of small sample sizes and provides a more reliable measure of uncertainty in our estimates. Based on the confidence intervals described above, we implemented a robust filtering process, which can be used for in-depth analyses of behavioral dynamics profiles.

Upon computing each X, two interconnected matrices, P and L, are generated to capture the aggregated data across all subjects. Matrix P contains the estimated binomial probabilities, while L holds the widths of the corresponding 95% confidence intervals. Specifically, each entry P(k, i) and L(k, i) jointly represent the estimate and its confidence interval while estimating X(k) for i^th subject.

To enhance the reliability of our estimates, we set the acceptance threshold from the distribution of widths stored in L. Estimates accompanied by confidence intervals exceeding this threshold were excluded from further analysis. In other words, we discarded P(k, i) if its corresponding L(k, i) exceeded the threshold.

As an additional step to ensure the robustness of our statistical analyses, we employed a listwise deletion strategy as a preprocessing procedure. If a subject had one or more discarded values, the entire dataset corresponding to that subject was excluded from the analysis using the behavioral dynamics profile X. More specifically, if any element in i^th column of P was discarded, the entire column was removed.

Lastly, we confirmed that our results remained stable across a reasonable range of acceptance thresholds for confidence interval widths. This was validated through sensitivity analyses across different threshold values, although these data are not presented. For the analyses conducted in this paper, the acceptance threshold was set at the median, except for analyses of the two-armed bandit tasks (Fig. 5) and the T-maze task (Fig. 6), where it was the 60^th percentile.

Multi-trial history regression analysis

We quantified the effect of past support or conflict events on the action-selection strategy after the conflict event using logistic regression analysis (Supplementary Fig. 3). We defined vectors for each of the two possible event types: support event (S), and conflict event (C), each taking on a value of +1 for trials of their type in which the subject selected the positive action, a value of −1 for trials of their type in which the subject selected the negative action and a value of 0 for trials of other types. We defined the following regression model:

$${{\rm{logit}}}\left[P\left({a}_{t}={a}_{+}| {e}_{t-1}\in {{\rm{C}}}\right)\right]={\sum }_{\tau=1}^{T}{\beta }_{{{\rm{C}}}}\left(\tau \right)\cdot {{\rm{C}}}\left(t-\tau \right)+{\sum }_{\tau=2}^{T}{\beta }_{{{\rm{S}}}}\left(\tau \right)\cdot {{\rm{S}}}\left(t-\tau \right),$$

where β_C and β_S are row vectors of regression weights that quantify the tendency to repeat the action that was made τ trials ago, which resulted in the corresponding event type, and T is a parameter governing the number of past trials used by the model to predict upcoming choice. Unless otherwise specified, T was set to 5 for all analyses. To evaluate the behavioral similarity between the subject and the fitted model, we first individually computed the normalized regression weight ${\widehat{\beta }}_{{{\rm{C}}}}$ and calculated the cosine similarities between ${\widehat{\beta }}_{{{\rm{C}}}}$ from the subject and the fitted model. Second, we individually computed the normalized regression weight ${\widehat{\beta }}_{{{\rm{S}}}}$ and calculated the cosine similarities between ${\widehat{\beta }}_{{{\rm{S}}}}$ from the subject and the fitted model.

$${\widehat{\beta }}_{{{\rm{C}}}}=\frac{{\beta }_{{{\rm{C}}}}}{\left\Vert {\beta }_{{{\rm{C}}}}\right\Vert },\,\,\,{\widehat{\beta }}_{{{\rm{S}}}}=\frac{{\beta }_{{{\rm{S}}}}}{\left\Vert {\beta }_{{{\rm{S}}}}\right\Vert },$$

Support-stay index (SSI)

We defined the support-stay index as the average regression weights β_S to represent the general effect of past support events on choosing the same action,

$${{\rm{SSI}}}=\frac{1}{T-1}{\sum }_{\tau=2}^{T}{\beta }_{{{\rm{S}}}}\left(\tau \right).$$

Conflict-shift index (CSI)

We defined the conflict-shift index as the average regression weights β_C multiplied by −1 to represent the general effect of past conflict events on choosing the alternative action,

$${{\rm{CSI}}}=\frac{-1}{T-1}{\sum }_{\tau=2}^{T}{\beta }_{{{\rm{C}}}}\left(\tau \right).$$

Model proposal

Based on observed discrepancies between animal behavior and reinforcement learning (RL) models in behavioral dynamics profiles and multi-trial history regression analyses (Fig. 2), we design a model to accurately describe different action-selection strategies after the conflict and support events. Here, we assumed that the animal understands the task structure well through extensive training, including anti-correlated reward probabilities for two output options and the likely outcomes it will experience after choosing one action under specific contexts.

Suppose there are two possible actions, X and Y. Note that the model cannot guarantee which one is the positive and which one is the negative action. This is because the model cannot know the ground-truth context currently active. Instead, the model only estimates it. For each possible action $a\in \left\{X,Y\right\}$, the model contains two decision variables, support-stay bias (support bias) ${b}_{{{\rm{S}}}}^{a}$ and conflict-shift bias (conflict bias) ${b}_{{{\rm{C}}}}^{a}$. Specifically, when the model chooses action a and experiences the support event of action a (S^a), the support bias of the action $a,{b}_{{{\rm{S}}}}^{a}$, governs the action selection for the next trial, explaining the action-selection strategy after the support event, observed in CI (Fig. 2a). On the other hand, when the model experiences the conflict event of the action a (C^a), the conflict bias of the action $a,{b}_{{{\rm{C}}}}^{a}$, governs the action selection for the next trial, explaining the action-selection strategy after the conflict event, observed in conditional CE (Fig. 2c) and β_C (Fig. 2d).

At the initialization of the model, the support bias of all actions is set to 0.5, and the conflict bias of all actions is set to ${b}_{{{\rm{C}}}}^{0}$, the constant parameter representing the innate value of conflict bias. At the current, t^th trial, suppose the model chooses action X (a_t = X) and experiences the event, which can occur after choosing action X (e_t ∈ S^X ∪ C^X). After each trial, our model performs four operations; (1) conflict bias update, (2) action selection, (3) support bias update, and (4) flag update.

Conflict bias update

The model updates the conflict bias of the chosen action X using the modified Rescorla-Wagner (RW) learning rule⁹,

$${b}_{{{\rm{C}}}}^{X}(t+1)={b}_{{{\rm{C}}}}^{X}(t)+{\alpha }_{{{\rm{C}}}}(t)\left({\lambda }_{{{\rm{C}}}}(t)-{b}_{{{\rm{C}}}}^{X}(t)\right),$$

(1)

where α_C(t) and λ_C(t) refer to the trial-varying learning rate and asymptote¹⁰ of conflict bias, respectively. Both variables depend on two factors: (1) the type of event e_t and (2) the flag f_t, the Boolean variable indicating whether the model repeats the same action, although it led to a conflict event in the last trial. The flag serves as a mental note to bet on the possibility that there was no context change. Mathematically, these factors can be represented as the indicator functions Y_e and Y_f, respectively;

$${Y}_{e}(t)={\mathbb{1}}\left[{e}_{t}\in {{{\rm{S}}}}^{X}\right],\,\,\,{Y}_{f}(t)={\mathbb{1}}\left[{f}_{t}=1\right]={\mathbb{1}}\left[{e}_{t-1}\in {{{\rm{C}}}}^{X}\right].$$

(2)

For different combinations of Y_e and Y_f, we used different pairs of α_C and λ_C. Specifically, for each trial, the values of α_C(t) and λ_C(t) are determined by the current combination of Y_e(t) and Y_f(t). This approach was used to characterize the observed results from the comparison between CE-C and CE-S while varying N_S (Fig. 2c), as well as the results observed from β_C while varying τ (Fig. 2d).

In addition to the update mechanism described in Eq. (1), we incorporated a forgetting mechanism to address scenarios where the model does not consistently adhere to one action over successive trials (a_t ≠ a_t−1). This situation indicates that the model lacks a strong belief in any particular context. If such a condition persists, the difference between the conflict biases of two actions - representing the model’s contextual belief shaped by past experiences - should converge toward 0. We assumed that this converge occurs as the conflict bias of all actions gradually converges to ${b}_{{{\rm{C}}}}^{0}$, the initial value of the conflict bias. We set the forgetting rates of the action chosen and unchosen at the current trial differently,

$${b}_{{{\rm{C}}}}^{a}\left(t+1\right)\leftarrow \left\{\begin{array}{ll}{b}_{{{\rm{C}}}}^{a}\left(t+1\right)+{\omega }_{{{\rm{C}}}}^{{{\rm{ch}}}}\left({b}_{{{\rm{C}}}}^{0}-{b}_{{{\rm{C}}}}^{a}\left(t+1\right)\right){,}&a=X\\ {b}_{{{\rm{C}}}}^{a}\left(t+1\right)+{\omega }_{{{\rm{C}}}}^{{{\rm{unc}}}}\left({b}_{{{\rm{C}}}}^{0}-{b}_{{{\rm{C}}}}^{a}\left(t+1\right)\right){,}&a\ne X\end{array}\right.,$$

(3)

where ${\omega }_{{{\rm{C}}}}^{{{\rm{ch}}}}$ and ${\omega }_{{{\rm{C}}}}^{{{\rm{unc}}}}$ are constants representing the forgetting rates of the conflict bias for the chosen and unchosen actions, respectively.

Action selection

After the action support event

After experiencing an action support event (e_t ∈ S^X), the model chooses whether to stay with the current action (a_t = X) based on the support bias. The stay probability is given by

$$P\left({a}_{t+1}=X| {e}_{t}\in {{{\rm{S}}}}^{X}\right)=\frac{\exp \left(\beta {b}_{{{\rm{S}}}}^{X}(t)\right)}{{\sum }_{i\in \left\{X,Y\right\}}\exp \left(\beta {b}_{{{\rm{S}}}}^{i}(t)\right)},$$

(4)

where ${b}_{{{\rm{S}}}}^{X}$ is the support bias of action X, and β is an inverse temperature parameter, which is constant.

After the action conflict event

After experiencing an action conflict event (e_t ∈ C^X), the model chooses whether to shift from the current action based on the conflict bias. The stay probability is given by

$$P\left({a}_{t+1}=X| {e}_{t}\in {{{\rm{C}}}}^{X}\right)=1-{b}_{{{\rm{C}}}}^{X}(t+1),$$

(5)

where ${b}_{{{\rm{C}}}}^{X}$ is the conflict bias of action X.

Support bias update

After selecting the action for the next trial, a_t+1, the model updates the support bias of the two actions based on what action has been chosen. The support bias of the chosen action increases towards 1, while the support bias of the action not chosen decreases towards 0. Mathematically, it follows the RW learning rule as

$${b}_{{{\rm{S}}}}^{a}\left(t+1\right)=\left\{\begin{array}{ll}{b}_{{{\rm{S}}}}^{a}\left(t\right)+{\alpha }_{{{\rm{S}}}}\left(1-{b}_{{{\rm{S}}}}^{a}\left(t\right)\right){,}&a={a}_{t+1}\\ {b}_{{{\rm{S}}}}^{a}\left(t\right)+{\alpha }_{{{\rm{S}}}}\left(0-{b}_{{{\rm{S}}}}^{a}\left(t\right)\right){,}&a\ne {a}_{t+1}\end{array}\right.,$$

(6)

where α_S is a constant learning rate of support bias. In addition, the support biases of two actions are always anti-parallel, by definition. That is, the sum of support biases is fixed to 1, and each support bias can be represented by the support bias difference solely.

Flag update

After selecting the action for the next trial, a_t+1, the model updates the flag. Despite that the action conflict event occurred (e_t ∈ C^X), if the model chooses the same action for the next trial (a_t+1 = a_t), the flag for the next trial is set to True. Mathematically,

$${f}_{t+1}={\mathbb{1}}\left[\left({e}_{t}\in {{{\rm{C}}}}^{X}\right)\&\left({a}_{t+1}={a}_{t}\right)\right].$$

Baseline models

In this section, we listed the update mechanism of baseline models used for comparative analyses in different tasks. At the current, t^th trial, suppose the model chooses action a_t, arrives at the outcome state o_t, and observes r_t. Here, r_t is a binary variable indicating whether rewarded.

Model-free RL (MF) model

The MF model²¹ maintains the action value of each action, Q^a, as well as the outcome value of each outcome state, V^o. After each trial, these quantities are updated according to

$$\begin{array}{rcl}{Q}^{{a}_{t}}(t+1)&=&{Q}^{{a}_{t}}(t)+\alpha \left[{V}^{{o}_{t}}(t)-{Q}^{{a}_{t}}(t)\right]+\alpha \lambda \left[{r}_{t}-{V}^{{o}_{t}}(t)\right],\\ {V}^{o}(t+1)&=&\left\{\begin{array}{ll}{V}^{o}(t)+\alpha \left[{r}_{t}-{V}^{o}(t)\right],\hfill &o={o}_{t}\\ {V}^{o}(t)+\alpha \left[1-{r}_{t}-{V}^{o}(t)\right],\quad &o \; \ne \; {o}_{t}\end{array}\right.,\end{array}$$

where α and λ are learning-rate and eligibility-trace parameters affecting the update process.

Q-learning with differential forgetting (DFQ) model

The DFQ model²⁸ maintains the action value of each action, Q^a. After each trial, these quantities are updated according to:

$${Q}^{a}(t+1)=\left\{\begin{array}{ll}\zeta {Q}^{a}(t),\hfill \quad &a\ne {a}_{t}\\ {Q}^{a}(t)+\alpha \left[{\kappa }_{R}-{Q}^{a}(t)\right],\hfill \quad &a={a}_{t},\quad {r}_{t} > 0\\ {Q}^{a}(t)+\alpha \left[-{\kappa }_{O}-{Q}^{a}(t)\right],\quad &a={a}_{t},\quad {r}_{t}\le 0\end{array}\right.,$$

where ζ is the forgetting rate parameter for the action unchosen, α is the learning rate parameter for the selected action, κ_R represents the strength of reinforcement by reward receipt, and κ_O represents the strength of aversion resulting from the reward omission.

Model-based RL (MB) model

The MB model²² maintains the outcome value of each outcome state V^o. It plans the next action based on the action value computed by multiplying the outcome value by T(o∣a), the transition probability with which each action will lead to each outcome state:

$${Q}^{a}(t)={\sum}_{o}{V}^{o}(t)\cdot T(o| a),$$

where T(o∣a) is fixed to the true transition function (0.8 for common and 0.2 for uncommon transitions). After each trial, the outcome value for both outcome states is updated according to:

$${V}^{o}(t+1)=\left\{\begin{array}{ll}{V}^{o}(t)+\alpha \left[{r}_{t}-{V}^{o}(t)\right],\hfill \quad &o={o}_{t}\\ {V}^{o}(t)+\alpha \left[1-{r}_{t}-{V}^{o}(t)\right],\quad &o\ne {o}_{t}\end{array}\right.,$$

where α is a learning-rate parameter.

Reduced (RD) model

The RD model⁵ is the mixture-of-agents model. It computes its action value as a weighted average of the action values of individual agents A, each of whom implements different behavioral strategies:

$${Q}_{{{\rm{Total}}}}^{a}(t)={\sum}_{A\in {\mathbb{P}}}{\beta }_{A}{Q}_{A}^{a}(t),$$

where ${\mathbb{P}}$ represents a set of agents, and each β is a weight determining the influence of each respective agent. The set ${\mathbb{P}}$ contains four agents: the MB model, novelty preference, perseveration, and bias. After each trial, these agents update their action values. Previously, we introduced the update mechanism of the MB model; here. we explain the remaining three agents.

Novelty preference This agent updates its action values based on whether an uncommon transition occurred in the last trial. Here, x_t is a binary variable indicating whether an uncommon transition occurred.

$${Q}_{{{\rm{np}}}}^{a}(t+1)=\left\{\begin{array}{ll}{x}_{t},\hfill \quad &a={a}_{t}\\ 1-{x}_{t},\quad &a \, \ne \, {a}_{t}\end{array}\right..$$

Perseveration This agent tends to repeat a_t.

$${Q}_{{{\rm{prsv}}}}^{a}(t+1)=\left\{\begin{array}{ll}1,\quad &a={a}_{t}\\ 0,\quad &a \, \ne \, {a}_{t}\end{array}\right..$$

Bias This agent tends to select the same action a^* in every trial.

$${Q}_{{{\rm{bias}}}}^{a}(t+1)=\left\{\begin{array}{ll}1,\hfill \quad &a={a}^{*}\\ -1,\quad &a \, \ne \, {a}^{*}\end{array}\right.,$$

Latent-state (LT) model

The LT model²³ treated the task as having a hidden context state h ∈ {Left, Right}, which determined the reward probabilities given the outcome state reached on the trial. The model maintained an estimate P^L, the probability the task was in the context Left. After each trial, the model first applies the Bayes rule to P^L to incorporate the information obtained such as the outcome state it arrives (o_t) and whether it gets a reward (r_t).

$${\tilde{P}}^{L}(t+1)=\frac{P({r}_{t}| {o}_{t},\,{\mbox{Left}})\cdot {P}^{L}(t)}{P({r}_{t})},$$

where P(r_t) is the marginal probability considering both contexts as follows:

$$P({r}_{t})=P({r}_{t}| {o}_{t},\,{\mbox{Left}}){P}^{L}(t)+P({r}_{t}| {o}_{t},{\mbox{Right}}){P}^{R}(t).$$

The conditional reward probability given the context and the outcome state is fixed to the true value. After the Bayesian update, the model next updates P^L considering the possibility of block reversal:

$${P}^{L}(t+1)=(1-P(\,{{\mbox{rev}}})){\tilde{P}}^{L}(t+1)+P(\,{{\mbox{rev}}}){\tilde{P}}^{R}(t+1),$$

where P(rev) is the probability of block reversal. After updating P^L, the model chooses the left action at the next trial with the probability calculated as:

$$P({a}_{t+1}=\,{\mbox{L}})=\left[1-P(\,{\mbox{lapse}})\right]\cdot {P}^{L}(t+1)+P({\mbox{lapse}})\cdot \frac{1}{2},$$

where P(lapse) is the probability of lapse, choosing the action with uniform probability.

Asymmetric Bayesian learning (ABL) model

The ABL model²⁵ implements a variant of the LT model. This treated rewards in each outcome state as different observations but considered reward omission at different outcome states as the same observation. The model maintained an estimate P^L, the probability the task was in the context Left. After each trial, the model first applies the Bayes rule to P^L following o_t and r_t as:

$${\tilde{P}}^{L}(t+1)=\frac{P({r}_{t},{o}_{t}| \,{\mbox{Left}})\cdot {P}^{L}(t)}{P({r}_{t},{o}_{t})},$$

where P(r_t, o_t) is the marginal probability considering both contexts as follows:

$$P({r}_{t},{o}_{t})=P({r}_{t},{o}_{t}| \,{\mbox{Left}}){P}^{L}(t)+P({r}_{t},{o}_{t}| {\mbox{Right}}){P}^{R}(t).$$

The conditional reward probability given the context is fixed to the true value. After the Bayesian update, the model next updates P^L considering the possibility of block reversal:

$${P}^{L}(t+1)=(1-P(\,{{\mbox{rev}}})){\tilde{P}}^{L}(t+1)+P(\,{{\mbox{rev}}}){\tilde{P}}^{R}(t+1),$$

where P(rev) is the probability of block reversal.

After updating P^L, the model computes the outcome values of the outcome states,

$${V}^{o}(t+1)=P(r=1,o| \,{\mbox{Left}}){P}^{L}(t+1)+P(r=1,o| {\mbox{Right}}){P}^{R}(t+1),$$

and the action values using the transition probability,

$${Q}^{a}(t)={\sum}_{o}{V}^{o}(t)\cdot T(o| a),$$

where T(o∣a) is fixed to the true transition function (0.8 for common and 0.2 for uncommon transitions). Then, the model plans the next action based on the action values with bias and multi-trial perseveration, following the best model shown in ref. ²⁵.

Meta-learning (MTL) model

We adopted and modified the meta-learning strategy outlined by ref. ²⁴ for application to the two-step task. The MTL model is based on the MB model, but it modulates RPE magnitude and negative outcome learning rate based on expected and unexpected uncertainty. After each trial, the model calculates the reward prediction error (RPE) δ(t), which is an actual reward (r_t) minus the outcome value of the arrived outcome state (o_t):

$$\delta (t)={r}_{t}-{V}^{{o}_{t}}(t).$$

Based on δ(t) and ϵ(t), the estimate of expected uncertainty calculated from the history of unsigned RPEs, the model calculates υ(t), the unexpected uncertainty:

$$\begin{array}{c}\upsilon (t)=| \delta (t)| -\epsilon (t)\\ \epsilon (t+1)=\epsilon (t+1)+{\alpha }_{\upsilon }(t)\end{array},$$

where α_υ is the parameter that controls the rate of RPE magnitude integration.

Large υ may indicate that an environmental change has occurred, which should drive learning for adaptive behavior. Consequently, α₋ varies as a function of how surprising recent outcomes are:

$${\alpha }_{-}(t)=\left\{\begin{array}{ll}{\alpha }_{-}(t-1),\hfill \quad &\delta (t) > 0\\ \psi \left[\upsilon (t)+{\alpha }_{-}(0)\right]+(1-\psi ){\alpha }_{-}(t-1)\quad &\delta (t) < 0\end{array}\right.,$$

where α₋(0) is the baseline learning rate from no reward, and ψ is the parameter that controls the integration rate of unexpected uncertainty to α₋. After surprising no-reward outcomes, α₋ increases and was not allowed to be less than 0.

After updating υ, ϵ, and α₋, the outcome value for both outcome states is updated according to:

$${V}^{o}(t+1)=\left\{\begin{array}{ll}\zeta {V}^{o}(t),\hfill \quad &o \, \ne \, {o}_{t}\hfill\\ {V}^{o}(t)+{\alpha }_{+}\delta (t)\left[1-\epsilon (t)\right],\quad &o={o}_{t},\quad \delta (t) \, > \, 0\\ {V}^{o}(t)+{\alpha }_{-}(t)\delta (t)\left[1-\epsilon (t)\right],\quad &o={o}_{t},\quad \delta (t) \, < \, 0\end{array}\right.,$$

where ζ is the forgetting rate parameter.

Stochastic logistic regression policy (SLRP) model

The SLRP model⁶ selects the next action given its past history of events:

$$P({a}_{t+1}| {a}_{1:t},{r}_{1:t})=\sigma \left[\psi (t+1)\right],$$

where σ is the logistic function and ψ is the log odds. After each trial, it calculates ψ as:

$$\psi (t+1)=\alpha {\overline{c}}_{t}+{\sum }_{i=0}^{5}{\beta }_{i}{\overline{c}}_{t-i}{r}_{t-i}$$

where ${\overline{c}}_{t}=2{c}_{t}-1$, and c_t is a binary variable indicating whether a_t is the left action. Consequently, ${\overline{c}}_{t}$ equals 1 when the left action was chosen, and −1 for when the right action was selected.

Model fitting

For model fitting, we utilized the pattern search algorithm, which is a derivative-free, global optimization algorithm. It is because we cannot guarantee the existence of smooth and continuous derivatives over the likelihood landscape, the key assumption of various derivative-based optimization solvers⁸⁵.

For model comparison, we used different baseline models for different tasks due to variations in task complexity. The two-step task incorporates probabilistic transitions from a chosen action to an outcome state, adding uncertainty that necessitates models accounting for transitions. In contrast, the two-armed bandit and T-maze tasks do not have this complexity, so we compared our SSCS model with baseline models that do not rely on transition information.

The two-step task

We prepared 6 different RL models as a baseline; the model-free (MF) RL model²¹, the model-based (MB) RL model²², the latent-state model²³, the meta-learning model²⁴, the asymmetric Bayesian learning model²⁵, and the “reduced model"⁵. For each subject, we repeated the procedure 40 times with different random seeds.

Two-armed bandit task with context reversal

As a baseline, we prepared 2 different RL models; the model-free (MF) RL model²¹ and the stochastic logistic regression policy (SLRP) model⁶. For each subject and each value of p (representing the reward probability), we separately inferred the parameters of the SLRP model. For the SLRP model, we utilized the Bayesian logistic regression, as conventional algorithms with maximum likelihood estimation can induce abnormal fitting results with a small number of trials. The parameters of the model-free RL model and the SSCS model were estimated in the following manner. First, for each subject, we generated 40 different initial priors by fitting the model with random seeds to the concatenated dataset, which includes three datasets from different p values. This preprocessing ensured that our prior distribution of parameters could explain the variances shared across different values of p. Second, from these 40 initial seeds, we conducted fine-tuning of the parameters by fitting the pretrained model to the dataset from a single value of p. By this procedure, we narrowed down the parameter distribution from the one capable of explaining common properties of one subject to the distribution specialized in explaining the dataset under a specific condition.

T-maze task with context reversal

We prepared 2 different RL models as a baseline; the model-free (MF) RL model²¹ and the DFQ model²⁸. For each subject, we repeated the procedure 40 times with different random seeds.

Two-armed bandit task with MSN inactivation

To analyze the behavior in⁷, we prepared 2 different RL models as a baseline; the model-free (MF) RL model²¹ and the DFQ model²⁸. First, for each subject, we generated 200 different initial priors by fitting the model with random seeds to the concatenated dataset, which includes both control and inactivation datasets, starting from random seeds.

We performed such preprocessing to ensure that our prior distribution of parameters can explain the variances within both control and inactivation conditions. Second, from these 200 initial seeds, we conducted fine-tuning of the parameters by fitting the pretrained model to the dataset from a single condition. By this procedure, we narrowed down the parameter distribution from the one capable of explaining common properties of one subject to the distribution specialized in explaining the dataset under a specific condition.

Model predictability comparison

To compare the accuracy of different models, we utilized two statistical measures: the normalized BIC score and the normalized cross-validation likelihood. First, to compare the accuracy of specific models while controlling for different model complexity, we computed the normalized BIC score of each model for every subject using the equation below,

$$n{{\rm{BIC}}}=\exp \left[-\frac{1}{2n}\cdot {{\rm{BIC}}}\right]=\exp \left[\frac{1}{n}\ln \left(\widehat{L}\right)-\frac{k}{2n}\ln \left(n\right)\right]$$

where k is the number of parameters of the model, n is the number of total trials performed by each subject, and $\widehat{L}$ is the maximum likelihood function of the given model.

Next, to compute the normalized cross-validation likelihood, we used two-fold cross-validation by dividing the data from entire sessions for each rat into even- and odd-numbered sessions. After calculating the log-likelihood of each partial dataset using parameters fit to the other, we computed the normalized cross-validated likelihood by summing the log-likelihoods from the two partial datasets, dividing it by the total number of trials, and computing its exponentiation. These two metrics can be interpreted as the average per-trial likelihood with which the model would have selected the action that the rat actually selected.

Neural network models

For the neural network modeling in the two-step task, we utilized two versions of the neural network model as described in ref. ²⁵. The architecture, inputs, outputs, loss functions, optimizer, and training hyperparameters are identical to those used in the original study²⁵. However, instead of the task environment used in ref. ²⁵, we employed the task environment used in ref. ⁵ to enable direct comparisons between rat behavior and model behavior.

The models were trained in episodes that terminated after 500 trials or 1200 time steps, whichever occurred first, with network weights updated between episodes. For each model version, we conducted 17 simulation runs using different random seeds, each trained for 500 episodes. These runs served as the experimental unit for statistical analysis, analogous to subjects in animal experiments. After training, the models underwent an additional 100,000 trials for further analyses.

Identification of neurons encoding task and decision variables

We used regression models to analyze neural spikes and identify corresponding neurons related to support bias or conflict bias. For each subject, we inferred the trial-by-trial values of support bias and conflict bias from the SSCS model with parameters showing the lowest BIC score.

From several considerations that the current methodology to identify neurons encoding decision variables can be problematic^30,31,86, we sought to resolve these issues with the autoregressive model, which is traditionally utilized to investigate the relationship between two time series. Among various options, we chose the autoregressive exogenous (ARX) model³². After fitting our SSCS model to the subject’s behavior, we computed trial-by-trial fluctuations of three decision variables: the support bias difference between the right and left action △b_S(t), the conflict bias of the left action ${b}_{{{\rm{C}}}}^{L}\left(t\right)$, and the conflict bias of the right action ${b}_{{{\rm{C}}}}^{R}\left(t\right)$ at trial t. Then, with task variables (choice and outcome), we fitted the regression model Z to the average firing rates of each neuron within four different sections, separately,

$$Z(t)=\left[{\sum }_{k=1}^{L}{\beta }_{-k}Z\left(t-k\right)\right]+{\beta }_{{{\rm{ch}}}}C(t)+{\beta }_{{{\rm{rw}}}}R(t)+{\beta }_{{{\rm{S}}}}\Delta {b}_{{{\rm{S}}}}(t)+{\beta }_{{{\rm{C}}}}^{L}{b}_{{{\rm{C}}}}^{L}(t)+{\beta }_{{{\rm{C}}}}^{R}{b}_{{{\rm{C}}}}^{R}(t),$$

where C(t) and R(t) represent the animal’s choice (0 for left, 1 for right), and its outcome (0 for unrewarded, 1 for rewarded) at trial t, respectively. In addition, the length of the autoregressive term L is automatically adjusted based on the result of the partial autocorrelation test for individual neurons.

To test the significance of the difference of each regression coefficient from 0, we performed the block-wise permutation test⁸. For this, we randomly shuffled spike data 1000 times across different trials within each block while preserving the original block sequence.

For the estimation of the single-trial firing rate of decision variable-encoding neurons within each section, we utilized the Bayesian adaptive kernel smoother⁸⁷. Since the length of the section is not constant, we focused on activity during fixed periods after the section starts and before the section ends. The length of these periods was fixed to half of the minimum section latencies for individual neurons across different trials.

To visualize the modulation of single-trial firing rate dependent on the decision variable $X\in \left\{\Delta {b}_{{{\rm{S}}}},\,{b}_{{{\rm{C}}}}^{L},\,{b}_{{{\rm{C}}}}^{R}\right\}$ during each section, we collected the firing rates across different trials for each neuron individually. After sorting them based on the value of the paired decision variable, which is estimated by our model, we grouped them into 6 bins and computed the average single-trial firing rate for each bin separately.

Statistical analyses

All data are represented as mean ± s.e.m, while Spearman correlation coefficients are represented as mean ± bootstrap standard error. Data were analyzed using MATLAB R2023a (The Mathworks, Inc., Natick, MA), R (Ver. 4.1.2, R Core Team, R Foundation for Statistical Computing, Vienna, Austria), and JASP (Ver. 0.18.3, JASP Team). The statistical significance level was set at p < 0.05. The number of permutations for entire permutation-based tests was set at N = 10⁵. To compare two correlations based on dependent groups (e.g., the same group), where two correlations are overlapping (they have a variable in common), and perform a test of significance for the difference between two correlations, we applied the Dunn and Clark’s Z test⁸⁸. In order to control for Type I errors arising from multiple comparisons, we applied the Benjamini–Yekutieli (BY) False Discovery Rate (FDR) adjustment method⁸⁹. For more details and a description of the test used for each figure, see Supplementary Tables 2 and 3.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.