Introduction

The ocean is turbulent, containing eddies with a wide range of sizes. Among them, the mesoscale eddies form the major fraction of the ocean kinetic energy reservoir1,2. These mesoscale eddies redistribute heat and materials in the ocean, contributing dominantly to the short-term (from daily to weekly time scales) variations of ocean thermohaline structures3,4, regulating the primary productivity and further marine ecosystem5,6, and acting as a major driver of extreme events like marine heatwaves7. They also interact strongly with the overlaying atmosphere, influencing air temperature, humidity, winds, cloud fraction, and rainfall within local marine atmospheric boundary layer8,9 as well as atmospheric synoptic variability10,11 and large-scale circulations12. Therefore, accurate eddy-resolving ocean forecasts are not only essential for supporting marine activities and managements but also necessary to improve weather forecast accuracy.

So far, ocean forecasts rely primarily on ocean general circulation models (OGCMs) that make forecasts by numerically discretizing and integrating the governing partial differential equations of the ocean. However, constructing an accurate eddy-resolving global ocean forecast system (GOFS) based on the OGCMs (i.e., the numerical GOFS) remains a challenging issue both computationally and scientifically. On the one hand, resolving mesoscale eddies requires a grid size of O(10 km) or even finer13,14, imposing a massive computational burden for operating global-scale OGCMs especially for implementing advanced data assimilation15 and making ensemble forecast16. In fact, the eddy-resolving numerical GOFSs did not emerge until the recent decade partially due to the enlarged computational resources. On the other hand, the chaotic nature of mesoscale eddies makes their forecast very sensitive to errors in initial conditions, boundary forcings, and OGCMs. In particular, despite development over about a half-century, there are still many uncertainties in OGCMs, including numerical errors caused by discretization, uncertainties in parameterizations of unresolved processes, and insufficient representation of interactions of the ocean with other components of the Earth system17.

Artificial intelligence (AI)-based methods provide a data-driven approach for making forecasts and have been successfully applied to the global medium-range weather forecasts18,19,20,21,22,23,24,25. Their success is achieved primarily from high-quality atmospheric reanalysis training datasets and customized deep neural network (DNN) designed to capture the hidden representations of atmospheric dynamics and alleviate accumulative error when rolling out multistep autoregressive forecasts18,19,20,21,22,23,24,25. These AI-based forecast systems show competitive forecast performance yet substantially reduce the computational burden compared to their numerical counterparts. The successful application of AI-based methods in medium-range weather forecasts has been inspiring their ocean-related usage, including the OGCM emulators, the short-term ocean forecast as well as the interannual-to-decadal ocean prediction26,27,28,29, although it has been well recognized that ocean reanalysis datasets are less robust compared to their atmospheric counterparts primarily due to the sparsity of ocean observations30.

It should be noted that the existing DNN architectures developed for the medium-range weather forecast may not be suitable for the eddy-resolving ocean forecast. Air-sea interactions play an important role in the short-term ocean variability, especially in the surface mixed layer31. However, these interactions have not been explicitly incorporated into the AI-based medium-range weather forecast systems except for providing the SST as an input. Furthermore, the existing AI-based methods tend to smooth out mesoscale weather phenomena32,33 and are expected to dampen ocean mesoscale eddies in a similar way. Such a blurring effect is tolerable for the medium-range weather forecast as its variability is generally dominated by synoptic processes34, but not so for short-term ocean forecast, at which time scale mesoscale eddies make a major contribution to the variability35 (Supplementary Fig. S1).

In this study, we present WenHai, an AI-based GOFS for short-term eddy-resolving forecast across the global upper ocean (0–643 m). WenHai explicitly incorporates atmospheric forcings into the DNN by exploiting the bulk formulae36 on air-sea fluxes. Furthermore, the design of WenHai’s architecture is guided by the characteristics of mesoscale eddies to better preserve their variabilities. As demonstrated below, these features make WenHai outperform state-of-the-art numerical and AI-based GOFSs in forecasting the eddying ocean.

Results

An AI-based eddy-resolving GOFS

Trained on a state-of-the-art eddy-resolving (1/12°) global ocean reanalysis dataset37 (See ‘GLORYS reanalysis’ in Methods), WenHai forecasts 1/12° daily averaged sea surface height (SSH) and three-dimensional temperature, salinity, and horizontal current in the upper 643 m across the global ocean in an autoregressive way. WenHai utilizes the Swin-Transformer38 as its backbone. The training process is decomposed into two stages. WenHai is first pre-trained to minimize the loss for the one-day forecast. Then we adopt a finetune technique20 to minimize the accumulative loss for a sequence of autoregressive forecasts over 5 days, which improves WenHai’s performance at long forecast lead times. The architecture of WenHai (Fig. 1) and its training details are elaborated in Methods (See ‘WenHai model’ in Methods).

Fig. 1: A schematic of WenHai’s architecture.
figure 1

The surface atmosphere and ocean variables on the day \(t+l\) are first combined to compute the air-sea momentum, heat, and freshwater fluxes based on the bulk formulae (green block), where t is an arbitrary date index and l is the forecast lead time (indexing in 1-day intervals). Then, the ocean variables and air-sea fluxes are sent to a deep neural network (red block) that forecasts temporal tendency between ocean variables on the days \(t+l\) and \(t+l+1\). The tendency field is added to the ocean variables on the day \(t+l\) to yield the ocean variable forecast on the day \(t+l+1\) (blue block). Finally, the above processes are iterated to generate a sequence of forecasts. Maps created with Cartopy65. Background land image provided by NASA Earth Observatory.

Full size image

We exploit domain knowledge in the air-sea interactions and ocean dynamics to guide WenHai’s architecture design, which enhances its capacity to forecast the eddying ocean. First, to explicitly represent the atmospheric forcings, we implement a specialized block for computing air-sea momentum, heat and freshwater fluxes from the surface atmosphere variables (e.g., air temperature, winds, etc.) based on the bulk formulae (Supplementary Note 1 and Supplementary Fig. S2). Second, the forecast output is chosen as the temporal tendency of an ocean variable between the two consecutive days rather than the ocean variable on the following day. This is essential to preserve the mesoscale eddy variabilities, as mesoscale eddies dominate the day-to-day variations not the absolute values of ocean variables (Supplementary Fig. S3). Similarly, we put more weight on the loss function in the upper part of the ocean, as mesoscale eddies are generally near-surface intensified39. Finally, the land region is masked to make WenHai focus on forecasting the ocean variability.

Supplementary Fig. S4 provides a visualization of sea surface kinetic energy (KE), sea surface height (SSH), and sea surface temperature (SST) forecast in the Kuroshio Extension region by WenHai. Here, the GLORYS reanalysis is approximated as the ground truth to test the capacity of WenHai to forecast the eddying ocean, with caution about the fidelity of the GLORYS reanalysis in representing reality. WenHai does capture the temporal evolution of KE, SSH, and SST reasonably well, outperforming the persistent forecast that assumes the future ocean state would be the same as the initial condition. In the following sections, we will provide more systematic and quantified assessments of the forecast performance of WenHai and compare it with a state-of-the-art numerical GOFS and AI-based GOFS.

Outperformance of WenHai against a state-of-the-art numerical GOFS

To evaluate the forecast performance of WenHai, we compare it with a state-of-the-art eddy-resolving numerical GOFS, i.e., the 1/12° operational ocean analysis and forecasting systems (GLO12v440,41) from the France Mercator Océan (See ‘GLO12v4’ in Methods). WenHai is initialized from the same initial condition and forced by the same atmospheric forecast product as GLO12v4 during April-November 2024. We remark that using the same initial condition is essential to make a fair comparison between different forecast systems, as errors in the initial condition could have substantial influences on the forecast performance (Supplementary Note 2 and Supplementary Fig. S5). The ocean variables involved in the comparison are selected following the GODAE Ocean-View Inter-comparison and Validation Task Team (IV-TT) Class 4 framework42, including the SST and 15-m current measured by drifting buoys, temperature and salinity profiles measured by Argo profiling floats and level-3 along-track sea level anomaly (SLA) measured by satellite altimeters (See ‘Observational datasets’ in Methods).

Two metrics are used to quantify the forecast performance of WenHai and GLO12v4 (See ‘Verification metrics’ in Methods). The first is the root mean square error (RMSE), a conventional point-to-point verification metric adopted by the GODAE Ocean-View IV-TT Class 4 framework. However, it has been recognized that verification on a point-to-point basis is less appropriate for assessing the performance of high-resolution (eddy-resolving) forecast systems because of the double-penalty issue43, i.e., features correctly forecast but misplaced in space are penalized twice: once for not occurring at the observational site, and secondly for occurring at the forecast site, where they are not observed. To overcome this problem, we adopt a neighborhood-based verification metric that has been routinely applied to evaluating high-resolution oceanic and atmospheric forecast systems44,45. Specifically, forecasts within the neighborhood centered on an observational location are collected to generate a pseudo ensemble which can then be compared to the observed value using typical ensemble and probabilistic forecast verification metrics such as the continuous ranked probability score (CRPS)46. Here the neighborhood is chosen as 1° × 1°. On the one hand, this neighborhood is large enough to contain many ensemble members for robust estimates of the probability. On the other hand, it is sufficiently small so that the observation is not only representative of its precise location but also has characteristics of the entire neighborhood.

Comparison based on RMSE

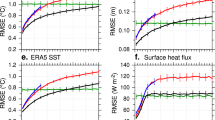
WenHai achieves lower RMSE for all the ocean variables compared to GLO12v4 (Fig. 2; Supplementary Fig. S6a, b). The superiority of WenHai over GLO12v4 becomes more evident as the forecast lead time increases. When forecasting 10 days in advance, WenHai has an RMSE for SST, SLA, 15-m zonal current, and 15-m meridional current 8.94%, 10.67%, 6.95% and 10.33% lower than GLO12v4. As to the 10-day-led temperature profile forecast, the RMSE of WenHai is lower than that of GLO12v4 throughout the upper 643 m (Supplementary Fig. S6a). So is the case for the salinity profile forecast (Supplementary Fig. S6b). The vertical mean RMSE for the temperature (salinity) profile forecast by WenHai is 6.02% (5.64%) lower than that by GLO12v4. We further assess the RMSE in different regions (Supplementary Fig. S7). The forecast performances of WenHai and GLO12v4 are region-dependent, with their RMSE varying from place to another. Nevertheless, the RMSE of WenHai is lower than that of GLO12v4 for most of the regions. Finally, the RMSE of WenHai is universally lower than that of GLO12v4 regardless of the time periods (Supplementary Fig. S8). This provides some support that WenHai should likely outperform GLO12v4 in boreal winter during which period their comparison is not conducted in this study due to the data limitation.

Fig. 2: Comparison of root mean square error (RMSE) between WenHai and a state-of-the-art numerical global ocean forecast system (GOFS) as a function of forecast lead time.
figure 2

Globally averaged RMSE (the lower, the better) of the forecast temperature profile (a), salinity profile (b), sea surface temperature (SST) (c), sea level anomaly (SLA) (d), 15-m zonal current (e) and 15-m meridional current (f) as a function of forecast lead time. The zero-lead time represents the initial conditions. The blue, red, and grey lines correspond to WenHai, GLO12v4 and persistent forecast, respectively. For the temperature and salinity profile forecast, the RMSE is vertically averaged over the upper 643 m. The shading corresponds to the 50% confidence interval computed from a bootstrap method.

Full size image

The RMSE quantifies the closeness of the forecast to the observation but doesn’t by itself indicate the skill in the forecast. The usefulness of a forecast is usually measured by comparing its RMSE to that of some readily available reference forecasts. Here we chose the reference forecast as the persistent forecast. Accordingly, the persistence skill score (PSS) (See ‘Verification metrics’ in Methods) is used to measure the forecast skills of WenHai and GLO12v4 relative to the persistent forecast. A positive PSS indicates superiority over the persistent forecast, while a negative PSS indicates the opposite. GLO12v4 does not beat the persistent forecast except for the SST, whereas WenHai is superior to the persistent forecast for all the ocean variables at most of the forecast lead times (Figs. 2 and 3). In particular, the PSS of WenHai shows a positive trend for all the ocean variables as the forecast lead time increases, suggesting that WenHai can capture the temporal variations of the eddying ocean reasonably well. In contrast, the PSS of GLO12v4 shows a positive trend only for the SST, yet its slope is smaller than that of WenHai.

Fig. 3: Comparison of persistence forecast skill (PSS) between WenHai and a state-of-the-art numerical global ocean forecast system (GOFS) as a function of forecast lead time.
figure 3

Globally averaged PSS (the higher, the better) for the forecast temperature profile (a), salinity profile (b), sea surface temperature (SST) (c), sea level anomaly (SLA) (d), 15-m zonal current (e) and 15-m meridional current (f) as a function of forecast lead time. The zero-lead time represents the initial conditions. The blue and red lines correspond to WenHai and GLO12v4, respectively. For the temperature and salinity profile forecast, the PSS is vertically averaged over the upper 643 m. The shading corresponds to the 50% confidence interval computed from a bootstrap method.

Full size image

Comparison based on CRPS

Verification based on the CRPS yields the same conclusion as verification based on the RMSE, further suggesting the outperformance of WenHai against GLO12v4 (Fig. 4; Supplementary Fig. S6c, d). The CRPS of WenHai is lower than that of GLO12v4 for all the ocean variables and their difference is generally enlarged with the increasing forecast lead time. For the forecasts led by 10 days, the CRPS of WenHai is 3.5% lower than that of GLO12v4 for the temperature profile, 5.5% lower for the salinity profile, 10.0% lower for the SST, 7.0% lower for the SLA, and 2.7% (4.5%) lower for the 15-m zonal (meridional) current, respectively. We remark that the lower CRPS of WenHai than GLO12v4 is not sensitive to the choice of neighborhood. Varying the area of the neighborhood from 0.3° × 0.3° to 2° × 2° leads to qualitatively the same conclusions (Supplementary Fig. S9).

Fig. 4: Comparison of the continuous ranked probability score (CRPS) between WenHai and a state-of-the-art numerical global ocean forecast system (GOFS) as a function of forecast lead time.
figure 4

Globally averaged CRPS (the lower, the better) of the forecast temperature profile (a), salinity profile (b), sea surface temperature (SST) (c), sea level anomaly (SLA) (d), 15-m zonal current (e) and 15-m meridional current (f) as a function of forecast lead time. The zero-lead time represents the initial conditions. The blue and red lines correspond to WenHai and GLO12v4, respectively. For the temperature and salinity profile forecast, the CRPS is vertically averaged over the upper 643 m. The shading corresponds to the 50% confidence interval computed from a bootstrap method.

Full size image

Outperformance of WenHai against the latest AI-based GOFS

In this subsection, we compare WenHai with the latest AI-based GOFS, i.e., XiHe28. Both WenHai and XiHe are trained in the GLORYS and ERA reanalysis and aimed to provide a global 1/12° ocean forecast in the upper 643 m, so that a fair comparison between their forecast performance can be made. We note that although WenHai preserves the ocean mesoscale eddy variabilities reasonably well, XiHe leads to severe underestimation (See ‘Computation of mesoscale eddy variabilities’ in Methods; Table 1; Supplementary Fig. S10). For instance, the variance of mesoscale temperature anomalies forecast by WenHai differs from that in the GLORYS reanalysis by 6.1% (Table 1). In contrast, the variance of mesoscale temperature anomalies forecast by XiHe is 30.0% lower than that in the GLORYS reanalysis (Table 1). Similar conclusions also hold for the variance of mesoscale salinity anomalies and eddy kinetic energy. The strong damping of mesoscale eddy variabilities in XiHe is likely to result from the blurring effect intrinsic to the AI-based forecast20,25,32,33. Such a blurring effect is largely alleviated in WenHai due to its customized design to preserve mesoscale eddy variabilities.

Table 1 Preservation of ocean mesoscale variabilities by artificial intelligence (AI)-based global ocean forecast systems (GOFSs)
Full size table

The above analysis suggests that WenHai has a higher effective resolution than XiHe. Accordingly, point-to-point verification metrics such as the RMSE are not suitable for comparing their forecast performance as these metrics tend to make higher-resolution forecast systems verify worse superficially, although they may provide more realistic forecasts44,47 (Supplementary Note 3 and Supplementary Fig. S11, 12). This issue is confirmed by the systematically reduced RMSE of WenHai by using the spatially smoothed initial condition to make forecast (Supplementary Fig. S11). For this reason, we only use the CRPS to quantify the forecast performance of WenHai and XiHe.

WenHai has much lower CRPS than XiHe for all the ocean variables at all the forecast lead times (Fig. 5). In terms of the temperature profile, salinity profile, SST, SLA, 15-m zonal current and 15-m meridional current forecast, the CRPS in WenHai is 6.8%-10.8%, 4.3%-10.0%, 24.5%-31.4%, 1.8%-21.0%, 1.4%-3.8%, and 0.02%-2.4% lower than that in XiHe, respectively, depending on the forecast lead times. In addition, the superiority of WenHai over XiHe is more evident in the upper 100 m, suggesting the advantage of explicit incorporation of air-sea fluxes into the DNN (Supplementary Fig. S13). Again, the lower CRPS in WenHai than XiHe holds for various choices of the area of neighborhood (Supplementary Fig. S9). In summary, WenHai has better skills in forecasting the eddying ocean than XiHe.

Fig. 5: Comparison of the continuous ranked probability score (CRPS) between WenHai and the latest AI-based global ocean forecast system (GOFS) as a function of forecast lead time.
figure 5

Globally averaged CRPS (the lower, the better) of the forecast temperature profile (a), salinity profile (b), sea surface temperature (SST) (c), sea level anomaly (SLA) (d), 15-m zonal current (e) and 15-m meridional current (f) as a function of forecast lead time. The zero-lead time represents the initial conditions. The blue and red lines correspond to WenHai and XiHe, respectively. For the temperature and salinity profile forecast, the CRPS is vertically averaged over the upper 643 m. The shading corresponds to the 50% confidence interval computed from a bootstrap method.

Full size image

Discussion

In this study, we present WenHai, an AI-based eddy-resolving GOFS whose design is guided by the domain knowledge in the air-sea interactions and ocean dynamics. It has a better representation of atmospheric forcing effects on the ocean by incorporating the bulk formulae of the air-sea fluxes into the DNN and shows a much-improved capacity to preserve ocean mesoscale variability compared to the latest AI-based GOFS through customized model architecture design guided by characteristics of mesoscale eddies. When initialized from the same initial condition and forced by the same atmospheric forecast product, WenHai surpasses the state-of-the-art eddy-resolving numerical GOFS for forecasting all the ocean variables led by one day to at least ten days. Nevertheless, it does not mean that AI-based GOFSs can substitute numerical GOFSs. In fact, the AI-based GOFSs, including WenHai, are trained based on high-quality ocean reanalysis datasets produced via numerical GOFSs in combination with data assimilation37,48. It is more appropriate to think that AI-based GOFSs stand on the shoulders of numerical GOFSs.

Despite the good forecast performance of WenHai, it has some limitations. First, WenHai provides daily average forecast that filters out the diurnal cycle and cannot resolve inertial oscillations or internal waves49 over most parts of the global ocean. The daily average forecast may also be deficient in representing upwelling/downwelling on the continental shelf and coastal trapped waves. Second, the maximum depth of WenHai is chosen as 643 m that is not a genuine lower boundary of the ocean. This may degrade the forecast performance near 643 m. Third, WenHai does not take into consideration the effects of river runoff and sea ice on the ocean and may have some deficiencies in coastal and polar regions. Finally, there is still a slight yet noticeable damping of mesoscale eddy variabilities in WenHai (Table 1) despite its customized design to alleviate this problem. This is partially because WenHai adopts a deterministic pointwise loss function that nudges WenHai to provide smoother forecasts at longer forecast lead times due to the double penalty issue. We envision that WenHai can be further improved by training a hierarchy of DNNs representing oceanic processes of different spatio-temporal scales, adopting probabilistic loss function or adding physical conservation constraints to the loss function, using hybrid model architectures combining deep learning and numerical solver, and utilizing higher-quality ocean reanalysis datasets for training. Achieving these improvements requires the expertise in the marine science and more oceanographers to get involved in the development of AI-based GOFSs.

Methods

GLORYS reanalysis

The Copernicus Global 1/12° Oceanic and Sea Ice GLORYS12 Reanalysis (GLORYS reanalysis for short), developed by Mercator Océan, provides a realistic representation of key oceanic quantities such as sea level, water mass properties, mesoscale activity or sea ice extent. The ocean and sea ice components are based on the NEMO platform50. It has a quasi-isotropic horizontal grid with a 1/12° resolution and 50 vertical levels with vertical spacing increasing progressively with depth. The ocean model is driven by the ERA-Interim atmospheric reanalysis51 provided by the European Centre for Medium-Range Weather Forecasts (ECMWF). Observations are assimilated using a reduced-order Kalman filter derived from a singular evolutive extended Kalman (SEEK) filter52 with a three-dimensional multivariate background error covariance matrix and a 7-day assimilation cycle53. Assimilated observations include the satellite-based SLA, SST, and sea ice concentration and in situ temperature and salinity profiles. The reanalysis dataset covers 1993-2020 with daily resolution.

It should be noted that ocean reanalysis datasets including the GLORYS reanalysis are less robust compared to their atmospheric counterparts primarily due to the sparsity of ocean observations30. In fact, some deficiencies of the GLORYS reanalysis have been reported37. First, a few zonal currents such as the Antarctic circumpolar current and Western Pacific south equatorial current are overly strong. In addition, inter-basins volume exchanges are larger compared to observations and other reanalyses. Finally, there is also unexpected behavior in the Tropical Indian and North East Atlantic basins.

WenHai model

Training and validation datasets

WenHai is trained on the GLORYS reanalysis and ERA5 reanalysis54 during 1993-2018 and validated based on the datasets during 2019.

Input and output details

WenHai is aimed to forecast a sequence of tendency of daily mean ocean variables in the upper ocean \(\{{{{{{\Delta }}}{{\bf{O}}}}_{t}^{l}={{{\bf{O}}}}_{t}^{l}{{{-}}}{{{\bf{O}}}}_{t}^{l-1}},l\in \left[1,N\right]\}\) in an autoregressive way, given the initial condition \({{{\bf{O}}}}_{t}^{0}\) and the surface atmospheric variables \(\{{{{\bf{A}}}}_{t}^{l},l\in \left[0,N-1\right]\}\), where t is an arbitrary date index and l is the forecast lead time (indexing in 1-day intervals). We use bold characters here to emphasize that \({{{\bf{O}}}}_{t}^{l}\) and \({{{\bf{A}}}}_{t}^{l}\) are tensors consisting of multiple variables at multiple grid points. The ocean variables forecast by WenHai are the same as the numerical GOFSs, including zonal velocity, meridional velocity, temperature, salinity, and SSH. WenHai shares the same horizontal grid points as the GLORYS reanalysis and has 23 depth levels selected from those of the GLORYS reanalysis in the upper 643 m (Supplementary Fig. 14). The different ocean variables are stacked along the vertical direction. Accordingly, \({{{\bf{O}}}}_{t}^{l}\) has a dimension size of \({N}_{O}\times {N}_{{lat}}\times {N}_{{lon}}\) with \({N}_{O}=4\times 23+1=93\), \({N}_{{lat}}=2041\) and \({N}_{{lon}}=4320\). Here \({N}_{O}\), \({N}_{{lat}}\) and \({N}_{{lon}}\) are analogous to the channel number, height and width of an image in the field of computer vision.

The surface atmosphere variables are 10-m zonal wind, 10-m meridional wind, mean sea level pressure, 2-m temperature, and 2-m dewpoint temperature, which are routinely forecast by numerical weather forecast systems55. It should be noted that the ocean is not directly forced by these surface atmosphere variables. Instead, it is directly forced by the net momentum, heat, and freshwater fluxes at the air-sea interface. For this reason, we implement a block to compute the fluxes based on the surface values of \({{{\bf{O}}}}_{t}^{l}\) and \({{{\bf{A}}}}_{t}^{l}\,\) using bulk formulae. Specifically, the surface atmosphere variables are first horizontally interpolated to the oceanic grids, and then the bulk formulae are used to transfer the surface atmosphere and ocean variables into the air-sea fluxes, including the surface latent heat flux, surface sensible heat flux, surface upward long-wave radiation flux, zonal wind stress, meridional wind stress, and evaporation rate. Finally, the surface net short-wave radiation flux, surface downward long-wave radiation flux, and precipitation rate from the numerical weather forecasts are included, and the surface downward and upward long-wave radiation fluxes are combined to yield the surface net long-wave radiation flux. This results in a total of eight air-sea flux variables denoted as \({{{\bf{F}}}}_{t}^{l}\) whose dimension size is \({N}_{F}\times {N}_{{lat}}\times {N}_{{lon}}\) with \({N}_{F}=8\). The \({{{\bf{F}}}}_{t}^{l}\) and \({{{\bf{O}}}}_{t}^{l}\) are fed into the DNN to forecast \({{{{\Delta }}}{{\bf{O}}}}_{t}^{l}\). Once \({{{{\Delta }}}{{\bf{O}}}}_{t}^{l}\) is obtained, it is added on \({{{\bf{O}}}}_{t}^{l}\) to obtain \({{{\bf{O}}}}_{t}^{l+1}\). Then \({{{\bf{F}}}}_{t}^{l+1}\) is computed based on the surface values of \({{{\bf{O}}}}_{t}^{l+1}\) and \({{{\bf{A}}}}_{t}^{l+1}\). The above processes are repeated to make a sequence of forecasts.

Architecture overview

For each channel, the values of \({{{\bf{O}}}}_{t}^{l}\) and \({{{\bf{F}}}}_{t}^{l}\) are normalized to range from 0 to 1. The normalized variables first go through two independent pre-processing modules designed to reduce dimensionality. The ocean and atmosphere outputs of pre-processing modules with a dimension of \(259\times 546\times {H}\) are then reshaped to \(141414\times H\) and added together before being fed into 10 homogeneous Swin-Transformer layers whose hidden dimension size \(H\) is 768 and window size is 7. Following this, a post-processing module is employed to restore the outputs of Swin-Transformer layers to the original dimension of ocean variables.

Pre- and post-processing

The pre-processing module consists of a patch embedding block and a down-sampling block. The patch embedding block is a convolution layer whose kernel size and stride (also known as the patch size) is chosen as 4 in this study. As \({N}_{{lat}}\) and \({N}_{{lon}}\,\) need to be divisible by both the window size 7 and patch size 4 to feed \({{{\bf{O}}}}_{t}^{l}\) and \({{{\bf{F}}}}_{t}^{l}\) into the patch embedding block, a zero-value padding is applied to change \({N}_{{lat}}\times {N}_{{lon}}\) of \({{{\bf{O}}}}_{t}^{l}\) and \({{{\bf{F}}}}_{t}^{l}\) to \(2072\times 4368\). The output of the patch embedding block is the embedded \({{{\bf{O}}}}_{t}^{l}\) and \({{{\bf{F}}}}_{t}^{l}\) with the same dimension of \(H\times 518\times 1092\) (i.e., \(H\times 2072/4\times 4368/4\)). It should be noted that using a larger patch size leads to more reduction of the dimensionality of \({{{\bf{O}}}}_{t}^{l}\) and potentially makes WenHai more difficult to preserve the mesoscale variabilities, which is confirmed by the stronger damping of EKE with the increasing patch size (Supplementary Fig. S15). The down-block uses a convolution layer with kernel size 3 and stride 2 to further reduce the data dimension to \(H\times 259\times 546\), followed by permuting the dimension to \(259\times 546\times H\). The post-processing module consists of an up-sampling block and a linear layer. The up-sampling block is a 2-D transposed convolution layer with kernel size 2 and stride 2, changing the dimension of reshaped output from the Swin-Transformer layers from \(H\times \,259\times 546\) to\(\,H\times 518\times 1092\), followed by permuting the dimension to \(518\times 1092\times H\). The linear layer changes the data dimension from \(518\times 1092\times H\) to \(518\times 1092\times 1488\). Then the data are rearranged to have a dimension of \(93\times 2072\times 4368\). Finally, the outputs are restored to the original dimension of \({{{\bf{O}}}}_{t}^{l}\) (i.e., \(93\times 2041\times 4320\)) by the pad-back module to remove redundant marginal zero values.

Window-based Transformer

After being processed by the pre-processing module, inputs are transformed into numerous patch tokens with a sequence length of 141414. As the memory consumption of the self-attention layer in the Vision Transformer (ViT) increases quadratically with the sequence length, we turn to using Swin-Transformer V2 with the window-attention mechanism. The long token sequences are divided into 2886 windows, and each window calculates self-attention with only 49 tokens, which greatly reduces the amount of computation and memory consumption. It should be noted that the down-sampling operations in Swin-Transformer V2 are not used in our model to ensure that the shapes of inputs and outputs are unchanged, making it convenient to increase the number of transformer layers.

Land-sea mask

A land-sea mask is adopted to handle the missing values of ocean variables on the land points. Specifically, the values on the land points are always replaced with 0 at any step of the processing. Accordingly, WenHai puts no attention on the land points, making it focus on the ocean forecast.

Two-stage training strategy

The training process is divided into two stages. The first stage is to pretrain a base model by optimizing a weighted mean absolute error (MAE) for \({{{{\Delta }}}{{\bf{O}}}}_{t}^{1}\) integrated over the global ocean, i.e.,

$$\min \int\!\!\!\!\int\!\!\!\! \int \left|\left|{{\bf{w}}}\cdot \left({\Delta \hat{{{\bf{O}}}}}_{t}^{1}-{\Delta {{\bf{O}}}}_{t}^{1}\right)\right|\right|_{1}{dV}\approx \min \mathop{\sum }\limits_{i}\left|\left|{{\bf{w}}}(i)\cdot \left(\Delta \hat{{{\bf{O}}}}_{t,i}^{1}-{\Delta {{\bf{O}}}}_{t,i}^{1}\right)\right|\right|_{1}\delta V\left(i\right)$$
(1)

where \({{{{\Delta }}}\hat{{{\bf{O}}}}}_{t,i}^{1}\) represents the forecast tendency by WenHai at the i-th grid cell, \({{{{\Delta }}}{{\bf{O}}}}_{t,i}^{1}\) is the ground truth obtained from the GLORYS reanalysis, \(\delta V(i)\) is the volume of the i-th ocean grid cell, \({{\bf{w}}}(i)\) is a weight vector for different ocean variables, and \({{||}\cdot {||}}_{1}\) is the L1 norm. The \({{\bf{w}}}(i)\) is chosen as:

$${{\bf{w}}}\left(i\right)=\frac{{{\bf{s}}}}{\delta h\left(i\right)}$$
(2)

where \(\delta h(i)\) is the layer thickness of the i-th ocean grid cell. As \(\delta h(i)\) becomes larger as the depth increases, the presence of \(\delta h(i)\) in the denominator makes WenHai put more attention on the shallower regions where mesoscale eddies are stronger56, enhancing its capacity to forecast mesoscale eddy variabilities. The value of \({{\bf{s}}}\) is chosen in a way so that the tendencies of different normalized ocean variables have similar variances. We find that the variances of tendency of the normalized variables have comparable magnitudes except the tendency of normalized salinity which is much smaller than the others. Accordingly, the component of \({{\bf{s}}}\) associated with salinity is set as 4.5 and components associated with the other variables as 1 to reduce the difference of variances among different normalized variables. It should be noted that the above choice of \({{\bf{w}}}\) is unlikely optimal. Nevertheless, it leads to better performance on the validation dataset than choosing \({{\bf{w}}}\left(i\right)={{\bf{1}}}/\delta h\left(i\right)\) or \({{\bf{w}}}\left(i\right)={{\bf{s}}}\).

During the second training stage, the pretrained-based model is finetuned to improve its performance at longer forecast lead times. This is done by optimizing the accumulated MAE over a sequence of autoregressive forecasts, i.e.,

$$\min \mathop{\sum }\limits_{l=1}^{M} \mathop{\sum }\limits_{i} \left|\left|{{{\bf{w}}}}(i)\cdot \big(\Delta \hat{{{\bf{O}}}}_{t,i}^{l}-{\Delta {{\bf{O}}}}_{t,i}^{l}\big)\right|\right|_{1}\delta V(i)$$
(3)

We try different values of \(M\) and find \(M=5\) gives rise to the overall best forecast performance on the validation dataset. Applying the finetune technique reduces the forecast RMSE for all the ocean variables (Supplementary Fig. S16).

Distributed training

During the second training stage, iterations on high-resolution inputs with patch size 4 consume considerable GPU memory beyond 80 GB. To address this issue, the model is strategically divided into several parts to share the overhead on different devices. Specifically, the 10 Transformer layers are segmented into five stages: 1, 3, 3, 3, and 0 Transformer layers, respectively, for optimal memory load balancing. The initial stage incorporates the model’s patch embedding and down-sampling block, while the final stage encompasses the up-sampling block and patch recovery module. Iterative finetune deviates from conventional pipeline model parallelism by creating a feedback loop, where the output of one iteration becomes the input for the next. The process begins by loading initial data into the first stage for forward computation. Results are then sequentially passed through subsequent stages. Upon reaching the final stage, the loss for the current iteration is calculated, and these results are transmitted back to the first device. Each iteration’s output serves as the input for the following iteration. This cycle continues until the 5-day computation is complete. The final stage aggregates losses from all iterations. By employing this pipeline model parallelism, the finetuning capacity has been significantly expanded from a single day to five days.

GLO12v4

GLO12v4 is the latest version of the Operational Mercator global ocean analysis and forecast system, providing global ocean forecasts in the next 10 days, updated daily. It includes an ocean component (NEMO3.6) with a horizontal resolution of 1/12° and 50 vertical levels and a sea ice component (LIM3 Multi-categories sea ice model)57. A reduced-order Kalman filter derived from a SEEK filter with a 3-D multivariate modal decomposition of the forecast error and a 7-day assimilation cycle is applied for assimilating observations including satellite-based SLA, SST and sea ice concentration and in situ temperature and salinity profiles.

The forecast is initialized from the hindcast simulation of GLO12v4 spanning the last 24 h leading to real-time (i.e., -24 to 0 h) without data assimilation. The atmosphere variables during the forecast period are obtained from the ECMWF IFS HRES forecast product58. We collect GLO12v4 forecasts along with the initial conditions and atmospheric forecast product during April, 2024-November, 2024 and use these data to assess the forecast performance.

Observational datasets

For temperature and salinity profiles, we use quality controlled (QC) near-real-time Argo59 profiles from E.U. Copernicus Marine Service Information60. For SLA, we use an along-track Level-3 near-real-time product from AVISO. The Ssalto/Duacs altimeter products were produced and distributed by the Copernicus Marine and Environment Monitoring Service (CMEMS) (http://www.marine.copernicus.eu). The product contains measurements of satellite altimeters including Sentinel-6A-HR, Jason-3 interleaved, Sentinel-3A, Sentinel-3B, SARAL-DP/AltiKa, Cryosat-2, HaiYang-2B, and SWOT-nadir. The filtered version of the product is chosen to suppress the effect of measurement noises. The SST and 15-m current are obtained from the near-real-time drifter observations provided by the Global Drifter Program61. The hourly drifter records are bin-averaged to produce the daily mean values. For the observations of all the ocean variables, only records passing all the real-time QC tests are retained.

It should be noted that GOFSs forecast SSH that differs from SLA by a reference sea level62. In the observation, the reference sea level is computed as the time mean SSH during 1993-2012. For the GOFSs, the reference sea level is computed as the time-mean SSH of the GLORYS reanalysis during the same period. There is likely a bias of SLA in GOFSs due to the difference between the observation and GLORYS reanalysis. To alleviate this bias, SLA in GOFSs is subtracted by the difference of SLA between the GLORYS reanalysis and observation averaged over the global ocean during 1993–2020.

Verification metrics

Point-to-point verification metrics

The forecasts of GOFSs are partitioned according to their initial time \(t\) and forecast lead time \(l\), and compared to observations at time \(t+l\). As the observations are distributed irregularly in space and not located on the grid points of GOFSs, forecasts are interpolated to individual sites of observations to form point-to-point match-ups between the forecasts and observations, so that the forecast errors can be computed, i.e.,

$${\varepsilon }_{t,l}^{i}={\hat{V}}_{t,l}^{i}-{V}_{t+l}^{i}$$
(4)

where \({V}_{t+l}^{i}\) is the observation and \({\hat{V}}_{t,l}^{i}\) is the interpolated forecast for the i-th match-up. To make a fair comparison among GOFSs, we only retain the match-ups for those having a forecast counterpart from every GOFS (Note that different GOFSs differ in their grids and land-sea masks).

Specifically, the match-ups of SST and SLA are obtained by horizontally interpolating the forecast values to the observational sites using the bilinear interpolation. The match-ups of 15-m zonal and meridional currents are obtained by horizontally interpolating the forecast values to the observational sites using the bilinear interpolation and vertically to 15 m using the linear interpolation. As to the match-ups of vertical profiles of temperature and salinity, the forecast values are horizontally interpolated to the sites of Argo profiles using the bilinear interpolation and vertically to the depths of Argo profiles using the linear interpolation. For each match-up of the observational and forecast profiles, we vertically bin-average the squared forecast errors in the prescribed 42 vertical bins containing approximately equal numbers of Argo measurements (Supplementary Fig. S17).

Two point-to-point verification metrics are used to measure the forecast performance of GOFSs, including the root mean square error (RMSE) and persistence skill scores (PSS). The RMSE is defined as42:

$${{{\rm{RMSE}}}}_{t,l}\,=\,\sqrt{\frac{\mathop{\sum }_{i=1}^{N}{\left({\varepsilon }_{t,l}^{i}\right)}^{2}}{N}}\,$$
(5)

where \(N\) is the number of total match-ups at the initial time \(t\) and forecast lead time \(l\). For the temperature and salinity profiles, \({({\varepsilon }_{t,l}^{i})}^{2}\) corresponds to the vertically bin-averaged squared forecast errors in the prescribed 42 vertical bins. In this case, the value of \(N\) differs among different vertical bins and \({{{\rm{RMSE}}}}_{t,l}\) is expressed as a function of center depth of these vertical bins.

The PSS is defined as42:

$${{{\rm{PSS}}}}_{t,l}\,=1-\,\frac{{{\rm{RMS}}}{{{\rm{E}}}}_{t,l}}{{{{\rm{RMSE}}}}_{t,l}^{p}}$$
(6)

where \({{{\rm{RMSE}}}}_{t,l}^{p}\) is the RMSE of a persistent forecast.

Once \({{{\rm{RMSE}}}}_{t,l}\) and \({{{\rm{PSS}}}}_{t,l}\) are obtained, their median values among different initial time \(t\) are computed and expressed as a function of forecast lead time \(l\) (Figs. 2 and 3).

Neighborhood-based verification metrics

The continuous ranked probability core (CRPS) of GOFSs evaluated based on some observation \({V}_{t+l}^{i}\) is defined as46:

$${{{\rm{CRPS}}}}_{t,l}^{i}={\int _{-\infty }^{+\infty }}{\left[F\left(x\right)-H\left(x\ge {V}_{t+l}^{i}\right)\right]}^{2}{dx}$$
(7)

where H represents the Heaviside function and \(F(x)\) denotes the cumulative distribution function of the pseudo ensemble forecast for \({V}_{t+l}^{i}\). The individual members of pseudo ensemble forecast of GOFSs are collected over the 1° × 1° box centered on the grid point closest to the site of \({V}_{t+l}^{i}\). For the temperature and salinity profiles, the collected forecast values are first interpolated to the depths of Argo profiles to compute the CRPS at each depth, and these CRPS values are then vertically bin-averaged in the prescribed 42 vertical bins.

The globally averaged CRPS at some initial time \(t\) and forecast lead time \(l\) (denoted as \({{{\rm{CRPS}}}}_{t,l}\)) is obtained by averaging \({{{\rm{CRPS}}}}_{t,l}^{i}\) over all the observational sites at the time \(t+l\). Once \({{{\rm{CRPS}}}}_{t,l}\) is obtained, its median values among different initial time \(t\) are computed and expressed as a function of forecast lead time \(l\) (Figs. 4 and 5).

Computation of mesoscale eddy variabilities

In this study, the mesoscale eddies are loosely defined as the processes with a horizontal scale ranging from tens to hundreds of kilometers, including fronts, filaments and coherent vortices1. To isolate anomalies induced by mesoscale eddies, we subtract a 4° × 4° spatially running mean from the original variables63. The eddy kinetic energy is computed as \(\big \langle \frac{1}{2}\big({{u}^{{\prime} }}^{2}+{{v}^{{\prime} }}^{2}\big)\big \rangle \,\) where \(u\) and \(v\) are zonal and meridional velocity, respectively, the primes denote the mesoscale anomalies and the brackets denote the spatio-temporal average. The variance of mesoscale temperature and salinity anomalies are computed as \( \langle {T^{\prime} }^{2} \rangle \) and \( \langle {{S}^{\prime} }^{2} \rangle\) where \(T\) and \(S\) denote the temperature and salinity, respectively. To evaluate the preservation of ocean mesoscale variabilities, eddy kinetic energy and variances of mesoscale temperature and salinity anomalies are integrated in the upper 643 m.