Abstract
Orthognathic surgery, or corrective jaw surgery, is performed to correct severe dentofacial deformities and is increasingly sought for cosmetic purposes. Accurate prediction of surgical outcomes is essential for selecting the optimal treatment plan and ensuring patient satisfaction. Here, we present GPOSC-Net, a generative prediction model for orthognathic surgery that synthesizes post-operative lateral cephalograms from pre-operative data. GPOSC-Net consists of two key components: a landmark prediction model that estimates post-surgical cephalometric changes and a latent diffusion model that generates realistic synthesizes post-operative lateral cephalograms images based on predicted landmarks and segmented profile lines. We validated our model using diverse patient datasets, a visual Turing test, and a simulation study. Our results demonstrate that GPOSC-Net can accurately predict cephalometric landmark positions and generate high-fidelity synthesized post-operative lateral cephalogram images, providing a valuable tool for surgical planning. By enhancing predictive accuracy and visualization, our model has the potential to improve clinical decision-making and patient communication.
Similar content being viewed by others
Introduction
Orthognathic surgery (OGS) is widely used to correct severe dentofacial deformities. Establishing the surgical treatment objective and predicting surgical results are necessary to obtain a balance among esthetics, function, and stability and ensure patient satisfaction1. Therefore, it is essential to compare various treatment options, such as whether to extract teeth or perform single-jaw surgery or double-jaw surgery, in terms of their expected results to select an optimal treatment plan for the patient. Such pre-procedural planning is even more important with the increased demand for appearance enhancements, as orthognathic surgeries are increasingly being done to improve facial esthetics, even for those who do not have severe facial deformities. Thus, the prediction of facial changes that would occur with orthognathic surgery serves as an important factor in deciding whether a patient should receive surgical treatment2,3. Traditionally, the prediction of OGS has been carried out by tracing lateral cephalometric radiographs. Changes in the facial appearance were predicted based on the ratio of the movement of the soft-tissue landmark corresponding to the hard-tissue landmark using a pre-operational cephalogram (pre-ceph)4,5. However, this ratio is affected by various factors, such as the direction of bony movement, thickness or tension of soft tissue, type of surgery, and type of malocclusion, and thus, the accuracy is low, and the deviation is exceedingly large for clinical usage. Commercial programs used for orthodontic diagnosis can provide clinically practical guidelines by simulating post-operational (post-op) changes based on the bone–skin displacement ratio but have limitations in describing actual changes. As a result, the post-op changes provided by these commercial programs do not accurately reflect real changes6,7,8,9. To overcome these problems, several researchers had developed various algorithms for accurately predicting soft-tissue changes. However, most of these algorithms have limited application, such as for mandibular surgery only or for mandibular advance surgery only10,11,12. Although there had been a rare attempt to develop a prediction algorithm for various surgical movements13, its prediction error was exceedingly large that it could not be applied in clinical situations. Recently, some investigators have been studied to predict surgical results in three dimensions(3D)14,15,16. CBCT was introduced into the field of dentistry from its early stages of development due to its advantages of being accurately reproducing the craniofacial structures in 3D without distortion, magnification, or overlap of images with low radiation dose17.
Initially, CBCT was mainly used to evaluate the alveolar bone region18, but as the field of view (FOV) gradually increased, its application has expanded to include the evaluation of impacted teeth19, assessment of diseases or trauma in the craniofacial region20, and analysis for orthodontics and OGS21,22. Lee et al.14 attempted to predict facial changes in 10 OGS patients using CBCT and facial scans. They achieved satisfactory results within 2.0 mm, but the sample size was too small. Resnick et al.15 also evaluated and predicted soft tissue changes in three dimensions after maxillary surgery, but obtained results that were unsatisfactory for clinical application. Bengtsson et al.16 compared soft tissue predictions using 2D cephalograms and 3D CBCT and found no significant difference in accuracy. However, they reported that 3D analysis is more advantageous in cases of facial asymmetry. With the application of CBCT to OGS, the amount of radiation exposed to patients has also increased as the FOV and image resolution have increased23.
Previous studies on CBCT dosimetry have shown that the mean organ dose (84–212 μSv) is significantly higher than that delivered for the acquisition of lateral cephalograms and panoramic radiographs24. Jha et al.25 investigated the cancer risk for various organs based on the median and maximum CBCT imaging conditions commonly used in Korea. The results showed that cancer risk was higher in women than in men, increased with younger age, and rose with the number of imaging sessions, as cancer risk is influenced by factors such as age, gender, equipment parameters, and the number of imaging sessions. Therefore, the ALARA (As Low As Reasonably Achievable) principle must be strictly followed when performing CBCT in clinical practice, and routine CBCT imaging for orthodontic treatment cannot be justified. For the analysis of OGS, CBCT can offer advantages in cases of severe skeletal discrepancies, such as pronounced facial asymmetry with a canted occlusal plane or developmental disorders26. While some studies advocate the use of CBCT for orthognathic or TMJ surgery, systematic reviews have failed to support their universal application27.
As the field of generative AI using deep-learning models dramatically improved, some researchers tried to apply synthetic images in medical and dental imaging. Kim et al. attempted to generate lateral cephalograms using deep learning28. They reported visual Turing test results showing that the synthetic lateral cephalograms were indistinguishable from real lateral cephalograms and that tracing on the synthetic images was possible. The use of diffusion models29,30,31,32,33,34 has led to advancements in multi-modal generation, such as text-to-image or layout-to-image generation, and various applications were demonstrated in the medical domain. For example, the method proposed by ref. 35, overcame the limitations of existing diffusion-based methods and improved 3D medical image reconstruction tasks such as MRI and CT, by effectively solving 3D inverse problems. Furthermore, the diffusion model can synthesize high-quality medical images, improving medical image analysis performance when data is scarce36,37,38,39. Among them, a latent diffusion model has been developed for a powerful and flexible generation with conditioning inputs and high-resolution synthesis with cross-attention layers into the model architecture16. With these advances, it could be possible to generate synthetic post-op lateral cephalograms (spost-cephs) for OGS to compare the outcomes of various treatment options. Therefore, the purpose of this study is to predict facial changes after OGS using a latent diffusion model. We utilized deep learning to generate spost-cephs, enabling surgical outcomes to be anticipated and images to be generated for various surgical planning scenarios through condition adjustments. Our approach relied on two methods. First, to enhance surgical planning accuracy, we employed GCNN to predict appropriate surgical movements from the pre-ceph. Second, we took the surgical movements predicted by GCNN and other information from pre-ceph and its profile line tracing as inputs to generate spost-cephs using a diffusion model. This generative prediction for orthognathic surgery using ceph network (GPOSC-Net) leveraged pre-cephs to generate spost-cephs based on the intended amount of surgical movement (IASM).
Afterward, we validated the spost-cephs through various methods. First, to assess the quality and medical realism of the spost-cephs, a visual Turing test (VTT) was performed with four doctors of dental surgery (DDSs), namely, two orthodontists (ODs) and two oral and maxillofacial surgeons (OMFSs), with an average of over 15 years of experience, to differentiate real post-op lateral cephalograms (post-ceph) from spost-cephs and achieved an average accuracy of 48%, which indicated that the spost-cephs exhibited medically plausible quality and features. Second, the spost-cephs were validated via a landmark comparison between the post-cephs and corresponding spost-cephs by two ODs. The distances of these 35 landmarks were grouped into five and evaluated. In each group, the mean Euclidean distance error of the landmarks was 1.5 mm, and the successful prediction rate40 (successful prediction rate, SPR; errors <2.0 mm) for each landmark averaged at ~90%. Third, by adjusting the weight of classifier-free guidance (CFG)31 in GPOSC-Net, we generated spost-cephs for various surgical planning scenarios. We requested an evaluation from the same two ODs and two OMFSs. After being shown simulated surgery images generated at guidance IASM ranging from under, exactly, and over setback amounts of 0.1 to 1.6 (where 0, pre-ceph; 1, exact setback amount, i.e., similar to those of post-ceph; 1.6, over setback amount, i.e., beyond the surgical movement of post-ceph), they selected the most appropriate surgical outcome images for those patients, resulting in an average selected IASM of 1.03 ± 0.31. Finally, a survey consisting of five questions was performed to evaluate the clinical utility of the proposed model.
Results
Comparison of landmarks between post-ceph and spost-ceph
To evaluate the accuracy of the model, two ODs traced the landmarks in both the post-cephs and spost-cephs (shown in Fig. 1a) from the test set. Figure 1b–d show the distance errors for the Euclidean, x-axis, and y-axis, respectively. We categorized all the landmarks into five anatomical groups: cranial base, dental, jaw, upper profile, and lower profile (Table 1). The average errors of the landmarks for the internal and external test sets were within 1.5 mm. This was smaller or similar to the inter-observer differences shown in past studies investigating the reproducibility of landmark selection in real cephalograms41,42. In the internal test, errors ranged from 1.01 ± 0.64 mm at the cranial base to 1.46 ± 0.93 mm at the lower profile, with an average error of ~1.27 ± 0.51 mm. In the external test, errors ranged from 0.85 ± 0.58 mm at the cranial base to 1.51 ± 1.01 mm at the jaw, with an average error of ~1.29 ± 0.62 mm (Fig. 1b). In the internal test, x-axis errors ranged from 0.59 ± 0.53 mm at the cranial base to 0.94 ± 0.81 mm at the lower profile, with an average error of approximately 0.80 ± 0.40 mm. In the external test, x-axis errors ranged from 0.52 ± 0.45 mm at the cranial base to 1.05 ± 0.96 mm at the lower profile, with an average error of approximately 0.80 ± 0.51 mm (Fig. 1c). In the internal test, y-axis errors ranged from 0.68 ± 0.6 mm at the cranial base to 0.94 ± 0.77 mm at the lower profile, with an average error of approximately 0.84 ± 0.43 mm. In the external test, y-axis errors ranged from 0.55 ± 0.48 mm at the cranial base to 0.93 ± 0.86 mm at the lower profile, with an average error of approximately 0.74 ± 0.42 mm (Fig. 1d). The results for each of the landmarks can be found in Supplementary Table 2 of the supplementary materials.
a Four typical cases of pre-ceph, post-ceph, and spost-ceph. Based on these pre-cephs, their landmarks, profile lines, and predicted amounts of surgical movement, GPOSC-Net generated corresponding spost-cephs. b Landmark distance errors (LDE, unit: mm) of post-ceph and spost-ceph measured by two orthodontists (ODs) for internal and external test sets. c LDEs of X-coordinates (unit: mm) of post-ceph and spost-ceph. d LDEs of Y-coordinates (unit: mm) of post-ceph and spost-ceph. Box plots illustrate the median, interquartile range (box), and whiskers extending to 1.5 times the range, with outliers represented as individual points. e Successful prediction rates (SPR) for each landmark in terms of percentages as determined by two ODs for internal and external test sets.
Comparison of accumulated SPRs
The distance errors between the gold standard landmarks and those predicted by the models for the five groups, namely, the cranial base, dental, jaw, upper profile, and lower profile, were evaluated. The SPRs for each group were assessed according to errors <2.0 mm as determined by an OD with more than 15 years of experience (Fig. 1e).
For both the internal and external test sets, landmarks at the cranial base that were not affected by OGS exhibited very high SPRs, whereas landmarks at the remaining parts whose positions changed as a result of OGS exhibited lower SPRs. The SPRs for soft-tissue landmarks appeared lower than those for hard-tissue landmarks, because the errors for the soft-tissue landmarks were generally larger than those for the hard-tissue landmarks40,41,43,44. In the internal test, the SPRs were 94% for the cranial base, 79.1% for dental, 78.1% for the jaw, 91.2% for the upper profile, and 76.5% for the lower profile. In the external test, the SPRs were 96.5% for the cranial base, 80% for dental, 81.2% for the jaw, 89.3% for the upper profile, and 74.9% for the lower profile (Table 1). The results for each of the landmarks can be found in Supplementary Table 2 of the supplementary materials.
Visual Turing test
A VTT was conducted with two ODs and two OMFSs, with an average of over 15 years of experience, to evaluate the quality of the spost-cephs. In general, a VTT for a generative model is considered ideal when the resulting accuracy is ~50%. We presented 57 pairs of randomly selected images consisting of both real and generated images (1:1 ratio). Although specificity was high for one examiner, the average accuracy of all examiners was 49.55%. The accuracies of the two ODs and two OMFSs were 45.6, 38.6, 64.9, and 49.1%, respectively. Meanwhile, the sensitivity values for OD1, OD2, OMFS1, and OMFS2 were 51.7, 41.4, 35.5, and 48.3%, respectively, whereas their specificity values were 39.3, 35.7, 96.4, and 50.0%, respectively. These results demonstrated that the quality of the spost-cephs was reasonably good because even expert DDSs were unable to differentiate between real and generated cephs in a blind condition.
Digital twin
After the serial generation of spost-cephs based on IASM, as shown in Fig. 2a, two ODs and two OMFSs were requested to choose the most proper images among the spost-cephs as a treatment goal. The spost-cephs were generated based on IASM 1.0, which denotes an amount of movement similar to that of actual surgical bony movement. On the other hand, the spost-cephs with IASMs corresponding to under or excessive movement were continuously generated as follows: an image generated based on IASM 0.8, for example, denotes setting the surgical movement to be 20% smaller than the actual setback amount, whereas an image generated based on IASM 1.2 denotes setting the surgical movement to be 20% larger than the actual amount. For IASM 0.1 to 1.6, five images, including for IASM 1.0, were thus randomly generated. The two ODs and two OMFSs were requested to select only one image as an appropriate treatment goal based on the pre-ceph. If a spost-ceph generated based on IASM 0.8 to 1.2 was selected, it was considered to be a correct answer, i.e., an appropriate treatment goal. If the selected spost-ceph was an image generated based on movement similar to actual surgical movement, then it may be used as a digital twin for predicting the simulated surgical result. The two ODs and two OMFSs independently selected a total of 35 cases each and demonstrated an average accuracy of 90.0%, as shown in Fig. 2b.
a Results of generating images based on the intended amount of surgical movement (IASM). As the IASM increased, the images moved away from the red dotted line, indicating a presumed increase in the magnitudes of movement. b Evaluation of usability as a digital twin by two orthodontists (ODs) and two oral & maxillofacial surgeons (OMFSs). c Questionnaire for digital-twin evaluation. d Responses to a questionnaire by the two ODs and two OMFSs.
The practicality of the clinical application of spost-ceph was evaluated using the questionnaire shown in Fig. 2c, which attempted to assess if spost-ceph would be useful in predicting surgical results and in patient consultation. As shown in Fig. 2d, the four DDSs indicated the positive utility of our generative model for most of the questions. However, with regard to question 4, this model has a limitation in its usefulness to assist surgical planning in clinical practice, because simply presenting post-op images would not be of much help in establishing a surgical plan.
Ablation study
We conducted various experiments comparing different conditions and networks. Initially, we compared the performance of generative models between generative adversarial networks (GAN)45,46,47 and diffusion models29,30,31,32. Subsequently, we enhanced the model by adding various conditions. The first condition used the pre-ceph coordinates of landmarks, whereas the second used surgical movement vectors, which significantly enhanced performance. During the experiments, we identified a problem with the incorrect generation of the mandible. To resolve this, we added the profile line of the pre-ceph as the final condition. This addition significantly enhanced the performance of the model, particularly improving the depiction of the mandibular of the patient. The results of these experiments are presented in Table 2. The hyperparameters of the model were set to default.
We used the same dataset for training both the GAN and diffusion model. The primary backbone model employed for training was StyleGAN46,47, and we utilized a pSp48 encoder for projection. Furthermore, to facilitate manipulation, we trained an additional encoder, specifically a graph network49,50, to learn surgical movement vectors40. However, during the training with GANs, we frequently observed mode collapse. Furthermore, no noticeable changes were observed as a result of surgical movements.
Discussion
In this paper, we propose the GPOSC-Net model, which is based on a GCNN and a diffusion model, which generates spost-cephs to predict facial changes after OGS. First, the GPOSC-Net model employs two modules, i.e., an image embedding module (IEM) and a landmark topology embedding module (LTEM), to accurately obtain the amounts of surgical movement that the cephalometric landmarks would undergo as a result of surgery. Afterward, the model uses the predicted post-op landmarks and profile lines segmented on the pre-ceph, among other necessary conditions, to generate accurate spost-cephs. In this study, we independently trained two models, which we then concatenated during the inference process.
We conducted training and evaluation using a dataset of high-quality patient data consisting of 707 pairs of pre-cephs and post-cephs dated from 2007 to 2019 provided by nine university hospitals and one dental hospital. To train and test the model, data from four of the institutions were used for internal validation to evaluate the accuracy of the model. Subsequently, to demonstrate the robustness of the model, data from the six other institutions were used for external validation.
The cephalometric landmarks of post-ceph and spost-ceph were then compared. In the internal validation, no statistically significant differences were observed for most of the landmarks (33 of the total 35 landmarks), whereas in the external validation, no statistically significant differences were observed for 23 of the 35 landmarks. Landmarks on the cranial base, which were not changed by surgery, had average errors of 0.85 ± 0.62 mm and 1.07 ± 0.79 mm for the internal and external test sets, respectively. These values were comparable to or smaller than the intra-observer errors observed in reproducibility studies with real cephalograms41,42. Thus, it could be said that the landmarks in spost-ceph were not significantly different from those of the real post-ceph.
Researches that predict the outcomes of OGS by training artificial intelligence on cephalometric radiographs are still relatively few, and some of them compared the accuracy of predictions using metrics such as F1 score or AUC for cephalometric measurements51. However, such evaluation methods may not always be appropriate for clinical application. Donatelli and Lee argued that in orthodontic research, when assessing the reliability of 2D data, it is more appropriate to represent errors based on horizontal and vertical axes and to evaluate them using Euclidean distance rather than simply relying on measurements of distance or angles52.
Previous studies that predicted the outcomes of OGS typically focused on the changes in soft tissue. Suh et al. investigated that the partial least squares (PLS) method was more accurate than the traditional ordinary least squares method in predicting the outcomes of mandibular surgery10. According to the study by Park et al., when predictions were made using the PLS algorithm, the Euclidean distance from the actual results ranged from 1.4 to 3.0 mm, whereas the AI (TabNet DNN algorithm) prediction error ranged from 1.9 to 3.8 mm53. In this study, the PLS algorithm predicted the soft tissue changes more accurately in the upper part of the upper lip, while the AI (TabNet DNN algorithm) provided more accurate predictions in the lower mandibular border and neck area. The prediction errors for soft tissue changes in our study were 0.8 to 1.22 mm in the upper profile and 1.32 to 1.75 mm in the lower profile, resulting in better outcomes compared to previous studies. Kim et al. predicted the positions of hard-tissue landmarks after surgery using linear regression, random forest regression, the LTEM, and the IEM They found that combining LTEM and IEM allowed for more accurate predictions, with errors ranging from 1.3 to 1.8 mm40.
Our study also achieved similar results, with prediction errors ranging from 1.3 to 1.6 mm. For the internal and external test sets, the average errors of cephalometric landmarks in the dental area were 1.34 ± 0.83 mm and 1.60 ± 1.08 mm, respectively, whereas the errors of landmarks in the jaw were 1.33 ± 0.86 mm and 1.57 ± 0.94 mm, respectively. Although the errors were larger than those of landmarks on the cranial base, they were comparable to the inter-observer errors demonstrated in a past study involving real cephalograms41,42, and thus, it could be inferred that the actual surgical results were accurately predicted. In particular, the dental area, which is difficult to accurately create in a generative model, was generated as accurately as the jaws. For the internal test set, there were no statistically significant differences among all 16 landmarks. However, for the external test set, there were significant differences in 6 of the landmarks, four of which were positioned at the jaws. It seemed that the prediction of these landmarks (A point, anterior nasal spine or ANS, protuberance menti, and pogonion) was made difficult by remodeling procedures after surgery, such as ANS trimming and genioplasty. The landmarks in the upper profile had relatively smaller errors than those of the landmarks in the lower profile, but there were more landmarks showing statistically significant differences in the upper profile than in the lower profile. This was probably due to the small standard deviation of the landmark errors in the upper profile. The upper profile undergoes relatively little or no change due to surgery, and thus, the measurement errors were small. By contrast, in the lower profile, it seemed that the prediction errors were relatively larger because of various changes in the chin position that could occur depending on whether genioplasty was done. However, nonetheless, the landmark errors in the lower profile were comparable to the inter-observer errors demonstrated in another study41,42.
VTT results revealed that the four examiners had ~50% accuracy, suggesting that the spost-cephs were perceived as realistic and could not be differentiated even by expert ODs and OMFSs with an average of over 15 years of experience.
Serial spost-cephs adjusted with different values for IASM were generated and evaluated in a test on selecting appropriate surgical results based on pre-cephs. Most of the answers chosen by the four examiners in a blind condition were within the criteria for preferred predictions (0.8 ≤ IASM ≤1.2), which meant that if an appropriate surgical movement could be presented, our generative model would be able to synthesize images that could be used as a simulated surgical goal. Therefore, with our proposed model, the surgical results could be reliably predicted and used in actual clinical practice. In the same test, most of the ODs and OMFSs responded positively to the usefulness of spost-cephs. In particular, spost-cephs would be of great help in explaining various kinds of surgical plans to patients and predicting their surgical results. However, the experts did not have a high expectation regarding the usefulness of spost-cephs in establishing an actual surgical plan. This might be because the actual amounts of bony movement could not be determined simply from spost-cephs. A more positive answer could have been obtained if the amounts of bony movement had been presented with a comparison of pre-ceph and spost-ceph.
This study had several limitations. First, our model depends on two-dimensional cephalometric images, which could not represent actual 3D movement and changes due to OGS. In the near future, this study could be extended to use 3D cone beam computed tomography (CBCT) of OGS. Second, this study was performed in a single nation and on an Asian population only. We need to extend our model to be applicable to various races from other nations. Lastly, in this study, there was a possibility of simulation-based digital twins for our model. For better clinical significance, we need more clinical evaluations on real-world clinical validation involving more examiners and performed in a prospective manner.
This study fundamentally aims to assist physicians in making better decisions in ambiguous cases, enhance communication between patients and doctors, and ultimately foster better rapport. However, there is concern that the outcomes of this study could potentially lead to misconceptions among patients, resulting in an increase in unnecessary surgeries or treatments. It is crucial for physicians to be aware of these risks, and there is a need for regulatory agencies to develop regulations that prevent unnecessary treatments. Our group is committed to actively addressing these concerns. Despite these concerns, our study demonstrates that AI-based prediction models, such as GPOSC-Net, can provide valuable insights for surgical planning and clinical decision-making.
In this paper, we propose GPOSC-Net, an automated and powerful OGS prediction model that uses lateral cephalometric X-ray images. In this study, these images were obtained from nine university hospitals and one dental hospital in South Korea. Our model predicted the movement of landmarks as a result of OGS between pre-cephs, post-cephs, and generated spost-cephs using pre-ceph and IASM (virtual setback ratio only). Based on a comparison with post-ceph, the spost-ceph not only accurately predicted the positions of the cephalometric landmarks but also generated accurate spost-cephs. Although 2D images have their limitations in formulating accurate surgical plans, our model has the potential to significantly contribute to simulations for surgical planning and communications with other dentists and patients.
Methods
Ethical approval
This retrospective study was conducted according to the principles of the Declaration of Helsinki. This nationwide study was reviewed and approved by the Institutional Review Board Committee of ten institutions: (A) Seoul National University Dental Hospital (SNUDH) (ERI20022), (B) Kyung Hee University Dental Hospital (KHUDH) (19-007-003), (C) Kooalldam Dental Hospital (KOO) (P01-202105-21-019), (D) Kyungpook National University Dental Hospital (KNUDH) (KNUDH-2019-03-02-00), (E) Wonkwang University Dental Hospital (WUDH) (WKDIRB201903-01), (F) Korea University Anam Hospital (KUDH) (2019AN0166), (G) Ewha Woman’s University Dental Hospital (EUMC) (EUMC 2019-04-017-003), (H) Chonnam National University Dental Hospital (CNUDH) (2019-004), (I) Ajou University Dental Hospital (AUDH) (AJIRB-MED-MDB-19-039), and (J) Asan Medical Center (AMC) (2019-0927). The requirement for patient consent was waived by each center’s Institutional Review Board Committee.
Overall procedure
Based on the IASM and pre-ceph, the spost-ceph is generated by GPOSC-Net. In this study, two ODs traced the spost-cephs and compared them with post-cephs to evaluate the accuracy of the landmark positions and the soft- and hard-tissue profile lines. 45 landmarks were digitized by experienced orthodontists using the V-ceph software (Version 8.0, Osstem, Seoul, Korea). Additionally, a VTT was conducted with two ODs and two OMFSs to validate the quality of the spost-cephs. During the spost-ceph generation process, additional images reflecting various amounts of surgical movement were generated and reviewed to establish an appropriate surgical plan (Fig. 3a, b). The proposed GPOSC-Net model is visualized in Fig. 3c.
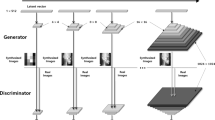
a Comparison of surgical outcome between real post-cephs and spost-cephs. b Evaluation of spost-cephs and assessment of their clinical utility. c Generative prediction for orthognathic surgery using ceph network (GPOSC-Net) model architecture, which utilizes a convolutional neural network (CNN)-based image embedding module (IEM) and a GCNN-based landmark topology embedding module (LTEM) to vectorize lateral cephalograms and landmark data, respectively. These vectors are concatenated and fed into a multi-layer perceptron (MLP) to predict the landmark movements caused by surgery. To generate spost-cephs, a latent diffusion model is employed with a few conditions, such as surgical movement value predicted by IEM and LTEM, pre-cephs, pre-operational landmarks, profile lines, and intended amount of surgical movement (IASM), which can control the virtual setback amounts of spost-cephs.
Data acquisition
A total of 707 patients with malocclusion who underwent orthognathic surgery (OGS) between 2007 and 2019 at one of nine university hospitals and/or one dental hospital and had lateral cephalograms taken before and after surgery (Fig. 4a) were included in this study (Fig. 4b). The age of the patients ranged from 16 to 50 years. All lateral cephalogram pairs were anonymized and stored in Digital Imaging and Communications in Medicine (DICOM) format as 12-bit grayscale images. The gender distribution of the patients was nearly equal (Fig. 4e). In this study, sex or gender was not considered as a factor in the experiments. The average duration of pre-surgical orthodontic treatment was 14 months, although some patients required 2 to 3 years to complete the pre-surgical phase (Fig. 4f).
a Paired lateral cephalograms before and after surgery (N = 707). Pre- and post-cephs were aligned using Sella and Nasion landmarks. b All pairs (N = 650) of pre- and post-cephs from three university hospitals and one dental hospital (A, B, C, and D) were used as internal datasets. Of these, 550, 50, and 50 pairs were used for training, validation, and internal tests, respectively. c Distribution of surgical movement for representative landmarks of hard and soft tissues, including (from upper left to lower right) anterior nasal spine (ANS), posterior nasal spine (PNS), B-point, Md 1crown (Mandible 1 crown), upper lip, lower lip, soft tissue pogonion, and soft-tissue menton. d Distribution of surgery types across the entire dataset and proportion of each type per hospital, where the horizontal axis of the bar graph represents the hospitals, and the vertical axis indicates the ratio of patients. Consequently, 57 pairs of pre- and post-cephs from six university hospitals (E, F, G, H, I, and J) were used for external tests. e Gender distribution of patients. f Distribution of pre-surgical orthodontic treatment time, where the horizontal axis represents the number of months, and the vertical axis denotes the number of patients.
We initially selected hospitals A, B, and C, which had the richest datasets, as our primary sources for the internal dataset. However, the majority of the patients from institutions A and B underwent two-jaw surgery (Fig. 4d). Consequently, to prevent a bias in the deep learning model toward patients that underwent one-jaw surgeries, we incorporated data from institution D, which had a higher proportion of patients who underwent one-jaw surgery, into our internal dataset. Through this process, a dataset comprising a total of 707 pairs was constructed, of which 550 were utilized as the training dataset, 50 as the validation dataset, and 50 as the internal test set. Additionally, we employed 57 pairs of pre-cephs and post-cephs from university hospitals E, F, G, H, I, and J as the external test set, because the different institutions had different cephalogram machines. In addition, there were variations in the imaging protocols and in the quality of the cephalograms.
With regard to the direction of surgical movement, the majority of anterior nasal spine (ANS), posterior nasal spine (PNS), and upper-lip landmarks moved anteriorly and superiorly, whereas the majority of B-point, Md 1 crown, lower lip, soft-tissue pogonion, and soft-tissue menton landmarks moved posteriorly and superiorly (Fig. 4c). The reason for these surgical movements was that most of the patients had skeletal Class III malocclusions, which needed anterior movement of the maxilla and posterior movement of the mandible. For most of the OGSs, the maxilla moved within 10 mm, whereas the mandible moved within 15 mm. Detailed information regarding the composition, demographic characteristics, and cephalography machines, among others, is provided in Supplementary Table 1 of the supplementary materials.
Model description
Overview of GPOSC-Net
Herein, we propose generative prediction for orthognathic surgery using ceph network (GPOSC-Net)40, which comprises two models: a two-module combination of our CNN-based image embedding module (IEM) and a GCNN-based landmark topology embedding module (LTEM), which predict the movement of landmarks that would occur as a result of OGS; and a latent diffusion model30, which is used to generate spost-cephs (Fig. 3c). The IEM utilizes a high-resolution network to maintain detailed representations of lateral cephalometric images. Before proceeding to the next step, the output of the IEM is subjected to channel coupling by the channel relation score module (CRSM), which calculates the relation score between channels of a feature map. On the other hand, the LTEM employs a GCNN to train the topological structures and spatial relationships of 45 hard- and soft-tissue landmarks. Finally, the movement of these landmarks is predicted by a multi-layer perceptron (MLP) module, which uses the combined outputs of IEM and LTEM.
To generate spost-cephs, the model uses a set of conditions that includes the movement of landmarks obtained through IEM and LTEM, along with segmented profile lines of pre-ceph. This approach aims to ensure a minimal generation ability for our system. To reinforce this capability, we trained an autoencoder on a dual dataset, including one with labeled pre-ceph and post-ceph images, and The other is an extensive unlabeled set of 30,000 lateral cephalograms, randomly collected between 2007 and 2020, which are unrelated to any pre- or post-surgical conditions or orthodontic treatment, and are sourced from an internal institution (Hospital J). The learning methods and model structure and description are explained in detail further in this paper.
Finally, we employed the IASM during the testing phase to generate serial spost-ceph images corresponding to various amounts of virtual surgical movement. IASM made it possible to calibrate the expected surgical movement ratio precisely across a continuous spectrum from 0 to 1.6, where a value of 0 represents no surgical movement (similar to pre-ceph, 0%), a value of 1 corresponds to the full predicted movement (similar to post-ceph, 100%), and a value of 1.6 equates to an enhanced projection with a 160% setback. This enabled the serial generation of spost-ceph images with nuanced variations in surgical movement. For IASM ranging from 0.1 to 1.6, five spost-ceph images, including for IASM 1, were randomly generated, and an appropriate treatment goal based on the pre-ceph was selected by two ODs and two OMFSs in a blind condition.
Surgical movement vector prediction modules
As indicated earlier, our model consists of IEM and LTEM40, which are trained using images and landmarks, respectively (Fig. 3c). The IEM adopted HR-NET54 as its backbone and was trained to represent a ceph as a low-dimensional feature map. To correspond to each landmark, the feature map outputs 45 channels, where each channel has dimensions of 45 × 45. CRSM is used to measure a relationship score matrix between distinct channels; similarly, the matrix has dimensions of 45 × 45. Finally, an image feature vector is evaluated using a weighted combination of the flattened feature map and relationship score matrix.
On the other hand, the LTEM was designed based on the GCNN49 to learn the topological structures of landmarks. The training process of the LTEM is as follows: \({{{\rm{GCNN}}}}({{{{\rm{f}}}}}_{{{{\rm{i}}}}}^{{{{\rm{k}}}}})\,={{{{\rm{f}}}}}_{{{{\rm{i}}}}}^{{{{\rm{k}}}}+1}={{{\rm{ReLU}}}}\left(\right.{{{{\rm{f}}}}}_{{{{\rm{i}}}}}^{{{{\rm{k}}}}}{{{{\rm{W}}}}}_{1}+{\sum}_{{{{\rm{j}}}}}{{{{\rm{e}}}}}_{{{{\rm{ij}}}}}{{{{\rm{f}}}}}_{{{{\rm{i}}}}}^{{{{\rm{j}}}}}({{{{\rm{W}}}}}_{2})\), where \({{{{\rm{W}}}}}_{1}\) and \({{{{\rm{W}}}}}_{2}\) are weight matrices learned from the training, \({{{\rm{f}}}}\) denotes node features, and \({{{\rm{e}}}}\) is the edge of the graph. Meanwhile, ReLU(·) = max(0, ·)55 is the nonlinear activation function, is the learnable connectivity at the ith node from A, denotes the data we want to train, and is expressed as input data. In our experiment, D = 92 and N = 45, where D is the input dimension of the graph, the position of the i-node, and the distance features from the neighborhood of node i; and N is the number of nodes, which is the same as the number of landmarks (Fig. 3c).
The encoder of the LTEM comprises two layers of the GCNN, which is the graph embedding, and the learned weight matrices in these layers. Herein, A is the connectivity of all nodes shared by both layers. The output dimensions of the first and second layers are set to 64 and 32, respectively. Our model utilizes IEM and LTEM to obtain embeddings of images and landmarks, and then concatenates these embedding vectors to ultimately predict the surgical movement vectors. We trained the model using the L1 loss between the predicted surgical movement vectors and the gold standard.
We also used the Adam optimizer56, which combined the momentum and exponentially weighted moving average gradients methods, to update the weights of our networks. The learning rate was initially set to 0.001, and then decreased by a factor of 10 when the accuracy of the networks on the validation dataset stopped improving. In total, the learning rate was decreased three times to end the training. The networks were constructed under the open-source machine learning framework of PyTorch 1.857 and Python 3.6, with training performed on an NVIDIA RTX A6000 GPU. For the model training, we adopted a data augmentation strategy to enhance its robustness and generalization ability. This data augmentation strategy could prevent overfitting and lead to robust model performance, particularly when a limited training dataset is used. Data augmentation was performed on the image and graph inputs to increase the training dataset. When the spatial information of an image was transformed, such as by random rotation and random shift, the same augmentation was applied to the input of the graph. For the gamma, sharpness, blurriness, and random noise, the spatial information of the image was not transformed; thus, these were applied only to the image and not to the graph input.
Generation module
Image compression (Fig. 3c). The objective of our generation module is to generate spost-cephs using pre-ceph as input. To achieve this, we employed a latent diffusion model30 consisting of an autoencoder58 for encoder \({{{\mathcal{E}}}}\) and decoder \({{{\mathcal{D}}}}\) and a diffusion model for generating the encoding latent (Fig. 3c). To train the autoencoder, we used not only pre-ceph and post-ceph data but also an unlabeled set of 30,000 lateral cephalograms sourced from an internal institution (Hospital J). This was important to ensure that the latent space of the autoencoder was well-formed, guaranteeing minimal generation capability30. Additionally, we employed vector quantization59,60, which uses a discrete codebook \({{{\mathcal{Z}}}}{{{\mathscr{\subset }}}}{{\mathbb{R}}}^{16\times 128\times 128}\), and adversarial learning techniques to enhance model stability and achieve high-quality results. The loss function is as follows.
where \(D\) is the patch-based discriminator, \(\hat{x}={{{\mathcal{D}}}}\left({{{\mathcal{E}}}}\left(x\right)\right)\), and \({{{{\mathcal{L}}}}}_{{GAN}}\left(\left\{{{{\mathcal{E}}}},{{{\mathcal{D}}}},{{{\mathcal{Z}}}}\right\},\,D\right)=\left[\log D\left(x\right)+\log \left(1-D\left(\hat{x}\right)\right)\right]\)
Diffusion model. The encoded data distribution \(q\left({z}_{0}\right)\) is gradually converted into a well-behaved distribution \({{{\rm{\pi }}}}\left(y\right)\) by repeated application of a Markov diffusion kernel \({T}_{{{{\rm{\pi }}}}}\left(\,{y|y;}{{{\rm{\beta }}}}\right)\) for π(y)32. Then,
Meanwhile, the forward trajectory, starting at the data distribution and performing \(T={{\mathrm{1000}}}\) steps of diffusion process, is as follows: \(q\left({z}_{0:T}\right)=q\left({z}_{0}\right){\prod }_{t=1}^{T}q\left({z}_{t} | {z}_{t-1}\right)\), where \({z}_{1},{z}_{2},\ldots {z}_{T}\) are latents of the same dimension as the data \({z}_{0}\). The forward process is that which admits sampling \({z}_{t}\) at an arbitary timestep \(t\) in closed form. Using the notation \({{{{\rm{\alpha }}}}}_{t}=1-{{{{\rm{\beta }}}}}_{t}\) and \({\bar{{{{\rm{\alpha }}}}}}_{t}={\sum }_{s=1}^{t}{{{{\rm{\alpha }}}}}_{s}\), then, we obtain the analytical form of \(q\left({z}_{t} | {z}_{0}\right)\) as follows.
We can easily obtain a sample in the immediate distribution of the diffusion process.
Diffusion models are latent variable models of the parameterized distribution \({p}_{{{{\rm{\theta }}}}}\left({z}_{0}\right)={\int {p}_{{{{\rm{\theta }}}}}\left({z}_{0:T}\right){dz}}_{1:T}\). The reverse trajectory, starting at the prior distribution, is as follows.
where \(p({z}_{T})={{{\rm{\pi }}}}\left({z}_{T}\right)\) and \({p}_{{{{\rm{\theta }}}}}\left({z}_{t-1}|{z}_{t}\right)={{{\mathcal{N}}}}\left({z}_{t-1};{\mu }_{\theta }\left({z}_{t},t\right),{\Sigma }_{\theta }\left({z}_{t},t\right)\right)\), and \({\mu }_{\theta }\left({z}_{t},t\right)\) and \({\Sigma }_{\theta }\left({z}_{t},t\right)\) are training targets defining the mean and covariance, respectively, of the reverse Markov transitions for a Gaussian distribution. To approximate between the parameterized distribution \({p}_{{{{\rm{\theta }}}}}\left({x}_{0}\right)\) and data distribution \(q\left({z}_{0}\right)\), training is performed by optimizing the variational lower bound on negative log likelihood.
For efficient training, further improvement is made by re-expressing \({{{{\mathcal{L}}}}}_{{vlb}}\) as follows.
The equation uses Kullback–Leibler divergence to directly compare \({p}_{{{{\rm{\theta }}}}}\left({z}_{t-1} | {z}_{t}\right)\) against forward process posteriors. The posterior distributions are tractable when conditioned on \({z}_{0}\).
where \({\widetilde{\mu }}_{t}\left({z}_{t},{z}_{0}\right)=\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_{t}}{1-{\bar{\alpha }}_{t}}{z}_{0}+\frac{\sqrt{{\alpha }_{t}}\left(1-{\bar{\alpha }}_{t-1}\right)}{1-{\bar{\alpha }}_{t}}{z}_{t}\) and \({\widetilde{\beta }}_{t}=\frac{1-{\bar{\alpha }}_{t}}{1-{\bar{\alpha }}_{t-1}}{\beta }_{t}\), and the values of \({\beta }_{0}\) and \({\beta }_{T}\) were 0.0015 and 0.0195, respectively. Then, the loss function can be defined as follows.
After training, samples can be generated by starting from \({z}_{T}{{{\mathscr{ \sim }}}}{{{\mathcal{N}}}}\left(0,{{{\boldsymbol{I}}}}\right)\) and following the parameterized reverse Markov chain.
Furthermore, we aimed to generate spost-cephs using multiple conditions in the diffusion model. We used a total of four conditions, including pre-cephs and their profile lines, which were concatenated, whereas the pre-ceph landmarks and the movement vectors predicted through IEM and LTEM were latentized using a graph network and subsequently embedded into the diffusion model via a cross-attention module. Then, we can train the conditional diffusion model using conditions c via
where, \(c=\left[{m,x}^{{pre}},\,{l}^{{pre}},\,{p}^{{pre}}\right]\) and \(m\in {{\mathbb{R}}}^{45\times 45}\) is the surgical movement vector predicted through the graph network, and \({x}^{{pre}}\in {{\mathbb{R}}}^{1\times 1024\times 1024}\), \({l}^{{pre}}\in {{\mathbb{R}}}^{45\times 45}\) and \({p}^{{pre}}\in {{\mathbb{R}}}^{1\times 1024\times 1024}\) represent the pre-ceph, the landmarks of pre-ceph, and the profile line of the pre-ceph. Additionally, we used the LTEM40 model to embed \(m\) and \({l}^{{pre}}\) into the diffusion model. We used an untrained model, which is trained together as the diffusion model is trained. After training, sampling is performed using the trained diffusion model. To reduce the generation time and maintain consistency, a DDIM29 was used. The formula for DDIM is as follows:
where \({{{\rm{\tau }}}}\) is a sub-sequence of timesteps of length \(T\).
To train the generation module, we utilized the Adam optimizer56, which combines momentum and exponentially weighted moving average gradient methods. The initial learning rate was set to 2e − 6, and we trained the model for a total of 1000 epochs. The networks were implemented using open-source machine learning frameworks such as PyTorch 1.857 and Python 3.6, with training performed on an NVIDIA RTX A6000 48GB GPU. However, we did not employ data augmentation in our training process.
Classifier-free guidance for digital twin
To conduct experiments for generating various surgical movements, we used classifier-free guidance (CFG)31. Unlike classifier guidance33,34, CFG is distinct in that the classifier model is not separate from the diffusion model but is trained together. CFG achieves an effect similar to modifying epsilon \({{{\rm{\epsilon }}}}\) for classifier guidance sampling, but without the separated classifier. The diffusion model can be trained by setting a condition c or a null token \({{\varnothing }}\) into the model for some probability. Then, we defined the estimated score61,62,63 using model θ for the input condition c as \({{{{\rm{\epsilon }}}}}_{{{{\rm{\theta }}}}}({z}_{t},t,{{{\rm{c}}}})\), and the estimated score for the null token as \({{{\epsilon }}}_{\theta }\left({z}_{t},t,\,{{\varnothing }}\right)={{{\epsilon }}}_{\theta }({z}_{t},t)\). After training, we modified the score using a linear combination of the unconditional score and conditional score by the IASM. The CFG sampling method is known to be robust against gradient-based adversarial attacks, whereas classifier guidance sampling by a poorly trained classifier may lead to problems in consistency and fidelity. The score estimated by the CFG sampling is shown as follows:
Preprocessing of dataset
Before training, all lateral cephalograms were standardized with a pixel spacing of 0.1 mm. Subsequently, the post-ceph was conventionally aligned with the pre-ceph based on the Sella–Nasion (SN) line. To include all landmarks in both pre-ceph and post-ceph, a rectangle encompassing the regions defined by the Basion, Soft-tissue menton, Pronasale, and Glabella points in both pre-ceph and post-ceph was cropped. Additionally, zero padding was applied horizontally and vertically to create a square image with a resolution of 1024 × 1024.
The cropped image was divided by the maximum pixel value of the image. Pixel normalization was performed such that the pixel value was within 0–1. In addition, the coordinates of each landmark and the distances among landmarks were expressed as vectors to train the model. Before input to the model, the x- and y-axis distances were divided by the width and height of the cropped picture, and normalization was performed such that the feature value was within the range of 0–1.
Statistical analysis
All statistical analysis was performed using IBM SPSS Statistics (IBM Corporation, Armonk, NY, USA) version 25.
Landmark distance comparison for post-ceph and spost-ceph
Two ODs traced post-cephs and spost-cephs in the internal (n = 50) and external (n = 57) test sets. The SN − 7° line was set as the horizontal reference line, and the line passing through the S point and perpendicular to the SN − 7° line was set as the vertical reference line. The horizontal and vertical distances from each landmark were used as coordinate values. The coordinate values of the same landmark in post-ceph and spost-ceph were compared, and the distance between landmarks was calculated. A paired equivalence test was performed for each landmark. In this case, the margin of error applied was 1.5 mm41, 42. The SPRs for each point were assessed according to errors <2.0 mm. Furthermore, we measured the distance between the profile lines of post-ceph and spost-ceph. Taking anatomical structures into account, we divided them into four lines, and the distances between the lines were measured using the Hausdorff distance. Details on the errors in the profile lines and the definition of the four profile lines can be found in the Supplementary Table 3 and Supplementary Fig. 1 of the supplementary materials.
Visual Turing test
For the VTT, 57 external test images (29 post-cephs and 28 spost-cephs) were used, as OMFSs and ODs had already observed the generated internal dataset during the digital twin experiment. VTT was conducted with two ODs and two OMFSs by displaying images one by one through a dedicated web-based interface. Each examiner had more than 15 years of clinical experience. To reduce environmental variability, the images were displayed in the same order, and revisiting previous answers was prohibited. The examiners were informed that there were 29 real and 28 synthesized images. In addition, none had prior experience with synthesized images before the test. All examiners successfully completed the test. Sensitivity, specificity, and accuracy were derived, with real images defined as positive and synthetic images as negative.
Digital twin
We investigated the clinical applicability of the spost-cephs as digital twins for simulated surgical planning. Two ODs and OMFSs were simultaneously shown pre-ceph and five spost-cephs randomly generated at different degrees of surgical movement. To focus on cases with significant surgical changes, patients with surgical movement of ≤5 mm were excluded, resulting in the selection of 35 cases from the initial internal test set of 50. Subsequently, the examiners were asked to select an appropriate surgical movement amount considering the pre-ceph. The percentage of spost-cephs reflecting real surgical movements was then calculated.
Ablation study
The ablation study was conducted using an internal dataset of 50 samples. A single OD manually measured landmarks for each experimental condition. Given the intensive nature of manual landmark annotation, only the internal dataset was used to ensure feasibility while maintaining evaluation consistency. Paired t-tests were performed at each of the five experimental stages to compare results with those from the preceding stage, assessing the impact of landmarks distance error. Statistical significance was set at p < 0.05, with p < 0.005 considered highly significant.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All data supporting the findings described in this manuscript are provided within the article and its Supplementary Information. The dataset utilized for model training and evaluation consists of lateral cephalometric radiographs from 707 patients who underwent orthognathic surgery. This dataset is divided into 600 samples for training, 50 samples for internal validation, and 57 samples for external validation. Additionally, 30,000 unlabeled lateral cephalometric radiographs from internal institutions were used for pre-training the generative model. These datasets are available upon request because certain restrictions on public availability apply, owing to national regulations and patient privacy laws in South Korea. Researchers interested in accessing these datasets should submit a formal request, which will be reviewed by the corresponding author, Namkug Kim (namkugkim@gmail.com), and the Institutional Review Board (IRB). The approval process typically requires one to two months, depending on the IRB meeting schedule. Researchers approved for data access are required to cite this manuscript when utilizing the dataset. Source Data containing the raw numerical values underlying all experimental results presented in this manuscript are provided with this paper. Source data are provided with this paper.
Code availability
The code and pretrained weight used in this research is available in the GitHub repository (https://github.com/Kim-Junsik/GPOSC-Net), which is publicly accessible to anyone. Information regarding usage, modification, and distribution of the code is specified in the LICENSE file within the repository. The code is intended for research purposes only and may be restricted to commercial use. Additionally, users must cite the related manuscript and code repository when utilizing this work in their research.
References
Musich, D. & Chemello, P. in Orthodontics: Current Principles and Techniques Ch. 23 (Elsevier, 2005).
Perkovic, V. et al. Facial aesthetic concern is a powerful predictor of patients’ decision to accept orthognathic surgery. Orthod. Craniofacial Res. 25, 112–118 (2022).
Broder, H. L., Phillips, C. & Kaminetzky S. Issues in decision making: Should I have orthognathic surgery? Semin. Orthod. 6, 249–258 (2000).
Kolokitha, O.-E. & Chatzistavrou, E. Factors influencing the accuracy of cephalometric prediction of soft tissue profile changes following orthognathic surgery. J. Maxillofac. Oral. Surg. 11, 82–90 (2012).
Wolford, L. M., Hilliard, F. W. & Dugan, D. J. STO Surgical Treatment Objective: A Systematic Approach to the Prediction Tracing (The C. V. Mosby Company, 1985).
Upton, P. M., Sadowsky, P. L., Sarver, D. M. & Heaven, T. J. Evaluation of video imaging prediction in combined maxillary and mandibular orthognathic surgery. Am. J. Orthod. Dentofac. Orthopedics 112, 656–665 (1997).
Cousley, R. R., Grant, E. & Kindelan, J. The validity of computerized orthognathic predictions. J. Orthod. 30, 149–154 (2003).
Kaipatur, N. R. & Flores-Mir, C. Accuracy of computer programs in predicting orthognathic surgery soft tissue response. J. Oral. Maxillofac. Surg. 67, 751–759 (2009).
Rasteau, S., Sigaux, N., Louvrier, A. & Bouletreau, P. Three-dimensional acquisition technologies for facial soft tissues–applications and prospects in orthognathic surgery. J. Stomatol. Oral. Maxillofac. Surg. 121, 721–728 (2020).
Suh, H.-Y. et al. A more accurate method of predicting soft tissue changes after mandibular setback surgery. J. Oral. Maxillofac. Surg. 70, e553–e562 (2012).
Yoon, K.-S., Lee, H.-J., Lee, S.-J. & Donatelli, R. E. Testing a better method of predicting postsurgery soft tissue response in Class II patients: a prospective study and validity assessment. Angle Orthod. 85, 597–603 (2015).
Lee, Y.-S., Suh, H.-Y., Lee, S.-J. & Donatelli, R. E. A more accurate soft-tissue prediction model for Class III 2-jaw surgeries. Am. J. Orthod. Dentofac. Orthopedics 146, 724–733 (2014).
Suh, H.-Y. et al. Predicting soft tissue changes after orthognathic surgery: the sparse partial least squares method. Angle Orthod. 89, 910–916 (2019).
Lee, K. J. C. et al. Accuracy of 3-dimensional soft tissue prediction for orthognathic surgery in a Chinese population. J. Stomatol. Oral. Maxillofac. Surg. 123, 551–555 (2022).
Resnick, C., Dang, R., Glick, S. & Padwa, B. Accuracy of three-dimensional soft tissue prediction for Le Fort I osteotomy using Dolphin 3D software: a pilot study. Int. J. Oral Maxillofac. Surg. 46, 289–295 (2017).
Bengtsson, M., Wall, G., Greiff, L. & Rasmusson, L. Treatment outcome in orthognathic surgery—a prospective randomized blinded case-controlled comparison of planning accuracy in computer-assisted two-and three-dimensional planning techniques (part II). J. Craniomaxillofac. Surg. 45, 1419–1424 (2017).
Arai, Y., Tammisalo, E., Iwai, K., Hashimoto, K. & Shinoda, K. Development of a compact computed tomographic apparatus for dental use. Dentomaxillofac. Radiol. 28, 245–248 (1999).
Lofthag‐Hansen, S., Grondahl, K. & Ekestubbe, A. Cone‐beam CT for preoperative implant planning in the posterior mandible: visibility of anatomic landmarks. Clin. Implant Dent. Relat. Res. 11, 246–255 (2009).
Momin, M. et al. Correlation of mandibular impacted tooth and bone morphology determined by cone beam computed topography on a premise of third molar operation. Surg. Radiol. Anat. 35, 311–318 (2013).
Patel, S., Dawood, A., Whaites, E. & Pitt Ford, T. New dimensions in endodontic imaging: part 1. Conventional and alternative radiographic systems. Int. Endod. J. 42, 447–462 (2009).
Silva, M. A. G. et al. Cone-beam computed tomography for routine orthodontic treatment planning: a radiation dose evaluation. Am. J. Orthod. Dentofac. Orthopedics 133, e641–640. e645 (2008). 640.
Protection R. Evidence-Based Guidelines on Cone Beam CT for Dental and Maxillofacial Radiology (European Commission, 2012).
Wrzesien, M. & Olszewski, J. Absorbed doses for patients undergoing panoramic radiography, cephalometric radiography and CBCT. Int. J. Occup. Med. Environ. Health 30, 705–713 (2017).
Ludlow, J. et al. Effective dose of dental CBCT—a meta analysis of published data and additional data for nine CBCT units. Dentomaxillofac. Radiol. 44, 20140197 (2015).
Jha, N. et al. Projected lifetime cancer risk from cone-beam computed tomography for orthodontic treatment. Korean J. Orthod. 51, 189–198 (2021).
Jung, Y.-J., Kim, M.-J. & Baek, S.-H. Hard and soft tissue changes after correction of mandibular prognathism and facial asymmetry by mandibular setback surgery: three-dimensional analysis using computerized tomography. Oral. Surg. Oral. Med. Oral. Pathol. Oral. Radiol. Endod. 107, 763–771.e768 (2009).
Kau, C. H. et al. Cone‐beam computed tomography of the maxillofacial region—an update. Int. J. Med. Robot. Comput. Assist. Surg. 5, 366–380 (2009).
Kim, M. et al. Realistic high-resolution lateral cephalometric radiography generated by progressive growing generative adversarial network and quality evaluations. Sci. Rep. 11, 12563 (2021).
Song, J., Meng, C. & Ermon, S. Denoising diffusion implicit models. In International Conference on Learning Representations. https://doi.org/10.48550/arXiv.2010.02502 (ICLR, 2020).
Rombach, R., Blattmann, A., Lorenz, D., Esser, P. & Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (IEEE, 2022).
Ho, J. & Salimans, T. Classifier-free diffusion guidance. In NeurIPS 2021 Workshop on Deep Generative Models and Downstream Applications. https://doi.org/10.48550/arXiv.2207.12598 (NIPS, 2021).
Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 33, 6840–6851 (2020).
Song, Y. et al. Score-based generative modeling through stochastic differential equations. In International Conference on Learning Representations. https://doi.org/10.48550/arXiv.2011.13456 (ICLR, 2020).
Dhariwal, P. & Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 34, 8780–8794 (2021).
Lee, S. et al. Improving 3D imaging with pre-trained perpendicular 2D diffusion models. In Proc. IEEE/CVF International Conference on Computer Vision (IEEE, 2023).
Pinaya, W. H. et al. Brain imaging generation with latent diffusion models. In MICCAI Workshop on Deep Generative Models. (Springer, 2022).
Takagi, Y. & Nishimoto, S. High-resolution image reconstruction with latent diffusion models from human brain activity. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition (IEEE, 2023).
Khader, F. et al. Denoising diffusion probabilistic models for 3D medical image generation. Sci. Rep. 13, 7303 (2023).
Lyu, Q. & Wang, G. Conversion between CT and MRI images using diffusion and score-matching models. Preprint at https://arxiv.org/abs/2209.12104 (2022).
Kim, I.-H. et al. Orthognathic surgical planning using graph CNN with dual embedding module: external validations with multi-hospital datasets. Comput Methods Prog. Biomed. 242, 107853 (2023).
Kim, I.-H., Kim, Y.-G., Kim, S., Park, J.-W. & Kim, N. Comparing intra-observer variation and external variations of a fully automated cephalometric analysis with a cascade convolutional neural net. Sci. Rep. 11, 7925 (2021).
Hwang, H.-W. et al. Automated identification of cephalometric landmarks: part 2-Might it be better than human? Angle Orthod. 90, 69–76 (2020).
Kim, J. et al. Accuracy of automated identification of lateral cephalometric landmarks using cascade convolutional neural networks on lateral cephalograms from nationwide multi‐centres. Orthod. Craniofac. Res. 24, 59–67 (2021).
Gil, S.-M. et al. Accuracy of auto-identification of the posteroanterior cephalometric landmarks using cascade convolution neural network algorithm and cephalometric images of different quality from nationwide multiple centers. Am. J. Orthod. Dentofac. Orthopedics 161, e361–e371 (2022).
Goodfellow, I. et al. Generative adversarial nets. In Proc. 28th International Conference on Neural Information Processing Systems 2672–2680 (MIT Press, 2014).
Karras, T., Laine, S. & Aila, T. A style-based generator architecture for generative adversarial networks. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition (IEEE, 2019).
Karras, T. et al. Analyzing and improving the image quality of stylegan. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition (2020).
Richardson, E. et al. Encoding in style: a stylegan encoder for image-to-image translation. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition (IEEE, 2021).
Kipf, T. N. & Welling, M. Semi-supervised classification with graph convolutional networks. In International Conference on Learning Representations (ICLR, 2017).
Sperduti, A. & Starita, A. Supervised neural networks for the classification of structures. IEEE Trans. Neural Netw. 8, 714–735 (1997).
de Oliveira, P. H. J. et al. Artificial intelligence as a prediction tool for orthognathic surgery assessment. Orthodont. Craniofac. Res. 27, 785–794 (2024).
Donatelli, R. E. & Lee, S.-J. How to report reliability in orthodontic research: Part 2. Am. J. Orthodont. Dentofac. Orthopedics 144, 315–318 (2013).
Park, J.-A. et al. Does artificial intelligence predict orthognathic surgical outcomes better than conventional linear regression methods? Angle Orthod. 94, 549–556 (2024).
Wang, J. et al. Deep high-resolution representation learning for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 43, 3349–3364 (2020).
Agarap, A. F. Deep learning using rectified linear units (ReLU). Preprint at https://arxiv.org/abs/1803.08375 (2018).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at https://arxiv.org/abs/1412.6980 (2014).
Paszke, A. et al. Pytorch: an imperative style, high-performance deep learning library. In Proc. 33rd International Conference on Neural Information Processing Systems 8026–8037 (Curran Associates Inc., 2019).
Baldi, P. Autoencoders, unsupervised learning, and deep architectures. In Proc. ICML Workshop on Unsupervised and Transfer Learning 37–49 (2012).
Razavi, A., Van den Oord, A. & Vinyals O. Generating diverse high-fidelity images with vq-vae-2. In Proc. 33rd International Conference on Neural Information Processing Systems 14866–14876 (Curran Associates Inc., 2019).
Van Den Oord, A. & Vinyals, O. Neural discrete representation learning. In 31st Conference on Neural Information Processing Systems (NIPS) (2017).
Vincent, P. A connection between score matching and denoising autoencoders. Neural Comput. 23, 1661–1674 (2011).
Song, Y., Garg, S., Shi, J. & Ermon, S. Sliced score matching: a scalable approach to density and score estimation. In Proc. 35th Uncertainty in Artificial Intelligence Conference, 574–584 (PMLR, 2020).
Hyvärinen, A. & Dayan, P. Estimation of non-normalized statistical models by score matching. J. Mach. Learn. Res. 6, 695−709 (2005).
Acknowledgements
This research was supported by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (grant number : HR20C0026). The authors thank Jongseon Lim, Minsu Kwon, Jongmin Hwang, Ji Youn Oh and Kyoung Hwa Oh for their helpful data analysis.
Author information
Authors and Affiliations
Contributions
I.-H.K., J.J., and J.-S.K. acquired and analyzed data, conducted deep learning experiments, and drafted the manuscript. N.K. and J.-W.P. has made substantial contribution to the conception and design and data interpretation, and critically revised the manuscript. M.K., S.-J.S., Y.-J.K., J.-H.C., M.H., K.-H.K., S.-H.L., S.-J.K., Y.H.K., and S-H.B. have made a substantial contribution to acquisition and interpretation of data, has made a substantial contribution to study design and interpretation of data. J.L. contributed to data preprocessing and figure preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Hyungjin Chung, Daeseok Hwang and Peer Kämmerer for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Kim, IH., Jeong, J., Kim, JS. et al. Predicting orthognathic surgery results as postoperative lateral cephalograms using graph neural networks and diffusion models. Nat Commun 16, 2586 (2025). https://doi.org/10.1038/s41467-025-57669-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-57669-x