Efficient and accurate framework for genome-wide gene-environment interaction analysis in large-scale biobanks

Abstract

Gene-environment interaction (G×E) analysis elucidates the interplay between genetic and environmental factors. Genome-wide association studies (GWAS) have expanded to encompass complex traits like time-to-event and ordinal traits, which provide richer phenotypic information. However, most existing scalable approaches focus only on quantitative or binary traits. Here we propose SPAGxE_CCT, a scalable and accurate framework for diverse trait types. SPAGxE_CCT fits a genotype-independent model and employs a hybrid strategy including saddlepoint approximation (SPA) for accurate p value calculation, especially for low-frequency variants and unbalanced phenotypic distributions. We extend SPAGxE_CCT to SPAGxEmix_CCT, which accounts for population stratification and is applicable to multi-ancestry or admixed populations. SPAGxEmix_CCT can further be extended to SPAGxEmix_CCT-local, which identifies ancestry-specific G×E effects using local ancestry. Through extensive simulations and real data analyses of UK Biobank data, we demonstrate that SPAGxE_CCT and SPAGxEmix_CCT are scalable to analyze large-scale study cohort, control type I error rates effectively, and maintain power.

Introduction

Gene-environment interaction (G×E) refers to the interplay effect of genetic and non-genetic factors on complex traits. Conducting genome-wide G×E analyses contributes to identifying genetic variants whose genetic effects are dependent on environmental conditions. Although holding promising applications in precision medicine¹, genome-wide G×E studies require larger sample sizes than regular GWAS for identifying marginal genetic effects, which greatly limits potential discoveries^{2,3,4,5,6,7,8,9,10}. Over the past decade, the emergence of biobanks with hundreds of thousands of participants has motivated a rapid growth of genome-wide G×E association studies^{11,12,13,14,15}.

Most of G×E analysis approaches are designed for quantitative or binary trait analysis, and are only applicable to a homogeneous population. Wald test and likelihood ratio test require fitting full models across the genome and thus are computationally intensive when applied to a large-scale study cohort^16,17. Recently, scalable methods such as fastGWA-GE¹⁴, GEM¹³, and SPAGE¹² have been proposed. As an extension of fastGWA, fastGWA-GE is developed for quantitative trait analysis. GEM can be applied to analyze binary traits but cannot control type I error rates in the presence of case-control imbalance¹³. SPAGE is a scalable and accurate method to analyze binary traits, in which a matrix projection is used to exclude the marginal genetic effects from G×E effect. SPAGE incorporates saddlepoint approximation (SPA) and thus is accurate to analyze low-frequency and rare variants even if case-control ratios are unbalanced. However, these approaches are only applicable to analyze quantitative or binary traits. Additionally, when analyzing a heterogeneous or admixed population, the scalable methods mentioned above have not been fully evaluated. There is still a lack of scalable G×E analytical frameworks for within-individual variability or diversity populations¹⁰.

With the advances in electronic health records (EHR), the response variables in GWAS have extended to complex traits with more intricate structures beyond quantitative and binary traits. For example, a time-to-event trait contains information not only whether an event occurred but also when the event occurred^18,19,20,21. An ordinal trait is an extension of a binary trait to measure more than two conditions^{22,23,24,25,26}. Despite these traits can embed richer phenotypic information, the proper tools for large-scale G×E analysis remain relatively scarce. R package gwasurvivr can be applied for G×E analyses of time-to-event traits but is not scalable to analyze a large-scale study cohort due to its low computation efficiency²⁷. Two-step methods can reduce computation time but the variants with G×E effect could be excluded in the screening step^28,29. An alternative approach is to convert the traits to quantitative or binary data, followed by G×E analysis using existing methods²². Although effective, this strategy may lead to reduced phenotypic information and thus statistical power. In general, a scalable and accurate G×E analytical framework applicable to a wide variety of complex traits are urgently needed.

Population stratification and admixture can result in inflated type I error rates if not properly controlled³⁰. This issue is particularly critical in large-scale biobank data analyses, in which the inclusion of diverse ancestries or admixed populations is common^31,32,33. It is crucial to conduct G×E analyses on diverse or admixed populations. For G×E analyses, the ancestry-specific diversities can manifest in the distribution of genotypes (e.g., minor allele frequency, MAF), environmental factors of interest, and phenotypes (e.g., case-control ratios or event rates)¹⁰. Due to these complex patterns, incorporating SNP-derived principal components (PCs) as covariates may not be sufficiently accurate. Moreover, sample relatedness is another major confounder that could inflate type I error rates if not properly accommodated. Additionally, unbalanced phenotypic distributions are frequently observed in biobanks. Examples include low case-control ratios for binary traits, low event rates for time-to-event traits, and unbalanced ratios for ordinal traits. Ignoring these features can lead to inaccurate analyses, especially for low-frequency and rare variants. This has been validated in previous studies for marginal genetic effect^18,25,34 and in SPAGE paper for G×E effect¹². However, the concerns related to population stratification, sample relatedness, and unbalanced phenotypic distribution have not been fully addressed in G×E analyses.

Recently, methods based on mixed effect model have been proposed to address the issues related to population stratification or sample relatedness in G×E analyses. Sul et al. proposed a linear mixed model approach for quantitative trait analysis and suggested using an additional kinship matrix to account for population structure on gene-environment interaction (GEI) statistics³⁵. fastGWA-GE is a fast and powerful linear mixed model-based approach¹⁴. StructLMM is a structured linear mixed model approach to identifying loci that interact with one or more environments, while it cannot account for sample relatedness³⁶. LEMMA is a linear mixed model-based approach based on a Bayesian whole-genome regression model for joint modeling of main genetic effects and G×E interactions³⁷. However, these methods are based on linear mixed models and not directly applicable to binary traits or other types of traits. GxEMM proposed a unifying mixed model for G×E interaction, which has the ability to model both quantitative and binary traits and is broadly applicable for testing and quantifying polygenic interactions³⁸. GxEMM can accommodate general environments, noise heterogeneity, and modest sample size. However, GxEMM is still computationally intensive. Consequently, there exists an urgent need to develop scalable and accurate G×E analytical frameworks that account for population structure or sample relatedness, while also being applicable to a broader spectrum of trait types.

Here, we propose a scalable and accurate analytical framework, SPAGxE_CCT, for a large-scale genome-wide G×E analysis. SPAGxE_CCT employs a retrospective strategy, which considers genotype as a random variable and conducts association analysis conditional on phenotype, environmental factor, and other covariates. The retrospective approaches are robust to model misspecifications and can be straightforwardly applied to complex trait types, such as time-to-event and ordinal traits^39,40. Similar to SPAGE and GEM, SPAGxE_CCT fits a covariates-only model and then uses a matrix projection to attenuate the marginal genetic effect, which greatly reduces computational burden across a genome-wide analysis. To calculate p values, a hybrid strategy combining normal distribution approximation and SPA is used to approximate the null distribution of test statistics. The precise approximation ensures SPAGxE_CCT to outperform conventional approaches, especially when testing low-frequency or rare variants in the presence of unbalanced phenotypic distributions.

SPAGxE_CCT can be extended to SPAGxEmix_CCT, an analytical framework robust to various patterns of ancestry-specific diversities, to address population stratification and admixture in G×E analyses. In addition, given local ancestry information, SPAGxEmix_CCT can test for ancestry-specific G×E effects, denoted as SPAGxEmix_CCT-local. Cauchy combination test (CCT) can combine p values from SPAGxEmix_CCT and SPAGxEmix_CCT-local to give a uniformly the most powerful testing in analyses of admixed populations^41,42. In addition, SPAGxE_CCT can be extended to SPAGxE+, which can effectively accommodate sample relatedness through leveraging genetic relationship matrix (GRM).

In this paper, we conducted extensive simulation studies to evaluate SPAGxE_CCT, SPAGxE+, and SPAGxEmix_CCT across various traits, including binary, time-to-event, ordinal, and quantitative traits. We applied SPAGxE_CCT, SPAGxEmix_CCT, and SPAGxE+ to analyze time-to-event and binary traits in UK Biobank. For the SPAGxE_CCT analyses, 281,299 White British (WB) individuals were included. For the SPAGxEmix_CCT analyses, 338,044 individuals from all ancestries were included and more loci were additionally identified compared to the analysis limited to White British individuals. For the SPAGxE+ analyses, 337,367 WB individuals with sample relatedness were included. We demonstrated that the proposed methods are computationally efficient to analyze large datasets with hundreds of thousands of individuals, can accurately control type I error rates while remaining powerful to identify G×E findings.

Results

An overview of SPAGxE_CCT

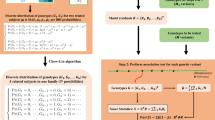
SPAGxE_CCT is an analytical framework developed for genome-wide G×E analyses in a large-scale study cohort. SPAGxE_CCT contains two main steps (Fig. 1). In step 1, SPAGxE_CCT fits a covariates-only model and then calculates model residuals. The covariates include confounding factors such as age, genetic sex, SNP-derived principal components (PCs), and environmental factors. The model specification and the corresponding model residuals vary depending on the type of trait. In the “Methods” section and Supplementary Note, we demonstrated regression models to fit time-to-event traits, binary traits, and ordinal traits, along with the corresponding model residuals. As the covariates-only model is genotype-independent, the model fitting and residuals calculation are only required once across a genome-wide analysis.

Fig. 1: Workflow of the SPAGxE_CCT framework.

The SPAGxE_CCT framework consists of two main steps: (1) fitting a genotype-independent model to calculate residuals, and (2) computing test statistics based on p values for marginal genetic effects and associating traits of interest with single genetic variant by approximating the null distribution of test statistics. Leveraging a hybrid strategy combining normal distribution approximation and saddlepoint approximation, SPAGxE_CCT is scalable for analyzing large-scale biobank data and maintains high accuracy for rare genetic variants, even under unbalanced phenotypic distributions.

In step 2, SPAGxE_CCT identifies genetic variants with marginal G×E effect on the trait of interest. First, SPAGxE_CCT tests for marginal genetic effect via score statistic ${S}_{G}^{c}={\sum }_{i=1}^{n}{G}_{i}{R}_{i}$, where $n$ is the number of individuals, and ${G}_{i}$ and ${R}_{i}$ denote the genotype and model residual for individual $i,\,i\le n$, respectively. If the marginal genetic effect is not significant, we use ${S}_{G\times E}={\sum }_{i=1}^{n}({G}_{i}{E}_{i}-\lambda {G}_{i}){R}_{i}$ as the test statistics to characterize marginal G×E effect, where ${E}_{i},i\le n$ denote the environmental factor and $\lambda={\sum }_{i=1}^{n}({E}_{i}{R}_{i}^{2})/{\sum }_{i=1}^{n}{R}_{i}^{2}$. Otherwise, statistics ${S}_{G\times E}$ is updated to ${\widetilde{S}}_{G\times E}={\sum }_{i=1}^{n}{G}_{i}{E}_{i}{\widetilde{R}}_{i}$ where ${\widetilde{R}}_{i},\,i \le n$ are genotype-adjusted residuals.

In a retrospective context, SPAGxE_CCT treats the genotypes ${G}_{i},\,i\le n$ as random variables and approximates the null distribution of ${S}_{G\times E}$ and ${\widetilde{S}}_{G\times E}$ conditional on model residuals and environmental factors. To balance the computational efficiency and accuracy, SPAGxE_CCT employs a hybrid strategy to combine normal distribution approximation and SPA to calculate p values, as in previous studies^12,19,34,43. For variants with significant marginal genetic effect, SPAGxE_CCT additionally calculates p value through Wald test and then uses Cauchy combination test (CCT) to combine p values from Wald test and statistics ${\widetilde{S}}_{G\times E}$.

As an extension of SPAGxE_CCT, SPAGxEmix_CCT is applicable to individuals from multiple ancestries or multi-way admixed populations. SPAGxEmix_CCT estimates individual-level allele frequencies using ancestry PCs and raw genotypes. SPAGxEmix_CCT can be extended to SPAGxEmix_CCT-local by integrating local ancestry information. In addition, as an extension of SPAGxE_CCT, SPAGxE+ is applicable to individuals with sample relatedness through incorporating a sparse GRM. Similar to SPAGxE_CCT, both SPAGxEmix_CCT and SPAGxE+ involve two main steps including genotype-independent model fitting and testing marginal G×E effects. More details can be found in the “Methods” section and Supplementary Note. A summary of existing G×E methods and those proposed in this work in terms of their key features is presented in Supplementary Table 1.

Association analysis in the UK Biobank data

We applied SPAGxE-based approaches to conduct genome-wide G×E analyses in which 281,299 White British individuals were included. We highlighted four combinations of environmental factors and time-to-event phenotypes: genetic sex and cardiac dysrhythmias (CDR, event rate in WB = 9.06%), genetic sex and colorectal cancer (event rate in WB = 1.86%), smoking status and chronic airway obstruction (CAO, event rate in WB = 4.03%), and smoking status and pulmonary heart disease (PHD, event rate in WB = 1.55%).

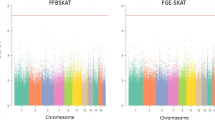
We compared four proposed methods including SPAGxE, SPAGxE_Wald, SPAGxE_CCT, and NormGxE. When marginal genetic effect p value is not significant, SPAGxE, SPAGxE_Wald, and SPAGxE_CCT are exactly the same, following strategies of matrix projection and a combination of normal distribution approximation and SPA to calculate p values. Otherwise, to test for marginal G×E effects, SPAGxE only uses ${\widetilde{S}}_{G\times E}$, SPAGxE_Wald only uses Wald test, SPAGxE_CCT uses Cauchy combination test to combine two p values from Wald test and ${\widetilde{S}}_{G\times E}$. NormGxE only uses normal distribution approximation without SPA. The Manhattan plots and QQ plots for the above four combinations are presented in Fig. 2, and QQ plots stratified by MAF are presented in Fig. 3. NormGxE cannot control type I error rates and identified a significant number of spurious loci, mostly low-frequency and rare variants (MAF < 0.05), especially when analyzing traits with low event rate. In contrast, SPAGxE, SPAGxE_Wald, and SPAGxE_CCT can well control type I error rates. The results are consistent with simulation results and previous studies, affirming the necessity of SPA to control type I error rates.

Fig. 2: Manhattan plots and quantile-quantile (QQ) plots for genome-wide G×E analyses of four combinations of environmental factors and time-to-event traits.

Manhattan plots display the results of genome-wide analyses using SPAGxE_CCT, SPAGxE, SPAGxE_Wald, and NormGxE for four combinations of environmental factors and time-to-event traits: a genetic sex and cardiac dysrhythmias (event rate in White British: 9.06%), b genetic sex and colorectal cancer (event rate in White British: 1.86%), c smoking status and chronic airway obstruction (event rate in White British: 4.03%), and d smoking status and pulmonary heart disease (event rate in White British: 1.55%). e Corresponding QQ plots for genome-wide G×E analyses of the four combinations of environmental factors and time-to-event traits shown in a–d. The QQ plots are color-coded based on methods used (SPAGxE_CCT, SPAGxE, SPAGxE_Wald, and NormGxE). The red line indicates the genome-wide significance level of $\alpha=5\times {10}^{-8}$. Genome-wide analyses included 281,299 individuals of White British ancestry. Tests conducted in the analysis were two-sided.

Fig. 3: Quantile-quantile (QQ) plots for genome-wide G×E analyses of four combinations of environmental factors and time-to-event traits, with genetic variants grouped based on minor allele frequency (MAF).

QQ plots display the results of genome-wide analyses using SPAGxE_CCT, SPAGxE, SPAGxE_Wald, and NormGxE for four combinations of environmental factors and time-to-event traits: a genetic sex and cardiac dysrhythmias (event rate in White British: 9.06%), b genetic sex and colorectal cancer (event rate in White British: 1.86%), c smoking status and chronic airway obstruction (event rate in White British: 4.03%), and d smoking status and pulmonary heart disease (event rate in White British: 1.55%). QQ plots are color-coded based on minor allele frequency categories. Genome-wide analyses included 281,299 individuals of White British ancestry. The red line indicates the genome-wide significance level of $\alpha=5\times {10}^{-8}$. Tests conducted in the analysis were two-sided.

Benefiting from the Cauchy combination test, SPAGxE_CCT identified more loci than SPAGxE and SPAGxE_Wald at a significant level of $\alpha=5\times {10}^{-8}$ (Fig. 2). For instance, in the analyses of genetic sex × CDR, SPAGxE_CCT was similarly powerful as SPAGxE and identified more loci than SPAGxE_Wald. Meanwhile, in the analyses of smoking status × PHD, SPAGxE_CCT was similarly powerful as SPAGxE_Wald and identified more loci than SPAGxE.

We clustered genetic variants within 200 kb region as one locus. The top SNPs in each locus and the complete list of SNPs with SPAGxE_CCT p values less than 5 × 10⁻⁸ are presented in Supplementary Table 2 and Supplementary Data 1. In the analysis of CDR, we identified a significant G×E effect of genetic sex and a variant rs2634073 (SPAGxE_CCT p value = 4.56 × 10⁻¹⁷) near PITX2. The gene PITX2 is instrumental in cardiac morphogenesis of the systemic and pulmonary venous inflow tracts^44,45,46. PITX2 plays an important role in cardiac development and diseases, and the incidence of cardiac development is known to be different for males and females^12,47,48,49. PITX2 encodes an evolutionarily conserved homeodomain transcription factor that is involved in the establishment of left-right asymmetry and cardiovascular development in the vertebrate embryo⁵⁰. PITX2 usually has the function of inhibiting irregular electrical signals, and if the expression level of PITX2 decreases, electrical signal disorder will occur in the heart, which is one of the causes of atrial fibrillation⁵¹. An association between rs2634073 and atrial fibrillation has been reported in previous studies^{44,50,52,53,54}.

In the analysis of colorectal cancer, we identified a significant G×E effect of genetic sex and variant rs9950013 (SPAGxE_CCT p value = 4.78 × 10⁻⁸) in gene ZNF521 (Zinc Finger Protein 521). Colorectal cancer is strongly influenced by biological sex differences and social-cultural gender components, with mortality rates in males significantly higher than females^{55,56,57,58,59,60,61,62,63}. ZNF521 is a protein coding gene and a co-transcriptional factor with multiple recognized regulatory functions in a range of normal, cancer and stem cell compartments⁶⁴. It has a variety of functions in multiple cells, including hematopoietic, osteo-adipogenic, neural progenitor, and cancer cells^65,66,67,68. ZNF521 has been identified as a candidate driver gene of colorectal cancer^69,70.

In the analysis of CAO, we identified a significant G×E effect of smoking status and highlighted a variant rs16969968 (SPAGxE_CCT p value = 6.36 × 10⁻⁹) in CHRNA5 and a variant rs1051730 (SPAGxE_CCT p value = 1.18 × 10⁻⁸) in CHRNA3. Smoking is an important risk factor to the CAO, and three neuronal nicotinic acetylcholine receptors encoding genes of CHRNA3 and CHRNA5 form a gene cluster and are well known to be associated with the smoking behavior and some smoking diseases such as chronic obstructive pulmonary disease, lung cancer^12,71,72,73. The variant of rs16969968 causes an amino acid substitution (D398N) and encodes the nicotinic acetylcholine receptor α5 subunit, predisposing to both smoking and Chronic Obstructive Pulmonary Disease (COPD)⁷⁴. It has been reported that rs16969968 involves in airway remodeling and related inflammatory response in COPD, and directly contributes to COPD-like lesions, sensitizing the lung to the action of oxidative stress and injury, and represents a therapeutic target⁷⁴. The allele A of the variant rs16969968 is a risk allele, and its risk effect will increase significantly smoker. The CHRNA3 gene encoding the neuronal nicotinic acetylcholine receptor has been associated to COPD, lung cancer and nicotine dependence in case–control studies with high smoking exposure^73,75. SNP rs1051730 is located in the exon of CHRNA3 gene and causes a synonymous nucleotide substitution. It has been reported in previous researches that smoking interacted with genotype of rs1051730 on forced expiratory in 1 s (FEV₁), and the association was observed only in smokers⁷⁵. In the analysis of PHD, we identified a significant G×E effect of smoking status and variant rs57198405 (SPAGxE_CCT p value = 5.52 × 10⁻¹¹) near genes MIR4539 and MIR4472-1. Epidemiological studies have concluded that active cigarette smoking caused heart disease^76,77,78,79.

To demonstrate the superiority of time-to-event traits over binary traits in real data analysis, we additionally used SPAGxE_CCT(CC0) to analyze the combination of smoking status and PHD in which event indicator ${\delta }_{i}$ was treated as a binary outcome. The QQ plot is presented in Supplementary Fig. 1. At a genome-wide significance level of α = 5 × 10⁻⁸, SPAGxE_CCT(CC0) identified no variants, whereas SPAGxE_CCT identified one locus. This suggested that time-to-event traits are more informative than binary traits, which could result in enhanced statistical powers and more discoveries. In addition, we applied the proposed SPAGxE-based approaches, NormGxE, and SPAGE to analyze the combination of genetic sex and CDR in which CDR was treated as a binary trait. The QQ plots illustrated that SPAGxE_CCT and SPAGxE were more powerful than SPAGxE_Wald and SPAGE (Supplementary Fig. 2). The consistent enhancement in statistical power across various trait types validates a superior performance of SPAGxE_CCT over other methods. We also applied SPAGE to analyze binary traits. In addition, we applied SPAGxE+ to analyze time-to-event traits for 337,367 WB individuals with sample relatedness. Compared to SPAGxE_CCT analyses, 56,068 additional related individuals were included. We scale up the real data analyses to 30 E-phenotype pairs (Supplementary Data 2). SPAGxE+ and SPAGxE_CCT identified more loci (or more significant SNPs) than SPAGE. Manhattan plots and QQ plots for several combinations of environmental factors and traits are illustrated in Supplementary Figs. 3–8. As related individuals were included, SPAGxE+ generally outperformed SPAGxE_CCT and SPAGE. For example, in the analyses of genetic sex and CDR, the signals identified by SPAGxE+ and SPAGxE_CCT are more significant than SPAGE. For top SNP rs2634073, p values of SPAGxE+, SPAGxE_CCT, and SPAGE are 1.19 × 10⁻¹⁸, 4.56 × 10⁻¹⁷, and 7.33 × 10⁻¹⁵, respectively. In the analysis of Townsend deprivation index (TDI) and Schizophrenia, SPAGxE+ and SPAGxE_CCT identified several loci, while SPAGE identified no significant SNPs. The advantage of time-to-event traits over binary traits in GWAS have been widely reported^{18,19,80,81,82}. However, due to the low effect size of G×E, testing for G×E effects generally identified much fewer findings than testing for marginal genetic effects at a stringent GWAS significance level. Thus, for most of the analyses, only one or two loci were identified, mostly by time-to-event trait analyses. For the loci identified by both time-to-event trait analyses and binary trait analysis, p values from time-to-event trait analyses were more significant. More discussion about the difference can be found in the Supplementary Note.

To demonstrate the superiority of SPAGxEmix_CCT over SPAGxE_CCT in terms of enhancing powers through incorporating more individuals from diverse ancestries in real data analysis, we additionally applied SPAGxEmix_CCT to analyze two combinations of environmental factors and time-to-event (and binary) traits including (1) genetic sex and CDR and (2) smoking status and CAO, in which 338,044 unrelated individuals from multiple ancestries were included. Compared to the previous real data analysis using SPAGxE_CCT, 56,745 more individuals from the other ancestries were included in the analysis. The QQ plots and Manhattan plots showed that SPAGxEmix_CCT was more powerful than SPAGxE_CCT (Fig. 4), which is expected as SPAGxE_CCT removed ~17% non-white British individuals. Genetic variants within 200 kb region were clustered as one locus. The top SNPs in each locus and the complete list of SNPs with SPAGxEmix_CCT p values less than 5 × 10⁻⁸ are presented in Supplementary Table 3 and Supplementary Data 3. Compared to the analysis limited to White British individuals, more significant genetic variants and loci were additionally identified. An elucidating example is the combination of smoking status and time-to-event trait CAO for which a locus with its top SNP rs76418688 was identified by SPAGxEmix_CCT (SPAGxEmix_CCT p value = 2.34 × 10⁻⁹) but missed by SPAGxE_CCT (SPAGxE_CCT p value = 0.595151). SNP rs76418688 is an intergenic variant between LINC02508 and LINC01262 on chromosome 4. For SNP rs76418688, its MAF in non-white British (0.012991) is approximately 93 times higher than that in White British (0.000139). Moreover, this locus was missed by either SPAGxEmix_CCT or SPAGxE_CCT in the binary trait analysis. The results highlight the necessity of incorporating individuals from diverse ancestries and analyzing time-to-event traits to increase statistical powers and discover more novel G×E findings. Generally speaking, the UK Biobank analyses validate that SPAGxE_CCT was close to the most powerful in the analysis of White British, making it optimal for G×E analysis across various types of traits. SPAGxE+ were generally more powerful than SPAGxE_CCT and SPAGE through including more related individuals into analyses. Meanwhile, as SPAGxEmix_CCT can include individuals from multiple ancestries, it was more powerful than SPAGxE_CCT as expected. Furthermore, the application of SPA is essential to control type I error rates for unbalanced phenotypic distribution, especially when testing for low-frequency and rare variants. The above conclusions align with the simulation studies and previous analyses^12,18,34,43.

Fig. 4: Manhattan plots and quantile-quantile (QQ) plots for genome-wide G×E analyses of two combinations of environmental factors and traits using SPAGxEmix_CCT and SPAGxE_CCT.

Manhattan plots and QQ plots display the results of genome-wide analyses for two combinations of environmental factors and traits: a genetic sex and cardiac dysrhythmias (event rate: 8.83%) and b smoking status and chronic airway obstruction (event rate: 3.92%). SPAGxEmix_CCT was applied to analyze 338,044 individuals of multiple ancestries for time-to-event traits (denoted as SPAGxEmix_CCT (Surv-ALL)) and binary traits (denoted as SPAGxEmix_CCT (Binary-ALL)). SPAGxE_CCT was applied to analyze 281,299 individuals of White British ancestry for time-to-event traits (denoted as SPAGxE_CCT (Surv-WB)) and binary traits (denoted as SPAGxE_CCT (Binary-WB)). The red line indicates the genome-wide significance level of $\alpha=5\times {10}^{-8}$. Tests conducted in the analysis were two-sided.

We selected two smoking-related values of pack years of smoking (field ID: 20161) and past tobacco smoking (field ID: 1249) to conduct additional sensitivity analyses. Note that in analysis of smoking status (E) and CAO (time-to-event trait) using SPAGxE_CCT, top SNPs rs16969968 (in CHRNA5) and rs146009840 (in CHRNA3) have significant p values of 6.36 × 10⁻⁹ and 9.36 × 10⁻⁹, respectively. Meanwhile, if we use pack years of smoking as environmental factor, the proposed methods (SPAGxE_CCT and SPAGxE+) and Wald tests show that the G×E effects of the two SNPs were not significant anymore, both in analysis of unrelated WB or all WB including related individuals, for both binary and time-to-event trait analyses. Similarly, when analyzing past tobacco smoking as phenotype, the two top SNPs of rs16969968 and rs146009840 were also only identified when using smoking status as environmental factor. The top SNPs influence smoking quantity specifically in smokers, which would show up as a pervasive G×E on smoking-related phenotypes. These findings suggest that gene-environment (G-E) correlation and mis-measured environmental factors would result in a true positive, statistically, although not aligning with the conventional understanding of G×E. Therefore, statistically valid G×E might have complicated relationships to the underlying biology. For further details, please refer to Supplementary Note.

SPAGxE_CCT is scalable to analyze large-scale biobank data

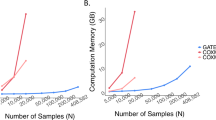
The projected computation time to conduct genome-wide G×E analyses via SPAGxE_CCT and gwasurvivr is presented in Fig. 5 and Supplementary Table 4. For smoking status × PHD and genetic sex × CDR, gwasurvivr took ~4418 and 4373 CPU hours, respectively. Meanwhile, SPAGxE_CCT only took 301 and 283 CPU hours, which were 14.7 and 15.5 times faster. The higher computational efficiency is mainly due to the projection, which is applied to genetic variants covering more than 99% of the genome (given a p value cutoff of 0.001). The superiority ensures that SPAGxE_CCT is scalable to a large-scale genome-wide G×E analysis including hundreds of thousands of individuals.

Fig. 5: Computational efficiency of SPAGxE_CCT and Wald test (gwasurvivr).

G×E analysis included 281,299 individuals of White British ancestry. CPU hours were recorded based on 10,000 randomly selected genetic variants from chromosome 1 and projected to a genome-wide analysis of 18,583,853 variants. SPAGxE_CCT and gwasurvivr were employed to analyze time-to-event traits using Cox PH regression models, incorporating age, genetic sex, environmental factors, and the top 10 SNP-derived PCs as covariates. All analyses were performed on a CPU model of Intel(R) Xeon(R) Gold 6342 CPU @ 2.80 GHz.

Type I error rates simulations

To assess type I error rates, we carried out extensive simulation studies for G×E analyses of time-to-event, binary, and ordinal traits. We simulated genotypes, covariates, environmental factors, and time-to-event, binary, and ordinal traits of $n={{\mathrm{10,000}}}$ individuals. The empirical type I error rates are shown in Supplementary Figs. 9–13 and Table 1 and Supplementary Tables 5–8. The QQ plots are presented in Supplementary Figs. 14–22.

Table 1 Empirical type I error rates and ratios of empirical type I error rates/significance level of SPAGxE_CCT, SPAGxE, SPAGxE_Wald, NormGxE at a significance level 5 × 10⁻⁷, and Wald test at a significance level 5 × 10⁻⁵ for time-to-event trait analysis under scenario 1

SPAGxE-based approaches can control type I error rates

For variants without marginal genetic effect (i.e., in scenario 1 that ${\beta }_{G\times E}={\beta }_{G}=0$), SPAGxE-based approaches and SPAGE generally performed well in terms of type I error rates. If the phenotypic distribution is unbalanced, Wald test produced deflated type I error rates when testing for rare or low-frequency variants. We considered extensive settings in terms of (1) genotypic distribution, (2) phenotypic distribution, (3) environmental distribution, (4) marginal genetic effect and G×E effect, etc. The large number of simulation settings results in massive computational burden. As a result, we conducted 10⁸ tests for each setting and then evaluated type I error rates under a significance level of 5 × 10⁻⁷. The results demonstrate that SPAGxE_CCT can well control type I error rates. Meanwhile, NormGxE had inflated type I error rates (Supplementary Figs. 9–12, 14–19). We additionally evaluated the type I error rates under the significance level of 5 × 10⁻⁸ (Supplementary Table 5 and Supplementary Fig. 11), which demonstrate that SPAGxE_CCT produced well-controlled type I error rates even under a stringent level of significance. The results indicate that SPA approaches outperform normal distribution approximation in a wide range of phenotypic distributions. The conclusion aligns with previous research and real data analysis, underscoring the need to employ SPA for accurately approximating the null distribution of test statistics.

For genetic variants with marginal genetic effect (i.e., in scenario 2 that ${\beta }_{G\times E}=0,\,{\beta }_{G}\ne 0$), SPAGxE-based methods can still control type I error rates across various trait types (Supplementary Figs. 13, 20–22). The results demonstrated that using matrix projection can well attenuate marginal genetic effects from the G×E effect.

Impact of environmental factor distribution to type I error rates

For Wald test and NormGxE, type I error rates are highly relevant to the distribution of environmental factor. When analyzing time-to-event traits and ordinal traits with an unbalanced phenotypic distribution, Wald test produced more deflated type I error rates if the environmental factor followed a Bernoulli distribution. For example, in the analysis of time-to-event trait, if the event rate was 0.01 and MAF was 0.01, the empirical type I error rates were 1.6 × 10⁻⁵ (0.32 alpha) and 0 (0 alpha) for normal and Bernoulli distributed environmental factors, respectively. The deflation of Wald test was also observed in previous binary trait G × E analysis¹². For NormGxE, if the environmental factors followed a Bernoulli distribution, the type I error rates were less inflated.

SPAGxE_CCT is accurate under heteroscedasticity of E-dependent noise and G-E dependence

To evaluate the impact of E-dependent noise on G × E tests of SPAGxE_CCT, we simulated binary traits of $n={{\mathrm{10,000}}}$ individuals. The empirical false positive rates (FPR) are shown in Supplementary Fig. 23. The results demonstrate that E-dependent noise cannot inflate G×E tests of SPAGxE_CCT. For further details, please refer to Supplementary Note.

To evaluate empirical type I error rates of SPAGxE_CCT in the case of G-E dependence, we simulated binary traits of $n={{\mathrm{10,000}}}$ individuals. The QQ plots are shown in Supplementary Fig. 24. The results indicate that SPAGxE_CCT produced well-calibrated p values and can control type I error rates even in the presence of G-E dependence. For further details, please refer to Supplementary Note.

SPAGxE+ can control type I error rates for related samples

We evaluated type I error rates of SPAGxE+, SPAGxE+ (SAIGE), and SPAGxE_CCT (SAIGE) in the presence of sample relatedness in binary and time-to-event trait analysis. SPAGxE+ (SAIGE) and SPAGxE_CCT (SAIGE) employ SAIGE to fit a null model, and then pass the model residuals to the proposed SPAGxE+ and SPAGxE_CCT framework, respectively. We simulated phenotypes of related samples and then calculated the variance ratio ${\rho=\hat{\sigma }}_{{GRM}}^{2}/{\hat{\sigma }}_{{UR}}^{2}$ (see “Method” section for details) for each phenotype. The distributions of the variance ratio for binary and time-to-event traits are shown in Supplementary Figs. 25 and 26, respectively. The QQ plots for binary and time-to-event trait analyses are presented in Supplementary Figs. 27–32. The results indicated that most of the ratios are close to 1, i.e., ${\hat{\sigma }}_{{GRM}}^{2}$ is close to ${\hat{\sigma }}_{{UR}}^{2}$, and thus SPAGxE_CCT (SAIGE) and SPAGE work well. Meanwhile, if the ratio is less than 1 or greater than 1, then SPAGxE_CCT (SAIGE) and SPAGxE_CCT are inflated or deflated. In contrast, SPAGxE+ and SPAGxE+ (SAIGE) can control type I error rates under all settings. As expected, type I error rates of NormGxE+ were inflated, emphasizing the necessity of SPA.

SPAGxEmix_CCT can control type I error rates in admixed population analyses

To assess the performance of SPAGxEmix_CCT in terms of type I error rates in admixed population analyses, we simulated genotypes, environmental factors, and time-to-event traits of $n={{\mathrm{10,000}}}$ subjects, mimicking an admixed population of European (EUR) and East Asian (EAS). Other types of traits were not simulated as the corresponding results and conclusions are expected to remain similar.

For each genetic variant, we simulated genotypes using ancestry vectors and allele frequency $\left({q}^{{EUR}},{q}^{{EAS}}\right)$ downloaded from the 1000 Genomes Project⁸³. Depending on the difference of MAFs (i.e., Diff_MAF = ${q}^{{EUR}}-{q}^{{EAS}}$) and the minimal MAF value (i.e., minMAF = $\min \left({q}^{{EUR}},{q}^{{EAS}}\right)$) in populations EUR and EAS, genetic variants were categorized into 15 groups. Two scenarios were used to simulate time-to-event traits. In scenario 1, the event rates in EUR and EAS were the same; and in scenario 2, the event rate in EUR was higher than that in EAS. In each scenario, we simulated traits with low event rates (ER_low), moderate event rates (ER_mod), and high event rates (ER_high). More details about the data simulation can be found in the “Data simulation” subsection of the “Methods” section.

The empirical type I error rates for the admixed population analyses based on 10⁷ association tests at a genome-wide significance level 5 × 10⁻⁶ are presented in Supplementary Fig. 33 and Supplementary Data 4 and 5. If event rates in EUR and EAS were the same (i.e., in scenario 1), SPAGxEmix_CCT and SPAGE generally performed well and can control type I error rates under all settings of MAFs and event rates (or disease prevalence rates). In a limited number of settings, SPAGE produced slightly deflated type I error rates (Supplementary Fig. 33a and Supplementary Data 4). Meanwhile, if event rates were low, NormGxEmix cannot control type I error rates when testing for low-frequency variants. For example, if Diff_MAF ~ 0, Min_MAF $<$ 0.01 (i.e., minMAF_low), and event rates in both EUR and EAS were 0.01 (i.e., ER_low), the empirical type I error rates corresponding to SPAGxEmix_CCT, SPAGE, and NormGxEmix were 3.2 × 10⁻⁶ (0.64α), 6 × 10⁻⁷ (0.12α), and 0.0032678 (>600 α), respectively.

If event rates in EUR and EAS were different (i.e., in scenario 2), SPAGxEmix_CCT can still control type I error rates well (Supplementary Fig. 33b and Supplementary Data 5). Meanwhile, SPAGE cannot control type I error rates if the disease prevalence rates were different across ancestries. If event rates were moderate or high, despite incorporating ancestry PCs to fit the null model, SPAGE resulted in inflated type I error rates for Diff_MAF << 0 or Diff_MAF >> 0. For example, if Diff_MAF >> 0, $\min \left({q}^{{EUR}},{q}^{{EAS}}\right) < 0.01$ (i.e., minMAF_low), and event rates in EUR and EAS are 0.5 and 0.2 (i.e., ER_high), respectively, the empirical type I error rate of SPAGE was 1.56 × 10⁻⁵ (3.12α). In addition, similar to scenario 1, NormGxEmix produced inflated type I error rates. The results demonstrated the accuracy of SPAGxEmix_CCT in the presence of ancestry-specific event rates and MAFs.

SPAGxEmix_CCT is well calibrated under heterogeneity of environmental factors

To assess the performance of SPAGxEmix_CCT in terms of type I error rates under heterogeneity of environmental factors, we simulated genotypes, environmental factors, and time-to-event traits of $n={{\mathrm{10,000}}}$ subjects, mimicking an admixed population of European (EUR) and East Asian (EAS). We simulated traits in scenario 2, the event rate in EUR was higher than that in EAS. The environmental factor distributions for individuals in EUR-dominant community and EAS-dominant community were different. The empirical type I error rates are presented in Supplementary Fig. 34. SPAGxEmix_CCT can still control type I error rates well, whereas SPAGE had inflated type I error rates. The results demonstrated that SPAGxEmix_CCT is robust to the heterogeneity of environmental factors.

Empirical power simulations

To assess empirical powers, we simulated genotypes, covariates, environmental factors, and time-to-event, binary, and ordinal traits of $n={{\mathrm{50,000}}}$ individuals. The empirical powers were evaluated based on 10⁴ tests at a significance level $\alpha=5\times {10}^{-8}$ under the alternative model (Fig. 6 and Supplementary Figs. 35–40). Across all simulation settings, SPAGxE_CCT was always close to the most powerful, indicating that SPAGxE_CCT can be an optimal unified approach to maximize power.

Fig. 6: Empirical powers of SPAGxE_CCT, Wald test, SPAGxE_CCT(CC), SPAGxE_CCT(CC0), and SPAGE methods at a significance level of 5 × 10⁻⁸ for time-to-event trait analysis under a normally distributed environmental factor.

Sample size was set to n = 50,000. Time-to-event traits were simulated with ${\beta }_{G}=0$ and ${\beta }_{G\times E}\ne 0$. Three MAFs were considered: 0.01, 0.05, and 0.3 (from top to bottom). Three event rates were evaluated: 0.01 (extremely unbalanced phenotypic distribution), 0.1 (moderately unbalanced phenotypic distribution), and 0.5 (balanced phenotypic distribution) (from left to right). The environmental factor was generated from a standard normal distribution. In each case, 10⁴ tests were conducted. Tests conducted in the analysis were two-sided.

Power simulation results for binary trait analysis

For binary trait analysis, if the environmental factor follows a normal distribution (Supplementary Fig. 35), SPAGxE and SPAGxE_CCT were more powerful than Wald test, SPAGxE_Wald, and SPAGE, especially for low disease prevalence (e.g., 0.1 or 0.01). If the environmental factor follows a Bernoulli distribution (Supplementary Fig. 36), SPAGxE was less powerful than SPAGxE_Wald, Wald, and SPAGE if the disease prevalence is 0.1 or 0.5; meanwhile, SPAGxE outperformed SPAGxE_Wald and Wald if the disease prevalence is 0.01. The empirical power in settings with a Bernoulli distributed environmental factor was consistently lower than that in settings with a normal distributed environmental factor. The results indicate that empirical powers were relevant to the distribution of environmental factor, with a trend similar as shown in type I error results. SPAGxE_CCT was always close to the most powerful, regardless of the environmental factor distribution settings and disease prevalence rates.

Power simulation results for time-to-event trait analysis

For time-to-event trait analysis, SPAGxE_CCT was always close to the most powerful, similar as in binary trait analysis. For both normal distributed (Fig. 6) and Bernoulli distributed (Supplementary Fig. 37) environmental factors, SPAGxE_CCT was more powerful than Wald if the event rate was 0.01. If the event rate was 0.1 or 0.5, SPAGxE_CCT and Wald were similarly powerful.

In all settings, SPAGxE_CCT was more powerful than the approaches designed for binary trait analyses, including SPAGxE_CCT(CC0), SPAGxE_CCT(CC), and SPAGE. The results underscore that time-to-event traits were more informative than binary traits. Meanwhile, SPAGxE_CCT(CC) was more powerful than SPAGxE_CCT(CC0) and SPAGE, which was logically reasonable as SPAGxE_CCT(CC) incorporated survival time as an additional covariate. Similar as the simulation results for binary trait analysis, SPAGxE_CCT(CC0) was more powerful than SPAGE if the event rate was 0.01. The results under scenarios of non-zero marginal genetic effects are consistent to those without marginal genetic effects, indicating that SPAGxE_CCT is powerful (Supplementary Fig. 38).

Power simulation results for ordinal trait analysis

For ordinal trait analysis, SPAGxE_CCT was still always close to the most powerful approach across all scenarios (Supplementary Figs. 39 and 40). If the ratio across the four categories was 100:1:1:1, SPAGxE_CCT was more powerful than Wald test, with the advantages being greater for the normal distributed environmental factor than the Bernoulli distributed environmental factor. For a balanced phenotypic distribution, SPAGxE_CCT and Wald test were similarly powerful. In all settings, SPAGxE_CCT was more powerful than the approaches designed for binary trait analyses including SPAGxE_CCT(CC0) and SPAGE. The power loss of SPAGxE_CCT(CC0) and SPAGE stemmed from the dichotomizing process.

SPAGxEmix_CCT is more powerful than cross-ancestry meta-analysis in multiple discrete populations

To assess empirical powers of SPAGxEmix_CCT and cross-ancestry meta-analysis based on SPAGxE_CCT in a cross-ancestry analysis, we simulated genotypes, environmental factors, and time-to-event phenotypes of n = 20,000 individuals, mimicking two discrete populations of European (EUR) and East Asian (EAS). We also simulated genotypes using allele frequencies downloaded from the 1000 Genomes Project and categorize genetic variants into 15 groups depending on the difference of MAFs and the minimal MAF value in populations EUR and EAS.

The empirical powers at a genome-wide significance level 5 × 10⁻⁸ are presented in Supplementary Fig. 41. The results demonstrated that jointly modeling multiple ancestries using SPAGxEmix_CCT is generally more powerful than cross-ancestry meta-analysis based on SPAGxE_CCT in both scenarios, particularly when DiffMAF << 0 and DiffMAF >> 0. Note that the meta-analysis can only support two or more than two discrete populations, while SPAGxEmix_CCT can allow for admixed individuals. Moreover, SPAGxEmix_CCT (PCxE) incorporating PC×E interaction terms as covariates into model fitting was similarly powerful as SPAGxEmix_CCT in our simulations.

SPAGxEmix_CCT can utilize local ancestry to maximize power across various cross-ancestry genetic architectures

To evaluate SPAGxEmix_CCT, SPAGxEmix_CCT-local, and SPAGxEmix_{CCT-local-global}, we simulated multiple cross-ancestry genetic architectures in an admixed population. The QQ plots demonstrated SPAGxEmix_CCT, SPAGxEmix_CCT-local, and SPAGxEmix_{CCT-local-global} can control type I error rates when analyzing binary and quantitative traits (Supplementary Figs. 42 and 43). For binary traits, normal distribution approximation (denoted as NormGxEmix_local) had inflated type I error rates if the prevalence was low (Supplementary Fig. 42), suggesting that incorporating SPA increased the accuracy. For quantitative traits, all approaches can well control type I error rates (Supplementary Fig. 43).

The empirical powers were evaluated for a binary trait with a prevalence of 0.2 (Fig. 7, Supplementary Figs. 44–46 for null marginal genetic effects, and Supplementary Figs. 51–54 for non-zero marginal genetic effects). If the marginal ancestry-specific G×E effect sizes were equal, SPAGxEmix_CCT was always more powerful than SPAGxEmix_CCT-local (Supplementary Fig. 44). In scenarios in which marginal ancestry-specific G×E effect sizes were different, we fixed the marginal G×E effect size of ancestry 1, i.e., ${\beta }_{G\times E}^{\left(1\right)}$, and increased marginal G×E effect size of ancestry 2, i.e., ${\beta }_{G\times E}^{\left(2\right)}$. The results demonstrated a power gain of SPAGxEmix_CCT-local over SPAGxEmix_CCT (Fig. 7 and Supplementary Figs. 45 and 46). For example, if ${\beta }_{G\times E}^{\left(1\right)}$ was fixed at 0.5, ${\beta }_{G\times E}^{\left(2\right)}$ was close to 0, and the MAF in ancestry 1 was 0.1 and the MAF in ancestry 2 was 0.3, the empirical powers of SPAGxEmix_CCT were close to 0 but SPAGxEmix_CCT-local can still identify the genetic variants with relatively high powers (Fig. 7). In all simulation scenarios, SPAGxEmix_{CCT-local-global} was always close to the most powerful methods across various cross-ancestry genetic architectures, demonstrating that SPAGxEmix_{CCT-local-global} can be an optimal unified approach to maximize powers. The empirical powers for quantitative traits (Supplementary Figs. 47–50 and 55–58) were consistent as the results for binary traits. As expected, the power results in scenarios with non-zero genetic effects are similar to scenarios without marginal genetic effects (Supplementary Figs. 51–58).

Fig. 7: Empirical powers of SPAGxEmix_CCT, SPAGxEmix_CCT-local (ance1), SPAGxEmix_CCT-local (ance2), and SPAGxEmix_{CCT-local-global} at a significance level of 5 × 10⁻⁸ for binary trait analysis under the scenario of G×E effect size heterogeneity, with the marginal G×E effect size of ancestry 1 fixed at 0.5.

SPAGxEmix_CCT-local (ance1) tests for ${\beta }_{G\times E}^{\left(1\right)}=0$, and SPAGxEmix_CCT-local (ance2) tests for ${\beta }_{G\times E}^{\left(2\right)}=0$. A two-way admixed population was simulated with a sample size n = 10,000. The disease prevalence of the simulated binary phenotypes was 0.2. Two minor allele frequencies (MAFs) in ancestry 1 (from top to bottom) and four MAFs in ancestry 2 (from left to right) were considered. The true G×E effect size of ancestry 1 was fixed at 0.5, and that of ancestry 2 was increased. In each case, 1000 tests were conducted. Tests conducted in the analysis were two-sided.

Discussion

In this paper, we proposed a scalable and accurate analytical framework, SPAGxE_CCT, to conduct G×E analyses in a large-scale GWAS. SPAGxE_CCT fits a genotype-independent model and then uses a matrix projection to adjust for marginal genetic effects. Thus, the computational burden is greatly reduced compared to conventional methods. SPAGxE_CCT treats genotype as a random variable and approximates the null distribution of the test statistic conditional on phenotypes and covariates. The retrospective framework allows SPAGxE_CCT to be applicable to complex traits with intrinsic structures including time-to-event and ordinal traits. A hybrid strategy including SPA ensures the stringent accuracy to analyze common, low-frequency, and rare variants, even if the phenotypic is extremely unbalanced. In addition, SPAGxE_CCT employs Cauchy combination test to maximize statistical power.

Through extensive simulation studies of binary, time-to-event, and ordinal traits, SPAGxE_CCT is demonstrated to be scalable to analyze hundreds of thousands of individuals and can control type I error rates while maintaining sufficient power. Meanwhile, regular approaches based on normal distribution approximation could be deflated or inflated. In general, SPAGxE_CCT is always close to the most powerful across all trait types, phenotypic distributions, genotype distributions, and environmental factor distributions.

We applied SPAGxE_CCT to analyze several time-to-event traits in UK biobank. SPAGxE_CCT is ~15 times faster than gwasurvivr and has identified multiple G×E findings. An elucidating example is the analysis of smoking status and pulmonary heart disease. If the outcome is a time-to-event trait, SPAGxE_CCT identified SNP rs57198405 (SPAGxE_CCT p value = 5.52 × 10⁻¹¹). Meanwhile, if the outcome is a binary trait defined as event occurrence status, no significant variant was identified. The example highlights that SPAGxE_CCT can fully leverage the rich information embedded in complex traits for identifying novel G×E signals. Moreover, the real data analysis of genetic sex and cardiac dysrhythmias validated that SPAGxE_CCT can be more powerful than SPAGE when analyzing binary traits. In addition, both simulation studies and real data analysis have demonstrated that SPAGxE_CCT outperforms regular approaches based on normal distribution approximation in terms of controlling type I error rates.

Admixed populations are groups of individuals with genetic contributions from multiple ancestral populations⁸⁴. Analyses in admixed or diverse populations can provide unique opportunities for G×E studies^{30,85,86,87,88,89}. Currently, there is a lack of G×E studies for diversity across ancestries¹⁰. The simulation studies have shown that regular methods such as SPAGE could still result in inflation, even if SNP-derived PCs were incorporated as covariates. An extension of SPAGxE_CCT, denoted as SPAGxEmix_CCT, can account for population stratification in admixed populations. We applied SPAGxEmix_CCT to analyze time-to-event and binary traits using 338,044 individuals from all ancestries in UK Biobank data. Compared to analyzing a homogeneous population with White British only, powers were enhanced and more loci were identified as ~ 17% additional individuals were incorporated into analysis. Additionally, it is also crucial to account for local ancestry^10,90,91. We extend SPAGxEmix_CCT to SPAGxEmix_CCT-local and SPAGxEmix_{CCT-local-global}, which can effectively and efficiently incorporate local ancestry information.

In large-scale genome-wide analyses, sample relatedness is another major confounder that could inflate type I error rates if not properly controlled. To address this issue, we extended SPAGxE_CCT to SPAGxE+, an analytical framework that can effectively and efficiently account for sample relatedness through leveraging a GRM. We applied SPAGxE+ to analyze time-to-event traits using 337,367 WB individuals with relatedness in UK Biobank data. Compared to analyzing unrelated White British individuals only, powers were enhanced and more loci were identified. Currently, mixed-model based methods have been widely used on biobank scales to address the concerns related to population stratification or sample relatedness. However, most mixed-model based G×E approaches are designed for quantitative or binary traits and not applicable to other complex types of traits. Our proposed scalable and accurate analytical frameworks, SPAGxEmix_CCT and SPAGxE+, can address the concerns related to population stratification and sample relatedness for a wide range of types of traits.

There are several limitations in SPAGxE_CCT. Firstly, SPAGxE_CCT is based on a modified score statistic without fitting a full model and thus cannot estimate the marginal G×E effect size. If marginal G×E effect size is required for the follow-up analysis, SPAGxE_CCT can serve as a screening process to prioritize variants to fit a full model. Secondly, SPAGxE_CCT cannot conduct gene- or region-based tests. Thirdly, SPAGxE_CCT does not test joint effects including both genetic main effect and G×E effect. In the future, we plan to expand the current analytical framework to allowing for gene- or region-based analysis and testing for joint effects of genetic main effect and G×E effect.

For the significant G×E interactions, it is important to acknowledge potential complexities that could arise from misclassified environmental factors. It is crucial to highlight that statistically valid G×E interactions may have complicated relationships to the underlying biology. Specifically, while G×E findings could be statistically robust, they still should be interpreted with caution. This complexity underscores the importance of cautious interpretation and highlights the need for further biological validation of G×E findings. Our real data analysis in the context of smoking behavior gives an intuitive example.

Currently, there is a noticeable trend towards leveraging complex traits with intricate structures in GWAS. For G×E studies, most existing tools are developed for binary or quantitative traits. However, for complex traits with intricate structures, researchers often resort to converting these traits into binary or quantitative traits before analysis, leading to a loss of phenotypic information and statistical power. We believe that SPAGxE_CCT, SPAGxE+, and SPAGxEmix_CCT can serve as a universal framework for genome-wide G×E studies to analyze complex traits.

Methods

Ethics approvals and compliance

This study complies with all relevant ethical regulations. The study protocol was approved by the UK Biobank (Application No. [78793]), and all participants provided informed consent. The use of UK Biobank data was conducted under approved protocols, and all analyses were performed in accordance with the UK Biobank’s data access guidelines.

Cox proportional hazard (PH) model for time-to-event traits

In the main text, we primarily demonstrated the use of SPAGxE_CCT with the Cox proportional hazards model to analyze time-to-event traits. For individual $i\le n$, we let ${{{{\bf{X}}}}}_{i}$ denote a $k\times 1$ vector of non-genetic confounder factors including age, genetic sex, SNP-derived PCs, etc., ${E}_{i}$ denote an environmental factor, ${G}_{i}$ denote a raw genotype call or imputation. Cox proportional hazard model specifies the hazard function ${{{\rm{\lambda }}}}\left({t;} {{{{\bf{X}}}}}_{i},{E}_{i},{G}_{i}\right)$ for the failure (i.e., event) time ${T}_{i}^{*}$ in the form of:

$${{{\rm{\lambda }}}}\left({t;}{{{{\bf{X}}}}}_{i},{E}_{i},{G}_{i}\right)= {{{{\rm{\lambda }}}}}_{0}\left(t\right)\exp \left({\eta }_{i}\right) \\= {{{{\rm{\lambda }}}}}_{0}\left(t\right)\exp \left({{{{\bf{X}}}}}_{i}^{{{{\rm{T}}}}}{{{{\boldsymbol{\beta }}}}}_{{{{\bf{X}}}}}+{E}_{i}{\beta }_{E}+{G}_{i}{\beta }_{G}+{G}_{i}{E}_{i}{\beta }_{G\times E}\right)$$

(1)

where ${{{{\rm{\lambda }}}}}_{0}\left(t\right)$ is the baseline hazard function and ${\eta }_{i}={{{{\bf{X}}}}}_{i}^{{{{\rm{T}}}}}{{{{\boldsymbol{\beta }}}}}_{{{{\bf{X}}}}}+{E}_{i}{\beta }_{E}+{G}_{i}{\beta }_{G}+{G}_{i}{E}_{i}{\beta }_{G\times E}$ is a linear predictor, ${{{{\boldsymbol{\beta }}}}}_{{{{\bf{X}}}}}$ and ${\beta }_{E}$ are coefficients for confounder factors and environmental factor, respectively. Coefficient ${\beta }_{G}$ is the marginal genetic effect, ${\beta }_{E}$ is the marginal environmental effect, ${\beta }_{G\times E}$ is the marginal G×E effect. The observed time-to-event phenotype is $\left({T}_{i},{\delta }_{i}\right)$, where ${C}_{i}$ is the censoring time, ${T}_{i}=\min ({T}_{i}^{*},{C}_{i})$ is the observed time-to-event, ${\delta }_{i}={{{\rm{I}}}}({T}_{i}^{*}\le {C}_{i})$ indicates that failure is observed, and ${{{\rm{I}}}}\left(.\right)$ is an indicator function. Null hypothesis to test for the marginal G×E effect is H₀$:$ ${\beta }_{G\times E}=0$.

Score statistics to test for G×E effect

Regular score test requires fitting a genotype-dependent model under the null hypothesis ${{{{\rm{H}}}}}_{0}:{\beta }_{G\times E}=0$ to estimate parameters $\left({\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{X}}}}}^{{H}_{0}},{\hat{\beta }}_{E}^{{H}_{0}},{\hat{\beta }}_{G}^{{H}_{0}}\right)$, followed by testing for marginal G×E effect via score statistics ${S}_{G\times E}^{{H}_{0}}={\sum }_{i=1}^{n}{G}_{i}{E}_{i}{R}_{i}^{{H}_{0}}$, where ${R}_{i}^{{H}_{0}},\,i\le n$ are the model residuals under model ${{{{\rm{H}}}}}_{0}$ (see Supplementary Note). This strategy is computationally expensive for a genome-wide analysis because it requires fitting a separate model for each genetic variant to test.

To improve computational efficiency, we fit a genotype-independent model under ${{{{\rm{H}}}}}_{{{{\rm{c}}}}}:{\beta }_{G}={\beta }_{G\times E}=0$ to estimate parameters $\left({\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{X}}}}}^{{H}_{c}},{\hat{\beta }}_{E}^{{H}_{c}}\right)$, followed by calculating a model residual vector ${{{\bf{R}}}}={\left({R}_{1},\ldots,{R}_{n}\right)}^{{{{\rm{T}}}}}$. If the marginal genetic effect ${\beta }_{G}=0$, score statistics ${S}_{G\times E}^{c}={\sum }_{i=1}^{n}{G}_{i}{E}_{i}{R}_{i}$ is asymptotically equivalent to ${S}_{G\times E}^{{H}_{0}}$ and can characterize the marginal G×E effect. However, if the marginal genetic effect ${\beta }_{G}\ne 0$, the underlying correlation between ${G}_{i}$ and ${R}_{i}$ can result in inflated type I error rates.

To adjust for the marginal genetic effect, we propose a modified score statistic:

$${S}_{G\times E}={S}_{G\times E}^{c}-\lambda {S}_{G}^{c}={{{{\bf{G}}}}}_{{{{\bf{E}}}}}^{{{{\rm{T}}}}}{{{\bf{R}}}}-\lambda {{{{\bf{G}}}}}^{{{{\rm{T}}}}}{{{\bf{R}}}}={\sum }_{i=1}^{n}\left({G}_{i}{E}_{i}-\lambda {G}_{i}\right){R}_{i}$$

(2)

where $\lambda={\sum }_{i=1}^{n}({E}_{i}{R}_{i}^{2})/{\sum }_{i=1}^{n}{R}_{i}^{2}$, genotype vector ${{{\bf{G}}}}={\left({G}_{1},\ldots,{G}_{n}\right)}^{{{{\rm{T}}}}}$, and G×E vector ${{{{\bf{G}}}}}_{{{{\bf{E}}}}}={\left({G}_{1}{E}_{1},\ldots,{G}_{n}{E}_{n}\right)}^{{{{\rm{T}}}}}$. If the marginal genetic effect is moderate, the correlation between ${S}_{G\times E}^{c}$ and ${S}_{G}^{c}$ is λ and the statistics ${S}_{G\times E}$ can reasonably approximate ${S}_{G\times E}^{{H}_{0}}$. The modification idea is initially proposed by SPAGE¹² and also used in GEM¹³. More details of the projection strategy can be seen in Supplementary Note.

Following Hardy-Weinberg Equilibrium (HWE), we employ a retrospective view to consider ${G}_{i},i\le n$ as independent and identically distributed random variables following a binomial distribution Binom(2, q), where q is minor allele frequency (MAF). Conditional on residual vector R and environment vector ${{{\bf{E}}}}={({E}_{1},\ldots,{E}_{n})}^{{{{\rm{T}}}}}$, the mean and variance of ${S}_{G\times E}$ under ${{{{\rm{H}}}}}_{{{{\rm{c}}}}}$ are $2q\cdot {\sum }_{i=1}^{n}{E}_{i}{R}_{i}-2\lambda q\cdot {\sum }_{i=1}^{n}{R}_{i}$ and $2q(1-q)\cdot {{\sum }_{i=1}^{n}({R}_{i}{E}_{i}-\lambda {R}_{i})}^{2}$, respectively, in which MAF q is estimated using $\hat{q}=(1/2n)\cdot {\sum }_{i=1}^{n}{G}_{i}$. Since ${\sum }_{i=1}^{n}{R}_{i}={\sum }_{i=1}^{n}{{E}_{i}R}_{i}=0$ holds for most of the regression models incorporating environmental factors as covariates, the mean of ${S}_{G\times E}$ is 0.

Limitation of the projection strategy and alternative solutions

In general, using ${S}_{G\times E}$ to approximate ${S}_{G\times E}^{{H}_{0}}$ is accurate while greatly boosting computational efficiency. However, the approximation could be inaccurate if ${\beta }_{G}$ is far away from 0. To avoid inflated type I error rates, SPAGxE_CCT uses score statistic ${S}_{G}^{c}={\sum }_{i=1}^{n}{G}_{i}{R}_{i}$ to test for marginal genetic effects and gives alternative solutions depending on the testing results.

Suppose that ${S}_{G}^{c}$ follows a normal distribution with a mean of 0 and a variance of $\widehat{{Var}}\left({S}_{G}^{c}|{{{\bf{R}}}}\right)=2\hat{q}\left(1-\hat{q}\right){\sum }_{i=1}^{n}{R}_{i}^{2}$ under the null hypothesis, we calculate a two-sided p value to characterize the marginal genetic effect. If the p value is greater than a pre-selected positive cutoff ϵ, we use ${S}_{G\times E}$ as the test statistic for the marginal G×E effect. Otherwise, we define a genotype-adjusted residual vector:

$$\widetilde{{{{\bf{R}}}}}=\left({\widetilde{R}}_{1},\ldots,{\widetilde{R}}_{n}\right)=\left({{{{\bf{I}}}}}_{n}-{{{\bf{W}}}}{\left({{{{\bf{W}}}}}^{{{{\rm{T}}}}}{{{\bf{W}}}}\right)}^{-1}{{{{\bf{W}}}}}^{{{{\rm{T}}}}}\right){{{\bf{R}}}}$$

(3)

in which marginal genetic effect is projected out from R through a linear regression on G. Here, ${{{{\bf{I}}}}}_{{\mathbf{n}}}$ is an $n\times n$ identity matrix and ${{{\bf{W}}}}=\left({{{{\mathbf{1}}}}}_{n},{{{\bf{G}}}}\right)$ is an n × 2 matrix including a column of genotype vector and a column of 1. We calculate ${\widetilde{S}}_{G\times E}={{{{\bf{G}}}}}_{{{{\bf{E}}}}}^{{{{\rm{T}}}}}\widetilde{{{{\bf{R}}}}}={\sum }_{i=1}^{n}{G}_{i}{E}_{i}{\widetilde{R}}_{i}$ as the test statistic for marginal G×E effect. To maximize statistical powers, we also calculate p values based on Wald test and then use Cauchy combination test (CCT) to combine two p values from Wald test and ${\widetilde{S}}_{G\times E}$. In numeric simulation and real data analysis, we followed SPAGE paper to set the cutoff $\epsilon=0.001$. For simulations of selecting the parameter ϵ, please refer to the Supplementary Note.

Normal distribution approximation and saddlepoint approximation

For both ${S}_{G\times E}$ and ${\widetilde{S}}_{G\times E}$, we use a hybrid strategy combining normal distribution approximation and saddlepoint approximation to calculate p values^{12,18,19,25,34}. In this section, we demonstrate the calculation for ${S}_{G\times E}$; the corresponding calculation for ${\widetilde{S}}_{G\times E}$ is similar.

Conditional on (R, E), the mean and variance of ${S}_{G\times E}$ under the null hypothesis are 0 and ${\hat{\sigma }}^{2}=2\hat{q}(1-\hat{q})\cdot {{\sum }_{i=1}^{n}\left({R}_{i}{E}_{i}-\lambda {R}_{i}\right)}^{2}$, respectively. Suppose that test statistic ${S}_{G\times E}$ follows a normal distribution, then the probability $\Pr \left({S}_{G\times E} < {s}_{G\times E}|{{{\bf{R}}}},{{{\bf{E}}}}\right)$ under the null hypothesis can be estimated by $\Phi \left({s}_{G\times E}/\hat{\sigma }\right)$, where $\Phi (.)$ is the cumulative distribution function (CDF) of a standard normal distribution and ${s}_{G\times E}$ is the observed statistics ${S}_{G\times E}$. The normal distribution approximation works well when the test statistic is close to the mean of 0⁴³. However, in the presence of unbalanced phenotypic distributions, the normal distribution approximation could perform poorly at tails and cannot control type I error rates.

We propose a retrospective SPA approach to approximate the null distribution of ${S}_{G\times E}$. Suppose that genotype ${G}_{i},i\le n$ follow a binomial distribution Binom$(2,\hat{q})$, the moment generating function (MGF) of ${G}_{i}$ is ${\widehat{M}}_{G}\left(t\right)={\left(1-\hat{q}+\hat{q}{e}^{t}\right)}^{2}$. Its derivatives are:

$${{\widehat{M}}_{G}^{{\prime} }\left(t\right)=2\hat{q}{e}^{t}\cdot \left(1-\hat{q}+\hat{q}{e}^{t}\right),\,\widehat{M}}_{G}^{{\prime} {\prime} }\left(t\right)=2{\left(\hat{q}{e}^{t}\right)}^{2}+2\hat{q}{e}^{t}\cdot \left(1-\hat{q}+\hat{q}{e}^{t}\right)$$

(4)

The corresponding cumulant generating function (CGF) is ${\hat{K}}_{G}\left(t\right)={{\mathrm{ln}}}{\widehat{M}}_{G}(t)$, and its derivatives are:

$${\hat{K}}_{G}^{{\prime} }\left(t\right)=\frac{{\widehat{M}}_{G}^{{\prime} }\left(t\right)}{{\widehat{M}}_{G}\left(t\right)},\,{\hat{K}}_{G}^{{\prime} {\prime} }\left(t\right)=\frac{{\widehat{M}}_{G}^{{\prime} {\prime} }\left(t\right){\widehat{M}}_{G}\left(t\right)-{\left[{\widehat{M}}_{G}^{{\prime} }\left(t\right)\right]}^{2}}{{\left[{\widehat{M}}_{G}\left(t\right)\right]}^{2}}$$

(5)

Hence, under ${{{{\rm{H}}}}}_{0}$, the estimated CGF of ${S}_{G\times E}$ conditional on (R,E) is:

$$\hat{H}\left(t\right)={\sum }_{i=1}^{n}{\hat{K}}_{G}\left(\left({R}_{i}{E}_{i}-\lambda {R}_{i}\right)t\right)={\sum }_{i=1}^{n}{{\mathrm{ln}}}{\widehat{M}}_{G}\left(\left({R}_{i}{E}_{i}-\lambda {R}_{i}\right)t\right)$$

(6)

and its derivatives are:

$${\hat{H}}^{{\prime} }\left(t\right)={\sum }_{i=1}^{n}\left({R}_{i}{E}_{i}-\lambda {R}_{i}\right){\hat{K}}_{G}^{{\prime} }\left(\left({R}_{i}{E}_{i}-\lambda {R}_{i}\right)t\right)$$

(7)

$${\hat{H}}^{{\prime} {\prime} }\left(t\right)={\sum }_{i=1}^{n}{\left({R}_{i}{E}_{i}-\lambda {R}_{i}\right)}^{2}{\hat{K}}_{G}^{{\prime} {\prime} }\left(\left({R}_{i}{E}_{i}-\lambda {R}_{i}\right)t\right)$$

(8)

Given an observed statistic ${s}_{G\times E}$, environmental factors ${E}_{i},i\le n$ and martingale residuals ${R}_{i},i\le n$, we calculate ${{{\rm{\zeta }}}}$ such that ${\hat{H}}^{{\prime} }\left({{{\rm{\zeta }}}}\right)={s}_{G\times E}$, and

$$\omega={{\mathrm{sgn}}}\left({{{\rm{\zeta }}}}\right)\sqrt{2\left({{{\rm{\zeta }}}}{s}_{G\times E}-\hat{H}\left({{{\rm{\zeta }}}}\right)\right)}$$

(9)

and

$$\nu={{{\rm{\zeta }}}}\sqrt{{\hat{H}}^{{\prime} {\prime} }\left({{{\rm{\zeta }}}}\right)}$$

(10)

Following Barndorff-Nielsen’s formula⁹², the null distribution of ${S}_{G\times E}$ can be approximated as:

$$\Pr \left({S}_{G\times E} \, < \, {s}_{G\times E}|{{{\bf{R}}}},{{{\bf{E}}}}\right)\approx \Phi \left\{\omega+\frac{1}{\omega }\cdot \log \left(\frac{\nu }{\omega }\right)\right\}$$

(11)

where $\Phi (.)$ is the CDF of the standard normal distribution.

We adopt a hybrid strategy to combine normal distribution approximation and SPA. If the absolute value of the observed statistics $\left|{s}_{G\times E}\right| < r\hat{\sigma }$, where r = 2 is a pre-specified value, we use normal distribution approximation. Otherwise, the retrospective SPA approach is used to calibrate p values in tail areas. We output a two-sided p value of ${p}_{l}+{p}_{r}$, where:

$${p}_{l}=\widehat{\Pr }\left({S}_{G\times E} < -\left|{s}_{G\times E}\right|\big|{{{\bf{R}}}},{{{\bf{E}}}}\right)$$

(12)

and

$${p}_{r}=\widehat{\Pr }\left({S}_{G\times E} > \left|{s}_{G\times E}\right|\big|{{{\bf{R}}}},{{{\bf{E}}}}\right)$$

(13)

are left-tailed and right-tailed p values, respectively, and $\widehat{\Pr }\left(.\right)$ denotes the probability estimated from the normal distribution approximation or SPA. The hybrid strategy can reduce computation time while avoiding false positive discoveries. For further details, please refer to Supplementary Note.

SPAGxE+ employs sparse GRM to account for sample relatedness

SPAGxE_CCT assumes that genotypes for different individuals distributed independently, which could be violated if the study cohort includes related samples. To address this issue, we propose SPAGxE+ following a similar idea from ROADTRIP⁹³, MASTOR⁴⁰, and L-GATOR⁹⁴ to incorporate a GRM Φ to characterize the correlation between the genotypes of related samples.

Test statistics adjusted for sample relatedness

Suppose that the study cohort includes n genetically related individuals. We let Φ denote an $n\times n$ genetic relationship matrix (GRM) to characterize sample relatedness. We update test statistics ${S}_{G\times E}$ to:

$${S}_{G\times E\left({GRM}\right)}={\sum }_{i=1}^{n}\left({G}_{i}{E}_{i}-{\lambda }_{{GRM}}{G}_{i}\right){R}_{i}$$

(14)

where ${\lambda }_{{GRM}}={{{{\bf{R}}}}}^{{{{\boldsymbol{T}}}}}{{{\mathbf{\Phi }}}}{{{{\bf{R}}}}}_{{{{\bf{E}}}}}/{{{{\bf{R}}}}}^{{{{\rm{T}}}}}{{{\mathbf{\Phi }}}}{{{\bf{R}}}}$, ${{{{\bf{R}}}}}_{{{{\bf{E}}}}}={\left({R}_{1}{E}_{1},\ldots,{R}_{n}{E}_{n}\right)}^{{{{\rm{T}}}}}$. More details about the GRM estimation can be found in Supplementary Note. SPAGxE+ follows a similar framework as SPAGxE_CCT to test for marginal genetic effect based on ${S}_{G}^{c}$ and to test for marginal G×E effects based on ${S}_{G\times E({GRM})}$ and ${\widetilde{S}}_{G\times E}$. Suppose that ${S}_{G}^{c}$ follows a normal distribution with a mean of 0 and a variance of $\widehat{{Var}}\left({S}_{G}^{c}|{{{\bf{R}}}}\right)=2\hat{q}\left(1-\hat{q}\right){{{{\bf{R}}}}}^{{{{\rm{T}}}}}{{{\mathbf{\Phi }}}}{{{\bf{R}}}}$ under the null hypothesis, we calculate a two-sided p value to characterize the marginal genetic effect. Note that when marginal genetic effect p value is smaller than $\epsilon$, SPAGxE+ only uses ${\widetilde{S}}_{G\times E}$ to test for marginal G×E effects, since it is computationally intensive to perform Wald test via fitting a mixed-effect model.

Normal distribution approximation and SPA adjusted for sample relatedness

Suppose that genotype ${G}_{i}$ follows a binomial distribution Binom$\left(2,q\right),$ the mean and variance of ${S}_{G\times E({GRM})}$ are 0 and ${\hat{\sigma }}_{{GRM}}^{2}=2q\left(1-q\right)\cdot ({{{{\bf{R}}}}}_{{{{\bf{E}}}}}^{{{{\rm{T}}}}}-{\lambda }_{{GRM}}{{{{\bf{R}}}}}^{{{{\rm{T}}}}}){{{\mathbf{\Phi }}}}({{{{\bf{R}}}}}_{{{{\bf{E}}}}}-{\lambda }_{{GRM}}{{{\bf{R}}}})$, respectively. SPAGxE+ follows previous strategies to calculate p values following a hybrid strategy combining normal distribution approximation and SPA.

We follow the SPA as in SPAGxE_CCT to approximate the null distribution of ${S}_{G\times E({GRM})}$ and ${\widetilde{S}}_{G\times E}$, respectively. For ${S}_{G\times E({GRM})}$, instead of the observed statistics ${s}_{G\times E({GRM})}$, we calculate an adjusted test statistics ${s}_{G\times E({adj})}=({\hat{\sigma }}_{{UR}}/{\hat{\sigma }}_{{GRM}})\cdot {s}_{G\times E({GRM})}$, where ${\hat{\sigma }}_{{UR}}^{2}=2\hat{q}(1-\hat{q})\cdot {{\sum }_{i=1}^{n}\left({R}_{i}{E}_{i}-{\lambda }_{{GRM}}{R}_{i}\right)}^{2}$. Then, the adjusted statistics ${s}_{G\times E({adj})}$ was used as in SPAGxE_CCT. For ${\widetilde{S}}_{G\times E}$, a similar adjustment was conducted to incorporate variance ratio in SPA. For further details, please refer to Supplementary Note.

SPAGxEmix_CCT uses individual-level allele frequency to adjust for population admixture

SPAGxE_CCT relies on an assumption that genotypes for different individuals follow an identical binomial distribution Binom (2,q). The assumption is usually valid in a homogeneous population. However, if the study cohort consists of individuals from multiple ancestries, this assumption could be violated. To address this issue, we propose SPAGxEmix_CCT in which genotypes for different individuals follow binomial distributions but the corresponding allele frequencies ${\hat{q}}_{1},{\hat{q}}_{2},\cdots {\hat{q}}_{n}$ could be different. We follow the idea from Conomos et al.⁹⁵ to estimate individual-level allele frequency using SNP-derived PCs and raw genotypes. More details can be found in Supplementary Note.

Test statistics adjusted for population admixture

For a genetic variant, given $\hat{{{{\bf{q}}}}}=({\hat{q}}_{1},{\hat{q}}_{2},\cdots {\hat{q}}_{n})$ where ${\hat{q}}_{i}$ is the estimated allele frequency for individual i, we update test statistics ${S}_{G\times E}$ to ${S}_{G\times E({mix})}={\sum }_{i=1}^{n}({G}_{i}{E}_{i}-{\lambda }_{{mix}}{G}_{i}){R}_{i}$, where ${\lambda }_{{mix}}={\sum }_{i=1}^{n}2{\hat{q}}_{i}(1-{\hat{q}}_{i})({E}_{i}{R}_{i}^{2})/{\sum }_{i=1}^{n}{2{\hat{q}}_{i}(1-{\hat{q}}_{i})R}_{i}^{2}$. SPAGxEmix_CCT follows the same analysis framework as SPAGxE_CCT to test for marginal genetic effect based on ${S}_{G}^{c}$ and to test for marginal G×E effects based on ${S}_{G\times E({mix})}$, ${\widetilde{S}}_{G\times E}$ and Wald test. Note that test statistic ${S}_{G}^{c}$ follows a normal distribution with a mean of ${\hat{E}}_{c}({S}_{G}^{c}|{{{\bf{R}}}})={\sum }_{i=1}^{n}2{\hat{q}}_{i}{R}_{i}$ and a variance of ${\widehat{{Var}}}_{c}\left({S}_{G}^{c}|{{{\bf{R}}}}\right)={\sum }_{i=1}^{n}{2{\hat{q}}_{i}(1-{\hat{q}}_{i})R}_{i}^{2}$.

Normal distribution approximation and SPA

Suppose that genotype ${G}_{i}$ follows a binomial distribution Binom$\left(2,{q}_{i}\right),i\le n,$ the mean and variance of ${S}_{G\times E({mix})}$ are:

$${\hat{\mu }}_{{mix}}={\sum }_{i=1}^{n}2{\hat{q}}_{i}\left({E}_{i}{R}_{i}-{\lambda }_{{mix}}{R}_{i}\right)$$

(15)

and

$${\hat{\sigma }}_{{mix}}^{2}={\sum }_{i=1}^{n}2{\hat{q}}_{i}\left(1-{\hat{q}}_{i}\right){\left({E}_{i}{R}_{i}-{\lambda }_{{mix}}{R}_{i}\right)}^{2}$$

(16)

respectively. The estimated MGF and CGF of ${G}_{i}$ are:

$${\widehat{M}}_{{G}_{i}}\left(t\right)={\left(1-{\hat{q}}_{i}+{\hat{q}}_{i}{e}^{t}\right)}^{2}$$

(17)

and

$${\hat{K}}_{{G}_{i}}\left(t\right)={{\mathrm{ln}}}{\widehat{M}}_{{G}_{i}}\left(t\right)$$

(18)

respectively. Conditional on $\left({{{\bf{R}}}},{{{\bf{E}}}},{\lambda }_{{mix}}\right)$, the estimated CGF of ${S}_{G\times E({mix})}$ under the null hypothesis is:

$${\hat{H}}_{{mix}}\left(t\right)={\sum }_{i=1}^{n}{\hat{K}}_{{G}_{i}}\left(\left({R}_{i}{E}_{i}-{\lambda }_{{mix}}{R}_{i}\right)t\right)={\sum }_{i=1}^{n}{{\mathrm{ln}}}{\widehat{M}}_{{G}_{i}}\left(\left({R}_{i}{E}_{i}-{\lambda }_{{mix}}{R}_{i}\right)t\right)$$

(19)

For observed statistics ${s}_{G\times E({mix})}$, SPAGxEmix_CCT follows previous strategies to calculate p values following a hybrid strategy combining normal distribution approximation and SPA. For further details, please refer to Supplementary Note.

SPAGxEmix_CCT-local tests for G×E allowing for ancestry-specific effects

Tractor proposed a framework in which local ancestry is used to enhance power of GWAS in an admixed population⁸⁴. Potential ancestry-specific patterns of G×E and the necessity to account for local ancestry in G×E analyses have been demonstrated in previous researches¹⁰. In this section, we extend SPAGxEmix_CCT to SPAGxEmix_CCT-local to incorporate local ancestry into analysis.

Ancestry-specific test statistics for G×E allowing for ancestry-specific effects

Suppose that the study cohort consists of n individuals from an admixed population composed of K ancestries, we let ${{{\bf{G}}}}={\left({G}_{1},\ldots,{G}_{n}\right)}^{{{{\rm{T}}}}}$ denote the genotype vector of a genetic variant and ${{{{\bf{G}}}}}^{\left(k\right)}={({G}_{1}^{\left(k\right)},\ldots,{G}_{n}^{\left(k\right)})}^{{{{\rm{T}}}}},k\le K$, denote the genotypes from the k-th ancestry, i.e., the vector of the number of copies coming from the k-th ancestry. SPAGxEmix_CCT-local is designed to test for G×E allowing ancestry-specific effects, i.e., to associate the interaction of ancestry-specific genotypes ${{{{\bf{G}}}}}^{\left(k\right)}$ and environmental factor E to the trait of interest. The latent linear predictor:

$${\eta }_{i}={{{{\bf{X}}}}}_{i}^{{{{\rm{T}}}}}{{{{\boldsymbol{\beta }}}}}_{{{{\bf{X}}}}}+{E}_{i}{\beta }_{E}+{\sum }_{k=1}^{K}\left({G}_{i}^{\left(k\right)}{\beta }_{G}^{\left(k\right)}+{E}_{i}{G}_{i}^{\left(k\right)}{\beta }_{G\times E}^{\left(k\right)}\right)$$

(20)

can well characterize the ancestry-specific effects to the phenotype, where coefficients ${\beta }_{G}^{\left(k\right)}$ and ${\beta }_{G\times E}^{\left(k\right)}$ are the ancestry-specific marginal genetic effect and ancestry-specific marginal G×E effect of the k-th ancestry, respectively. Testing for ancestry-specific G×E effect of the k-th ancestry is equal to testing for a null hypothesis ${{{{\rm{H}}}}}_{0}^{\left(k\right)}:{\beta }_{G\times E}^{\left(k\right)}=0$.

For individual $i,i\le n$, we let ${h}_{i}^{\left(k\right)}$ denote the number of haplotypes, i.e., local ancestry counts, of the k-th ancestry at one locus, and let ${{{{{\bf{h}}}}}^{\left(k\right)}=({h}_{1}^{\left(k\right)},\ldots,{h}_{n}^{\left(k\right)})}^{T}$ denote the corresponding vector for all individuals. Suppose that the ancestry-specific allele frequencies ${q}^{\left(1\right)},\ldots,{q}^{\left(K\right)}$ are available. We assume that ancestry-specific genotype ${G}_{i}^{\left(k\right)},\,i\le n$ follow a binomial distribution Binom$({h}_{i}^{\left(k\right)},{q}^{\left(k\right)})$ in which ${h}_{i}^{\left(k\right)}=0,\,1,$ or 2. Similar to SPAGxEmix_CCT, SPAGxEmix_CCT-local calculates ancestry-specific score statistics ${S}_{G}^{c\left(k\right)}={\sum }_{i=1}^{n}{R}_{i}{G}_{i}^{\left(k\right)}$ and then tests for ancestry-specific marginal genetic effects. The mean and variance of ${S}_{G}^{c\left(k\right)}$ under the hypothesis ${{{{\rm{H}}}}}_{{{{\rm{c}}}}}^{\left(k\right)}:{\beta }_{G\times E}^{\left(k\right)}={\beta }_{G}^{\left(k\right)}=0$ are:

$${E}_{c}\left({S}_{G}^{c\left(k\right)}|{{{\bf{R}}}}\right)={q}^{\left(k\right)}\cdot {\sum }_{i=1}^{n}{R}_{i}\cdot {h}_{i}^{\left(k\right)}$$

(21)

and

$${Va}{r}_{{{{\rm{c}}}}}\left({S}_{G}^{c\left(k\right)}|{{{\bf{R}}}}\right)={\sum }_{i=1}^{n}{R}_{i}^{2}\cdot {h}_{i}^{\left(k\right)}\cdot {q}^{\left(k\right)}\left(1-{q}^{\left(k\right)}\right)$$

(22)

respectively. For SPAGxEmix_CCT-local, the ancestry-specific allele frequency ${q}^{\left(k\right)}$ is estimated by using ${\hat{q}}^{\left(k\right)}={\sum }_{i=1}^{n}{G}_{i}^{\left(k\right)}/{\sum }_{i=1}^{n}{h}_{i}^{\left(k\right)}$. If the p value from ${S}_{G}^{c\left(k\right)}$ is greater than a pre-selected positive cutoff $\epsilon$, we use statistic:

$${S}_{G\times E}^{\left(k\right)}={S}_{G\times E}^{c\left(k\right)}-{\lambda }^{\left(k\right)}{S}_{G}^{c\left(k\right)}={\sum }_{i=1}^{n}\left({G}_{i}^{\left(k\right)}{E}_{i}-{\lambda }^{\left(k\right)}{G}_{i}\right){R}_{i}$$

(23)

to test for marginal G×E effect corresponding to k-th ancestry, where ${\lambda }^{(k)}={\sum }s_{i=1}^{n}({h}_{i}^{(k)}{E}_{i}{R}_{i}^{2})/{\sum }_{i=1}^{n}{h}_{i}^{(k)}{R}_{i}^{2}$. Otherwise, we define an ancestry-specific genotype-adjusted residual vector:

$${\widetilde{{{{\bf{R}}}}}}^{\left(k\right)}=\left({\widetilde{R}}_{1}^{\left(k\right)},\ldots,{\widetilde{R}}_{n}^{\left(k\right)}\right)=\left({{{{\bf{I}}}}}_{n}-{{{{\bf{W}}}}}^{\left(k\right)}{\left({{{{{\bf{W}}}}}^{\left(k\right)}}^{{{{\rm{T}}}}}{{{{\bf{W}}}}}^{\left(k\right)}\right)}^{-1}{{{{{\bf{W}}}}}^{\left(k\right)}}^{{{{\rm{T}}}}}\right){{{\bf{R}}}}$$

(24)

and use ${\widetilde{S}}_{G\times E}^{\left(k\right)}={\sum }_{i=1}^{n}{G}_{i}^{\left(k\right)}{E}_{i}{\widetilde{R}}_{i}^{\left(k\right)}$ to test for the marginal G×E effect, where ${{{{\bf{W}}}}}^{\left(k\right)}=({{{{\mathbf{1}}}}}_{{{{\mathbf{ n}}}}},{{{{\bf{G}}}}}^{(k)})$. Then, SPAGxEmix_CCT-local uses CCT to combine two p values from ${\widetilde{S}}_{G\times E}^{(k)}$ and Wald test. For ${S}_{G\times E}^{\left(k\right)}$ and ${\widetilde{S}}_{G\times E}^{\left(k\right)}$, the hybrid strategy to combine normal distribution approximation and SPA to calculate p values is the same as in previous sections. Further details can be found in Supplementary Note.

Combining p values of SPAGxEmix_CCT and SPAGxEmix_CCT-local to maximize powers

Suppose that the admixed population is composed of K ancestries. SPAGxEmix_CCT-local outputs K ancestry-specific p values, and the original SPAGxEmix_CCT outputs one p value assuming that the G×E effects are the same for all ancestries. We proposed SPAGxEmix_{CCT-local-global} in which Cauchy combination test is used to combine the K + 1 p values. Benefiting from the advantage of Cauchy combination test, SPAGxEmix_{CCT-local-global} can control type I error rates while remaining powerful regardless of whether ancestry-specific G×E effect sizes are homogeneous or heterogeneous.

The framework can be applied to other types of traits

The above proposed analysis framework only requires score statistics with a format of:

$${S}_{G\times E}^{c}={\sum }_{i=1}^{n}{G}_{i}{E}_{i}{R}_{i},\,{S}_{G}^{c}={\sum }_{i=1}^{n}{G}_{i}{R}_{i}$$

(25)

to test for marginal G×E effect and marginal genetic effect, respectively. For other types of traits and regression models, SPAGxE_CCT and SPAGxEmix_CCT are also applicable. The below gives two examples.

Binary traits and logistic model

For individual i, we let ${Y}_{i}$ denote a binary trait (0 or 1, e.g., disease status), ${\mu }_{i}=\Pr \left({Y}_{i}=1|{{{{\bf{X}}}}}_{i},{E}_{i},{G}_{i}\right)$ denote the probability of ${Y}_{i}=1$ conditional on ${{{{\bf{X}}}}}_{i}$, ${E}_{i}$, and ${G}_{i}$. We consider the following logistic model:

$${{{\rm{logit}}}}\left({\mu }_{i}\right)={\eta }_{i}={{{{\bf{X}}}}}_{i}^{{{{\rm{T}}}}}{{{{\boldsymbol{\beta }}}}}_{{{{\bf{X}}}}}+{E}_{i}{\beta }_{E}+{G}_{i}{\beta }_{G}+{G}_{i}{E}_{i}{\beta }_{G\times E},\,i\le n$$

(26)

where the denotations of ${{{{\bf{X}}}}}_{i}$ (including an intercept term), ${E}_{i}$, ${G}_{i}$, ${{{{\boldsymbol{\beta }}}}}_{{{{\bf{X}}}}}$, ${\beta }_{G}$, ${\beta }_{E}$, ${\beta }_{G\times E}$, and ${\eta }_{i}$ are the same as those in Cox PH model. We are interested in testing for the marginal G×E effect with a null hypothesis ${{{{\rm{H}}}}}_{0}:{\beta }_{G\times E}=0$. More details, including model fitting, theoretical derivations about the score statistics, and the model residuals ${R}_{i}$, can be found in Supplementary Note.

Ordinal traits and proportional odds logistic model

Ordinal traits are widely available in biobanks to measure human behaviors, satisfaction, and preferences. For individual $i\le n$, we let ${Y}_{i}$ = 1, 2, …, J denote the ordinal phenotype, in which J is the number of category levels. We let ${\nu }_{{ij}}=\Pr \left({Y}_{i}\le {j|}{{{{\bf{X}}}}}_{i},{E}_{i},{G}_{i}\right)$ denote a cumulative probability of ${Y}_{i}\le j$ conditional on ${{{{\bf{X}}}}}_{i}$, ${E}_{i}$, and ${G}_{i}$. We consider the proportional odds logistic regression model as below:

$${{{\rm{logit}}}}\left({\nu }_{{ij}}\right)={\varepsilon }_{j}-{\eta }_{i}={\varepsilon }_{j}-{{{{\bf{X}}}}}_{i}^{T}{{{{\boldsymbol{\beta }}}}}_{{{{\bf{X}}}}}-{E}_{i}{\beta }_{E}-{G}_{i}{\beta }_{G}-{G}_{i}{E}_{i}{\beta }_{G\times E},\,i\le n,\,j\le J$$

(27)

where the denotations of ${{{{\bf{X}}}}}_{i}$, ${E}_{i}$, ${G}_{i}$, ${{{{\boldsymbol{\beta }}}}}_{{{{\bf{X}}}}}$, ${\beta }_{G}$, ${\beta }_{E}$, ${\beta }_{G\times E}$, and ${\eta }_{i}$ are the same as those in Cox PH model. The cutpoints ${\varepsilon }_{j},j\le J$ are used to categorize the data. More details, including model fitting, theoretical derivations about the score statistics, and the model residuals ${R}_{i}$, can be found in Supplementary Note and previous work²⁵.

Data simulation

In this section, we demonstrated the simulation of genotypes, covariates, environmental factors, and time-to-event traits. The simulation of binary and ordinal traits can be seen in Supplementary Note.

For individual i, we first generated an underlying failure time ${T}_{i}^{*}$ and a censoring time ${C}_{i}$, and then calculated a time-to-event value ${T}_{i}=\min ({T}_{i}^{*},{C}_{i})$ and an indicator ${\delta }_{i}={{{\rm{I}}}}({T}_{i}^{*}\le {C}_{i})$. We simulated the censoring time ${C}_{i}$ following a Weibull distribution with a scale parameter of 0.15 and a shape parameter of 1. The underlying failure time ${T}_{i}^{*}$ was generated from a Cox PH model with a Weibull baseline hazard function as:

$${T}_{i}^{*}=\alpha \sqrt{\frac{-{{{\mathrm{ln}}}}{U}_{i}}{\exp \left({\eta }_{i}\right)}}$$

(28)

where ${U}_{i}$ was simulated following a uniform distribution U(0,1), and linear predictor ${\eta }_{i}=0.5{X}_{i1}+0.5{X}_{i2}+0.5{E}_{i}+{\beta }_{G}{G}_{i}+{\beta }_{G\times E}{G}_{i}{E}_{i}$, where a binary covariate ${X}_{i1}$ was simulated following a Bernoulli(0.5) distribution, a continuous covariate ${X}_{i2}$ was simulated following a standard normal distribution, and genotype ${G}_{i}$ was simulated following Hardy-Weinberg equilibrium, i.e., Binom(2, MAF) distribution. Parameters ${\beta }_{G}$ and ${\beta }_{G\times E}$ are to characterize marginal genetic effect and the marginal G×E effect, respectively. The scale parameter α was chosen to correspond to a given event rate, i.e., ${\sum }_{i=1}^{n}{\delta }_{i}/n$.

We considered two settings to simulate an environmental factor E_i: (1) E_i was simulated following a standard normal distribution N(0,1) to mimic a quantitative value, and (2) E_i was simulated following a Bernoulli(0.5) distribution to mimic a binary value. For time-to-event traits, we considered three event rates of 1%, 10%, and 50% to mimic extremely unbalanced, moderately unbalanced, and balanced phenotypic distribution, respectively.

In the simulation studies within a homogeneous population, we evaluated SPAGxE-based approaches including SPAGxE, SPAGxE_Wald, and SPAGxE_CCT. If the marginal genetic effect p value is greater than $\epsilon$, all the three SPAGxE-based approaches employ ${S}_{G\times E}$ as test statistics and output the same marginal G×E effect p value. However, if the p value is less than or equal to $\epsilon$, the SPAGxE-based approaches calculate p values following different strategies: SPAGxE takes ${\widetilde{S}}_{G\times E}$ as the test statistic, SPAGxE_Wald employs Wald test, and SPAGxE_CCT applies Cauchy combination test to combine the two p values from ${\widetilde{S}}_{G\times E}$ and Wald test. In addition, we also evaluated Wald test and NormGxE. Similar to SPAGxE, NormGxE also calculates p values based on ${S}_{G\times E}$ and ${\widetilde{S}}_{G\times E}$, with the exception that only normal distribution approximation is used. For binary trait analyses, we additionally evaluated SPAGE.

Type I error rates simulation

To evaluate type I error rates, we fixed sample size n = 10,000 and simulated traits under null model ${\beta }_{G\times E}=0$. We simulated genotypes and traits to assess type I error rates under the below two scenarios.

• Scenario 1. Test for variants without marginal genetic effect, that is, ${{{{\boldsymbol{\beta }}}}}_{{{{\boldsymbol{G}}}}{{{\mathbf{\times }}}}{{{\boldsymbol{E}}}}}={{{{\boldsymbol{\beta }}}}}_{{{{\boldsymbol{G}}}}}={{{\boldsymbol{0}}}}$. We considered three fixed MAFs of 0.3, 0.05, and 0.01 to mimic common, low-frequency, and rare variants. For each MAF, we simulated genotypes of 10,000 independent variants following HWE. Traits were simulated using a linear predictor ${\eta }_{i}=0.5{X}_{i1}+0.5{X}_{i2}+0.5{E}_{i}$. For each phenotypic distribution setting, we simulated 10,000 datasets of phenotypes and covariates. Thus, for each pair of MAF and phenotypic distribution setting, a total of 10⁸ tests were conducted to associate time-to-event traits to genetic variants without marginal genetic effect.

• Scenario 2. Test for variants with marginal genetic effect, that is, ${{{{\boldsymbol{\beta }}}}}_{{{{\boldsymbol{G}}}}{{{\mathbf{\times }}}}{{{\boldsymbol{E}}}}}={{{\boldsymbol{0}}}},\,{{{{\boldsymbol{\beta }}}}}_{{{{\boldsymbol{G}}}}}{{{\mathbf{\ne }}}}{{{\boldsymbol{0}}}}$. We simulated m = 1000 variants with MAFs following a uniform(0.05, 0.5) distribution. Traits were simulated using a linear predictor ${\eta }_{i}=0.5{X}_{i1}+0.5{X}_{i2}+0.5{E}_{i}+{\sum }_{k=1}^{m}{{G}_{{ki}}\beta }_{{G}_{k}}$, where ${G}_{{ki}}$ is the genotype value of the k^th variant and marginal genetic effects ${\beta }_{{G}_{k}}$ were simulated following a uniform(−0.4, 0.4) distribution. For each phenotypic distribution setting, we simulated 1000 datasets of phenotypes and covariates. Thus, 10⁶ tests were conducted for variants with marginal genetic effect.

Power simulation

We fixed sample size n = 50,000 and simulated traits under an alternative model in which linear predictor:

$${\eta }_{i}=0.5{X}_{i1}+0.5{X}_{i2}+0.5{E}_{i}+{G}_{i}{E}_{i}{\beta }_{G\times E},i \, \le \, n$$

(29)

where ${G}_{i}$ was the genotype value of a causal genetic variant. We considered three fixed MAFs of 0.3, 0.05, and 0.01 to mimic common, low-frequency, and rare variants. The settings of phenotypic distribution and environmental factor distribution were the same as in previous sections. For each parameter setting, we simulated 10⁴ datasets to evaluate empirical powers.

For time-to-event trait analysis, we considered two settings of marginal genetic effect of ${\beta }_{G}=0$ and ${\beta }_{G}\ne 0$, similar as in the previous section of type I error simulations. We treated event indicator ${\delta }_{i}$ as a binary outcome (0 or 1) and additionally evaluated the methods designed for binary trait analyses, including SPAGE, SPAGxE_CCT(CC), and SPAGxE_CCT(CC0). Both SPAGxE_CCT(CC) and SPAGxE_CCT(CC0) fit a logistic model to adjust for covariates and then pass model residuals to SPAGxE_CCT framework. When fitting a logistic model, SPAGxE_CCT(CC0) incorporates covariates of ${X}_{i1}$ and ${X}_{i2}$, and SPAGxE_CCT(CC) additionally incorporates a covariate of time-to-event ${T}_{i}$. For ordinal trait analysis, we dichotomized ordinal traits to binary traits depending on whether the individual is in level 1 or not²⁵. Then, we evaluated SPAGxE_CCT(CC0) which fits a logistic regression model with covariates of ${X}_{i1}$ and ${X}_{i2}$.

Type I error simulations in related samples

We carried out simulations to evaluate type I error rates of SPAGxE+ and SPAGxE_CCT (SAIGE) in the presence of sample relatedness for binary and time-to-event trait analysis. We simulated n = 10,000 individuals consisting of 5000 related individuals from 1250 four-member families and 5000 unrelated individuals. We considered three fixed MAFs of 0.3, 0.05, and 0.01. For each MAF, we simulated genotypes of 10⁶ independent variants following HWE. We conducted the gene-dropping simulation using these variants as the founding haplotypes, which were then passed down through the pedigrees of four-member families, as illustrated in Supplementary Fig. 59.

We simulated binary and time-to-event phenotypes using a linear predictor ${\eta }_{i}=0.5{X}_{i1}+0.5{X}_{i2}+0.5{E}_{i}+{b}_{i}$, where ${b}_{i}$ denotes random effect simulated from multivariate normal distribution $N\left(0,\tau {{{\mathbf{\phi }}}}\right)$, ${{{\mathbf{\phi }}}}$ is an $n\times n$ GRM, and $\tau$ is the additive genetic variance. We set $\tau=1$ in our simulations. The covariates ${X}_{i1}$ was simulated following a Bernoulli(0.5) distribution, ${X}_{i2}$ was simulated following a standard normal distribution, and the environmental factor ${E}_{i}$ was simulated following a standard normal distribution.

For each phenotypic distribution setting, we simulated 1000 datasets of phenotypes of related samples and then calculated the variance ratio $\rho={\hat{\sigma }}_{{GRM}}^{2}/{\hat{\sigma }}_{{UR}}^{2}$ for each phenotype. We analyzed the phenotypes corresponding to the variance ratio distribution quantiles 0, 0.5, and 1. Thus, for each setting of quantile, MAF, and phenotypic distribution, a total of 10⁶ tests were conducted.

Type I error simulation in an admixed population

For individual $i\le n$, we let ${{{{\bf{a}}}}}_{i}={\left({a}_{i}^{{EUR}},{a}_{i}^{{EAS}}\right)}^{T}$ denote an ancestry vector, where $1\ge {a}_{i}^{{EUR}}\ge 0$ and $1\ge {a}_{i}^{{EAS}}\ge 0$ are to represent ancestry proportions of EUR and EAS, respectively, and ${a}_{i}^{{EUR}}+{a}_{i}^{{EAS}}=1$. We assumed that the first $n/2={{\mathrm{5,000}}}$ individuals were from a EUR-dominant community with an ancestry vector ${{{{\bf{a}}}}}_{i}$ following a Dirichlet(9, 1) distribution, and the remaining 5000 individuals were from an EAS-dominant community with an ancestry vector ${{{{\bf{a}}}}}_{i}$ following a Dirichlet(1, 9) distribution^{95,96,97,98,99}. The distribution of ${{{{\bf{a}}}}}_{i},i\le n$ can be found in Supplementary Fig. 60.

In this paper, we used the real MAF values from 1000 Genome Projects to mimic the allele frequency diversity between EUR and EAS⁸³. For a genetic variant, we let ${q}^{{EUR}}$ and ${q}^{{EAS}}$ denote the MAFs in EUR and EAS, respectively. Depending on the difference of MAFs corresponding to the two populations, i.e., Diff_MAF = ${q}^{{EUR}}-{q}^{{EAS}}$, we categorized variants into five groups: Diff_MAF << 0, Diff_MAF < 0, Diff_MAF ~ 0, Diff_MAF > 0, and Diff_MAF >> 0 based on cutoffs of −0.05, −0.01, 0.01, and 0.05. Depending on the minimal MAF value, i.e., $\min \left({q}^{{EUR}},{q}^{{EAS}}\right)$, we categorized variants into three groups of minMAF_low, minMAF_mod, minMAF_high based on two cutoffs of 0.01 and 0.05. Thus, all variants were categorized into 15 (5 × 3) groups. In each group, we randomly sampled 1000 pairs of $\left({q}^{{EUR}},{q}^{{EAS}}\right)$ and simulated 1000 SNPs. For each variant, ${q}_{i}={a}_{i}^{{EUR}}{q}^{{EUR}}+{a}_{i}^{{EAS}}{q}^{{EAS}}$ is the allele frequency of individual i and the genotype ${G}_{i}$ follows a Binom(2, ${q}_{i}$) distribution. In addition, we simulated 100,000 common SNPs with ${q}^{{EUR}}+{q}^{{EAS}} > 0.1$ to calculate SNP-derived PCs (Supplementary Fig. 60).

To simulate time-to-event traits in an admixed population, we simulated a linear predictor ${\eta }_{i}={\beta }_{1}{X}_{i1}+0.5{X}_{i2}+0.5{X}_{i3}+0.5{E}_{i}+ {\beta }_{G}{G}_{i}+{\beta }_{G\times E}{G}_{i}{E}_{i}$. Covariate ${X}_{i1}={a}_{i}^{{EAS}}=1-{a}_{i}^{{EUR}}$ was the proportion of EAS ancestry, ${X}_{i2}$ was simulated following a Bernoulli(0.5) distribution, ${X}_{i3}$ was simulated following a standard normal distribution, and environmental factor ${E}_{i}$ was simulated following a standard normal distribution. We selected a scale parameter $\lambda$ and a coefficient ${\beta }_{1}$ to obtain desired event rates ${{{{\rm{ER}}}}}_{{EUR}}$ and ${{{{\rm{ER}}}}}_{{EAS}}$ in EUR and EAS populations. Here, ${{{{\rm{ER}}}}}_{{EUR}}$ and ${{{{\rm{ER}}}}}_{{EAS}}$ are the expected event rates for a pure EUR population (i.e., ${X}_{i1}=0,i\le n$) and pure EAS population (i.e., ${X}_{i1}=1,i\le n$), respectively. Then, we followed the same procedures in previous homogeneous population simulations to simulate a censoring time ${C}_{i}$ and an underlying failure time ${T}_{i}^{*}=\lambda \sqrt{-{{{\mathrm{ln}}}}{U}_{i}/\exp \left({\eta }_{i}\right)}$.

To assess type I error rates, we simulated traits under two scenarios, either of which followed the null hypothesis of no G×E effects and genetic effects (${{{\rm{i}}}}.{{{\rm{e}}}}.{\beta }_{G\times E}={\beta }_{G}=0$).

• Scenario 1. The event rates in EUR and EAS were the same, that is, ${{{{\bf{ER}}}}}_{{{{\boldsymbol{EUR}}}}}={{{{\bf{ER}}}}}_{{{{\boldsymbol{EAS}}}}}$. We consider three events rates including 0.01 (low event rate, ER_low), 0.05 (moderate event rate, ER_mod), and 0.2 (high event rate, ER_high).

• Scenario 2. The event rates in EUR were higher than those in EAS, that is, ${{{{\bf{ER}}}}}_{{{{\boldsymbol{EUR}}}}}{{{\boldsymbol{ > }}}}{{{{\bf{ER}}}}}_{{{{\boldsymbol{EAS}}}}}$. We considered three pairs of event rates $\left({{{{\rm{ER}}}}}_{{EUR}},{{{{\rm{ER}}}}}_{{EAS}}\right)$ = (0.1, 0.01) (low event rate, ER_low), (0.3, 0.05) (moderate event rate, ER_mod), and (0.5, 0.2) (high event rate, ER_high).

We did not consider a scenario in which the event rates in EAS were higher than those in EUR since it is exactly the opposite direction of scenario 2. In either scenario, 10,000 datasets of phenotypes and covariates were simulated, and thus a total of 10⁷ tests were conducted for each pair of MAF group and event rate.

Null model fitting incorporates covariates ${{{{\bf{X}}}}}_{{{{\boldsymbol{2}}}}}={\left({X}_{12},{X}_{22},\cdots,{X}_{n2}\right)}^{{{{\rm{T}}}}},{{{{\bf{X}}}}}_{{{{\bf{3}}}}}={\left({X}_{13},{X}_{23},\cdots,{X}_{n3}\right)}^{{{{\rm{T}}}}},{{{\bf{E}}}}={\left({E}_{1},{E}_{2},\cdots,{E}_{n}\right)}^{{{{\rm{T}}}}}$, and the top 4 PCs derived from genotype data. In addition to SPAGxEmix_CCT, we also evaluated NormGxEmix and SPAGE. For NormGxEmix, p values of all variants are calculated using only normal distribution approximation without SPA. For SPAGE, we treated event indicator ${\delta }_{i}$ as a binary trait.

Type I error simulation under heterogeneity of environmental factors

To evaluate the impact of environmental factors heterogeneity on type I error rates, we simulated a scenario in which the distribution of environmental factors varies between EUR-dominant and EAS-dominant communities. The environmental factor ${E}_{i}$ was simulated following a standard normal distribution in the EUR-dominant community and a normal distribution N (1,10) in the EAS-dominant community. We simulated traits under scenario 2, that is, the event rates in EUR were higher than those in EAS. We simulated 1000 datasets of phenotypes, environmental factors, and covariates, and thus a total of 10⁶ tests were conducted for each pair of MAF group and event rate. Although the environmental factors heterogeneity seems too extreme to be available in real data analyses, it can demonstrate the advantage of SPAGxEmix_CCT in terms of the robustness and accuracy.

Power simulation in cross-ancestry analyses

We simulated two discrete populations of EUR and EAS with a total sample size n = 20,000 (10,000 individuals were from a EUR population, and the remaining 10,000 individuals were from EAS population). We also used the real MAF values from 1000 Genome Projects to mimic the allele frequency diversity between EUR and EAS. We simulate time-to-event phenotypes using a linear predictor ${\eta }_{i}={\beta }_{1}{X}_{i1}+0.5{X}_{i2}+0.5{X}_{i3}+0.5{E}_{i}+{\beta }_{G\times E}{G}_{i}{E}_{i}$. The settings of event rates and processes of categorizing variants, generating genotypes and SNP-derived PCs, and covariates were the same as in previous section of type I error simulation in an admixed population. We simulated ${\beta }_{G\times E}=-2{\log }_{10}\widehat{{{{\rm{MAF}}}}}$ where $\widehat{{{{\rm{MAF}}}}}=\frac{1}{2n}{\sum }_{i=1}^{n}{G}_{i}$. Null model fitting incorporates covariates ${{{{\bf{X}}}}}_{{{{\bf{2}}}}}={\left({X}_{12},{X}_{22},\cdots,{X}_{n2}\right)}^{{{{\rm{T}}}}},{{{{\bf{X}}}}}_{{{{\bf{3}}}}}= {\left({X}_{13},{X}_{23},\cdots,{X}_{n3}\right)}^{{{{\rm{T}}}}},{{{\bf{E}}}}={\left({E}_{1},{E}_{2},\cdots,{E}_{n}\right)}^{{{{\rm{T}}}}}$, and the top 4 PCs (see Supplementary Fig. 61) derived from genotype data. In addition to SPAGxEmix_CCT, we also evaluated SPAGxEmix_CCT (PCxE), SPAGxE_CCT (EUR), SPAGxE_CCT (EAS), and SPAGxE_CCT (meta). SPAGxEmix_CCT (PCxE) denotes SPAGxEmix_CCT method fitting null model including the interaction term of PCs-by-E as covariates. SPAGxE_CCT (EUR), SPAGxE_CCT (EAS), and SPAGxE_CCT (meta) denote SPAGxE_CCT method analyzing 10,000 individuals from EUR population, 10,000 individuals from EAS population, and cross-ancestry meta-analysis based on SPAGxE_CCT (EUR) and SPAGxE_CCT (EAS), respectively.

Simulation studies considering ancestry-specific marginal G×E effect sizes

To evaluate the performance of SPAGxEmix_CCT-local and SPAGxEmix_{CCT-local-global}, we simulated a two-way admixed population with sample size n = 10,000, including ancestry-specific genotypes, local ancestry counts, genotype-derived PCs, and phenotypes. We considered extensive scenarios of ancestry-specific G×E effect sizes and MAFs.

We followed procedure as in Mester et al.⁴¹ to simulate genotypes. First, we generated an individual-level global ancestry proportion of ancestry 2 (denoted as ${d}_{i},i\le n$) from a normal distribution $N\left(\theta,{\sigma }^{2}\right)$ for each individual, in which θ is the expected global ancestry proportion and σ is the corresponding standard deviation. We let $\sigma=0.125$ and coerced ${d}_{i}$ between [0,1]. For individual $i,i\le n$, we simulated local ancestry count ${h}_{i}^{\left(1\right)}$ and ${h}_{i}^{\left(2\right)}$, in which ${h}_{i}^{\left(2\right)}$ follows a binomial distribution ${{{\rm{Binom}}}}\left({d}_{i},2\right)$ and ${h}_{i}^{\left(1\right)}=2-{h}_{i}^{\left(2\right)}$. Then, we simulated ancestry-specific genotype ${G}_{i}^{\left(k\right)}$ following a binomial distribution ${{{\rm{Binom}}}}({h}_{i}^{\left(k\right)},{q}^{\left(k\right)})$, where ${q}^{\left(k\right)}$ is the allele frequency corresponding to the ancestry k. Genotype ${G}_{i}={G}_{i}^{\left(1\right)}+{G}_{i}^{\left(2\right)}$. In simulation studies, we considered two fixed MAFs of 0.01 and 0.1 in ancestry 1 and four fixed MAFs of 0.01, 0.05, 0.1, and 0.3 in ancestry 2. A total of 100,000 common SNPs were simulated to calculate SNP-derived PCs. Supplementary Fig. 62 showed the global ancestry distribution and the top PCs and for the 10,000 two-way admixed individuals.

Type I error simulations

We simulated binary and quantitative traits following a logistic regression model and a linear regression model as below:

$${{{\rm{logit}}}}\left({\mu }_{i}\right)={\beta }_{0}+0.5{Z}_{i1}+0.5{Z}_{i2},\,+0.5{E}_{i},i \, \le \, n$$

(30)

$${Y}_{i}=0.5{Z}_{i1}+0.5{Z}_{i2}+0.5{E}_{i}+{\varepsilon }_{i},\,i \, \le \, n$$

(31)

where covariates ${Z}_{i1}$ and ${Z}_{i2}$ were simulated with a standard normal distribution and a Bernoulli(0.5) distribution, environmental factor ${E}_{i}$ was simulated a standard normal distribution, ${\mu }_{i}$ is the probability of being a case for a binary trait, and ${Y}_{i}$ is a quantitative trait. For a binary trait, the intercept ${\beta }_{0}$ was determined to correspond to a certain disease prevalence. We considered disease prevalence of 0.01 and 0.2. For a quantitative trait, random term ${\varepsilon }_{i}$ was simulated following a standard normal distribution. We simulated 100 datasets of phenotypes and covariates for each phenotypic distribution and 10,000 SNPs for each setting of MAF, and thus a total of 10⁶ tests were conducted in each scenario.

Power simulations

We simulated binary and quantitative traits under an alternative hypothesis to evaluate powers. For both binary and quantitative traits, we simulated phenotypes under an alternative model by using the linear predictor:

$${\eta }_{i}={\beta }_{0}+0.5{Z}_{i1}+0.5{Z}_{i2}+0.5{E}_{i}+{\sum }_{j=1}^{10}\left[{\beta }_{G}^{\left(1\right)}{G}_{i,j}^{\left(1\right)}+{\beta }_{G}^{\left(2\right)}{G}_{i,j}^{\left(2\right)}\right]+{E}_{i}{\sum }_{j=1}^{10}\left[{\beta }_{G\times E}^{\left(1\right)}{G}_{i,j}^{\left(1\right)}+{\beta }_{G\times E}^{\left(2\right)}{G}_{i,j}^{\left(2\right)}\right]$$

(32)

where ${Z}_{i1}$, ${Z}_{i2}$, and ${E}_{i}$ were simulated following the same distribution as in type I error simulations, ${G}_{i,j}^{\left(1\right)}$ and ${G}_{i,j}^{\left(2\right)}$ were the ancestry-specific genotype of individual i in SNP j from ancestry 1 and 2, respectively, and ${\beta }_{G\times E}^{\left(1\right)}$ and ${\beta }_{G\times E}^{\left(2\right)}$ were corresponding ancestry-specific marginal G×E effect sizes. For binary traits, we fixed disease prevalence at 0.2. For quantitative traits, we set ${\beta }_{0}=0$.

We considered two scenarios including homogeneity and heterogeneity of marginal genetic effect sizes and G×E effect sizes for ancestries 1 and 2. For heterogeneous marginal G×E effect sizes, we fixed ${\beta }_{G\times E}^{\left(1\right)}$ and increased ${\beta }_{G\times E}^{\left(2\right)}$ from 0. For both homogeneous and heterogeneous marginal G×E effect sizes, we consider three pairs of marginal genetic effect sizes of (0, 0), (0.1, 0.1), and (0.2, 0.1) in ancestries 1 and 2, respectively. We simulated 100 datasets of phenotypes and covariates for each scenario, and thus a total of 1000 tests were conducted to evaluate powers. We calculated empirical powers at a genome-wide significance level 5 × 10⁻⁸.

Association analysis of SPAGxEmix_CCT-local in simulation studies

SPAGxEmix_CCT-local fitted a null model with covariates of ${Z}_{i1}$, ${Z}_{i2}$, ${E}_{i}$, and top 4 SNP-derived PCs. Regular linear model and logistic model were used to fit quantitative and binary traits, respectively. SPAGxEmix_CCT-local returned two p values corresponding to ancestry-specific marginal G×E effect sizes ${\beta }_{G\times E}^{\left(1\right)}$ and ${\beta }_{G\times E}^{\left(2\right)}$. SPAGxEmix_{CCT-local-global} calculated one p value by combining the two p values outputted by SPAGxEmix_CCT-local and one p value outputted by SPAGxEmix_CCT.

Application to UK Biobank data

To assess the performance in a real-data application, we applied the proposed approaches to conduct genome-wide gene-environmental interaction analyses of time-to-event traits in UK Biobank. Environmental factors and traits were defined based on UK Biobank field ID (FID) and PheWAS codes (PheCodes), respectively. The analyses of White British participants (sample size = 281,299) comprised 8 pairs of environmental factors and time-to-event traits, including two environmental factors: smoking status (FID: 20116) and genetic sex (FID: 22001), along with four time-to-event traits: cardiac dysrhythmias (CDR), pulmonary heart disease (PHD), chronic airway obstruction (CAO), and colorectal cancer. Smoking status was encoded into variables of 0, 1, and 2, representing never, former, and current smoker, respectively. Genetic sex was encoded into categorical variables of 0 and 1, representing male and female, respectively. Further detailed summary information about these time-to-event traits was provided in the Supplementary Table 9.

UK Biobank contains 338,044 unrelated individuals with in-patient diagnosis data, of which 281,299 (83.2%) are White British participants and the remaining participants (16.8%) are from other ancestries including African, Asian, and other ethnic groups (field ID: 21000). To construct time-to-event traits, we leveraged the PheWAS code system based on the International Statistical Classification of Diseases (ICD) codes version 9 and 10. If at least one in-patient diagnosis was observed, we designated an event indicator ${\delta }_{i}=1$ and let time-to-event ${T}_{i}$ be the age at the initial in-patient diagnosis date. For individuals without related in-patient diagnosis, we set ${\delta }_{i}=0$ and let time-to-event ${T}_{i}$ be the age at the right-censoring date or the date of being lost to follow-up. Furthermore, the observed survival time was left truncated at the in-patient data collection date¹⁵.

To demonstrate the superiority of time-to-event trait over binary trait (i.e., case or control), in real data analysis, we conducted additional G×E analyses using SPAGxE_CCT(CC0) and SPAGE in which event indicator ${\delta }_{i}$ was treated as a binary outcome. To highlight the importance of ancestry diversities in genome-wide G×E analyses and the superiority of SPAGxEmix_CCT over SPAGxE_CCT in real data analysis, we additionally applied SPAGxEmix_CCT to analyze time-to-event traits in which 338,044 unrelated individuals from multiple ancestries were included.

For each trait, top ten principal components (PCs), genetic sex, age, and the relevant environmental factor were incorporated as covariates to fit null models. Markers imputed by the Haplotype Reference Consortium (HRC) panel with a minor allele counts (MAC) > 20 and imputation INFO score > 0.6 were used in the analysis.

Comparison of computation time in analyzing large-scale biobank data

To assess computation time in analyzing a large-scale biobank data, we selected smoking status × PHD and genetic sex × CDR in UK Biobank as two examples (sample size = 281,299) corresponding to low and high event rates, respectively. All analyses were conduct on a CPU model of Intel(R) Xeon(R) Gold 6342 CPU @ 2.80 GHz. In addition to SPAGxE_CCT, we also evaluated an R package gwasurvivr in which Wald test was used to calibrate p values for G×E analyses. As the package gwasurvivr does not support BGEN format, we converted the genotype data to plink format. It is expected that reading text-based formats (such as VCF format) is slower than reading binary format (such as plink and BGEN formats). To mimic a genome-wide analysis, we analyzed 10,000 genetic variants randomly selected in chromosome 1, recorded the computation time, and then projected it to all chromosomes including 18,583,853 genetic variants.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.