Cu supraparticles with enhanced mass transfer and abundant C-C coupling sites achieving ampere-level CO₂-to-C₂₊ electrosynthesis

Abstract

The efficient electrochemical CO₂ reduction to C₂₊ products at high current densities remains a significant challenge. Here we show inherently hydrophobic and hierarchically porous Cu supraparticles comprising sub-10 nm Cu constituent particles for ampere-level CO₂-to-C₂₊ electrosynthesis. These supraparticles feature abundant grain boundaries for high C₂₊ selectivity, coupled with interconnected mesopores and interparticle macropore cavities to enhance the accessibility of the active sites and mass transfer, breaking the trade-off between activity and mass transfer in Cu-based catalysts. Moreover, the intrinsic hydrophobicity of the supraparticles mitigates the water-flooding issue of catalytic layer in flow cells, improving the stability at high current densities. Consequently, the Cu supraparticles achieve ampere-level CO₂ electrolysis up to 3.2 A cm^-2 with a C₂₊ Faradaic efficiency of 74.9% (compared to 1.21 A cm^-2 and 55.4% for Cu nanoparticles) and maintain stability at 1 A cm^-2 for over 100 h. This work provides profound insights into the effect of the coupling of mass transfer and catalytic reaction under a high current and presents a corresponding solution by superstructure design.

Introduction

The electrocatalytic CO₂ reduction reaction (ECO₂RR), powered by the renewable electricity, holds great potential not only for producing valuable fuels and chemicals but also for contributing to a sustainable carbon cycle^1,2,3. Among the various electrocatalysts developed CO₂RR^4,5,6, Cu-based materials have emerged as the most effective for producing valuable multicarbon products (C₂₊), such as ethylene (C₂H₄) and ethanol (C₂H₅OH), ascribe to the moderate CO* binding energy, which facilitates the C–C coupling^{7,8,9,10,11,12,13}. Moreover, the ECO₂RR in the electrolytic cell equipped with the gas diffusion electrode (GDE) is predominantly a gas-liquid-solid triple-phase interface reaction (TPIR), with gas diffusion limitation^14,15,16. Therefore, for practical applications, ECO₂RR catalysts must exhibit both superb activity and excellent mass transfer capabilities to ensure efficient operation at high current densities for the production of C₂₊ products^17,18,19,20.

Grain boundary sites have been recognized as efficient sites for the formation of C₂₊ product^21,22,23,24. However, in conventional nanoparticle (NPs)-based catalyst layers, smaller particle sizes promote the formation of the grain boundary sites and improve active site exposure, while larger interparticle voids, resulting from larger particle sizes, facilitate mass transfer. As a result, a trade-off exists between optimizing mass transfer and maximizing catalytic activity^25,26,27. To address this issue, the design of porous Cu-based materials has been identified as an effective strategy to integrate interfacial mass transportation and active site modulation for achieving CO₂-to-C₂₊ conversion at high current densities^25,28,29,30.

However, the fabrication of well-defined porous Cu based materials often involves complex and time-consuming processes, such as chemical etching or sacrificial template methods^25,30,31,32. Moreover, the resulting catalysts often exhibit large particle or crystallite sizes, ranging from tens to hundreds of nanometers^25,30,31, which compromises the activity for C₂₊ products and limits active site exposure. Therefore, addressing the trade-off between mass transfer and the catalytic activity in Cu-based materials remains a significant challenge.

Herein, we prepared Cu₂O supraparticles composed of sub-10 nm-sized Cu₂O constituent particles via the spontaneous evolution of copper hydride (CuH) supraparticles, which possess abundant inherent mesopores (3–10 nm) and large interparticle voids (>100 nm). During the ECO₂RR process, Cu₂O supraparticles are in situ reduced to metallic Cu while maintaining a similar supraparticle structure, and abundant grain boundaries form between the supraparticle interfaces. The maintained interconnected porous suprastructure significantly enhances the active site exposure and mass transfer, while the formation of abundant grain boundary sites greatly facilitates the *OC–CHO coupling pathway, effectively breaking the trade-off between efficient mass transfer and the superior activity. Additionally, the intrinsic hydrophobicity of the supraparticles alleviates water-flooding in the catalytic layer of flow cell, enhancing stability, especially under high current densities. Benefiting from this effective coupling of mass transfer and catalytic reaction, the well-defined metallic Cu supraparticles demonstrate remarkable capability for ampere-level CO₂ electrolysis, achieving a high C₂₊ current density of 2.40 A cm⁻² with corresponding Faradic efficiency (FE) of 74.9% (1.21 A cm⁻² and 55.4% for Cu nanoparticles counterpart), and demonstrating a satisfactory stability at 1 A cm⁻² for over 100 h.

Results and discussion

Design and characterization of Cu₂O supraparticles

Interface-connected Cu₂O supraparticles (SP-Cu₂O) were synthesized via the spontaneous evolution of assembled CuH supraparticles under ambient condition (Fig. 1a; the detailed synthesis process is described in the “Methods” section). The dynamic structure evolution of CuH was tracked by X-ray diffraction (XRD) and X-ray absorption spectroscopy (XAS). Based on the XRD spectra (Fig. 1b), the initial sample undergoes a transformation into a mixed phase of CuH and Cu₂O within the first 10 h, followed by complete conversion to pure Cu₂O phase after 30 h, which remains stable in air. According to Scherrer equation, the crystalline diameters of initial CuH and derived Cu₂O are estimated to be 5.0 and 8.5 nm (Supplementary Table 1), respectively. Moreover, the Cu K-edge X-ray absorption near-edge structure (XANES) spectra reveal that both CuH and its spontaneously-derived Cu₂O exhibit oxidation states similar to that of standard Cu₂O (Supplementary Fig. 1). The FT k³χ(k) functions of extended X-ray absorption fine structure (EXAFS) data in R-space show gradually intensified Cu-O bond signal strength, indicating the transformation of CuH to Cu₂O (Fig. 1c).

Fig. 1: Synthesis and characterization of SP-Cu₂O.

a Schematic demonstration for the synthesis of CuH-derived SP-Cu₂O. XRD patterns (b) and Cu K-edge EXAFS spectra (c) for CuH evolving process under ambient condition. SEM (d, e) and TEM (f) images, inset in (d) is the size distribution diagram. g pore-size distribution curve obtained from N₂ adsorption-desorption measurements. Finite element simulation of triple-phase reaction interfaces: the hydroxide concentration flux for the models without (h) and with (i) mesopores (10 nm in diameter); the current distribution at the triple-phase reaction interfaces based on simplified 2D catalyst models without (j) and with (k) mesopores. Source data are provided as a Source Data file.

Scanning electron microscopy (SEM) images (Fig. 1d, e) show that the derived Cu₂O supraparticles (SP-Cu₂O) are assembled from smaller NPs and exhibit an open porous structure with an average diameter of 468 ± 78 nm. Transmission electron microscopy (TEM) and high resolution (HR)-TEM images of SP-Cu₂O further demonstrate that the average diameter of the constituent NPs is 8.3 ± 0.9 nm (Fig. 1f and Supplementary Fig. 2), consistent with the XRD results. Moreover, these smaller constituent NPs are interconnected, giving the assembled SP-Cu₂O an inherent porous structure (Supplementary Fig. 3). As confirmed by the N₂ adsorption-desorption measurements (Fig. 1g and Supplementary Fig. 4), SP-Cu₂O possess abundant mesopores (pore diameters primarily from 3 to 10 nm), which could facilitate the exposure of interior active sites.

As for the ECO₂RR, the effective diffusion of in situ produced OH⁻ is essential for mitigating alkalinity, which obstructs CO₂ transfer to active sites^33,34,35. To reveal the diffusion behavior of OH⁻ within pores of supraparticles, we conducted the finite element simulation of the triple-phase interface using simplified two-dimensional (2D) catalyst models with/without mesopores (ca. 10 nm in diameter; Fig. 1h–k). Clearly, the model without mesopores shows severe OH⁻ accumulation in the catalyst, as indicated by the OH⁻ concentration distribution (Fig. 1h). For the model with mesopores, the porous channels provide efficient transport path for OH⁻ flux (Fig. 1i), facilitating CO₂ transfer to the interior pores of supraparticles for subsequent conversion. The mesopore-intensified reaction interfaces generate much higher current density compared to that without mesopores (Fig. 1j, k), highlighting the potential of suprastructure in achieving the efficient ECO₂RR performance.

Characterization and finite element simulation of catalyst layer

The ECO₂RR performance of SP-Cu₂O relies not only on the accessibility of active sites provided by their intrinsic mesopores but also the efficient gas-liquid transport through the packing pore network of catalyst layer. To elucidate the effect of packing pores on mass transfer, we carried out the structure characterization and gas-liquid transport simulation of catalytic layer, comparing SP-Cu₂O with conventional Cu nanoparticles (NP-Cu) of similar particle sizes but lacking supraparticle structure (Supplementary Fig. 5; see the synthesis process for NP-Cu in “Methods” section). From the results of mercury intrusion porosimetry (Supplementary Fig. 6), SP-Cu₂O possesses a bimodal pore system comprising intrinsic mesopore and interparticle macropores centered at ~250 nm, whereas NP-Cu exhibits monomodal packing macropores centered at ~116 nm. Notably, SP-Cu₂O demonstrates the higher geometric tortuosity (τ = 38.4 vs. 25 for NP-Cu) yet paradoxically shows the superior permeability (191.2 mDarcy vs. 176.2 mDarcy). This apparent deviation from classical tortuosity-permeability correlation suggests the presence of interconnected macroporous “highways” in SP-Cu₂O, which enables low-resistance mass transport.

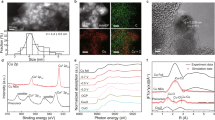
Moreover, focused ion beam (FIB)-SEM tomography was performed to directly visualize the packing pore structure of SP-Cu₂O and NP-Cu (Fig. 2a–d). Evidently, SP-Cu₂O presents a homogeneous distribution of interconnected macropores (Fig. 2a, c), forming continuous transport routes. In contrast, NP-Cu features dispersed macropores with limited interconnectivity (Fig. 2b, d). To quantitatively analyze these findings, we reconstructed 2D pore networks from the high-resolution FIB-SEM images (Fig. 2c, d) using a validated contrast correction algorithm³⁶. The resultant models clearly confirm that the SP-Cu₂O catalyst layer forms the interconnected macropore pathways, whereas NP-Cu only has fragmented macropores and interconnected narrow pore channels.

Fig. 2: Characterization and mass transport simulation of catalytic layer.

FIB-SEM images of SP-Cu₂O (a) and NP-Cu (b) catalyst layers. Extract process of packing pore models for (c) SP-Cu₂O and (d) NP-Cu. Finite element simulation of gas-liquid transport within the packing pores: diffusion velocity of (e) OH⁻ and (f) CO₂ for SP-Cu₂O; diffusion velocity of (g) OH⁻ and (h) CO₂ for NP-Cu. For (e–h), the electrolyte (1 M KOH) and CO₂ flow in opposite directions through the upper and lower boundaries of the porous model, respectively.

Beyond the hierarchical porosity, the supraparticle architecture endows SP-Cu₂O with intrinsic hydrophobicity as evidenced by a water contact angle of 145° (Supplementary Fig. 7), in sharp contrast to the hydrophilic NP-Cu with a value of 14° (Supplementary Fig. 8). The strong hydrophobicity has the potential to alleviate the water flooding phenomenon prevalent in conventional catalytic layers, thereby enhancing the three-phase boundary dynamics in GDEs³⁷. To factor in this critical property during our mass-transfer analyses, we incorporated the hydrophilicity/hydrophobicity characteristics into the subsequent simulations, enabling the more precise assessment of the gas-liquid transport behavior within the catalytic layer.

Figure 2e–h shows the results of finite element simulations of coupled gas-liquid transport. Under counter-current flow conditions (the electrolyte flowing downward and CO₂ flowing upward), the interconnected macroporous network substantially increases the OH⁻ diffusion velocity (Fig. 2e) compared to the narrow pore pathways in NP-Cu (Fig. 2g). This accelerated OH⁻ transport in turn facilitates CO₂ mass transfer, as indicated by the significantly enhanced CO₂ diffusion velocity within the macropore transport pathway in SP-Cu₂O (Fig. 2f, h). The simplification of disregarding the contribution of intrinsic mesopores results in an underestimation of the overall mass transport capacity of SP-Cu₂O. Nevertheless, compared with conventional nanoparticle assemblies, the characteristic macroporous channels in the supraparticle catalytic layer fundamentally enhance gas-liquid transport during ECO₂RR. In the context, multiscale characterization and simulations have established that the supraparticle structure enables the synergistic optimization of active site accessibility (through intrinsic mesopores) and mass transport efficiency (via macroporous networks), providing a paradigm for designing high-performance catalytic systems.

Monitoring the evolution of SP-Cu₂O during ECO₂RR

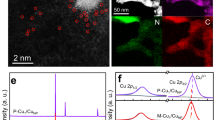
Due to the tendency of non-zero-valent Cu-based catalysts to undergo reduction during the ECO₂RR, identifying their valence state changes during is crucial for determining the true active sites. This understanding is essential for the design and synthesis of effective Cu-based CO₂RR catalyst^8,38,39. However, the oxidation of low-valence Cu in air complicates the investigation of the surface chemical information of post-reaction samples. To address this issue, we conducted flow-cell tests in an argon-filled glovebox and the catalysts were then transferred to a vacuum suitcase before being moved to the XPS chamber. These quasi-in-situ XPS measurements allowed us to exclude the influence of ambient gas and accurately capture the chemical states of the Cu surfaces after reaction. Clearly, the Cu LMM Auger spectra (Fig. 3a) and XPS valence spectra (Fig. 3b) exhibit major peaks at 918.6 and 2.9 eV, respectively, evidencing the chemical state of Cu^040,41. Moreover, XPS depth profiles for the post-reaction SP-Cu₂O shows no difference between its surface and inner chemical states (Fig. 3a, b), indicating that SP-Cu₂O was fully transformed into metallic Cu.

Fig. 3: Chemical-state and structural characterizations for SP-Cu₂O.

Quasi-in-situ XPS characterization and depth profiles at −0.6 V: Cu LMM Auger spectra (a) and band spectra (b). In situ XRD characterization: c spectra at different applied potentials, d time-evolved XRD heatmap at −1.0 V and e time-dependent crystal size of reduced SP-Cu₂O. In situ XAFS at −1.0 V: f XANES spectra and g the corresponding first derivative spectra, h EXAFS spectra and i wavelet transforms of the Cu K-edge EXAFS. a–i Potentials are not iR corrected. Source data are provided as a Source Data file.

Furthermore, time-evolved in situ XRD characterization was employed to track the dynamic structure evolution of SP-Cu₂O during ECO₂RR (Fig. 3c–e). As depicted in Fig. 3c, SP-Cu₂O partially transforms into metallic Cu after just 10 min at −0.4 V vs. RHE (unless otherwise stated, all potentials are referenced to the reversible hydrogen electrode, RHE), with almost no Cu₂O remaining after 30 min at the same potential. At higher overpotentials (−0.6, −0.8, −1.0 V), only metallic Cu is observed, which is consistent with the results of quasi-in-situ XPS characterizations. The time-evolved XRD patterns of SP-Cu₂O at −1.0 V (Fig. 3d) indicate that SP-Cu₂O is reduced to metallic Cu within 300 s. According to the Scherrer equation, the time-dependent crystalline diameters of the constituent NPs of SP-Cu₂O after 300 s at −1.0 V are estimated (Fig. 3e). The initial size of the constituent NPs is ca. 6.7 nm, gradually increasing to ca. 9.0 nm (Supplementary Table 2) before stabilizing, demonstrating good size stability during ECO₂RR.

In situ XAS was further employed to track the changes in the average chemical states and atomic structures of SP-Cu₂O during ECO₂RR (Fig. 3f-i). According to the XANES spectra of Cu K-edge and their first derivative spectra (Fig. 3f, g), SP-Cu₂O is reduced to metallic Cu within the first 10 min at −1.0 V and remain stable during the subsequent reaction process. In addition, the corresponding k³-weighted FT-EXAFS show that Cu-Cu peak of metallic Cu at 2.23 Å emerges and Cu-O bond at 1.54 Å disappears concurrently in the SP-Cu₂O (Fig. 3h and Supplementary Table 3) as the reaction progresses, indicating the reduction of SP-Cu₂O and the formation of metallic Cu. Moreover, the coordination number of Cu for the sample after 60 min of reaction is determined to be ca. 9.2, much lower than that of bulk Cu foil, suggesting the presence of abundant low-coordination sites (such as step or grain boundary sites) within the reduced SP-Cu₂O. We further applied the wavelet transforms of the Cu K-edge EXAFS to visually examine the changes in coordination features during ECO₂RR. Two regions are observed at ca. 1.54 and 2.23 Å (Fig. 3i), corresponding to the Cu-O and Cu-Cu coordination of initial Cu₂O and the Cu-Cu coordination of metallic Cu, respectively. As the reaction progresses, the peak at 1.54 Å gradually diminishes, while the peak at 2.23 Å progressively intensifies, further confirming that SP-Cu₂O is gradually reduced to metallic Cu during the ECO₂RR. Furthermore, SEM (Supplementary Fig. 9), TEM and HAADF-STEM (Supplementary Fig. 10) were conducted on reduced SP-Cu₂O collected in an argon-filled glovebox. The mesoporous structure of the post-reduction samples is well preserved (Supplementary Fig. 10a, b) with rich grain boundaries containing Cu(111) and Cu(100). The above results indicate that the prepared SP-Cu₂O is in situ reduced to metallic Cu during the ECO₂RR, featuring abundant defects and grain boundary sites, while the size of its constituent particles remains largely unchanged.

To disentangle structural and chemical state effects, a CuH-derived Cu supraparticle catalyst with primary particle size of 22.1 nm (SP-Cu) was synthesized (Supplementary Figs. 11–13 and Supplementary Table 1 in the Supplementary Information). In situ XRD (Supplementary Fig. 14 and Supplementary Table 2) and quasi-in situ XPS (Supplementary Fig. 15) confirm identical metallic states for SP-Cu and conventional NP-Cu, eliminating chemical state variability as a performance determinant. This controlled comparison isolates structural advantages (e.g., grain boundaries, pore structure) as the origin of the disparity in the ECO₂RR performance. In addition, from the hydroxide electrosorption (OH_ad) studies (Supplementary Fig. 16), the three-investigated catalysts have the similar distribution of exposed Cu(100), Cu(110), and Cu(111) facets, further excluding the crystal face effect on the ECO₂RR.

ECO₂RR performance evaluation

The ECO₂RR performances of SP-Cu₂O, SP-Cu, and NP-Cu were evaluated in a home-made flow cell (Supplementary Fig. 17) with CO₂-saturated 1 M KOH as the electrolyte. To maintain consistency throughout the text, we will continue to refer to the prepared catalyst as SP-Cu₂O in this section, even though it was converted to metallic Cu during the ECO₂RR. Linear scanning voltammogram (LSV) curves (Fig. 4a) show that the instantaneous current densities of the SP-Cu₂O reach 3.48 A cm⁻² at −0.9 V, higher than that of both SP-Cu (2.62 A cm⁻²) and NP-Cu (1.21 A cm⁻²), indicating the combination of supraparticle structure and abundant grain boundary sites endows SP-Cu₂O with higher ECO₂RR activity. To further evaluate product selectivity, the gas and liquid products were determined and quantified by gas chromatography (Supplementary Fig. 18) and ¹H NMR spectrometer (Supplementary Fig. 19), respectively. The Faradaic efficiencies (FE) of the products on SP-Cu₂O, SP-Cu, and NP-Cu at different applied current densities are depicted in Fig. 4b and Supplementary Figs. 20–22. As the current density increases, the C₂₊ selectivity of all catalysts gradually rises while the FE of CO decreases, suggesting that adsorbed CO (CO*) acts as a key intermediate for C–C coupling^42,43. Consequently, the increased C₂₊ formation suppresses the desorption of CO* into CO.

Fig. 4: Performance evaluation of ECO₂RR in a flow cell.

a LSV curves of SP-Cu₂O, SP-Cu, and NP-Cu in 1 M KOH solution fed with CO₂ gas. b FE of all detected products at different applied current densities on SP-Cu₂O. c FE of C₂₊ products; d C₂H₄ partial current densities, e C₂H₅OH partial current densities and f C₂₊ partial current densities of SP-Cu₂O, SP-Cu, and NP-Cu. g full-cell energy conversion efficiency (ECE_full-cell) for C₂H₄, C₂H₅OH, and C₂₊ production of SP-Cu₂O in 3 M KOH solution. h Stability test on SP-Cu₂O at 1 A cm⁻² in 3 M KOH solution. a, c–f The 90% iR compensation was conducted to calculate the applied potential. The error bars represent standard deviations from at least three independent measurements. Source data are provided as a Source Data file.

As for the potential-dependent FE (Fig. 4c), SP-Cu₂O achieves a high FE 74.9% for C₂₊ at −0.94 V, which is significantly higher than those of SP-Cu (63.1%) and NP-Cu (55.4%). Specifically, C₂H₄ and C₂H₅OH are the main C₂₊ products and their partial current densities are shown in Fig. 4d and Fig. 4e, respectively. At −0.94 V, the SP-Cu₂O exhibits partial current densities of 1.23 and 0.79 A cm⁻² for C₂H₄ and C₂H₅OH, respectively, which are 1.95 and 1.40 times higher than those of SP-Cu, and 4.03 and 3.21 times than those of NP-Cu. These values also exceed most previously reported results (Supplementary Table 4)^44,45,46, indicating the decent C₂₊ product selectivity of SP-Cu₂O. Overall, SP-Cu₂O exhibits significantly higher total C₂₊ partial current densities (2.40 A cm⁻²) than that of SP-Cu (1.52 A cm⁻²) and NP-Cu (0.66 A cm⁻²) in 1 M KOH electrolyte (Fig. 4f). These results underscore the importance of hierarchically porous suprastructure and abundant in situ derived grain boundary sites in achieving high C₂₊ activity and selectivity. To evaluate the intrinsic CO₂RR activity, Pb underpotential deposition (UPD) experiments²¹ (Supplementary Fig. 23) were conducted to determine the ECSAs of SP-Cu₂O, SP-Cu, and NP-Cu for the calculation of ECSA-normalized C₂₊ partial current densities. As shown in Supplementary Table 5, SP-Cu₂O exhibits a higher ECSA-normalized C₂₊ partial current densities than that of SP-Cu and NP-Cu, indicating a high intrinsic activity of SP-Cu₂O. The C₂₊ selectivity of SP-Cu₂O can be further optimized by tuning the electrolyte concentration^47,48,49 and the FE of C₂₊ can reach as high as 83.4% at 1.6 A cm⁻² in 3 M KOH electrolyte (Supplementary Fig. 24).

Subsequently, a full electrolyzer system (Supplementary Table 6) was constructed, incorporating a cost-effective NiFe/Ni foam anode³ (Supplementary Fig. 25) with the anode’s geometric surface area intentionally scaled to fourfold that of the cathode. This design strategy serves dual purposes: (1) mitigating the oxygen evolution reaction overpotential by reducing anodic current density through enhanced active site availability, and (2) minimizing mass transport limitations at high current densities. The resultant configuration establishes well-defined kinetic conditions that enables the evaluation of the ultimate performance of SP-Cu₂O within the specific full-electrolyzer setup. As a result, the system achieves a total current density of 1.24 A cm⁻² with 79.4% C₂₊ Faradaic efficiency at 3.0 V without iR compensation (Supplementary Fig. 26). Notably, it attains 30.0% full-system energy-conversion efficiency at a C₂₊ partial current density of 1.04 A cm⁻² (Fig. 4g). Moreover, SP-Cu₂O maintains the total ECO₂RR FEs and C₂₊ FEs around 90.0 % and 70.0 % over 108-h electrolysis at 1 A cm⁻² in 3 M KOH solution (Fig. 4h and Supplementary Fig. 27), demonstrating the significant stability of SP-Cu₂O.

Additionally, Pb-UPD curves (Supplementary Fig. 23) show that SP-Cu₂O presents a Pb-stripping peak at −0.55 V vs. Hg/Hg₂SO₄, which is correlated to the undercoordinated and defective Cu sites, probably as grain boundaries²¹. Clearly, the intensity of such a Pb-stripping peak on SP-Cu₂O is significantly higher than that on SP-Cu, proving more grain boundaries on SP-Cu₂O. The enriched grain boundaries probably act as highly-active sites and the well-reserved mesoporous structure of supraparticles promotes the mass transfer, thus enabling SP-Cu₂O with high activity, selectivity, and stability for ECO₂RR.

Operando probing ECO₂RR intermediates and interfacial sites

It is known that triple-phase reaction region spans tens to hundreds of nanometers and is nearly impossible to quantify for evaluating the GDE quality. In this case, the electrolysis performance serves as an indicator to draw conclusions, but a deep understanding is lacking. To address this, we performed operando Raman tests with a flow cell to probe the evolution of reaction intermediates and interfacial sites on GDE during ECO₂RR (Fig. 5a). It should be noted that the laser beam of Raman spectrometer can reach the surface or near-surface of GDE-electrolyte interface through the pore channels of catalytic layer. As a result, the reaction interface containing information about intermediates and catalytic sites information can be inferred from the collected Raman signals (Fig. 5a).

Fig. 5: Operando Raman characterizations in a flow cell.

a Schematic illustration of operando Raman tests for probing the reaction intermediates and interfacial sites. Raman spectra collected at −0.6 V vs. RHE in 1 M KOH (pH = 13.5) on b SP-Cu₂O, c SP-Cu and d NP-Cu. e, f Continues Raman spectra collected at different applied potentials on SP-Cu₂O. g In situ FTIR spectra in CO₂-saturated 0.1 M KHCO₃ (pH = 6.8) at different applied potentials on SP-Cu₂O. b–g Potentials are not iR corrected. Source data are provided as a Source Data file.

Figure 5b-d show the Raman spectra collected at −0.6 V for SP-Cu₂O, SP-Cu, and NP-Cu, respectively. No characteristic peak assigned to Cu₂O is observed for all three catalysts during ECO₂RR, indicating the metallic Cu serve as the active site, in accordance with above in situ structural analyses of SP-Cu₂O. The detailed assignments of Raman peaks are listed in Supplementary Table 7. Typically, two noticeable Raman peaks at ~2045 cm⁻¹ and ~2088 cm⁻¹ appear on the surface of SP-Cu₂O and SP-Cu (Fig. 5b, c), which are attributed to the low frequency band (LFB) from *CO on terrace sites and the high frequency band (HFB) from CO* on step sites^50,51, respectively. Analysis of the ratio of HFB/(HFB + LFB) reveals that much more step sites are present on the SP-Cu₂O, further verifying that the SP-Cu₂O possess more grain boundaries. Additionally, SP-Cu₂O presents a dominated Cu-CO stretching vibration peak at 364 cm⁻¹ and a greatly suppressed frustrated rotational mode at ca. 280–300 cm⁻¹, indicating a higher CO coverage on SP-Cu₂O than SP-Cu (Fig. 5c) and NP-Cu (Fig. 5d)^52,53,54,55. This implies that the enriched grain boundaries serve as effective sites for concentrating CO* and thereby promote subsequent C-C coupling.

Raman spectra of SP-Cu₂O at different applied potentials are shown in Figs. 5e, f. Similar peaks to those in Fig. 5b are observed at −0.1 to −0.5 V. Nevertheless, as the overpotential increases, the Raman signals correspond to ECO₂RR intermediates disappear and peaks located at 384 and 615 cm^-1 (Fig. 5e and Supplementary Fig. 28) that attributed to adsorbed oxygen (Cu-O_ad) emerge^56,57. We speculated that the continuous Raman laser beam of SP-Cu₂O GDE leads to the infiltration of surface and near-surface pore channels, preventing effective triple-phase reactions from occurring in these regions and resulting in the disappear of corresponding signal. To investigate the evolution of observable metallic Cu sites on GDE, we conducted deconvolution analyses of Raman signals at 2000–2100 cm⁻¹, as shown in Fig. 5f. As the overpotential increases, the peak intensity associated with terrace and defect sites presents an increasing trend, both originating from the reduction of Cu oxides. Moreover, the ratio of HFB/(HFB + LFB) increases with the increasing overpotential, suggesting that the evolution of Cu₂O supraparticles preferentially generates defect sites, likely in the form of grain boundaries at the supraparticle interfaces. Additionally, in situ FTIR measurements on SP-Cu₂O shows the obvious *COOH, *CO, and OCCHO* signals (Fig. 5g and Supplementary Fig. 29)^58,59, demonstrating that the in situ-produced grain boundaries sites facilitate the C₁ intermediates formation and the subsequent C–C coupling reaction.

Density functional theory simulations

To elucidate the enhanced C₂₊ product selectivity at grain boundary sites, we performed density functional theory (DFT) calculations to evaluate free energy profiles for three C–C coupling pathways (CO*-CO*, CO*-CHO*, and CO*-COH*) on Cu(111), Cu(100), and Cu(100)/Cu(111) boundary surfaces (Fig. 6a, Supplementary Figs. 30–32 and Supplementary Data 1). Following our established methodology⁶⁰, we calculated effective free energy barriers to compare pathway preferences (see “Computational Methods”). Figure 6b and Supplementary Fig. 33 present the potential-dependent effective free energy barriers for these pathways across the three surfaces. Since CO-CO dimerization is a non-electrochemical step, the systematic comparison of the optimal pathways (Fig. 6c) suggests a critical potential-dependent transition: the dominant C-C coupling mechanism shifts from CO*-CO* to CO*-CHO* as the applied potential becomes more negative. Under optimized operational conditions, the CO*-CHO* pathway dominates across all surfaces and presents a negative ∆G of the CO* transformation to CHO* step. In this case, the effective free energy barrier of the CO*-CHO* pathway is solely determined by CO* and CHO* dimerization. As shown in Fig. 6d, the Cu(100)/Cu(111) boundary exhibits the lowest C-C formation barrier of 0.63 eV, outperforming 0.92 eV for Cu(111) and 0.75 eV for Cu(100). This hierarchy directly correlates with experimental C₂₊ selectivity trends, confirming grain boundaries as kinetically favorable sites for the C-C coupling.

Fig. 6: DFT simulations of C–C coupling reactions.

a Top view of slabs of Cu(111), Cu(100), and Cu(100)/Cu(111) grain boundary, the yellow spheres represent the atoms on the surface, and the orange spheres represent bulk Cu atoms. b, c The effective free energy barriers of three C₂ production process under varied potentials. d Free energy profiles of the preferred C–C coupling step, i.e., CO*-CHO*, over Cu(111), Cu(100), and grain boundary (GB)-enriched surface. e Reaction network of C₂H₄ and C₂H₅OH formation following the formation of OCCHO. Source data are provided as a Source Data file.

We further investigated the reaction pathways of C₂H₄ and C₂H₅OH formation on Cu(100) and Cu(100)/Cu(111) boundary surfaces. A reaction network consisting of 45 intermediates, 106 elementary steps, and 799 possible reaction pathways was generated from OCCHO* to C₂H₄ and C₂H₅OH (Fig. 6e). More details related to all elementary steps are provided in Supplementary Table 8. The C₂H₄ formation is slightly preferred than C₂H₅OH formation on both Cu(100) and Cu(100)/Cu(111) boundary. The grain boundary-enriched surface is energetically favored for C₂ formation, which is consistent with our experimental observation that the grain boundary-enriched SP-Cu₂O catalyst can achieve an enhanced C₂₊ selectivity and production compared to SP-Cu.

Discussion

In conclusion, hierarchically-porous and inherently-hydrophobic Cu supraparticles, composed of sub-10 nm constituent nanoparticles, were prepared by in situ electrochemical reduction of SP-Cu₂O for efficient ECO₂RR. The as synthesized catalyst possesses rich grain boundaries for high C₂₊ selectivity, abundant mesopores, and interparticle voids for enhanced mass transfer, and hydrophobicity for alleviated water-flooding. Consequently, the metallic Cu supraparticles achieve efficient C₂₊ product preparation at 3.2 A cm⁻² with a high FE of 74.9%. Moreover, the as-assembled full-cell CO₂ electrolysis operates stably at 1 A cm⁻² in 3 M KOH solution for over 108 h, demonstrating the application potential of the prepared Cu supraparticles. Furthermore, the assembled full-cell with SP-Cu₂O as cathode, reaches an energy-conversion efficiency of 30.0% at C₂₊ current density of 1.04 A cm⁻² (and total CO₂RR current density of 1.24 A cm⁻²). This work highlights the importance and efficiency of coupling mass transfer and activity for application-oriented catalyst design.

Methods

Chemicals

Potassium bicarbonate (KHCO₃, ≥99.5%), ethanol (C₂H₅OH, ≥99.8%), perchloric acid and sodium perchlorate monohydrate (NaClO₄·H₂O, ≥98.0%) were purchased from Sinopharm Chemical Reagent Co., Ltd. Tert-butylamine borane (TBAB, ≥97%) was purchased from Shanghai Excellent Chemical Co., Ltd. Deuterium Oxide (D₂O, ≥99.9%), dimethyl sulfoxide (DMSO, ≥99.9%), cupric chloride anhydrous (CuCl₂, ≥99.0%), potassium hydroxide (KOH, ≥90.0%) and lead perchlorate trihydrate [Pb(ClO₄)₂·3H₂O, ≥97%] were purchased from Adamas. All materials were used as received without further purification. Ultrapure water from a Millipore autopure system was used in all our experiments.

Synthesis of CuH

1 mmol of CuCl₂ and 5 mL of 1 mol L⁻¹ TBAB solution (C₂H₅OH as the solvent) were added into 200 mL of C₂H₅OH. After the reaction under ultrasonic water bath at a temperature of 30 ± 2 °C for 30 min, the CuH product was then filtered and washed with C₂H₅OH at least three times.

Synthesis of CuH-derived catalysts

The freshly prepared CuH was exposed under ambient conditions (temperature: 25 ± 2 °C, humidity: 50 ± 10%) for >30 h to obtain the spontaneously-derived catalyst with Cu₂O crystal phase (designated as SP-Cu₂O). For a comparison, the freshly prepared CuH was treated by Ar-saturated water to obtain the derived catalyst with Cu crystal phase (designated as SP-Cu).

Synthesis of Cu nanoparticles catalyst

10 mmol of CuCl₂ dissolved in 200 mL of H₂O was quickly reduced by 20 mL of 1 mol L⁻¹ TBAB solution to form the Cu nanoparticles catalyst (designated as NP-Cu).

Characterization

Powder X-ray diffraction (XRD) patterns were collected on a Bruker AXS D8 ADVANCE powder X-ray diffractometer with a Cu Kα (λ = 1.5418 Å) radiation source, operating at 40 kV and 40 mA. SEM images were obtained on a field-emission scanning electron microscopy (Zeiss Gemini 300, Germany). TEM, HRTEM, HAADF-STEM images, and EDX mapping images were collected on an FEI talos F200x G2 operated at 200 kV. X-ray photoelectron spectroscopy (XPS) was carried out on a ThermoFisher ESCA 250XI with a monochromatic excitation source of Al Kα radiation (hν = 1486.6 eV) performed under 12 kV and 4 mA. Brunauer-Emmett-Teller (BET) surface area and Barrett-Joyner-Halenda (BJH) pore volume (desorption branch) were calculated from N₂-physisorption measurements on ASAP2460. The pore size distribution curves were calculated by the nonlocal density functional theory. The water contact angles of the samples were measured using a Contact Angle Meter (Model OCA15EC).

Simulation of triple-phase reaction interface within a mesoporous particle

Finite element method (FEM) simulation was employed with COMSOL Multiphysics to simulate the triple-phase reaction interface, surface reaction and OH⁻ concentration distribution by combining the modules of “Transport of Diluted Species”, “Electric Current” “Laminar Flow” and “Phase Field”. Two-dimensional (2D) models with and without mesoporous (10 nm in diameter) were constructed. In the module of “Transport of Diluted Species”, a reaction interface that electrolyte and CO₂ gas come cross at the catalyst model from two different directions was specified. Since the reaction rate of triple-phase interface is controlled by the local OH⁻ concentration (cOH⁻), as evidenced in previous work, a simplified pseudo surface reaction (CO₂ + H₂O + e⁻ → CO + 2OH⁻, k_OH- = 1/cOH⁻) was added for simulating current density at the triple-phase reaction interface. The OH⁻ diffusion constant is 5.273 • 10⁻⁹ m² s⁻¹⁶¹. The initial OH⁻ concentration in the electrolyte is 1 mol L⁻¹ and a constant 0.0001 mol L⁻¹ OH⁻ boundary condition was set on the top of the simulation box. In the “Electric Current” module, the potentials of the upper and lower boundaries were set to be 0 and 1 V, respectively. In the “Laminar Flow” module, we added two-point constraints with zero pressure on the upper boundary to ensure convergence of the model. In the “Phase Field” module, a wetting wall with a contact angle of pi/4 was used on the surface of the catalyst particles to simulate the electrolyte infiltrating.

Simulation of gas-liquid transport in the packing pores of catalyst layer

The simulation framework integrates advanced image processing techniques with multiphysics modeling in COMSOL Multiphysics. High-resolution FIB-SEM images were processed and imported for geometric reconstruction, where machine learning algorithms were employed to capture void edge features, and the Edge Difference method was applied to enhance pore boundary definition through contrast optimization between pores and particles. This approach enables precise extraction of pore-defining particle morphology and subsequent inverse selection for pore model generation. The model establishes experimentally validated boundary conditions, with the upper surface configured as the electrolyte inlet and gas outlet, and the lower surface as the electrolyte outlet and gas inlet, with other specific parameters keeping consistency with the above simulation. The computational framework incorporates the Creeping Flow module for solving Stokes equations under isothermal conditions, coupled with the Electrochemistry module to simulate the CO₂ electroreduction process, utilizing reaction parameters derived from the aforementioned simulations. Furthermore, to account for material-specific interfacial properties, the Phase Field Method was implemented to resolve wettability-dependent fluid dynamics, enabling detailed analysis of liquid and gas flow behaviors under varying hydrophilic and hydrophobic conditions.

Preparation of gas diffusion electrode

To enhance the waterproofness of gas diffusion electrode (GDE) specially at the ampere-level current density, a porous PTFE membrane with 8 μm of thickness was closely attached onto the carbon fiber of the gas diffusion layer (GDL, YLS-30T, Toray) assisted by the PTFE emulsion pasting and subsequent high-temperature treatment in air at 350 °C for 2 h. To construct the catalytic layer of GDE, 20 mg of catalyst and 50 uL of Nafion solution (Dupont, 5 wt%) were ultrasonically dispersed into 0.95 mL of C₂H₅OH. Afterward, the catalyst ink was sprayed onto the microporous carbon layer of GDL on a hot plate at a temperature of 80 °C, to form the catalytic layer with an active area of 0.5 × 0.5 cm² and the catalyst loading of 1.0 ± 0.1 mg cm⁻².

Evaluation of Electrochemical Active Surface Area (ECSA)

ECSAs of all-investigated Cu-based catalysts were evaluated by Pb underpotential deposition (UPD) in a H-cell, with Hg/Hg₂SO₄ (saturated K₂SO₄ solution as the filling solution) and Pt foil as the reference electrode and counter electrode, respectively. Before Pb UPD, oxides within Cu electrodes were reduced at −0.4 V vs. RHE in Ar-saturated 1 M KOH solution. Afterward, the obtained electrodes were cleaned by Ar-saturated ultrapure water and then quickly transferred into an Ar-saturated solution of 0.1 M NaClO₄, 10 mM HClO₄, and 3 mM Pb(II)(ClO₄)₂²¹. Subsequently, cyclic voltammetry (CV) with a scan rate of 10 mV s⁻¹ was performed in a potential range of −0.50 to −0.85 V vs. Hg/Hg₂SO₄ to obtain the Pb UPD curves. The Cu ECSA calculation is based on the integrated charge values of Pb UPD and a conversion factor of 357.5 μC cm⁻² from the benchmark of polished Cu foil⁶². The tests were conducted at room temperature (25 ± 2 °C) and pressure (1.01 × 10⁵Pa).

Electrosorption of hydroxide (OH_ad)

Investigations of OH_ad on the reduced Cu GDEs were carried out by flowing Ar through the flow-cell electrolyzer. To prevent bulk oxidation of Cu, a potential window of -0.2 to 0.55 V (vs. RHE) was employed⁶³. Prior to testing, Cu oxides were electrochemically reduced at −0.6 V (vs. RHE) for 30 min in the flow cell under a CO₂ atmosphere. Immediately following electrolysis, the gas feed was switched back to Ar, the electrolyte flow was halted, and cyclic voltammetry was subsequently performed. The test was carried out at room temperature (25 ± 2 °C) and pressure (1.01 × 10⁵Pa).

Electrochemical measurements and products analyses

Electrochemical measurements were carried out in a home-made flow cell (separated by Alkymer® anion exchange membrane) with three electrodes connected to a CHI 660e electrochemical workstation equipped with a high current amplifier CHI 680c. The anion exchange membrane (3.0 × 3.0 cm²) was soaked in 1.0 M KOH for 24 h and then rinsed with deionized water before use. Pt foil and Ag/AgCl electrode (with saturated KCl as the filling solution) were used as the counter and reference electrodes, respectively. The electrolyte used is 1 M KOH (pH = 13.5) and was freshly prepared for each test. Constant current electrolysis at room temperature (25 ± 2 °C) and pressure (1.01 × 10⁵Pa) was conducted for the performance evaluation. All potentials were converted to the RHE scale the following formulas:

${{\rm{E}}}({{\rm{RHE}}})={{\rm{E}}}({{\rm{Ag}}}/{{\rm{AgCl}}})+0.197+0.0591 \times {{\rm{pH}}}+0.9 \times {iR}$

The 90% iR compensation was conducted in flow cell experiment at each potential, where the resistance was determined by extrapolating high-frequency impedance data. The potential of the reference electrode (vs. RHE) in 1 M KOH solution was calibrated to 1.00 ± 0.01 V using a reversible hydrogen electrode purchased from Phychemi Co., Ltd., which was in close agreement with the theoretical calculation of 0.99 V (vs. RHE). As for the full-cell electrolysis, the used electrolyte is 3 M KOH solution, and a high-performance NiFeO_x catalyst with the area of 1 cm² was adopted as the anode, and the distance between anode and cathode is 1.0 cm. All electrolytes mentioned above were stored under airtight conditions in volumetric flasks at room temperature (25 ± 2 °C) and used within 1 week of preparation. For all performance tests, the electrolyte was circulated through the electrolyte chambers of flow cell with a flow rate of 5 mL min⁻¹ via a peristaltic pump. High-purity CO₂ was supplied to the gas chamber of flow cell with a constant flow rate of 80 mL min⁻¹. The volumetric flowrate of outlet gas was monitored by the electronic soap-film flowmeter (BL100, Beijing Ke’an Labor Insurance New Technology Co., Ltd.). Meanwhile, the outlet gas was collected in a gas sampling bag (300 mL) during the ECO₂RR and then quantified by gas chromatography (Agilent 7890B) equipped with FID and TCD detectors for analyzing the gas phase composition. The GC was calibrated by standard gases (H₂, CO, CH₄, and C₂H₄ in CO₂) before use.

Faradaic efficiencies of gas products can be calculated as below:

$${{FE}}_{x}=\frac{{Q}_{x}}{{Q}_{{total}}}=\frac{t{z}_{x}{{\rm{F}}}{v}_{x}{G}_{{out}}{{{\rm{P}}}}_{0}}{{{\rm{R}}}{{{\rm{T}}}}_{0}{it}}\times 100\%=\frac{{z}_{x}{{\rm{F}}}{v}_{x}{G}_{{out}}{{{\rm{P}}}}_{0}}{{{\rm{R}}}{{{\rm{T}}}}_{0}i}\times 100\%$$

(1)

Wherein, ${Q}_{x}$ is the spent charge for product (x) production; ${Q}_{{total}}$ is the total charge passed during the electrolysis; i is the applied current (A); t is the electrolysis time (s); z_x is the number of transferred electrons for producing a molecule of product (x); ${v}_{x}$ is the volume concentration of product (x) measured by gas chromatography; ${G}_{{out}}$ is the volumetric flowrate of outlet gas; F = 96485 C/mol, P₀ = 1.01 × 10⁵Pa, R = 8.314 J mol^–1 K^–1, T₀ = 298 K.

Liquid products from both anolyte and catholyte, along with those carried by the outlet gas, were collected and analyzed using a Bruker Avance-III 400 MHz ¹H NMR spectrometer with dimethyl sulfoxide (DMSO) as the internal standard. Sample preparation involved mixing 700 µL of electrolyte with 35 µL of 5 mM DMSO in D₂O. Faradaic efficiencies of liquid products can be calculated as below:

$${{FE}}_{x}=\frac{{Q}_{x}}{{Q}_{{total}}}=\frac{{z}_{x}{{\rm{F}}}{n}_{x}}{{Q}_{{total}}}\times 100\%=\frac{{z}_{x}{{\rm{F}}}{n}_{x}}{{it}}\times 100\%$$

(2)

Wherein, ${Q}_{x}$ is the spent charge for product (x) production; ${Q}_{{total}}$ is the total charge passed during the electrolysis; z_x is the number of transferred electrons for producing a molecule of product (x); ${n}_{x}$ is the quantity (mol) for the products (x); i is the applied current (A); t is the electrolysis time (s); F = 96485 C/mol.

Full-cell energy conversion efficiencies of C₂H₄, C₂H₅OH and C₂₊ can be calculated as below:

$${{ECE}}_{x}=\frac{1.23-{E}_{0}}{E}\times {{FE}}_{x}$$

(3)

$${{ECE}}_{{{{\rm{C}}}}_{2+}}={{ECE}}_{{{{\rm{C}}}}_{2}{{{\rm{H}}}}_{4}}+{{ECE}}_{{{{\rm{C}}}}_{2}{{{\rm{H}}}}_{5}{{\rm{OH}}}}+{{ECE}}_{{{\rm{C}}}{{{\rm{H}}}}_{3}{{\rm{CO}}}{{{\rm{O}}}}^{-}}+{{ECE}}_{{n{{\rm{\hbox{-}}C}}}_{3}{{{\rm{H}}}}_{7}{{\rm{OH}}}}$$

(4)

Wherein, E₀ is the thermodynamic potential (vs. RHE) for CO₂RR to species x, which is 0.06 V for C₂H₄, 0.12 V for CH₃COO^-, 0.08 V for C₂H₅OH and 0.10 V for n-C₃H₇OH. E is the cell voltage in two-electrode system.

Operando Raman spectra measurements

Operando Raman spectra tests were performed using a Horiba LabRAM HR Evolution Raman spectroscopy with 633 nm excitation laser. A home-made operando cell was used for Raman signal collection. Similar to the used flow cell for performance evaluation, the GDE was equipped between the electrolyte chamber of cathodic side and gas chamber. The electrolyte chambers of cathodic side and anodic side were also separated by Alkymer® anion exchange membrane to avoid any cross-contamination.

In situ FTIR measurements

In situ FTIR spectra tests were performed using a custom-built three-electrode H-cell on a Zolix Foli20-Z-B FTIR spectrometer. The working electrode was prepared by drop-casting the catalyst ink onto a polished Au-coated Si wafer with an active area of 1 cm². The electrolyte was CO₂-saturated 0.1 M KHCO₃ (pH = 6.8). To simulate the gas flow behavior within GDE, continuous CO₂ gas was bubbled at a flow rate of 10 sccm onto the surface of the catalytic layer.

Ex Situ and in situ XAFS measurements

Ex situ and in situ XAFS measurements were conducted at the BL14W1 beamline in Shanghai Synchrotron Radiation Facility (SSRF) with the electron beam energy of 3.5 GeV and stored currents of 180 mA (decay)⁶⁴. A 38-pole wiggler with the maximum magnetic field of 1.2 T inserted in the straight section of the storage ring was used. XAFS data were collected using a fixed-exit double-crystal Si(111) monochromator. For the in situ XAFS measurements, a custom-designed in situ electrolytic cell was utilized. The catalyst ink was dropped onto the hydrophobic carbon paper to prepare the working electrode. During the measurements, CO₂ was bubbled into 0.1 M KOH. Lytle detector was used to collect the fluorescence signal of the Cu K-edge (8979 eV) XAFS spectra, and the energy was calibrated using Cu foil. The photon flux at the sample position was 2.6 × 10¹² photons per second.

The raw data analysis was carried out using IFEFFIT software package in light of the standard data analysis procedure⁶⁵. The spectra were calibrated, averaged, pre-edge background subtracted, and post-edge normalized, and then Cu-K edge XANES spectra and their first derivative spectra were exported using Athena program in IFEFFIT software package. The Fourier transformation of the k³-weighted EXAFS oscillations, k³·χ(k), from k space to R space was carried out to obtain a radial distribution function and data fitting was done by Artemis program in IFEFFIT.

In situ XRD measurements

In situ synchrotron XRD characterizations were conducted at the BL02U2 beamline in Shanghai Synchrotron Radiation Facility (SSRF). The XRD data were collected using a custom-designed three-electrode cell, with Ag/AgCl electrode and Pt wire as reference and counter electrodes, respectively. The working electrode was obtained as the preparation procedure of GDE, with an active area of 1 cm⁻². During the measurement, the cell was filled with CO₂-saturated 0.1 M KHCO₃ (8 mL, pH = 6.8) and meanwhile CO₂ was bubbled into the electrolyte (0.1 M KHCO₃) with a flow rate of 20 mL min⁻¹. Continuous data collection (10 s per record) was carried out in transmission geometry throughout the cell during the ECO₂RR at −1.0 V/RHE. To present the comparable results, the value of 2-theta (2θ_synchrotron) corresponding to the synchrotron X-ray wavelength of 0.6887 Å (λ_synchrotron) was transformed into the data (2θ_{Cu Kα}) corresponding to the routine Cu Kα X-ray wavelength of 1.5418 Å (λ_{Cu Kα})⁶⁶.

Computational methods

DFT calculations were performed employing the Vienna Ab initio Simulation Package (VASP) code⁶⁷ with projector augmented wave (PAW) method⁶⁸. All the calculations were based on the generalized gradient approximation (GGA) with revised Perdew-Burke-Ernzerhof (RPBE) exchange-correlation functional⁶⁹. Four-layer slabs with 4 × 4 supercells were used for Cu(111) and Cu(100) surfaces. The top-view and side-view of of Cu(111), Cu(100) and Cu(100)/Cu(111) surfaces are shown in Supplementary Fig. 30. Specifically, the Cu(100)/Cu(111) interface was constructed by removing two rows of surface Cu atoms from a 2 × 4 Cu(211) slab, as illustrated in Supplementary Fig. 31. The most favorable transition-state coupling structures for the three surfaces are shown in Supplementary Fig. 32. The Cu atoms of bottom two layers were fixed during the optimizations and the vacuum region were higher than 12 Å. The Monkhorst–Pack mesh k-point grids was 2 × 2 × 1 for Cu(100) and grain boundary-enriched surface, 3 × 3 × 1 for Cu(111) surface. The plane wave cutoff was 500 eV and the convergence criteria was 0.05 eV/Å in force and 1 × 10⁻⁴ eV in energy. The transition states were obtained by constrained minimization method^70,71. As for solvent effect, we used the VASPsol method for an implicit model with the relative permittivity of 80⁷². To compare the preference of different C-C coupling pathways, effective free energy barriers of these pathways have been calculated as suggested in our recent work⁶⁰. Supplementary Figs. 34–37 and Supplementary Note 1 illustrate the method used in the current work to calculate the effective free energy barriers for the C-C bond formation through the coupling of CO* and CHO*/COH*, with the example of OCCHO* formation. All transition state structures are provided in Supplementary Data 1.